Число 1 в двоичной системе: Перевод чисел из десятичной системы в двоичную

Двоичная система счисления: пресловутые нолики и единички

О чем речь? Можно с уверенностью назвать двоичную систему счисления одной из основных, которые используются в вычислительной технике. А значит, привычные нам компьютер и смартфон применяют 0 и 1 для расчетов.

На что обратить внимание? Стоит отметить, что такая «популярность» – это дань традиции, заложенной праотцом вычислительных машин Блезом Паскалем. И все же, порой, нужно переводить показатели двоичной системы в 10-ю или 16-ю. Как же это сделать?

В статье рассказывается:

1. Общепринятые системы счисления
2. Числа, используемые в двоичной системе счисления
3. Сложение, вычитание и умножение в двоичной системе счисления
4. Как переводить числа в двоичной системе счисления в десятичную
5. Алгоритм перевода из двоичной системы счисления в шестнадцатеричную

6. Пройди тест и узнай, какая сфера тебе подходит:
   айти, дизайн или маркетинг.

   Бесплатно от Geekbrains

Общепринятые системы счисления

Человечество в ходе своего развития со временем стало нуждаться в способах подсчета. Нужно было считать, например, количество добычи или убитых врагов из других племен. И эта нужда у древних людей только возрастала. Поначалу пользовались абстрактными понятиями типа «нисколько», «один», «много». Затем в употребление вошла «пара», означающая два каких-то предмета. Уже одно это нововведение существенно упростило жизнь древнему человеку.

Общепринятые системы счисления

В дальнейшем люди стали считать единицами, используя в качестве таковых пальцы на руках и ногах, зарубки на деревьях, кости зверей, узелки на веревках. Благодаря изобретению таких примитивных счетных машин человечество спустя тысячелетия смогло понять, что в древности люди умели не только считать, но также фиксировать результаты счета.

С течением времени возникла необходимость в символьном обозначении любого количества больше единицы. В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.

Система чисел, состоящая из определенных знаков (цифр), фактически и является системой счисления. Другими словами, это способ численного выражения с помощью принятых правил и специальных знаков, называемых цифрами.

Любая система счисления принадлежит к одной из двух категорий:

Позиционные СС

Конкретное значение числа определяется не только цифрами, но и их позицией. Сюда относят арабскую систему, где первый разряд справа отведен для единиц, второй разряд справа — для десятков, третий разряд справа — для сотен и т. д. Таким образом, для записи числа 475 необходимо в крайней правой позиции расположить пятерку (пять единиц), после нее — семерку (семь десятков) и затем — четверку (четыре сотни). Позиционными считаются также системы счисления с основаниями (2, 8, 16).

Непозиционные СС

Значение числа определяется только знаком (цифрой). Для обозначения единиц, десятков, сотен и тысяч используются отдельные символы.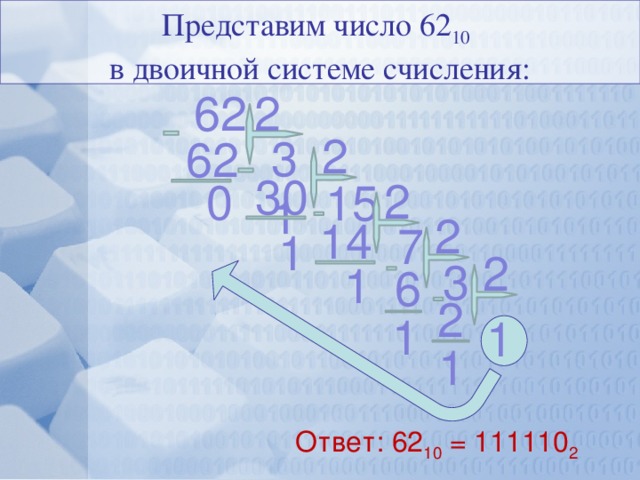 Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.

К примеру, число 475 римскими цифрами может выглядеть как CCCCXXXXXXXIIIII либо, в сокращенном виде, как CDLXXV. В последнем варианте используются именно вычитание и прибавление. Значение цифры, стоящей слева от большего числа, отнимается соответственно от этого числа. Если эта цифра стоит справа, то значение прибавляется.

Впервые позиционная система счисления была введена в Вавилоне. Примечательно, что она была шестнадцатеричная. К 19 веку распространение получила двенадцатеричная система.

Прежде чем разбирать, как записывается двоичная система счисления, определимся с терминами. Алфавит любой СС состоит из знаков, обозначающих отдельные цифры. Основанием называют значение, равное количеству знаков для кодирования чисел и представляющее собой целое число от 2 и выше.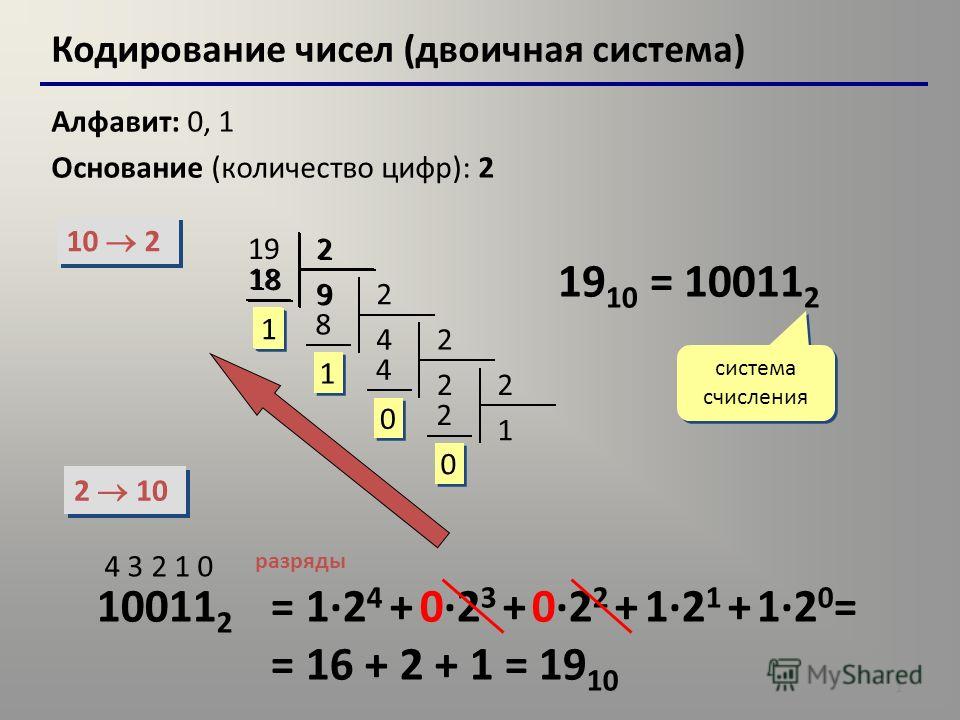

Непозиционные СС

Когда рассматривается несколько разных СС, тип каждой из них обычно обозначается подстрочным знаком. По умолчанию, если не указано основание, число является десятичным. Позиция цифры в числе называется разрядом.

Числа, используемые в двоичной системе счисления

Состав двоичной системы счисления — цифры 0 и 1. Основание равно 2. В крайней правой позиции числа указывается количество единиц, левее — количество двоек, затем количество четверок и т. д.

Таким образом, любое натуральное число кодируется в последовательный ряд из нулей и единиц — это и будет являться двоичной системой счисления. Решение такой задачи покажем на примере ниже.

10112 = 1*23 + 0*2*2+1*21+1*20 =1*8 + 1*2+1=1110

Как известно, двоичная система счисления используется вычислительной техникой для хранения информации, а также для преобразования данных в графические изображения. В свою очередь обработка двоичного кода требует предварительного размещения каждой цифры внутри особой электронной схемы (триггера). Эта схема может пребывать в одном из двух состояний — «ноль» или «единица».

Отдельное число, состоящее из нескольких цифр, сохраняется группой триггеров — регистром. Оперативная память компьютера фактически является совокупностью таких регистров.

Топ-30 самых востребованных и высокооплачиваемых профессий 2023

Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ ресурсов об IT-сфере

Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT

ТОП 50+ сервисов и приложений от Geekbrains

Безопасные и надежные программы для работы в наши дни

pdf 3,7mb

doc 1,7mb

Уже скачали 19919

С точки зрения вычислительной техники любое сохраняемое число представляет собой машинное слово, арифметические и логические операции над которым выполняет арифметико-логическое устройство (АЛУ). Чтобы компьютеру было проще работать с регистрами, они нумеруются (или наделяются адресами).

Так, для сложения двух чисел используются адреса регистров, где они расположены, а не сами эти числа. Данные записываются в восьмеричной и шестнадцатеричной системах для более быстрого и простого перевода чисел в двоичный формат.

Тем не менее, конечный пользователь видит всю числовую информацию в привычном ему десятичном виде. Почему так происходит? Изначально, нажимая на клавишу, пользователь передает компьютеру соответствующую последовательность электрических сигналов (нулей и единиц). Для каждого символа определен конкретный набор этих импульсов.

Специальные программы (драйверы клавиатуры и экрана) преобразуют эти сигналы в читаемый вид путем обращения к кодовой таблице. Например, стандарт Unicode позволяет закодировать таким образом 65536 символов. Именно так используется двоичная система счисления в информатике — нули и единицы преобразуются программным способом в текст и изображения на экране.

исла, используемые в двоичной системе счисления

Далее приведем очевидные достоинства использования двоичного способа представления информации.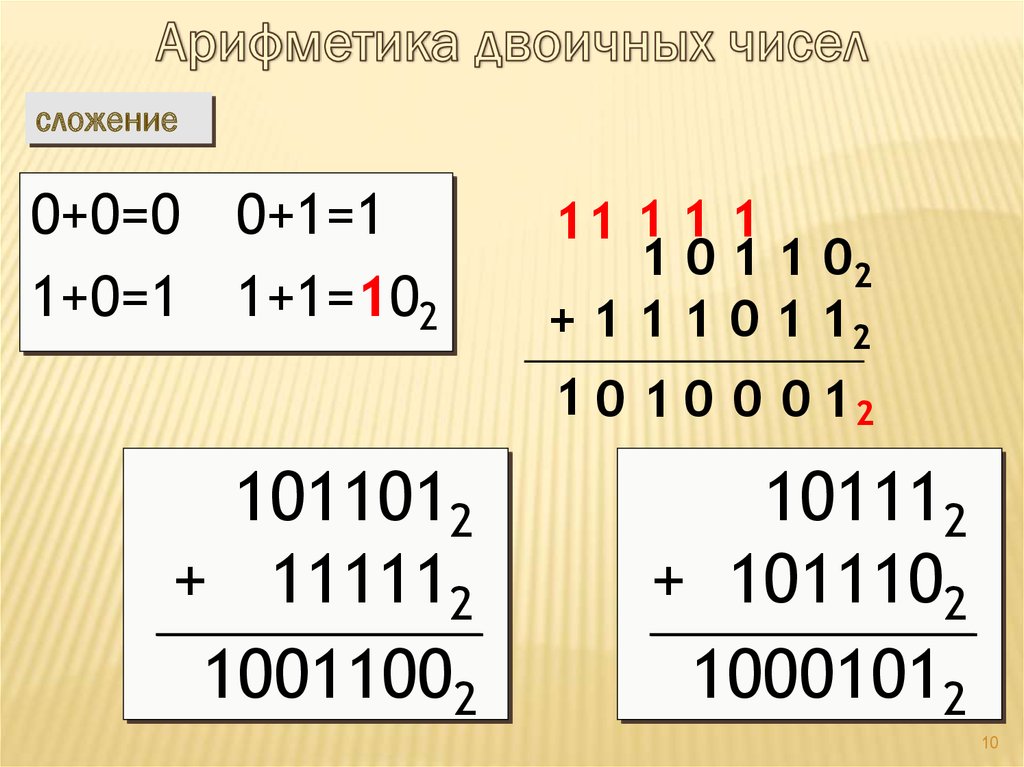

• От технических устройств требуется лишь два устойчивых состояния (например, наличие тока и отсутствие тока и т. д.).
• Вычислительной технике значительно проще выполнять операции с двоичными данными, чем с десятичными.
• Таблицы сложения и умножения в двоичной системе имеют гораздо меньший размер по сравнению с такими же таблицами для десятичной системы.

Недостатки:

• возможное превращение конечных десятичных дробей в бесконечные двоичные;
• большее количество занимаемых разрядов по сравнению с десятичной записью;
• сложность с восприятием записи чисел, поскольку двоичная система счисления — этопредставление только в виде нулей и единиц.

Сложение, вычитание и умножение в двоичной системе счисления

Для того, чтобы складывать числа, пользуются следующей таблицей:

+	0	1
0	0	1
1	1	10 (переход в старший разряд)

Таблица вычитания в двоичной системе счисления выглядит так:

—	0	1
0	0	1
1	(взятие из старшего разряда) 1	0

Точный инструмент «Колесо компетенций»

Для детального самоанализа по выбору IT-профессии

Список грубых ошибок в IT, из-за которых сразу увольняют

Об этом мало кто рассказывает, но это должен знать каждый

Мини-тест из 11 вопросов от нашего личного психолога

Вы сразу поймете, что в данный момент тормозит ваш успех

Регистрируйтесь на бесплатный интенсив, чтобы за 3 часа начать разбираться в IT лучше 90% новичков.

Только до 13 марта

Осталось 17 мест

Умножение выполняется по следующей таблице:

*	0	1
0	0	0
1	0	1

Как переводить числа в двоичной системе счисления в десятичную

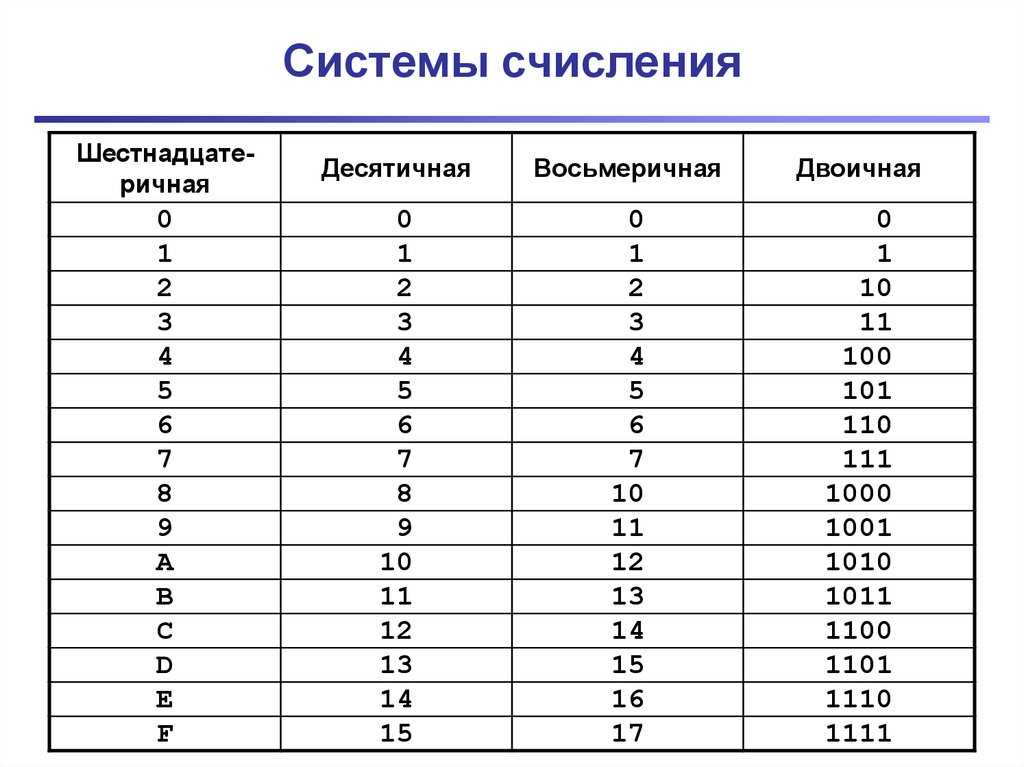
Сперва приведем алфавиты трех используемых систем — двоичной, десятичной и шестнадцатеричной.

Основание	Наименование системы	Алфавит
2	Двоичная	0, 1
10	Десятичная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
16	Шестнадцатеричная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Как уже упоминалось, двоичная система счисления имеет основание 2. Чтобы перевести число в десятичный формат, можно воспользоваться такой таблицей степеней данного основания:

512

256

128

64

32

16

8

4

2

1

Здесь ряд начинается с единицы, а каждая последующая цифра является результатом умножения предыдущей на двойку.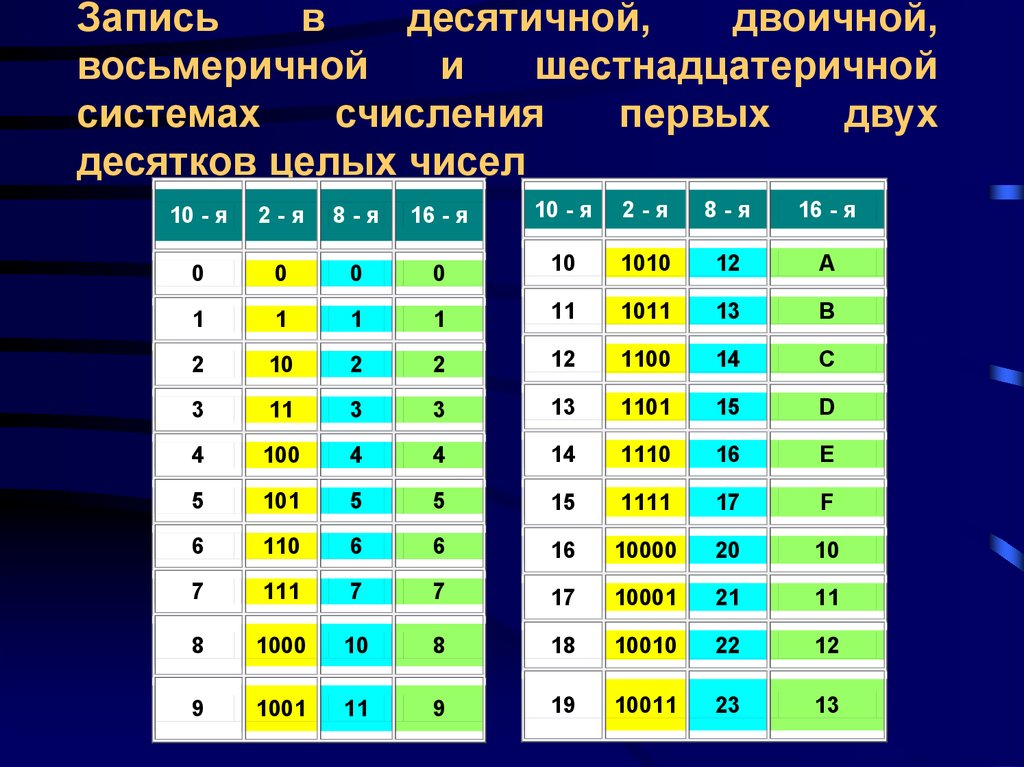 После 1 ставится так называемая двоичная точка.

В качестве примера переведем число 1011011 двоичной системы счисления в 10-ный формат (число 91):

0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>>11*2+0=22>>22*2+1=45>> 45*2+1=91.

А конвертация 101111 в десятичную систему даст число 47:

0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>> 11*2+1=23 >> 23*2+1=47

НУЖНА КАРТИНКА

Таким же образом можно переводить и дробные числа. Для примера возьмем 1011010, 101 в двоичной системе счисления. Перевод чисел в десятичную можно осуществлять в таком виде:

1*26 + 0*25 + 1*24 + 1*2 + 0 *22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 0 * 2-2 + 1 * 2-3 = 90,625

Иначе говоря, расчет будет следующим:

1*64+0*32+1*16+1*8+0*4+1*2+0*1+1*0,5+0*0,25+1*0,125 = 90,625

Полученное значение в десятичной системе также высчитывается по таблице:

64	32	16	8	4	2	1	0,5	0,25	0,125
1	0	1	1	0	1	0.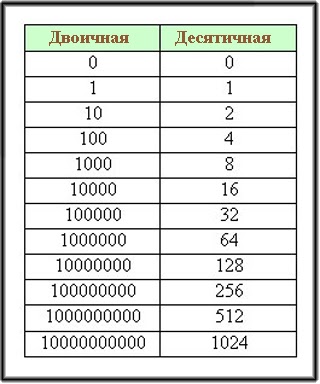	.1	0	1
+64	+0	+16	+8	+0	+2	+0	+0.5	+0	+1.125

Алгоритм перевода из двоичной системы счисления в шестнадцатеричную

Здесь необходимо выполнить 2 шага:

1. Перевод числа из двоичной системы в десятичную
2. Преобразование полученного значения в шестнадцатеричный формат

К примеру, имеется число 1011101 в двоичной системе счисления. Запись чисел для выполнения первого шага осуществляется по формуле:

A2 = an-1 ∙ 2n-1 + an-2 ∙ 2n-2 + ∙∙∙ + a0 ∙ 20

Подставляем значения:

10111012=1 ∙ 26 + 0 ∙ 25 + 1 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 1 ∙ 20 = 1 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 64 + 0 + 16 + 8 + 4 + 0 + 1 = 9310

Теперь полученное десятичное число необходимо преобразовать в шестнадцатеричное. Для этого 93 многократно последовательно делим на 16 до тех пор, пока остаток не станет меньше 16.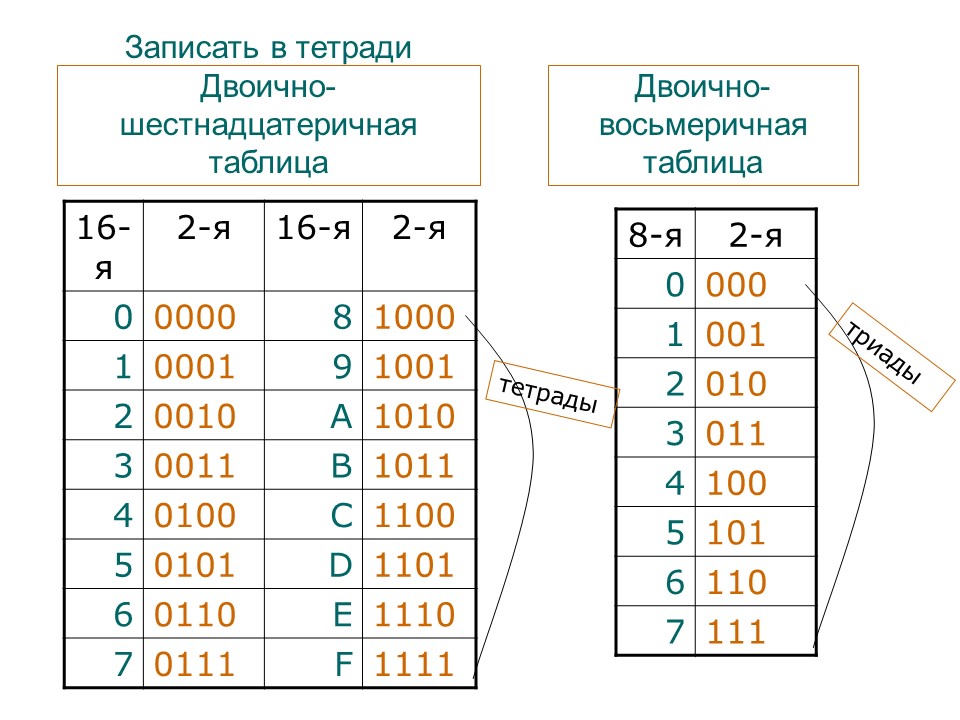

В процессе деления остатки нужно записывать в обратном порядке. Результатом всех операций будет число 9310=5D16.

НУЖНА КАРТИНКА

Перевод дробных чисел в шестнадцатеричный формат выполняется аналогичным образом — через промежуточный этап перевода в десятичную систему.

Вновь покажем это на примере. Преобразуем двоичное число 10001100.110 сначала в десятичную систему по формуле:

An = an-1 ∙ qn-1 + an-2 ∙ qn-2 + ∙∙∙ + a0 ∙ q0 + a-1 ∙ q-1 + ∙∙∙ + a-m ∙ q-m

Подставляем наши значения:

10001100.1102=1 ∙ 27 + 0 ∙ 26 + 0 ∙ 25 + 0 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 0 ∙ 20 + 1 ∙ 2-1 + 1 ∙ 2-2 + 0 ∙ 2-3 = 1 ∙ 128 + 0 ∙ 64 + 0 ∙ 32 + 0 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 + 1 ∙ 0.5 + 1 ∙ 0.25 + 0 ∙ 0.125 = 128 + 0 + 0 + 0 + 8 + 4 + 0 + 0 + 0.5 + 0.25 + 0 = 140.7510

Следует отметить сильное сходство формул расчетов дробного и целого десятичных чисел. Тем не менее, отличия также имеются.

Вторым этапом переводим число 140,75 в шестнадцатеричный формат. Это делается в два подэтапа:

1. Перевод отдельно целой части числа.
2. Перевод отдельно дробной части числа.

Итак, нам необходимо сначала преобразовать 140 в шестнадцатеричную систему счисления, последовательно деля это число на 16, пока остаток не станет меньше делителя.

После записи остатков в обратном порядке получаем результат: 14010=8C16

Операции с дробной частью отличаются тем, что мы многократно и последовательно умножаем ее, пока она не станет равной нулю (или значению в соответствии с заданной точностью).

В нашем случае это будет выглядеть так: 0.75 * 16 = 12.0 (C).

Поскольку после первого же умножения дробная часть обнулилась, дальнейшие итерации прекращаем. Итоговый результат: 0.12 (0.С) или, иначе, 0.75 ∙ 16 = 12.0 (C)

Остался последний этап — соединение преобразованных целой и дробной частей: 140.7510=8C.C16. Это и будет общим решением всей задачи.

Сперва может показаться, что изложенный здесь материал слишком сложен и запутан для простого обывателя.

На самом деле двоичная арифметика предельно логична и понятна. Пользование таблицами сложения и умножения не представляет сложности, если в них разобраться.

Рейтинг: 5

( голосов 1 )

Поделиться статьей

Глава 31. Двоичная система исчисления . Введение в электронику

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Описать двоичную систему счисления.

• Перечислить значения разрядов для каждого бита двоичного числа.

• Преобразовывать двоичные числа в десятичные.

• Преобразовывать десятичные числа в двоичные.

• Преобразовывать десятичные числа в двоично-десятичный код.

• Преобразовывать числа в двоично-десятичном коде в десятичные.

Система счисления — это не более, чем код. Для каждой отдельной величины существует приписанный ей символ. Когда код известен, можно выполнять вычисления. Это возможно с помощью арифметики и высшей математики.

Простейшей системой счисления является двоичная. Двоичная система содержит только две цифры — 0 и 1. Эти цифры имеют такое же значение, как и в десятичной системе счисления.

Двоичная система счисления используется в цифровых и микропроцессорных цепях благодаря ее простоте. Двоичные данные представляются двоичными цифрами, называемыми битами. Термин бит означает двоичная цифра (разряд) (binary digit).

31-1. ДВОИЧНЫЕ ЧИСЛА

Десятичная система счисления называется системой с основанием 10, поскольку она использует десять цифр от 0 до 9. Двоичная система — это система с основанием два, поскольку она использует две цифры, 0 и 1. Положение 0 или 1 в двоичном числе показывает их значение в числе и называется значением разряда или его весом.

Значения разрядов двоичного числа увеличиваются как степени 2.

Счет в двоичной системе начинается с чисел 0 и 1. Как и в десятичной системе счисления, каждая двоичная цифра отличается от предыдущей на единицу. Сумма единицы и нуля дает единицу, а сумма двух единиц дает нуль, и при этом прибавляется единица в старшем разряде. На рис. 31-1 показана последовательность двоичных чисел, образованная по описанному алгоритму.

Рис. 31-1. Десятичные числа и эквивалентные двоичные числа.

Для определения наибольшего значения, которое может быть представлено данным количеством разрядов с основанием 2, используйте следующую формулу:

Наибольшее число = 2ⁿ — 1,

где n — число битов (или число использованных значений разрядов).

_{ПРИМЕР: два бита могут быть использованы для счета от 0 до 3, так как}

_{2ⁿ — 1 = 2² — 1 = 4–1 = 3.}

_{Четыре бита необходимы для счета от 0 до 15, так как}

_{2ⁿ — 1 = 2⁴ — 1 = 16 — 1 = 15.}

31-1. Вопросы

1. В чем преимущество двоичной системы счисления перед десятичной при использовании в цифровых цепях?

2. Как определить наибольшее значение двоичного числа при заданном числе разрядов?

3. Каково наибольшее значение двоичного числа с:

а. 4 битами,

б. 8 битами,

в. 12 битами,

г. 16 битами.

31-2. ПРЕОБРАЗОВАНИЕ ДВОИЧНЫХ ЧИСЕЛ В ДЕСЯТИЧНЫЕ И НАОБОРОТ

Как установлено, двоичное число представляет собой число с весом каждого разряда. Значение двоичного числа может быть определено суммированием произведений каждой цифры на вес ее разряда. Метод вычисления двоичного числа показан на следующем примере:

_{ПРИМЕР:} 

_{Число 45 является десятичным эквивалентом двоичного числа 101101.}

_{Дробные числа также могут быть представлены в двоичной форме путем размещения двоичных цифр справа от двоичной запятой, так же как и десятичные цифры размещаются справа от десятичной запятой. Все цифры справа от запятой имеют вес, представленный отрицательными степенями 2 или дробными значениями разрядов.}

_{Степень 2 ∙ Значение разряда}

_{2⁵ = 32}

_{2⁴ = 16}

_{2³ = 8}

_{2² = 4}

_{2¹ = 2}

_{2⁰ = 1}

_{десятичная запятая}

_{2^-1 = 1/2¹ = 1/2 = 0,5}

_{2^-2 = 1/2² = 1/4 = 0,25}

_{2^-3 = 1/2³ = 1/8 = 0,125}

_{2^-4 = 1/2⁴ = 1/16 = 0,0625}

_{ПРИМЕР: Определить десятичное значение двоичного числа 111011,011.}

При работе с цифровым оборудованием часто бывает необходимо преобразовывать числа из двоичной системы в десятичную, и наоборот. Наиболее популярный способ преобразования десятичных чисел в двоичные — это последовательное деление десятичного числа на 2, с записью остатка после каждого деления. Остатки, взятые в обратном порядке, образуют двоичное число.

_{ПРИМЕР: Преобразовать 11 в двоичное число последовательным делением на 2. (Самый Младший Разряд).}

_{(1/2 = 0 означает, что 1 не делится на 2, так что 1 является остатком). Десятичное число 11 равно 1011 в двоичной системе.}

_{Этот процесс может быть упрощен путем записи чисел упорядоченным образом, как это показано на примере преобразования 25 в двоичное число.}

_{ПРИМЕР:}

_{Десятичное число 25 равно двоичному числу 11001.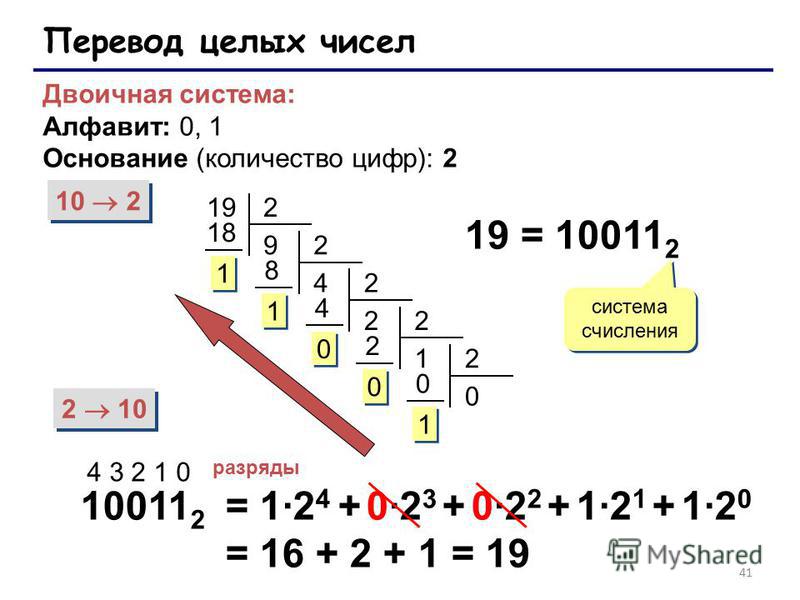 Дробные числа преобразовываются по другому: число умножается на 2 и целая часть записывается как двоичная дробь.}

_{ПРИМЕР: Преобразовать десятичную дробь 0,85 в двоичную дробь последовательным умножением на 2.}

_{Умножение на 2 продолжается до тех пор, пока не будет достигнута необходимая точность. Десятичная дробь 0,85 равна 0,110110 в двоичной форме.}

_{ПРИМЕР: Преобразовать десятичное число 20,65 в двоичное число. Разделите 20,65 на целую часть 20 и дробную 0,65 и примените описанные выше методы.}

_{Десятичное 20 — двоичному 10100}

_и

_{Комбинируя два числа, получим} 20,65₁₀ = 10100,1010011₂.

_{Это 12-разрядное число является приближенным, потому что преобразование дроби было прервано после получения 7 разрядов.}

31-2. Вопросы

1. Чему равно значение каждого разряда 8-разрядного двоичного числа?

2. Чему равно значение каждого разряда для 8 разрядов правее десятичной точки?

3. Преобразуйте следующие двоичные числа в десятичные:

а. 1001;

б. 11101111;

в. 11000010;

г. 10101010,1101;

д. 10110111,0001.

4. В чем состоит процесс преобразования десятичных чисел в двоичные?

5. Преобразуйте следующие десятичные числа в двоичные:

а. 27;

б. 34,6;

в. 346;

г. 321,456;

д. 7465.

31-3. КОД 8421

Код 8421 — это двоично-десятичный код (ДДК), состоящий из четырех двоичных разрядов.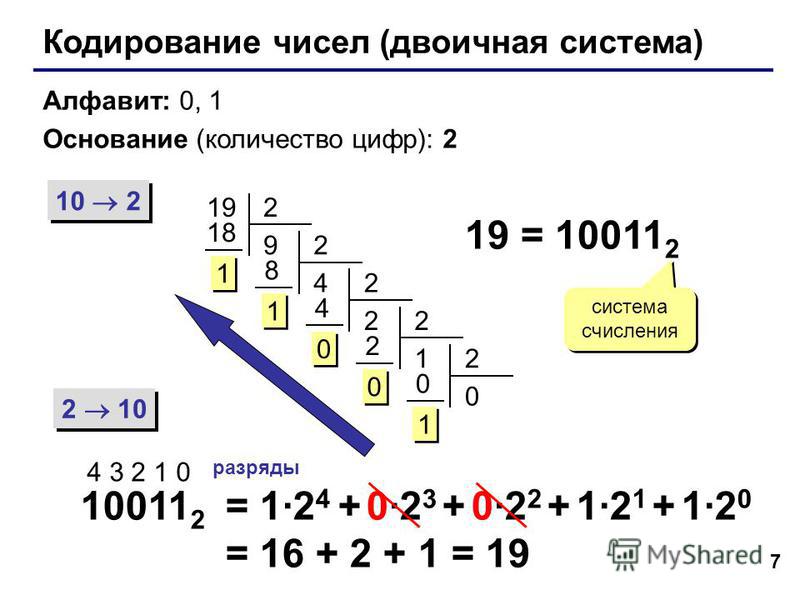 Он используется для представления цифр от 0 до 9. Обозначение 8421 относится к двоичному весу 4 разрядов.

Степени 2: 2³ 2² 2¹ 2⁰

Двоичный вес: 8 4 2 1

Основным достоинством этого кода является то, что он допускает легкое преобразование из десятичной формы в двоичную, и наоборот. Поэтому двоично-десятичный код используется всегда, если не оговорено другое.

Каждая десятичная цифра (от 0 до 9) представляется двоичной комбинацией следующим образом:

Хотя с помощью четырех двоичных разрядов можно представить 16 чисел (2⁴), шесть кодовых комбинаций для чисел, больших 9 (1010,1011,1100, 1101, 1110 и 1111), в коде 8421 не используются.

Для того чтобы выразить любое десятичное число с помощью кода 8421, замените каждую десятичную цифру соответствующим 4-разрядным кодом.

_{ПРИМЕР: Преобразовать следующие десятичные числа в двоично-десятичный код: 5, 13, 124, 576, 8769.}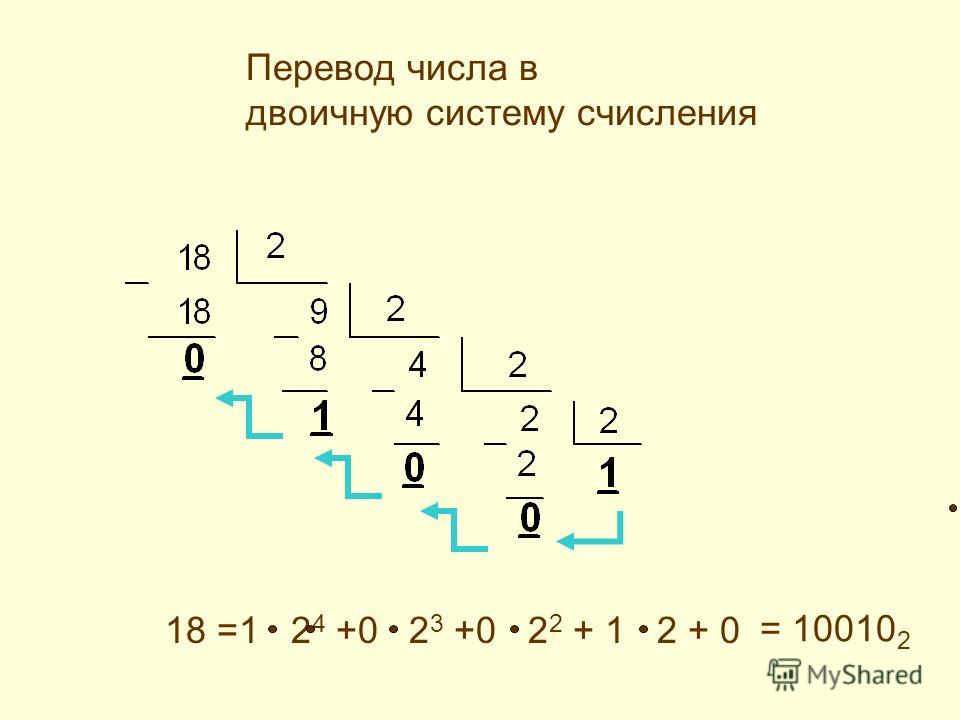

_{Для преобразования числа из двоично-десятичного кода в десятичную систему, разбейте число на группы по 4 разряда. После этого запишите десятичные цифры, соответствующие каждой 4-разрядной группе.}

_{ПРИМЕР: Преобразуйте числа, записанные двоично-десятичным кодом в десятичную систему: 10010101, 1001000, 1100111, 1001100101001, 1001100001110110.}

Замечание: Если в крайней группе слева не хватает разрядов до четырех, то к ней добавляются нули.

31-3. Вопросы

1. Что такое код 8421 и как он используется?

2. Преобразуйте следующие десятичные числа в двоично-десятичный код:

а. 17;

б. 100;

в. 256;

г. 778;

д. 8573.

3.  Преобразуйте следующие двоично-десятичные коды в десятичные числа:

а. 1000 0010;

б. 0111 0000 0101;

в. 1001 0001 0011 0100;

г. 0001 0000 0000 0000;

д. 0100 0110 1000 1001.

РЕЗЮМЕ

• Двоичная система счисления — это простейшая система счисления.

• Двоичная система счисления содержит две цифры — 0 и 1.

• Двоичная система счисления используется для представления данных в цифровых и компьютерных системах.

• Двоичные данные представляются двоичными разрядами, которые называются битами.

• Термин бит происходит от названия двоичный разряд (binary digit)

• Значение каждого более высокого разряда двоичного числа увеличивается как степень 2.

• Наибольшее число, которое может быть представлено данным количеством разрядов в двоичной системе равно 2ⁿ — 1, где n — количество разрядов.

• Значение двоичного числа может быть определено суммированием произведений каждой цифры на вес ее разряда.

• Дробные числа представляются отрицательными степенями 2.

• Для преобразования десятичного числа в двоичное, десятичное число последовательно делится на 2, и после каждого деления записывается остаток. Эти остатки, расположенные в обратном порядке, образуют двоичное число.

• Код 8421 или двоично-десятичный код используется для представления цифр от 0 до 9.

• Достоинством двоично-десятичного кода является возможность легкого преобразования чисел из десятичной формы в двоичную и наоборот.

Глава 31. САМОПРОВЕРКА

1. Запишите в двоичной форме десятичные числа от 0 до 27.

2. Сколько двоичных разрядов нужно для представления десятичного числа 100?

3. Опишите процесс преобразования десятичного числа в двоичное число.

4. Преобразуйте следующие двоичные числа в десятичные:

а. 100101,001011;

б. 111101110,11101110;

в. 10000001,00000101.

5. Опишите процесс преобразования десятичных чисел в двоично-десятичный код.

6. Преобразуйте следующие двоично-десятичные коды в десятичные числа:

а. 0100 0001 0000 0110;

б. 1001 0010 0100 0011;

в. 0101 0110 0111 1000.

1 в двоичном формате — Как преобразовать 1 из десятичного в двоичный?

1 в двоичной системе равно 1. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 1 бит для представления 1 в двоичном формате. В этой статье мы покажем, как преобразовать десятичное число 1 в двоичное.

• 1 в двоичном виде: 1₁₀ = 1₂
• 1 в восьмеричной системе: 1₁₀ = 1₈
• 1 в шестнадцатеричном формате: 1₁₀ = 1₁₆
• 1₂ в десятичном формате: 1₁₀

Как преобразовать 1 в двоичный код?

Шаг 1: Разделите 1 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0.

Дивиденд	Остаток
1/2 = 0	1

Шаг 2: Запишите остаток снизу вверх, т.е. в обратном хронологическом порядке. Это даст двоичный эквивалент 1.

Следовательно, двоичный эквивалент десятичного числа 1 равен 1.

☛ Калькулятор преобразования десятичной дроби в двоичную

Постановка задачи:

Часто задаваемые вопросы о 1 в двоичной системе

Что такое 1 in Бинарный?

1 в двоичном формате равен 1. Чтобы найти десятичный эквивалент в двоичном, последовательно делите 1 на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.

☛ Двоичный код в десятичный

Сколько бит имеет 1 в двоичном формате?

Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 1 в двоичном формате, т. е. 1. Таким образом, мы использовали 1 бит для представления 1 в двоичном формате.

Что такое двоичный эквивалент 1 + 5?

1 в двоичной системе счисления равно 1, а 5 равно 101. Мы можем сложить двоичный эквивалент 1 и 5, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (1)₂ + (101)₂ = (110)₂, что есть не что иное, как 6,9.0003

☛ Двоично-десятичный калькулятор

Найдите значение 3 × 1 в двоичной форме.

Мы знаем, что 1 в двоичном формате равно 1, а 3 равно 11.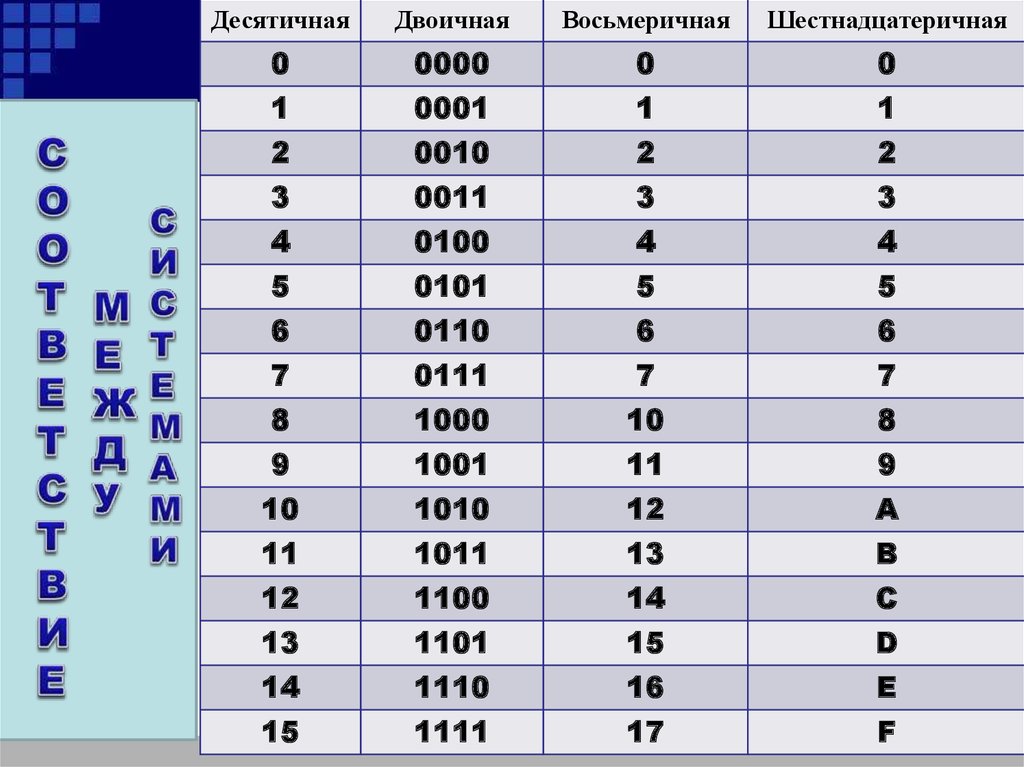 Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0 , 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 1 × 11 = 11, что равно 3 в десятичной системе счисления. [1 × 3 = 3]

Как преобразовать 1 в двоичный эквивалент?

Мы можем разделить 1 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге. 1 по модулю 2 = 1. Следовательно, десятичное число 1 в двоичном виде можно представить как 1.

☛ Также проверьте:

• 73 в двоичном формате — 1001001
• 225 в двоичном формате — 11100001
• 3000 в двоичном формате — 101110111000
• 69 в двоичном формате — 1000101
• 120 в двоичном формате — 1111000
• 5 в двоичном формате — 101
• 222 в двоичном формате — 11011110

Рабочие листы по математике и визуальный учебный план

Двоичная система счисления | Определение, пример и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.