Арифметические операции с плавающей запятой могут давать неточный результат в Excel — Office
- Статья
-
- Применяется к:
- Excel 2010, Excel 2013, Excel for Microsoft 365, Microsoft Excel for Mac 2011, Excel for Mac for Microsoft 365
Сводка
В этой статье рассматривается, как Microsoft Excel хранит и вычисляет числа с плавающей запятой. Это может повлиять на результаты некоторых чисел или формул из-за округления или усечения данных.
Обзор
Microsoft Excel был разработан на основе спецификации IEEE 754 для определения способа хранения и вычисления чисел с плавающей запятой. IEEE — институт инженеров электротехники и электроники, международный орган, который, помимо прочего, определяет стандарты для компьютерного программного и аппаратного обеспечения. Спецификация 754 — это широко используемая спецификация, которая описывает, как числа с плавающей запятой должны храниться в компьютере, использующем двоичную систему счисления. Она популярна по той причине, что позволяет хранить числа с плавающей запятой в разумных объемах и выполнять вычисления относительно быстро. Стандарт 754 используется в модулях операций с плавающей запятой и арифметических сопроцессорах почти всех современных микропроцессоров на базе ПК, реализующих вычисления с плавающей запятой, включая процессоры Intel, Motorola, Sun и MIPS.
IEEE — институт инженеров электротехники и электроники, международный орган, который, помимо прочего, определяет стандарты для компьютерного программного и аппаратного обеспечения. Спецификация 754 — это широко используемая спецификация, которая описывает, как числа с плавающей запятой должны храниться в компьютере, использующем двоичную систему счисления. Она популярна по той причине, что позволяет хранить числа с плавающей запятой в разумных объемах и выполнять вычисления относительно быстро. Стандарт 754 используется в модулях операций с плавающей запятой и арифметических сопроцессорах почти всех современных микропроцессоров на базе ПК, реализующих вычисления с плавающей запятой, включая процессоры Intel, Motorola, Sun и MIPS.
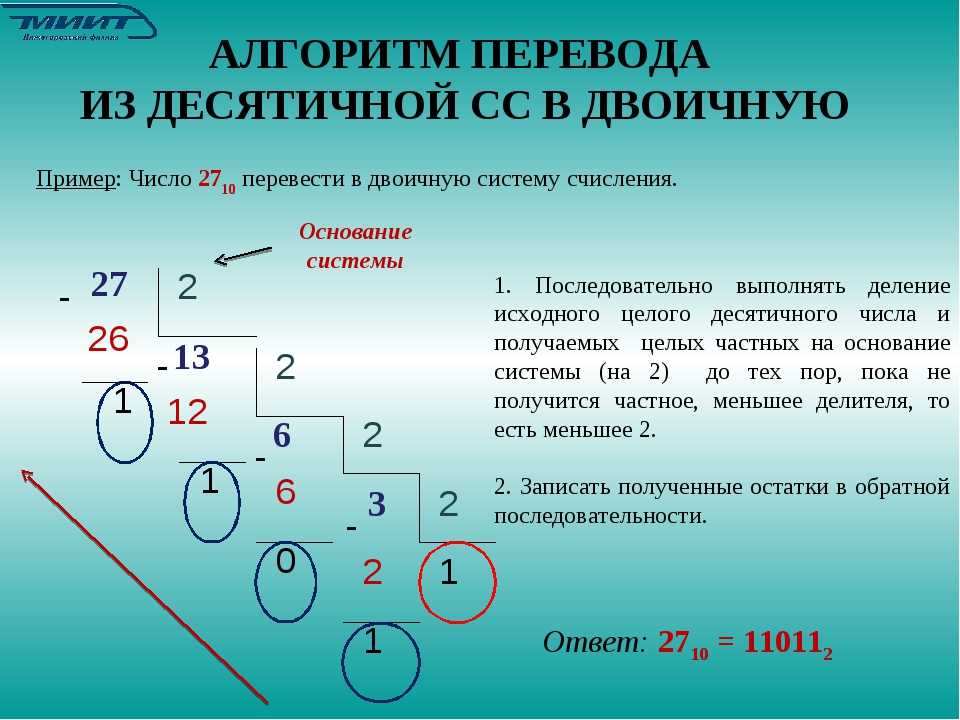
При хранении чисел соответствующее двоичное число может представлять каждое число или дробное число. Например, дробь 1/10 может быть представлена в десятичной системе счисления как 0,1. Однако то же самое число в двоичном формате становится следующим повторяющимся двоично-десятичным числом:
0001100110011100110011 (и т. д.)
д.)
Это число можно бесконечно повторять. Это число не может быть представлено в конечном (ограниченном) пространстве. Поэтому при хранении это число округляется примерно на -2.8E-17 в меньшую сторону.
Однако существуют некоторые ограничения спецификации IEEE 754, которые делятся на три общие категории:
- Максимальные/минимальные ограничения
- Точность
- Повторяющиеся двоичные числа
Максимальные/минимальные ограничения
Все компьютеры имеют максимальное и минимальное количество, которое может быть обработано. Поскольку количество битов памяти, в которых хранится число, является конечным, из этого следует, что максимальное или минимальное число, которое может храниться, также является конечным. Максимальное число, которое может храниться в Excel, — 1.79769313486232E+308, а минимальное положительное число — 2.2250738585072E-308.
Случаи, в которых мы придерживаемся стандарта IEEE 754
- Потеря точности. Потеря точности возникает в том случае, если генерируется число, которое слишком мало для представления.
 В IEEE и Excel результат равен 0 (за исключением того, что в IEEE есть понятие -0, а в Excel — нет).
В IEEE и Excel результат равен 0 (за исключением того, что в IEEE есть понятие -0, а в Excel — нет). - Переполнение. Переполнение возникает в том случае, если число слишком велико для представления. Excel использует свое специальное представление для этого случая (#NUM!).
Случаи, в которых мы не придерживаемся стандарта IEEE 754
Ненормализованные числа. Ненормализованное число содержит 0 в экспоненте. В этом случае все число хранится в мантиссе, которая не имеет неявной ведущей единицы. В результате теряется точность, и чем меньше число, тем больше теряется точность. Числа на малом конце этого диапазона имеют только одну цифру точности.
Пример: нормализованное число имеет неявную ведущую единицу. Например, если мантисса представляет собой 0011001, нормализованное число становится 10011001 из-за неявной ведущей единицы. Ненормализованное число не имеет неявной ведущей единицы, поэтому в нашем примере ненормализованное число 0011001 не изменяется.
 В данном случае нормализованное число имеет восемь значащих цифр (10011001), а ненормализованное — пять значащих цифр (11001), причем ведущие нули являются несущественными.
В данном случае нормализованное число имеет восемь значащих цифр (10011001), а ненормализованное — пять значащих цифр (11001), причем ведущие нули являются несущественными.Ненормализованные числа — это, по сути, обходной путь, позволяющий хранить числа, которые меньше обычного нижнего предела. Корпорация Майкрософт не реализует эту необязательную часть спецификации, поскольку ненормализованные числа по своей природе имеют переменное количество значащих цифр. Это может привести к существенной ошибке в расчетах.
Положительная/отрицательная бесконечность: бесконечность возникает при делении на 0. Excel не поддерживает бесконечность и выдает ошибку #DIV/0! в таких случаях.
Не число (NaN): используется для представления недопустимых операций (таких как бесконечность/бесконечность, бесконечность-бесконечность или квадратный корень из -1). NaNs позволяют программе продолжать работу с недопустимой операцией. Вместо этого Excel немедленно выдает ошибку типа #NUM! или #DIV/0!.

Точность
Число с плавающей запятой хранится в двоичном формате в виде трех частей в 65-битном диапазоне: знак, экспонента и мантисса.
| Знак | Экспонента | Мантисса |
|---|---|---|
| 1 бит знака | 11-битная экспонента | 1 неявный бит + 52-битная дробь |
Знак хранит знак числа (положительный или отрицательный), экспонента хранит степень 2, в которую возводится или на которую понижается число (максимальная/минимальная степень 2 равна +1.023 и -1.022), а мантисса хранит действительное число. Конечная область хранения мантиссы ограничивает то, насколько близкими могут быть два соседних числа с плавающей запятой (то есть точность).
Мантисса и экспонента хранятся как отдельные компоненты. В результате возможная точность зависит от размера числа (мантиссы), над которым выполняется операция. Хотя Excel может хранить числа от 1.79769313486232E308 до 2.2250738585072E-308, это возможно только в пределах 15 разрядов.
Дробь — это нормализованная дробная часть числа, нормализованная по той причине, что экспонента корректируется таким образом, чтобы ведущий бит всегда был равен 1. Таким образом, ее не нужно хранить, и вы получаете еще один бит точности. Вот почему существует неявный бит. Это похоже на экспоненциальное представление, где вы управляете экспонентой, чтобы слева от десятичной запятой располагалась одна цифра; за исключением двоичной системы счисления, вы всегда можете управлять экспонентой так, чтобы первый бит был 1, потому что имеются только 1 и 0.
Смещение — это значение смещения, используемое для предотвращения хранения отрицательных экспонент. Смещение для чисел одинарной точности равно 127 и 1,023 (десятичное) для чисел двойной точности. Excel хранит числа с двойной точностью.
Пример с использованием очень больших чисел
Введите следующие данные в новую рабочую книгу:
A1: 1.2E+200 B1: 1E+100 C1: =A1+B1
Результирующее значение в ячейке C1 будет 1. 2E+200, то же значение, что и в ячейке A1. На самом деле, если сравнить ячейки A1 и C1 с помощью функции IF, например IF(A1=C1), результатом будет TRUE. Это вызвано тем, что спецификация IEEE предусматривает хранение только 15 значащих цифр точности. Для хранения приведенного выше расчета Excel потребуется точность не менее 100 разрядов.
2E+200, то же значение, что и в ячейке A1. На самом деле, если сравнить ячейки A1 и C1 с помощью функции IF, например IF(A1=C1), результатом будет TRUE. Это вызвано тем, что спецификация IEEE предусматривает хранение только 15 значащих цифр точности. Для хранения приведенного выше расчета Excel потребуется точность не менее 100 разрядов.
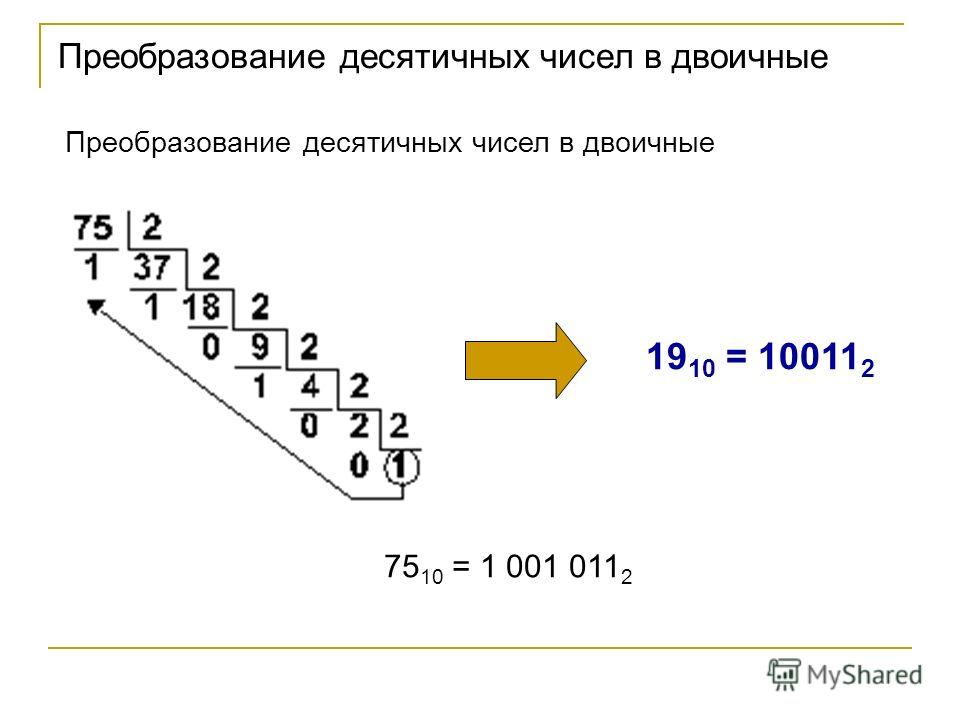
Пример с использованием очень маленьких чисел
Введите следующие данные в новую рабочую книгу:
A1: 0.000123456789012345 B1: 1 C1: =A1+B1
В результате значение в ячейке C1 будет равно 1.00012345678901 вместо 1.000123456789012345. Это вызвано тем, что спецификация IEEE предусматривает хранение только 15 значащих цифр точности. Для хранения приведенного выше расчета Excel потребуется точность не менее 19 разрядов.
Исправление ошибок точности
Excel предлагает два основных метода компенсации ошибок округления: функцию ROUND и параметр в рабочей книге Точность как на экране или Задать точность как на экране.
Метод 1. Функция ROUND
Используя предыдущие данные, в следующем примере функция ROUND используется для приведения числа к пяти цифрам. Это позволяет успешно сравнить результат с другим значением.
A1: 1.2E+200 B1: 1E+100 C1: =ROUND(A1+B1,5)
В результате получается 1.2E+200.
D1: =IF(C1=1.2E+200, TRUE, FALSE)
В результате получается значение TRUE.
Метод 2. Точность как на экране
В некоторых случаях можно предотвратить влияние ошибок округления на работу с помощью параметра Точность как на экране. Этот параметр заставляет значение каждого числа в рабочем листе быть отображаемым значением. Чтобы включить этот параметр, выполните следующие действия.
- В меню Файл нажмите Параметры, затем выберите категорию Дополнительно.
- В разделе При пересчете этой книги выберите необходимую книгу, а затем установите флажок Задать точность как на экране.

Например, если выбрать формат чисел, отображающий два знака после запятой, а затем включить параметр Точность как на экране, все знаки кроме двух символов после запятой теряются при сохранении книги. Этот параметр применяется к открытой книге и всем ее листам. Отменить этот параметр для восстановления утерянной информации невозможно. Перед его включением рекомендуется сохранить книгу.
Повторение двоичных чисел и вычислений с результатами, близкими к нулю
Еще одна проблема, возникающая при хранении чисел с плавающей точкой в двоичном формате, связана с тем, что некоторые числа в десятичной системе являются конечными, но становятся бесконечными и повторяющимися в двоичной. Наиболее распространенным примером этого является значение 0,1 и похожие. Несмотря на то, что эти значения могут быть представлены в десятичной системе, такие же значения в двоичном формате становятся следующим повторяющимся двоичным числом при их сохранении в мантиссе:
000110011001100110011 (и т. д.)
д.)
Спецификация IEEE 754 не допускает особых ограничений для любого значения. Все, что можно сохранить, хранится в мантиссе, а остальное удаляется. Неточность в таком случае случае составляет около -2.8E-17 или 0,000000000000000028 при хранении.
Даже обычные десятичные дроби, например 0,0001, невозможно точно представить в двоичном формате. (0,0001 — это повторяющаяся двоичная дробь с периодом в 104 бита). Этот явление похоже на невозможность точно представить дробь 1/3 в десятичной системе (повторяющаяся дробь 0.33333333333333333333).
Например, рассмотрим следующий простой пример в Microsoft Visual Basic для приложений:
Sub Main()
MySum = 0
For I% = 1 To 10000
MySum = MySum + 0.0001
Next I%
Debug.Print MySum
End Sub
В таком случае в качестве выходных данных будет выведено значение 0,999999999999996. Небольшая неточность в представлении 0,0001 в двоичном формате распространяется на сумму.
Пример: добавление отрицательного числа
Введите следующие данные в новую рабочую книгу:
A1: =(43,1-43,2)+1
Щелкните правой кнопкой мыши ячейку A1 и выберите пункт Формат ячеек.
 На вкладке «Числовые форматы» выберите «Инженерный» в разделе «Категория». Установите значение Знаки после запятой на 15.
На вкладке «Числовые форматы» выберите «Инженерный» в разделе «Категория». Установите значение Знаки после запятой на 15.
Вместо значения 0,9 Excel отображает 0,899999999999999. Так как сначала вычисляется (43,1-43,2), значение -0.1 временно сохраняется и к расчету добавляется неточность, возникшая при хранении -0.1.
Пример, когда значение достигает нуля
В Excel 95 или более ранней версии введите в новую книгу следующее:
A1: =1,333+1,225-1,333-1,225
Щелкните правой кнопкой мыши ячейку A1 и выберите пункт Формат ячеек. На вкладке «Числовые форматы» выберите «Инженерный» в разделе «Категория». Установите значение Знаки после запятой на 15.
Вместо 0 Excel 95 отображает -2,22044604925031E-16.
В Excel 97 добавлена оптимизация для устранения этой проблемы. Если в результате операции добавления или вычитания получается значение равно или близко к нулю, Excel 97 и более поздние версии компенсируют неточность, полученную в результате конвертации операнда в двоичную систему и обратно.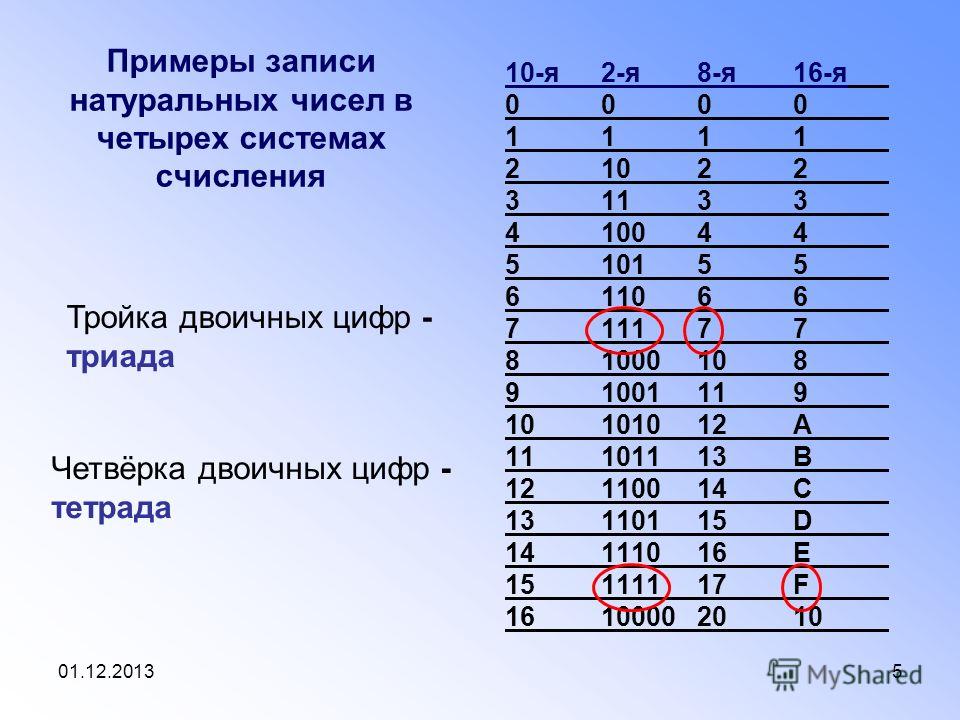 При выполнении примера, указанного выше, в Excel 97 и более поздней версии в экспоненциальном представлении отображается правильное значение 0 или 0.000000000000000E+00.
При выполнении примера, указанного выше, в Excel 97 и более поздней версии в экспоненциальном представлении отображается правильное значение 0 или 0.000000000000000E+00.
Дополнительные сведения о числах с плавающей точкой и спецификации IEEE 754 см. на следующих веб-сайтах:
- https://www.ieee.org
- https://steve.hollasch.net/cgindex/coding/ieeefloat.html
Числа в памяти компьютера. 9 класс. Семакин
Числа в памяти компьютера
Цели: иметь представление о способах представления числовых данных в памяти компьютера; иметь представление о способах оперирования числовой информацией в памяти компьютера.
Ход урока
- Организационный момент
- Актуализация знаний
Самостоятельная работа по индивидуальным карточкам.
Проверка домашней работы
2. Какие двоичные числа соответствуют следующим десятичным числам:
128; 256; 512; 1024?
Решение:
12810 = 100000002; 25610 = 1000000002; 51210 = 10000000002; 102410 = 100000000002.
3. Чему в десятичной системе равны следующие двоичные числа:
1000001; 10000001; 100000001; 1000000001?
Решение:
10000012 = 1 . 26 + 0 . 25 + 0 . 24 + 0 . 23 + 0 . 22 + 0 . 21 + 1 . 20 = 64 + 1 = 6510;
100000012 = 1 . 27 + 1 . 20 = 128 + 1 = 12910;
1000000012 = 1 . 28 + 1 . 20 = 256 + 1 = 25710;
10000000012 = 1 . 29 + 1 . 20 = 512 + 1 = 51310.
4. Переведите в десятичную систему следующие двоичные числа:
101; 11101; 101010; 100011; 10110111011.
Решение:
1012 = 1 . 22 + 0 . 21 + 1 . 20 = 4 + 1 = 510;
111012 = 1 . 24 + 1 . 23 + 1 . 22 + 0 . 21 + 1 . 20 = 16 + 8 + 4 + 1 = 2910;
1010102 = 1 . 25 + 0 . 24 + 1. 23 + 0 . 22 + 1 . 21 + 0 . 20 = 32 + 0 + 8 + 0 + 2 + 0 = 4210;
1000112 = 1 . 25 + 0 . 24 + 0 .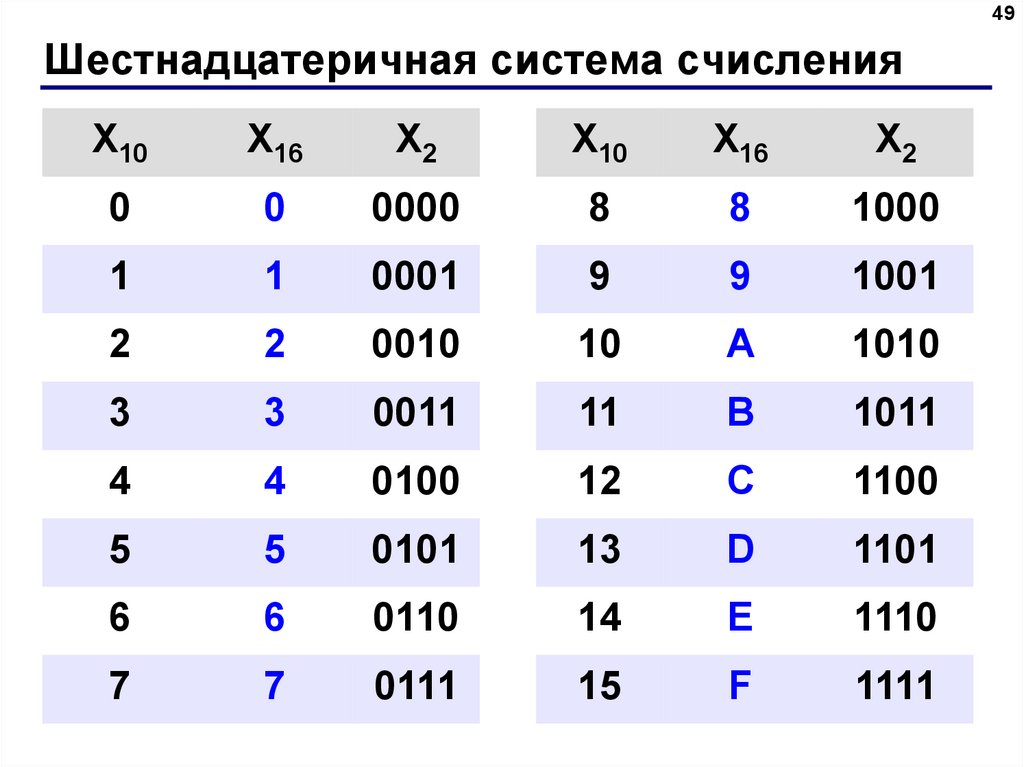 23 + 0 . 22 + 1 . 21 + 1 . 20 = 32 + 2 + 1 = 3510;
23 + 0 . 22 + 1 . 21 + 1 . 20 = 32 + 2 + 1 = 3510;
101101110112 = 1 . 210 + 0 . 29 + 1 . 28 + 1 . 27 + 0 . 26 + 1 . 25 + 1 . 24 + 1 . 23 + 0 . 22 + 1 . 21 + 1 . 20 = 1024 + 256 + 128 + 32 + 16 + 8 + 2 + 1 = 146710.
5. Переведите в двоичную систему счисления следующие десятичные числа:
2; 7; 17; 68; 315; 765; 2047.
Решение:
210 = 102;
710 = 1112;
1710 = 100012;
6810 = 10001002;
31510 = 1001110112;
76510 = 11111111012;
204710 = 111111111112.
6. Выполните сложение в двоичной системе счисления:
11 + 1; 111 + 1; 1111 + 1; 11111 + 1.
Решение:
11 + 1 = 100;
111 + 1 = 1000;
1111 + 1 = 10000;
11111 + 1 = 100000.
7. Выполните умножение в двоичной системе счисления:
111 • 10; 111 • 11; 1101 • 101; 1101 • 1000.
Решение:
111 • 10 = 1110;
111 • 11 = 10101;
1101 • 101 = 1000001;
1101 • 1000 = 11010002.
3. Теоретический материал уроки
Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры, были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном счете сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр — 0 и 1. Поэтому современные компьютерные технологии называют цифровыми технологиями.
В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.
Представление целых чисел
Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальная ячейка, в которой может храниться целое число, имеет размер 8 битов – 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете. Результат перевода: 2510 = 110012.
Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так: 00011001.
Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями.
Самый старший разряд — первый слева, хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код:
Самому большому положительному целому числу соответствует следующий код:
01111111.
Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 27 = 128. Значит:
011111112 = 128 – 1 = 127.
Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127.
Теперь рассмотрим представление целых отрицательных чисел. Как, например, в 8-разрядной ячейке памяти будет представлено число -25? Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. К сожалению, в компьютере все несколько сложнее.
Для представления отрицательных целых чисел используется дополнительный код.
Получить дополнительный код можно по следующему алгоритму:
1) записать внутреннее представление положительного числа X;
2) записать обратный код этого числа заменой во всех разрядах 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.
Определим по этим правилам внутреннее представление числа –2510 в 8-разрядной ячейке:
- 00011001
- 11100110
- +1
11100111 – это и есть представление числа –25.
В результате выполнения такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения.
Проверим полученный результат. Очевидно, что при сложении чисел +25 и – 25 должен получиться ноль.
Для представления отрицательных целых чисел используется дополнительный код.
00011001
+ 11100111
1 00000000
Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается ноль!
Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом.
Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 28.
Размер ячейки и диапазон значений чисел
Наибольшее по модулю отрицательное значение в 8-разрадной ячейке равно – 27 = –128. Его внутреннее представление: 10000000. Таким образом, диапазон представления целых чисел в восьмиразрядной ячейке следующий: –128£Х£127, или –27<Х<27–1.
Восьмиразрядное представление целых чисел обеспечивает слишком узкий диапазон значений. Если требуется больший диапазон, нужно использовать ячейки большего размера. Для 16-разрядной ячейки диапазон значений будет следующим: –
215 £ X < 215 – 1, или –32 768 £ X £ 32 767.
Теперь становится очевидной обобщенная формула для диапазона целых чисел в зависимости от разрядности N ячейки: –2N–1 £ X £ 2N–1 – 1.
Диапазон для 32-разрядной ячейки получается достаточно большим:
–231 £ Х £ 231 – 1, или –2 147 483 648 £ X £ 2 147 483 647.
Особенности работы компьютера с целыми числами
Выполняя на компьютере вычисления с целыми числами, нужно помнить об ограниченности диапазона допустимых значений. Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.
Представление вещественных чисел
Целые и дробные числа в совокупности называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с вещественными числами.
Всякое вещественное число (X) можно записать в виде произведения мантиссы т и основания системы счисления р в некоторой целой степени п, которую называют порядком: X = m . pn.
pn.
Например, число 25,324 можно записать в таком виде: 0,25324 • 102. Здесь т = 0,25324 — мантисса, п = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.
Чаще всего для хранения вещественных чисел в памяти компьютера используется либо 32-разрядная, либо 64-разрядная ячейка. Первый вариант называется представлением с обычной точностью, второй — представлением с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел. Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.
Особенности работы компьютера с вещественными числами
- Диапазон вещественных чисел ограничен. Но он значительно шире, чем для рассмотренного ранее способа представления целых чисел.
 Например, при использовании 32-разрядной ячейки этот диапазон следующий:
Например, при использовании 32-разрядной ячейки этот диапазон следующий:
-3,4 • 1038 £ X £ 3,4 • 1038.
- Выход за диапазон (переполнение) – аварийная ситуация для процессора, который прерывает свою работу.
- Результаты машинных вычислений с вещественными числами содержат погрешность. При использовании удвоенной точности эта погрешность уменьшается.
4. Закрепление изученного материала
В памяти компьютера целые числа представляются в двоичной системе счисления и могут занимать ячейку размером 8, 16, 32 и т. д. битов.
Диапазон значений целых чисел ограничен. Чем больше размер ячейки, тем шире диапазон.
При выходе результатов вычислений с целыми числами за допустимый диапазон работа процессора не прерывается. При этом результаты могут оказаться неверными.
Вещественные числа представляются в виде совокупности мантиссы и порядка в двоичной системе счисления. Обычный размер ячейки — 32 или 64 бита.
Результаты вычислений с вещественными числами приближенные. Переполнение приводит к прерыванию работы процессора.
5. Выполнение практического задания
6. Подведение итогов урока
Домашнее задание: § 17 упражнение 2 – 4 на стр. 109.
Просмотр содержимого документа
«Числа в памяти компьютера»
Урок 24.
Числа в памяти компьютера
Цели: иметь представление о способах представления числовых данных в памяти компьютера; иметь представление о способах оперирования числовой информацией в памяти компьютера.
Ход урока
Организационный момент
Актуализация знаний
Самостоятельная работа по индивидуальным карточкам.
Проверка домашней работы
2. Какие двоичные числа соответствуют следующим десятичным числам:
128; 256; 512; 1024?
Решение:
12810 = 100000002; 25610 = 1000000002; 51210 = 10000000002; 102410 = 100000000002.
3. Чему в десятичной системе равны следующие двоичные числа:
1000001; 10000001; 100000001; 1000000001?
Решение:
10000012 = 1 . 26 + 0 . 25 + 0 . 24 + 0 . 23 + 0 . 22 + 0 . 21 + 1 . 20 = 64 + 1 = 6510;
100000012 = 1 . 27 + 1 . 20 = 128 + 1 = 12910;
27 + 1 . 20 = 128 + 1 = 12910;
1000000012 = 1 . 28 + 1 . 20 = 256 + 1 = 25710;
10000000012 = 1 . 29 + 1 . 20 = 512 + 1 = 51310.
4. Переведите в десятичную систему следующие двоичные числа:
101; 11101; 101010; 100011; 10110111011.
Решение:
1012 = 1 . 22 + 0 . 21 + 1 . 20 = 4 + 1 = 510;
111012 = 1 . 24 + 1 . 23 + 1 . 22 + 0 . 21 + 1 . 20 = 16 + 8 + 4 + 1 = 2910;
1010102 = 1 . 25 + 0 . 24 + 1. 23 + 0 . 22 + 1 . 21 + 0 . 20 = 32 + 0 + 8 + 0 + 2 + 0 = 4210;
23 + 0 . 22 + 1 . 21 + 0 . 20 = 32 + 0 + 8 + 0 + 2 + 0 = 4210;
1000112 = 1 . 25 + 0 . 24 + 0 . 23 + 0 . 22 + 1 . 21 + 1 . 20 = 32 + 2 + 1 = 3510;
101101110112 = 1 . 210 + 0 . 29 + 1 . 28 + 1 . 27 + 0 . 26 + 1 . 25 + 1 . 24 + 1 . 23 + 0 . 22 + 1 . 21 + 1 . 20 = 1024 + 256 + 128 + 32 + 16 + 8 + 2 + 1 = 146710.
5. Переведите в двоичную систему счисления следующие десятичные числа:
2; 7; 17; 68; 315; 765; 2047.
Решение:
210 = 102;
710 = 1112;
1710 = 100012;
6810 = 10001002;
31510 = 1001110112;
76510 = 11111111012;
204710 = 111111111112.
6. Выполните сложение в двоичной системе счисления:
11 + 1; 111 + 1; 1111 + 1; 11111 + 1.
Решение:
11 + 1 = 100;
111 + 1 = 1000;
1111 + 1 = 10000;
11111 + 1 = 100000.
7. Выполните умножение в двоичной системе счисления:
111 • 10; 111 • 11; 1101 • 101; 1101 • 1000.
Решение:
111 • 10 = 1110;
111 • 11 = 10101;
1101 • 101 = 1000001;
1101 • 1000 = 11010002.
Теоретический материал уроки
Любая информация в памяти компьютера представляется в двоичном виде: последовательностью нулей и единиц. Исторически первым типом данных, с которыми стали работать компьютеры, были числа. Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном счете сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр — 0 и 1. Поэтому современные компьютерные технологии называют цифровыми технологиями.
Теперь это и числа, и тексты, и изображение, и звук. Работа с данными любого типа в конечном счете сводится к обработке двоичных чисел — чисел, записываемых с помощью двух цифр — 0 и 1. Поэтому современные компьютерные технологии называют цифровыми технологиями.
В компьютере различаются два типа числовых величин: целые числа и вещественные числа. Различаются способы их представления в памяти компьютера.
Представление целых чисел
Часть памяти, в которой хранится одно число, будем называть ячейкой. Минимальная ячейка, в которой может храниться целое число, имеет размер 8 битов – 1 байт. Получим представление десятичного числа 25 в такой ячейке. Для этого нужно перевести число в двоичную систему счисления. Как это делается, вы уже знаете. Результат перевода: 2510 = 110012.
Теперь осталось «вписать» его в восьмиразрядную ячейку (записать так называемое внутреннее представление числа). Делается это так: 00011001.
Делается это так: 00011001.
Число записывается «прижатым» к правому краю ячейки (в младших разрядах). Оставшиеся слева разряды (старшие) заполняются нулями.
Самый старший разряд — первый слева, хранит знак числа. Если число положительное, то в этом разряде ноль, если отрицательное — единица. Самому большому положительному целому числу соответствует следующий код:
01111111.
Чему он равен в десятичной системе? Можно расписать это число в развернутой форме и вычислить выражение. Но можно решить задачу быстрее. Если к младшему разряду этого числа прибавить единицу, то получится число 10000000. В десятичной системе оно равно 27 = 128. Значит:
011111112 = 128 – 1 = 127.
Максимальное целое положительное число, помещающееся в 8-разрядную ячейку, равно 127.
Теперь рассмотрим представление целых отрицательных чисел. Как, например, в 8-разрядной ячейке памяти будет представлено число -25? Казалось бы, очевидным ответом является следующий: нужно в представлении числа 25 заменить старший разряд с 0 на 1. К сожалению, в компьютере все несколько сложнее.
К сожалению, в компьютере все несколько сложнее.
Для представления отрицательных целых чисел используется дополнительный код.
Получить дополнительный код можно по следующему алгоритму:
1) записать внутреннее представление положительного числа X;
2) записать обратный код этого числа заменой во всех разрядах 0 на 1 и 1 на 0;
3) к полученному числу прибавить 1.
Определим по этим правилам внутреннее представление числа –2510 в 8-разрядной ячейке:
00011001
11100110
+1
11100111 – это и есть представление числа –25.
В результате выполнения такого алгоритма единица в старшем разряде получается автоматически. Она и является признаком отрицательного значения.
Проверим полученный результат. Очевидно, что при сложении чисел +25 и – 25 должен получиться ноль.
Для представления отрицательных целых чисел используется дополнительный код.
00011001
+ 11100111
1 00000000
Единица в старшем разряде, получаемая при сложении, выходит за границу ячейки и исчезает. В ячейке остается ноль!
Из этого примера теперь можно понять, почему представление отрицательного числа называется дополнительным кодом.
Представление восьмиразрядного отрицательного числа -X дополняет представление соответствующего положительного числа +Х до значения 28.
Размер ячейки и диапазон значений чисел
Наибольшее по модулю отрицательное значение в 8-разрадной ячейке равно – 27 = –128. Его внутреннее представление: 10000000. Таким образом, диапазон представления целых чисел в восьмиразрядной ячейке следующий: –128Х127, или –277–1.
Восьмиразрядное представление целых чисел обеспечивает слишком узкий диапазон значений. Если требуется больший диапазон, нужно использовать ячейки большего размера. Для 16-разрядной ячейки диапазон значений будет следующим: –
Для 16-разрядной ячейки диапазон значений будет следующим: –
215 X 15 – 1, или –32 768 X 32 767.
Теперь становится очевидной обобщенная формула для диапазона целых чисел в зависимости от разрядности N ячейки: –2N–1 X 2N–1 – 1.
Диапазон для 32-разрядной ячейки получается достаточно большим:
–231 Х 231 – 1, или –2 147 483 648 X 2 147 483 647.
Особенности работы компьютера с целыми числами
Выполняя на компьютере вычисления с целыми числами, нужно помнить об ограниченности диапазона допустимых значений. Выход результатов вычислений за границы допустимого диапазона называется переполнением. Переполнение при вычислениях с целыми числами не вызывает прерывания работы процессора. Машина продолжает считать, но результаты могут оказаться неправильными.
Представление вещественных чисел
Целые и дробные числа в совокупности называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с вещественными числами.
Всякое вещественное число (X) можно записать в виде произведения мантиссы т и основания системы счисления р в некоторой целой степени п, которую называют порядком: X = m . pn.
Например, число 25,324 можно записать в таком виде: 0,25324 • 102. Здесь т = 0,25324 — мантисса, п = 2 — порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместиться десятичная запятая в мантиссе.
Чаще всего для хранения вещественных чисел в памяти компьютера используется либо 32-разрядная, либо 64-разрядная ячейка. Первый вариант называется представлением с обычной точностью, второй — представлением с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел. Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.
В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядок. Здесь мы не будем подробно рассматривать правила представления вещественных чисел. Отметим лишь основные следствия, вытекающие из этих правил, которые важно знать пользователю компьютера, занимающемуся математическими вычислениями.
Особенности работы компьютера с вещественными числами
Диапазон вещественных чисел ограничен. Но он значительно шире, чем для рассмотренного ранее способа представления целых чисел. Например, при использовании 32-разрядной ячейки этот диапазон следующий:
-3,4 • 1038 X 3,4 • 1038.
Выход за диапазон (переполнение) – аварийная ситуация для процессора, который прерывает свою работу.
Результаты машинных вычислений с вещественными числами содержат погрешность. При использовании удвоенной точности эта погрешность уменьшается.
Закрепление изученного материала
В памяти компьютера целые числа представляются в двоичной системе счисления и могут занимать ячейку размером 8, 16, 32 и т. д. битов.
д. битов.
Диапазон значений целых чисел ограничен. Чем больше размер ячейки, тем шире диапазон.
При выходе результатов вычислений с целыми числами за допустимый диапазон работа процессора не прерывается. При этом результаты могут оказаться неверными.
Вещественные числа представляются в виде совокупности мантиссы и порядка в двоичной системе счисления. Обычный размер ячейки — 32 или 64 бита.
Результаты вычислений с вещественными числами приближенные. Переполнение приводит к прерыванию работы процессора.
Выполнение практического задания
Подведение итогов урока
Домашнее задание: § 17 упражнение 2 – 4 на стр. 109.
Самостоятельная работа Вариант 1
1100112 + 1100102 =
101112. | Самостоятельная работа Вариант 2
1011012 + 110112 =
101012. 1012 = |
Самостоятельная работа Вариант 3
1101112 + 1110112 =
111012. 1012 = | Самостоятельная работа Вариант 4
10100112 + 1010012 =
110012. 0112 = |
Самостоятельная работа Вариант 5
101112 + 100112 =
110012. 1012 = | Самостоятельная работа Вариант 6
10100112 + 1010012 =
101012. |
Самостоятельная работа Вариант 7
11010112 + 1010012 =
1011012. 1012 = | Самостоятельная работа Вариант 8
1100112 + 100012 =
111012. 0112 = |
двоичных чисел в десятичные ✔️ ConvertBinary.com
Этот преобразователь двоичных чисел в десятичные позволяет быстро и легко преобразовывать двоичные числа в десятичные.
Десятичное число:
Сохранить
Оцените этот конвертер
[Всего: 74 Среднее значение: 4,4]
Как использовать конвертер двоичных чисел в десятичные
Необходимое время: 1 минута.
- Введите двоичное число
Введите двоичное число в первое поле.
- Нажмите кнопку Convert
Нажмите кнопку Convert под полем двоичного числа.
- Просмотрите вывод
Во втором поле появится вывод десятичного числа.
- Копировать или сохранить
Дополнительно , вы можете скопировать вывод в буфер обмена или сохранить его как файл на вашем устройстве.
Функции преобразователя
| 🔟 Длина двоичного ввода: | До 25 цифр |
| ⚡ Скорость преобразования: | Мгновенно! |
| ➡️ Десятичный Вывод: | Показать, скопировать, сохранить |
| 9000 3 🎯 Точность преобразования: | 100% |
Прочитайте (или посмотрите) наш учебник о том, как преобразовать двоичные числа в десятичные, чтобы узнать больше о процессе преобразования двоичных чисел в десятичные.
Попробуйте также конвертер десятичных чисел в двоичные !
Как преобразовать двоичное число в десятичное
Итак, вам нужно знать, как преобразовать двоичное число в десятичное? Все эти единицы и нули могут быть пугающими. Вы можете найти конвертер из двоичного кода в десятичный здесь или научиться конвертировать самостоятельно — компьютер не требуется.
Видео кредит
Если вы думали, что для преобразования двоичного кода в десятичный необходимы сложные формулы, вы можете вздохнуть с облегчением. Для перевода из двоичной системы счисления в десятичную систему счисления вам действительно нужно знать только три вещи . Сначала , помните, что единицы и нули, составляющие двоичный код, можно рассматривать как ответ на вопрос «да» или «нет». Единица за «да» и ноль за «нет». Next , если вы понимаете силу числа 2, это будет несложно. Последний шаг является основным дополнением.
(Супер) Сила Двойки
Мы можем поблагодарить силы Двойки за то, что они сделали это так просто. Если вы не знакомы с ними, наличие таблицы для справки сделает вашу работу еще проще. Вам не понадобится обширная таблица, если только вы не конвертируете очень большие двоичные числа. Например, если двоичное число, которое вы хотите преобразовать, равно три цифры длиной , вам понадобятся только первые три степени числа 2 (2 0 , 2¹ и 2²).
Давайте рассмотрим трехзначное двоичное число 101 .
Чтобы преобразовать 101 из двоичной системы в десятичную, мы должны использовать первые три степени двойки. Самый простой способ визуализировать это — написать свое двоичное число, а над ним указать степень двойки. Просто помните чтобы начать с 2 0 справа и двигаться влево, пока не закончатся двоичные цифры.
У нас есть 1, 0 и 1, а также степень двойки для каждой двоичной цифры. Начнем с самой правой цифры, которая является наименее значащим битом (LSB): посмотрите на 2 0 ; что под ним? Один. Это означает, что мы будем использовать 2 0 в десятичном выводе.
Начнем с самой правой цифры, которая является наименее значащим битом (LSB): посмотрите на 2 0 ; что под ним? Один. Это означает, что мы будем использовать 2 0 в десятичном выводе.
Теперь давайте поработаем со следующей крайней левой цифрой. Что меньше 2¹? Ноль. Это означает, что мы будем , а не использовать 2¹. А под 2²? Другой. Чтобы узнать, что такое 101 в десятичном виде, нам понадобится 2 0 и 2².
Остальное просто — 2 0 и 2² это 1 и 4 соответственно. Теперь просто добавьте 1 + 4. Двоичное число 101 — это десятичное число 5 .
Не забывайте всегда двигаться справа налево или от младшего значащего бита (LSB, самая правая цифра) к старшему значащему биту (MSB, самая левая цифра).
Это невероятно просто, если вы можете представить 1 как «да», а 0 как «нет». Аналогичным образом работают и большие числа. Давайте добавим в смесь несколько лишних нулей и воспользуемся 100001. Это длинно, но метод идентичен. На этот раз нам просто нужно 6 степеней двойки; по одному на каждую цифру двоичного числа.
Это длинно, но метод идентичен. На этот раз нам просто нужно 6 степеней двойки; по одному на каждую цифру двоичного числа.
Какие степени числа 2 соответствуют единице? Только 2 6 и 2 0 . Теперь мы складываем эти степени двойки вместе. 100001 в виде десятичного числа равно 33 .
Просто чтобы показать, насколько просто преобразовать двоичное число в десятичное, давайте посмотрим на еще более длинное двоичное число: 11001100 . Для этого преобразования нам нужно пройти весь путь до 2 7 .
Все, что нам нужно сделать, это сложить степени двойки, которые мы использовали. Помните, мы «используем» их только тогда, когда они соответствуют единице. В этом случае нам нужно сложить 128, 64, 8 и 4, чтобы найти десятичную дробь. Все остальное обозначено нулем, поэтому нам не нужно их включать! 11001100 в двоичном формате — это десятичное число 204 .
Если вы хотите попробовать сами, вы можете использовать двоично-десятичный калькулятор на этой странице, чтобы проверить свою работу. Потренируйтесь несколько раз, и вы с легкостью заговорите на языке компьютеров.
Таблица первой сотни двоичных чисел в десятичном формате
Для вашего удобства в следующей таблице показаны двоичные числа от 0 до 1100100 вместе с их десятичным представлением.
| Двоичный | Десятичный |
|---|---|
| 0 | 0 |
| 1 900 56 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 90 056 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 900 51 7|
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 12 | |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 1001 0 | 18 |
| 10011 | 19 |
| 10100 | 20 |
| 10101 | 21 |
| 10110 | 90 051 22|
| 10111 | 23 |
| 11000 | 24 |
| 11 001 | 25 |
| 11010 | 26 |
| 11011 | 27 |
| 11100 | 28 9005 6 |
| 11101 | 29 |
| 11110 | 30 |
| 11111 | 31 |
| 100000 | 32 9005 6 |
| 100001 | 33 |
| 100010 | 34 |
| 100011 9005 6 | 35 |
| 100100 | 36 |
| 100101 | 37 |
| 100110 | 38 | 100111 | 39 |
| 101000 | 40 |
| 101001 | 41 |
| 101010 | 42 | 101011 | 43 |
| 101100 | 44 |
| 101101 | 45 |
| 101110 | 46 |
| 101111 | 47 |
| 110000 | 48 |
| 11 0001 | 49 |
| 110010 | 50 |
| 110011 | 51 |
| 110100 | 52 |
| 53 | |
| 110110 | 54 |
| 110111 | 55 |
| 111000 | 56 |
| 111001 | 57 |
| 111010 | 58 |
| 11101 1 | 59 |
| 111100 | 60 |
| 111101 | 61 |
| 111110 | 62 |
| 111111 | 63 |
| 1000000 | 64 |
| 1000001 | 65 | 1000010 | 66 |
| 1000011 | 67 |
| 1000100 | 68 |
| 1000101 | 9 0051 69|
| 1000110 | 70 |
| 1000111 | 71 |
| 1001000 | 72 |
| 1001 001 | 73 |
| 1001010 | 74 |
| 1001011 | 75 | 9005 9
| 1001100 | 76 |
| 1001101 | 77 |
| 1001110 | 78 |
| 1001111 | 9 0051 79|
| 1010000 | 80 |
| 1010001 | 81 |
| 1010010 | 82 |
| 83 | |
| 1010100 | 84 |
| 1010101 | 85 9 0056 |
| 1010110 | 86 |
| 1010111 | 87 |
| 1011000 | 88 |
| 101 1001 | 89 |
| 1011010 | 90 |
| 1011011 | 91 |
| 1011100 | 92 | 1011101 | 93 |
| 1011110 | 94 |
| 1011111 | 9005 1 95|
| 1100000 | 96 |
| 1100001 | 97 |
| 1100010 | 98 |
| 1100011 | 99 |
| 1100100 | 100 |
Вопросы и ответы о преобразовании двоичных чисел в десятичные
👉 Как вы используете конвертер двоичных чисел в десятичные?
Конвертер из двоичного кода в десятичный на сайте ConvertBinary. com очень прост в использовании.
com очень прост в использовании.
Просто выполните следующие действия: введите двоичное число в первое поле, затем нажмите кнопку «Конвертировать».
Десятичное представление вашего двоичного числа немедленно появится в поле ниже.
✏️ Как преобразовать двоичное число в десятичное?
Чтобы преобразовать двоичные числа в их десятичные эквиваленты, у вас есть два варианта: вы можете использовать онлайн-конвертер (например, тот, который бесплатно предоставляется ConvertBinary.com), или вы можете сделать это вручную.
Если вы хотите научиться вручную преобразовывать двоичные числа в десятичные, вы можете прочитать это руководство или просмотреть соответствующий учебник.
⚙️ Как работает конвертер двоичных чисел в десятичные?
Он использует функцию сценария, которая анализирует ввод (в нашем случае двоичное число) и возвращает целое число.
Вызов функции указывает, что следует использовать двоичную систему.
Процесс автоматический и настолько быстрый, что кажется мгновенным даже для очень больших чисел.
🔟 Могу ли я конвертировать числа из десятичных в двоичные?
Конечно! Если вы хотите преобразовать любое десятичное число в двоичное, вы можете использовать Конвертер десятичных чисел в двоичные .0004 на ConvertBinary.com.
Как преобразовать двоичную систему в десятичную?
Двоичные числа — это числа, понятные компьютерам. Это комбинация 0 и 1. Поскольку компьютеры и несколько электронных устройств понимают только двоичный язык, они принимают ввод только в двоичном формате и возвращают результат в двоичном формате.
В этой статье мы узнаем, как преобразовать двоичное число в десятичное.
Двоичная формула в десятичную
Чтобы преобразовать двоичное число в десятичное, нам нужно выполнить операцию умножения каждой цифры двоичного числа справа налево со степенями 2, начиная с 0, и сложить каждый результат, чтобы получить десятичное число это.
Это можно лучше объяснить с помощью следующих примеров:
Пример 1: Рассмотрим двоичное число 1111. Нам нужно преобразовать это двоичное число в десятичное число.
Решение:
Как упоминалось в предыдущем абзаце, при преобразовании из двоичного числа в десятичное мы должны рассматривать каждую цифру в двоичном числе справа налево.
Таким образом, мы можем преобразовать двоичное число в десятичное.
Примечание: Мы представляем любое двоичное число в формате (xxxx) 2 и десятичное число в формате (xxxx) 10 .
Пример 2. Преобразование (101010) 2 ->(?) 10
Решение:
Продолжаем увеличивать степень числа 2 до тех пор, пока количество цифр в двоичном коде число увеличивается.
Пример 3: Преобразование (11100) 2 ->(?) 10
Решение:
Результирующее десятичное число = 0+0+4+8+16 = 28
Итак, (11100) 2 ->(28) 10
Есть Это также еще один метод, называемый удвоением, который можно использовать для преобразования двоичных чисел в десятичные.
Метод удвоения
Чтобы объяснить этот метод, мы рассмотрим пример и попытаемся решить его пошагово.
Пример 1: преобразование двоичного числа (10001) 2 до десятичной.
Решение:
Подобно описанному выше подходу, в этом подходе также рассматривается каждая цифра, но слева направо, и выполняются пошаговые вычисления над ней.
Шаг-1 Сначала нам нужно умножить 0 на 2 и добавить 1-ю цифру двоичного числа.
0 x 2 + 1 = 0 + 1 = 1
Шаг 2 Теперь используйте результат предыдущего шага и умножьте на 2 и добавьте вторую цифру двоичного числа.
1 x 2 + 0 = 2 + 0 = 2
Тот же шаг 2 повторяется до тех пор, пока не останется ни одной цифры. Конечным результатом будет результирующее десятичное число.
2 х 2 + 0 = 4 + 0 = 4
4 х 2 + 0 = 8 + 0 = 8
8 х 2 + 1 = 16 + 1 = 17
Таким образом, мы выполнили шаг 2 для всех оставшихся чисел и, наконец, у нас осталось 9.
 1102 =
1102 =
 0112 =
0112 =