Разное

Арктангенс в матлабе: How does the MATLAB calculate the arctan? — MATLAB Answers

Самоучитель Matlab (ч.1)

Если этого не сделать, то
• atan(X) – возвращает арктангенс для каждого элемента X. Для действи
тельных значений X atan(X) находится в области [–?/2, ??????Пример:
>> Y=atan(1)
Y=
0.7854
• atan2 (Y, X) – возвращает массив P той же размерности что X и Y, содер
жащий поэлементно арктангенсы отношения вещественных частей Y и X.
Мнимые части игнорируются. Элементы P находятся в интервале [–?, ???.
Специфический квадрант определен функциями sign(Y) и sign(X). Это

174
Программные средства математических вычислений
отличает полученный результат от результата atan(Y/X), который огра
ничен интервалом [–?/2, ??????Пример:
>> atan2(1,2)
ans = 0.4636
Встроенные элементарные функции
175
• cos(X) – возвращает косинус для каждого элемента X. Пример:
>> X=[1 2 3];
>> cos(X)
ans =
0.5403
>> Y = cot(2)
Y=
-0.4577
-0.

4161
-0.9900
• cot(X) – возвращает котангенс для каждого элемента X. Пример:
• csc(O) – возвращает косеканс для каждого элемента X. Пример:
>> X=[2 4.678 5;0.987 1 3];
>> Y = csc(X)
Y=
1.0998 -1.0006 -1.0428
1.1985
1.1884
7.0862
• sec(X) – возвращает массив той же размерности, что и X, состоящий из
секансов элементов X. Пример:
>> X=[pi/10 pi/3 pi/5];
>> sec(X)
ans = 1.0515 2.0000 1.2361
Рис. 3.2. Графики четырех тригонометрических функций
• sin(X) – возвращает синус для каждого элемента X. Пример:
>> X=[pi/2 pi/4 pi/6 pi];
>> sin(X)
ans = 1.0000 0.7071 0.5000
тронных устройств. Следующая программа строит графики для таких комбина
ций, создающих из синусоиды три наиболее распространенных сигнала – прямо
угольные, пилообразные и треугольные импульсы1 :
% I?ia?aiia iino?iaiey a?aoeeia neaiaeia
x=-10:0.01:10;
subplot(2,2,1),plot(x,0.
8*sin(x)),…
xlabel(\’0.8*sin(x)\’)
subplot(2,2,2),plot(x,0.8*sign(sin(x))),…
xlabel(\’0.8*sgn(sin(x))\’)
subplot(2,2,3),plot(x,atan(tan(x/2))),…
xlabel(\’atan(tan(x/2))\’)
subplot(2,2,4),plot(x,asin(sin(x))),…
xlabel(\’asin(sin(x))\’)
0.0000
• tan(X) – возвращает тангенс для каждого элемента X.

<< Назад   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 Вперед >>

пример функции в матлаб

Графики функций/ Исследовать

Учитель очень удивится увидев твоё верное решение😉

Введите график функции

Исследуем график функции y=f(x), для этого задайте функцию f(x). 2*arctgh(x)*arcctgh(x)

Что исследует?

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

  • Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
  • Умеет определять точки пересечения графика функции с осями координат: Да
  • Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
  • Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
  • Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
  • Горизонтальные асимптоты графика функции: Да
  • Наклонные асимптоты графика функции: Да
  • Четность и нечетность функции: Да
  • Минимум и максимум функции: Да
Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)
Абсолютное значение x
(модуль x или |x|)
arccos(x)
Функция — арккосинус от x
arccosh(x)
Арккосинус гиперболический от x
arcsin(x)
Арксинус от x
arcsinh(x)
Арксинус гиперболический от x
arctg(x)
Функция — арктангенс от x
arctgh(x)
Арктангенс гиперболический от x
exp(x)
Функция — экспонента от x (что и e^x)
log(x) or ln(x)
Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
sin(x)
Функция — Синус от x
cos(x)
Функция — Косинус от x
sinh(x)
Функция — Синус гиперболический от x
cosh(x)
Функция — Косинус гиперболический от x
sqrt(x)
Функция — квадратный корень из x
sqr(x) или x^2
Функция — Квадрат x
ctg(x)
Функция — Котангенс от x
arcctg(x)
Функция — Арккотангенс от x
arcctgh(x)
Функция — Гиперболический арккотангенс от x
tg(x)
Функция — Тангенс от x
tgh(x)
Функция — Тангенс гиперболический от x
cbrt(x)
Функция — кубический корень из x
gamma(x)
Гамма-функция
LambertW(x)
Функция Ламберта
x! или factorial(x)
Факториал от x
DiracDelta(x)
Дельта-функция Дирака
Heaviside(x)
Функция Хевисайда

Интегральные функции:

Si(x)
Интегральный синус от x
Ci(x)
Интегральный косинус от x
Shi(x)
Интегральный гиперболический синус от x
Chi(x)
Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа
вводить в виде 7. 3
— возведение в степень
x + 7
— сложение
x — 6
— вычитание
15/7
— дробь

Другие функции:

asec(x)
Функция — арксеканс от x
acsc(x)
Функция — арккосеканс от x
sec(x)
Функция — секанс от x
csc(x)
Функция — косеканс от x
floor(x)
Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x)
Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x)
Функция — Знак x
erf(x)
Функция ошибок (или интеграл вероятности)
laplace(x)
Функция Лапласа
asech(x)
Функция — гиперболический арксеканс от x
csch(x)
Функция — гиперболический косеканс от x
sech(x)
Функция — гиперболический секанс от x
acsch(x)
Функция — гиперболический арккосеканс от x

Постоянные:

pi
Число «Пи», которое примерно равно ~3. 14159..
e
Число e — основание натурального логарифма, примерно равно ~2,7183..
i
Комплексная единица
oo
Символ бесконечности — знак для бесконечности

×

Где учитесь?

Для правильного составления решения, укажите:

(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое

Функция «атан», поддерживаемая в CVX？ — невыпуклая

Иван

#1

Привет всем,

В моем ограничении есть функция арктангенса. На самом деле я использую встроенную функцию Matlab «atan». Выражение этого ограничения:
x — atan(y) <= 0,
, где x и y — скалярные переменные, а y>=0.

Однако появляется ошибка: Неопределенная функция «atan» для входных аргументов типа «cvx».
Означает ли это, что функция «атан» не поддерживается в CVX？

Спасибо!
Иван

Mark_L_Stone (Марк Л. Стоун)

#2

`atan не является ни выпуклым, ни вогнутым, поэтому не поддерживается CVX.

Иван

#3

Спасибо, Марк. В моем случае y>=0, поэтому -atan(y) выпукла в этой области определения. А ограничение x-atan(y) — выпуклое множество.

Можно ли что-нибудь сделать, чтобы CVX принял это ограничение? (Может быть, что-то вроде встроенной функции CVX «square_pos»?)

Mark_L_Stone (Марк Л.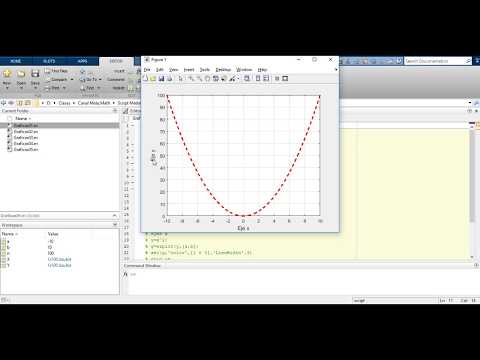 Стоун)

28 января 2021 г., 19:09

#4

См. мой ответ в разделе Как ввести функцию arctan в cvx

Иван

#5

Спасибо! Это полезно. Я решаю попробовать последовательное приближение.

Кстати, будут ли в будущем CVX включать функции для работы с такими функциями, как арктангенс и тангенс? Может быть:

  1. добавить встроенную функцию, например, «atan_pos»?
  2. включает встроенную последовательную аппроксимацию для арктангенса, как это было сделано для log 9.0016 функция?

Mark_L_Stone (Марк Л.

Стоун)

#6

Я сомневаюсь, что что-либо из этого когда-либо будет добавлено в CVX, который не находится в очень активной стадии разработки (я не разработчик).

Иван

#7

Хорошо, понятно. Спасибо за ответ!

бинси

#8

Здравствуйте, я тоже столкнулся с такой же проблемой, но я не знаю, как сделать непрерывную аппроксимацию этой функции атана. Как вы это решаете? С нетерпением жду вашего ответа

Mark_L_Stone (Марк Л. Стоун)

#9

Способ, которым вы «решаете это», заключается в использовании какого-либо инструмента, отличного от CVX. Например, YALMIP, который допускает невыпуклости и поддерживает atan (а также поддерживает atan2 в своей ветке разработки https://groups.google.com/g/yalmip/c/diLhQLh5bN8)

bingxi

18 ноября 2021 г., 15:14

#10

Спасибо! Это полезно. Я попробую.

Функция арктангенса | Академия роботов

УРОК

Стенограмма

Мы собираемся сделать краткий обзор тригонометрической функции Tan и ее обратной функции. Ничто на этом слайде пока не должно вас удивить. Это довольно стандартная школьная математика. Мы можем перестроить его, чтобы изолировать тангенс тета, и мы запишем это в терминах Y, деленного на X, а затем мы можем ввести обратную функцию тангенса, чтобы мы могли записать тета в терминах обратного тангенса Y, деленного на мой X.

Функция обратного загара обозначается по-разному, но чаще всего она записывается как загар в степени минус один, иногда записывается как A загар, а иногда записывается как Arc загар. Это, пожалуй, самые распространенные способы представления функции арктангенса. Теперь давайте рассмотрим несколько более сложных случаев, но начнем мы с самого простого из этих случаев. И у нас есть треугольник, его высота равна единице, его ширина равна двум и угол, отмеченный в треугольнике, равен 0,4636 лучистости.

Если я применю функцию обратного загара к пропорции один к двум, то получу точно такое же значение, 0,4636. Это верно для случая, когда угол отрицательный. В этом случае ширина равна двум, а высота равна минус единице.

Я могу вычислить арктангенс деления минус один на два и получить результат минус 0,4636, как и ожидалось. Теперь давайте рассмотрим случай, когда угол больше Пи на два. В этом случае высота равна единице, а ширина равна минус двум. В этом случае тета равна 2,6779 радиации. Если я вычислю арктангенс единицы на минус два, то я получу результат минус 0,4636. Мы видим, что есть несоответствие между реальным углом этой линии и углом, который дает нам функция арктангенса. И аналогично для этого случая ширина минус два, высота минус один, и если я вычислю арктангенс этого, я получу результат 0,4636. Проблема в этом последнем случае заключается в том, что деление отрицательного числа на два дает результат, аналогичный делению числа на два. Это положительное число, и это то же самое, что и в примере, который мы сделали в начале здесь.

Основная проблема заключается в том, что функция обратного тангенса имеет диапазон, который охватывает только от минус Пи для двух до плюс Пи для двух. Чтобы обойти эту проблему, мы вводим новую функцию, которую обычно называют «Tan Two», вы найдете функцию с таким названием в математической библиотеке многих языков программирования и обязательно найдете ее в MATLAB. Он принимает во внимание знак А и знак В и на основе этой информации может определить, в каком квадранте круга лежит угол. Таким образом, диапазон этой функции составляет от минус Пи до плюс Пи включительно. А вот простой пример с использованием MATLAB, вычисляющий арктангенс единицы, деленный на минус два, он дает нам ответ 2,6779.сияние и это угол во втором квадранте круга.

Очень важной функцией при выполнении инверсной кинематики является функция арктангенса или арктангенса. Мы пересматриваем, как эта функция работает для углов во всех квадрантах окружности, и вводим полезный вариант, известный как atan2.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *