Арифметические действия над числами: Арифметические действия над числами

Арифметические действия над числами

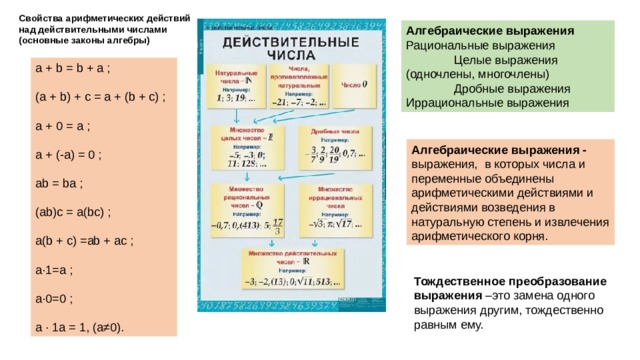
Советы → Полезные сведения → Арифметика → Арифметические действия

Нахождение по нескольким данным числам одного нового числа называется арифметическим действием. В арифметике рассматривается шесть действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

 

1. Сложение. Это действие состоит в том, что по нескольким числам, называемым слагаемыми, находится число, называемое их суммой.

Пример: 4+3=7, где 4 и 3 – слагаемые, а 7 – их сумма.

 

2. Вычитание – действие, посредством которого по данной сумме (уменьшаемое) и данному слагаемому (вычитаемое) находят искомое слагаемое (разность).
Это действие обратно сложению.

Пример: 7 – 3 = 4, где 7 – уменьшаемое, 3 – вычитаемое, а 4 – разность.

 

3.

Умножение. Умножить некоторое число (множимое) на целое число (множитель) – значит повторить множимое слагаемым столько раз, сколько единиц содержится в множителе. Результат умножения называется произведением.

Пример: 2 ∙ 3 = 6, где 2 – множимое, 3 – множитель, а 6 – произведение. (2 ∙ 3 = 2 + 2+ 2 = 6)

Если множитель и множимое меняются ролями, то произведение остается тем же. Поэтому множитель и множимое также называются сомножителями.

Пример: 2 ∙ 3 = 3 ∙ 2, то есть (2 + 2 + 2 = 3 + 3)

 

Полагают, что если множителем является 1, то a ∙ 1 = a.

Например: 2 ∙ 1 = 2, 44 ∙ 1 = 44, 13 ∙ 1 = 13.

 

4. Деление. Посредством деления по данному произведению (делимое) и данному сомножителю (делитель) находят искомый сомножитель (частное).
Это действие обратно умножению.

Пример: 8 : 2 = 4, где 8 – делимое, 2 – делитель, а 4 – частное.

Проверка деления

: произведение делителя 2 и частного 4 дает делимое 8. 2 ∙ 4 = 8

 

Деление с остатком

Если при делении целого числа на целое число в частном получается целое число, то такое деление целых чисел называется точным, или, что первое число нацело делится (или просто – делится) на второе.

Например: 35 делится (нацело) на 5, частное есть целое число 7.

Второе число при этом называется делителем первого, первое же – кратным второго.

Во многих случаях можно, не выполняя деления, узнать, делится ли нацело одно целое число на другое (см. признаки делимости).

Точное деление возможно далеко не всегда. В таком случае выполняют так называемое деление с остатком. В этом случае находят такое наибольшее число, которое при умножении на делитель даст произведение, не превосходящее делимого. Это число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком от деления.

Делимое равно делителю, умноженное на неполное частное, плюс остаток. Остаток всегда меньше делителя.

Пример: Неполное частное от деления числа 27 на 4 равно 6, а остаток равен 3. Очевидно, 27 = 4∙6 + 3 и 3˂4.

 

5. Возведение в степень. Возвести некоторое число в целую степень (во вторую, в третью и т.д.) – значит взять это число сомножителем два, три раза и т.д. Иначе говоря, возведение в степень выполняется повторным умножением.
Число, которое берётся сомножителем, называется основанием степени; число, показывающее, сколько раз повторяется основание, называется показателем степени; результат возведения числа в степень называется степенью этого числа.

Пример: 2∙2∙2 = 2³ = 8; где 2 – основание степени, 3 – показатель степени, 8 – степень.

 

Вторую степень числа иначе называют квадратом, третью степень – кубом. Первой степенью числа называют само это число.

 

6. Извлечение корня есть действие, посредством которого по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят искомое основание (корень).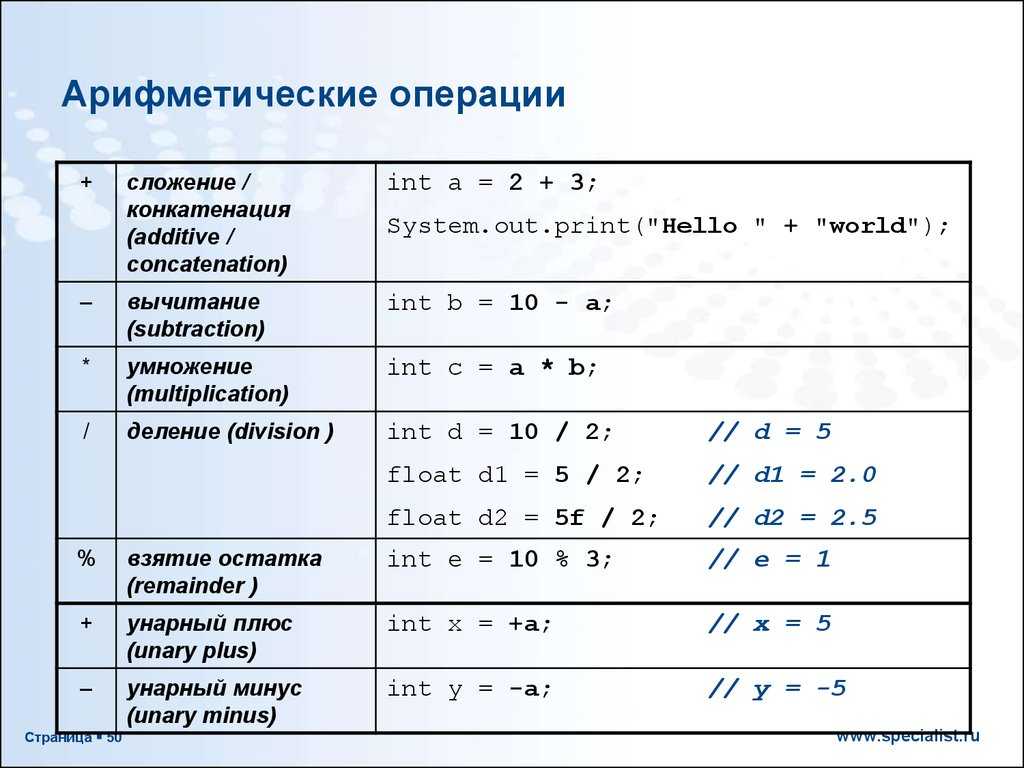
Это действие обратно возведению в степень.

Пример: ³√64 = 4; где 64 – подкоренное число, 3 – показатель корня, 4 – корень.

Проверка извлечения корня: 4³=64. Возведение числа 4 в 3-ю степень даёт 64.

 

Корень второй степени иначе называют квадратным; корень третьей степени – кубическим.
При знаке квадратного корня показатель корня принято опускать: √36 = 6 означает ²√36 = 6.

---

Использованная лит-ра:
Справочник по элементарной математике — Выгодский М.Я., «Наука», 1974 г.
Справочник по математике. Пособие для учащихся 9—11 кл. — Шахно К. У., «Учпедгиз», 1961 г.

 

→ Читайте по теме: Признаки делимости

→ Арифметика

→ В раздел Советы

При полной или частичной публикации статьи в Интернете обязательно указание активной гиперссылки на источник http://programmistan.narod.ru

Арифметические действия с целыми числами

Понятия арифметических действий

По двум или нескольким целым числам можно составить новое целое число. Способов составлять новое целое число очень много. Так, по двум целым числам 6 и 2 можно составить новое число различным образом.

1. Можно по двум целым числам составить такое число, которое будет заключать в себе столько единиц, сколько их содержится в обоих числах.

   Для 6 и 2 это будет число 8. В этом случае число 8 равно обоим числам, вместе взятым.

2. Можно по двум целым числам составить такое число, которое будет показывать, насколько единиц одно число больше другого. Для 6 и 2 это будет число 4.

3. Можно по двум целым числам составить число, которое будет показывать, сколько единиц получим, если одно число повторим количество раз, равное второму числу. Для 6 и 2 это будет число 12.

4. Можно попробовать по двум целым числам составить такое число, которое покажет, сколько раз второе число содержится в первом. В случае 6 и 2 число два называют парой, следовательно, новое число будет показывать, сколько пар содержится в шести, или сколько пар содержит число 6. Такое число есть 3. Оно показывает, во сколько раз 6 больше 2.

Таким образом, по двум числам 6 и 2 разными способами мы составили 4 новых числа: 8, 4, 12 и 3.

Арифметическое действие. Способ составлять новое число по двум или нескольким числам называется арифметическим действием.

Данные и искомые. Те числа, по которым составляют новое число, всегда даются и называются данными числами, а новое число, которое составляют по данным, называют искомым, ибо цель арифметического действия состоит в том, чтобы отыскать его. Искомое число называют также результатом действия.

Основные арифметические действия

Вообще арифметических действий много, но основных только четыре: сложение, вычитание, умножение и деление. Они названы основными, ибо все остальные действия приводятся к ним.

1. По двум числам 6 и 2 найти число 8, равное двум числам, взятым вместе, значит сложить два числа. Само действие называется сложением, и связь между тремя числами выражают словесно: 6 да 2 составляют 8.

2. По двум числам 6 и 2 найти число 4, показывающее, чем число 6 больше 2, значит 2 отнять от 6. Отнять 2 от 6 значит вычесть 2 из 6. Само действие называется вычитанием. Связь между тремя числами выражается словесно: 6 без 2 составляет 4.

3. По двум числам 6 и 2 составить 12 или иначе повторить 6 два раза, значит умножить 6 на 2. Действие называется умножением. Связь между числами 6, 2 и 12 выражается словесно: 6, повторенное 2 раза, составляет 12, или 6, умноженное на 2, составляет 12.

4. По двум числам 6 и 2 составить число 3, указывающее, сколько раз 6 содержит число 2, значит 6 разделить на 2. Действие называется делением. Связь между числами 6, 2 и 3 выражают словесно: 6 содержит число два 3 раза, или 6, деленное на 2, составляет 3.

Знак равенства. Слово «составляет» заменяют знаком =, который называется

знаком равенства, ибо это слово может быть заменено словом равно.

Равенство. Совокупность равных чисел по обе стороны знака = называется равенством.

Четыре арифметических действия над двумя числами могут быть выражены словами:

Во всех этих действиях 6 и 2 являются данными числами, а 8, 4, 12 и 3 — искомыми числами.

Знаки основных действий. Слова «да», «без», «умноженное», «деленное» заменяют особыми знаками:

• слово «да» — знаком + (плюс)

• слово «без» — знаком — (минус)

• слово «умноженное» («повторенное») — знаком × или · (точкой)

• слово «деленное» — знаком : (÷)

Заменяя слова знаками, мы можем зависимость между числами выразить письменно:

• 6 + 2 = 8 (сложение)

• 6 — 2 = 4 (вычитание)

• 6 × 2 = 12 (умножение)

• 6 ÷ 2 = 3 (деление)

Знаки + и — были введены Родольфи (Rodolphi) в 1522 году, знак × ввел англичанин Отред (Oughtred) в 1631 г. , знак = ввел английский геометр Рекор (Recort) в 1552 г.

 

Арифметические операции — Примеры | Основные арифметические операции

Арифметические операции являются основой математики. В основном он состоит из таких операций, как сложение, вычитание, умножение и деление. Они также известны как математические операции. В нашей повседневной жизни мы используем арифметические операции, чтобы узнать общие доходы и расходы бизнеса, составить месячный или годовой бюджет, измерить длину и т. д. Мы используем их почти в любое время дня, например, при расчете общего числа вопросов, заданных в домашнем задании, при подсчете времени, денег, количества съеденных конфет, количества полученных баллов по всем предметам и т. д.

1.	Определение арифметических операций
2.	Четыре основных арифметических операции
3.	Арифметические операции с целыми числами
4.	Арифметические операции с рациональными числами
5.	Часто задаваемые вопросы по арифметическим операциям

Определение арифметических операций

Арифметические операции представляют собой набор из четырех основных операций, которые необходимо выполнить для сложения, вычитания, умножения или деления двух или более величин. Они включают изучение чисел, включая порядок операций, которые полезны во всех других частях математики, таких как алгебра, обработка данных и геометрия. Мы не можем решить задачу без использования правил арифметических действий. Арифметические операции включают четыре основных правила: сложение, вычитание, умножение и деление. Для каждой из четырех арифметических операций, показанных на изображении ниже, используется определенный символ.

Четыре основных арифметических операции

Здесь мы обсуждаем четыре основных правила арифметических операций для всех действительных чисел.

• Дополнение (сумма; «+»)
• Вычитание (разница; «-»)
• Умножение (произведение; ‘×’ )
• Отдел (÷)

Давайте подробно обсудим приведенные выше арифметические операции.

Сложение

Сложение — это базовый математический навык нахождения или вычисления суммы двух или более чисел, или мы можем сказать простыми словами сложение вещей. Обозначается символом «+». Когда мы складываем два или более чисел, получается один термин. Порядок цифр в сложении не имеет значения.

Например: 367 + 985 = 1352

Вычитание

Арифметическая операция вычитания показывает разницу между двумя числами. Обозначается символом «-». Вычитание в основном используется, чтобы узнать, что останется, когда вещи уберут, или, другими словами, вычитание одного числа из другого числа.

Например: 20 — 9 = 11

Умножение

Повторное сложение называется умножением. Он представлен символом «×». Умножение как арифметическая операция помогает нам узнать сумму, когда число повторяется несколько раз. Например, 2 умножить на 3 равно 6. Математически мы можем записать это как 2 × 3 = 6. Множитель и множитель — это термины, используемые в процессе умножения. Произведение — это термин, который мы используем для обозначения результата умножения множимого и множителя.

Например: 20 × 31 = 620

В приведенном выше примере «20» — это множитель, «31» — множимое, а результат «620» известен как произведение.

Деление

Деление — это акт деления чего-либо на равные части или группы. Это одна из четырех основных арифметических операций, которая дает справедливый результат равного распределения. Деление является обратным умножению. Например, 2 группы по 3 карандаша в каждой дают при умножении 6 карандашей (2×3), а в случае деления 6 карандашей, разделенных на 2 равные группы, дают по 3 карандаша в каждой группе. Обозначается символом «÷». Итак, здесь мы можем записать это как 6 ÷ 2 = 3,

Арифметические операции с целыми числами

С целыми числами мы можем легко выполнять четыре основных арифметических действия. Целые числа — это набор чисел, который начинается с 0 и продолжается до бесконечности. Такие числа не имеют дробных или десятичных частей. Сложение двух и более целых чисел всегда приводит к увеличению конечной суммы. Например, если мы сложим три числа 4, 5 и 6, то получим 4 + 5 + 6 = 9 + 6 = 15. Итак, здесь 15 больше, чем все три слагаемых. Добавление любого числа к 0 всегда приводит к одному и тому же числу, и если мы добавляем 1 к любому целому числу, мы получаем его последовательный номер или преемник.

В случае целых чисел мы всегда вычитаем меньшую величину из большей, чтобы получить разность, которая меньше уменьшаемого. Вычитание 0 из любого числа всегда приводит к одному и тому же числу, а вычитание 1 из числа дает его предшественник. Умножение двух и более целых чисел можно выполнить с помощью таблицы умножения. Произведение всегда больше обоих чисел, за исключением случая умножения на 1 и 0. Число, умноженное на 0, всегда дает 0, а умножение на 1 дает нам то же число, что и произведение.

Деление двух целых чисел может дать или не дать целые числа. Если частное является целым числом, это означает, что делимое кратно делителю. Если это не так, то в качестве частного будет десятичное число.

Арифметические операции с рациональными числами

Арифметические операции с рациональными числами такие же, как и с целыми числами. Единственное отличие состоит в том, что рациональные числа представлены в виде p/q, где p и q — целые числа, а q не равно 0. При сложении или вычитании двух рациональных чисел мы должны взять НОК знаменателей. Чтобы узнать об арифметических операциях над рациональными числами, нажмите здесь.

Связанные статьи по арифметическим операциям

Ознакомьтесь со следующими страницами, посвященными арифметическим операциям.

• Арифметика
• Порядок действий
• правило PEMDAS
• Сложение и вычитание дробей

Часто задаваемые вопросы по арифметическим операциям

Каковы основные правила арифметических операций?

В математике сложение (+), вычитание (-), умножение (×) и деление — четыре основных арифметических действия.

Что представляют четыре арифметические операции?

Четыре арифметических действия — сложение, вычитание, умножение и деление представляют собой:

• Сложения представляют собой сумму двух значений.
• Вычитание представляет разницу между двумя числами
• Умножение показывает произведение двух чисел.
• Деление — это процесс деления одного числа на другое и получения значений частного и остатка.

Каков порядок арифметических операций?

Порядок, в котором должны выполняться арифметические операции в выражении, известен как PEMDAS или BODMAS. В этом правиле четко указано, что порядок выполнения операций следующий: круглые скобки, возведения в степень, умножение или деление, сложение или вычитание.

Является ли вычитание арифметической операцией?

Да, вычитание — это арифметическая операция, показывающая процесс удаления объектов из коллекции. Вычитание предполагает вычитание одного числа из другого числа. Символ вычитания выглядит так «-«. Имя символа представляет собой знак минус. Например, у Рэйчел 6 яблок, и из них 2 яблока она отдала своему брату Джону. Значит, чтобы найти оставшиеся яблоки с Рэйчел, отнимем от 6 2. Разница и будет ответом, то есть 6 — 2 = 4.

Является ли сложение арифметической операцией?

Да, сложение — одно из правил арифметической операции. Сложение означает подсчет суммы или нахождение суммы двух или более чисел. Символ добавления выглядит так: «+». Например, 25 + 10 + 4 = 39.

Каковы символы основных арифметических операций?

Символы основных арифметических операций:

• Символ сложения ⇒ «+»
• Символ вычитания ⇒ ‘-’
• Символ умножения ⇒ «×»
• Символ деления ⇒ «÷»

Основные арифметические операции: четыре основных оператора

Изучение арифметических операций

Как сказала нам Джули Эндрюс в Звуки музыки , мы должны «начать с самого начала», потому что это «очень хорошее место для начала». В математике мы не начинаем с До-Ре-Ми, а строим на основах, известных как арифметические операции!

Овладение арифметическими операциями означает создание прочной основы для успешного изучения математики на всю жизнь, поэтому мы настоятельно рекомендуем не торопиться, чтобы действительно посвятить себя этим навыкам!

Если вам нужен более широкий обзор арифметического раздела математики, давайте сделаем шаг назад, чтобы сначала пройтись по арифметике в целом.

Готовы приступить к арифметическим операциям?

Прежде всего, что такое «арифметические операции»?

Арифметические операции являются строительными блоками для всех математических процессов и методов. (Да, они очень важны!) Эти типы операций являются частью «арифметической» ветви математики.

Арифметические операции сводят математику к основам, которыми мы пользуемся каждый день, осознаем мы это или нет. Этими основами являются сложение, вычитание, умножение и деление.

Не так уж и страшно, правда?

Базовая арифметика

Иногда можно услышать, что арифметические операции называют «основной арифметикой», что означает наиболее фундаментальные математические операции.

Основные арифметические операции

Основными арифметическими операциями обычно считаются сложение, вычитание, умножение и деление.

Через мгновение мы углубимся в каждое из них!

Некоторые школы также включают сравнение чисел и оценку степеней (или показателей степени) как часть арифметических операций. Если вы еще не там, не волнуйтесь! Каждый движется в своем собственном темпе, и мы всегда можем помочь вам, когда вы туда доберетесь.

Четыре основных математических действия

Независимо от того, балансируете ли вы свою чековую книжку или заказываете пиццу на вечеринку, скорее всего, вы ежедневно используете некоторые из четырех основных арифметических действий.

Но иногда, когда что-то настолько второстепенно, трудно объяснить это хорошо. Вот таблица терминов и примеров, которые вы можете использовать при описании четырех основных операций:

Операция	Глагол	Пример	Словарь результатов
Дополнение	Добавить	$$1 + 1 = 2$$	Результатом сложения является «сумма»
Вычитание	Вычесть	$3 — 2 = 1$$	Результат вычитания – «разность»
Умножение	Умножить	$$\displaylines{4 × 2 = 8 \\ 2 * 3 = 6 \\ 5 ⋅ 2 = 10}$$	Результат умножения — «произведение»
Отдел	Разделить	$$\displaylines{12 ÷ 3 = 4 \\ 10/2=5}$$	Результат деления — «частное»

Теперь, когда мы знаем больше о каждой операции, мы можем углубиться еще глубже и взглянуть на оператора каждой операции.

Что такое арифметические операторы?

Арифметические операторы — это символы, которые мы видим в математических задачах и которые обозначают действие, которое мы должны предпринять. Они как маленькие математические инструкции GPS, говорящие нам, что должно произойти, чтобы мы достигли конечного пункта назначения.

Другими словами, оператор говорит нам, какую операцию выполнять! Например, оператор $$-$$ говорит нам, что мы должны вычесть.

Давайте рассмотрим каждый оператор более подробно:

Арифметические операторы: руководство

Изучение арифметических операторов (и связанных с ними операций) похоже на обучение вождению автомобиля — вам нужно знать, какая педаль за что отвечает, прежде чем вы сможете нажать на педаль. газ и начать рулить.

Вот удобная таблица, объясняющая, что означает каждый оператор и как он может выглядеть на странице:

Оператор	Операция
$$+$$	Дополнение
$$-$$	Вычитание
$$×, *, ⋅$$	Умножение
$$÷ , /$$	Подразделение

Иногда вы можете увидеть более одного оператора в одной и той же задаче. Если эти операторы разные — например, «+» и «÷» в одной и той же задаче — вам нужно следовать структуре PEMDAS.

Напоминаем, что PEMDAS означает:

1. Скобки
2. Экспоненты
3. Умножение (слева направо)
4. Отдел (слева направо)
5. Дополнение (слева направо)
6. Вычитание (слева направо)

Примеры арифметических операций

Понимание контекста, лежащего в основе арифметических операций, поможет укрепить обучение, но то, что действительно укрепит эти навыки, — это попробовать их! Работа над проблемами — и, честно говоря, несколько неправильных — гарантирует, что учащийся будет полностью вовлечен.

Итак, когда будете готовы, попробуйте решить следующие примеры задач:

1. $$3 + 4$$
2. $$6 ÷ 2$$
3. $$2 \times1$$
4. $$8 – 5 + 2$$
5. $$3 \times4 – 1$$
6. $$\frac{4}{2} + \frac{6}{3}$$
7. $$5 – 1 + 3$$
8. $$7 \times 3 \times 2$$
9. $$12 ÷ 3 + 5$$
10. $$2 \раз 0$$

Проблемы? Это нормально! Нравится нам это или нет, чувство неуверенности или застревания на самом деле является частью процесса обучения. Хорошая новость заключается в том, что вам не нужно оставаться на месте! Отсканируйте сложную задачу с помощью приложения Photomath, и мы проведем вас через каждый шаг.

P.S.: Вы также можете проверить свои ответы на примеры задач, отсканировав их с помощью приложения!

Вот как это выглядит:

00:00 / 00:00

И еще: какие два основных арифметических действия коммутативны?

Сложение и умножение известны как «коммутативные» (другими словами, они следуют свойству коммутативности). Это означает, что вы можете изменить порядок чисел и получить тот же результат.

Вы можете заметить это при работе с примерами задач, но свойство перестановочности означает, что $$2 + 3$$ равняется той же сумме, что и $$3 + 2$$. Точно так же $$4 \times 5$$ дает нам тот же продукт, что и $$5 \times4$$.

Однако , а не означает, что мы можем переключаться между сложением и умножением.