Урок 5. Аргумент комплексного числа. Тригонометрическая форма комплексных чисел.
Напомним, что углом между лучами ОА и ОВ с общим началом называется угол, на который надо повернуть луч ОА вокруг т. О против часовой стрелки, чтобы получить луч ОВ. Если вращение происходит по часовой стрелке, то углу приписывается знак «минус». При этом угол определяется не однозначно, а с точностью до слагаемого 2kπ , где k∈z – любое. Определение.
Пусть т.О – начало координат, и пусть вектор ОА (а, в) соответствует комплексному числу z=a+вi ≠0 . Аргументом комплексного числа z (обозначение arg z) называется угол между положительным
направлением оси ОХ и лучом ОА, вычисленный при вращении ОХ по кратчайшему
направлению. Иными словами, arg
z – это тот угол φ=(ОХ,
ОА), для которого -π<φ≤π . Если z=0, то arg z не определяется. Прокомментируем данное определение. Если z а) для точек верхней полуплоскости числа arg z положительны: argZ∈0,π б) для точек нижней полуплоскости числа arg z отрицательны: argZ∈—π,0 в) для точек, лежащих на положительной полуплоскости ОХ: arg z=0 г) для точек, лежащих на отрицательной полуплоскости ОХ: arg z=π Зная а = Rez и в = Jmв, мы можем вычислить arg z, пользуясь тем, что как видно из рисунка: tgargZ=ва Однако, необходимо иметь в виду, что отсюда еще не следует, что argZ=argtgвa . Это не всегда так по той причине, что числа arg z и argtg вa могут принадлежать разным промежуткам, ибо, по определению-π<argZ≤π —π2<argва<π2 Поэтому
следует рассмотреть различные случаи расположения точки z на плоскости. 1)
a > 0, в – любое.
Тогда т. z
= a+вi лежит в правой полуплоскости. При этом
обязательно
А т.к. и —π2<argва<π2 , а числа argz и argва имеют одинаковый тангенс, равный ва , то argz= argва при а>0, в – любом 2) а=0, в>0. Тогда т. z = a+вi лежит на положительной мнимой полуоси и, следовательно, по определению argZ=π2 при а=0, в>0 3) а=0, в<0. Тогда т. z = a+вi лежит на отрицательной мнимой полуоси, и argZ=—π2 при а=0, в<0 4) а<0, в≥0. Тогда т. z = a+вi лежит во втором квадранте: π2<argz≤π следовательно, —π2< argZ-π≤0 а поскольку tgargz-π=tgargz=ва , то argz=π+argtgва при а<0, в≥0 5)
а<0,
в<0. —π< argz<—π2 следовательно, 0<π+argz<π2 , а посколькуtgπ+argz=tgargz=ва при а<0, в<0 Задача 6.1. Вычислить аргументы чисел: а) 1+i, б) 1-i, в) -1+i, г) -1-i, д) 2i, е) -2i, ж) 2, з) -2. Определение. Запись комплексного числа z в виде z = r (cos φ+isinφ ), где r=z, φ= argz называется тригонометрической формой записи комплексного числа z. Поскольку число О не имеет аргумента, то оно не имеет тригонометрической формы. Задача 6.2. Представить в тригонометрической форме комплексные числа: a) 1+i, б) -1+3i , в) 1, г) 3i, д) -5, е) 1+2i. Запись комплексного
числа в виде z=(cos φ +isin φ ),
где φ∈ Argz тоже называется тригонометрической
формой комплексного числа. Из закона равенства (=) комплексных чисел и из того, что z=a2+в2 , φ∈ Argz⇒ ⇒ φ= argz+2kπ вытекает следующие утверждение. Два комплексных числа z1 = r1 (cos φ1+isinφ1 ) и z2 = r2 (cos φ2+isinφ2 ) равны тогда и только тогда, когда модули их равны: r1= r2, а аргументы φ1 и φ2 отличаются на число, краткое 2π : φ1=φ2+2kπ (где k – любое целое число). |
Комплексные числа
Плакаты > Фракталы
Напомним необходимые сведения о комплексных числах.
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)
.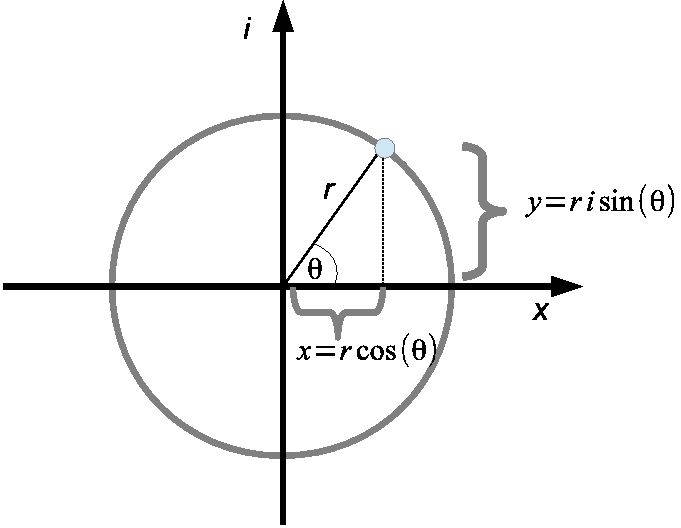
(Например, .)
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами ( a; b) равна . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор.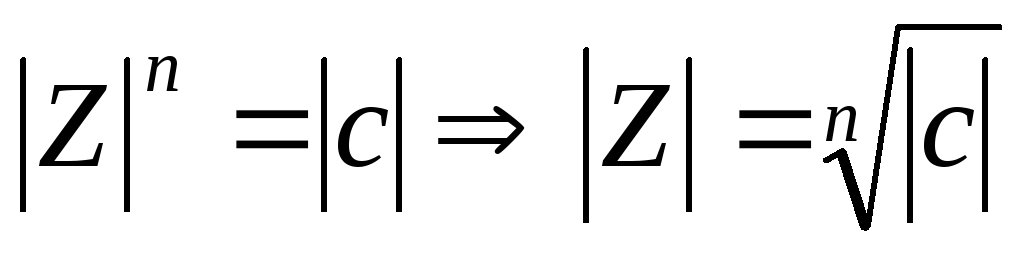 Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается
Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается
 Корень n-й степени из числа z — это такое комплексное число w, что wn = z. Видно, что , а , где k может принимать любое значение из множества {0, 1, …, n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).
Корень n-й степени из числа z — это такое комплексное число w, что wn = z. Видно, что , а , где k может принимать любое значение из множества {0, 1, …, n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).Далее: Фрактальные размерности
3
Показать комментарии (3)
Свернуть комментарии (3)
Написать комментарий
Общие предки кольчатых червей, моллюсков и брахиопод были ползающими животными
30.10 • Андрей Журавлёв
Яркое оперение у самок играет не менее важную сигнальную роль, чем у самцов
27.10 • Антон Морковин
Поздние алтайские неандертальцы были малочисленны и патрилокальны
24.10 • Александр Марков
Создана новая система контролируемой экспрессии генов на основе Cre-рекомбиназы
23. 10 • Галина Клинк
10 • Галина Клинк
Все новости
комплексный анализ — Доказательство непрерывности функции $f(z)=\arg(z)$ на определенном множестве
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 6к раз
$\begingroup$
Докажите, что $f: \{z \in \mathbb C : |z|=1\} \setminus \{-1\} \to \mathbb R$, $f(z)=\arg(z)$ , является непрерывным.
Я запутался в этом упражнении, я не знаю, какое тождество использовать, чтобы показать, что если $z \to z_0$ в этом множестве, то $\arg(z) \to \arg(z_0)$.
Извините, если я спрашиваю что-то тривиальное, но я не понимаю, почему точка $-1$ исключена из этого набора. И, рассматривая общий случай комплексной плоскости как области: если последовательность комплексных чисел $\{z_n\}_{n \in \mathbb N}$ сходится к некоторому числу $z$, не будет ли это означать что аргумент $z_n$ все ближе и ближе к аргументу $z$? Я не понимаю, почему это неправда. 9{- i \pi} = -1$
9{- i \pi} = -1$
$arg (z) = \theta $ и $\log(z) = -i arg(z)$, где $z \in A$
На множестве $A — \{-1\}$ комплексный логарифм $\log(z)$ однозначен и непрерывен.
Возьмем любую точку $z \in A$ $z \neq -1$. Пусть последовательность $\{z_n\}$ в $A$ сходится к $z$. Мы увидим, что последовательность $\{\log(z_n)\}$ будет сходиться к $Arg(z)$ из-за непрерывности функции $\log(z)$
При $z = -1$ функция $\log(z)$ многозначна и не непрерывна. Таким образом, $arg(z)$ также не будет непрерывным при $z = -1$. 9н я $. Это явно сходится к $0$, но аргумент колеблется (не сходится).
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.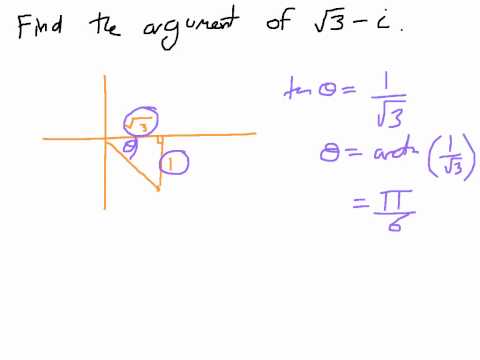
комплексный анализ — Где $Arg(z)$ дифференцируем?
Задавать вопрос
спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 906 раз
$\begingroup$ 92} $$ и $v_x(x,y)=v_y(x,y)=0$. Следовательно, уравнения Коши-Римана не выполняются, если $(x,y)=(0,0)$. Поэтому $f$ не дифференцируема в каждой точке с $x\neq0$.
Комментарий: мы говорим, что $f$ дифференцируема в $z_0$ , если существует следующий предел $$ \lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0} $$
(a) Как насчет дифференцируемости в точках с $x=0$ ?
(b) Как доказать недифференцируемость $f(z)=Arg(z)$ без использования уравнений Коши-Римана?
- комплексный анализ
$\endgroup$
$\begingroup$
Это всего лишь частичное решение, но, возможно, оно представляет интерес: зафиксируйте $z_0$ и рассмотрите разностное частное
$$\frac{f(z_0+h)-f(z_0)}{h} = \frac {\text{Arg}(z_0+h)-\text{Arg}(z_0)}{h}$$
Если положить $h \rightarrow 0$ вдоль прямой (или луча) $\text{Arg} (z) = \text{Arg}(z_0)$ это выражение явно стремится к $0$.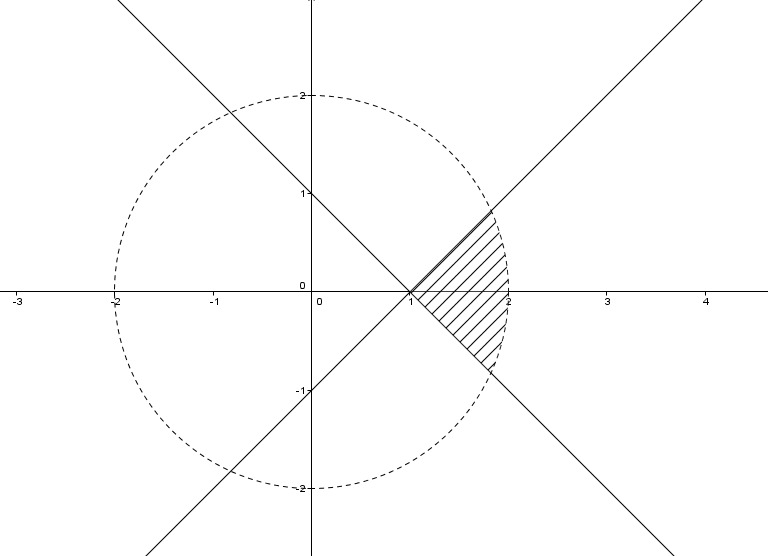


 Тогда т. z
= a+вi лежит в третьем квадранте:
Тогда т. z
= a+вi лежит в третьем квадранте: