Полиномиальная аппроксимация и методы точечного оценивания
Применение
методов исключения интервалов, которые
рассматривались в предыдущем разделе,
накладывает единственное требование
на исследуемую функцию: она должна быть
унимодальной. Следовательно, указанные
методы можно использовать для анализа
как непрерывных, так и разрывных функций,
а также в случаях, когда переменные
принимают значения из дискретного
множества. Логическая структура поиска
с помощью методов исключения интервалов
основана на простом сравнении значений
функции в двух пробных точках. Кроме
того, при таком сравнении в расчет
принимается только отношение порядка
на множестве значений функции и не
учитывается величина разности между
значениями функции. В данном разделе
рассматриваются методы поиска, которые
позволяют учесть относительные
изменения значений функции и как
следствие в ряде случаев оказываются
более эффективными, чем методы исключения
интервалов. Однако выигрыш в эффективности
достигается ценой введения дополнительного
требования, согласно которому исследуемые
функции должны быть достаточно гладкими.
Основная идея рассматриваемых методов
связана с возможностью аппроксимации
гладкой функции полиномом и последующего
использования аппроксимирующего
полинома для оценивания координаты
точки оптимума. Необходимыми условиями
эффективной реализации такого подхода
являются унимодальность и непрерывность
исследуемой функции. Согласно теореме
Вейерштрасса об аппроксимации [3],
если функция непрерывна в некотором
интервале, то ее с любой степенью точности
можно аппроксимировать полиномом
достаточно высокого порядка. Следовательно,
если функция унимодальна и найден
полином, который достаточно точно ее
аппроксимирует, то координату точки
оптимума функции можно оценить путем
вычисления координаты точки оптимума
полинома. Согласно теореме Вейерштрасса,
качество оценок координаты точки
оптимума, получаемых с помощью
аппроксимирующего полинома, можно
повысить двумя способами: использованием
полинома более высокого порядка и
уменьшением интервала аппроксимации.
Однако выигрыш в эффективности
достигается ценой введения дополнительного
требования, согласно которому исследуемые
функции должны быть достаточно гладкими.
Основная идея рассматриваемых методов
связана с возможностью аппроксимации
гладкой функции полиномом и последующего
использования аппроксимирующего
полинома для оценивания координаты
точки оптимума. Необходимыми условиями
эффективной реализации такого подхода
являются унимодальность и непрерывность
исследуемой функции. Согласно теореме
Вейерштрасса об аппроксимации [3],
если функция непрерывна в некотором
интервале, то ее с любой степенью точности
можно аппроксимировать полиномом
достаточно высокого порядка. Следовательно,
если функция унимодальна и найден
полином, который достаточно точно ее
аппроксимирует, то координату точки
оптимума функции можно оценить путем
вычисления координаты точки оптимума
полинома. Согласно теореме Вейерштрасса,
качество оценок координаты точки
оптимума, получаемых с помощью
аппроксимирующего полинома, можно
повысить двумя способами: использованием
полинома более высокого порядка и
уменьшением интервала аппроксимации.
Простейшим вариантом полиномиальной интерполяции является квадратичная аппроксимация, которая основана на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть по крайней мере квадратичной. Если же функция линейная, то ее оптимальное значение может достигаться только в одной из двух граничных точек интервала. Таким образом, при реализации метода оценивания с использованием квадратичной аппроксимации предполагается, что в ограниченном интервале можно аппроксимировать функцию квадратичным полиномом, а затем использовать построенную аппроксимационную схему для оценивания координаты точки истинного минимума функции.
Если задана последовательность точек x1, х2, х3 и известны соответствующие этим точкам значения функции f1f2 и f3, то можно определить постоянные величины а0, а1 и а2 таким образом, что значения квадратичной функции
совпадут
со значениями f(x) в
трех указанных точках. Перейдем к
вычислению q(x) в
каждой из трех заданных точек. Прежде
всего, так как
Перейдем к
вычислению q(x) в
каждой из трех заданных точек. Прежде
всего, так как
имеем a0=f1
. Далее, посколькуполучаем a1=(f2—f1)/(x2—x1).
Наконец, при х=х3
Разрешая последнее уравнение относительно а2, получаем
Таким образом, по трем заданным точкам и соответствующим значениям функции можно оценить параметры а0, a1 и а2 аппроксимирующего квадратичного полинома с помощью приведенных выше формул.
Если
точность аппроксимации исследуемой
функции в интервале от х1 до х3 с
помощью квадратичного полинома
оказывается достаточно высокой, то
в соответствии с предложенной стратегией
поиска построенный полином можно
использовать для оценивания координаты
точки оптимума.
можно получить
Поскольку функция f(x) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина х окажется приемлемой оценкой координаты точки истинного оптимума х*.
Пример 2.8. Поиск с использованием квадратичной аппроксимации
Рассмотрим процедуру оценивания координаты точки минимума функции
в интервале 1 x 5. Пусть x1=l, х3=5, а х2 есть средняя точка, интервала, т. е. х2=3. Вычислим соответствующие значения функции:
Для
того чтобы оценить х, необходимо
найти значения параметров а1 и
а2 аппроксимирующей функции.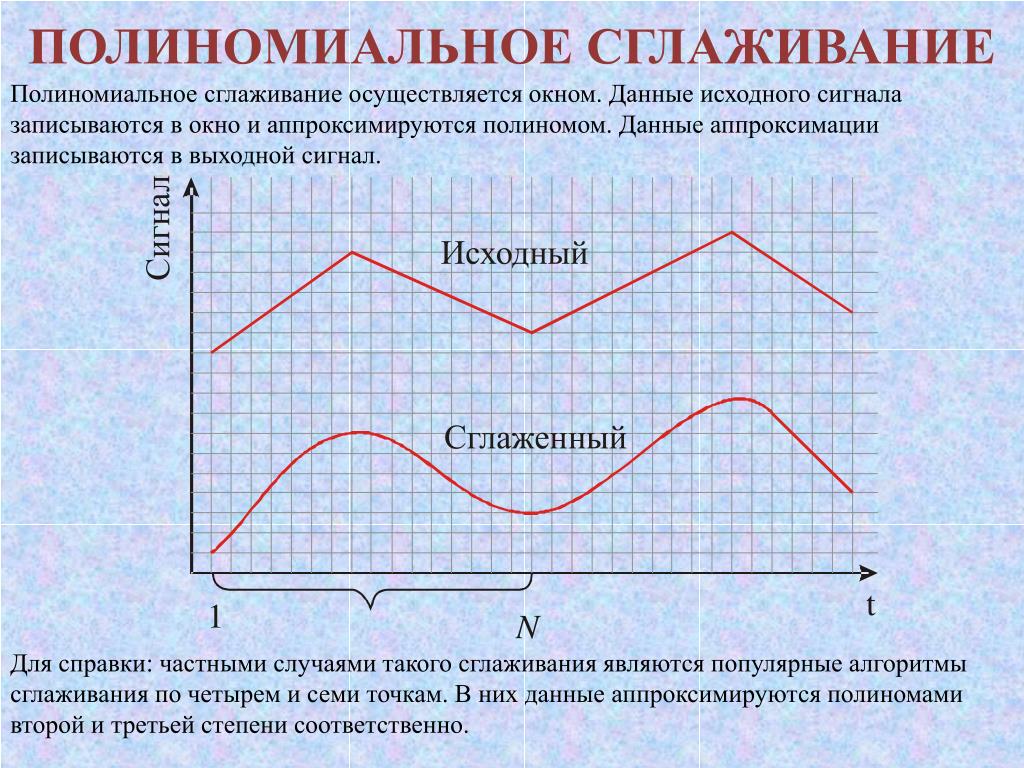 Имеем
Имеем
Подстановка этих значений в формулу для х позволяет получить
Точный минимум достигается при х* = 1,5874.
Полиномиальная аппроксимация — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Полиномиальная аппроксимация не служит единственной основой построения математических моделей по данным наблюдений. В качестве аппроксимирующих выражений могут успешно использоваться стандартные функции, а также функции, задаваемые пользователем. Для решения таких задач в среде MathCAD Pro удобно использовать встроенные функции, перечисленные в табл. 5.1. Типовые задачи, в которых применены функции этого класса ( Unfit, sinfit), были рассмотрены в разд. Применение остальных функций, табл. 5.1 и 5.2 аналогично. [1]
Полиномиальная аппроксимация соответствует выбору gr — хг. [2]
Полиномиальная аппроксимация ( Polynomial) используется для описания величин, попеременно возрастающих и убывающих. Ее целесообразно применять для анализа большого набора данных нестабильной величины. Степень полинома определяется количеством экстремумов ( максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум. Полином третьей степени имеет один или два экстремума. Полином четвертой степени может иметь не более трех экстремумов.
[3]
Ее целесообразно применять для анализа большого набора данных нестабильной величины. Степень полинома определяется количеством экстремумов ( максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум. Полином третьей степени имеет один или два экстремума. Полином четвертой степени может иметь не более трех экстремумов.
[3]
| Температурные и спектральные зависимости показателя преломления монокристалла кремния. [4] |
Полиномиальным аппроксимациям
свойственно ограничение: их нельзя применять за пределами того диапазона параметров, в котором они получены. Причина в том, что обоснованные ограничения на выбор коэффициентов полинома ( например, минимизация среднеквадратичного отклонения полинома от экспериментальных точек) накладываются только в том диапазоне, где имеются экспериментальные точки. Для полуэмпирических аппроксимаций, основанных на физических моделях явления, небольшое продолжение зависимостей за пределы диапазона не является столь опасным. [5]
[5]Метод полиномиальной аппроксимации заключается в определении полинома, аппроксимирующего функцию F () ( чаще всего — квадратичного полинома), и поиске его минимума. [6]
Кроме линейной и полиномиальной аппроксимации можно выбрать сплайн-аппроксимацию — когда на каждом интервале приближения используется кубический полином с новыми коэффициентами. В этом случае нельзя получить выражение для аппроксимирующей функции, т.е. такая аппроксимация является неполной. Аналогичными свойствами обладает и Эрмитовая аппроксимация. Она имеет только графическую интерпретацию. [7]
С помощью полиномиальной аппроксимации ( см. разд. [8]
| Зависимость полной погрешности R от количества разбиений N интервала интегрирования. [9] |
Методы Ньютона-Котеса основаны на полиномиальной аппроксимации подынтегральной функции. Алгоритмы методов просты и легко поддаются программной реализации.
[10]
Алгоритмы методов просты и легко поддаются программной реализации.
[10]
Следует помнить, что при полиномиальной аппроксимации максимальная степень полинома на 1 меньше числа экспериментальных точек. [11]
Следует помнить, что при полиномиальной аппроксимации максимальная степень полинома на 1 меньше числа экспериментальных точек. [12]
Таким образом, не существует более точной полиномиальной аппроксимации ( по переменной г) к функции г — 1 в указанном кольце, чем рп — Разумеется, наиболее простая рациональная аппроксимация дает точное решение. [13]
| Структурные обозначения фильтров. а — прямого. и — обра тного. [14] |
F есть желаемый выходной сигнал полиномиальной аппроксимации обратного фильтра, а выходной сигнал фильтра F есть входной сигнал обратного фильтра. [15]
Страницы: 1 2 3 4
Building Approximents for Sin(x)
Возраст от 16 до 18 лет
Уровень сложности
Александр из Гдыни Двуязычный Высокий
Школа № 3, Польша, использовала свойства функции синуса для
найти полиномиальную аппроксимацию.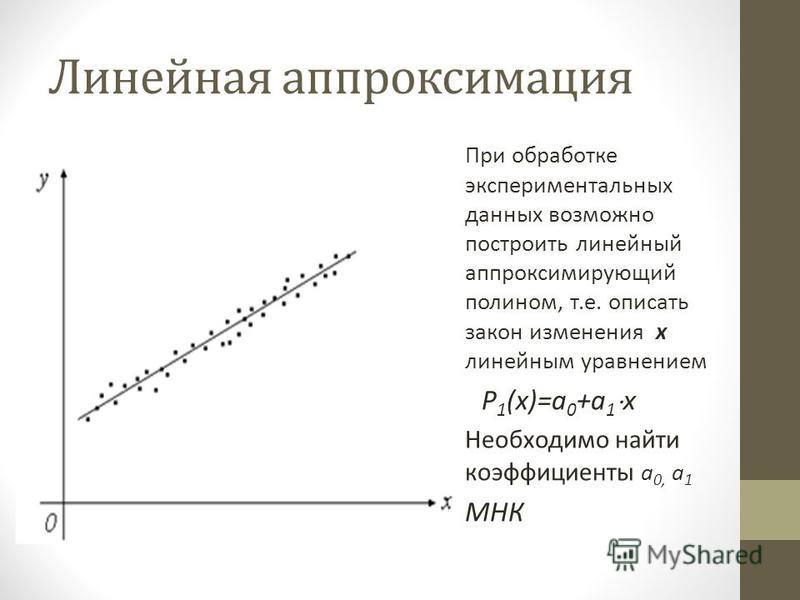
Функция sin(x) представлена белым цветом, первый порядок многочлен красным цветом, третий — голубым, пятый — зеленым и седьмой желтый. Можно заметить, что точность выше и лучше. С увеличением порядка полинома точность увеличивается.
Примечательно, что при использовании только до седьмого порядка многочлен, я получаю очень хорошее приближение функции. Грех является периодической функцией, поэтому достаточно работать над интервал $[-\pi, \pi]$, и, заметив, что sin является нечетной функцией достаточно интервала $[0, \pi]$. Около $\pi$, на самом деле я должен используйте расширение функции вокруг этого значения. Это эквивалентно перемещению оси Y $\pi$ вправо. 96\over 6!} +…$$
Синим цветом обозначена функция, фиолетовым — полином второго порядка,
четвертый — в белом и шестой — в красном. Я вижу, что шестой порядок
полином является довольно хорошим приближением в целом
интервал. 5\более 160}1 …$$
5\более 160}1 …$$
Цвета следующие: функция красного цвета, первый порядок
многочлен в голубом, второго порядка в зеленом, третьего в
желтый, четвертый синий и пятый фиолетовый.
§3.11 Методы аппроксимации ‣ Площади ‣ Глава 3 Численные методы
Содержимое
- §3.11(i) Минимаксные полиномиальные приближения
- §3.11(ii) Расширения серии Чебышева
- §3.11(iii) Минимаксные рациональные приближения
- §3.11(iv) Приближения Паде
- §3.11(v) Метод наименьших квадратов
- §3.11(vi) Сплайны
§3.11(i) Минимаксные полиномиальные приближения
Пусть f(x) непрерывна на отрезке [a,b]. Тогда существует единственный многочлен pn(x) степени n, называемый минимакс (или наилучшая равномерная ) полиномиальное приближение к f(x) на [а, б], что минимизирует maxa≤x≤b|ϵn(x)|, где ϵn(x)=f(x)−pn(x).
Достаточное условие для того, чтобы pn(x) было минимаксным полиномом, состоит в том, что
|ϵn(x)| достигает своего максимума в n+2 различных точках на [a,b]
и ϵn(x) меняет знак в этих последовательных максимумах.
Если у нас есть достаточно близкое приближение
| 3.11.1 | pn(x)=anxn+an−1xn−1+⋯+a0 | ||
в f(x), то коэффициенты ak можно вычислить итеративно. Предположить, что f′(x) непрерывна на [a,b] и пусть x0=a, xn+1=b и x1,x2,…,xn — нули ϵn′(x) в (a,b), расположенные так что
| 3.11.2 | x0 | ||
Также пусть
| 3.11.3 | мдж=(−1)jϵn(xj), | ||
| j=0,1,…,n+1. | |||
(Таким образом, mj являются приближениями к m, где ±m — максимальное значение |ϵn(x)| на [а,б].)
Тогда (в общем) лучшее приближение к pn(x) дается выражением
3. 11.4 11.4 | ∑k=0n(ak+δak)xk, | ||
где
| 3.11.5 | ∑k=0nxjkδak=(−1)j(mj−m), | ||
| j=0,1,…,n+1. | |||
Это набор n+2 уравнений для n+2 неизвестных δa0,δa1,…,δan и m.
Итерационный процесс сходится локально и квадратично (§3.8(i)).
Описан метод получения достаточно точного первого приближения в следующем подразделе.
О теории минимаксных приближений см. Meinardus (1967) . За примеры минимаксных полиномиальных аппроксимаций элементарных и специальных функции см. Hart et al. (1968) . См. также Коди (1970) и Ральстон (1965) .
§3.11(ii) Расширения серии Чебышева
Многочлены Чебышева Tn задаются как
3.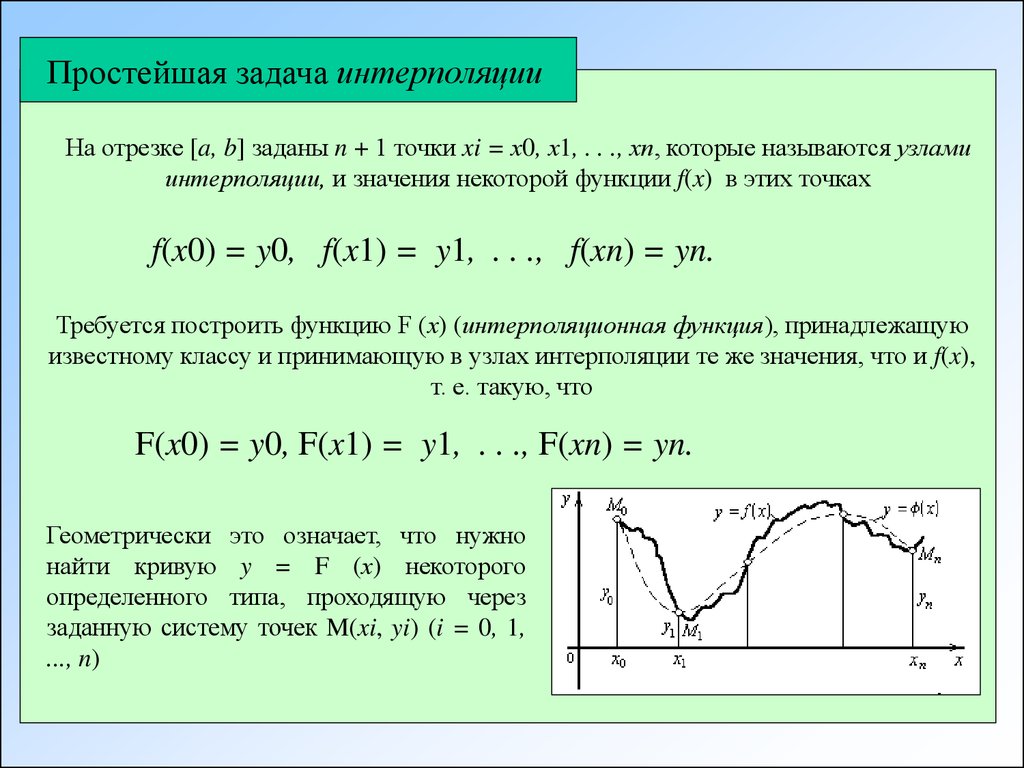 11.6 11.6 | Tn(x)=cos(narccosx), | ||
| −1≤x≤1. | |||
Они удовлетворяют рекуррентному соотношению
| 3.11.7 | Tn+1(x)−2xTn(x)+Tn−1(x)=0, | ||
| n=1,2,…, | |||
с начальными значениями T0(x)=1, T1(x)=x. Они наслаждаются свойство ортогональности относительно интегралов:
| 3.11.8 | ∫−11Tj(x)Tk(x)1−x2dx={π,j=k=0,12π,j=k≠0,0,j≠k, | ||
, а также свойство ортогональности по отношению к суммам следующим образом. Когда n>0 и 0≤j≤n, 0≤k≤n,
| 3.11.9 | ∑′′ℓ=0′′n′′Tj(xℓ)Tk(xℓ)={n,j=k=0 или n,12n,j=k≠0 или n,0,j≠k, | ||
где xℓ=cos(πℓ/n) и двойное штрих означает, что первое и
последние сроки сокращаются вдвое.
Об этих и других свойствах многочленов Чебышева см. Глава 18, Гил и др. (2007a, глава 3) и Мейсон и Хэндскомб (2003) .
Расширения Чебышева
Если f непрерывно дифференцируема на [−1,1], то с
| 3.11.10 | cn=2π∫0πf(cosθ)cos(nθ)dθ, | ||
| n=0,1,2,…, | |||
расширение
| 3.11.11 | f(x)=∑′n=0′∞′cnTn(x), | ||
| −1≤x≤1, | |||
сходится равномерно. Здесь единственный штрих на символе суммирования означает, что первый срок должен быть уменьшен вдвое. На самом деле (3.11.11) есть Разложение f(cosθ) в ряд Фурье; сравнивать (3.11.6) и §1.8(i).
Кроме того, если f∈C∞[−1,1], то сходимость
(3.11.11) обычно очень быстро; сравнить (1. 8.7)
с произвольным k.
8.7)
с произвольным k.
Для общих интервалов [a,b] масштабируем:
| 3.11.12 | f(x)=∑′n=0′∞′dnTn(2x−a−bb−a). | ||
Поскольку ряд (3.11.12) быстро сходится, мы получаем очень хорошее первое приближение к минимаксному многочлену pn(x) для [a,b], если мы усекаем (3.11.12) на (n+1)-м члене. Это потому что в обозначениях §3.11(i)
| 3.11.13 | ϵn(x)=dn+1Tn+1(2x−a−bb−a), | ||
примерно, и правая часть обладает именно такими свойствами относительно его максимумов и минимумов, необходимых для минимакса приближение; сравните рисунок 18.4.3.
Точнее, известно, что для интервала [a,b] отношение максимальное значение остатка
| 3.11.14 | |∑k=n+1∞dkTk(2x−a−bb−a)| | ||
к максимальной ошибке минимаксного полинома pn(x) ограничено 1+Ln,
где Ln — n-я постоянная Лебега для ряда Фурье; видеть
§1.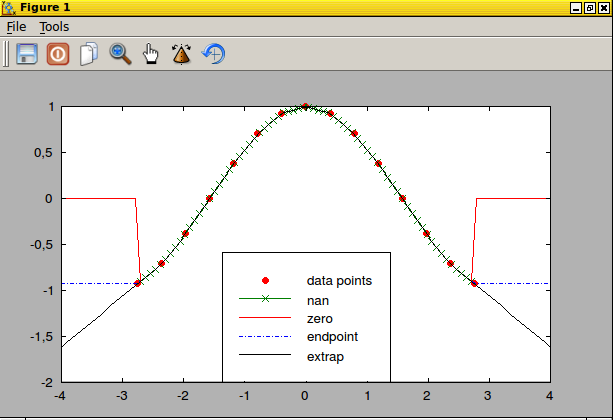 8(i). Поскольку L0=1, Ln — монотонно возрастающая
функция от n, и (например) L1000=4,07…, это означает, что в
попрактиковаться в замене усеченного разложения в ряд Чебышева на
соответствующая минимаксная полиномиальная аппроксимация вряд ли имеет смысл.
При этом множество минимаксных приближений
p0(x),p1(x),p2(x),…,pn(x) требует вычисления и хранения
12(n+1)(n+2) коэффициентов, тогда как соответствующий набор
Аппроксимация ряда Чебышева требует только n+1 коэффициентов.
8(i). Поскольку L0=1, Ln — монотонно возрастающая
функция от n, и (например) L1000=4,07…, это означает, что в
попрактиковаться в замене усеченного разложения в ряд Чебышева на
соответствующая минимаксная полиномиальная аппроксимация вряд ли имеет смысл.
При этом множество минимаксных приближений
p0(x),p1(x),p2(x),…,pn(x) требует вычисления и хранения
12(n+1)(n+2) коэффициентов, тогда как соответствующий набор
Аппроксимация ряда Чебышева требует только n+1 коэффициентов.
Расчет коэффициентов Чебышева
Значение cn в (3.11.11) можно рассчитать из (3.11.10), но в целом эффективнее использовать свойство ортогональности (3.11.9). Кроме того, в случаях, когда f(x) удовлетворяет линейному обыкновенному дифференциальному уравнению с полиномиальными коэффициентами, разложение (3.11.11) можно подставить в дифференциал уравнение, чтобы получить рекуррентное соотношение, которому удовлетворяет cn.
Для получения подробной информации и примеров этих методов см. Clenshaw (1957, 1962) и Миллер (1966) . Смотрите также Мейсон и Хэндскомб (2003 г., глава 10) и Фокс и Паркер (1968 г., глава 5) .
Смотрите также Мейсон и Хэндскомб (2003 г., глава 10) и Фокс и Паркер (1968 г., глава 5) .
Суммирование рядов Чебышева: алгоритм Кленшоу
Для разложения (3.11.11) численные значения чебышевского полиномы Tn(x) могут быть сгенерированы применением рекуррентного соотношение (3.11.7). Более эффективная процедура выглядит следующим образом. Позволять cnTn(x) — последний член усеченного ряда. Начиная с un+1=0, un=cn, мы применяем
| 3.11.15 | великобритания=2xuk+1−uk+2+ск, | ||
| k=n−1,n−2,…,0. | |||
Тогда сумма усеченного разложения равна 12(u0−u2). За анализ ошибок и модификации алгоритма Кленшоу см. Оливер (1977) .
Комплексные переменные
Если x заменить комплексной переменной z и f(z) является аналитической, то
разложение (3.11.11) сходится внутри эллипса. Однако в
общее (3.11.11) не дает преимущества в ℂ для
числовых целях по сравнению с разложением Маклорена f(z).
Однако в
общее (3.11.11) не дает преимущества в ℂ для
числовых целях по сравнению с разложением Маклорена f(z).
Подробнее о разложениях в ряды Чебышева на комплексной плоскости см. Мейсон и Хэндскомб (2003, §5.10) .
§3.11(iii) Минимаксные рациональные приближения
Пусть f непрерывна на отрезке [a,b] и w непрерывна. ненулевая функция на [a,b]: w называется весовой функцией . затем минимакс (или наилучшая равномерная ) рациональное приближение
| 3.11.16 | Rk,ℓ(x)=p0+p1x+⋯+pkxk1+q1x+⋯+qℓxℓ | ||
типа [k,ℓ] to f на [a,b] минимизирует максимальное значение |ϵk,ℓ(x)| на [а,б], где
| 3.11.17 | ϵk,ℓ(x)=Rk,ℓ(x)−f(x)w(x). | ||
Теория полиномиальной минимаксной аппроксимации, данная в §3. и ±m — максимум |ϵk,ℓ(x)| на [а, б]. Набор минимаксных рациональных аппроксимаций элементарных и специальных
функции можно найти в Hart et al. (1968) . Широко реализованный и используемый алгоритм расчета коэффициентов
pj и qj в (3.11.16) равно Второй алгоритм Ремеза .
См. Remez (1957) , Werner et al. (1967) и Джонсон и Блэр (1973) . При w(x)=1 и 14-значном вычислении мы получаем следующее рациональное
приближение типа [3,3] к функции Бесселя J0(x)
(§10. с коэффициентами, указанными в таблице 3.11.1. Кривая ошибок показана на рис. 3.11.1. Лет — формальный степенной ряд. Рациональная функция называется аппроксимацией Паде в нуле f if Обозначается [p/q]f(z). Таким образом, если b0≠0, то маклореновская
разложение (3.11.21) согласуется с (3.11.20) до и
включая член в zp+q. Требование (3.11.22) подразумевает где cj=0, если j<0. При b0=1 последние q уравнений дают
b1,…,bq как решение системы линейных уравнений. Массив аппроксимаций Паде называется столом Паде . Аппроксимации с той же степенью знаменателя
находятся в одном столбце таблицы. Для результатов сходимости аппроксимаций Паде и связи с
непрерывные дроби и квадратуры Гаусса, см. Бейкер и Грейвс-Моррис (1996, §4.7) . Аппроксимации Паде можно вычислить с помощью перекрестного правила Винна . Любые пять
аппроксимации, расположенные в таблице Паде как удовлетворить Начиная с первого столбца [n/0]f, n=0,1,2,…, и инициализируя
предыдущего столбца на [n/−1]f=∞, n=1,2,…, мы можем вычислить
нижняя треугольная часть таблицы через (3. О рекурсивном вычислении [n+k/k]f с помощью эпсилон-алгоритма Винна см.
(3.9.11) и последующий текст. Численное обращение преобразования Лапласа (§1.14(iii)) требует, чтобы f=ℒ−1F было получено из числовых значений
F. Общая процедура состоит в том, чтобы аппроксимировать F рациональной функцией R
(исчезающий в бесконечности), а затем аппроксимировать f на r = ℒ−1R.
Когда F имеет явное разложение в степенной ряд, возможный выбор R — это
Приближение Паде к F. См. Люк (1969b, §16.4) для нескольких
примеры со специальными функциями. Для получения дополнительной информации о аппроксимациях Паде см. Бейкер и Грейвс-Моррис (1996, §4. Предположим, что функция f(x) аппроксимируется многочленом минимизирует Здесь xj, j=1,2,…,J, — заданный набор различных вещественных точек и
J≥n+1. Из уравнений ∂S/∂ak=0, k=0,1,…,n получаем
вывести нормальное уравнение где (3.11.29) представляет собой систему n+1 линейных уравнений для
коэффициенты a0,a1,…,an. Матрица симметрична и
положительно определена, но система плохо обусловлена, когда n велико, потому что
нижние строки матрицы примерно пропорциональны друг другу. Если
J=n+1, то pn(x) — интерполяционный полином Лагранжа для множества
x1,x2,…,xJ (§3.3(i)). В более общем случае пусть f(x) аппроксимируется линейной комбинацией заданных функций ϕk(x), k=0,1,…,n, минимизирующих w(x) является заданным положительным числом весовая функция и снова J≥n+1. с и Поскольку Xkℓ=Xℓk, матрица снова симметрична. Если функции ϕk(x) линейно независимы на множестве
x1,x2,…,xJ, то есть единственное решение системы уравнений равно c0=c1=⋯=cn=0, то аппроксимация Φn(x) равна
определяется однозначно. Теперь предположим, что Xkℓ=0, когда k≠ℓ, то есть функции
ϕk(x) ортогональны относительно взвешенного суммирования на
дискретный набор x1,x2,…,xJ. Тогда система (3.11.33)
является диагональным и, следовательно, хорошо обусловленным. Набор функций ϕ0(x),ϕ1(x),…,ϕn(x), линейно
не зависят от множества x1,x2,…,xJ (ср. (3.11.36))
всегда можно ортогонализовать в смысле, указанном в предыдущем абзаце, с помощью
процедура Грамма-Шмидта ; см. Гаучи (1997а) . Возьмем n комплексных экспонент ϕk(x)=eikx,
k=0,1,…,n−1, и аппроксимировать f(x) линейной комбинацией
(3.11.31).
Функции ϕk(x) ортогональны на множестве x0,x1,…,xn−1,
xj=2πj/n относительно весовой функции w(x)=1 в смысле
что δk,ℓ — символ Кронекера, а черта обозначает комплекс
сопряженный. и получить При таком выборе ak и fj=f(xj) соответствующая сумма
(3.11.32) исчезает. Пара векторов {f,a} называется парой дискретного преобразования Фурье . Прямое вычисление дискретного преобразования Фурье
(3. требует приблизительно n2 умножений. Метод быстро
Преобразование Фурье (БПФ) использует структуру матрицы Ω
с элементами ωnjk, j,k=0,1,…,n−1. Если n=2m, то
Ω можно разложить на m матриц, строки которых содержат
только несколько ненулевых записей, и ненулевые записи равны, за исключением
знаки. Благодаря такой структуре количество операций может быть уменьшено.
до nm=nlog2n операций. Имущество имеет фундаментальное значение в алгоритме БПФ. Если n не является степенью числа 2,
тогда возможны модификации. Для получения дополнительной информации о аппроксимации методом наименьших квадратов, включая примеры, см.
см. Гаучи (1997a, глава 2) и Бьорк (1996, главы 1 и 2) . Сплайны задаются кусочно и обычно полиномами низкой степени. Данный
n+1 различных точек xk на действительном интервале [a,b], с
(a=)x0 Для сплайнов, основанных на полиномах Бернулли и Эйлера, см. §24.17(ii). Для многих приложений сплайн-функция является более адаптируемой аппроксимирующей
инструмент, чем интерполяционный полином Лагранжа, включающий сравнимый
количество параметров;
см. 11(i)
можно распространить на случай замены pn(x) рациональной функцией
Рк,ℓ(х). Существует единственное решение этой минимаксной задачи и
существует не менее k+ℓ+2 значений xj,
a≤x0
11(i)
можно распространить на случай замены pn(x) рациональной функцией
Рк,ℓ(х). Существует единственное решение этой минимаксной задачи и
существует не менее k+ℓ+2 значений xj,
a≤x0 3.11.18 мдж=(−1)jϵk,ℓ(xj), j=0,1,…,k+ℓ+1, Пример
 2(ii)) на интервале 0≤x≤j0,1,
где j0,1 — первый положительный нуль J0(x):
2(ii)) на интервале 0≤x≤j0,1,
где j0,1 — первый положительный нуль J0(x): 3.11.19 R3,3(x)=p0+p1x+p2x2+p3x31+q1x+q2x2+q3x3, §3.11(iv) Приближения Паде
3.11.20 f(z)=c0+c1z+c2z2+⋯ 3.11.21 Np,q(z)Dp,q(z)=a0+a1z+⋯+apzpb0+b1z+⋯+bqzq 3.  11.22
11.22 Np,q(z)−f(z)Dp,q(z)=O(zp+q+1), z→0. 3.11.23 а0 =с0b0, а1 =с1b0+c0b1, ⋮ ап =cpb0+cp−1b1+⋯+cp−qbq, 0 =cp+1b0+cpb1+⋯+cp−q+1bq, ⋮ 0 =cp+qb0+cp+q−1b1+⋯+cpbq,  Первый
тогда p+1 уравнений дают a0,…,ap.
Первый
тогда p+1 уравнений дают a0,…,ap. 3.11.24 [0/0]ж[0/1]ж[0/2]ж⋯[1/0]ж[1/1]ж[1/2]ж⋯[2/0]ж[2/1] ж[2/2]ф⋯⋮⋮⋮⋱ 3.11.25 (N-C)-1+(S-C)-1=(W-C)-1+(E-C)-1.  11.25).
Аналогично верхняя треугольная часть следует из первой строки [0/n]f,
n=0,1,2,…, инициализируя [−1/n]f=0, n=1,2,….
11.25).
Аналогично верхняя треугольная часть следует из первой строки [0/n]f,
n=0,1,2,…, инициализируя [−1/n]f=0, n=1,2,…. Инверсия преобразования Лапласа
3.11.26 F(s)=ℒf(s)=∫0∞e−stf(t)dt  7) , Брезинский (1980, стр. 9–39 и 126–177) и Лорентцен и Вааделанд (1992, стр. 367–395) .
7) , Брезинский (1980, стр. 9–39 и 126–177) и Лорентцен и Вааделанд (1992, стр. 367–395) . §3.11(v) Аппроксимации методом наименьших квадратов
3.11.27 pn(x)=anxn+an−1xn−1+⋯+a0 3.11.28 S=∑j=1J(f(xj)−pn(xj))2. 3.11.29 [X0X1⋯XnX1X2⋯Xn+1⋮⋮⋱⋮XnXn+1⋯X2n][a0a1⋮an]=[F0F1⋮Fn], 3.  11.30
11.30 Кк =∑j=1Jxjk, ФК =∑j=1Jf(xj)xjk. 3.11.31 Φn(x)=anϕn(x)+an−1ϕn−1(x)+⋯+a0ϕ0(x) 3.11.32 ∑j=1Jw(xj)(f(xj)−Φn(xj))2,  Затем (3.11.29) заменяется на
Затем (3.11.29) заменяется на 3.11.33 [X00X01⋯X0nX10X11⋯X1n⋮⋮⋱⋮Xn0Xn1⋯Xnn][a0a1⋮an]=[F0F1⋮Fn], 3.11.34 Xkℓ=∑j=1Jw(xj)ϕk(xj)ϕℓ(xj), 3.11.35 Fk=∑j=1Jw(xj)f(xj)ϕk(xj). 3.11.36 ∑k=0nckϕk(xj)=0, j=1,2,…,J, 
Пример. Дискретное преобразование Фурье
3.11.37 ∑j=0n−1ϕk(xj)ϕℓ(xj)¯=nδk,ℓ, k,ℓ=0,1,…,n−1,  Следовательно, мы можем решить систему
Следовательно, мы можем решить систему 3.11.38 fj=∑k=0n−1akϕk(xj), j=0,1,…,n−1, 3.11.39 ак=1n∑j=0n−1fjϕk(xj)¯, k=0,1,…,n−1. 3.11.40 ф = [f0,f1,…,fn−1]T, и = [a0,a1,…,an−1]T, Быстрое преобразование Фурье
 11.38), то есть из
11.38), то есть из 3.11.41 фдж =∑k=0n−1akωnjk, ωn =e2πi/n, j=0,1,…,n−1, 3.11.42 ωn2(k−(n/2))=ωn/2k 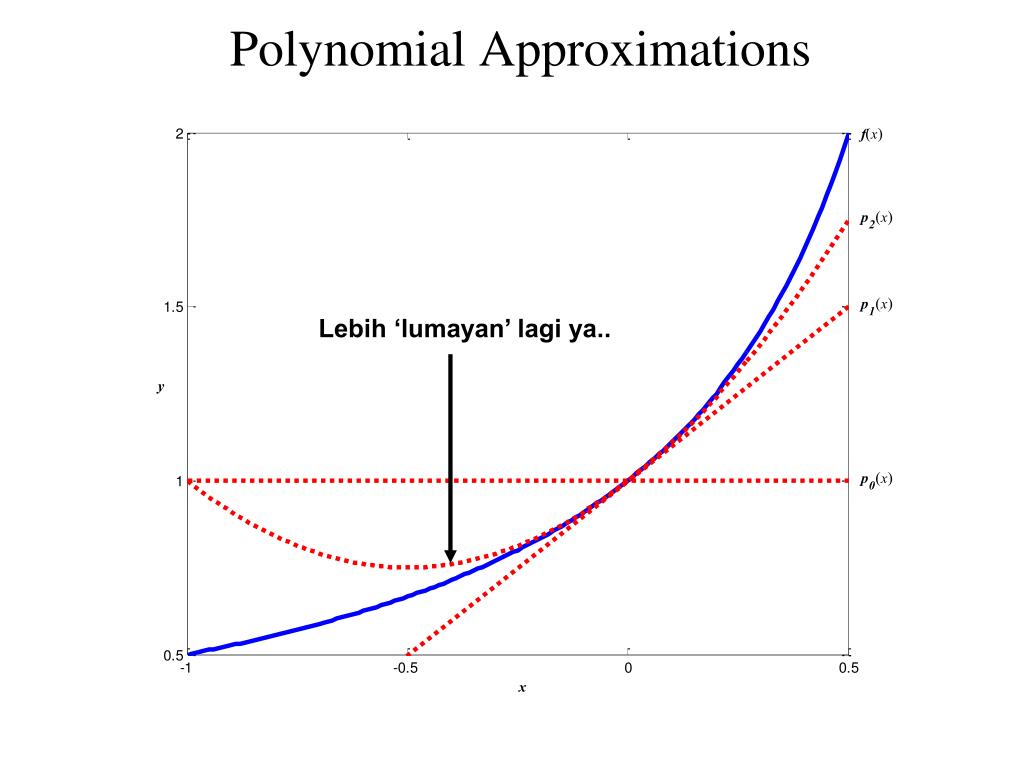 Оригинальную ссылку см. Кули и Тьюки (1965) . Подробности и алгоритмы см. Ван Лоан (1992) .
Оригинальную ссылку см. Кули и Тьюки (1965) . Подробности и алгоритмы см. Ван Лоан (1992) . §3.11(vi) Сплайны