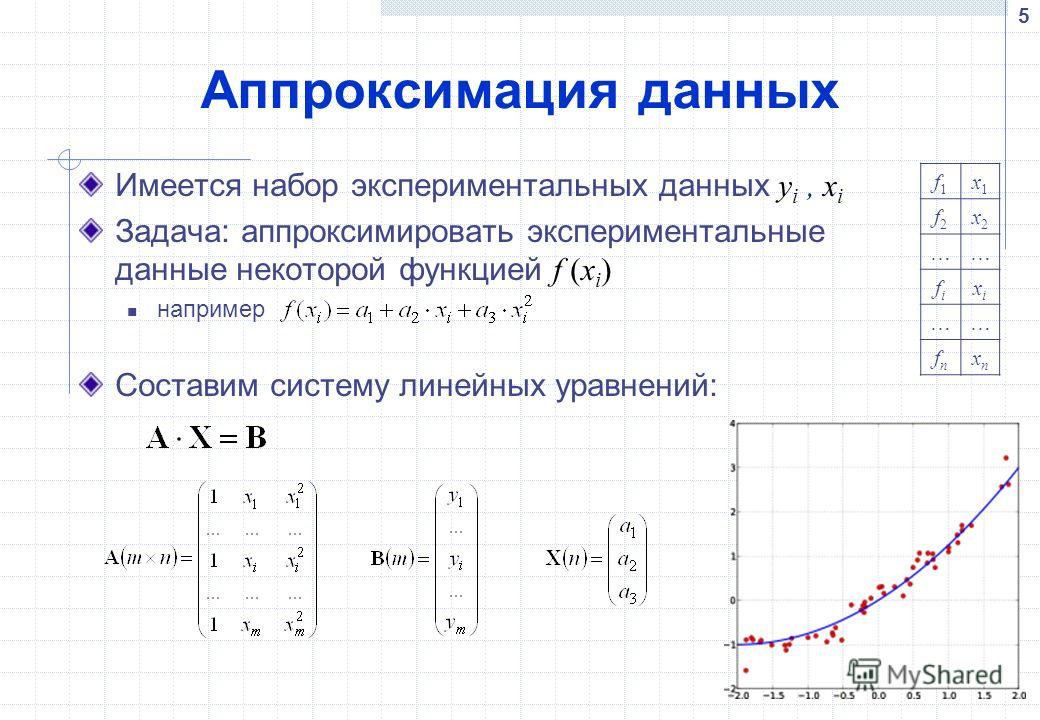
[n/m]=[n/m]f.[n/m]=[n/m]_f.[n/m]=[n/m]f.Для эффективного вычисления аппроксимации Паде удобнее пользоваться не явными формулами, а реккурентными соотношениями, существующими в таблице Паде. Разработано большое число алгоритмов для машинного вычисления аппроксимаций Паде.
Название аппроксимация Паде получила по имени французского математика А. Паде, применявшего её (1892) в рамках классической теории непрерывных дробей. Частные случаи аппроксимации Паде изучались начиная с 1820 г. О. Коши, К. Якоби, Ф. Г. Фробениусом. Фундаментальные результаты о диагональных аппроксимациях Паде получены П. Л. Чебышёвым, А. А. Марковым и Т. Стилтьесом. С начала 20 в. аппроксимация Паде стала самостоятельным объектом анализа и составляет важную часть теории рациональных приближений аналитических функций.
Аппроксимация Паде | это… Что такое Аппроксимация Паде?
|
Аппроксимация Паде — классический метод рациональной аппроксимации аналитических функций, названный по имени французского математика Анри Паде. Метод заключается в представлении функции в виде отношения двух полиномов, коэффициенты которых определяются коэффициентами разложения функции в ряд Тейлора.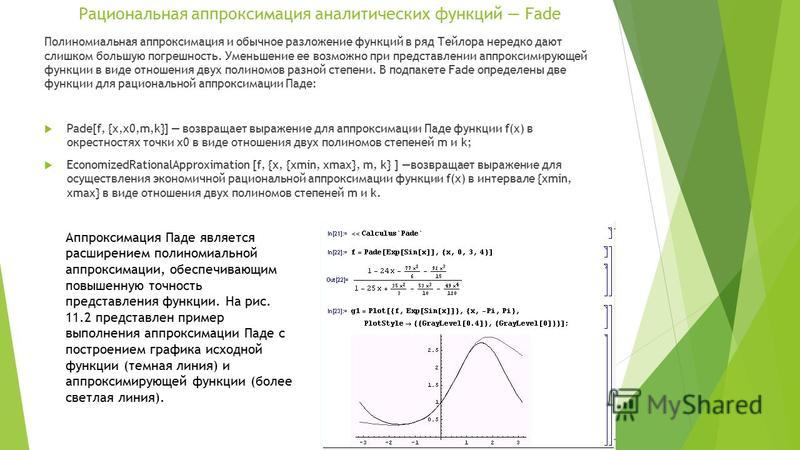
с помощью аппроксимации Паде можно оптимальным способом выбрать коэффициенты и и получить аппроксимант
Использование этой простой идеи и её обобщений привело ко многим результатам и превратилось практически в фундаментальный метод исследования.
История
Авторство Паде основывается на его диссертации 1892 года[1] (копия диссертации хранится в библиотеке Корнелльского университета). В этой работе он изучил подобные аппроксимации и расположил их в таблицу, уделив при этом большое внимание экспоненциальной функции.
Определение
Пусть имеется разложение функции в степенной ряд Тейлора:
- ,
где — коэффициенты ряда.
Аппроксимация Паде представляет собой рациональную функцию вида
разложение которой в ряд Тейлора (с центром в нуле) совпадает с разложением функции до тех пор, пока это возможно. Функция такого вида имеет коэффициентов в числителе и — в знаменателе.
Таблица Паде
Основная статья: Таблица Паде
Обобщения
- Многоточечные аппроксимации Паде
- Аппроксимации Бейкера — Гаммеля
- Аппроксимация функции нескольких переменных
- Матричные аппроксимации Паде
- Аппроксимация Паде — Чебышёва
- Аппроксимация Паде — Фурье
Численные методы нахождения
Примечания
- ↑ H. Padé. Sur la représentation approchée d’une fonction par des fractions rationnelles Thèse de Doctorat présentée à l’Université de la Sorbonne, 1892
Библиография
- Jeorge A. Baker, Jr.; Peter Graves-Morris Аппроксимации Паде = Padé approximants / пер. с англ. Е. А. Рахманова, С. П. Суетина; ред. А. А. Гончар. — М.: Мир, 1986. — 502 с. — 6400 экз.
Ссылки
- Eric W. Weisstein Padé Approximant (англ.). «MathWorld». Проверено 1 августа 2009.
- Бочканов С., Быстрицкий В. Паде-аппроксимация (англ.). «Библиотека алгоритмов».(недоступная ссылка — история) Проверено 1 августа 2009.
- Буслаев В. И. Рекуррентные соотношения и рациональные аппроксимации. Общеинститутский семинар «Математика и ее приложения» Математического института им. В. А. Стеклова РАН (17 апреля 2008). — Видеозапись. Проверено 1 августа 2009.
- Калюжный О., Коковин В. Применение аппроксимаций Паде к вибрации турбореактивного двигателя (рус.). Проверено 2012-17-12.
ca.classical analysis and odes — Необоснованная эффективность приближения Паде
Уолтер Ван Аш дает современное описание приближения Паде, вариант которого использовался в доказательстве трансцендентности e.
В случае, когда $f(z)$ является преобразованием Коши финитной меры $\mu(x)$,
\[ f(z) = \int \frac{1}{z-x} d \mu(x) \]
Тогда $P_n(x)$ является ортогональным многочленом относительно $\mu(x)$, тогда как
\[ Q_{n-1}(z) = \int_a^b \ frac{P_n(z) — P_n(x)}{z-x} \, \mu(x) \] 92 \]
Ряд Тейлора точен, а аппроксимация 1-1 расходится.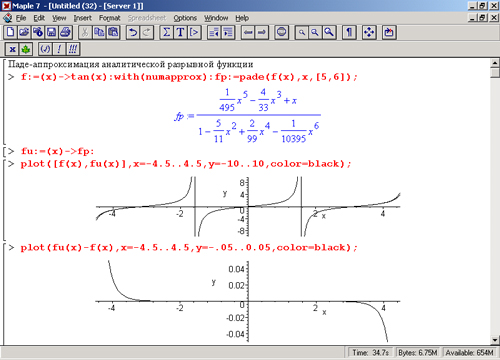
В вашем примере $\sqrt{\frac{1+\frac{z}{2} }{1+2z}} \to \frac{1}{2}$ для больших значений и, вероятно, 1,1 аппроксимант делает то же самое, что делает его хорошим глобальным соответствием. Приближения 0,2 или 2,0 будут иметь различное глобальное поведение. Я не смог найти никакого точного сравнения, в общем.
Известно, что непрерывные дроби в определенном смысле являются «наилучшими приближениями».
Наилучшее рациональное приближение к действительное число х является рациональным числом d/n, d > 0, то есть ближе к x, чем любое приближение с меньшим знаменатель.
Пример из Википедии:
\[ 0,84375 = \cfrac{1}{1 + \cfrac{1}{5 + \cfrac{1}{2 + \cfrac{1}{2}}}} = [ 0;1,5,2,2]\]
Мы можем остановиться в середине этого процесса, чтобы получить близкую дробь с учетом верхней границы знаменателя.
\[ 0,84375 \приблизительно 1,\frac{5}{6}, \frac{11}{13} , \frac{27}{32}\]
Дроби Фареев до знаменателя 6 равны
$ $0,\frac{1}{6}, \frac{1}{5},\frac{1}{4},\frac{1}{3},\frac{2}{5},\frac{ 1} {2}, \ гидроразрыва {3} {5}, \ гидроразрыва {2} {3}, \ гидроразрыва {3} {4}, \ гидроразрыва {4} {5}, \ mathbf {\ гидроразрыва {27} {32}},\frac{5}{6} 1$$ 92 & x & 1 \end{array} \right|}\]
na.
numerical analysis — Паде-аппроксимация распределения Гаусса с заданной точностьюЗадавать вопрос
спросил
Изменено 3 года, 6 месяцев назад
Просмотрено 69{-7}$ над $\mathbb{R}$), желательно с рациональными функциями.
Увы, я не знаком с теорией приближения. Google указал мне на приближение Паде как путь. Увы, я до сих пор не знаю, как вывести аппроксимацию Паде для заданной функции, не говоря уже о том, как гарантировать, что аппроксимация будет соответствовать заданной точности. Не могли бы вы указать мне на соответствующую информацию?
РЕДАКТИРОВАТЬ:
Вот немного предыстории. Для некоторых инженерных вычислений мне нужны аналитические выражения для некоторых интегралов; в этом конкретном случае для $e^{-x^2} \operatorname{erf}(x+a)$, где $a$ — параметр, изменяющийся на протяжении всего вычисления.
2}\operatorname{erf}(x+a)\,dx$, как и I. 92}$ и $\operatorname{erf}(x+a)$ (и, возможно, некоторые другие, которые мне могут понадобиться), чтобы их произведения были аналитически интегрируемыми?
Хорошо известно, что можно получить аналитическое выражение для интеграла от рациональной функции и что произведения рациональных функций рациональны. Таким образом, идея: аппроксимировать соответствующие функции рациональными, используя аппроксимацию Паде, и проинтегрировать произведения аппроксимаций Паде. Это в основном заменит интеграл, который я хочу, выражением, содержащим кучу рациональных функций и $\log$s и $\arctan$s.
Я должен жестко контролировать точность приведенных выше приближений, чтобы модель работала должным образом. Таким образом вопрос.
- na.численный анализ
- теория приближения
$\endgroup$
7
$\begingroup$
Стоит посмотреть на хитрый трюк Шраудольфа, если ваша цель — производительность.