c# — Оптимизация алгоритма расчёта CRC32 (MPEG-2) с помощью векторов
Из глубоких глубин глубокого интернета был поднят кусок кода на С в котором я нашёл табличный вариант расчёта CRC32 для стандарта MPEG-2. к сожалению первоисточника этого метода не знаю. После некоторых доработок этот метод заработал под c#:
private static readonly uint[] CRC32_table = new uint[] {0x00000000, 0x04c11db7, 0x09823b6e, 0x0d4326d9,
0x130476dc, 0x17c56b6b, 0x1a864db2, 0x1e475005,
0x2608edb8, 0x22c9f00f, 0x2f8ad6d6, 0x2b4bcb61,
0x350c9b64, 0x31cd86d3, 0x3c8ea00a, 0x384fbdbd,
0x4c11db70, 0x48d0c6c7, 0x4593e01e, 0x4152fda9,
0x5f15adac, 0x5bd4b01b, 0x569796c2, 0x52568b75,
0x6a1936c8, 0x6ed82b7f, 0x639b0da6, 0x675a1011,
0x791d4014, 0x7ddc5da3, 0x709f7b7a, 0x745e66cd,
0x9823b6e0, 0x9ce2ab57, 0x91a18d8e, 0x95609039,
0x8b27c03c, 0x8fe6dd8b, 0x82a5fb52, 0x8664e6e5,
0xbe2b5b58, 0xbaea46ef, 0xb7a96036, 0xb3687d81,
0xad2f2d84, 0xa9ee3033, 0xa4ad16ea, 0xa06c0b5d,
0xd4326d90, 0xd0f37027, 0xddb056fe, 0xd9714b49,
0xc7361b4c, 0xc3f706fb, 0xceb42022, 0xca753d95,
0xf23a8028, 0xf6fb9d9f, 0xfbb8bb46, 0xff79a6f1,
0xe13ef6f4, 0xe5ffeb43, 0xe8bccd9a, 0xec7dd02d,
0x34867077, 0x30476dc0, 0x3d044b19, 0x39c556ae,
0x278206ab, 0x23431b1c, 0x2e003dc5, 0x2ac12072,
0x128e9dcf, 0x164f8078, 0x1b0ca6a1, 0x1fcdbb16,
0x018aeb13, 0x054bf6a4, 0x0808d07d, 0x0cc9cdca,
0x7897ab07, 0x7c56b6b0, 0x71159069, 0x75d48dde,
0x6b93dddb, 0x6f52c06c, 0x6211e6b5, 0x66d0fb02,
0x5e9f46bf, 0x5a5e5b08, 0x571d7dd1, 0x53dc6066,
0x4d9b3063, 0x495a2dd4, 0x44190b0d, 0x40d816ba,
0xaca5c697, 0xa864db20, 0xa527fdf9, 0xa1e6e04e,
0xbfa1b04b, 0xbb60adfc, 0xb6238b25, 0xb2e29692,
0x8aad2b2f, 0x8e6c3698, 0x832f1041, 0x87ee0df6,
0x99a95df3, 0x9d684044, 0x902b669d, 0x94ea7b2a,
0xe0b41de7, 0xe4750050, 0xe9362689, 0xedf73b3e,
0xf3b06b3b, 0xf771768c, 0xfa325055, 0xfef34de2,
0xc6bcf05f, 0xc27dede8, 0xcf3ecb31, 0xcbffd686,
0xd5b88683, 0xd1799b34, 0xdc3abded, 0xd8fba05a,
0x690ce0ee, 0x6dcdfd59, 0x608edb80, 0x644fc637,
0x7a089632, 0x7ec98b85, 0x738aad5c, 0x774bb0eb,
0x4f040d56, 0x4bc510e1, 0x46863638, 0x42472b8f,
0x5c007b8a, 0x58c1663d, 0x558240e4, 0x51435d53,
0x251d3b9e, 0x21dc2629, 0x2c9f00f0, 0x285e1d47,
0x36194d42, 0x32d850f5, 0x3f9b762c, 0x3b5a6b9b,
0x0315d626, 0x07d4cb91, 0x0a97ed48, 0x0e56f0ff,
0x1011a0fa, 0x14d0bd4d, 0x19939b94, 0x1d528623,
0xf12f560e, 0xf5ee4bb9, 0xf8ad6d60, 0xfc6c70d7,
0xe22b20d2, 0xe6ea3d65, 0xeba91bbc, 0xef68060b,
0xd727bbb6, 0xd3e6a601, 0xdea580d8, 0xda649d6f,
0xc423cd6a, 0xc0e2d0dd, 0xcda1f604, 0xc960ebb3,
0xbd3e8d7e, 0xb9ff90c9, 0xb4bcb610, 0xb07daba7,
0xae3afba2, 0xaafbe615, 0xa7b8c0cc, 0xa379dd7b,
0x9b3660c6, 0x9ff77d71, 0x92b45ba8, 0x9675461f,
0x8832161a, 0x8cf30bad, 0x81b02d74, 0x857130c3,
0x5d8a9099, 0x594b8d2e, 0x5408abf7, 0x50c9b640,
0x4e8ee645, 0x4a4ffbf2, 0x470cdd2b, 0x43cdc09c,
0x7b827d21, 0x7f436096, 0x7200464f, 0x76c15bf8,
0x68860bfd, 0x6c47164a, 0x61043093, 0x65c52d24,
0x119b4be9, 0x155a565e, 0x18197087, 0x1cd86d30,
0x029f3d35, 0x065e2082, 0x0b1d065b, 0x0fdc1bec,
0x3793a651, 0x3352bbe6, 0x3e119d3f, 0x3ad08088,
0x2497d08d, 0x2056cd3a, 0x2d15ebe3, 0x29d4f654,
0xc5a92679, 0xc1683bce, 0xcc2b1d17, 0xc8ea00a0,
0xd6ad50a5, 0xd26c4d12, 0xdf2f6bcb, 0xdbee767c,
0xe3a1cbc1, 0xe760d676, 0xea23f0af, 0xeee2ed18,
0xf0a5bd1d, 0xf464a0aa, 0xf9278673, 0xfde69bc4,
0x89b8fd09, 0x8d79e0be, 0x803ac667, 0x84fbdbd0,
0x9abc8bd5, 0x9e7d9662, 0x933eb0bb, 0x97ffad0c,
0xafb010b1, 0xab710d06, 0xa6322bdf, 0xa2f33668,
0xbcb4666d, 0xb8757bda, 0xb5365d03, 0xb1f740b4 };
public static bool CRC32V3(byte[] buffer, uint crc)
{
uint result = 0xFFFFFFFF;
for (int i = 0; i < buffer.
(buffer[i] & 0xff)) & 0xff];
}
return result == crc;
}
Оптимизация получилась поистине хрестоматийная. Так как в библиотеке насчитывающей более 60 классов, сотни методов и почти 8000 строк кода замена только одного, вот этого метода, позволила сократить обработку тестового файла с записанным транспортным потоком с 8.5 сек до 4.2 сек. С точки зрения оптимизации этого метода — вопрос решён. Но вот с точки зрения изучения векторизации методов — нет. @aepot возможно этот табличный вариант лучше поддастся векторизации?
Crc32 Класс (System.IO.Hashing) | Microsoft Learn
Twitter LinkedIn Facebook Адрес электронной почты
- Ссылка
Определение
- Пространство имен:
- System. IO.Hashing
IO.Hashing- Сборка:
- System.IO.Hashing.dll
Важно!
Некоторые сведения относятся к предварительной версии продукта, в которую до выпуска могут быть внесены существенные изменения. Майкрософт не предоставляет никаких гарантий, явных или подразумеваемых, относительно приведенных здесь сведений.
Предоставляет реализацию алгоритма CRC-32, используемого в ITU-T V.42 и IEEE 802.3.
public ref class Crc32 sealed : System::IO::Hashing::NonCryptographicHashAlgorithm
public sealed class Crc32 : System.IO.Hashing.NonCryptographicHashAlgorithm
type Crc32 = class
inherit NonCryptographicHashAlgorithmPublic NotInheritable Class Crc32 Inherits NonCryptographicHashAlgorithm
- Наследование
Object
NonCryptographicHashAlgorithm
Crc32
Эта реализация выдает ответ в порядке байтов Little Endian, чтобы отношение остатков CRC (CRC(message concat CRC(message)было фиксированным значением).
Для CRC-32 этот стабильный результат является последовательностью 0x2144DF1CLittle Endian .
Существует несколько несовместимых определений 32-разрядной циклической проверки избыточности (CRC). При взаимодействии с другой системой убедитесь, что используется то же определение. Определение, используемое этой реализацией, несовместимо с проверкой циклической избыточности, описанной в ITU-T I.363.5.
Конструкторы
| Crc32() | Инициализирует новый экземпляр класса Crc32. |
Свойства
| HashLengthInBytes | Возвращает количество байтов, полученных из этого хэш-алгоритма. (Унаследовано от NonCryptographicHashAlgorithm) |
Методы
| Append(Byte[]) | Добавляет содержимое |
| Append(ReadOnlySpan<Byte>) | Добавляет содержимое |
| Append(Stream) | Добавляет содержимое |
| AppendAsync(Stream, CancellationToken) | Asychronously считывает содержимое |
| Equals(Object) | Определяет, равен ли указанный объект текущему объекту. (Унаследовано от Object) |
| GetCurrentHash() | Возвращает текущее вычисленное хэш-значение без изменения накопленных состояний. |
| GetCurrentHash(Span<Byte>) | Записывает вычисляемое хэш-значение |
| GetCurrentHashCore(Span<Byte>) | При переопределении в производном классе записывает вычисляемое хэш-значение |
| GetHashAndReset() | Возвращает текущее вычисленное хэш-значение и очищает накопленный состояние. (Унаследовано от NonCryptographicHashAlgorithm) |
| GetHashAndReset(Span<Byte>) | Записывает вычисленное хэш-значение, чтобы |
| GetHashAndResetCore(Span<Byte>) | Записывает вычисленное хэш-значение, чтобы |
| GetHashCode() | Является устаревшей. Этот метод не поддерживается и не должен вызываться. Вызов GetCurrentHash() или GetHashAndReset() вместо этого. (Унаследовано от NonCryptographicHashAlgorithm) |
| GetType() | Возвращает объект Type для текущего экземпляра. (Унаследовано от Object) |
| Hash(Byte[]) | Вычисляет хэш CRC-32 предоставленных данных. |
| Hash(ReadOnlySpan<Byte>) | Вычисляет хэш CRC-32 предоставленных данных. |
| Hash(ReadOnlySpan<Byte>, Span<Byte>) | Вычисляет хэш CRC-32 предоставленных данных в указанном месте назначения. |
| MemberwiseClone() | Создает неполную копию текущего объекта Object. (Унаследовано от Object) |
| Reset() | Сбрасывает хэш-вычисления в исходное состояние. |
| ToString() | Возвращает строку, представляющую текущий объект. (Унаследовано от Object) |
| TryGetCurrentHash(Span<Byte>, Int32) | Пытается записать вычисляемое хэш-значение |
| TryGetHashAndReset(Span<Byte>, Int32) | Пытается записать вычисляемое хэш-значение в |
| TryHash(ReadOnlySpan<Byte>, Span<Byte>, Int32) | Пытается вычислить хэш CRC-32 предоставленных данных в указанном месте назначения. |
В случае успешного выполнения очищает накопленный состояние.Применяется к
Алгоритм расчета контрольной суммы CRC32
Однако проблема состоит в том, что контроль с помощью 32-разрядного значения CRC (CRC32) обладает определенными недостатками. Так, он устойчиво обнаруживает случайные изменения во входной информации (например, возникающие в результате сбоев при передаче данных), однако недостаточно надежен в случае преднамеренных действий. Если для идентификации некоторого файла используется его 32-разрядный параметр CRC, то для злоумышленника не так уж сложно с помощью компьютера создать совершенно другой файл с тем же значением CRC.
Вот почему в целях безопасности в электронной подписи для выработки контрольной суммы (дайджеста) используются особые алгоритмы хэширования.
Хорошая хэш-функция работает таким образом, что принципиально невозможно создать два различных документа с одинаковой контрольной суммой. Первые алгоритмы хэширования допускали возможность существования текстов-близнецов. Это явление получило название «эффект дня рождения». Современные хэш-функции не содержат подобных «дыр».
Криптографические хэш-функции используются обычно для генерации дайджеста сообщения при создании цифровой подписи. Хэш-функции отображают сообщение в имеющее фиксированный размер хэш-значение (hash value) таким образом, что все множество возможных сообщений распределяется равномерно по множеству хэш-значений.
При этом криптографическая хэш-функция делает это таким образом, что практически невозможно подогнать документ к заданному хэш-значению.
Хэш-функцией называется такое математическое или алгоритмическое преобразование заданного блока данных, которое обладает следующими свойствами:
· Хэш-функция имеет бесконечную область определения;
· Хэш-функция имеет конечную область значений;
· Она необратима;
· Изменение входного потока информации на один бит меняет около половины всех бит выходного потока, то есть результата хэш-функции.
Эти свойства позволяют подавать на вход хэш-функции текстовые строки произвольной длины на любом национальном языке и, ограничив область значений функции диапазоном 0..2N-1, где N – длина ключа в битах, получать на выходе достаточно равномерно распределенные по области значения блоки информации – ключи.
Рассмотрим применение хэш-функций для проверки достоверности пароля. Пусть имеется криптографическая функция F, расшифровывающая ключом K последовательность Аi в последовательность Aj.
Разумеется, только для одного единственного K мы получим исходную последовательность Aj, а для всех остальных K – «мусор». Каким способом можно удостовериться, что полученная Aj и есть искомая последовательность? Можно сохранить фрагмент исходной последовательности и затем сверить его с полученным результатом. Однако это очень ненадежно, так как не гарантируется, что совпадение одного фрагмента обеспечивает совпадение всей последовательности.
Развитие криптографии привело к исследованию так называемых односторонних или однонаправленных функций. Однако, несмотря на внешнюю схожесть действий хэш и однонаправленных функций, это разные функции, которые изучаются различными разделами математики и обладают разными свойствами. Однако среди них есть и такие, которые удовлетворяют двум критериям сразу. Их называют однонаправленными хэш-функциями.
Однонаправленные хэш-функции
Вообще однонаправленными называют функции, которые вычислить сравнительно легко, но их обратные функции для вычисления требуют неприемлемых трудозатрат, то есть, более формально, однонаправленную функцию F(x) несложно рассчитать для каждого значения аргумента х, но очень трудно для известного значения F(x) вычислить соответствующее значение аргумента х. Примером однонаправленных функций могут служить полиномы. В этом случае вычисление обратной функции равносильно нахождению корней полинома, что, как известно из школьной алгебры, затруднительно даже для полинома третьей степени.
Особой разновидностью однонаправленных функций являются однонаправленные функции с тайной лазейкой. Такие функции, кроме однонаправленности, обладают дополнительным свойством – знание некой информации об этой функции делает подсчет обратной функции сравнительно нетрудным. Более формально, для однонаправленных функций с лазейкой нетрудно вычислить F(x) по заданному значению аргумента х, если не знать некую секретную информацию z. Собственно однонаправленные функции с тайной лазейкой служат математической основой для криптографии с открытым ключом.
Однонаправленной хэш-функцией, которую мы будем обозначать Н(М), называется такая однонаправленная функция, которая в качестве аргумента получает сообщение М произвольной длины и возвращает число h фиксированной разрядности m, то есть более формально
h = H(M),
где значение h называемое хэшем (или необратимым хэшем), имеющим разрядность m.
Вдобавок к указанному свойству, чтобы быть пригодными для практического применения однонаправленные хэш-функции должны иметь дополнительные свойства, которые, собственно, и позволяют использовать их для создания цифровой подписи:
· зная М легко вычислить h.
· зная h, трудно определить значение M, для которого H(M) = h.
· зная M, трудно определить другое сообщение M’, для которого H(M) = H(M’).
Простейшей функцией, обладающей перечисленными свойствами, является следующее преобразование h = H(M)
, ,
где H0 и p – параметры хэш-функции, h – результирующее значение хэша (его разрядность совпадает с разрядностью p).
Если же хэш-функция, использованная для вычисления дайджеста, обладает последним из указанных выше дополнительных свойств, то дайджест, по сути, становится уникальным идентификатором сообщения. В этом случае, если Участник-1 зашифрует дайджест сообщения своим закрытым ключом, то Участник-2 сможет удостовериться в его подлинности, восстановив дайджест с помощью открытого ключа Участника-1, далее самостоятельно вычислив дайджест сообщения и сравнив результат с дайджестом, полученным в сообщении.
Именно так и создается цифровая подпись документов средствами современных криптосистем.
Наиболее популярными функциями хэширования являются MD5 (Message Digest 5 – профиль сообщения 5), создающий 16-байтовый результат (128-битное значение хэш-функции), и алгоритм SHA (Secure Hash Algorithm – надежный алгоритм хэширования), формирующий 20-байтовый результат (160-битное значение хэш-функции). В настоящее время алгоритм SHA принят правительством США как стандарт.
Существует отечественный стандарт для хэш-функций ‑ ГОСТ Р34.11‑94; он используется совместно со стандартами ГОСТ Р34.10‑ 94/2001 для ЭЦП.
Стойкость функции хеширования примерно равна 2n/2, где п – длина выходного значения функции. В связи с разработкой в США новых стандартов шифрования с длиной ключа 128, 192 и 256 бит потребовалось создать «сопровождающие» алгоритмы, обеспечивающие такой же уровень стойкости. В качестве нового стандарта США предполагается перейти на алгоритмы вычисления хэш-функции с длиной выходного значения 256, 384 и 512 бит, имеющие название SHA-256, SHA-384, SHA-512 соответственно.
Насколько надежны хэш-функции? Например, возможна ли эффективная атака на RSA и другие, применяющие хэш-преобразования асимметричные системы? Над проблемой разложения на простые сомножители безуспешно бились многие знаменитые математики. Но до сих пор не доказано, что это невозможно. Впрочем, так же как не доказано существование идеальной однонаправленной функции. Но пока не появился математический гений, который решит эти задачи, ничего другого, кроме перебора, предложить не удается. Единственным выходом является не полный, а самоорганизующийся табличный поиск. Это может быть реализовано аппаратно (например, в виде чипа).
Системы, построенные на односторонних функциях при условии отсутствия ошибок реализации, взлому, как правило, не подлежат. Но такие программы сегодня – редкость (вспомним обнаруженные ошибки в продуктах таких гигантов как Microsoft, Novell). Использование контрольной суммы – это один из способов этот пароль найти. Крайне редко в системах массового применения используют односторонние хэш-функции.
Процесс подписания сообщения закрытым ключом К формально будем обозначать так:
SK(M).
Процесс проверки подлинности подписи с помощью соответствующего открытого ключа формально записывается так:
VK(M).
Цифровой подписью будем называть необратимый хэш документа, зашифрованный закрытым ключом. В компьютерном представлении цифровая подпись реализуется в виде строки двоичного кода, которая присоединяется к документу после его подписания (рис. 8).
Протокол, в котором сообщение подписывается закрытым ключом отправителя, а затем шифруется открытым ключом получателя сообщения (это обеспечивает конфиденциальность сообщения и подтверждение его авторства), выглядит следующим образом:
· Участник-1 подписывает сообщение своим закрытым ключом;
· Участник-1 шифрует подписанное сообщение открытым ключом и отправляет его Участнику-2;
· Участник-2 расшифровывает сообщение своим закрытым ключом;
· Участник-2 проверяет подлинность подписи.
Используя открытый ключ Участника-1, и восстанавливает сообщение.
| Рис. 8. Протокол работы цифровой электронной подписи |
Сделаем несколько замечаний к этому протоколу. Во-первых, для шифрования и подписания документов нет никакой необходимости использовать одну и ту же пару открытый/закрытый ключ; вместо этого каждый Участник может обзавестись несколькими парами ключей, имеющими разные сроки действия и разные разрядности. Во-вторых, примененное в протоколе подписание сообщения до шифрования позволяет избежать подмены подписи шифрованного сообщения. Кроме того, с юридической точки зрения законную силу имеет подпись только под доступным для прочтения документом. В-третьих, для предотвращения повторного использования сообщений в этом протоколе должны использоваться метки времени.
Возможности, открываемые с использованием криптосистем с открытыми ключами, практически безграничны. С развитием таких криптосистем появились реальные возможности для сетевой идентификации пользователей и придания цифровым электронным подписям юридического статуса (в РФ соответствующий закон был подписан Президентом в начале 2002 года).
Правовые условия использования электронной цифровой подписи в электронных документах регламентирует федеральный закон от 10.01.2002 N 1-ФЗ «Об электронной цифровой подписи».
В основе стандартов электронной цифровой подписи в США и России лежит схема Эль-Гамаля.
3.12. Алгоритмы работы с большими числами
В процессе работы с большими простыми числами очень часто возникает ситуация в которой алгоритмы прямого перебора работают слишком медленно и неэффективно, поэтому проектировщику асимметричных криптографических систем приходится использовать вероятностные методы и математические алгоритмы для оптимизации. Критичными с точки зрения производительности здесь являются следующие алгоритмы:
· поиска больших простых чисел;
· нахождения взаимно простых больших чисел;
· возведения в степень в конечном поле.
Расчет CRC32 — процессор LXP32
Простой пример: расчет CRC32 — процессор LXP32Введение
В этом документе мы будем использовать пример вычисления CRC32, чтобы проиллюстрировать различные методы оптимизации, которые можно использовать в языке ассемблера LXP32.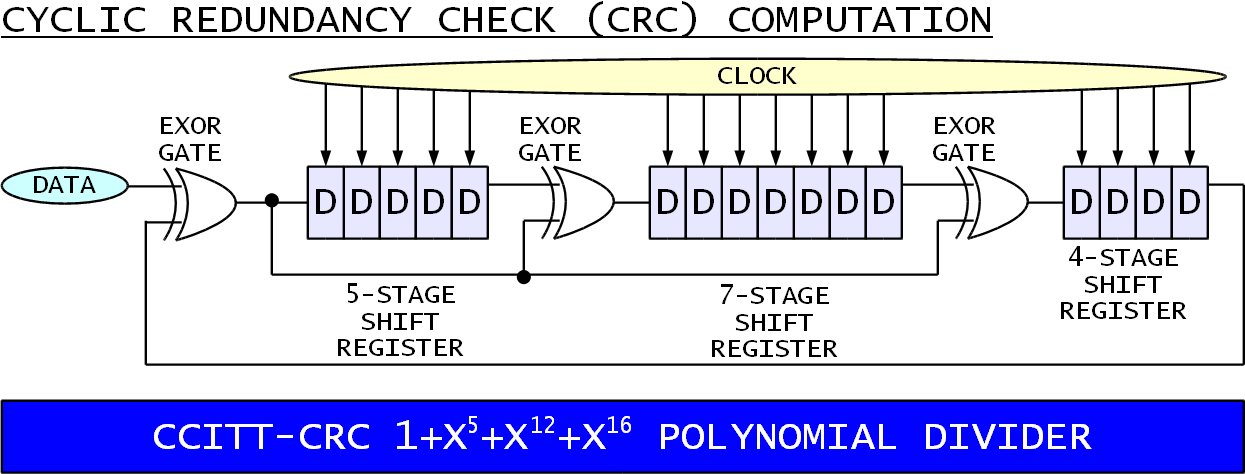
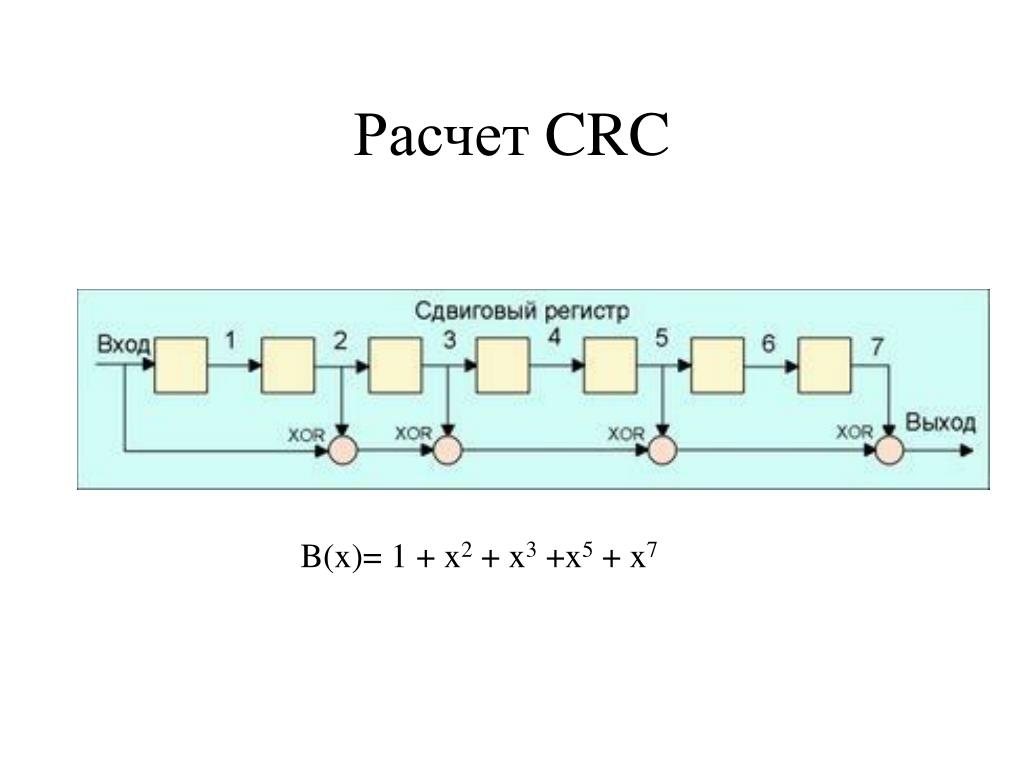
CRC32 — это популярный алгоритм контрольной суммы, используемый для обнаружения повреждения данных. Существует несколько вариантов алгоритма со схожими математическими свойствами. Наиболее распространенный вариант контрольной суммы CRC32, иногда называемый CRC-32b, основан на следующем порождающем полиноме:
g ( x ) = x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + х + 1,90xEDB88320; ч>>=1; } } возврат ~CRC; }
Этот код обрабатывает по одному биту за раз. 0xEDB88320 — это так называемое обратное
представление полинома генератора CRC32, предназначенное для работы с реализациями с первым младшим битом, подобным этой.
Тот же полином может быть также представлен как 0x04C11DB7 для реализаций с первым старшим битом (это называется обычным представлением
).
При вызове со строкой «123456789» в качестве аргумента (без завершающего нулевого символа) эта функция вернет 0xCBF439.26.
Побитовая реализация
Ниже представлена реализация этого алгоритма на языке ассемблера LXP32, которая более или менее эквивалентна приведенному выше коду:
#экспорт Crc32_proc
/*
* Crc32_proc
*
* Рассчитывает наиболее распространенный вариант контрольной суммы CRC32
*
* Пример: CRC32("123456789") = 0xCBF43926.
*
* Входы
* r1: crc (начальное значение CRC, обычно 0, см. ниже)
* r2: p (указатель строки)
* r3: n (длина строки в байтах)
* Выходы
* r1: значение CRC
*
* Примечание: аргумент "crc" должен быть первоначально установлен в 0. Чтобы продолжить
* вычисление, установите его на значение, возвращенное предыдущим вызовом.
* Это может быть полезно для вычисления контрольной суммы для длинного потока данных.
*/
#define crc r1
#define p r2
#define n r3
#define ch r4
#define j r5
#define b r6
#define полином r7
#define string_end_ptr r8
#определить dont_xor_ptr r9
# определить bit_loop_ptr r10
# определить byte_loop_ptr r11
Crc32_proc:
cjmpe rp, n, 0 // Немедленный возврат, если строка пуста
lc полином, 0xEDB88320
добавить string_end_ptr, p, n
lcs dont_xor_ptr, Crc32_dont_xor
lcs bit_loop_ptr, Crc32_bit_loop
lcs byte_loop_ptr, Crc32_byte_loop
вместо контрольная сумма, контрольная сумма
Crc32_byte_loop:
луб ч, р
мов й, 0
Crc32_bit_loop:
xor b, ch, crc
и б, б, 1
sru crc, crc, 1
cjmpe dont_xor_ptr, b, 0
xor crc, crc, многочлен
Crc32_dont_xor:
сру ч, ч, 1
добавить й, й, 1
cjmpul bit_loop_ptr, j, 8 // конец цикла битов
добавить р, р, 1
cjmpul byte_loop_ptr, p, string_end_ptr // конец цикла байтов
вместо контрольная сумма, контрольная сумма
повторно 
*/
#define crc r1
#define p r2
#define n r3
#define ch r4
#define j r5
#define b r6
#define полином r7
#define string_end_ptr r8
#определить dont_xor_ptr r9
# определить bit_loop_ptr r10
# определить byte_loop_ptr r11
Crc32_proc:
cjmpe rp, n, 0 // Немедленный возврат, если строка пуста
lc полином, 0xEDB88320
добавить string_end_ptr, p, n
lcs dont_xor_ptr, Crc32_dont_xor
lcs bit_loop_ptr, Crc32_bit_loop
lcs byte_loop_ptr, Crc32_byte_loop
вместо контрольная сумма, контрольная сумма
Crc32_byte_loop:
луб ч, р
мов й, 0
Crc32_bit_loop:
xor b, ch, crc
и б, б, 1
sru crc, crc, 1
cjmpe dont_xor_ptr, b, 0
xor crc, crc, многочлен
Crc32_dont_xor:
сру ч, ч, 1
добавить й, й, 1
cjmpul bit_loop_ptr, j, 8 // конец цикла битов
добавить р, р, 1
cjmpul byte_loop_ptr, p, string_end_ptr // конец цикла байтов
вместо контрольная сумма, контрольная сумма
повторно Примечания:
- Эта процедура соответствует соглашению о вызовах, рекомендованному руководством. Поскольку он не вызывает никаких вложенных процедур, а регистры r0–r31 обозначены как сохраняемые вызывающей стороной, ему не нужно использовать стек.
- Предполагается, что код расположен в начале или конце адресного пространства, поэтому для загрузки указателей используется lcs ( Load Constant Short ). Если компоновщик жалуется на то, что указатели находятся вне допустимого диапазона, замените lcs на lc .
- Чтобы сократить время выполнения цикла, все указатели ветвления предварительно загружаются. Кроме того, чтобы не отслеживать как i, так и текущий указатель байта, мы вычисляем string_end_ptr в начале и вообще не используем переменную i.
- Циклы реализованы как постусловия для сокращения времени выполнения. Сравните цикл предварительного условия:
Crc32_byte_loop: cjmpuge loop_end_ptr, p, string_end_ptr луб ч, р ... jmp byte_loop_ptr
с постусловием:
Crc32_byte_loop: луб ч, р .
В версии с предварительным условием cjmpuge выполняется за 2 цикла (при условии, что переход не выполнен) и за 9 циклов.0071 jmp требует 4 цикла. В версии с пост-условием нам нужно всего 5 циклов для cjmpul (при условии, что прыжок выполнен). ..
cjmpul byte_loop_ptr, p, string_end_ptr - Самый внутренний оператор if можно заменить умножением:
Crc32_bit_loop: xor b, ch, crc и б, б, 1 sru crc, crc, 1
Эта модификация выгодна только тогда, когда ЦП сконфигурирован с множителем «dsp».cjmpe dont_xor_ptr, b, 0mul b, b, полиномиальныйxor crc, crc, многочленxor контрольная сумма, контрольная сумма, бCrc32_dont_xor:сру ч, ч, 1 добавить й, й, 1 cjmpul bit_loop_ptr, j, 8 - Условные переходы или любые переходы с использованием косвенной адресации могут быть дорогостоящими в конвейерных процессорах, поскольку конвейер должен очищаться. Более продвинутые процессоры смягчают эту проблему, используя предсказание переходов (или даже спекулятивное выполнение), но в LXP32 эта функция отсутствует. Чтобы повысить производительность за счет размера кода, внутренний цикл (т. е.
битовый цикл
) можно развернуть полностью. В этом случае переменная j не нужна:Crc32_byte_loop: луб ч, р // бит 0 xor b, ch, crc и б, б, 1 sru crc, crc, 1 lcs r0, Crc32_dont_xor_bit0 cjmpe р0, б, 0 xor crc, crc, многочлен Crc32_dont_xor_bit0: сру ч, ч, 1 // бит 1 xor b, ch, crc и б, б, 1 sru crc, crc, 1 lcs r0, Crc32_dont_xor_bit1 cjmpe р0, б, 0 xor crc, crc, многочлен Crc32_dont_xor_bit1: сру ч, ч, 1 ... // бит 7 xor b, ch, crc и б, б, 1 sru crc, crc, 1 lcs r0, Crc32_dont_xor_bit7 cjmpe р0, б, 0 xor crc, crc, многочлен Crc32_dont_xor_bit7: добавить р, р, 1 cjmpul byte_loop_ptr, p, string_end_ptr
Поскольку он не вызывает никаких вложенных процедур, а регистры r0–r31 обозначены как сохраняемые вызывающей стороной, ему не нужно использовать стек.
..
cjmpul byte_loop_ptr, p, string_end_ptr 
Более продвинутые процессоры смягчают эту проблему, используя предсказание переходов (или даже спекулятивное выполнение), но в LXP32 эта функция отсутствует. Чтобы повысить производительность за счет размера кода, внутренний цикл (т. е. Побайтовая реализация
Также можно вычислять CRC32 побайтно, полностью устраняя битовый цикл.
Этот подход примерно в шесть раз быстрее предыдущего, но требует дополнительной памяти для предварительно рассчитанной таблицы поиска из 256 слов. Идея описана в Todd K. Moon, Error Correction Coding. Математические методы и алгоритмы
, Wiley, 2005, ISBN 0-471-64800-0 .
Побайтовая реализация алгоритма CRC32 может быть проиллюстрирована следующим кодом: 9crc32_table[т]; } возврат ~CRC; }
build_crc32_table() необходимо вызывать перед первым вызовом функции crc32_fast().
Ниже представлена реализация этого алгоритма на языке ассемблера LXP32. Он включает в себя всю таблицу поиска, чтобы избежать ее вычисления во время выполнения.
#экспорт Crc32_fast_proc
/*
* Crc32_fast_proc
*
* Рассчитывает наиболее распространенный вариант контрольной суммы CRC32
* с использованием быстрого побайтового алгоритма.
*
* Пример: CRC32("123456789") = 0xCBF43926.
*
* Входы
* r1: crc (начальное значение CRC, обычно 0, см.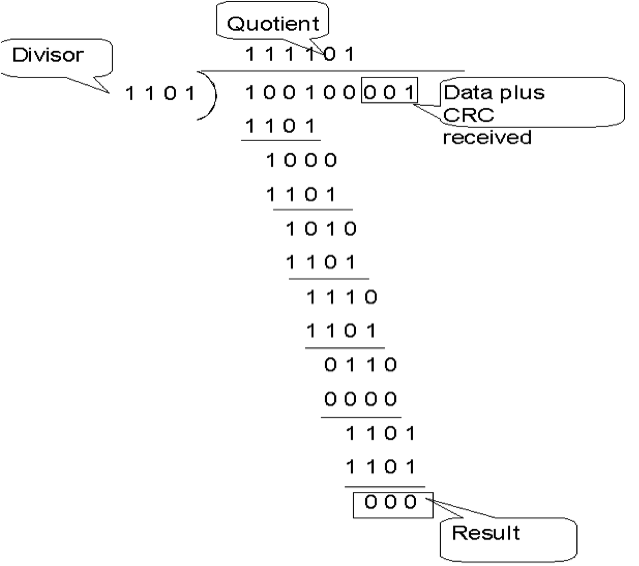 ниже)
* r2: p (указатель строки)
* r3: n (длина строки в байтах)
* Выходы
* r1: значение CRC
*
* Примечание: аргумент "crc" должен быть первоначально установлен в 0. Чтобы продолжить
* вычисление, установите его на значение, возвращенное предыдущим вызовом.
* Это может быть полезно для вычисления контрольной суммы для длинного потока данных.
*/
#define crc r1
#define p r2
#define n r3
# определить х р4
#define string_end_ptr r5
#define константа_ff r6
#define table_ptr r7
#define loop_ptr r8
Crc32_fast_proc:
cjmpe rp, n, 0 // Немедленный возврат, если строка пуста
добавить string_end_ptr, p, n
lcs константа_ff, 0xFF
lcs table_ptr, Crc32_fast_table
lcs loop_ptr, Crc32_fast_loop
вместо контрольная сумма, контрольная сумма
Crc32_fast_loop:
смазка х, стр // х := ч
xor x, x, crc
и х, х, константа_ff // х := т
сл х, х, 2
добавить x, table_ptr, x // x := &crc32_table[t]
lw х, х // х := crc32_table[t]
sru crc, crc, 8
xor контрольная сумма, контрольная сумма, х
добавить р, р, 1
cjmpul loop_ptr, p, string_end_ptr
вместо контрольная сумма, контрольная сумма
рет
Crc32_fast_table:
. слово 0x00000000, 0x77073096, 0xEE0E612C, 0x9BA
.word 0x076DC419, 0x706AF48F, 0xE963A535, 0x9E6495A3
.word 0x0EDB8832, 0x79DCB8A4, 0xE0D5E91E, 0x97D2D988
.word 0x09B64C2B, 0x7EB17CBD, 0xE7B82D07, 0x90BF1D91
.word 0x1DB71064, 0x6AB020F2, 0xF3B97148, 0x84BE41DE
.word 0x1ADAD47D, 0x6DDDE4EB, 0xF4D4B551, 0x83D385C7
.word 0x136C9856, 0x646BA8C0, 0xFD62F97A, 0x8A65C9EC
.word 0x14015C4F, 0x63066CD9, 0xFA0F3D63, 0x8D080DF5
.word 0x3B6E20C8, 0x4C69105E, 0xD56041E4, 0xA2677172
.word 0x3C03E4D1, 0x4B04D447, 0xD20D85FD, 0xA50AB56B
.word 0x35B5A8FA, 0x42B2986C, 0xDBBBC9D6, 0xACBCF940
.word 0x32D86CE3, 0x45DF5C75, 0xDCD60DCF, 0xABD13D59
.слово 0x26D930AC, 0x51DE003A, 0xC8D75180, 0xBFD06116
.word 0x21B4F4B5, 0x56B3C423, 0xCFBA9599, 0xB8BDA50F
.word 0x2802B89E, 0x5F058808, 0xC60CD9B2, 0xB10BE924
.word 0x2F6F7C87, 0x58684C11, 0xC1611DAB, 0xB6662D3D
.word 0x76DC4190, 0x01DB7106, 0x98D220BC, 0xEFD5102A
. word 0x71B18589, 0x06B6B51F, 0x9FBFE4A5, 0xE8B8D433
.слово 0x7807C9A2, 0x0F00F934, 0x9609A88E, 0xE10E9818
.word 0x7F6A0DBB, 0x086D3D2D, 0x91646C97, 0xE6635C01
.word 0x6B6B51F4, 0x1C6C6162, 0x856530D8, 0xF262004E
.слово 0x6C0695ED, 0x1B01A57B, 0x8208F4C1, 0xF50FC457
.слово 0x65B0D9C6, 0x12B7E950, 0x8BBEB8EA, 0xFCB9887C
.слово 0x62DD1DDF, 0x15DA2D49, 0x8CD37CF3, 0xFBD44C65
.слово 0x4DB26158, 0x3AB551CE, 0xA3BC0074, 0xD4BB30E2
.word 0x4ADFA541, 0x3DD895D7, 0xA4D1C46D, 0xD3D6F4FB
.word 0x4369E96A, 0x346ED9FC, 0xAD678846, 0xDA60B8D0
.слово 0x44042D73, 0x33031DE5, 0xAA0A4C5F, 0xDD0D7CC9
.слово 0x5005713C, 0x270241AA, 0xBE0B1010, 0xC90C2086
.word 0x5768B525, 0x206F85B3, 0xB966D409, 0xCE61E49F
.word 0x5EDEF90E, 0x29D9C998, 0xB0D09822, 0xC7D7A8B4
.word 0x59B33D17, 0x2EB40D81, 0xB7BD5C3B, 0xC0BA6CAD
.слово 0xEDB88320, 0x9ABFB3B6, 0x03B6E20C, 0x74B1D29A
.word 0xEAD54739, 0x9DD277AF, 0x04DB2615, 0x73DC1683
. word 0xE3630B12, 0x94643B84, 0x0D6D6A3E, 0x7A6A5AA8
.word 0xE40ECF0B, 0x9309FF9D, 0x0A00AE27, 0x7D079EB1
.слово 0xF00F9344, 0x8708A3D2, 0x1E01F268, 0x6906C2FE
.word 0xF762575D, 0x806567CB, 0x196C3671, 0x6E6B06E7
.слово 0xFED41B76, 0x89D32BE0, 0x10DA7A5A, 0x67DD4ACC
.слово 0xF9B9DF6F, 0x8EBEEFF9, 0x17B7BE43, 0x60B08ED5
.word 0xD6D6A3E8, 0xA1D1937E, 0x38D8C2C4, 0x4FDFF252
.word 0xD1BB67F1, 0xA6BC5767, 0x3FB506DD, 0x48B2364B
.word 0xD80D2BDA, 0xAF0A1B4C, 0x36034AF6, 0x41047A60
.word 0xDF60EFC3, 0xA867DF55, 0x316E8EEF, 0x4669BE79
.слово 0xCB61B38C, 0xBC66831A, 0x256FD2A0, 0x5268E236
.word 0xCC0C7795, 0xBB0B4703, 0x220216B9, 0x5505262F
.word 0xC5BA3BBE, 0xB2BD0B28, 0x2BB45A92, 0x5CB36A04
.word 0xC2D7FFA7, 0xB5D0CF31, 0x2CD99E8B, 0x5BDEAE1D
.слово 0x9B64C2B0, 0xEC63F226, 0x756AA39C, 0x026D930A
.word 0x9C0906A9, 0xEB0E363F, 0x72076785, 0x05005713
.word 0x95BF4A82, 0xE2B87A14, 0x7BB12BAE, 0x0CB61B38
. слово 0x92D28E9B, 0xE5D5BE0D, 0x7CDCEFB7, 0x0BDBDF21
.слово 0x86D3D2D4, 0xF1D4E242, 0x68DDB3F8, 0x1FDA836E
.слово 0x81BE16CD, 0xF6B9265Б, 0x6FB077E1, 0x18B74777
.word 0x88085AE6, 0xFF0F6A70, 0x66063BCA, 0x11010B5C
.word 0x8F659EFF, 0xF862AE69, 0x616BFFD3, 0x166CCF45
.word 0xA00AE278, 0xD70DD2EE, 0x4E048354, 0x3903B3C2
.word 0xA7672661, 0xD06016F7, 0x4969474D, 0x3E6E77DB
.word 0xAED16A4A, 0xD9D65ADC, 0x40DF0B66, 0x37D83BF0
.word 0xA9BCAE53, 0xDEBB9EC5, 0x47B2CF7F, 0x30B5FFE9
.слово 0xBDBDF21C, 0xCABAC28A, 0x53B39330, 0x24B4A3A6
.word 0xBAD03605, 0xCDD70693, 0x54DE5729, 0x23D967BF
.word 0xB3667A2E, 0xC4614AB8, 0x5D681B02, 0x2A6F2B94
.word 0xB40BBE37, 0xC30C8EA1, 0x5A05DF1B, 0x2D02EF8D 
ниже)
* r2: p (указатель строки)
* r3: n (длина строки в байтах)
* Выходы
* r1: значение CRC
*
* Примечание: аргумент "crc" должен быть первоначально установлен в 0. Чтобы продолжить
* вычисление, установите его на значение, возвращенное предыдущим вызовом.
* Это может быть полезно для вычисления контрольной суммы для длинного потока данных.
*/
#define crc r1
#define p r2
#define n r3
# определить х р4
#define string_end_ptr r5
#define константа_ff r6
#define table_ptr r7
#define loop_ptr r8
Crc32_fast_proc:
cjmpe rp, n, 0 // Немедленный возврат, если строка пуста
добавить string_end_ptr, p, n
lcs константа_ff, 0xFF
lcs table_ptr, Crc32_fast_table
lcs loop_ptr, Crc32_fast_loop
вместо контрольная сумма, контрольная сумма
Crc32_fast_loop:
смазка х, стр // х := ч
xor x, x, crc
и х, х, константа_ff // х := т
сл х, х, 2
добавить x, table_ptr, x // x := &crc32_table[t]
lw х, х // х := crc32_table[t]
sru crc, crc, 8
xor контрольная сумма, контрольная сумма, х
добавить р, р, 1
cjmpul loop_ptr, p, string_end_ptr
вместо контрольная сумма, контрольная сумма
рет
Crc32_fast_table:
.
слово 0x00000000, 0x77073096, 0xEE0E612C, 0x9BA
.word 0x076DC419, 0x706AF48F, 0xE963A535, 0x9E6495A3
.word 0x0EDB8832, 0x79DCB8A4, 0xE0D5E91E, 0x97D2D988
.word 0x09B64C2B, 0x7EB17CBD, 0xE7B82D07, 0x90BF1D91
.word 0x1DB71064, 0x6AB020F2, 0xF3B97148, 0x84BE41DE
.word 0x1ADAD47D, 0x6DDDE4EB, 0xF4D4B551, 0x83D385C7
.word 0x136C9856, 0x646BA8C0, 0xFD62F97A, 0x8A65C9EC
.word 0x14015C4F, 0x63066CD9, 0xFA0F3D63, 0x8D080DF5
.word 0x3B6E20C8, 0x4C69105E, 0xD56041E4, 0xA2677172
.word 0x3C03E4D1, 0x4B04D447, 0xD20D85FD, 0xA50AB56B
.word 0x35B5A8FA, 0x42B2986C, 0xDBBBC9D6, 0xACBCF940
.word 0x32D86CE3, 0x45DF5C75, 0xDCD60DCF, 0xABD13D59
.слово 0x26D930AC, 0x51DE003A, 0xC8D75180, 0xBFD06116
.word 0x21B4F4B5, 0x56B3C423, 0xCFBA9599, 0xB8BDA50F
.word 0x2802B89E, 0x5F058808, 0xC60CD9B2, 0xB10BE924
.word 0x2F6F7C87, 0x58684C11, 0xC1611DAB, 0xB6662D3D
.word 0x76DC4190, 0x01DB7106, 0x98D220BC, 0xEFD5102A
.
word 0x71B18589, 0x06B6B51F, 0x9FBFE4A5, 0xE8B8D433
.слово 0x7807C9A2, 0x0F00F934, 0x9609A88E, 0xE10E9818
.word 0x7F6A0DBB, 0x086D3D2D, 0x91646C97, 0xE6635C01
.word 0x6B6B51F4, 0x1C6C6162, 0x856530D8, 0xF262004E
.слово 0x6C0695ED, 0x1B01A57B, 0x8208F4C1, 0xF50FC457
.слово 0x65B0D9C6, 0x12B7E950, 0x8BBEB8EA, 0xFCB9887C
.слово 0x62DD1DDF, 0x15DA2D49, 0x8CD37CF3, 0xFBD44C65
.слово 0x4DB26158, 0x3AB551CE, 0xA3BC0074, 0xD4BB30E2
.word 0x4ADFA541, 0x3DD895D7, 0xA4D1C46D, 0xD3D6F4FB
.word 0x4369E96A, 0x346ED9FC, 0xAD678846, 0xDA60B8D0
.слово 0x44042D73, 0x33031DE5, 0xAA0A4C5F, 0xDD0D7CC9
.слово 0x5005713C, 0x270241AA, 0xBE0B1010, 0xC90C2086
.word 0x5768B525, 0x206F85B3, 0xB966D409, 0xCE61E49F
.word 0x5EDEF90E, 0x29D9C998, 0xB0D09822, 0xC7D7A8B4
.word 0x59B33D17, 0x2EB40D81, 0xB7BD5C3B, 0xC0BA6CAD
.слово 0xEDB88320, 0x9ABFB3B6, 0x03B6E20C, 0x74B1D29A
.word 0xEAD54739, 0x9DD277AF, 0x04DB2615, 0x73DC1683
.
word 0xE3630B12, 0x94643B84, 0x0D6D6A3E, 0x7A6A5AA8
.word 0xE40ECF0B, 0x9309FF9D, 0x0A00AE27, 0x7D079EB1
.слово 0xF00F9344, 0x8708A3D2, 0x1E01F268, 0x6906C2FE
.word 0xF762575D, 0x806567CB, 0x196C3671, 0x6E6B06E7
.слово 0xFED41B76, 0x89D32BE0, 0x10DA7A5A, 0x67DD4ACC
.слово 0xF9B9DF6F, 0x8EBEEFF9, 0x17B7BE43, 0x60B08ED5
.word 0xD6D6A3E8, 0xA1D1937E, 0x38D8C2C4, 0x4FDFF252
.word 0xD1BB67F1, 0xA6BC5767, 0x3FB506DD, 0x48B2364B
.word 0xD80D2BDA, 0xAF0A1B4C, 0x36034AF6, 0x41047A60
.word 0xDF60EFC3, 0xA867DF55, 0x316E8EEF, 0x4669BE79
.слово 0xCB61B38C, 0xBC66831A, 0x256FD2A0, 0x5268E236
.word 0xCC0C7795, 0xBB0B4703, 0x220216B9, 0x5505262F
.word 0xC5BA3BBE, 0xB2BD0B28, 0x2BB45A92, 0x5CB36A04
.word 0xC2D7FFA7, 0xB5D0CF31, 0x2CD99E8B, 0x5BDEAE1D
.слово 0x9B64C2B0, 0xEC63F226, 0x756AA39C, 0x026D930A
.word 0x9C0906A9, 0xEB0E363F, 0x72076785, 0x05005713
.word 0x95BF4A82, 0xE2B87A14, 0x7BB12BAE, 0x0CB61B38
.
слово 0x92D28E9B, 0xE5D5BE0D, 0x7CDCEFB7, 0x0BDBDF21
.слово 0x86D3D2D4, 0xF1D4E242, 0x68DDB3F8, 0x1FDA836E
.слово 0x81BE16CD, 0xF6B9265Б, 0x6FB077E1, 0x18B74777
.word 0x88085AE6, 0xFF0F6A70, 0x66063BCA, 0x11010B5C
.word 0x8F659EFF, 0xF862AE69, 0x616BFFD3, 0x166CCF45
.word 0xA00AE278, 0xD70DD2EE, 0x4E048354, 0x3903B3C2
.word 0xA7672661, 0xD06016F7, 0x4969474D, 0x3E6E77DB
.word 0xAED16A4A, 0xD9D65ADC, 0x40DF0B66, 0x37D83BF0
.word 0xA9BCAE53, 0xDEBB9EC5, 0x47B2CF7F, 0x30B5FFE9
.слово 0xBDBDF21C, 0xCABAC28A, 0x53B39330, 0x24B4A3A6
.word 0xBAD03605, 0xCDD70693, 0x54DE5729, 0x23D967BF
.word 0xB3667A2E, 0xC4614AB8, 0x5D681B02, 0x2A6F2B94
.word 0xB40BBE37, 0xC30C8EA1, 0x5A05DF1B, 0x2D02EF8D python — Расчет Ethernet CRC32 — программное обеспечение и алгоритмический результат
Вопрос задан
Изменено 2 месяца назад
Просмотрено 33k раз
Я пытаюсь побайтно вычислить последовательность проверки кадра (FCS) пакета Ethernet.
Многочлен равен 0x104C11DB7 .
Я следовал алгоритму XOR-SHIFT, показанному здесь http://en.wikipedia.org/wiki/Cyclic_redundancy_check или здесь http://www.woodmann.com/fravia/crctut1.htm
Предположим, что информация, которая должна иметь CRC состоит только из одного байта. Допустим, это 0x03.
шаг: дополнить 32 битами вправо
0x0300000000выровняйте полином и данные в левой части с их первым битом, который не равен нулю, и выполните операцию xor
0x300000000 xor 0x209823B6E = 0x109823b6eвыровнять остаток и снова выполнить операцию xor
0x109823b6e xor 0x104C11DB7 = 0x0d4326d9
Поскольку больше не осталось битов, CRC32 0x03 должен быть 0x0d4326d9
К сожалению, все программные реализации говорят мне, что я не прав, но что я сделал не так или что они делают по-другому?
Python говорит мне:
"0x%08x" % binascii.
crc32(chr(0x03))
0x4b0bbe37
Онлайн-инструмент http://www.lammertbies.nl/comm/info/crc-calculation.html#intr дает тот же результат. В чем разница между моим расчетом руки и алгоритмом, который использует упомянутое программное обеспечение?
ОБНОВЛЕНИЕ:
Оказывается, подобный вопрос уже был о переполнении стека:
Вы найдете ответ здесь Python CRC-32 woes
Хотя это не очень интуитивно понятно. Если вам нужно более формальное описание того, как это делается для кадров Ethernet, вы можете посмотреть документ стандарта Ethernet 802.3, часть 3 — глава 3.2.9.Поле последовательности проверки кадра
Давайте продолжим пример выше:
Поменяйте порядок битов вашего сообщения на обратный. Это представляет собой способ, которым они будут поступать в приемник по крупицам.
0x03поэтому0xC0Дополните первые 32 бита сообщения. Обратите внимание, что мы снова дополняем один байт 32 битами.
0xC000000000 xor 0xFFFFFFFF = 0x3FFFFFFFF00Снова выполните Xor и метод сдвига сверху. Примерно через 6 шагов вы получите:
0x13822f2dЗатем указанная выше последовательность битов дополняется.
0x13822f2d xor 0xFFFFFFFF = 0xec7dd0d2Помните, что мы изменили порядок битов, чтобы получить представление о проводе Ethernet на первом шаге. Теперь нам нужно отменить этот шаг, и мы, наконец, выполним наш квест.
0x4b0bbe37
Тот, кто придумал этот способ, должен быть …
Много раз вы действительно хотите знать, что полученное вами сообщение верно. Для этого вы берете полученное сообщение, включая FCS, и выполняете те же шаги с 1 по 5, что и выше. В результате должно получиться то, что они называют остатком. Что является константой для данного многочлена. В данном случае это 0xC704DD7B .
Как упоминает mcdowella , вы должны поиграть со своими битами, пока не получите правильный результат, в зависимости от используемого приложения.
- питон
- алгоритм
- Ethernet
- crc32
7
Этот фрагмент записывает правильную CRC для Ethernet.
Python 3
# запись полезной нагрузки
для байта в данных:
f.write(f'{byte:02X}\n')
# пишем ФКС
crc = zlib.crc32 (данные)
для я в диапазоне (4):
байт = (CRC >> (8*i)) & 0xFF
f.write(f'{byte:02X}\n')
Python 2
# запись полезной нагрузки
для байта в данных:
f.write('%02X\n' % порядок(байт))
# пишем ФКС
crc = zlib.crc32(данные) и 0xFFFFFFFF
для я в диапазоне (4):
байт = (CRC >> (8*i)) & 0xFF
f.write('%02X\n' % байт)
Если бы я нашел это здесь, это сэкономило бы мне время.
3
Обычно требуется немного проб и ошибок, чтобы добиться совпадения вычислений CRC, потому что вы никогда не прочитаете, что именно нужно сделать. Иногда вам нужно инвертировать входные байты или полином, иногда вам нужно начинать с ненулевого значения и так далее.
Один из способов обойти это — посмотреть на исходный код программы, которая делает это правильно, например, http://sourceforge.net/projects/crcmod/files/ (по крайней мере, он утверждает, что соответствует, и поставляется с модульным тестом для этого).
Другой вариант — поэкспериментировать с реализацией. Например, если я использую калькулятор по адресу http://www.lammertbies.nl/comm/info/crc-calculation.html#intr, я вижу, что при вводе 00000000 получается CRC 0x2144DF1C, а при вводе FFFFFFFF получается FFFFFFFF — так что это не совсем полиномиальное деление, которое вы описываете, для которого 0 будет иметь контрольную сумму 0
. Из беглого взгляда на исходный код и эти результаты я думаю, что вам нужно начать с CRC 0xFFFFFFFF — но я могу ошибаться, и вы могли бы в конечном итоге отладьте свой код рядом с реализацией, используя соответствующие printfs, чтобы узнать, где первые отличаются, и исправляя различия одно за другим.
В Интернете есть несколько мест, где вы прочтете, что перед вычислением FCS необходимо изменить порядок битов, но спецификация 802.
3 не входит в их число. Цитата из версии спецификации 2008 года:
3.2.9 Поле Frame Check Sequence (FCS)
Проверка циклическим избыточным кодом (CRC) используется алгоритмами передачи и приема для
генерировать значение CRC для поля FCS. Поле FCS содержит 4 октета (32 бита)
значение CRC. Это значение вычисляется как функция содержимого защищенного
поля кадра MAC: адрес назначения, адрес источника, длина/тип
поле, Данные клиента MAC и Pad (то есть все поля, кроме FCS). Кодировка
определяется следующим производящим полиномом.
G(х) = х32 + х26 + х23 + х22 + х16 + х12 + х11
+ х10 + х8 + х7 + х5 + х4 + х2 + х + 1
Математически значение CRC, соответствующее данному кадру MAC, определяется как
следующую процедуру:
а) Дополняются первые 32 бита кадра.
b) Затем n битов защищенных полей считаются коэффициентами
полинома M(x) степени n – 1. (Первый бит адреса назначения
Поле соответствует термину x(n–1) и последнему биту клиентских данных MAC.
поле (или поле Pad, если оно присутствует) соответствует термину x0. )
c) M(x) умножается на x32 и делится на G(x), что дает остаток R(x) от
степень ≤ 31.
г) Коэффициенты R(x) считаются 32-битной последовательностью.
e) Битовая последовательность дополняется, и результатом является CRC.
32 бита значения CRC помещаются в поле FCS, так что термин x31 равен
крайний левый бит первого октета, а термин x0 является крайним правым битом
последний октет. (Таким образом, биты CRC передаются в порядке x31, x30,...,
x1, x0.) См. Hammond, et al. [Б37].
)
c) M(x) умножается на x32 и делится на G(x), что дает остаток R(x) от
степень ≤ 31.
г) Коэффициенты R(x) считаются 32-битной последовательностью.
e) Битовая последовательность дополняется, и результатом является CRC.
32 бита значения CRC помещаются в поле FCS, так что термин x31 равен
крайний левый бит первого октета, а термин x0 является крайним правым битом
последний октет. (Таким образом, биты CRC передаются в порядке x31, x30,...,
x1, x0.) См. Hammond, et al. [Б37].
Конечно, остальные биты кадра передаются в обратном порядке, но это не включает FCS. Опять же из спецификации:
3.3 Порядок передачи битов Каждый октет кадра MAC, за исключением FCS, передается как минимум значащий бит первым.
2
http://en.wikipedia.org/wiki/Cyclic_redundancy_check
содержит все данные для Ethernet и множество важных деталей, например, есть (по крайней мере) 2 соглашения для кодирования полинома в 32-битное значение, наибольшее первым термином или первым наименьшим термином.
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
справочная страница crc32 раздел n
|
| ||||||||||
..123456789lncrc32(n) Циклические проверки избыточности crc32(n) ____________________________________________________________________________
ИМЯ
crc32 — выполнить 32-битную циклическую проверку избыточности
ОБЗОР
пакет требует Tcl 8.2
пакет требует crc32 ?1.3?
::crc::crc32 ?-формат формат ? ?-seed значение ? [ -канал чан | -имя файла
файл | сообщение ]
::crc::Crc32Init ? семян ?
::crc::Crc32Update токен данные
::crc::Crc32Final токен
_________________________________________________________________
ОПИСАНИЕ
Этот пакет предоставляет Tcl-реализацию алгоритма CRC-32.
на основе информации, представленной на http://www.naaccr.org/stan-
dard/crc32/document.html Если либо пакет critcl , либо пакет Trf ,
age доступны, то скомпилированная версия может быть использована внутренне для
ускорить вычисление контрольной суммы.
на основе информации, представленной на http://www.naaccr.org/stan-
dard/crc32/document.html Если либо пакет critcl , либо пакет Trf ,
age доступны, то скомпилированная версия может быть использована внутренне для
ускорить вычисление контрольной суммы.
КОМАНДЫ
::crc::crc32 ?-формат формат ? ?-seed значение ? [ -канал чан | -имя файла
файл | сообщение ]
Команда принимает либо строковые данные, либо канал, либо имя файла.
и возвращает значение контрольной суммы, рассчитанное с использованием алгоритма CRC-32.
ритм. Результат форматируется с использованием спецификатора format(n) .
при условии. По умолчанию значение возвращается как беззнаковое.
целое число (формат %u).
ОПЦИИ
-канал имя
Возвращает контрольную сумму для данных, считанных из канала.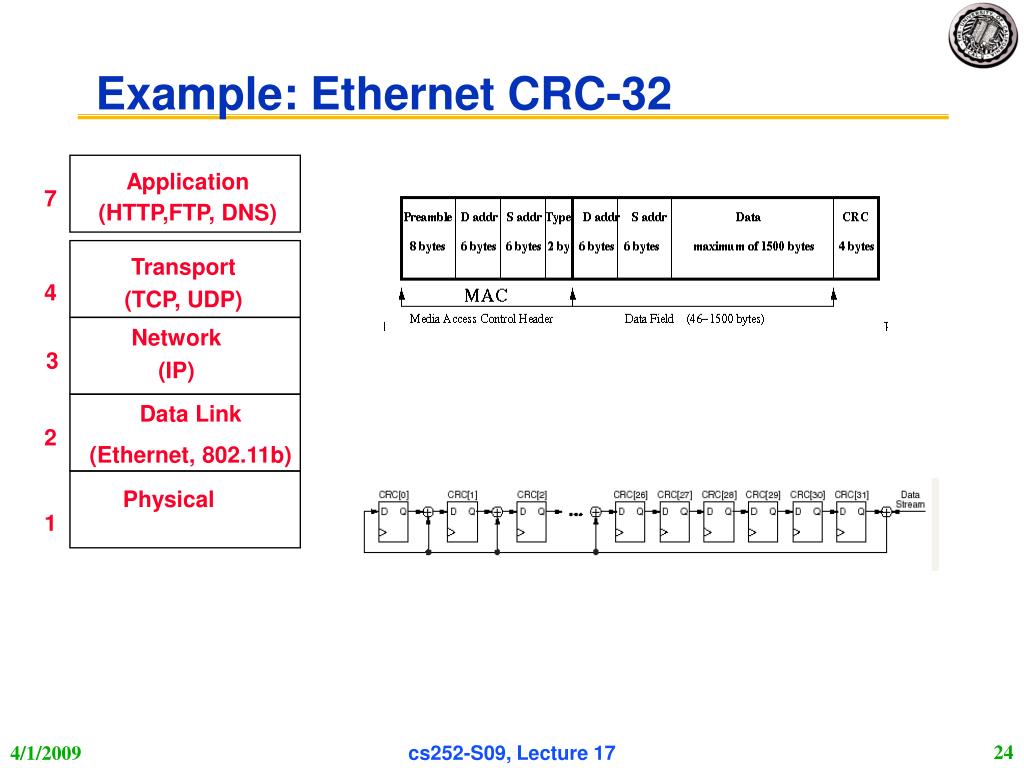 Команда
будет считывать данные из канала до тех пор, пока значение из не станет истинным. если ты
необходимо иметь возможность обрабатывать события во время этого расчета см.
раздел ПРОГРАММИРОВАНИЕ ИНТЕРФЕЙС
-filename имя
Это удобная опция, которая открывает указанный файл, устанавливает
кодирование в двоичное, а затем действует так, как если бы -опция канала
был использован. Файл закрывается по завершении.
-формат строка
Верните контрольную сумму, используя шаблон альтернативного формата.
-seed значение
Выберите альтернативное начальное значение для вычисления CRC.
по умолчанию 0xffffffff. Это может быть полезно для расчета
CRC для структур данных без предварительного преобразования всего
структурировать в строку. CRC предыдущего члена может быть
используется в качестве начального значения для вычисления CRC следующего члена.
Обратите внимание, что алгоритм crc32 включает последний шаг XOR. Если
желательна инкрементная обработка, тогда это необходимо отменить
перед использованием вывода алгоритма в качестве начального значения для дальнейшего
обработка. Более простой альтернативой является использование ПРОГРАММИРОВАНИЕ
ИНТЕРФЕЙС , который предназначен для этого режима работы.
Команда
будет считывать данные из канала до тех пор, пока значение из не станет истинным. если ты
необходимо иметь возможность обрабатывать события во время этого расчета см.
раздел ПРОГРАММИРОВАНИЕ ИНТЕРФЕЙС
-filename имя
Это удобная опция, которая открывает указанный файл, устанавливает
кодирование в двоичное, а затем действует так, как если бы -опция канала
был использован. Файл закрывается по завершении.
-формат строка
Верните контрольную сумму, используя шаблон альтернативного формата.
-seed значение
Выберите альтернативное начальное значение для вычисления CRC.
по умолчанию 0xffffffff. Это может быть полезно для расчета
CRC для структур данных без предварительного преобразования всего
структурировать в строку. CRC предыдущего члена может быть
используется в качестве начального значения для вычисления CRC следующего члена.
Обратите внимание, что алгоритм crc32 включает последний шаг XOR. Если
желательна инкрементная обработка, тогда это необходимо отменить
перед использованием вывода алгоритма в качестве начального значения для дальнейшего
обработка. Более простой альтернативой является использование ПРОГРАММИРОВАНИЕ
ИНТЕРФЕЙС , который предназначен для этого режима работы.
ИНТЕРФЕЙС ПРОГРАММИРОВАНИЯ
Пакет CRC-32 реализует контрольную сумму, используя контекстную переменную для
какие дополнительные данные могут быть добавлены в любое время. Это особенно полезно-
в среде, основанной на событиях, такой как приложение Tk или веб-сайт.
серверный пакет. Данные для контрольной суммы могут обрабатываться постепенно
во время события fileevent 9Обработчик 0072 в дискретных фрагментах. Это может улучшить
интерактивный характер приложения с графическим интерфейсом и может помочь избежать чрезмерного
потребление памяти.
::crc::Crc32Init ? семян ?
Начинает новый контекст CRC32. Возвращает идентификатор токена, который необходимо использовать
для остальных функций. Можно указать необязательное семя
если необходимо.
::crc::Crc32Update токен данные
Добавьте данные в контрольную сумму, идентифицированную токеном. Вызов
Crc32Update $token "abcd" эквивалентно вызову Crc32Update
$token "ab" , за которым следует Crc32Update $token "cb" . См. ПРИМЕРЫ .
::crc::Crc32Final токен
Возвращает значение контрольной суммы и освобождает все ресурсы, удерживаемые
этот токен. После выполнения этой команды токен будет
инвалид. Результатом является 32-битное целочисленное значение.
::crc::Crc32Init ? семян ?
Начинает новый контекст CRC32. Возвращает идентификатор токена, который необходимо использовать
для остальных функций. Можно указать необязательное семя
если необходимо.
::crc::Crc32Update токен данные
Добавьте данные в контрольную сумму, идентифицированную токеном. Вызов
Crc32Update $token "abcd" эквивалентно вызову Crc32Update
$token "ab" , за которым следует Crc32Update $token "cb" . См. ПРИМЕРЫ .
::crc::Crc32Final токен
Возвращает значение контрольной суммы и освобождает все ресурсы, удерживаемые
этот токен. После выполнения этой команды токен будет
инвалид. Результатом является 32-битное целочисленное значение.
ПРИМЕРЫ
% crc::crc32 "Привет, мир!" 3964322768 % crc::crc32 -format 0x%X "Привет, мир!" 0xEC4AC3D0 % crc::crc32 -файл crc32.
