Коэффициент альфа после исключения переменных и задания дополнительных параметров — Мегаобучалка
Приведенные на рис. 19.4 результаты формируются после удаления из шкалы трех упомянутых переменных (шаг 5а). Первая таблица Статистики пригодности содержит величину Альфа Кронбаха для шкалы, содержащей 9 переменных. Вто-рая таблица содержит основные статистические показатели для шкалы: средние, дисперсии и корреляции. Таблица Статистики соотношения пункта с суммарным баллом по своему содержанию аналогична одноименной таблице, приведенной ранее на рис. 19.3, однако здесь вместо 12 исходных переменных содержатся лишь 9. Как легко видеть, значение коэффициента α увеличилось и составля-ет 0,825. Данное значение α больше нельзя увеличить, удалив какую-либо из 9 оставшихся переменных, так как Альфы Кронбаха при дальнейшем исключении любого из оставшихся пунктов получаются меньше, чем α, полученная по всем 9 пунктам. Таким образом, оставшиеся 9 пунктов образуют оптимальный состав шкалы.
Ниже дана трактовка новых терминов, используемых программой в окне выво-да и относящихся к вычислению коэффициента α после исключения нескольких переменных и задания дополнительных параметров.
ff Средние пунктов — описательная информация о средних значениях 9 пунктов шкалы. Среднее полученных средних значений равно 0,547, наименьшее из 9 средних равно 0,5 и т. д.
ff Дисперсии пунктов — статистика, аналогичная средним элементов, но получен-ная для их дисперсий.
| Представление результатов |
ff Межпунктовые корреляции — описательная статистика, характеризующая кор-реляцию между каждой переменной шкалы и суммой остальных переменных. Для каждой переменной вычисляется коэффициент корреляции, а в окне вы-вода приводятся среднее значение, минимум и т. д. полученных коэффици-ентов. Среднее значение коэффициентов корреляции является величиной r в формуле расчета α.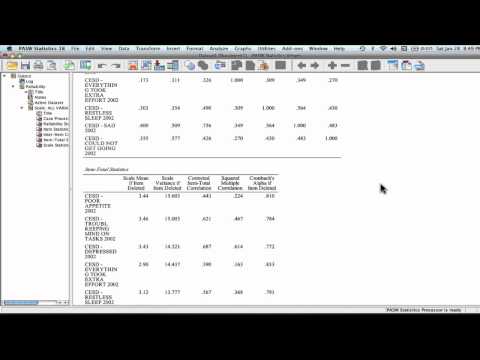
Рис. 19.4.Фрагмент окна вывода после выполнения шага5а
ff Квадрат коэффициента множественной корреляции — представленные в этой секции величины вычислены с помощью уравнения множественной регрессии, позволяющего получать прогнозируемый коэффициент корреляции данной переменной с остальными переменными, участвующими в анализе.
ff Альфа Кронбаха — коэффициент α, вычисляемый по формуле, приведенной
и начале главы. Число элементов шкалы (k) в данном случае равно 9. Посколь-ку α зависит от числа элементов шкалы, нельзя четко определить критерий
276 Глава 19.Анализ надежности
приемлемости полученного значения α. Для большинства случаев можно при-держиваться следующих рекомендаций по оценке внутренней согласованности шкалы:
ff α > 0,9 — отличная;
ff α > 0,8 — хорошая;
ff α > 0,7 — приемлемая;
ff α > 0,6 — сомнительная;
ff α > 0,5 — малопригодная;
ff α < 0,5 — недопустимая.
ff Альфа Кронбаха, основанная на стандартизованных пунктах — коэффициент α, вычисляемый в предположении, что элементы шкалы заранее стандартизова-ны. Как можно видеть, значения обычного и стандартизованного коэффициен-тов α в данном случае не отличаются.
Анализ надежности
При помощи разнообразных критериев определяется, какие задания (переменные) можно считать надежными, а какие нет .
Этап 1
Ø
в список «переменные» вносим все переменные (метрические, порядковые), которые хотим проверить на надежность;
Ø
в графе «модель» выбираем модель проверки на надежность – альфа:
·
Альфа – коэффициент внутренней согласованности, значения близкие «1» означает высокую внутреннюю согласованность, значения близкие «0» и отрицательным значениям – свидетельствуют о несогласованности данного вопроса с остальными вопросами теста.
·
Деление пополам – делит группу вопросов на 2 части и считает коэффициент корреляции между ними.
·
Гутман – определение нижней границы пригодности.
·
Параллельно – оценка максимального правдоподобия пригодности теста при условии наличия одинаковых дисперсий пунктов.
·
Строго параллельно – оценка максимального правдоподобия пригодности теста при условии наличия одинаковых средних значений пунктов и одинаковых дисперсий пунктов.
·
Метки объектов – вопросы будут отображены с метками.
Ø
галочки в меню «статистика»: масштаб, масштабировать если пункт удален, средние, вариации, корреляции (в подгруппе «итоги»), корреляции (в подгруппе «между пунктами»).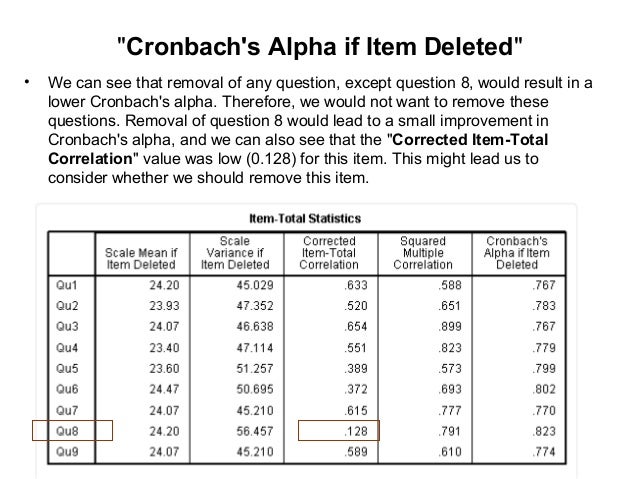
Сводка обработки наблюдений
1.
N – количество респондентов.
Статистики пригодности
1.
Альфа Кронбаха – статистика надежности внутренней согласованности:
·
Больше 0,9 – отличная;
·
Больше 0,8 – хорошая;
·
Больше 0,7 – приемлемая;
·
Больше 0,6 – сомнительная;
·
Больше 0,5 – малопригодная;
·
Меньше 0,5 – недопустимая.
2.
Альфа Кронбаха, основанная на стандартизованных пунктах – статистика надежности с учетом стандартизации пунктов.
3.
Матрица корреляций между пунктами
1.
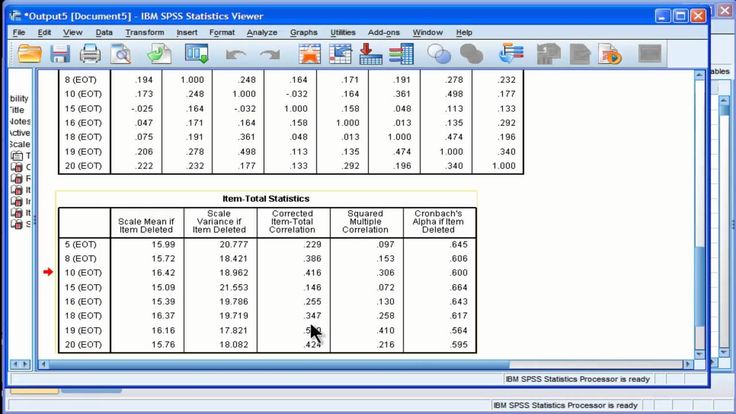Корреляция (r) – два органа считаются коррелируемые если изменение одного из них сопровождается большим или меньшим изменением другого в том же направлении – Ф.Гальтон. Коэффициент Пирсона всегда лежит в пределах от -1 (отрицательная корреляция) до 1 (положительная корреляция). Значения близкие 0 свидетельствует о том, что переменные практически не коррелируемы между собой.
Итоговые статистики пунктов
1.
Средние пунктов – средние арифметические значения всех пунктов.
2.
Дисперсии пунктов – вспомогательная величина для стандартного отклонения.
3.
Межпунктовые корреляции – см. выше.
·
Среднее.
·
Минимум.
·
Максимум.
·
Размах.
·
Максимум / Минимум.
·
Дисперсия.
·
Количество пунктов.
Общие статистики пунктов
1.
Среднее шкалы при удалении пункта – величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной.
2.
Дисперсия шкалы при удалении пункта – величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной.
3.
Общая корреляция коррелированных пунктов – это главная в этой таблице величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной. Нам необходимо удалить из списка «переменных» все те переменные, которые имеют в этом столбике значения меньше чем 0,2 (условно), включая все отрицательные значения.
После чего повторить проверку заданий на надежность.
4.
Квадрат коэффициента множественной корреляции – величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной.
5.
Альфа Кронбаха при удалении пункта – статистика надежности внутренней согласованности всех переменных при удалении конкретного задания.
Статистики шкалы
1.
Среднее (арифметическое) – сумма всех значений деленное на их количество.
2. Дисперсия – вспомогательная величина для стандартного отклонения.
3. Стд. отклонение (от среднего) – величина, характеризующая изменчивость (равняется квадратному корню из дисперсии).
4. Количество пунктов – количество переменных.
Этап 2
Ø
в список «переменные» вносим все переменные (метрические, порядковые), которые в первом анализе дали корреляцию больше 0,2;
Ø
в графе «модель» выбираем модель проверки на надежность – деление пополам;
Ø
галочки в меню «статистика»: масштаб, масштабировать если пункт удален, средние, вариации, корреляции (в подгруппе «итоги»), корреляции (в подгруппе «между пунктами»).
Быстрый способ проверки надежности теста путем определения коэффициента корреляции между 2-мя частями теста. Стоит все же провести повторное тестирование и сделать проверку на ретестовую надежность (чаще всего используют при делении на четные и не четные вопросы).
Сводка обработки наблюдений (данная таблица уже была рассмотрена выше)
Статистики пригодности
1.
Альфа Кронбаха – статистика надежности внутренней согласованности:
·
Больше 0,9 – отличная;
·
Больше 0,8 – хорошая;
·
Больше 0,7 – приемлемая;
·
Больше 0,6 – сомнительная;
·
Больше 0,5 – малопригодная;
·
Меньше 0,5 – недопустимая.
2.
Количество пунктов – количество заданий (переменных) проверяемых на надежность.
3.
Корреляция между формами – приближенное значение надежности шкал, рассчитанное в предположении, что она содержит 5 элементов.
4.
Коэффициент Спирмена-Брауна – коэффициент показывает корреляцию между 2-мя частями теста (стоит обратить внимание на: равно ли количество вопросов или нет):
·
Больше 0,9 – отличная;
·
Больше 0,8 – хорошая;
·
Больше 0,7 – приемлемая;
·
Больше 0,6 – сомнительная;
·
Больше 0,5 – малопригодная;
·
Меньше 0,5 – недопустимая.
5.
Коэффициент половинного расщепления Гутмана – аналог выше наведенного коэффициента .
Матрица корреляций между пунктами (данная таблица уже была рассмотрена выше)
Итоговые статистики пунктов (данная таблица уже была рассмотрена выше)
Общие статистики пунктов (данная таблица уже была рассмотрена выше)
Меню статистики:
·
Элемент – средние значения и их стандартное отклонение.
·
Масштаб – общее среднее значение, дисперсия, стандартное отклонение и количество пунктов в сумме.
·
Масштаб если пункт удален – альфа для каждого из пунктов.
·
Средние – средние значения для всех пунктов.
·
Вариации – средние для дисперсий всех пунктов.
·
Ковариации – вычисления ковариаций между каждой переменной и суммой всех остальных.
·
Корреляции – вычисления корреляций между каждой переменной и суммой всех остальных.
·
Корреляции – корреляционная матрица для всех пунктов.
·
Ковариации – ковариационная матрица для всех пунктов.
·
Т квадрат – сравнения различий между средними значениями всех пунктов.
·
Тьюки тест – проверка линейности зависимости.
· Меню А NOVA
Альфа Кронбаха: определение, интерпретация, SPSS
Содержание:
- Что такое Альфа Кронбаха?
- Альфа Кронбаха в SPSS.
Альфа Кронбаха , α (или коэффициент альфа ), разработанный Ли Кронбахом в 1951 году, измеряет надежность или внутреннюю согласованность. «Надежность» — это другое название постоянства.
Альфа-тесты Кронбаха для проверки надежности опросов по шкале Лайкерта с несколькими вопросами. Эти вопросы измеряют латентные переменные — скрытые или ненаблюдаемые переменные, такие как: добросовестность человека, невроз или открытость. Их очень трудно измерить в реальной жизни. Альфа Кронбаха расскажет вам, насколько тесно связан набор тестовых заданий как группа.
Посмотрите видео с обзором и расчетом формулы:
Альфа Кронбаха: определение и расчет
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Формула альфа Кронбаха
Формула альфа Кронбаха:
Где:
- N = количество элементов.
- c̄ = средняя ковариация между парами элементов.
- v̄ = средняя дисперсия.
Хотя полезно знать формулу, лежащую в основе этой концепции, на самом деле вам не нужно работать с ней. Вы часто будете вычислять альфу в SPSS или подобном программном обеспечении.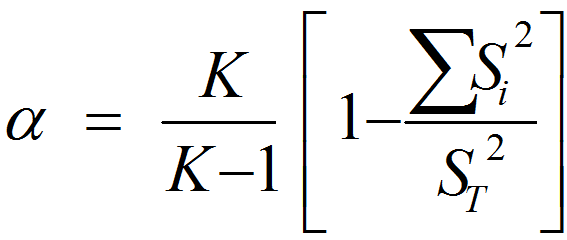
Посмотрите видео с шагами и анализом низких значений:
Cronbachs Alpha SPSS
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Чтобы запустить альфа-тест Кронбаха в SPSS, убедитесь, что вы измеряете скрытые переменные по шкале Лайкерта. Альфа Кронбаха расскажет вам, насколько тесно связан набор тестовых заданий как группа.
Шаги:
Шаг 1: Нажмите «Анализ», затем нажмите «Масштаб», а затем нажмите «Анализ надежности».
Шаг 2: Перенесите ваши переменные (от q1 до q5) в «Элементы». Модель по умолчанию должна быть установлена как «Альфа».
Шаг 3: Нажмите «Статистика» в диалоговом окне.
Шаг 4: Выберите «Элемент», «Масштаб» и «Масштаб, если элемент удален» в описании окна. Выберите «Корреляция» в поле между элементами.
Шаг 5: Нажмите «Продолжить», а затем нажмите «ОК».
Шаг 4 можно пропустить, но это позволит вам проанализировать проблемы с отдельными тестовыми вопросами.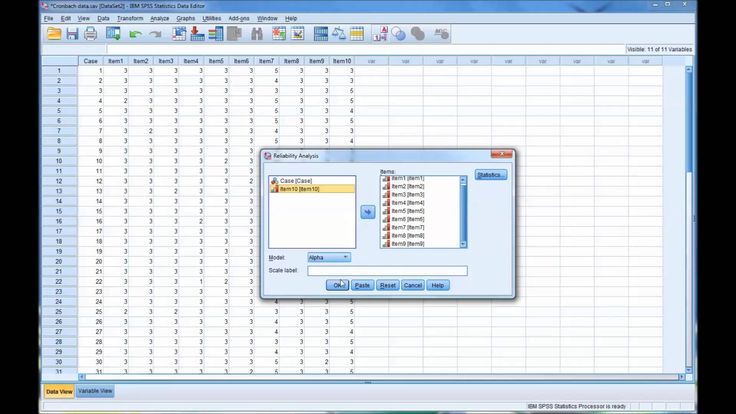
В частности, он может выделить один или несколько вопросов с низкими значениями альфа (я работаю над конкретным примером в видео).
Эмпирическое правило для результатов
Эмпирическое правило для интерпретации альфа для дихотомических вопросов (т. е. вопросов с двумя возможными ответами) или вопросов по шкале Лайкерта:
В целом, оценка более 0,7 обычно является удовлетворительной. Однако некоторые авторы предлагают более высокие значения от 0,90 до 0,95.
Как избежать проблем с Cronbach’s Alpha
С осторожностью используйте приведенные выше эмпирические правила. Высокий уровень альфы может означать, что элементы в тесте сильно коррелированы. Однако α также чувствителен к количеству элементов в тесте. Большее количество элементов может привести к большему α, а меньшее количество элементов — к меньшему α. Если альфа высокая, это может означать избыточные вопросы (то есть они задают одно и то же).
Низкое значение для альфы может означать, что в тесте недостаточно вопросов.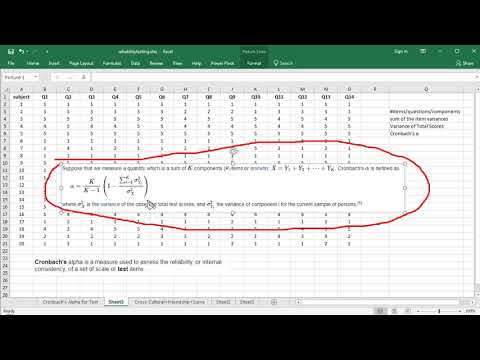
Добавление в тест еще релевантных элементов может увеличить альфу. Плохая взаимосвязь между тестовыми вопросами также может привести к низким значениям, как и измерение более чем одной скрытой переменной.
Путаница часто связана с причинами высоких и низких показателей альфа. Это может привести к неправильному отбрасыванию тестов или тестам, ошибочно помеченным как ненадежные. Профессор психометрии Мохсен Тавакол и профессор медицинского образования Рег Денник предполагают, что улучшение ваших знаний о внутренней согласованности и одномерности приведет к правильному использованию альфа-9 Кронбаха.0089 1 :
Одномерность в альфе Кронбаха предполагает, что вопросы измеряют только одну скрытую переменную или измерение. Если вы измеряете более одного измерения (сознательно или неосознанно), результат теста может быть бессмысленным. Вы можете разбить тест на части, измеряя разные скрытые переменные или измерения в каждой части.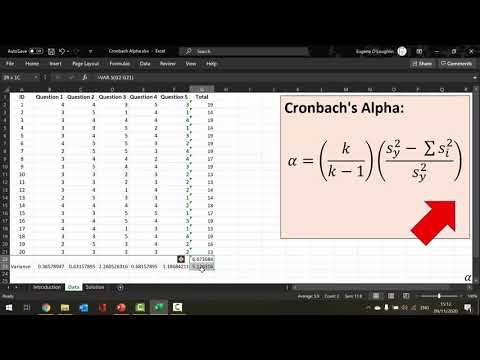
Если вы не уверены, является ли ваш тест одномерным или нет, запустите факторный анализ, чтобы определить измерения в вашем тесте.
Ссылки
Лавракас, П. (2008). Энциклопедия методов обследования, 1-е издание. МУДРЕЦ.
Мохсен Тавакол и Рег Денник. Разбираемся с альфой Кронбаха. Международный журнал медицинского образования. 2011 г.; 2:53-55 От редакции
Салкинд, Н. (2015). Энциклопедия измерений и статистики, 1-е издание. МУДРЕЦ.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Альфа Кронбаха: определение, интерпретация, SPSS» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/cronbachs-alpha-spss/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.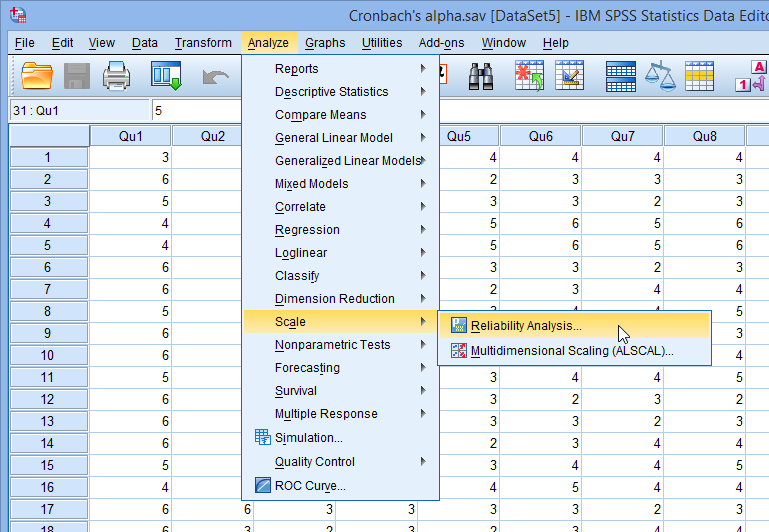
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Альфа Кронбаха: определение, расчеты и пример
Что такое Альфа Кронбаха?
Коэффициент альфа Кронбаха измеряет внутреннюю согласованность или надежность набора элементов обследования. Используйте эту статистику, чтобы определить, последовательно ли набор элементов измеряет одну и ту же характеристику. Альфа Кронбаха количественно определяет уровень согласия по стандартизированной шкале от 0 до 1. Более высокие значения указывают на более высокое согласие между элементами.
Высокие значения альфа Кронбаха указывают на то, что значения ответов для каждого участника на набор вопросов согласованы. Например, когда участники дают высокие ответы по одному из пунктов, они, вероятно, также дадут высокие ответы по другим пунктам. Эта согласованность указывает на то, что измерения надежны, и элементы могут измерять одну и ту же характеристику.
И наоборот, низкие значения указывают на то, что набор элементов не позволяет надежно измерить одну и ту же конструкцию. Высокие ответы на один вопрос не означают, что участники высоко оценили другие вопросы. Следовательно, вопросы вряд ли будут измерять одно и то же свойство, потому что измерения ненадежны.
Для этой статистики данные обычно берутся из ответов на опросы, инструментов оценки и результатов тестов. Данные могут быть непрерывными, но часто представляют собой значения Лайкерта и двоичные значения. Расчеты предполагают, что все элементы измеряют одну и ту же черту с использованием одной и той же шкалы. Статистики называют это моделью, эквивалентной тау.
Читайте дальше, чтобы узнать больше об использовании, интерпретации и расчете альфы Кронбаха. Я заканчиваю анализом примера.
Для чего используется альфа Кронбаха?
Аналитики часто используют альфа-канал Кронбаха при разработке и тестировании нового опроса или инструмента оценки.
Эта статистика помогает им оценить качество инструмента на этапе проектирования перед его полным развертыванием. Это показатель надежности.
Опросы и инструменты оценки часто задают несколько вопросов об одном и том же понятии, характеристике или конструкции. Включив несколько вопросов по одному и тому же аспекту, тест может дать более тонкую оценку явления.
Аналитики могут комбинировать несколько связанных элементов, чтобы сформировать шкалу конструкции. Однако, прежде чем включать различные вопросы в шкалу, они должны быть уверены, что все пункты надежно измеряют одну и ту же конструкцию. Альфа Кронбаха помогает в этом процессе.
Представьте, что исследователи разрабатывают шкалу самооценки и разрабатывают несколько пунктов для измерения этой конструкции. Если все пункты действительно оценивают самооценку, то баллы по всем пунктам в целом должны совпадать, что дает высокий коэффициент альфа Кронбаха. Например, люди с высокой самооценкой, как правило, получают высокие баллы по всем пунктам.
И наоборот, люди с низкой самооценкой, как правило, получают низкие баллы по всем пунктам.
Однако, если не все пункты оценивают самооценку, люди могут получить высокие оценки по одним вопросам и низкие по другим. Оценки по пунктам расходятся, что приводит к более низкой альфе Кронбаха.
Обычно исследователи используют альфу Кронбаха, чтобы убедиться, что элементы совпадают, но им необходимо использовать его с другими анализами, которые оценивают, измеряют ли элементы правильную характеристику. Подробнее об этом в разделе ограничений!
Интерпретация альфа Кронбаха
Интерпретация альфа Кронбаха немного сложнее, чем выше, тем лучше. Давайте рассмотрим основные моменты, а также некоторые предостережения и предупреждения.
Альфа Кронбаха находится в диапазоне от 0 до 1.
- Ноль указывает на отсутствие корреляции между элементами. Они полностью независимы. Знание ценности ответа на один вопрос не дает информации об ответах на другие вопросы.
- Один указывает на то, что они идеально коррелированы. Знание значения одного ответа дает полную информацию о других элементах.
Конечно, ваше значение обычно будет где-то посередине. Каков приемлемый диапазон для альфы Кронбаха?
Аналитики часто используют 0,7 в качестве контрольного значения для альфа Кронбаха. На этом уровне и выше пункты достаточно согласованы, чтобы указать, что мера надежна. Как правило, значения около 0,7 минимально приемлемы, но не идеальны. Однако в некоторых областях и отраслях минимальные значения различаются. Обязательно проверьте область обучения.
Это может вас удивить, но альфа Кронбаха может быть слишком высокой. Чрезвычайно высокие значения могут указывать на то, что вопросы избыточны. Например, если респонденты всегда дают один и тот же ответ на два вопроса, можно удалить один из них. Опять же, разные аналитики/области исследования расходятся во мнениях относительно того, что считать «слишком высоким». Часто это либо альфа Кронбаха > 0,95 или 0,99.
Предупреждения и ограничения
Наконец, вот несколько предостережений о том, о чем вам не сообщает альфа-канал Кронбаха.
Альфа Кронбаха является мерой надежности, но не валидности. Он может указать, согласуются ли ответы между элементами (надежность), но не может определить, измеряют ли элементы правильную концепцию (валидность). Например, ответы на вопросы могут быть очень последовательными, но они могут измерять позитивный настрой, а не самооценку, как вы предполагали. Узнайте больше о надежности и достоверности.
Кроме того, хотя высокие значения Кронбаха указывают на согласованность, они не обязательно доказывают, что ваши элементы являются одномерными, измеряя одну характеристику. Элементы могут измерять несколько связанных понятий и, таким образом, давать высокие значения альфа.
В этом свете вы должны рассматривать получение высокой альфы Кронбаха как необходимый шаг для установления надежности, но одного этого недостаточно для определения достоверности.
Чтобы гарантировать, что набор элементов измеряет правильную характеристику, и только эту характеристику, аналитики часто используют факторный анализ и анализ основных компонентов.
Узнайте о других способах оценки достоверности.
Как рассчитать альфу Кронбаха
Обычно статистическое программное обеспечение рассчитывает альфу Кронбаха за вас. Однако знание того, как рассчитать его самостоятельно, может помочь вам понять его.
Ниже приведена формула альфа Кронбаха.
Где:
- N = количество предметов
- c̅ = средняя ковариация между элементами.
- v̅ = средняя дисперсия элемента.
Вычисления альфа Кронбаха включают взятие средней ковариации и деление ее на среднюю общую дисперсию. Следовательно, высокое значение альфа требует, чтобы ковариация была высокой по отношению к дисперсии элемента. Другими словами, на отношения между вопросами приходится большая часть общей изменчивости.
Кроме того, большое значение имеет количество предметов.
Альфа Кронбаха имеет тенденцию увеличиваться по мере добавления новых элементов.
Пример анализа
Представьте, что банк хочет опросить клиентов, чтобы оценить, насколько они удовлетворены своевременностью обслуживания. Вы разрабатываете следующие четыре вопроса для опроса:
- Пункт 1. На мой телефонный, электронный или письменный запрос ответили в разумные сроки.
- Пункт 2 – Я удовлетворен своевременностью оказанной услуги.
- Пункт 3. Время ожидания услуг было разумным.
- Пункт 4 – Я доволен полученными услугами.
Во всех этих вопросах используется 5-балльная шкала Лайкерта в диапазоне от 1 «Очень неудовлетворен» до 5 «Очень удовлетворен». Вы просите 60 клиентов принять участие в опросе на этапе пилотного исследования, прежде чем распространять опрос более широко. Загрузите набор данных CSV: Cronbachs_alpha.
Для этого анализа статистическое программное обеспечение вычисляет общий коэффициент альфа Кронбаха.