Аксонометрическая проекция — Википедия
Материал из Википедии — свободной энциклопедии
Проецирование параллелепипеда на плоскость П’.Аксонометри́ческая прое́кция (от др.-греч. ἄξων «ось» + μετρέω «измеряю») — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.
Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.
Стандартизированные аксонометрические проекции [1][править | править код]
Аксонометрическая проекция- прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции):
ru.wikipedia.org
Аксонометрическая проекция — это… Что такое Аксонометрическая проекция?
Проецирование параллелепипеда на плоскость П’.Аксонометрическая проекция (от др.-греч. ἄξων «ось» и др.-греч. μετρέω «измеряю») — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.
Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получается две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.
Стандартизированные аксонометрические проекции [1]
Аксонометрическая проекция- прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции):
- косоугольная проекция (направление проецирования не перпендикулярно к плоскости проекции):
- фронтальная изометрическая проекция;
- фронтальная диметрическая проекция;
- горизонтальная изометрическая проекция.
См. также
Проекция (геометрия)
Источники
- ↑ По ГОСТ 2.317-69 — Единая система конструкторской докуметации. Аксонометрические проекции.
Литература
- Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7
- Под ред. Ишлинский А. Ю. Новый политехнический словарь. — М.: Большая Российская энциклопедия, 2003. — С. 671. — ISBN 5-7107-7316-6
- Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.
dic.academic.ru
Инженерная графика | Лекции | Аксонометрические проекции
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.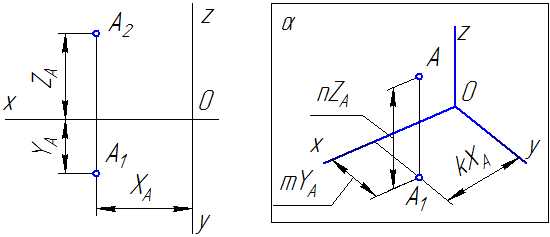
Рисунок 4.2
Здесь буквами k,
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:
- прямоугольные изометрические и диметрические;
- косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;
Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.
4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается
Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.
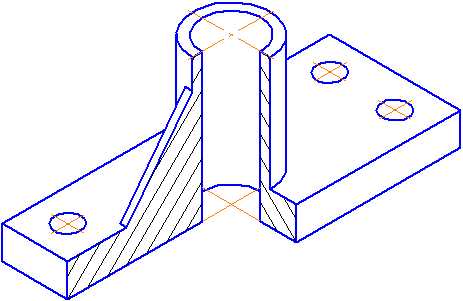
Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции
4.1.2. Диметрическая проекция
Положение аксонометрических осей проводится на Рисунке 4.5.
Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.
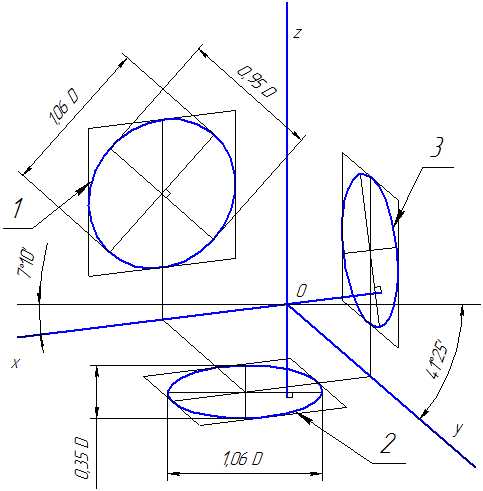
Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции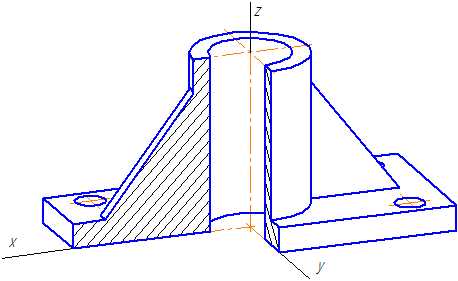
Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 300 и 600.
Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.
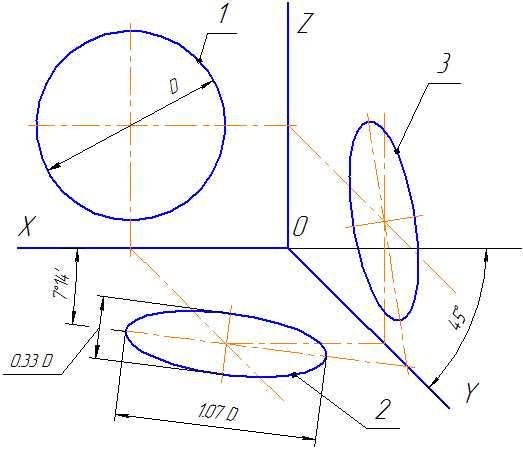
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.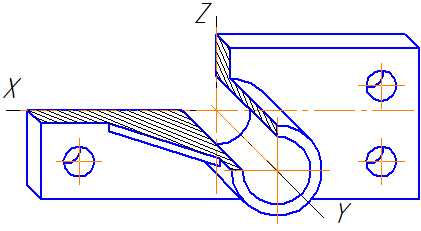
Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из этих окружностей делится на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).
4.4 Штриховка сечений
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).
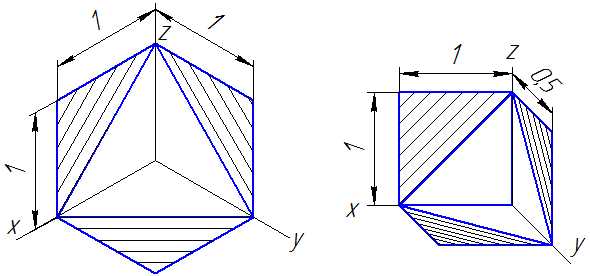
а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях
cadinstructor.org
Лекция 6 Аксонометрические проекции
Лекция 6. Аксонометрические проекции
Вопросы:
1.Общие сведения об аксонометрических проекциях.
2.Классификация аксонометрических проекций.
3.Примеры построения аксонометрических изображений .
1 Общие сведения об аксонометрических проекциях
При составлении технических чертежей иногда возникает необходимость наряду с изображениями предметов в системе ортогональных проекций иметь более наглядные изображения. Для таких изображений применяют метод аксонометрического проецирования (аксонометрия — греческое слово, в дословном переводе оно означает измерение по осям; аксон — ось, метрео — измеряю).
Сущность метода аксонометрического проецирования: предмет вместе с осями прямоугольных координат, к которым он отнесен в пространстве, проецируется на некоторую плоскость так, что ни одна из его координатных осей не проецируется на нее в точку, а значит сам предмет спроецируется на эту плоскость проекций в трех измерениях.
На черт. 88 на некоторую плоскость проекций Р спроецирована находящаяся в пространстве система координат х, y, z. Проекции хр, yр ,
zр осей координат на плоскость Р называются аксонометрическими осями.
Рисунок 88
На осях координат в пространстве отложены равные отрезки е. Как видно из чертежа, их проекции ех, еy, еz на плоскость Р в общем
случае не равны отрезку е и не равны между собой. Это значит, что размеры предмета в аксонометрических проекциях по всем трем осям искажаются. Изменение линейных размеров вдоль осей характеризуется показателями (коэффициентами) искажения вдоль осей.
Показателем искажения называется отношение длины отрезка на аксонометрической оси к длине такого же отрезка на соответствующей оси прямоугольной системы координат в пространстве.
Показателем искажения вдоль оси х обозначим буквой k, по оси y
– буквой m, по оси z – буквой n, тогда: k= ех/е; m= еy/е; n= еz/е.
Величина показателей искажения и соотношение между ними зависят от расположения плоскости проекций и от направления проецирования.
В практике построения аксонометрических проекций обычно пользуются не самими коэффициентами искажения, а некоторыми величинами, пропорциональными величинам коэффициентов искажения: К:М:N = k:m:n. Эти величины называют приведенными коэффициентами искажения.
2 Классификация аксонометрических проекций
Все множество аксонометрических проекций подразделяется на две группы:
1 Прямоугольные проекции – получены при направлении проецирования, перпендикулярном аксонометрической плоскости .
2 Косоугольные проекции – получены при направлении проецирования, выбранном под острым углом к аксонометрической плоскости.
Кроме того, каждая из указанных групп делится еще и по признаку соотношения аксонометрических масштабов или показател ей (коэффициентов) искажения. Пo этому признаку аксонометрические проекции можно разделить на следующие виды:
а) Изометрические — показатели искажения по всем трем осям одинаковы (изос — одинаковый).
б) Диметрические — показатели искажения по двум осям равны между собой, а третий не равен (ди — двойной).
в) Триметрические — показатели искажения по всем трем осям не рав-
ны между собой. Это аксонометрия (большого практического применения не имеет).
2.1 Прямоугольные аксонометрические проекции
Прямоугольная изометрическая проекция
Впрямоугольной изометрии все коэффициенты равны ме жду
собой:
k = m = n , k2 + m2 + n2=2 ,
тогда это равенство можно записать в виде 3k2=2, откуда k = .
Таким образом, в изометрии показатель искажения равен ~ 0,82. Это означает, что в прямоугольной
изометрии все размеры изображаемого предмета сокращаются в 0,82 раза. Для
упрощения | построений | используют | |
приведенные | коэффициенты | искажения | |
k=m=n=1, | что | соответствует | |
увеличению | размеров | изображения по | |
сравнению с действительными в 1,22 | |||
раза (1:0,82 | 1,22). | Расположение осей | |
изометрической проекции показано на рис. | |||
89. |
|
| Рисунок 89 |
Прямоугольная диметрическая проекция
В прямоугольной диметрии показатели искажения по двум осям одинаковы, т. е. k = п. Третий
показатель искажения выбираем вдвое меньше двух других, т. е. m =1/2k. Тогда равенство k2+m2+n2= 2 примет такой вид: 2k2+1/4k2=2; откуда k=0,94;
m = 0,47. |
|
| |
В целях упрощения построений |
| ||
используем | приведенные |
| |
коэффициенты искажения: k=n=1; |
| ||
m=0,5. Увеличение в этом случае |
| ||
составляет 6% (выражается числом | Рисунок 90 | ||
1,06=1:0,94). | Расположение осей | ||
| |||
диметрической | проекции показано на |
| |
рис. 90. |
|
| |
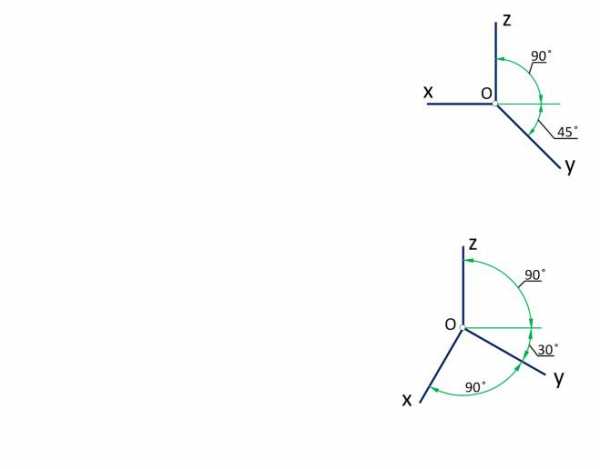
Рисунок 91
Рисунок 92
равны: k = n=1.
2.2 Косоугольные проекции
Фронтальная изометрическая проекция
На рис. 91 дано положение аксонометрических осей для фронтальной изометрии.
Согласно ГОСТ 2.317-69, допускается применять фронтальные изометрические проекции с углом наклона оси y 30° и 60°. Коэффициенты искажения являются точными и равны:
k = m = n=1.
Горизонтальная изометрическая проекция
На рис. 92 дано положение аксонометрических осей для фронтальной изометрии. Согласно ГОСТ 2.317-69, допускается применять горизонтальные изометрические проекции с углом наклона оси y 45° и 60° при сохранении угла между осями x и y 90°. Коэффициенты искажения являются точными и равны: к=m= n= 1.
Фронтальная диметрическая проекция
Положение осей такое же, как для фронтальной изометрии (рис.91) . Также допускается применение фронтальной диметрии с углом наклона оси y 30° и 60°.
Коэффициенты искажения являются точными и m=0.5
Все три вида стандартных косоугольных проекций получены при расположении одной из координатных плоскостей (горизонтальной или фронтальной) параллельно плоскости аксонометрии. Поэтому все фигуры, расположенные в этих плоскостях или им параллельных, проецируются на плоскость чертежа без искажения.
3 Примеры построения аксонометрических изображений
Как в прямоугольных (ортогональных проекциях), так и в аксонометрических одна проекция точки не определяет ее положения в пространстве. Помимо аксонометрической проекции точки необходимо иметь еще одну проекцию, называемую вторичной. Вторичная проекция точки – это аксонометрия одной из ее прямоугольных проекций (чаще горизонтальной).
Приемы построения аксонометрических изображений не зависят от вида аксонометрических проекций. Для всех проекций приемы построений одинаковы. Аксонометрическое изображение обычно строят на основе прямоугольных проекций предмета.
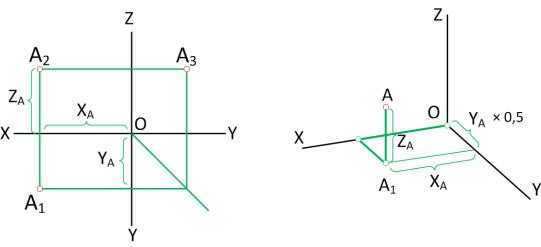
3.1 Аксонометрия точки
Построение аксонометрии точки по заданным ее ортогональным проекциям (рис. 93,а) начинаем с определения ее вторичной проекции (рис. 93,б). Для этого на аксонометрической оси х от начала координат откладываем величину координат Х точки А – ХA ; по оси y– отрезок YA (для диметрии YA×0.5 , т.к. показатель искажения по этой оси m=0.5).
В пересечении линий связи, проведенных параллельно осям из концов отмеренных отрезков, получают точку А1- вторичную проекцию точки А.
Аксонометрия точки А будет находиться на расстоянии Z A от вторичной проекции точки А.
Рисунок 93

3.2 Аксонометрия отрезка прямой (рис. 94)
Находим вторичные проекции точек А, В. Для этого откладываем вдоль осей х и у соответствующие координаты точек А и В. Затем отмечают на прямых, проведенных из вторичных проекций параллельно оси z, высоты точек А и В (Z A и ZB).Соединяем полученные точки – получаем аксонометрию отрезка.
Рисунок 94
3.3 Аксонометрия плоской фигуры
На рис. 95 показано построение изометрической проекции треугольника АВС. Находим вторичные проекции точек А, В, С. Для этого откладываем вдоль осей х и у соответствующие координаты точек А, В и С. Затем отмечаем на прямых, проведенных из вторичных проекций параллельно оси z, высоты точек А, В и С. Полученные точки соединяем линиями – получаем аксонометрию отрезка.
Рисунок 95
Если плоская фигура лежит в плоскости проекций, то аксонометрия такой фигуры совпадает с ее проекцией .
3.4 Аксонометрия окружностей, расположенных в плоскостях проекций
Окружности в аксонометрии изображаются в виде эллипсов. Для упрощения построений построение эллипсов заменяется построением овалов, очерченных дугами окружностей.
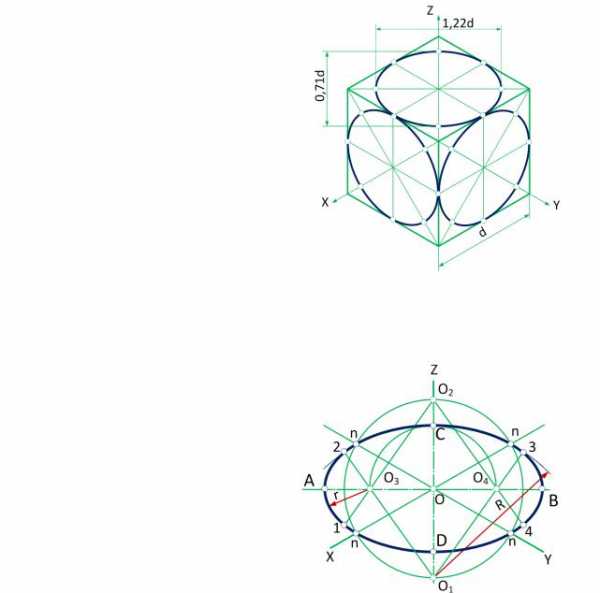
Прямоугольная изометрия окружности
На рис. 96 в | прямоугольной |
| |||
изометрии изображен куб, в грани |
| ||||
которого | вписаны |
| окружности. |
| |
Грани | куба в | прямоугольной |
| ||
изометрии будут ромбами, а |
| ||||
окружности – эллипсами. Длина |
| ||||
большой оси эллипса равна 1.22d, |
| ||||
где d — диаметр окружности. Малая |
| ||||
ось составляет 0.7 d. |
|
| |||
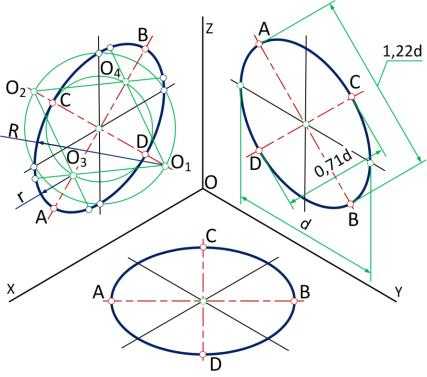
На | рис. | 97 | показано |
| |
построение овала, лежащего в |
| ||||
плоскости, параллельной π1. Из |
| ||||
точки пересечения осей О проводят |
| ||||
вспомогательную |
| окружность | Рисунок 96 | ||
диаметром d, равным действитель- | |||||
| |||||
ной величине диаметра изображаемой окружности, и находят точки n пересечения этой окружности с аксонометрическими осями х и у.
Из точек О1, О2 пересечения вспомогательной окружности с осью z, как
из центров радиусом R = О1n= О2n , проводят две дуги nDn и пСп окружности, принадлежащие овалу.
Из центра О радиусом ОС, |
| ||
равным половине малой оси овала, |
| ||
засекают на большой оси овала | АВ |
| |
точки О3 и О4. Из этих точек |
| ||
радиусом r = О31 = О32 = О43 | = |
| |
О44 проводят две дуги. Точки 1, 2, 3 |
| ||
и 4 сопряжений дуг радиусов R и r |
| ||
находят, соединяя точки О1 и О2 с |
| ||
точками О3 и О4 и продолжая | Рисунок 97 | ||
прямые до пересечения с дугами | |||
| |||
пСп и nDn. |
|
| |
Аналогичным образом строят овалы, | расположенные в | ||
плоскостях, параллельных плоскостям π2, | и π3, (рисунок 98). | ||
Построение овалов, лежащих в плоскостях, параллельных плоскостям π2 и π3, начинают с проведения горизонтальной АВ и вертикальной СD осей овала:
-АВ оси x для овала, лежащего в плоскости, параллельной плоскостям π3;
-АВ оси y для овала, лежащего в плоскости, параллельной
плоскостям π2; Дальнейшие построения овалов аналогичны построениям овала,
лежащего в плоскости, параллельной π1.
Рисунок 98
Прямоугольная диметрия окружности (рис. 99)
На рис. 99 в прямоугольной изометрии изображен куб с ребром α, в грани которого вписаны окружности. Две грани куба изобразятся в виде равных параллелограммов со сторонами 0,94d и 0,47 d, третья грань — в виде ромба со сторонами, равными 0,94d. Две окружности, вписанные в грани куба, проецируются в виде одинаковых эллипсов, третий эллипс по форме близок к окружности.
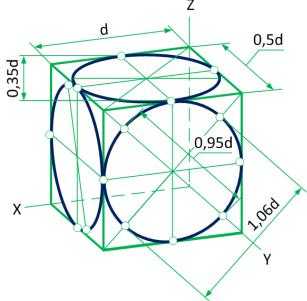
Направление больших | осей |
| |||
эллипсов (как и в изометрии) |
| ||||
перпендикулярно | к | соот- |
| ||
ветствующим аксонометрическим |
| ||||
осям, малые оси параллельны |
| ||||
аксонометрическим осям. |
|
| |||
Размер | большой | оси | всех |
| |
трех эллипсов равен | d, | т. е. |
| ||
диаметру окружности, | размеры |
| |||
малых осей | двух | одинаковых |
| ||
эллипсов равны d/3 | размер малой |
| |||
оси эллипса, близкого по форме к |
| ||||
окружности, | равен |
| 0,9d. |
| |
Практически | при | приведенных |
| ||
показателях искажения | (1 и | 0,5) | Рисунок 99 | ||
большие оси всех трех эллипсов |
| ||||
равны 1,06 d, малые оси двух эллипсов равны 0,35 d, малая ось третьего эллипса равна 0,94 d.
Построение эллипсов | в диметрии иногда заменяется более | ||||
простым построением овалов (рис. 100) |
|
| |||
На рисунке 100 | приведены примеры построения диметрических | ||||
проекций, | где | эллипсы заменены | овалами, | построенными | |
упрощенным | способом. | Рассмотрим | пример | построения | |
диметрической проекции окружности, расположенной параллельно плоскости π2 (рисунок 100, а).
Через точку О проводим оси, параллельные осям х и z. Из центра О радиусом, равным радиусу данной окружности, проводим вспомогательную окружность, которая пересекается с осями в точках 1, 2, 3, 4. Из точек 1 и 3 (по направлению стрелок) проводим горизонтальные линии до пересечения с осями АВ и CD овала и получаем точки О1, О2 , О3, О4. Приняв за центры точки О1, О4, радиусом R проводим дуги 1 2 и 3 4. Приняв за центры точки О2, О3, проводим радиусом R1 замыкающие овал дуги.
Разберем упрощенное построение диметрической проекции окружности, лежащей в плоскости π1 (рисунок 100, в).
Через намеченную точку О проводим прямые, параллельные осям х и y, а также большую ось овала АВ перпендикулярно малой оси CD. Из центра О радиусом, равным радиусу данной окружности, проводим вспомогательную окружность и получаем точки n и n1.
На прямой, параллельной оси z, вправо и влево от центра O
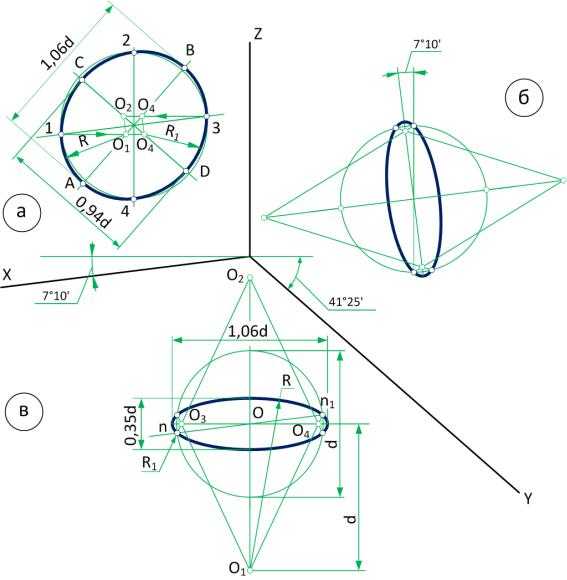
откладываем отрезки, равные диаметру вспомогательной окружности, и получаем точки О1 и О2. Приняв эти точки за центры, проводим радиусом R = О1n1 дуги овалов. Соединяя точки О2 прямыми с концами дуги n1n2, на линии большой оси АВ овала получим точки О4 и О3. Приняв их за центры, проводим радиусом R1 замыкающие овал дуги.
Рисунок 100
3.5 Аксонометрия геометрического тела
Аксонометрия шестигранной призмы (рис.101)
В основании прямой призмы лежит правильный шестиугольник
studfiles.net
Аксонометрическая проекция
Аксонометрической называется проекция, полученная проецированием оригинала вместе с пространственной системой координат, к которой он отнесен, параллельными лучами на некоторую плоскость П.
В черчении из множества аксонометрических проекций стандартизировано в ГОСТ 2.317-69 два вида прямоугольных проекций (прямоугольная изометрия и диметрия) и три вида косоугольных проекций (фронтальная изометрия и диметрия и горизонтальная изометрия).
В технической практике наибольшее распространение получили прямоугольные виды аксонометрических проекций.
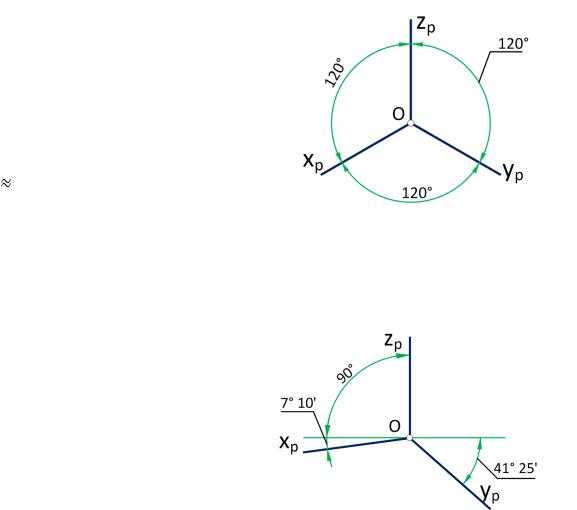
Прямоугольная изометрическая проекция
В прямоугольной изометрии аксонометрические оси располагаются под углом 120 друг к другу (рис. 18а). Способ построения осей прямоугольной изометрии показан на рис. 18б, истинный коэффициент искажения по всем трем осям равен 0,82. С целью упрощения построений ГОСТ 2.317-69 рекомендует выполнять изометрическую проекцию условно, с приведенным коэффициентом искажения, равным единице, т.е. по всем трем осям откладываются действительные размеры оригинала.
Направление штриховки в координатных плоскостях при выполнении разрезов изображено на рис. 18а.
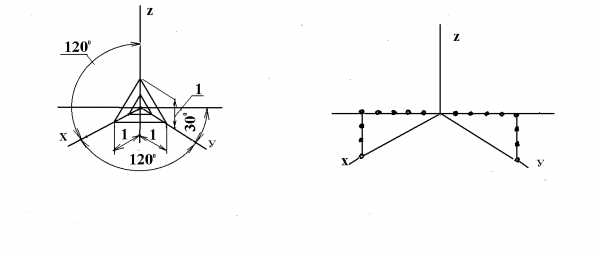
Рис. 18. Направление штриховки в координатных плоскостях (а) и осей (б) в изометрии
а
б
П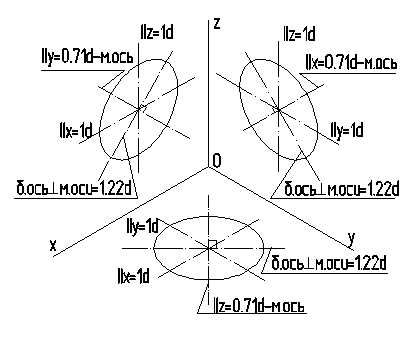 остроение
аксонометрических проекций окружностей,
лежащих в координатных плоскостях,
показано на рис. 19.
остроение
аксонометрических проекций окружностей,
лежащих в координатных плоскостях,
показано на рис. 19.
Рис. 19. Изометрия. Изображение окружностей,
расположенных в координатных плоскостях
Так как показатели искажения в изометрии по всем осям одинаковые, то окружности одного диаметра, расположенные в разных координатных плоскостях, изображены равными эллипсами. При этом для каждой координатной плоскости малая ось эллипса располагается параллельно аксонометрической проекции оси, отсутствующей в этой плоскости, т.е. если окружность лежит в плоскости XOY, то малая ось эллипса параллельна оси Z.
Прямоугольная диметрическая проекция
В диметрической проекции оси координат располагают так, как показано на рис. 20.

Рис. 20. Направление осей в диметрии
П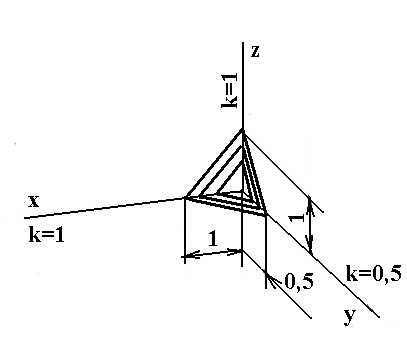 риведенные
коэффициенты искажения по осям Х иZ
равны единице, т.е. размеры отрезков,
расположенных на осях Х и Z
или им параллельных, не искажаются; по
оси Y
равны 0,5, т.е. размеры уменьшаются вдвое.
Штриховка в разрезах в координатных
плоскостях показана на рис. 21. Диметрические
проекции окружностей, расположенных в
координатных плоскостях, показаны на
рис. 22.
риведенные
коэффициенты искажения по осям Х иZ
равны единице, т.е. размеры отрезков,
расположенных на осях Х и Z
или им параллельных, не искажаются; по
оси Y
равны 0,5, т.е. размеры уменьшаются вдвое.
Штриховка в разрезах в координатных
плоскостях показана на рис. 21. Диметрические
проекции окружностей, расположенных в
координатных плоскостях, показаны на
рис. 22.
Рис. 21. Диметрия. Направление штриховки в координатных плоскостях
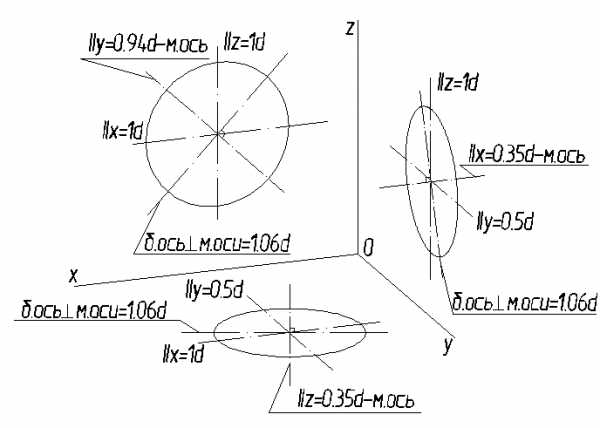
Рис. 22. Диметрия. Изображение окружностей, расположенных
в координатных плоскостях
Выполнение аксонометрической проекции с разрезом
При выполнении аксонометрических изображений деталей, имеющих внутренние полости, применяют разрезы. Их осуществляют двумя или тремя секущими плоскостями, каждая из которых параллельна какой-либо из координатных плоскостей. Полный разрез выполнять не рекомендуется, так как при этом теряется наглядность изображения. Следует удалять одну четвертую часть детали.
В рассматриваемом примере дана деталь, состоящая из нижней части, представляющей собой параллелепипед, и верхней части – цилиндра. В данной детали существует сквозное цилиндрическое отверстие. Нижняя и верхняя части детали соединены, треугольными в данном случае, ребрами жесткости.
Ребра жесткости – тонкая стенка или перегородка, которая препятствует смещению основных частей детали относительно друг друга. В разрезах их принято, согласно ГОСТа, не заштриховывать, даже если они попадают в секущую плоскость. В аксонометрической проекции, при вырезе четверти детали, данные ребра жесткости, попав в секущую плоскость, штрихуются на общих основаниях.
studfiles.net
Аксонометрия
9. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Суть аксонометрического проецирования.
Для получения наглядного «объемного» изображения предмета с трех сторон на одной плоскости проекций применяют аксонометрию. (с греческого аксонометрия – «измерение по осям»). Суть аксонометрического проецирования заключается в том, что предмет вместе с осями системы прямоугольных координат (образующих плоскости π1, π2, π3) к которым этот предмет отнесен в пространстве, проецируют параллельно на плоскость аксонометрических проекций.
Т.о., аксонометрическая проекция – это наглядное изображение предмета с трех сторон на плоскости вместе с осями прямоугольных координат, к которым предмет отнесен в пространстве, полученное параллельным проецированием (прямоугольным или косоугольным) на некоторую плоскость аксонометрических проекций. Направление проецирования не должно быть параллельным какой либо из осей X, Y, Z.
На рис. 9.1 дана аксонометрическая проекция т. А: А!. Аксонометрическая проекция ортогональной проекции (А1!) называется вторичной.
π! | Z |
|
|
|
| При аксонометрическом проецировании предмета его | |
| |||||||
|
|
|
|
|
| A! | размеры искажаются. Если на каждой из трех осей |
|
|
|
|
|
|
| прямоугольной системы координат отложить отрезок длиной l , |
|
|
|
|
|
|
| |
| lZ |
|
|
|
|
| то на плоскость аксонометрических проекций π! он |
|
|
|
|
|
| ||
|
|
|
|
|
|
| спроецируется вместе с соответствующими осями как lХ, lY, lZ |
|
|
|
|
|
|
| (рис. 9.1). Значения lХ, lY, lZ зависят от угла проецирования и |
|
|
|
|
|
|
| |
lX |
|
|
|
|
| lY | положения системы ортогональных осей по отношению к π!. |
|
|
|
|
|
|
| Отношение аксонометрической проекции отрезка (lХ, lY, lZ), |
X |
|
|
|
|
| Y | лежащей на аксонометрической проекции ортогональной оси к |
|
|
|
| А1! |
|
| истинной длине этого отрезка называется коэффициентом |
|
|
|
|
| |||
|
|
|
|
|
|
| искажения для данной оси в аксонометрии (X, Y, Z). |
|
|
|
|
|
|
| |
Рис. 9.1
kX = llX , kY = llY , kZ = llZ — коэффициенты искажения в аксонометрии по осям X, Y, Z.
Согласно основной теореме аксонометрии, три произвольно выбранные отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельную аксонометрическую проекцию трех равных и взаимно перпендикулярных отрезков, отложенных на осях прямоугольной системы координат.
В зависимости от соотношения коэффициентов искажения аксонометрические проекции могут быть трех видов: изометрическая, когда все коэффициенты искажения равны между собой; диметрическая, когда два коэффициента искажения равны между собой; триметрическая, когда все коэффициенты искажения различны.
Аксонометрия может быть косоугольной – когда проецирующие лучи не перпендикулярны плоскости аксонометрических проекций, а также прямоугольной – когда проецирующие лучи перпендикулярны плоскости аксонометрических проекций.
Плоскость аксонометрических проекций при прямоугольном проецировании не параллельна π1, π2 или π3, а при косоугольном проецировании может быть параллельна любой из этих плоскостей проекций.
Стандартные аксонометрические проекции.
В практике для построения аксонометрических проекций применяют наиболее удобные комбинации направлений аксонометрических осей и, соответствующих им коэффициентов искажения, принятые как стандартные. В практике наибольшее распространение получили прямоугольная изометрия и прямоугольная диметрия.
|
| z |
|
|
| Прямоугольная изометрия (рис. 9.2): оси расположены под углом | |
|
|
|
|
| 120º относительно друг друга. Коэффициенты искажения по всем осям | ||
|
|
|
|
| |||
|
|
|
|
|
| составляет k ≈ 0,82, однако для | удобства принято использовать |
|
|
|
|
|
| приведенные коэффициенты искажения. Для получения приведенных | |
|
| 0 |
| 0 |
| коэффициентов искажения больший из коэффициентов увеличивают до | |
| 12 |
|
| 12 |
| 1, а остальные пропорционально. | Т.о для прямоугольной изометрии |
|
|
|
|
| вместо kX = kY = kZ ≈ 0,82 используют kX = kY = kZ =1. | ||
|
|
|
|
| |||
x |
| 120 | y |
| z | ||
|
|
|
| Рис. 9.2 | |||
|
|
|
|
| |||
|
|
|
|
| ‘ | 4 |
|
|
|
|
| 1 | |
В прямоугольной диметрии оси расположены следующим |
|
| 0 |
| ||
|
|
| 1 |
| 2 | |
образом: ось х – под углом 7º10 ‘ по отношению к горизонту, ось y — |
|
|
| |||
|
| 5′ | ||||
под углом 41º25′ по отношению к горизонту. Коэффициенты | 7 |
|
|
|
| |
|
|
|
|
| ||
искажения по осям: по x и z — kx = kz ≈ 0,94, по | y — ky ≈ 0,47; | x |
|
|
|
|
значения приведенных коэффициентов искажения | соответственно: |
|
|
|
| |
kx = kz = 1, ky = 0,5 (рис. 9.3). |
|
|
|
|
|
|
|
|
|
|
| Рис. 9.3 | y |
Построения в прямоугольной изометрии и диметрии.
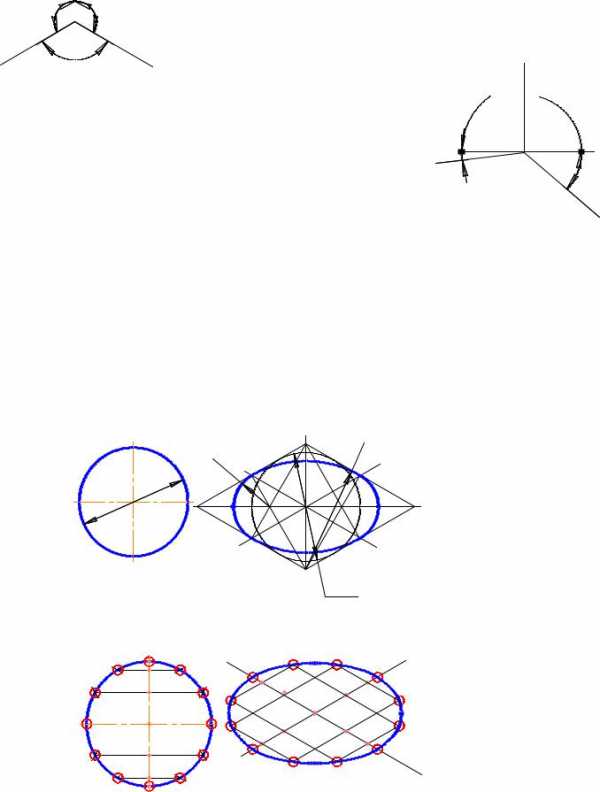
Существует ряд способов построения геометрических фигур в аксонометрии. На рис. 9.4 приведен пример построения окружности в изометрии. Для построения эллипса необходимо построить две взаимноперпендикулярные прямые и из этого центра — оси изометрии, расположенные под углом 1200 относительно друг друга. В центре пересечения осей строим окружность заданного диаметра D. К окружности проводим касательные, параллельные осям х и у, которые при пересечении друг с другом образуют ромб. Из вершины тупого угла, образованного касательными, радиусом R описываем дугу от точки пересечения оси у с одной стороной ромба до точки пересечения оси х с другой стороной ромба. Далее из точек О и О1 радиусом R1 описываем малые дуги. Эллипс построен.
|
|
| z |
| R | 1 | R |
|
|
| |
|
|
|
|
D |
|
|
|
|
| О | О |
|
|
| 1 |
| х | у | |
| Рис. 9.4 | D | |
На рис. 9.5 приведен еще один способ построения эллипса. Этот способом универсален и применим к любой аксонометрической проекции с учетом коэффициентов искажения по осям.
| 7 |
|
|
|
|
| e |
|
| 7 |
|
|
| 6 |
|
| |
d | 5 |
| 6 | 5 | |
| e | ||||
|
|
|
| ||
|
|
|
| 4 | |
|
|
|
|
|
x | c |
| 4 |
|
| 3 |
|
|
|
| d |
| 2 | ||
|
|
|
|
|
| ||
|
|
| 3 |
|
|
| |
| b |
|
| c |
|
| |
|
|
| х | a | 1 | ||
|
|
|
| b | |||
|
|
| 2 | y | |||
|
| a |
|
| |||
|
| 1 | y | Рис. 9.5 |
|
| |
|
|
|
|
|
| ||
|
|
|
|
|
|
|

Этот способ построения заключается в следующем: заданную окружность на комплексном чертеже (рис. 9.5 слева) делим на некоторое число частей ( в нашем случае на 12) 1, a, b, c, d, e, 7… Из каждой точки деления, кроме 1 и 7, проводим отрезки параллельно оси х до пересечения с окружностью в симмеричных точках деления. Эти отрезки пересекли ось у в точках2, 3, 4, 5, 6. Далее переходим к построению эллипса – проекции данной окружности в прямоугольной изометрии в плоскости осей ху. Для этого строим изометрические оси под углом 1200 (рис. 9.5 справа) относительно друг друга и по оси у откладываем точки 1…7. Из точек 2, 3, 4, 5,6 проводим прямые параллельные оси х. На каждой прямой необходимо отложить соответствующие отрезки: 2a, 3b, 4c, 5d, 6e по обе стороны от оси у. Полученные точки, включая точки 1 и 7 необходимо соединить плавной кривой с помощью лекала.
|
|
|
|
|
|
|
|
|
|
|
|
| Таким методом можно строить окружность, | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| например, в диметрии с учетом коэффициентов искажения | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| по осям. |
|
|
|
|
|
|
z |
| Имеет | смысл | рассмотреть | примеры построения | ||||||||||||||
| геометрических тел в аксонометрии (рис. | 9.6). В | качестве | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
| примера рассмотрены призмы с шестиугольным и | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| четырехугольным | основаниями. | Соответствующими | ||||
|
|
|
|
|
|
|
|
|
|
|
| y | засечками | показаны | отрезки, которые | измеряются на | |||
|
|
|
|
|
|
|
|
|
|
|
| комплексном чертеже, а после откладывают на | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
| аксонометрических осях. Следует обратить внимание на то, | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| что, если в основании геометрического тела лежит квадрат | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| или ромб, используют диметрические оси, т.к. в этом случае | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| наглядность будет наилучшей. В нашем примере призма с | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
| y |
| квадратом | в | основании построена | в диметрии с | учетом | ||
|
|
| z |
| коэффициентов искажения по осям. |
|
|
| |||||||||||
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y
y Рис. 9.6
Штриховка разрезов в аксонометрии
На вырезах в аксонометрии штриховые линии должны быть параллельны диагоналям вписанных в плоскости π1, π2, π3. квадратов. Т.о. направление штриховых линий зависит от вида аксонометрической проекции (рис. 9.7). Т.е. линии штриховки разрезов и сечений в аксонометрических проекциях наносят параллельно одной из диагоналей, вписанных в плоскости XY, YZ, XZ квадратов. Стороны этих квадратов отложены на осях с учетом коэффициентов искажения.
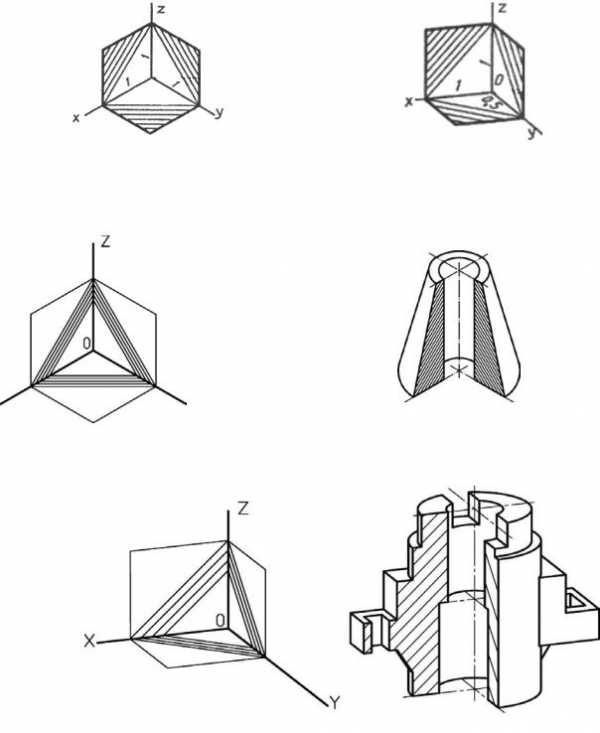
Прямоугольная изометрия | Прямоугольная диметрия |
Рис. 9.7
Направление штриховки разрезов в изометрической проекции показано на рис. 9.8
Рис. 9.8
Направление штриховки разрезов в диметрической проекции показано на рис. 9.9.
Рис. 9.9
studfiles.net
Аксонометрические проекции — это… Что такое Аксонометрические проекции?
- Аксонометрические проекции
- (от греч. axon — ось и metreo — измеряю * a. axonometric projections; н. axonometric Projektionen; ф. projections axonometriques; и. proyecciones axonometricas) — наглядное изображение предмета путём его параллельного проецирования вместе co связанной c ним системой трёх взаимно перпендикулярных координат на плоскость.B зависимости от угла s между направлением проецирования и плоскостью проекции различают прямоугольные и косоугольные A.
п. Прямоугольные пространств. координаты (и параллельные им осн. размеры изображаемого объекта) при аксонометрич. проецировании искажаются в определённых отношениях. Pазличают A. п. изометрические (показатели искажения вдоль всех координатных осей одинаковы), диметрические (одинаковы по двум осям), триметрические (по всем осям различны). При косоугольном проецировании (на основании теоремы Польке) за аксонометрич. оси принимают любые три прямые на плоскости чертежа, пересекающиеся в одной точке, a за показатели искажения — три произвольных конечных числа, обеспечивающих простоту построения, наглядность и удобоизмеряемость чертежа.
A. п. в горн. деле используют для изображения отд. сложных узлов горн. выработок (рис.) или геол. структур и составления спец. планов горн. работ (вентиляционных, аварийных, энергооборудования и т.д.).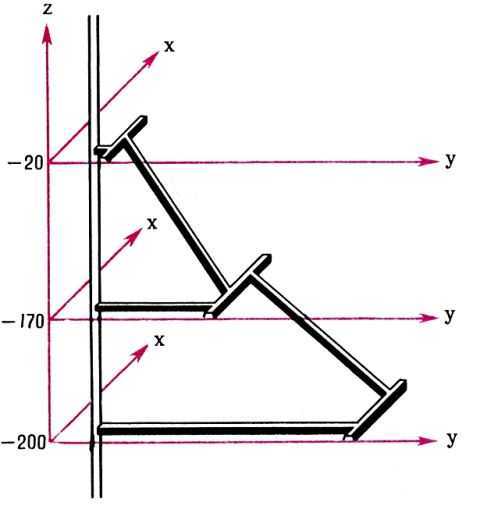
Изображение горных выработок в аксонометрической диаметрической проекции
Исходными материалами для построения A. п. горн. выработок и геол. структур являются горизонтальные (погоризонтные планы) и вертикальные разрезы. Построение аксонометрич. изображений проводят по координатам c помощью вспомогат. сеток и аксонографов. H. И. Cтенин.
Горная энциклопедия. — М.: Советская энциклопедия. Под редакцией Е. А. Козловского. 1984—1991.
- Аксинит
- Активатор
Смотреть что такое «Аксонометрические проекции» в других словарях:
ГОСТ 2.317-2011: Единая система конструкторской документации. Аксонометрические проекции — Терминология ГОСТ 2.317 2011: Единая система конструкторской документации. Аксонометрические проекции оригинал документа: 3.1 аксонометрическая проекция: Проекция на плоскость с помощью параллельных лучей, идущих из центра проецирования (который… … Словарь-справочник терминов нормативно-технической документации
Изометрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия
Аксонометрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия
Косоугольная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия
Диметрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия
аксонометричні проекції — аксонометрические проекции axonometric projections, isometric projections axonometrische Projektionen зображення предмета шляхом його паралельного проекціювання разом із пов’язаною з ним системою трьох взаємноперпендикулярних координат на площину … Гірничий енциклопедичний словник
коэффициент искажения — 3.4 коэффициент искажения: Отношение длины проекции отрезка оси на плоскость к его истинной длине. Источник: ГОСТ 2.317 2011: Единая система конструкторской документации. Аксонометрические проекции … Словарь-справочник терминов нормативно-технической документации
Аксонометрия — (от греч. áxōn ось и …метрия (См. …метрия) способ изображения предметов на чертеже при помощи параллельных проекций (См. Параллельная проекция). Аксонометрические чертежи характеризуются большой наглядностью. Для построения… … Большая советская энциклопедия
2.317 — ГОСТ 2.317{ 69} ЕСКД. Аксонометрические проекции. ОКС: 01.100.01 КГС: Т52 Система проектно конструкторской документации Взамен: ГОСТ 2.305 68 в части приложения Действие: С 01.01.71 Изменен: ИУС 11/80 Примечание: переиздание 2004 в сб. ЕСКД. ГОСТ … Справочник ГОСТов
аксонометрическая проекция — 3.1 аксонометрическая проекция: Проекция на плоскость с помощью параллельных лучей, идущих из центра проецирования (который удален в бесконечность) через каждую точку объекта до пересечения с плоскостью, на которую проецируется объект. 3.2… … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru