Разное

9 в двоичной системе: Перевод чисел из десятичной системы в двоичную

Содержание

Перевод в двоичную систему счисления

Пример №1. Перевести число 87,4510 в двоичное представление.
Используем калькулятор Перевод чисел.
Целая часть от деленияОстаток от деления
87 div 2 = 4387 mod 2 = 1
43 div 2 = 2143 mod 2 = 121 div 2 = 1021 mod 2 = 110 div 2 = 510 mod 2 = 05 div 2 = 25 mod 2 = 12 div 2 = 12 mod 2 = 01 div 2 = 01 mod 2 = 1

Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 1010111
87 = 10101112

Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.45*2 = 0.9 (целая часть 0)
0.9*2 = 1.8 (целая часть 1)
0.8*2 = 1.6 (целая часть 1)
0.

6*2 = 1.2 (целая часть 1)
Получаем число в 2-ой системе счисления: 0111
0.45 = 01112
Таким образом, число 87,45 в двоичной системе счисления записывается как 1010111,0111.

Пример №2. Перевести число 321,18 в двоичное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная СС Восьмеричная СС
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
Получаем число: 3218 = 0110100012

Переводим дробную часть числа.
Получаем число: 1

8 = 0012
Таким образом, число 321,18 в двоичной системе счисления записывается как 011010001,001.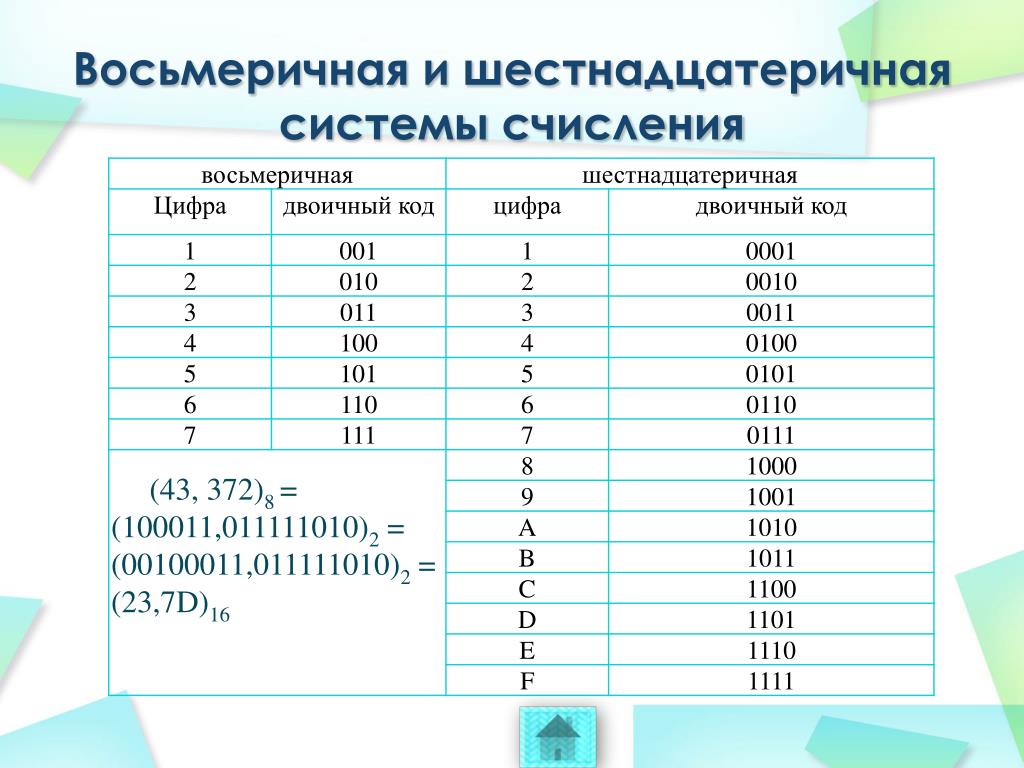

Пример №3. Перевести число AD,6716 в двоичное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная ССШестнадцатеричная СС
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F
Получаем число: AD16 = 101011012

Переводим дробную часть числа.
Получаем число: 6716 = 011001112
Таким образом, число AD,6716 в двоичной системе счисления записывается как 10101101,01100111.

Перейти к онлайн решению своей задачи

Пример №2. Перевести числа 581,10610, 115,7078, D21,E616 в двоичную систему.

Решение

Для проверки решения используем автоматический перевод чисел в двоичную систему счисления.

а) 581,10610;

Целая часть от деления
Остаток от деления
581 div 2 = 290581 mod 2 = 1
290 div 2 = 145290 mod 2 = 0145 div 2 = 72145 mod 2 = 172 div 2 = 3672 mod 2 = 036 div 2 = 1836 mod 2 = 018 div 2 = 918 mod 2 = 09 div 2 = 49 mod 2 = 14 div 2 = 24 mod 2 = 02 div 2 = 12 mod 2 = 01 div 2 = 01 mod 2 = 1

Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 1001000101
581 = 10010001012

Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.106*2 = 0.212 (целая часть 0)
0.212*2 = 0.424 (целая часть 0)
0.424*2 = 0.848 (целая часть 0)

0.848*2 = 1.696 (целая часть 1)
Получаем число в 2-ой системе счисления: 0001
0.106 = 00012

б) 115,7078;
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная система счисления Восьмеричная система счисления
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
Получаем число: 1158 = 0010011012

Переводим дробную часть числа.
Получаем число: 7078 = 111000111

2

в) D21,E616.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная система счисления шестнадцатеричная система счисления
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F
Получаем число: D21
16 = 1101001000012

Переводим дробную часть числа.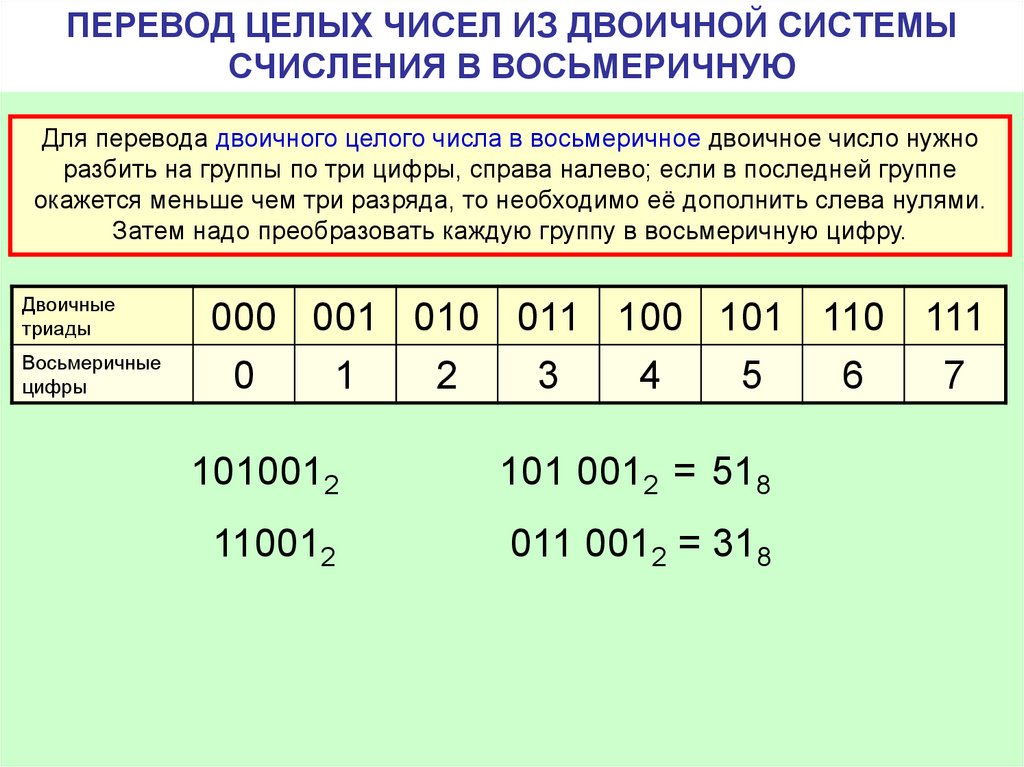
Получаем число: E616 = 111001102

Перейти к онлайн решению своей задачи

«Двоичная система счисления». 9-й класс

Разделы: Информатика, Конкурс «Презентация к уроку»

Класс: 9

Презентация к уроку

Загрузить презентацию (102 кБ)

Цель: сформировать понятия «двоичная система счисления» и основ арифметических вычислений в двоичной системе.

Требования к знаниям и умения

Учащиеся должны знать:

  • десятичную и двоичную системы счисления;
  • развернутую форму записи числа;
  • правила перевода из двоичной системы счисления в десятичную и наоборот;
  • правила сложения и умножения двоичных чисел.

Учащиеся должны уметь:

  • переводить двоичные числа в десятичную систему;
  • переводить десятичные числа в двоичную систему;
  • складывать и умножать двоичные числа.

Программно-дидактическое сопровождение: презентация «Двоичная система счисления»; учебник Семакин И.Г. Информатика и информационно-коммуникационные технологии. Базовый курс: Учебник для 9 класса; проектор.

ХОД УРОКА

1. Организационный момент

2. Постановка целей урока

– С какими числами работает компьютер? Почему?
– Как ими оперировать?

3. Ход урока

(Урок сопровождается презентацией «Двоичная система счисления»)

Двоичная система счисления является основной системой представления информации в памяти компьютера. Эта идея принадлежит Джону фон Нейману, сформулировавшему в 1946 году принципы устройства и работы ЭВМ.
Системы счисления
А что же такое система счисления? Это правила записи чисел и связанные с ними способы выполнения вычислений.
Система счисления, к которой мы все привыкли, называется десятичной. Объясняется это название тем, что в ней используются только 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число цифр определяет основание системы счисления. В двоичной же системе существуют всего две цифры: 0 и 1. Основание равно двум.

Вспомним принцип записи чисел в десятичной системе счисления. Значение цифры в записи числа зависит не только от самой цифры, но и от ее места расположения в числе (от позиции цифры). Например, в числе 473 первая справа цифра обозначает единицы, следующая – десятки, следующая – сотни. Этот факт можно выразить как сумму разрядных слагаемых:

47310 = 4 * 100 + 7 * 10 + 3 * 1 = 4 * 102 + 7 * 101 + 3 * 100.

Таким же образом можно записать число в двоичной системе счисления:

1012 = 1 * 22 + 0 * 21 + 1*20.

Такая запись называется развернутой формой записи числа.

Задание 1.

Запишите развернутую форму записи чисел:

5 789 = 5 * 103 + 7 * 102 + 8 * 101 + 9 * 100
51,89 = 5 * 101 + 1 * 100 + 8 * 10–1 + 9 * 10–2
32 478 = 3 * 104 + 2 * 103 + 4 * 102 + 7 * 101 + 8 * 100
26,378 = 2 * 101 + 6 * 100 + 3 * 10–1 + 7 * 10–2 + 8 * 10–3

Перевод чисел

Одним из способов перевода чисел из десятичной системы счисления в двоичную является деление столбиком на основания системы, т.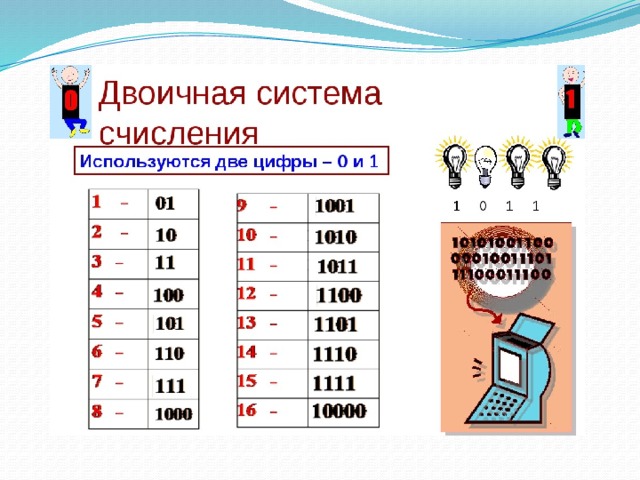 е. на 2. Деление производится до тех пор, пока в остатке не получится 1. Ответ в двоичной системе счисления записывается по остаткам от деления с конца.
Таким образом, 1910 = 100112.

Перевод из двоичной системы счисления в двоичную выполняется с помощью развернутой записи числа.

1012 = 1 * 22 + 0 * 21 + 1 * 20 = 4 + 0 + 1 = 510.

Задание 2.

Переведите числа:

3710 = 1001012
111012 = 2910

Арифметика двоичных чисел

Правила двоичной арифметики гораздо проще правил десятичной арифметики. Вот все возможные варианты сложения и умножения однозначных двоичных чисел:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 102		 0 х 0 = 0
0 х 1 = 0
1 х 0 = 0
1 х 1 = 1

Своей простотой и согласованностью с битовой структурой компьютерной памяти двоичная система и привлекла изобретателей компьютера. Ее гораздо проще реализовать техническими средствами, чем десятичную систему.

Вот пример сложения столбиком двух многозначных двоичных чисел:

Задание 3.

Выполните сложение в двоичной системе счисления:

1011012 + 111112; 101112 + 1011102 (ответ: 10011002; 10001012).

А теперь внимательно посмотрите на следующий пример умножения многозначных двоичных чисел:

Задание 4.

Выполните умножение в двоичной системе счисления:

1011012х112; 101012х112 (ответ: 100001112; 1111112).

4. Подведение итогов урока

– Что такое система счисления? (это правила записи чисел и связанные с ними способы выполнения вычислений)
– Какие цифры используются в записи двоичных чисел? (0 и 1)

5. Домашнее задание

  • §16 учебника;
  • Стр. 104 вопросы 2-7 письменно.

Урок по информатике «Двоичная система счисления» (9-й класс)

Разделы: Информатика

Класс: 9

Цели урока:

  1. Обучающая – формирование новых знаний, умений и навыков по теме “Двоичная система счисления”, осознанное понимание представления чисел в двоичной системе счисления, перевода десятичных чисел в двоичную систему счисления, контроль за усвоением учебного материала.
  2. Развивающая – развивать мышление учащихся посредством анализа, сравнения и обобщения изучаемого материала, самостоятельность, развитие речи;
  3. Воспитательная – активизация познавательной и творческой активности учащихся, воспитание чувства ответственности, коммуникативности.

Тип урока: изучение нового материала.

Вид урока: комбинированный, продолжительность 40 минут.

Возраст учащихся: 9 класс.

Оборудование урока:

  1. Компьютер с видеопроектором;
  2. Презентация;
  3. Карточки с заданиями;
  4. Листы для проставления итоговых баллов

Ход урока

1. Оргмомент.

2. Подготовка к восприятию нового материала, мотивация.

Сегодня на уроке вы имеете возможность показать свои знания не только по информатике, но и по математике и заработать отличные оценки. Каждый полный и правильный ответ на мой вопрос оценивается жетонами, дополнительно будут выставляться баллы за работу по карточкам. 1 жетон = 1баллу

“5” -– 14 балов, “4” — 12 балов, “3” — 10 балов

Деятельность учителя Деятельность учащихся
1. С каким универсальным техническим устройством мы работаем на уроках информатики? Это устройство называется компьютер.
2. Для чего была изобретена ЭВМ? ЭВМ изобретена для работы с числами
3. Зачем нужны числа? Для практически
4. На каком школьном учебном предмете вас учат работать с числами? С числами работаем на математике.
5. Сколько цифр используется для представления чисел? 10

0,1,2,3,4,5,6,7,8,9
6. Какие сигналы используются в компьютере и как они обозначаются? включено, выключено; 0,1
7. Сколько цифр используется? Используется 2 цифры: 0 и 1.
8. Какая это система счисления? Это двоичная система счисления.
9. Тема сегодняшнего урока? “Двоичная система счисления”

(Презентация, слайд 1)
10. Попробуйте поставить задачи урока.

Правильный ответ- 3 балла

 Научиться работать с двоичными числами:
  • Переводить из двоичной в десятичную СС;
  • Переводить из десятичной в двоичную СС;
  • Изучить арифметику двоичных чисел.

(Презентация, слайд 2)
11. Вспомним принцип записи числа в десятичной СС. Число 333

(Презентация, слайд 3)

Представьте это число в виде суммы разрядных единиц

Этот факт выражаем равенством: 33310=3*102 +3*101+3*100

Это развернутая форма записи многозначного числа. Договорились основание записывать подстрочно. (Презентация, слайд 4)

 333=300+30+3

(Правильный ответ 1 балл)
12. Задание: запишите в развернутой форме число

1 вариант 356210

2 вариант 286410

 Работа в тетрадях по вариантам:

356210=3*103 +5*102+6*101 +2*100

286410=2*103 +8*102+6*101 +4*100

(правильная запись – 1 балл)

(Презентация, слайд 5)
13.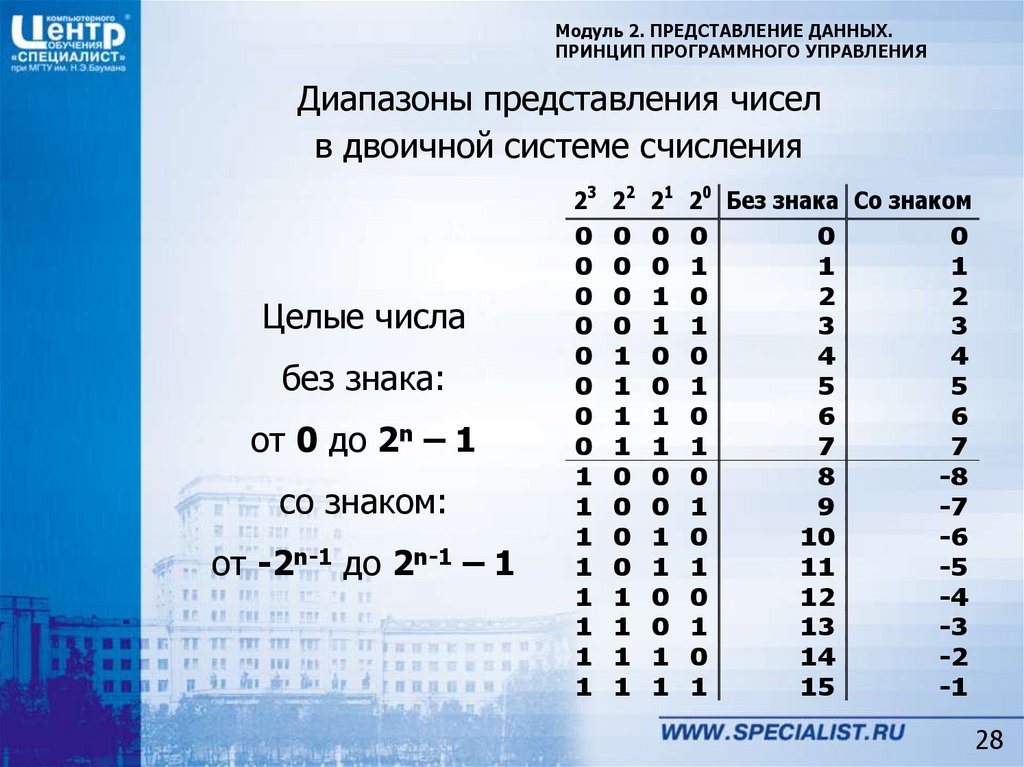 Запишите в развернутой форме двоичное число 10010012

(Презентация, слайд 6)

 10010012=1*26 +0*25+0*24+ 1*23 +0*22+0*21+ 1*20

(правильная запись – 1 балл)

(Презентация, слайд 6)
14. Можете ли вы вычислить какое это число в десятичной системе счисления? Да. 64+8+1=7310

(Правильный ответ 1 балл)
15. Переведите в десятичную систему счисления двоичное число 111012

(Презентация, слайд 7)

 111012=1*24+ 1*23 +1*22+0*21+ 1*20 =16+8+4+1=2910

(правильная запись – 1 балл)

(Презентация, слайд 7)
16. У каждого из вас есть карточка с заданием. Выполните задание №1 в тетрадях. Работа по карточкам.

(Приложение 1)
17. Поменяйтесь тетрадями, проверьте друг друга и выставьте баллы (1 за правильный ответ) Работают в парах.
18. Переводить двоичные числа в десятичную СС вы научились.

Как осуществить обратный перевод десятичного числа в двоичную СС? Например число 1810

(Презентация, слайд 8)

 Необходимо разложить на слагаемые, степени двоек.

1810=16+2=1*24+ 0*23 +0*22+1*21+ 0*20=100102
Есть другой способ. (Число 37)

В результате перевода получаем:

3710=1001012 (Презентация, слайд 9)

  
18. Выполните задание 2 на вашей карточке в тетради. Работают по карточкам. (Приложение 1)
19. Поменяйтесь тетрадями, проверьте друг друга и выставьте баллы (1 балл за правильный ответ) Работают в парах.
20. Нам необходимо познакомиться с правилами двоичной арифметики: сложением и умножением. Выпишите все варианты сложения и умножения двоичных чисел.

0+0=0 0*0=0

0+1=1 0*1=0

1+0=1 1*0=0

1+1=10 1*1=1
21. Складывать и умножать столбиком двоичные числа очень просто. Давайте попробуем.

Задание: 1010112+10012

 Складываем столбиком:

1010112+10012=1101002
22.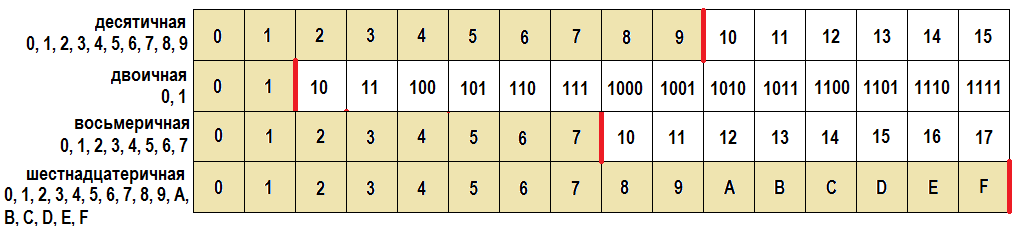 Сложите и умножьте два двоичных числа, полученных в результате выполнения задания 2 на вашей карточке в тетради. Работают по карточкам.

(Приложение 1)
23. Поменяйтесь тетрадями, проверьте друг друга и выставьте баллы (1 за правильный ответ) Работают в парах.

Рефлексия
Что такое двоичные числа?

Чем хороша двоичная система счисления?

Недостаток двоичной системы счисления.

 Числа, в записи которых используется только 0 и 1.

Простота двоичной арифметики.

(3 балла)

Многозначность двоичного числа. (3балла)
Посчитайте свои жетоны, приплюсуйте свои баллы.

Выставляем оценки в журнал.

 Считают, Проставляют в листы для проставления итоговых баллов., Выставляют оценки в дневники.
Дома: §16 читать, №4, 5,6,7 выполнить в тетради

Работа с дневниками. (Презентация, слайд 10)

  

Литература:

  1. Учебник Семакин И.Г. и др. Информатика и ИКТ. 9 класс М.:БИНОМ. Лаборатория знаний, 2005
  2. Семакин И.Г. и др. Преподавание базового курса информатики в средней школе: методическое пособие М.:БИНОМ. Лаборатория знаний, 2005

Двоичная система счисления | Информатика

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, десятичная двойка является основанием двоичной системы счисления, аналогично тому, как в десятичной системе основанием является число десять.

Чтобы научиться считать в двоичной системе счисления, рассмотрим, как формируются числа в привычной для нас десятичной.

В десятичной системе счисления мы располагаем десятью знаками-цифрами: от 0 до 9. Когда счет достигает числа 9, вводится новый более старший разряд – десятки. При этом разряд единиц обнуляется и счет в этом разряде опять начинается с нуля. После числа 19 разряд десятков увеличивается на 1, а разряд единиц снова обнуляется. Получается число 20. Когда десятки дойдут до 9, впереди них появится третий разряд – сотни.

Формирование каждого последующего числа в двоичной системе счисления аналогично тому, как это происходит в десятичной за исключением того, что используются всего-лишь две цифры: 0 и 1. Как только разряд достигает своего предела, то есть единицы, появляется новый разряд, а старый обнуляется.

  0
  1
 10
 11
100
101
110
111

Итак, число три в двоичной системе записывается как 11, в десятичной – как 3. Количественно это одинаковые числа.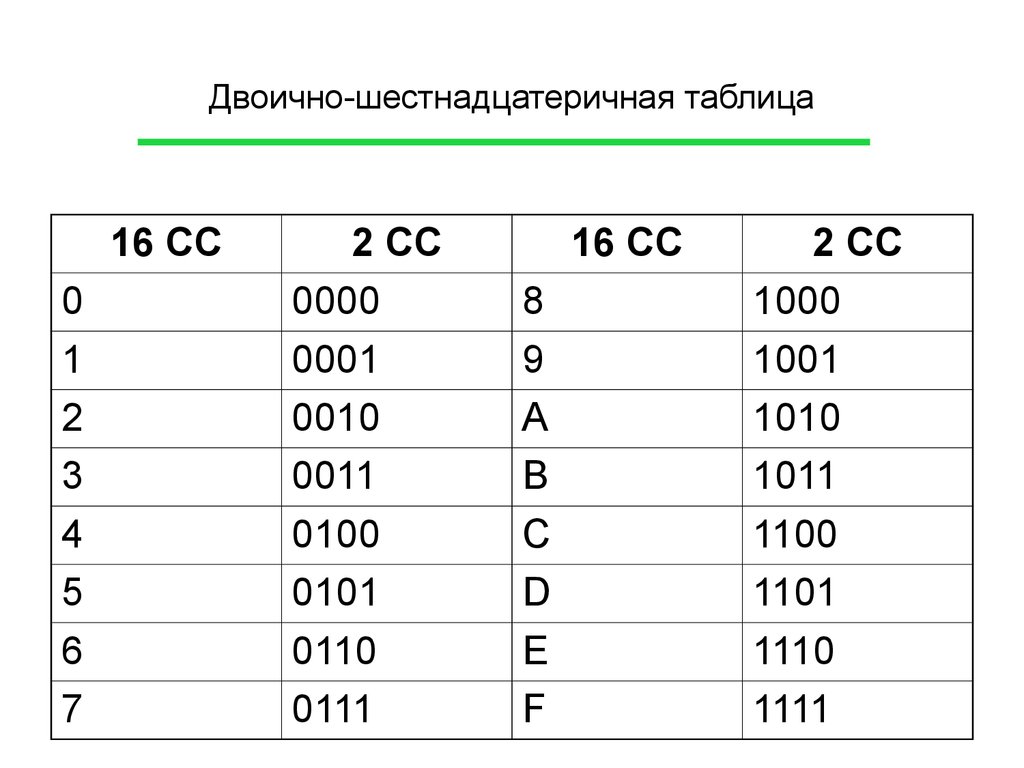 Это одно и то же число, выраженное в различных системах счисления. Если есть вероятность неоднозначной трактовки числа, к нему приписывается нижний индекс в десятичной системе счисления, обозначающий, в какой системе счисления выражено данное число:

112 = 310

Индекс для числа, выраженного в десятичной системе, обычно опускается.

Перевод чисел из двоичной системы счисления в десятичную

В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:

5476 = 5000 + 400 + 70 + 6

Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:

5476 = 5 * 103 + 4 * 102 + 7 * 101 + 6 * 100

После равенства числа 5, 4, 7 и 6 – это набор цифр из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10(1-1). Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.

Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:

10001001 = 1 * 27 + 0 * 26 + 0 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 0 * 21 + 1 * 20

Результат вычислений дает десятичное число, количественно равное двоичному 10001001:

1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 =
= 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:

100010012 = 13710

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык современной вычислительной техники.

Когда любые данные сохраняются на компьютере, они кодируются числами. С числами же компьютер выполняет операции, изменяя эти данные.

Допустим, у нас есть десятичное число 14, которое требуется сохранить в компьютерной памяти. Мы задействуем участок памяти, в данном случае состоящий как минимум из двух элементов, отводимых под разряды. В одном из разрядов мы сохраняем десятичное число 1, в другом – число 4.

Элемент памяти – это физическое устройство. Если проектировать его для хранения десятичной цифры, потребуется создать такое устройство, которое может находиться в десяти разных физических состояниях и способно переключаться между ними. Каждое из этих состояний будет соответствовать числу от 0 до 9.

Создать такой элемент памяти возможно, однако сложнее и дороже, чем создать элемент, способный находиться только в двух состояниях. Одно состояние сопоставить нулю, второе – единице. Кроме того, подобное хранение данных является более надежным.

Поэтому оказалось проще перевести число 14 в двоичную систему счисления, получив число 1110, и именно его сохранить в памяти. И пусть даже при этом будут задействованы не два, а четыре разряда, то есть четыре элементарных единиц памяти.

Перевод десятичного числа в двоичное

Одним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим «сбором» двоичного числа из остатков. Переведем таким образом число 14 в двоичное представление.

14 / 2 = 7, остаток 0
 7 / 2 = 3, остаток 1
 3 / 2 = 1, остаток 1
 1 / 2 = 0, остаток 1

Собирать остатки надо с конца, то есть с последнего деления. Получаем 1110.

Выполним то же самое для числа 77:

77 / 2 = 38, остаток 1
38 / 2 = 19, остаток 0
19 / 2 =  9, остаток 1
 9 / 2 =  4, остаток 1
 4 / 2 =  2, остаток 0
 2 / 2 =  1, остаток 0
 1 / 2 =  0, остаток 1

Собираем остатки вместе, начиная с конца: 1001101.

Проверим, выполнив обратный перевод:

1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Число 9, 0x000009, девять — BiKubik.

com

Энциклопедия чисел

Свойства натурального числа 9, 0x000009, 0x9:

Системы счисления Основные свойства Степени, корни

Тригонометрия Хэши, криптография Языки программирования

Дата и время Цвет по числу Интернет

Другие свойства

Рейтинг 7.9 из 10, оценок: 22.

Системы счисления, перевод в систему счисления

Десятичное число 9

  • 9 в шестнадцатеричной системе счисления
    9
  • 9 в двоичной системе счисления
    1001
  • 9 в восьмеричной системе счисления
    11

Шестнадцатеричное число 9

  • 9 в десятичной системе
    9
  • 9 в двоичной системе
    1001
  • 9 в восьмеричной системе
    11

Двоичное число 1001

  • 1001 в десятичной системе
    9
  • 1001 в шестнадцатеричной системе
    9
  • 1001 в восьмеричной системе
    11

Восьмеричное число 11

  • 11 в десятичной системе
    9
  • 11 в шестнадцатеричной системе
    9
  • 11 в двоичной системе
    1001

Основные арифметические и алгебраические свойства

  • Число 9 на русском языке, number in Russian, число 9 прописью:
    девять
  • Четность
    Нечетное число 9
  • Разложение на множители, делители числа 9
    3, 3, 1
  • Простое или составное число
    Составное число 9
  • Числа делящиеся на целое число 9
    18, 27, 36, 45, 54, 63, 72, 81
  • Число 9 умноженное на число два
    18
  • 9 деленное на число 2
    4. 5
  • Список 8-ми простых чисел перед числом
    7, 5, 3, 2
  • Сумма десятичных цифр
    9
  • Количество цифр
    1
  • Является ли число 9 цифрой
    Да, цифра 9
  • Десятичный логарифм 9
    0.95424250943932
  • Натуральный логарифм 9
    2.1972245773362
  • Это число Фибоначчи?
    Нет
  • Число на 1 больше числа 9,
    следующее число
    число 10
  • Число на 1 меньше числа 9,
    предыдущее число
    8

Степени числа, корни

  • 9 во второй степени (в квадрате)
    (функция x в степени 2 — x²)
    81
  • В третьей степени (в кубе, 9 в степени 3, x³) равно
    729
  • Корень квадратный из 9
    3
  • Корень кубический из числа 9 =
    2. 0800838230519

Тригонометрические функции, тригонометрия

  • Синус, sin 9 градусов, sin 9°
    0.156434465
  • Косинус, cos 9 градусов, cos 9°
    0.9876883406
  • Тангенс, tg 9 градусов, tg 9°
    0.1583844403
  • Синус, sin 9 радиан
    0.41211848524176
  • Косинус, cos 9 радиан
    -0.91113026188468
  • Тангенс, tg 9 радиан равно
    -0.45231565944181
  • 9 градусов, 9° =
    0.15707963267949 радиан
  • 9 радиан =
    515.66201561774 градуса, 515.66201561774°

Контрольные суммы, хэши, криптография

  • MD-5 хэш(9)
    45c48cce2e2d7fbdea1afc51c7c6ad26
  • CRC-32, CRC32(9)
    2366072709
  • SHA-256 hash, SHA256(9)
    19581e27de7ced00ff1ce50b2047e7a567c76b1cbaebabe5ef03f7c3017bb5b7
  • SHA1, SHA-1(9)
    0ade7c2cf97f75d009975f4d720d1fa6c19f4897
  • ГОСТ Р 34. 11, GOST R 34.11-94, GOST(9)
    ceb4ca741fc5b919262b4bc9b8d0df90119216cc645a3320d92b350ad99b841b
  • Base64
    OQ==

Языки программирования

  • C++, CPP, C значение 9
    0x000009, 0x9
  • Delphi, Pascal значение числа 9
    $000009

Дата и время

  • 9-й день простого и високосного года
    9 января
  • Конвертация UNIX timestamp 9 в дату и время
    UTC
    в Москве, Россия
    в Лондоне, Великобритания
    в Нью-Йорке, США

Интернет

  • Конвертация в IPv4 адрес Интернет
    0.0.0.9
  • 9 в Википедии:
    9

Другие свойства числа

  • Короткая ссылка на эту страницу, DEC
    https://bikubik.com/ru/9
  • Короткая ссылка на эту страницу, HEX
    https://bikubik.com/ru/x9
  • Номер телефона
    9
  • Телефонный код страны
    +9

Цвет по числу 9, цветовая гамма

  • html RGB цвет 9, 16-ричное значение
    #000009 — (0, 0, 9)
  • HTML CSS код цвета #000009
    .color-mn { color: #000009; }
    .color-bg { background-color: #000009; }

Цвет для данного числа 9

 

Здесь вы можете изменить составляющую цвета для данного числа 9 или цвета 000009:

Двоичное счисление на пальцах — Журнал «Код»

Если у вас в школе была информатика, не исключено, что там было упражнение на перевод обычных чисел в двоичную систему и обратно. Маловероятно, что кто-то вам объяснял практический смысл этой процедуры и откуда вообще берётся двоичное счисление. Давайте закроем этот разрыв.

Эта статья не имеет практической ценности — читайте её просто ради интереса к окружающему миру. Если нужны практические статьи, заходите в наш раздел «Где-то баг», там каждая статья — это практически применимый проект.

Отличный план

Чтобы объяснить всё это, нам понадобится несколько тезисов:

  1. Система записи числа — это шифр.
  2. Мы привыкли шифровать десятью знаками.
  3. Но система записи чисел может быть любой. Это условность.
  4. Двоичная система — это тоже нормальная система.
  5. Всё тлен и суета.

Система записи — это шифр

Если у нас есть девять коров, мы можем записать их как 🐄🐄🐄🐄🐄🐄🐄🐄🐄  или как 9 × 🐄.

Почему 9 означает «девять»? И почему вообще есть такое слово? Почему такое количество мы называем этим словом? Вопрос философский, и короткий ответ — нам нужно одинаково называть числа, чтобы друг друга понимать. Слово «девять», цифра 9, а также остальные слова — это шифр, который мы выучили в школе, чтобы друг с другом общаться.

Допустим, к нашему стаду прибиваются еще 🐄🐄🐄. Теперь у нас 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄  — двенадцать коров, 12. Почему мы знаем, что 12 — это «двенадцать»? Потому что мы договорились так шифровать числа.

Нам очень легко расшифровывать записи типа 12, 1920, 100 500 и т. д. — мы к ним привыкли, мы учили это в школе. Но это шифр. 12 × 🐄  — это не то же самое, что 🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄🐄. Это некая абстракция, которой мы пользуемся, чтобы упростить себе счёт.

Мы привыкли шифровать десятью знаками

У нас есть знаки 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — всего десять знаков. Этим числом знаков мы шифруем количество единиц, десятков, сотен, тысяч и так далее.

Мы договорились, что нам важен порядок записи числа. Мы знаем, что самый правый знак в записи означает число единиц, следующий знак (влево) означает число десятков, потом сотен и далее.

Например, перед нами число 19 547. Мы знаем, что в нём есть:

1 × 10 000

9 × 1000

5 × 100

4 × 10

7 × 1

Если приглядеться, то каждый следующий разряд числа показывает следующую степень десятки:

1 × 104

9 × 103

5 × 102

4 × 101

7 × 100

Нам удобно считать степенями десятки, потому что у нас по десять пальцев и мы с раннего детства научились считать до десяти.

Система записи — это условность

Представим бредовую ситуацию: у нас не 10 пальцев, а 6. И в школе нас учили считать не десятками, а шестёрками. И вместо привычных цифр мы бы использовали знаки ØABCDE. Ø — это по-нашему ноль, A — 1, B — 2, E — 5.

Вот как выглядели бы привычные нам цифры в этой бредовой системе счисления:

0 — Ø
1 — A
2 — B
3 — C
4 — D
5 — E		6 — AØ
7 — AA
8 — AB
9 — AC
10 — AD
11 — AE		12 — BØ
13 — BA
14 — BB
15 — BC
16 — BD
17 — BE		18 — CØ
19 — CA
20 — CB
21 — CC
22 — CD
23 — CE		24 — DØ
25 — DA
26 — DB
27 — DC
28 — DD
29 — DE		30 — EØ
31 — EA
32 — EB
33 — EC
34 — ED
35 — EE		36 — AØØ
37 — AØA
38 — AØB
39 — AØC
40 — AØD
41 — AØE

В этой системе мы считаем степенями шестёрки. Число ABADØ можно было бы перевести в привычную нам десятичную запись вот так:

A × 64 = 1 × 1296 = 1296

B × 63 = 2 × 216 = 432

A × 62 = 1 × 36 = 36

D × 61 = 4 × 6 = 24

Ø × 60 = 0 × 1 = 0

1296 + 432 + 36 + 24 + 0 = 1788. В нашей десятичной системе это 1788, а у людей из параллельной вселенной это ABADØ, и это равноценно.

Выглядит бредово, но попробуйте вообразить, что у нас в сумме всего шесть пальцев. Каждый столбик — как раз шесть чисел. Очень легко считать в уме. Если бы нас с детства учили считать шестёрками, мы бы спокойно выучили этот способ и без проблем всё считали. А счёт десятками вызывал бы у нас искреннее недоумение: «Что за бред, считать числом AD? Гораздо удобнее считать от Ø до E!»

То, как мы шифруем и записываем числа, — это следствие многовековой традиции и физиологии. Вселенной, космосу, природе и стадам коров глубоко безразлично, что мы считаем степенями десятки. Природа не укладывается в эту нашу систему счёта.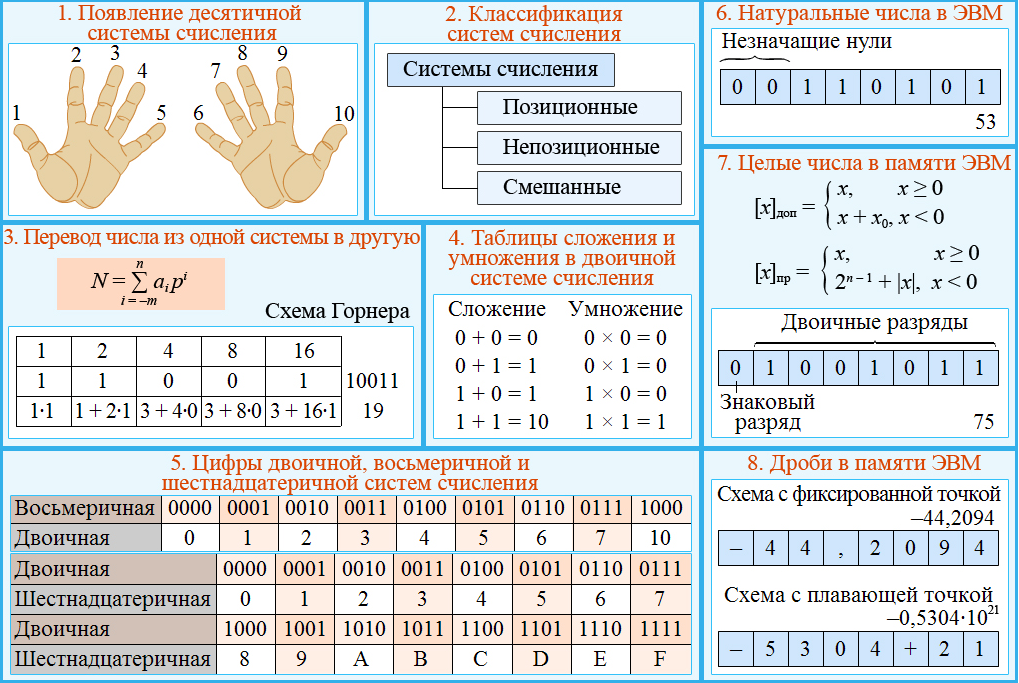

Например, свет распространяется в вакууме со скоростью 299 792 458 метров в секунду. Ему плевать, что нам для ровного счёта хотелось бы, чтобы он летел со скоростью 300 тысяч километров в секунду. А ускорение свободного падения тела возле поверхности Земли — 9,81 м/с2. Так и хочется спросить: «Тело, а ты не могло бы иметь ускорение 10 м/с2?» — но телу плевать на наши системы счисления.

Двоичная система (тоже нормальная)

Внутри компьютера работают транзисторы. У них нет знаков 0, 1, 2, 3… 9. Транзисторы могут быть только включёнными и выключенными — обозначим их 💡 и ⚫.

Как это устроено: транзисторы

Мы можем научить компьютер шифровать наши числа этими транзисторами так же, как шестипалые люди шифровали наши числа буквами. Только у нас будет не 6 букв, а всего две: 💡 и ⚫. И выходит, что в каждом разряде будет стоять не число десяток в разной степени, не число шестёрок в разной степени, а число… двоек в разной степени. И так как у нас всего два знака, то получается, что мы можем обозначить либо наличие двойки в какой-то степени, либо отсутствие:

0 — ⚫
1 — 💡

2 — 💡⚫
3 — 💡💡

4 — 💡⚫⚫
5 — 💡⚫💡
6 — 💡💡⚫
7 — 💡💡💡

8 — 💡⚫⚫⚫
9 — 💡⚫⚫💡
10 — 💡⚫💡⚫
11 — 💡⚫💡💡
12 — 💡💡⚫⚫
13 — 💡💡⚫💡
14 — 💡💡💡⚫
15 — 💡💡💡💡		16 — 💡⚫⚫⚫⚫
17 — 💡⚫⚫⚫💡
18 — 💡⚫⚫💡⚫
19 — 💡⚫⚫💡💡
20 — 💡⚫💡⚫⚫
21 — 💡⚫💡⚫💡
21 — 💡⚫💡💡⚫
23 — 💡⚫💡💡💡
24 — 💡💡⚫⚫⚫
25 — 💡💡⚫⚫💡
26 — 💡💡⚫💡⚫
27 — 💡💡⚫💡💡
28 — 💡💡💡⚫⚫
29 — 💡💡💡⚫💡
30 — 💡💡💡💡⚫
31 — 💡💡💡💡💡		32 — 💡⚫⚫⚫⚫⚫
33 — 💡⚫⚫⚫⚫💡
34 — 💡⚫⚫⚫💡⚫
35 — 💡⚫⚫⚫💡💡
36 — 💡⚫⚫💡⚫⚫
37 — 💡⚫⚫💡⚫💡
38 — 💡⚫⚫💡💡⚫
39 — 💡⚫⚫💡💡💡
40 — 💡⚫💡⚫⚫⚫
41 — 💡⚫💡⚫⚫💡
42 — 💡⚫💡⚫💡⚫
43 — 💡⚫💡⚫💡💡
44 — 💡⚫💡💡⚫⚫
45 — 💡⚫💡💡⚫💡
46 — 💡⚫💡💡💡⚫
47 — 💡⚫💡💡💡💡
48 — 💡💡⚫⚫⚫⚫
49 — 💡💡⚫⚫⚫💡
50 — 💡💡⚫⚫💡⚫
51 — 💡💡⚫⚫💡💡
52 — 💡💡⚫💡⚫⚫
53 — 💡💡⚫💡⚫💡
54 — 💡💡⚫💡💡⚫
55 — 💡💡⚫💡💡💡
56 — 💡💡💡⚫⚫⚫
57 — 💡💡💡⚫⚫💡
58 — 💡💡💡⚫💡⚫
59 — 💡💡💡⚫💡💡
60 — 💡💡💡💡⚫⚫
61 — 💡💡💡💡⚫💡
62 — 💡💡💡💡💡⚫
63 — 💡💡💡💡💡💡

Если перед нами число 💡 ⚫💡⚫⚫ 💡💡⚫⚫, мы можем разложить его на разряды, как в предыдущих примерах:

💡 = 1 × 28 = 256

⚫ = 0 × 27 = 0

💡 = 1 × 26 = 64

⚫ = 0 × 25 = 0

⚫ = 0 × 24 = 0

💡 = 1 × 23 = 8

💡 = 1 × 22 = 4

⚫ = 0 × 21 = 0

⚫ = 0 × 20 = 0

256 + 0 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 332

Получается, что десятипалые люди могут записать это число с помощью цифр 332, а компьютер с транзисторами — последовательностью транзисторов 💡⚫💡⚫⚫ 💡💡⚫⚫.

Если теперь заменить включённые транзисторы на единицы, а выключенные на нули, получится запись 1 0100 1100. Это и есть наша двоичная запись того же самого числа.

Почему говорят, что компьютер состоит из единиц и нулей (и всё тлен)

Инженеры научились шифровать привычные для нас числа в последовательность включённых и выключенных транзисторов.

Дальше эти транзисторы научились соединять таким образом, чтобы они умели складывать зашифрованные числа. Например, если сложить 💡⚫⚫ и ⚫⚫💡, получится 💡⚫💡.  Мы писали об этом подробнее в статье о сложении через транзисторы.

Дальше эти суммы научились получать супербыстро. Потом научились получать разницу. Потом умножать. Потом делить. Потом всё это тоже научились делать супербыстро. Потом научились шифровать не только числа, но и буквы. Научились их хранить и считывать. Научились шифровать цвета и координаты. Научились хранить картинки. Последовательности картинок. Видео. Инструкции для компьютера. Программы. Операционные системы. Игры. Нейросети. Дипфейки.

И всё это основано на том, что компьютер умеет быстро-быстро складывать числа, зашифрованные как последовательности включённых и выключенных транзисторов.

При этом компьютер не понимает, что он делает. Он просто гоняет ток по транзисторам. Транзисторы не понимают, что они делают. По ним просто бежит ток. Лишь люди придают всему этому смысл.

Когда человека не станет, скорость света будет по-прежнему 299 792 458 метров в секунду. Но уже не будет тех, кто примется считать метры и секунды. Такие дела.

Двоичная система счисления

Двоичное число состоит только из 0 с и 1 с.

110100

Пример двоичного числа

В двоичном формате нет 2, 3, 4, 5, 6, 7, 8 или 9!

Двоичные числа широко используются в математике и не только.


На самом деле в цифровом мире используются двоичные числа.

Как считать с помощью двоичного кода?

Это похоже на десятичный счет, за исключением того, что мы достигаем 10 гораздо раньше.

Двоичный    
0   Мы начинаем с 0
1   Затем 1
???   Но тогда нет символа 2… что делать?

 

Ну как считать в десятичной системе?
  0   Начать с 0
  …   Сосчитайте 1,2,3,4,5,6,7,8, а затем…
  9   Это последняя цифра в десятичном формате
  10   Итак, мы снова начинаем с 0, но добавляем 1 слева

То же самое делается в двоичном коде. ..

  Двоичный    
  0   Начать с 0
• 1   Затем 1
•• 10   Теперь снова начните с 0, но добавьте 1 слева
••• 11   еще 1
•••• ???   Но что СЕЙЧАС… ?

 

Что происходит в Decimal?
  99   Когда у нас заканчиваются цифры, мы…
  100   … снова начать с 0, но добавить 1 слева

И это то, что мы делаем в двоичном формате . ..

  Двоичный    
  0   Начать с 0
• 1   Затем 1
•• 10   Снова начать с 0, но добавить 1 слева
••• 11    
•••• 100   снова начать с 0 и добавить единицу к числу слева…
… но это число уже равно 1, поэтому оно также возвращается к 0…
… и 1 добавляется к числу слева. следующая позиция слева
••••• 101    
•••••• 110    
••••••• 111    
•••••••• 1000   Снова начать с 0 (для всех 3 цифр),
добавить 1 слева
••••••••• 1001   И так далее!

 

Посмотрите, как это делается в этой небольшой демонстрации (нажмите кнопку воспроизведения):

Десятичный против двоичного

Вот некоторые эквивалентные значения:

Десятичный: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Двоичный: 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111

Симметрия

Двоичные числа также имеют красивый и элегантный узор:

Вот несколько больших значений:

Десятичный: 20 25 30 40 50 100 200 500
Двоичный: 10100 11001 11110 101000 110010 1100100 11001000 111110100

«Двоичный код так же прост, как 1, 10, 11. »

Теперь посмотрите, как использовать Binary для счета на пальцах после 1000:

Деятельность: Бинарные пальцы

 

Позиция

В десятичной системе есть единицы, десятки, сотни и т. д.

В Двоичный есть Единицы, Двойки, Четверки и т. д., например:

Это 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8)
= 13,625 в десятичной системе счисления

 

Цифры можно размещать слева или справа от точки, чтобы показать значения больше единицы и меньше одного.

10.1
Число слева от точки целое число (например, 10)
   
По мере того, как мы двигаемся дальше влево, каждый числовой разряд
получает 2 раз больше .
   
Первая цифра справа означает половинки (1/2).
   
  По мере того, как мы движемся дальше вправо, каждый числовой разряд
становится в 2 раза меньше (в два раза больше).

Пример: 10.1

  • «10» означает 2 в десятичной системе,
  • «.1» означает половину,
  • Итак, «10,1» в двоичном формате равно 2,5 в десятичном

Вы можете выполнять преобразования в Конвертер двоичных и десятичных чисел в шестнадцатеричные.

Слов

Слово двоичное происходит от «Би-», что означает два. Мы видим «би-» в таких словах, как «велосипед» (два колеса) или «бинокль» (два глаза).

Когда вы произносите двоичное число, произносите каждую цифру (например, двоичное число «101» произносится как «один ноль один» , или иногда «один-о-один» ). Таким образом, люди не путаются с десятичным числом.

Одна двоичная цифра (например, «0» или «1») называется «бит».

Например, 11010 имеет длину пять бит.

Слово бит составлено из слов » b inary dig it »

Как показать, что число является двоичным

Чтобы показать, что число является двоичным числом, добавьте к нему маленькую двойку, например: 101 2

Таким образом, люди не будут думать, что это десятичное число «101» (сто один).

Примеры

Пример: Что такое 1111

2 в десятичном формате?
  • «1» слева стоит в позиции «2×2×2», значит, 1×2×2×2 (=8)
  • Следующая «1» находится в позиции «2×2», что означает 1×2×2 (=4)
  • Следующая «1» находится в позиции «2», значит, 1×2 (=2)
  • Последняя «1» стоит в позиции единиц, значит 1
  • Ответ: 1111 = 8+4+2+1 = 15 в десятичной системе счисления

Пример: Что такое 1001

2 в десятичном формате?
  • «1» слева находится в позиции «2×2×2», что означает 1×2×2×2 (=8)
  • «0» находится в позиции «2×2», так что это означает 0×2×2 (=0)
  • Следующий «0» находится в позиции «2», что означает 0×2 (=0)
  • Последняя «1» стоит в позиции единиц, значит 1
  • Ответ: 1001 = 8+0+0+1 = 9 в десятичной системе счисления

Пример: Что такое 1.

1 2 в десятичном формате?
  • «1» слева стоит в позиции единиц, поэтому это означает 1.
  • 1 справа находится в положении «половинки», значит, 1×(1/2)
  • Итак, 1,1 — это «1 и 1 половина» = 1,5 в десятичной системе счисления

Пример: Что такое 10.11

2 в десятичном формате?
  • «1» стоит в позиции «2», значит, 1×2 (=2)
  • «0» стоит в позиции единиц, значит 0
  • «1» справа от точки находится в положении «половинки», поэтому это означает 1×(1/2)
  • Последняя «1» справа стоит в позиции «четверти», значит, 1×(1/4)
  • Итак, 10,11 равно 2+0+1/2+1/4 = 2,75 в десятичной системе счисления
    • .

«В мире есть 10 типов людей,
тех, кто понимает двоичные числа, и тех, кто не понимает.»

 

 

Конвертер десятичных чисел в двоичные

Конвертер десятичных чисел в двоичные

Главная›Преобразование›Преобразование чисел›Десятичное число в двоичное

От BinaryDecimalOctalHexadecimalText

Кому BinaryDecimalOctalHexadecimalText

Введите десятичное число

Двоичный номер

Дополнение до 2 с двоичной подписью

Шестнадцатеричный номер

Группировка цифр

Little endian

Адрес
Данные

Big endian

Адрес
Данные

Шаги преобразования десятичного числа в двоичное

Разделите на основание 2, чтобы получить цифры из остатков:

Деление
на 2		 Частное

Остаток

(Цифра)		 Бит #

Двоичное преобразование в десятичное ►

Как преобразовать десятичное число в двоичное

Шаги преобразования:
  1. Разделите число на 2.
  2. Получить целое частное для следующей итерации.
  3. Получить остаток двоичной цифры.
  4. Повторяйте шаги, пока частное не станет равным 0,
Пример #1

Преобразование 13 10 в двоичное:

Пример #2
Разделение
на 2		 Частное Остаток Бит #
13/2 6 1 0
6/2 3 0 1
3/2 1 1 2
1/2 0 1 3 Частное Остаток Бит #
174/2 87 0 0
87/2 43 1 1
43/2 21 1 2
21/2 10 1 3
10/2 5 0 4
5/2 2 1 5
2/2 1 0 6
1/2 0 1 7

Так 174 10 = 10101110 2

Таблица преобразования десятичных чисел в двоичные

Десятичное число
Число		 Двоичный
Число		 Шестнадцатеричный
Числовой
0 0 0
1 1 1
2 10 2
3 11 3
4 100 4
5 101 5
6 110 6
7 111 7
8 1000 8
9 1001 9
10 1010 А
11 1011 Б
12 1100 С
13 1101 Д
14 1110 Е
15 1111 Ф
16 10000 10
17 10001 11
18 10010 12
19 10011 13
20 10100 14
21 10101 15
22 10110 16
23 10111 17
24 11000 18
25 11001 19
26 11010 1А
27 11011 1Б
28 11100 1С
29 11101 1Д
30 11110 1Е
31 11111 1F
32 100000 20
64 1000000 40
128 10000000 80
256 100000000 100

 

См.

также
  • Преобразователь двоичного кода в десятичный
  • Преобразователь десятичных чисел в шестнадцатеричные
  • Преобразователь десятичного числа в восьмеричное
  • Преобразователь десятичных чисел в дроби
  • Преобразователь десятичных чисел в проценты
  • Двоичный калькулятор
  • Преобразователь текста ASCII в двоичный код
  • Как преобразовать десятичную систему в двоичную
  • Системы счисления
  • 16 из десятичной в двоичную
  • 64 из десятичного в двоичный
  • 255 десятичный в двоичный

Напишите как улучшить эту страницу

ПРЕОБРАЗОВАНИЕ ЧИСЕЛ
  • ASCII, шестнадцатеричный, двоичный, десятичный преобразователь
  • Преобразователь текста ASCII в двоичный код
  • Преобразователь текста ASCII в шестнадцатеричный
  • Базовый преобразователь
  • Двоичный преобразователь
  • Преобразователь двоичного кода в текст ASCII
  • Преобразователь двоичного кода в десятичный
  • Преобразователь двоичного кода в шестнадцатеричный
  • Конвертер даты в римские цифры
  • Преобразователь десятичной дроби в дробную
  • Преобразователь десятичных чисел в проценты
  • Преобразователь десятичной системы в двоичную
  • Преобразователь десятичного числа в восьмеричное
  • Преобразователь десятичного числа в шестнадцатеричный
  • Преобразователь градусов в градусы, минуты, секунды
  • Перевод градусов,мин,сек в градусы
  • Перевод градусов в радианы
  • Преобразователь дроби в десятичную дробь
  • Преобразователь дробей в проценты
  • Шестнадцатеричный/десятичный/восьмеричный/двоичный преобразователь
  • Преобразователь текста Hex в ASCII
  • Преобразователь шестнадцатеричного кода в двоичный
  • Преобразователь шестнадцатеричного кода в десятичный
  • Преобразователь восьмеричной системы в десятичную
  • Преобразователь процентов в десятичные числа
  • Преобразователь процентов в дроби
  • Конвертер процентов в ppm
    • Конвертер
  • ppm в проценты
    • Конвертер
  • ppm в ppb
    • Конвертер
  • ppm в ppt
    • Конвертер
  • ppb в ppm
    • Конвертер
  • ppt в ppm
    • Преобразователь
  • частей на миллион
  • Перевод радиан в градусы
  • Преобразователь римских цифр
  • Преобразователь экспоненциальной записи
RAPID TABLES
  • Рекомендовать сайт
  • Отправить отзыв
  • О

Преобразование шестнадцатеричного числа 9 в двоичное шестнадцатеричное в двоичный калькулятор

Как записать 9 в двоичном формате (с основанием 2)?

9 равно 1001 в двоичной форме

Котировки

Преобразование в другие базы

Бинарный:
Четвертичный:
Восьмеричный:
Десятичный:
Шестнадцатеричный:
База 32:

Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования шестнадцатеричной базы. Здесь вы можете найти ответы на такие вопросы, как: Конвертировать шестнадцатеричное число 9в двоичный
hex в двоичный калькулятор или Hex в двоичное преобразование.

Dec Hex Oct Bin
0 0 0 0
1 1 1 1
2 2 2 10
3 3 3 11
4 4 40014 4 100
5 5 5 101
6 6 6 110
7 7 7 111
8 8 10 1000
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14 1100
13 D
. 16 1110
15 F 17 1111

Dec Hex Oct Bin
16 10 20 10000
17 11 21 10001
18 12 22 10010
19 13 23 10011
20 14 24 10100
21 15 25 10101
22 16 26 10110
23 17 27 10111
24 18 30 11000
25 19 31 11001
26 1A 32 11010
27 1B 33 11011
28 1C 34 11100
29 1D 35 11101
30 1E 36 11110
31 1F 37 11111

DEC HEX OCOM BIN
32 20 40 20 40 20 401111111111114. 0011 21 41 100001
34 22 42 100010
35 23 43 100011
36 24 44 ​​ 100100
37.0014 47 100111
40 28 50 101000
41 29 51 101001
42 2A 52 101010
43 2B 53 101011
44 ​​ 2C 54 101100
45 2D 55 101101
46 2E 56 101110
47 2F 57 101111

Dec Hex Oct Bin
48 30 60 110000
49 31 61 110001
50 32
50 32
50 32
50 32
50 32
. 0014 62 110010
51 33 63 110011
52 34 64 110100
53 35 65 110101
54 36 66 110110
55 37 67 110111
56 38 70 111000
57 39 71 111001
58 3A 72 111010
59 3B 73 111011
60 3C 74 111100
61 3D 75 111101
62 3E 76 111110
63 3F 77 111111

Dec Hex Oct Bin
64 40 100 1000000
65 41 101 1000001
66 42 102 1000010
67 43
67 43
67 43
67 43
. 0014 1000011
68 44 ​​ 104 1000100
69 45 105 1000101
70 46 106 1000110
71 47 107 1000111
72 48 110 1001000
73 49 111 1001001
74 4A 112 1001010
75 4B 113 1001011
76 4C 114 1001100
77 4D 115 1001101
78 4E 116 1001110
79 4F 117 1001111

Dec Hex Oct Bin
80 50 120 1010000
81 51 121 1010001
82 52 122 1010010
83 53 123 1010011
84 54 124 1010100
85 55 125 1010101
86 56 126 1010110
87 57 127 1010111
88 58 130 1011000
89 59 131 1011001
90 5A 132 1011010
91 5B 133 1011011
92 5C 134 1011100
93 5D 135 1011101
94 5E 136 1011110
95 5F 137 1011111

Dec Hex Oct Bin
96 60 140 1100000
97 61 141 1100001
98 62 142 1100010
99. 0015
101 65 145 1100101
102 66 146 1100110
103 67 147 1100111
104 68 150 1101000
105.0014
107 6B 153 1101011
108 6C 154 1101100
109 6D 155 1101101
110 6E 156 1101110
111 6F 157 11011119

DECE9

де.9

де.0360 Oct Bin
112 70 160 1110000
113 71 161 1110001
114 72 162 1110010
115 73 163 1110011
116 74 164 1110100
117 75 165 1110101
118 76 166 1110110
119 77 167 1110111
120 78 170 1111000
121 79 171 1111001
122 7A 172 1111010
123 7B 173 1111011
124 7C 174 1111100
125 7D 175 1111101
126 7E 176 1111110
127 7F 177 1111111

Dec Hex Oct Bin
128 80 200 10000000
129 81 201 10000001
130 82 202 10000010
131 83 203 10000011
132 84 204 10000100
133 85 205 10000101
134 86 206 10000110
135 87 207 10000111
136 88 210 10001000
137 89 211 10001001
138 8A 212 10001010
139 8B 213 139 8B 213 8B 213 8B 213 8B 213 8B13 10001011
140 8C 214 10001100
141 8D 215 10001101
142 8E 216 10001110
143 8F 217 10001111

Dec Hex Oct Bin
144 90 220 10010000
145 91 221 10010001
146 92 222 10010010
147 93 223 10010011
148 94 224 10010100
149 95 225 10010101
150 96 226 10010110
151 97 227 10010111
152 98 230 10011000
153 99 231 10011001
154 9A 232 10011010
155 9B 233 10011011
156 9C 234 10011100
157 9D 235 10011101
158 9E 236 10011110
159 9F 237 10011111

Dec Hex Oct Bin
160 A0 240 10100000
161 A1 241 10100001
162 A2 242 10100010
163 A3 243 10100011
164 A4 244 10100100
165 A5 245 10100101
166 A6 246 10100110
167 A7 247 10100111
168 A8 250 10101000
169 A9 251 10101001
170 AA 252 10101010
171 AB 253 10101011
172 AC
172 AC
172 AC
172 AC
172 AC
172. 0011 254 10101100
173 AD 255 10101101
174 AE 256 10101110
175 AF 257 10101111

Dec Hex Oct Bin
176 B0 260 10110000
177 B1 261 10110001
178 B2 262 10110010
179 B3 263 10110011
180 B4 264 10110100
181 B5 265 10110101
182 B6 26611011014 B6 266110110110110.0015
183 B7 267 10110111
184 B8 270 10111000
185 B9 271 10111001
186 BA 272 10111010
187 BB 273 10111011
188 BC 274 10111100
189 BD 275 10111101
190 BE 276 10111110
191 BF 277 10111111

9 9
Dec Hex Oct Bin
192 C0 300 11000000
193 C1 301 11000001
194 C2 302 11000010
195 C3 303 11000011
196 C4 304 11000100
197 C5 305 11000101
198 C6 306 11000110
19910
19910
1990011 C7 307 11000111
200 C8 310 11001000
201 C9 311 11001001
202 CA 312 11001010
. 0014 CD 315 11001101
206 CE 316 11001110
207 CF 317 11001111

Dec Hex Oct Bin
208 D0 320 11010000
209 D1 321 11010001
210 D2 322 11010010
211 D3 323 11010011
212 D4 324 11010100
213 D5 325 11010101
214 D6 326 11010110
215 D7 327 11010111
216 D8 330 11011000
217 D9 331 11011001
218 DA 332 11011010
219 DB 333 11011011
220 DC 334 11011100
221 DD
221 DD
221 DD
221 DD
221. 0014 11011101
222 DE 336 11011110
223 DF 337 11011111

2
Dec Hex Oct Bin
224 E0 340 11100000
225 E1 341 1100001
2 1100001
2 1100001
2 1100001
111 20014 E2 342 11100010
227 E3 343 11100011
228 E4 344 11100100
229 E5 345 11100101
230 E6 346 11100110
231 E7 347 11100111
232 E8 350 11101000
233 E9 351 11101001
234 EA 352 11101010
235 EB 353 11101011
236 EC 354 11101100
237 ED 355 11101101
238 EE 356 11101110
239 EF 357 11101111

Dec Hex Oct Bin
240 F0 360 11110000
241 F1 361 11110001
242 00014
242 00014
242 00014
242 00014
242 10
242 00014
242. 0011 362 11110010
243 F3 363 11110011
244 F4 364 11110100
245 F5 365 11110101
246 F6 366 11110110
247 F7 367 11110111
248 F8 370 11111000
249 F9 371 11111001
250 FA 372 11111010
251 FB 373 11111011
252 FC 374 11111100
253 FD 375 11111101
254 FE 376 11111110
255 FF 377 1111111119

Номерная базовая конвертер

9

Собрание с номером

.

Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.

  • 7E2 преобразование из шестнадцатеричного в восьмеричное
  • 11011100000 преобразование из двоичного в шестнадцатеричное
  • 2A преобразование из шестнадцатеричного в двоичное
  • 10000 преобразование из шестнадцатеричного в восьмеричное
  • 5400 octal to decimal
  • 2016 decimal to binary
  • 5A0 hexadecimal to binary
  • 10101101 binary to octal
  • 101000000 binary to octal

Table / List of Binary Numbers ▶️ from 0 to 100

At ConvertBinary вы можете найти числа от 0 до 100 в их двоичном кодовом представлении.

Если вы хотите узнать двоичное представление любого десятичного числа до 7 цифр, воспользуйтесь конвертером десятичных чисел в двоичные.

DECIMAL NUMBERS IN BINARY

0014
Decimal Binary
0 0
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
16 10000
17 10001
17 100019
17 100019
100019
100019
100019
100019
0011 18 10010
19 10011
20 10100
21 10101
22 10110
23 10111
24 11000
25 11001
26 11010
27 11011
28 11100
29 11101
30 11110
31 11111
32 100000
33 100001
34 100010
35 100011
36 100100
37 1001019
3811111111111111111111111111111114
38111111111111111111111111111111111111111111111191111111111111111111111111111. 0014
39 100111
40 101000
41 101001
42 101010
43 101011
44 ​​ 101100
45 101101
46 101110
47 101111
48 110000
49 110001
50 110010
51 110011
52 110100
53 110101
54 110110
55 110111
56 111000
57 111001
58 111010
59 111011
60 111100
61 111101
62 111110
63 111111
64 1000000
65 1000001
66 1000010
67 1000011
68 1000100
. 0036 69 1000101
70 1000110
71 1000111
72 1001000
73 1001001
74 1001010
75 1001011
76 1001100
77 1001101
78 100110
7811110
1110
11100015
79 1001111
80 1010000
81 1010001
82 1010010
83 1010011
84 1010100
85 10101019
86 1010110
1010111
8810000
89 1011001
90 1011010
91 1011011
92 1011100
93 1011101
94 1011110
95 1011111
96 1100000
97 1100001
98 110010
98 110010
98 110010
98 110010
. 0014
99 1100011
100 1100100

Также обратите внимание на двоичный алфавит!

Вопросы и ответы о двоичных числах

🔟 Как вы читаете двоичные числа?

Чтобы прочитать двоичные числа и преобразовать их в эквивалентные десятичные числа, у вас есть два варианта: вы можете использовать конвертер двоичных чисел в десятичные числа на сайте ConvertBinary.com или сделать это вручную.

Короче говоря, чтобы преобразовать двоичные числа в десятичные числа, вы должны умножить каждую двоичную цифру на два в степени ее разряда справа налево, а затем сложить все результаты вместе. При вычислении разрядного номера самая правая цифра разрядного разряда имеет нулевое значение.

Так, например, если вы хотите преобразовать двоичное число 1010 в десятичное, вы начинаете с самого правого 0.

Давайте сделаем это с двоичным числом 1010:
0 × 2 0 = 0
1 × 2 1 = 2
0 × 2 2 = 0
1 × 2 3 = 8

Добавьте 0+2+0+8 и получите десятичное число 10.

🔟 Как считать до 10 в двоичном формате?

Чтобы считать в двоичном формате, вы начинаете с 0, затем переходите к 1. Затем добавляете еще одну цифру, как при десятичном счете, когда переходите от 9 к 10. Вы добавляете еще одну цифру, так что теперь у вас есть две цифры . Итак, в двоичном формате вы переходите от 1 к 10, поскольку 1 — ваше последнее счетное число.

Итак, считая в двоичном виде, вы считаете так:

0
1
10
11
100
101
110
111
1000
1001
1010

Вы можете найти десятичные числа от 0 до 100 (сто) в Таблице бинарных номеров на конверте. com

✏️ Как преобразовать десятичную систему в двоичную?

Чтобы преобразовать десятичные числа в их двоичный эквивалент, у вас есть два варианта: вы можете использовать конвертер десятичных чисел в двоичные на ConvertBinary. com или сделать это вручную.

Если вы хотите научиться преобразовывать десятичные числа в двоичные вручную, вы можете прочитать это руководство или просмотреть соответствующий учебник.

🎓 Что представляют собой двоичные числа?

В математике и цифровой электронике двоичное число — это число, выраженное в системе счисления с основанием 2 или в двоичной системе счисления, в которой используются только два символа: обычно «0» (ноль) и «1» (единица). Система счисления с основанием 2 представляет собой позиционную систему счисления с основанием 2. Каждая цифра называется битом.

Преобразователь десятичных чисел в двоичные

Чтобы использовать этот инструмент для преобразования десятичных чисел в двоичные числа , вы должны ввести десятичное значение, например 308, в левое поле ниже, а затем нажмите кнопку «Конвертировать». Таким образом, вы можете преобразовать до 19 десятичных символов (макс. значение72036854775807) в двоичных значений .

Десятичное значение (макс.:72036854775807) Прокладка

Двоичное значение преобразование подкачки: двоично-десятичный преобразователь

Преобразование десятичной системы в двоичную приводит к базовым числам

Десятичная система счисления

Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. В качестве основы (основания) используется число 10. Следовательно, он имеет 10 символов: цифры от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями. Трудность представления очень больших чисел в десятичной системе была преодолена индо-арабской системой счисления. Индо-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степени основания 10; цифры возводятся до n -я -я власть, в соответствии со своим положением.

Например, возьмем число 2345,67 в десятичной системе:

  • Цифра 5 стоит на позиции единиц (10 0 , что равно 1),
  • 4 стоит на позиции десятков (10 1 )
  • 3 стоит на позиции сотен (10 2 )
  • 2 находится в позиции тысяч (10 3 )
  • При этом цифра 6 после запятой находится в десятых долях (1/10, что равно 10 -1 ), а 7 в сотых (1/100, то есть 10 -2 ) позиции
  • Таким образом, число 2345,67 также можно представить следующим образом: (2 * 10 3 ) + (3 * 10 2 ) + (4 * 10 1 ) + (5 * 10 0 ) + (6 * 10 -1 ) + (7 * 10 -2 )

Двоичная система счисления

В двоичной системе счисления в качестве основания (основания) используется число 2. Система счисления с основанием 2 состоит только из двух чисел: 0 и 1. 

В то время как двоичная система применялась в Древнем Египте, Китае и Индии для различных целей, в современном мире двоичная система стала языком электроники и компьютеров. Это наиболее эффективная система для обнаружения выключенного (0) и включенного (1) состояния электрического сигнала. Это также основа для двоичного кода, который используется для составления данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.

Чтение двоичного числа проще, чем кажется: это позиционная система; следовательно, каждая цифра двоичного числа возводится в степень 2, начиная с самой правой с 2 ​​ 0 . В двоичной системе каждая двоичная цифра соответствует 1 биту.

Примеры преобразования десятичной системы в двоичную
  • (51) 10 = (110011) 2
  • (217) 10 = (11011001) 2
  • (8023) 10 = (1111101010111) 2

Таблица преобразования десятичной системы в двоичную

000011 000101010011 3111 9 9
Десятичная Двоичная
1 00000001
2 00000010
3 00000011
4 00000100
5 00000101
6 00000110
7 00000111
8 00001000
9 00001001
10 00001010
11 00001011
12 00001100
13 00001101
14 00001110
15 00001111
16 00010000
17 00010001
18 00010010
19 00010011
20 00010100
21
21
22 00010110
23 00010111
24 00011000
25 00011001
26 00011010
27 00011011
28 000111100
29 00011101
30 00011110
000110
00011111
32 00100000
33 00100001
34 00100010
35 00100011
36 00100100
37 00100101
38 00100110
39 00100111
40 0010150159
40 00101000
40 00101000
40 00101000
. 0015
41 00101001
42 00101010
43 00101011
44 ​​ 00101100
45 00101101
46 00101110
47 001011119
48 00110000
49 00110001
50 00110010
50 00110010
50 00110010
.0014
51 00110011
52 00110100
53 00110101
54 00110110
55 00110111
56 00111000
57 001111001
58 0011101010
59 00111011
60
6014
601114
. 0011 00111100
61 00111101
62 00111110
63 00111111
64 01000000

9 9 9 9 90011 01101011
Decimal Binary
65 01000001
.0014
69 01000101
70 01000110
71 01000111
72 01001000
73 01001001
74 01001010
75 01001011
76 01001100
77 01001101
7801
78
78
78
78
78
010011 01001110
79 01001111
80 01010000
81 01010001
82 01010010
83 01010011
84 01010100
85 01010101
86 01010110
87 01010111
01010111
01010111
01010111
01010111
01010111
01010111
0011 88 01011000
89 01011001
90 01011010
91 01011011
92 01011100
93 01011101
94 01011110
95 010111119
96 01100000
97 011000019
97 01100001
97 011000019
. 0015
98 01100010
99 01100011
100 01100100
101 01100101
102 01100110
103 01100111
104 01101000
105 01101001
106 01101010
107
107
108 01101100
109 01101101
110 01101110
111 01101111
112 01110000
113 01110001
114 01110010
115 01110011
116 01110100
116 01110100
0036 117 01110101
118 01110110
119 01110111
120 01111000
121 01111001
122 01111010
123 01111011
124 01111100
125 01111101
126101
126 01111110
127 0111111
128 10000000

ДЕРЕВИМАЛЬНЫЙ
9
00150014001511000140015
129 10000001
130 10000010
131 10000011
132 10000100
133 10000101
134 10000110
135 10000111
136 10001000
137 10001001
138 10001010
139 10001011
140 10001100
141 10001101
142 10001110
143 1000111114
143 10001111114
144 10010000
145 10010001
146 10010010
147 10010011
148 10010100
149 10010101
150 10010110
151 10010111
152 1001000
153 000
153 10011001
154 10011010
155 10011011
156 10011100
157 10011101
158 10011110
159 10011111
160 10100000
161 10100001
162 10100010 162 10100010
163 10100011
164 10100100
165 10100101
166 10100110
167 10100111
168 10101000
169 10101001
170 10101010
171 10101011
172. 0014 10101100
173 10101101
174 10101110
175 10101111
176 10110000
177 10110001
178 10110010
179 10110011
180 10110100
181 10110101
181 10110101
182 10110110
183 10110111
184 10111000
185 10111001
186 10111010
187 10111011
188 10111100
189 10111101
190 10111110
1911110
1911110
191
191 919Двоичный
193 11000001
194 11000010
195 11000011
196 11000100
197 11000101
198 11000110
199 11000111
200 11001000
201 11001001
202 11001010
203 11001011
204 11001100
205 11001101
206 11001110
207 1100111119
208 11010000
208 11010000
2080014
209 11010001
210 11010010
211 11010011
212 11010100
213 11010101
214 11010110
215 11010111
216 11011000
217 11011001
218 11011001
2180014 11011010
219 11011011
220 11011100
221 11011101
222 11011110
223 11011111
224 11100000
225 11100001
226 11100010
227 11100011 227 11100011
228 11100100
229 11100101
230 11100110
231 11100111
232 11101000
233 11101001
234 11101010
235 11101011
236 11101100
237 11101101
238 11101110
239 11101111
240 11110000
241 11110001
242 11110010
243 11110011
244 11110100
245 11110101
246 11110110
246 1110110
247 11110111
248 11111000
249 11111001
250 11111010
251 11111011
252 11111100
253 11111101
254 11111110
255 111111


0000 9 в двоичном формате | Работа, решение

Как написать 9 в двоичном формате?

9 записывается как 1001 в двоичном формате

Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: 9 в двоичном формате | Работа, решение или десятичное преобразование в двоичное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.

Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.

С помощью этого конвертера вы можете получить ответы на такие вопросы, как:

  • Что такое 9 в двоичном формате?
  • Что такое 9 в шестнадцатеричном формате?
  • Что такое восьмеричное число 9?
  • Как преобразовать число 9 в двоичное?
  • Как преобразовать число 9 в двоичное? И так далее.

Decimal to Binary Chart — Including Hexa and Octal

Dec Hex Oct Bin
0 0 0 0
1 1 1 1
2 2 2 10
3 3 3 11
4 4 4 100
5 5 5 101
6 6. 0011 8 10 1000
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14 1100
13 D 15 1101
14 E 16 1110
15 F 17 1111

Dec Hex Oct Bin
16 10 20 10000
17 11 21 10001
18 12 22 10010
19 13 23 10011
20 14 24 10100
21 15 25 10101
22 16 26 10110
23 17 27 10111
24 18 30 11000
25 19 31 11001
26 1A 32 11010
27 1B 33 11011
28 1C 34 11100
29 1D 35 11101
30 1E 36 11110
31 1F 37 11111

0015
Dec Hex Oct Bin
32 20 40 100000
33 21 41 100001
34 22 42 100010
35 23 43 100011
36 24 44 ​​ 100114 24 44 ​​ 1001144 44 ​​11114 24 44 ​​11114
37 25 45 100101
38 26 46 100110
39 27 47 100111
40 28 50 101000
41 29 51 101001
42 2A 5211114 2A 521111149 52111114
521111149111 5211114
.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *