Перевод из двоичной в восьмеричную систему счисления, калькулятор
Реклама
- CALCUS.RU
- Перевод систем счисления
- Перевод из двоичной в восьмеричную
Исходное число
Направление перевода
2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
Сообщить об ошибке
В избранное
Виджет
Вы можете сохранять ваши расчеты и они будут отображаться здесь.
Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.
Перевести число из двоичной системы в восьмеричную без калькулятора можно тремя способами.
Способ 1:
Перевести сначала в десятичную систему счисления, затем из нее в конечную.
Способ 2:
Для перевода в восьмеричную систему нужно разбить двоичное число на группы по 3 цифры справа налево. В последней (самой левой) группе вместо недостающих цифр поставить слева нули. Для каждой полученной группы произвести умножение каждого разряда на 2n
11012 = (001) (101) = (0*22 + 0*21 + 1*20) (1*22 + 0*21 + 1*20) = (0+0+1) (4+0+1) = (1) (5) = 158
Способ 3:
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
| Триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
101110102 = (010) (111) (010) = 2728
Смотрите также
- Перевод из двоичной в десятичную
- Перевод из двоичной в шестнадцатеричную
- Перевод из десятичной в двоичную
- Перевод из десятичной в восьмеричную
- Перевод из десятичной в шестнадцатеричную
- Перевод из восьмеричной в двоичную
- Перевод из восьмеричной в десятичную
- Перевод из шестнадцатеричной в двоичную
- Перевод из шестнадцатеричной в десятичную
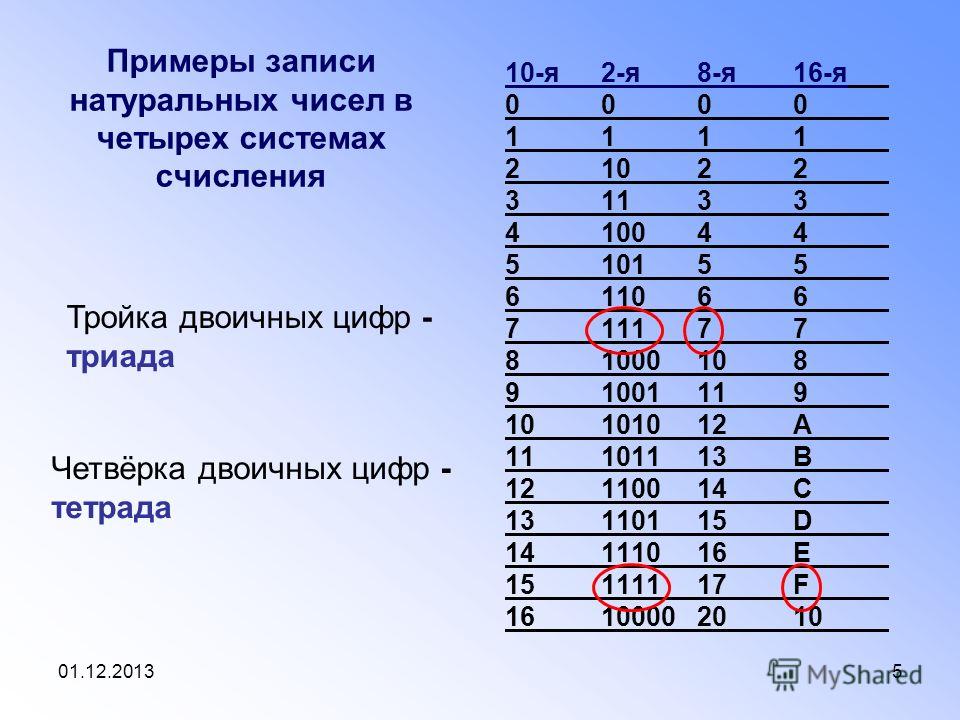
IKT-prosvet: Системы счисления
Позиционная система счисления
Позиционная
система счисления это система
счисления, в которой значение цифры зависит от разряда.
Разрядом числа называется место цифры в числе.
Наибольший вес имеет самый левый разряд, наименьший вес имеет самый правый
разряд.
Нумерация разрядов увеличивается справа налево.
Например: в числе 54510 цифра 5 имеет различный вес: первая цифра 5 — показывает количество сотен, вторая цифра 5 — показывает количество единиц.
5
4 5
число сотен число десятков
число единиц
У чисел
в позиционной системе счисления имеется основание системы — n.
Основанием системы счисления n называют количество цифр в числе
используемых для записи чисел.
n принадлежит числовому промежутку от 0 до n-1 включительно.
Например: В десятичной системе счисления n=10. Первая цифра будет
0, последней будет 9 9=10-1.
Действительно в данной системе используется 10 цифр для записи различных чисел
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В двоичной системе будет всего два числа, т.к. n=2.
А как будет в восьмеричной системе?
n=8. Восемь цифр, первая — 0, последняя — ???. Верно — 7.
Вот эти цифры: 0, 1, 2, 3, 4, 5, 6, 7.
Давайте посмотрим, что происходит в шестнадцатиричной системе.
n=16. Цифр должно быть 16, первая — 0, последняя — какая??15? — Ведь у нас всего десять цифр.
Здесь на помощь приходят буквы.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.
Непозиционная система счисления
Непозиционная система счисления — это система счисления, в которой значение цифры не изменяется в зависимости от ее расположения.
Примером непозиционной системы счисления служит римская система, в которой вместо цифр используются латинские буквы
Например: Число 242 можно записать ССXLII (т.е. 100+100+(50-10) +1+1).
Число 96 запишем IXVI=(-1+10)+(5+1).
Значение 1=I в данном случае не изменяется от ее местоположения.
Соответствие римской и арабской системы записи
I V
X L
C D M
1 5 10
50 100 500 1000
Перевод из любой системы счисления в десятичную систему счисления
Для перевода целого числа из любой системы счисления в десятичную, необходимо записать данное число в общем виде:
anbn+an-1bn-1+an-2bn-2+…+a2b2+a1b1+a0b0
Например: переведем число 12568 в десятичную систему счисления.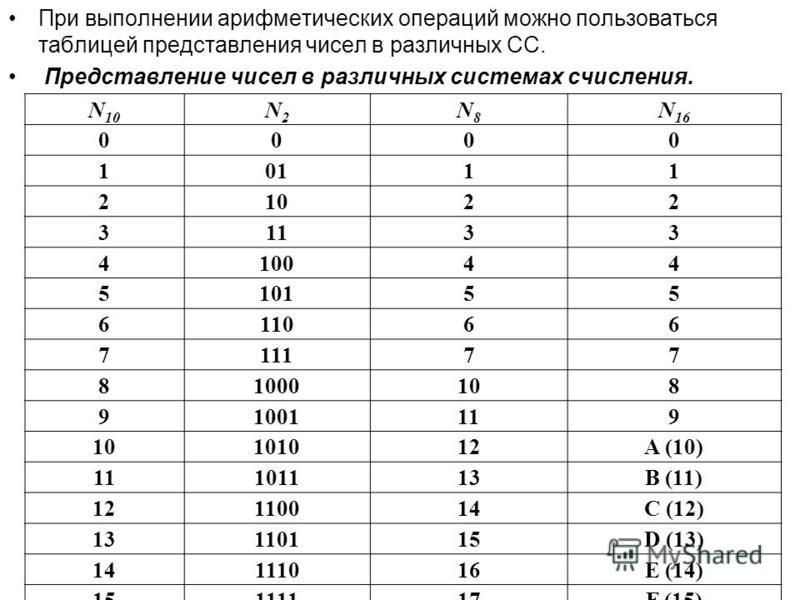
12568=1·83+2·82+5·81+6·80=1·512+2·64+5·8+6·1=68610
Правило перевода числа из десятичной системы счисления в другую систему.
1)
Делим данное число на основание той системы, в которую необходимо перевести число.
2) Полученное число делим
аналогично на
основание системы, в которую необходимо перевести число.
3) Пункт 2 повторяем до тех пор пока, полученное частное не будет меньше
основания.
4) Выписываем остатки от деления в порядке от последнего к первому.
Например:
1 способ записи: | ||||||
242510 | 2425:8=303+(1остаток) | |||||
остаток 1 | 303:8=37+(7остаток) | |||||
остаток 7 | 37:8=4+(5остаток) | |||||
остаток 5 | 4 | Т. | ||||
Ответ: 242510=45718 | ||||||
2 способ записи: | ||
242510 | ||
остаток 1 | ||
остаток 7 | ||
остаток 5 | 4 | |
Т. | ||
Ответ: 242510=45718 | ||
Правило перевода чисел из двоичной системы счисления в восьмеричную
1) Разбиваем
число по три цифры на группы начиная с младшего разряда.
Если не хватает до целой тройки цифр, то добавляем необходимое
количество нулей справа.
2) Каждую полученную тройку цифр заменяем цифрой из восьмеричной системы
счисления.
(Можно использовать «Таблицу Систем Счисления» — первым
смотрим столбик А2, затем — столбик А8).
3) Дробную часть разбиваем на тройки вправо от запятой.
Если не хватает цифр, то припысываем нули слева.
Правило перевода чисел из двоичной системы счисления в шестнадцатиричную
1) Разбиваем
число по четыре цифры на группы начиная с младшего разряда.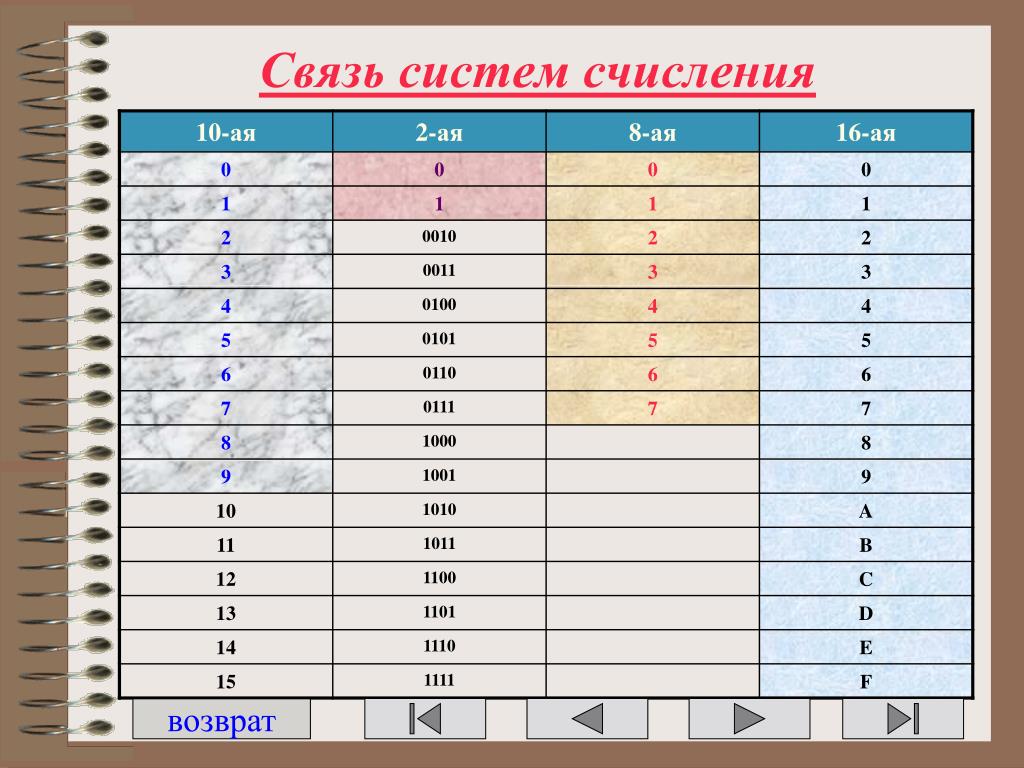
Если не хватает до целой четверки цифр, то добавляем
необходимое количество нулей справа.
2) Каждую полученную четверку цифр заменяем цифрой из восьмеричной системы
счисления.
(Можно использовать «Таблицу Систем
Счисления» — первым смотрим столбик А2, затем — столбик А16).
3) Дробную часть разбиваем на четверки вправо от запятой.
Если не хватает цифр, то припысываем нули слева.
Правило перевода чисел из восьмеричной системы счисления в двоичную
Заменяем
каждую цифру данного восьмеричного числа соответсвующим ей двоичным
эквивалентом.
(Можно использовать «Таблицу Систем Счисления» — первым смотрим столбик А8, затем — столбик А2).
Если до полной тройки не хватает цифр, то в данной тройке добавлем недостающее
количество нулей справа.
Правило перевода чисел из шестнадцатиричной системы счисления в двоичную
Заменяем
каждую цифру данного шестнадчатиричного числа соответсвующим ей двоичным
эквивалентом.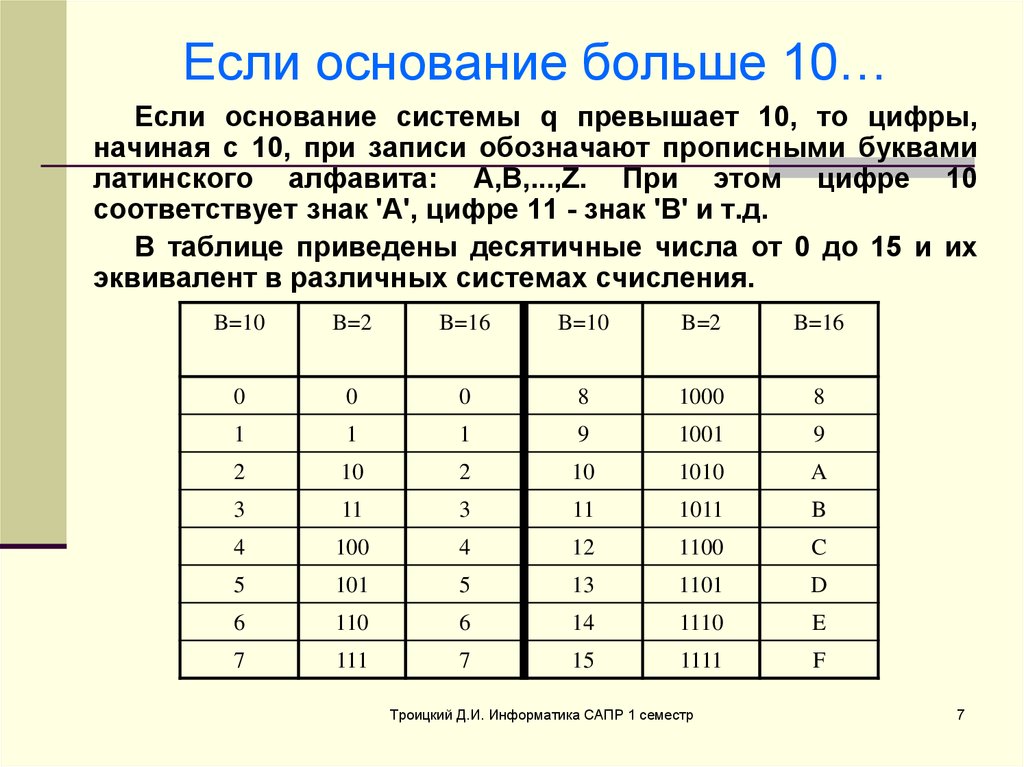 0=2·4096+10·256+3·16+12·1=1081210
0=2·4096+10·256+3·16+12·1=1081210
Ответ: 2А3С16=1081210
Перевод чиcла из двоичной системы счисления А2 в восьмериную А8
Задание. Перевести число 11110111012 в восмеричную систему счисления.
-Разбиваем данное число на группы по три цифры слева:
1 111 011 1012
-Используем таблицу систем счисления: в столбике А2 находим число 1, далее
находим, соответствующее ему число из столбика А8. Выписываем найденное число
-1.
1 111 011 1012
1
-В столбике А2 находим число 111, далее находим, соответствующее ему число из
столбика А8 — 7. Выписываем найденное число -7.
1 111 011 1012
1 7
-В столбике А2 находим число 011 или 11, далее находим, соответствующее ему
число из столбика А8 — 3. Выписываем найденное число — 3.
1 111 011 1012
1 7 3
-В столбике А2 находим число 101, далее находим, соответствующее ему число из
столбика А8 — 5. Выписываем найденное число — 5.
Выписываем найденное число — 5.
1 111 011 1012
1
7 3 5
Ответ: 17358.
Перевод из восьмеричной системы счисления в двоичную
Задание: Перевести число из 13468 в двоичную систему счисления.
Для перевода используем таблицу систем счисления.
Каждую цифру данного числа находим в столбике А8, выписываем ниже ее
соответсвие из столбика А2, образовывая тройки чисел.
Если до тройки не хватает, то подписываем справа 0, например для 3 подписали
один 0 и для 1 — два 0.
Первые 0 полученного числа можно удалить!
3 4
1 6
011 100 001 110
Ответ: 13468=11 100 001 1102
Перевод из шестнадцатеричной системы счисления в двоичную систему
Задание: Перевести число из В40Е16 в двоичную систему счисления.
Для перевода используем таблицу систем счисления.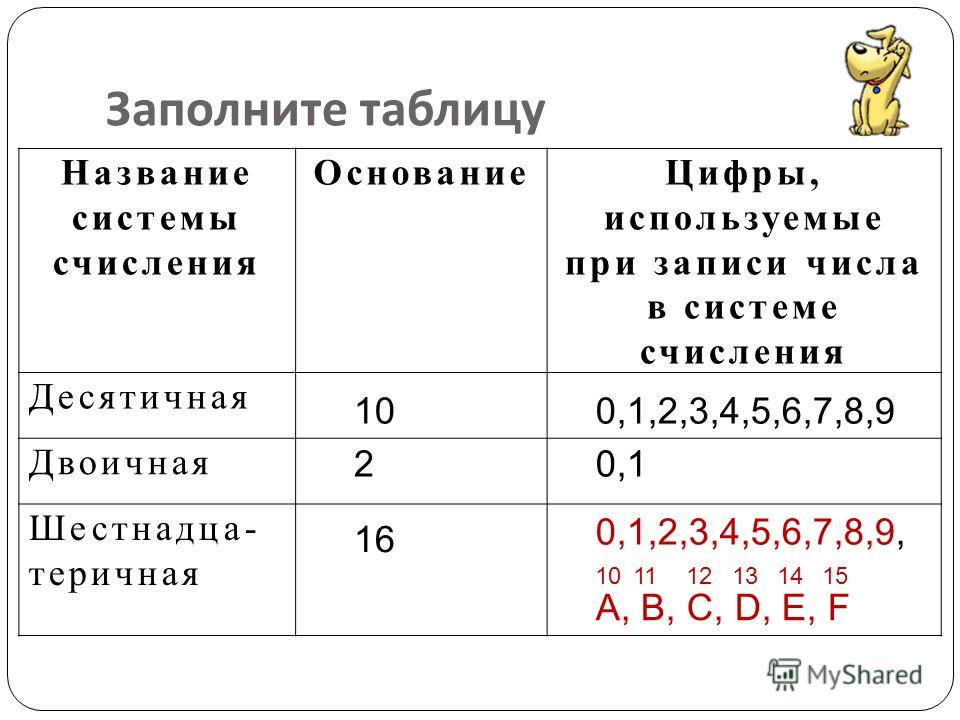
Каждую цифру данного числа находим в столбике А16, выписываем ниже ее соответствие из столбика А2, образовывая четверки чисел.
Если до тройки не хватает, то подписываем справа 0, например, для 4 подписали
один 0 и для 0 — четыре 0.
Первые 0 полученного числа можно удалить!
В 4
0 Е
1011 0100 0000 1110
Ответ: В40Е16=1011 0100 0000 11102
Сложение чисел в двоичной системе счисления
Выполните сложение чисел 1С5216+89116 :
Сложение двух чисел в восьмеричной системе счисления
Выполните сложение 63548+7058:
4 | |||||
5 | |||||
1 | 1 | ||||
4+5=9=1*8+1 | |||||
5+0+1=6 | |||||
3+7=10 |
Сложение в восьмеричной системе счисления
Выполните сложение чисел 63548+7058:
Ответ: 73618.
Сложение в шестнадцатиричной системе счисления
Выполните сложение чисел 1С5216+89116 :
Ответ: 24Е316.
Вычитание в двоичной системе счисления
Выполните вычитание 10112-1012:
Ответ: 1102.
Вычитание в восьмеричной системе счисления
Выполните вычитание 63548-7058:
Ответ: 74478.
Умножение в двоичной системе
Выполните умножение 11012*1112.
Ответ: 10110112.
Умножение в восьмеричной системе счисления
Выполните
умножение чисел 63548*7058 в восьмеричной системе счисления.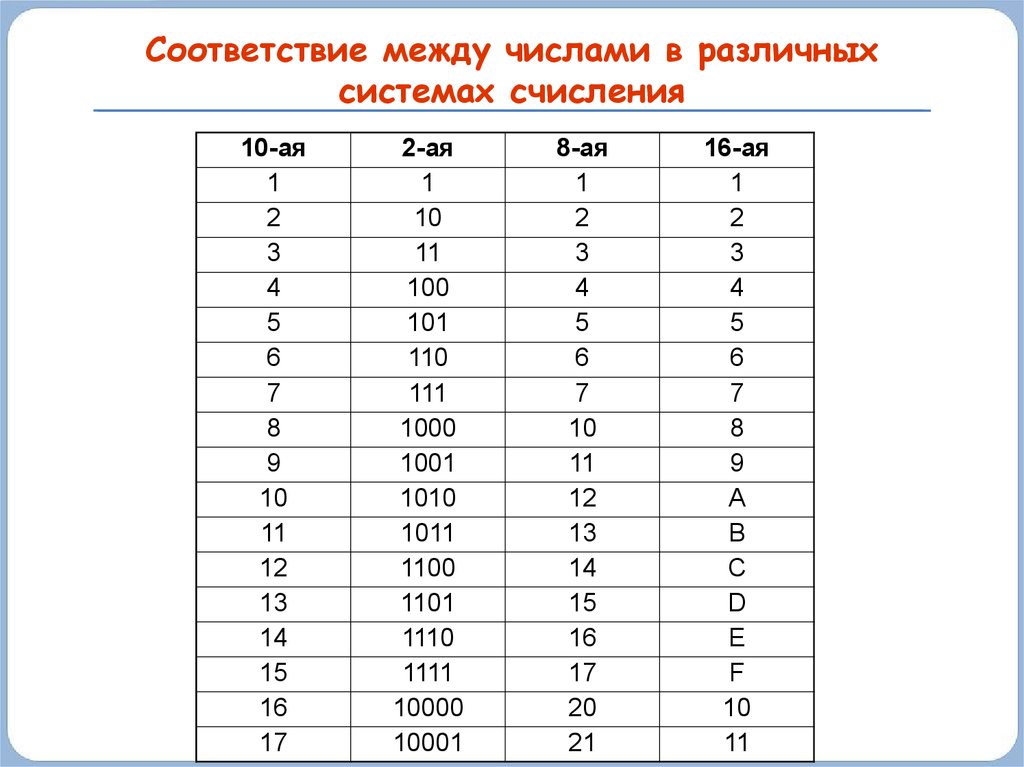
Ответ: 55636248
Умножение в шестнадцатиричной системе счисления
Выполните умножение чисел 20А416+В1516.
Ответ: 169B98416.
Таблица систем счисления
Десятичная | Двоичная | Восьмеричная | Шестнадцатиричная |
Восьмеричная система счисления 1 — 100
Восьмеричная система счисления — это система счисления с основанием 8.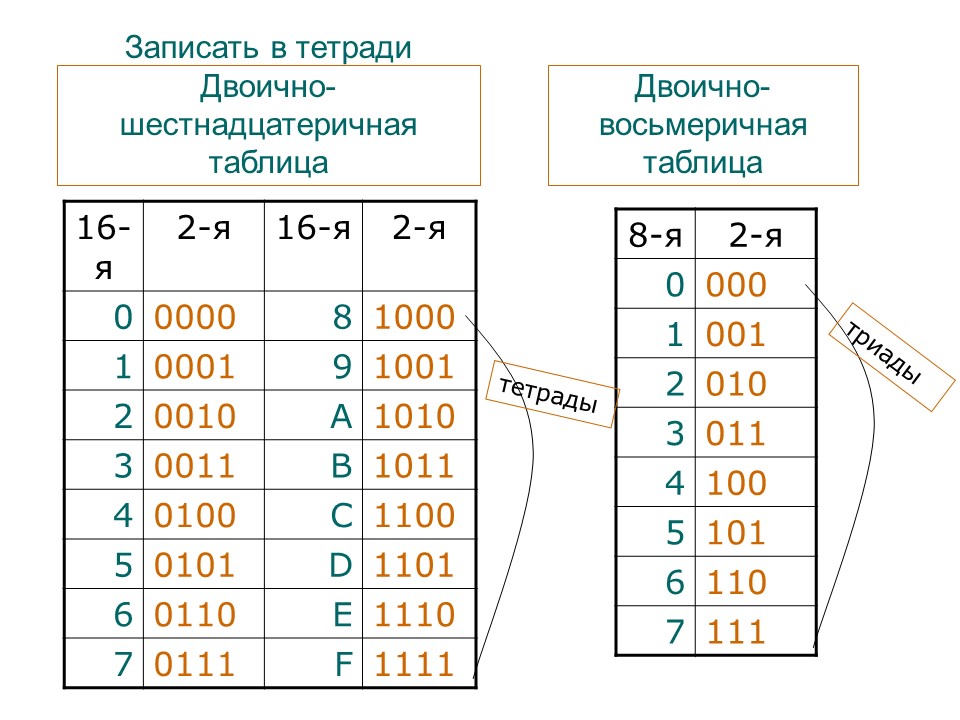 Представление числовых значений с использованием восьми символов: 0, 1, 2, 3, 4, 5, 6 и 7. В восьмеричной системе счисления нет 8 или 9.
Представление числовых значений с использованием восьми символов: 0, 1, 2, 3, 4, 5, 6 и 7. В восьмеричной системе счисления нет 8 или 9.
В таблице ниже представлены восьмеричные числа от 1 до 144, эквивалентные десятичным числам от 1 до 100.
| Восьмеричный | Десятичный | Восьмеричный | Десятичный |
|---|---|---|---|
| 1 | 2 5 1 | 60020021||
| 2 | 2 | 64 | 52 |
| 3 | 3 | 65 | 53 |
| 4 | 4 | 66 | 54 |
| 5 | 5 | 67 | 55 |
| 6 | .0021 | 72 | 58 |
| 11 | 9 | 73 | 59 |
| 12 | 10 | 74 | 60 |
| 13 | 11 | 75 | 61 |
| 14 | 12 | 76 | 62 |
| 15 | 13 | 77 | 63 |
| 16 | 14 | 100 | 64 |
| 17 | 15 | 101 | 65 |
| 20 | 16 | 102 | 66 |
| 21 | 17 | 103 | 67 |
| 22 | 18 | 104 | 68 |
| 23 | 19 | 105 | 69 |
| 24 | 20 | 106 | 70 |
| 25 | 21 | 107 | 71 |
| 26 | 22 | 110 | 72 |
| 27 | 23 | 111 | 73 |
| 30 | 24 | 112 | 74 |
| 31 | 25 | 113 | 75 |
| 32 | 26 | 114 | 76 |
| 33 | 27 | 115 | 77 |
| 34 | 28 | 116 | 78 |
| 35 | 29 | 117 | 79 |
| 36 | 30 | 120 | 80 |
| 37 | 31 | 121 | 81 |
| 40 | 32 | 122 | 82 |
| 41 | 33 | 123 | 83 |
| 42 | 34 | 124 | 84 |
| 43 | 35 | 125 | 85 |
| 44 | 36 | 126 | 86 |
| 45 | 37 | 127 | 87 |
| 46 | 38 | 130 | 88 |
| 47 | 39 | 131 | 89 |
| 50 | 40 | 132 | 90 |
| 51 | 41 | 133 | 91 |
| 52 | 42 | 134 | 92 |
| 53 | 43 | 135 | 93 |
| 54 | 44 | 136 | 94 |
| 55 | 45 | 137 | 95 |
| 56 | 46 | 140 | 96 |
| 57 | 47 | 141 | 97 |
| 60 | 48 | 142 | 98 |
| 61 | 49 | 143 | 99 |
| 62 | 50 | 144 | 100 |
NEXT →
← PREV
Связанные статьи
Выбрать этикетку
Подробнее
. Почтовые комментарии (Атом)
Почтовые комментарии (Атом)
Системы счисления
Системы счисленияКому преобразовать в основание 10 из оснований 2, 8 и 16, используя метод остатка.
Преобразование из основание 2 в основании 8
Для преобразования от основания 2 до основания 16
Кому преобразовать из базы 10 в базу 2, 8 или 16 использовать расширенную нотацию
Кому преобразовать из базы 10 в базу 2, 8 или 16, используя метод вычитания
Конвертировать до дополнения до двух из двоичного кода
Значения оснований счисления 10, 2, 8, 16
| Основание 10 Десятичный | Основание 2 Двоичный | Основание 8 Восьмеричный | Основание 16 Шестнадцатеричный |
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | А |
| 11 | 1011 | 13 | Б |
| 12 | 1100 | 14 | С |
| 13 | 1101 | 15 | Д |
| 14 | 1110 | 16 | Е |
| 15 | 1111 | 17 | Ф |
| 16 | 10000 | 20 | 10 |
- Вернуться к началу
Преобразование между системами счисления
Позиционное обозначение означает, что
значение цифры в числе зависит от ее положения в числе.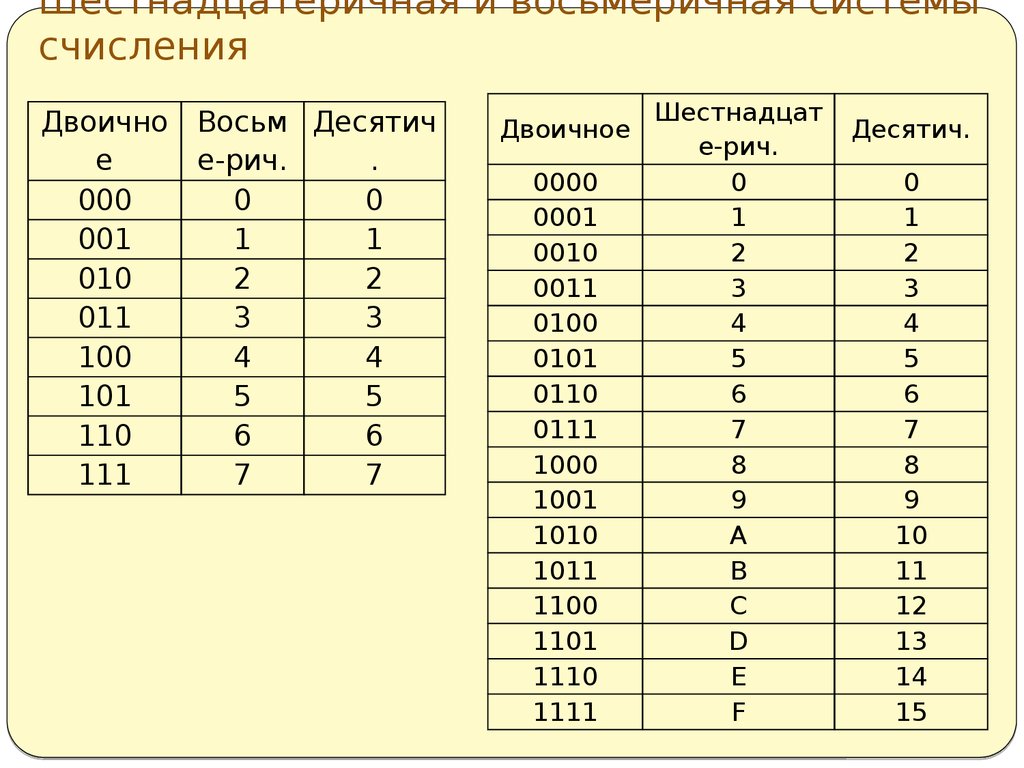 В
в десятичной системе счисления позиционное значение является степенью основания 10.
В
в десятичной системе счисления позиционное значение является степенью основания 10.
| Тысячи | Сотни | Десятки | Единицы |
| 10 3 | 10 2 | 10 1 | 10 0 |
| 1000 | 100 | 10 | 1 |
| (1 * 1000) | + | (2*100) | + | (3*10) | + | 2 | или |
| 1000 | + | 200 | + | 30 | + | 2 |

Вы можете оценить число в другом систему счисления таким же образом.
Восьмеричная система счисления позиционное значение является степенью основания 8.
| Пятьсот двенадцать | Шестьдесят четыре | Восьмерки | Единицы |
| 8 3 | 8 2 | 8 1 | 8 0 |
| 512 | 64 | 8 | 1 |
| (1*512) | + | (2*64) | + | (3*8) | + | 2 | или |
| 512 | + | 128 | + | 24 | + | 2 | или 666 10 |
Вернуться к началу
Шестнадцатеричная система счисления позиционная
значение является степенью основания 16.
| Два-пять-шесть | Шестнадцать | Единицы | |
| 16 3 | 16 2 | 16 1 | 16 0 |
| 4096 | 256 | 16 | 1 |
| (1 * 4096) | + | (2*256) | + | (3*16) | + | 2 | или |
| 4096 | + | 512 | + | 48 | + | 2 | или 4658 10 |

Вернуться к началу
| Восьмерки | Четверки | Двойки | Единицы |
| 2 3 | 2 2 | 2 1 | 2 0 |
| 8 | 4 | 2 | 1 |
Двоичное число 1101 понято означает:
| (1*8) | + | (1*4) | + | (0 * 2) | + | 1 | или |
| 8 | + | 4 | + | 0 | + | 1 | или 13 10 |
Для преобразования в 10 с основанием 2, 8 и 16
использовать расширенную нотацию, используя соответствующие позиционные значения для базы
вы конвертируете из.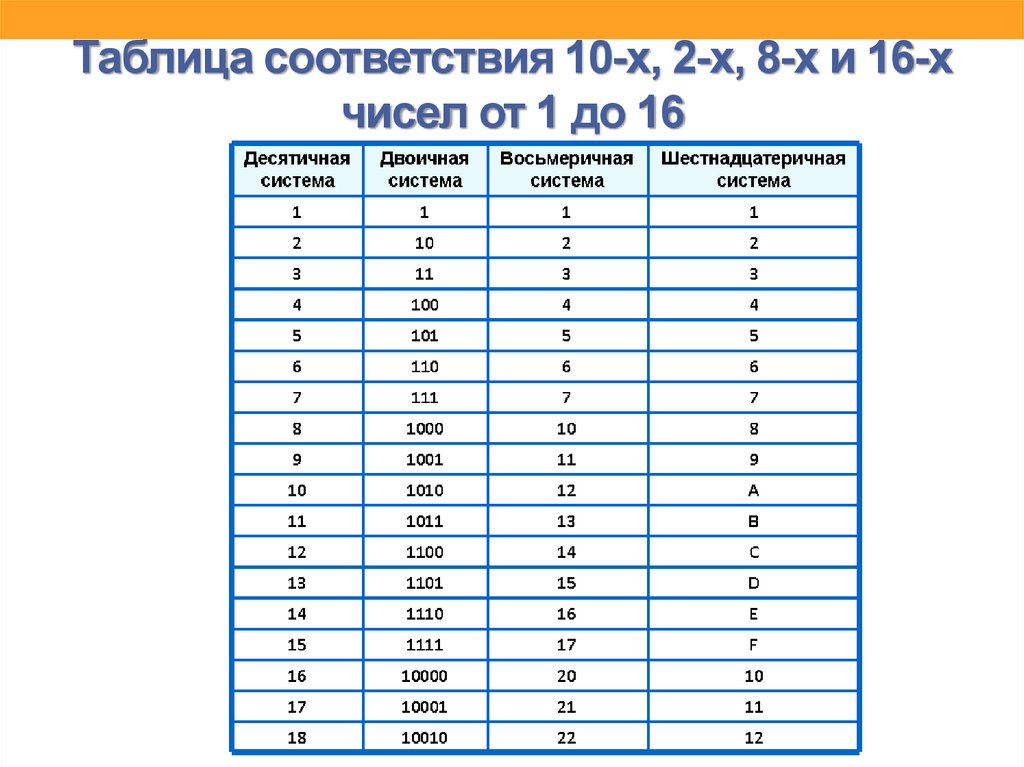
|
Для преобразования числа с основанием 10 в число 2, 8 или 16 используйте метод остатка.
| разделить на основание | дивидендов частное предыдущего деления | остатки | |
| 8 | 7146 | Остатки в обратном порядке решение | |
| 8 | 893 | 2 | |
| 8 | 111 | 5 | |
| 8 | 13 | 7 | |
| 8 | 1 | 5 | |
| 0 | 1 | Продолжайте делить пока частное не станет равным нулю |
Вернуться к началу
Для преобразования числа с основанием 10 в число 2, 8 или 16 используйте
метод вычитания.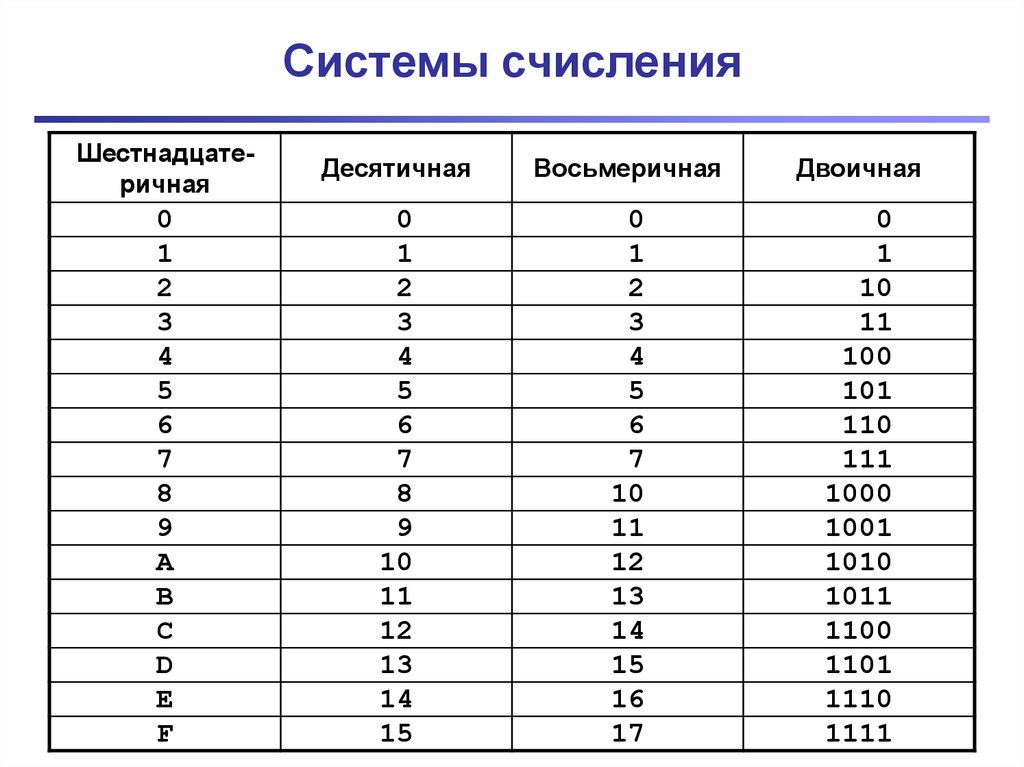
Заполните оставшуюся часть таблицы нули. |
| Чтобы преобразовать в основание 2 из основания 16, преобразуйте каждый шестнадцатеричный
цифра отдельно до четырех двоичных цифр. 2 4 В 16 = 0010 0100 1011 = 001001001011 2 Чтобы преобразовать основание 2 в основание 16, преобразуйте каждую группу
из четырех двоичных разрядов в восьмеричный разряд. 6 9 F = 69F 16 |
Вернуться к началу
| Чтобы преобразовать в основание 2 из основания 8, преобразовать каждый восьмеричный
цифра отдельно до трех двоичных цифр. 001 101 111 101 010 = 0011011111101010 2 Чтобы преобразовать основание 2 в основание 8, преобразуйте каждую группу из трех двоичных разрядов в восьмеричный разряд. (Начните с правого конца двоичного числа для создания групп.)3 2 3 7 = 3237 8 |
Преобразование в дополнение до двух из двоичного, обратное
все биты и добавить 1. |
 к. 4<8 деление
прекращаем
к. 4<8 деление
прекращаем к. 4<8 деление
прекращаем
к. 4<8 деление
прекращаем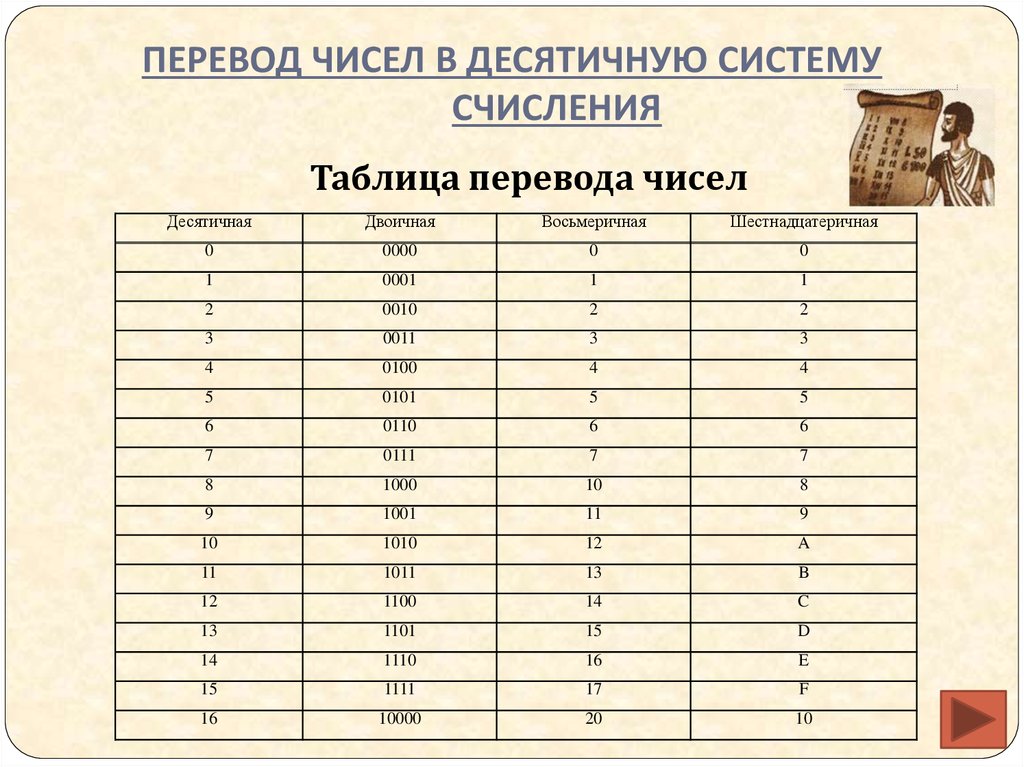 (Начните с правого конца
двоичного числа для создания групп.) 11010011111 2 = 110 1001 1111
знак равно
(Начните с правого конца
двоичного числа для создания групп.) 11010011111 2 = 110 1001 1111
знак равно