5 в восьмеричной системе счисления: Перевод 5 из десятичной в восьмеричную систему счисления

Перевод из восьмеричной в десятичную систему счисления, калькулятор

Исходное число

Направление перевода

2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Сообщить об ошибке

В избранное

Виджет

Вы можете сохранять ваши расчеты и они будут отображаться здесь.

Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.

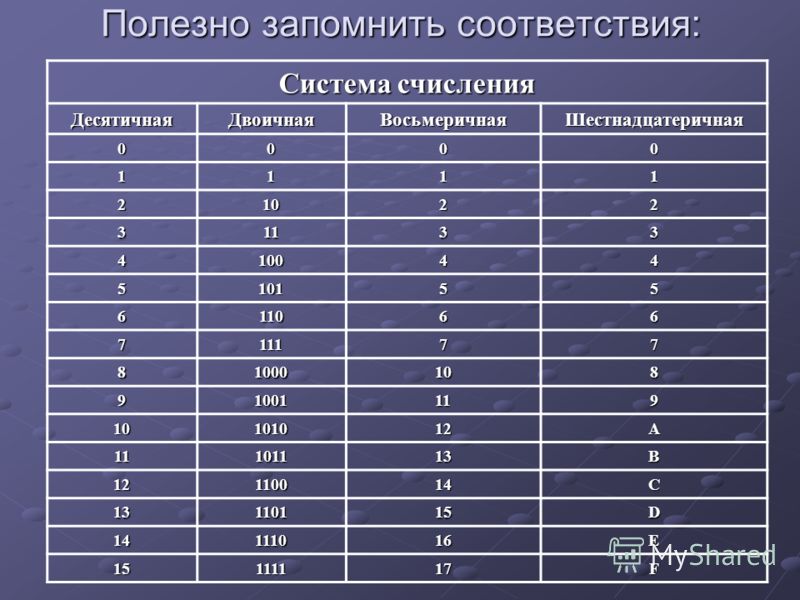
Преобразовать число из восьмеричной системы счисления в десятичную можно следующим образом: каждый разряд числа необходимо умножить на 8ⁿ, где n — номер разряда, начиная с 0. Затем суммировать полученные значения.

abc₂ = (a×8² + b×8¹ + c×8⁰)

10

56₈ = (5*8¹ + 6*8⁰)₁₀ = 46₁₀

467₈ = (4*8² + 6*8¹ + 7*8⁰)₁₀ = 311₁₀

Смотрите также

• Перевод из двоичной в десятичную
• Перевод из двоичной в восьмеричную
• Перевод из двоичной в шестнадцатеричную
• Перевод из десятичной в двоичную
• Перевод из десятичной в восьмеричную
• Перевод из десятичной в шестнадцатеричную
• Перевод из восьмеричной в двоичную
• Перевод из шестнадцатеричной в двоичную
• Перевод из шестнадцатеричной в десятичную

Перевод из восьмеричной системы в десятичной системе

Лабораторная работа №3

Тема: Использование восьмеричную систему счисления.

Цель работы: научиться использовать

восьмеричную систему счисления

Двоичная система счисления неудобна для использования человеком, поэтому программисты используют восьмеричную систему счисления.

Используемые символы: 0, 1, 2, 3, 4, 5, 6 и 7;

Для восьмеричной системы счисления соответствие чисел базиса системы с трехзначными числами двоичной системы следующее:

0₈=000₂ 4₈=100₂

1₈=001₂ 5₈=101₂

2₈=010₂ 6₈=110₂

3₈=011₂ 7₈=111₂

Представим в виде таблицы:

Двоичная система счисления	000	001	010	011	100	101	110	111
Восьмеричная система счисления	0	1	2	3	4	5	6	7

Примеры:

1) 1447₈=001 100 100 111₂=1100100111₂.

2) 256,773₈= 010 101 110, 111 111 011₂ = 10101110,111111011₂;

Задания: Используя таблицу переведите числа из восьмеричной в двоичную:

1. 436₈ 6. 15,423₈

2. 1674₈

7. 24,55₈

3. 6074₈ 8. 73,23₈

4. 1254₈ 9. 124,32₈

5. 5677₈ 10. 364,45₈

Перевод из восьмеричной системы в десятичную систему производится путем сложения произведений соответствующего десятичного эквивалента символа числа в восьмеричной системе на вес i-го знакоместа.

Примеры перевода из восьмеричной системы счисления в десятичную систему:

1. 461₈ = 4*8²+6*8¹+1*8⁰ = 4*64+6*8+1*1 = 256+49 = 305₁₀.

2. 172,54

   8 = 1*8²+7*8¹+2*8⁰+5*8^-1+4*8^-2 = 64+56+2+5*

Задания: Переведите восьмеричные числа в десятичную систему счисления.

1. 555₈ 7. 235,43₈

2. 633₈ 8. 731_,45₈

3. 434₈ 9.115,456₈

4. 2555₈ 10. 25,456₈

5. 7411₈ 11. 56,321₈

6. 325₈ 12. 231,44₈

Самостоятельная работа студента:

1. Преобразовать восьмеричные числа в десятичную систему:

1. 124; 6) 4407; 11) 125,64;

2. 357; 7) 3556; 12) 321,45;

3. 706; 8) 6754; 13) 654,21;

4. 235; 9) 3701; 14) 332,21;

5. 663; 10) 5564; 15) 32,654;

2. Перевести в двоичную систему следующие восьмеричные числа:

1. 45; 6) 365; 11) 1657; 16) 741,21;

2. 73; 7) 321; 12) 2566; 17) 256,74;

3. 35; 8) 257; 13) 3265; 18) 654,31;

4. 61; 9) 652; 14) 7415; 19) 257,36;

5. 72; 10) 234; 15) 3614; 20) 741,32;

Самостоятельная работа студента с преподователями:

1. Перевести в двоичную систему следующие восьмеричные числа:

1. 2322₈ 8. 7006₈

2. 7524₈ 9. 125₈

3. 223,245₈ 10. 224₈

4. 425₈ 11. 47₈

5. 315,075₈ 12. 21,25₈

6. 181,361₈ 13. 206,125₈

7. 176,526₈ 14. 640₈

2. Преобразовать восьмеричные числа в десятичную систему:

1. 122₈ 8. 3167₈

2. 450,706₈ 9. 125₈

3. 253,245₈ 10. 224₈

4. 426₈ 11. 13₈

5. 315,075₈ 12. 37,25₈

6. 131₈ 13. 206,125₈

7. 176,526₈ 14. 47,53₈

Контрольные вопросы:

1. Что такое позиционная система счисления?

2. Назовите правило перевода чисел из восьмеричной системы счисления в десятичную систему.

3. Назовите правило перевода чисел из восьмеричной системы счисления в двоичную систему счисления.

Лабораторная работа №4

Тема: Использование шестнадцатеричную систему счисления

Цель работы: научиться использовать шестнадцатеричную систему счисления

Перевод из шестнадцатеричной системы в десятичную систему производится путем сложения произведений соответствующего десятичного эквивалента символа числа в шестнадцатеричной системе на вес i-го знакоместа.

Пример перевода из 16-ричной системы счисления в десятичную систему:

15В₁₆=116²+516¹+1116⁰=256+80+11=347₁₀.

Для шестнадцатеричной системы счисления соответствие чисел базиса системы с четырехзначными числами двоичной системы следующее:

0₁₆=0000₂ 4₁₆=0100₂ 8₁₆=1000₂ C₁₆=1100₂

1₁₆=0001₂ 5₁₆=0101₂ 9₁₆=1001₂ D₁₆=1101₂

2₁₆=0010₂ 6₁₆=0110₂ A₁₆=1010₂ E₁₆=1110₂

3₁₆=0011₂ 7₁₆=0111₂ B₁₆=1011₂ F₁₆=1111₂

Представим в виде таблицы:

Двоичная система счисления	0000	0001	0010	0011	0100	0101	0110	0111
Шестнадцатеричная система счисления	0	1	2	3	4	5	6	7

Двоичная система счисления	1000	1001	1010	1011	1100	1101	1110	1111
Шестнадцатеричная система счисления	8	9	A	B	C	D	E	F

Используя таблицу переведите числа из шестнадцатеричной системы в двоичную:

1. А36₁₆ 6. 102,9E₁₆

2. В7С₁₆ 7. 456,EA₁₆

3. 2Е1₁₆ 8. B03,DF₁₆

4. 8DF4₁₆ 9. EA2,E3₁₆

5. AB47₁₆ 10. ED7,87₁₆

Примеры:

1) 3Е5А1₁₆=3*16⁴+E*16³+5*16²+A*16¹+1*16⁰ .

2) 48С,В7₁₆ = 4*16²+8*16¹+C*16⁰+B*16^-1+7*16^-2 =

4*16²+8*16¹+12*16⁰+11*16^-1+7*16^-2 =

Перевести шестнадцатеричные числа в десятичную систему счисления.

1. A87E₁₆ 7. BE,741₁₆

2. 23DF₁₆ 8. F11,567₁₆

3. EA12₁₆ 9. 981,DA₁₆

4. 1A22₁₆ 10. 23,3B₁₆

5. 91₁₆ 11. F54,47₁₆

6. 7C31₁₆ 12. 235,F₁₆

Преобразование чисел в Linux между десятичными, шестнадцатеричными, восьмеричными и двоичными

Unix как второй язык

Сандра Генри-Стокер, Юникс Двиб, Сетевой мир |

Linux предоставляет команды для преобразования чисел из одного основания в другое. Узнайте, как использовать эти команды и как упростить процесс с помощью сценариев и псевдонимов.

Матеймо / Getty Images

Возможно, вам нечасто приходится преобразовывать числа из одной системы счисления в другую, но если вам это нужно, вы можете сделать это с помощью любой из двух довольно простых команд в командной строке Linux.

Преобразование в уме может быть утомительным, особенно для длинных чисел. В то время как десятичная система счисления позволяет любой цифре в числе иметь любое из десяти значений (0-9), цифры в шестнадцатеричных числах могут иметь 16 (0-F), цифры в восьмеричных числах только восемь (0-7) и цифры в двоичных чисел всего два (0-1).

И, нравится вам это или нет, время от времени вы, вероятно, сталкиваетесь с числами, отображаемыми в шестнадцатеричном или восьмеричном формате, и знание того, как преобразовать их из одной системы счисления в другую, может пригодиться.

Для начала десятичные числа от 5 до 16 в четырех системах счисления выглядят так:

 5 6 7 8 9 10 11 12 13 14 15 16 <== десятичное 
 5 6 7 8 9 a b c d e f 10 <== шестнадцатеричный
  5 6 7 10 11 12 13 14 15 16 17 20 <== восьмеричное число
101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 <== двоичный 

Использование команды

printf для преобразования десятичных чисел

Чтобы преобразовать число из десятичного в шестнадцатеричное, вы можете использовать команду printf , подобную приведенной ниже, которая преобразует десятичное число 15 в шестнадцатеричное:

 $ printf '%x\ № 15
ф
 

Чтобы вместо этого преобразовать в восьмеричный формат, замените «%x» (шестнадцатеричный) на «%o» (восьмеричный):

 $ printf ‘%o\n’ 15
17
 

Для числа 17, показанного во втором примере выше, напомним, что первая цифра (1) имеет десятичное значение 8, а вторая (7) — значение 7.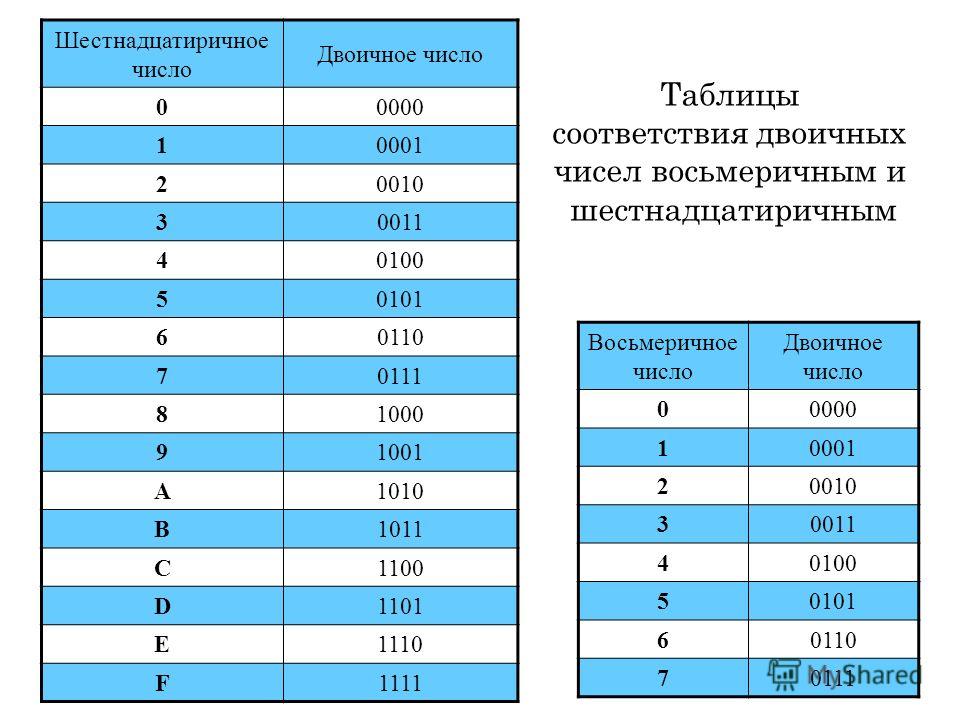 Следовательно, восьмеричный результат равен десятичному 15.

Превратить эти преобразования в скрипты несложно. Вот два сценария, которые запрашивают преобразование числа, а затем запускают команду printf , чтобы выполнить преобразование за вас.

dec2hex

 #!/bin/bash
echo -n «Введите десятичное число>»
читать номер
printf ‘%x\n’ $number
 

dec2oct

 #!/bin/bash
echo -n «Введите десятичное число>»
читать номер
printf ‘%o\n’ $number
 

Примечание. Команда printf не имеет возможности преобразования в двоичный формат.

Использование команды

bc для преобразования десятичных чисел

Используя команду bc (калькулятор), вы можете выполнять аналогичный тип преобразования с помощью команд, подобных приведенным ниже.

В первом примере десятичное число 16 преобразуется в основание 16 (шестнадцатеричное). Поскольку в шестнадцатеричном формате вторая цифра справа представляет 16-ю позицию (это десятичное число 16), 1 означает десятичное число 16. Параметр «obase» означает «выходное основание». Это формат, в который вы хотите преобразовать число. Поскольку «ibase» (база ввода) не указана, предполагается, что она десятичная.

 $ echo "obase=16; 16” | До нашей эры
10
 

Следующая команда преобразует то же число в восьмеричное. Поскольку в восьмеричной системе вторая цифра справа представляет десятичную позицию восьмерок, 2 означает десятичные 16 (две восьмерки).

 $ echo "obase=8; 16” | До нашей эры
20
 

Со следующим большим числом, десятичным числом 17, мы получаем 21 — две десятичные восьмерки и одну единицу.

 $ echo "obase=8; 17” | До нашей эры
21
 

Команда bc работает так же хорошо с двоичными, как и с шестнадцатеричными и восьмеричными числами, поэтому мы также можем преобразовывать числа в двоичные. Вот команда для отображения десятичного числа 16 в виде двоичного числа:

 $ эхо "obase=2; 16” | До нашей эры
10000
 

Описано в системе счисления 10, то есть одно число 16, без восьмерок, без четверок, без двоек и без единиц.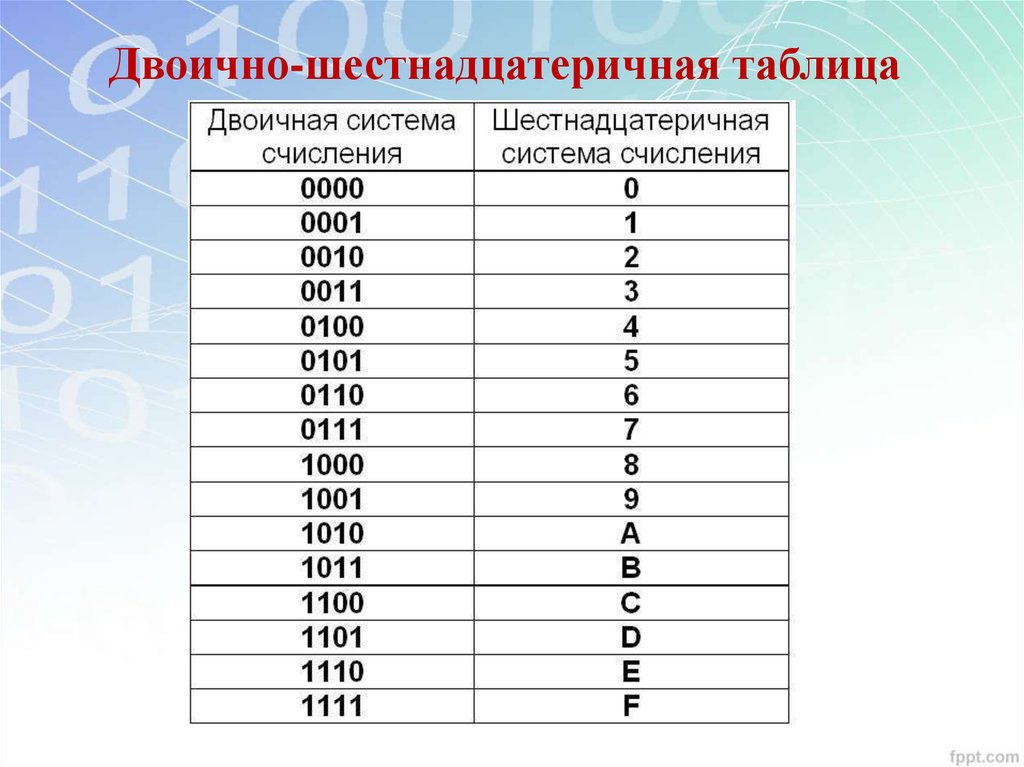

В то время как двоичная система вошла в обиход, потому что она работает непосредственно с состоянием включения/выключения электроники, восьмеричная и шестнадцатеричная системы обеспечивают простое преобразование, так что нам, людям, не нужно смотреть на длинные строки нулей и единиц. Даже это не ограничивает работу команды bc , которая без проблем работает с основанием 3, основанием 7 или любым другим основанием счисления, с которым вы, возможно, захотите поэкспериментировать.

 $ echo "obase=3; 16” | До нашей эры
121
 

Описанные как десятичные числа, 121 в приведенном выше примере представляет одну 9, две тройки и одну 1. Вот версия с основанием 7:

 $ echo "obase=7; 16” | До нашей эры
22
 

Приведенные выше цифры представляют собой две десятичные семерки и две единицы.

Преобразование чисел в десятичные числа с помощью

bc

При всем сказанном вы также можете использовать команду bc для преобразования чисел, выраженных в шестнадцатеричном, восьмеричном или двоичном формате, в десятичные.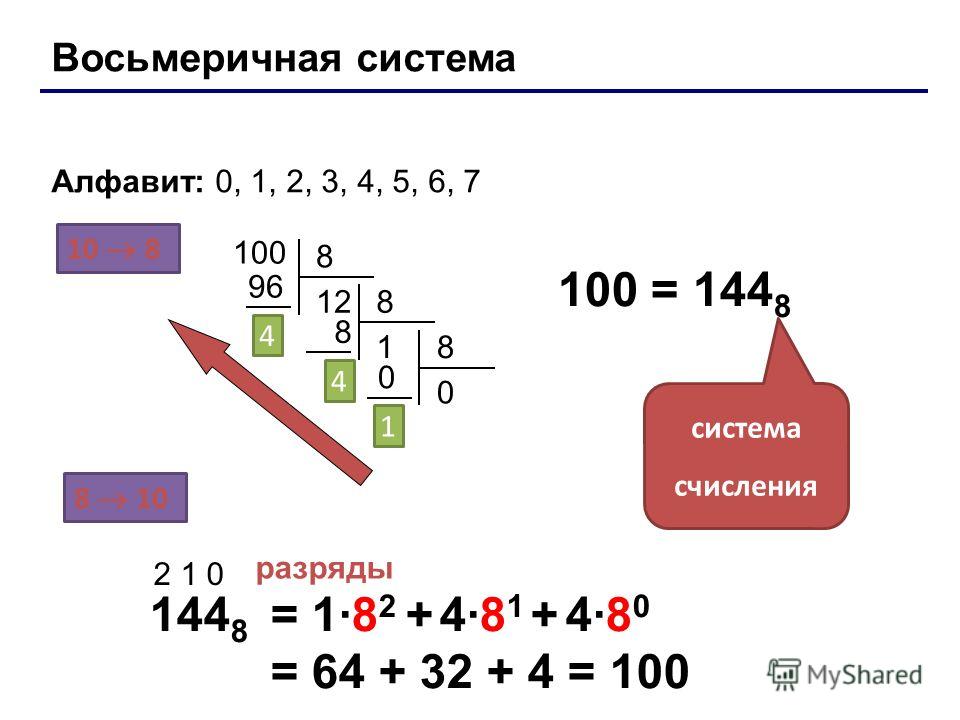 Просто укажите obase (выходное основание) равно 10, ibase (входное основание) равно 16, если начальное число шестнадцатеричное, 8, если оно восьмеричное, и 2, если оно двоичное, как в примерах, показанных ниже.

 $ echo "obase=10; ибаза=16; Ф” | До нашей эры
15
$ эхо "obase=10; ибаза=8; 15” | До нашей эры
13
$ эхо "obase=10; ибаза=2; 112” | До нашей эры
7
 

Как и в предыдущем сценарии, преобразование этих команд в сценарии требует совсем немного усилий.

hex2dec

 #!/bin/bash
echo -n «Введите шестнадцатеричное число>»
читать номер
эхо "obase=10; ибаза=16; $ число” | До нашей эры
 

oct2dec

 #!/bin/bash
echo -n «Введите восьмеричное число>»
читать номер
эхо "obase=10; ибаза=8; $ число” | До нашей эры
 

bin2dec

 #!/bin/bash
echo -n «Введите двоичное число>»
читать номер
эхо "obase=10; ибаза=16; $ число” | до н.э. 

Использование псевдонимов для преобразований с числовой основой

Хотя сценарии, показанные выше, легко настроить, вероятно, наиболее удобный способ реализовать любое из показанных преобразований — настроить их как группу псевдонимов. Добавление псевдонима ниже к вашему ~/.bashrc сделает их доступными при следующем входе в систему или сразу после получения файла (например, запустив  . ~/.bashrc ).

 # преобразовать из десятичной
псевдоним dec2hex=’f(){ echo «obase=16; ибаза=10; $1” | До нашей эры; сбросить -f f; }; ж’
псевдоним dec2oct=’f(){ echo «obase=8; ибаза=10; $1” | До нашей эры; сбросить -f f; }; ж’
псевдоним dec2bin=’f(){ echo «obase=2; ибаза=10; $1” | До нашей эры; сбросить -f f; }; ж’
# преобразовать в десятичную
псевдоним hex2dec=’f(){ echo «obase=10; ибаза=16; $1” | До нашей эры; сбросить -f f; }; ж’
псевдоним oct2dec=’f(){ echo «obase=10; ибаза=8; $1” | До нашей эры; сбросить -f f; }; ж’
псевдоним bin2dec=’f(){ echo «obase=10; ибаза=2; $1” | До нашей эры; сбросить -f f; }; ж’
 

После этого вы можете запустить псевдонимы следующим образом:

 $ dec2hex 15
Ф
$ дек2окт 15
17
$ dec2bin 15
1111
$ hex2dec F
15
$ окт2дек 17
15
$ bin2dec 1111
15
 

Резюме

Преобразование чисел из одной системы счисления в другую может быть утомительным, но вы можете избавить себя от многих проблем, используя команды printf и bc , особенно если вы настроите их как скрипты или псевдонимы.

Связанный:

• Linux

Copyright © 2022 IDG Communications, Inc.

10 самых влиятельных компаний в области корпоративных сетей 2022 г.

Как преобразовать восьмеричную систему счисления в двоичную | Система счисления

Итак, ребята, сегодня мы собираемся обсудить, как преобразовать восьмеричное число в двоичное. Прежде чем мы начнем, давайте вспомним двоичные и восьмеричные числа.

Восьмеричное число: Восьмеричное число представляет собой 8-основную систему счисления, в которой используются цифры от 0 до 8 (0,1,2,3,4,5,6,7). Они известны как восьмеричные числа. Вот несколько примеров восьмеричных чисел: 12 ₈ , 27 ₈ , 143 ₈ , 276 _8, и т. д., а также многие другие числа.

Двоичное число: Двоичное число представляет собой систему счисления с двумя основаниями, в которой используются только цифры 0 и 1. Они известны как двоичные числа. Вот несколько примеров двоичных чисел: 010 _2, 10 ₂ , 101 ₂ , 10010 ₂

Для получения более подробной информации по этой теме перейдите по этой ссылке «Компьютерная система счисления»

Для лучшего понимания начнем с примера.

Пример 1: Преобразовать восьмеричное число (10) ₈ в двоичное?

Сол:

Шаг 1: Во-первых, мы должны преобразовать данное число 10 ₈ в десятичное число. Итак, давайте посмотрим, как преобразовать

= 1 x 8 ¹ + 0 x 8 ⁰

= 8 ₁₀

Шаг 2: Теперь мы должны преобразовать число 8 60 1 в двоичное число. Преобразуем…

As В нашем блоге «Как преобразовать десятичную систему счисления в двоичную» мы обсуждали, как преобразовать ее в двоичную… Остаток 8 ÷ 2 4 0 4 ÷ 2 2 0 2 ÷ 2 1 0 1 ÷ 2 0 1

Напишите все остальные от нисходящего до восходящего манера

= 1000

. Таким образом, наш ответ - (1000) ₂

. восьмеричной цифры 10 ₈ это (1000) ₂ .

Пример 2: Преобразовать восьмеричное число (74) ₈ в двоичное?

Sol:

Шаг 1: Сначала мы должны преобразовать данное число 74 ₈ в десятичное число. Итак, давайте посмотрим, как преобразовать...

= 7 х 8 ¹ + 4 х 8 ⁰

= 56 + 4

= 60 ₁₀

Шаг 2: Теперь нам нужно преобразовать число 60 ₁₀ в двоичное число. Let's convert…

Decimal No. ÷ by 2	Quotient	Remainder
60 ÷ 2	30	0
30 ÷ 2	15	0
15 ÷ 2	7	1
7 ÷ 2	3	1
3 ÷ 2	1	1
1 ÷ 2	0	1

Запишем весь остаток снизу вверх

= 111100

Итак, наш ответ: (111100) ₂

Следовательно, преобразование восьмеричного числа 74 9 0159 2 .

Пример 3: Преобразовать восьмеричное число (531) ₈ в двоичное?

Sol:

Шаг 1: Сначала мы должны преобразовать данное число 531 ₈ в десятичное число. Итак, давайте посмотрим, как преобразовать…

= 5 x 8 ² + 3 x 8 ¹ + 1 x 8 ⁰

= 320 + 24 + 1

= 345 ₁₀

Шаг. 2: Теперь нам нужно преобразовать число 345 ₁₀ в двоичное число. Let's convert…

Decimal No. ÷ by 2	Quotient	Remainder
345 ÷ 2	172	1
172 ÷ 2	86	0
86 ÷ 2	43	0
43 ÷ 2	21	1
21 ÷ 2	10	1
10 ÷ 2	5	0
5 ÷ 2	2	1
2 ÷ 2	1	0
1 ÷ 2	0	1

Write all the remainder from вниз к восходящему

= 101011001 ₂

Итак, наш ответ: (101011001) ₂

Следовательно, преобразование восьмиугольника 531 ₈ - (101011001001) ₂ .

Пример 4: Преобразовать восьмеричное число (1624) ₈ в двоичное?

Sol:

Шаг 1: Сначала мы должны преобразовать данное число 1624 ₈ в десятичное число. Итак, давайте посмотрим, как конвертировать…

= 1 x 8 ³ + 6 x 8 ² + 2 x 8 ¹ + 4 x 8 ⁰

= 512 + 384 + 16 +

= 916 ₁₀

02020202020202020202 Шаг 2: Теперь нам нужно преобразовать число (916) ₁₀ в двоичное число. Let’s convert…

Decimal No. ÷ by 2	Quotient	Remainder
916 ÷ 2	458	0
458 ÷ 2	229	0
229 ÷ 2	114	1
114 ÷ 2	57	0
57 ÷ 2	28	1
28 ÷ 2	14	0
14 ÷ 2	7	0
7 ÷ 2	3	1
3 ÷ 2	1	1
1 ÷ 2	0	1

Запишем весь остаток снизу вверх

= 1110010100

Итак, наш ответ: (1110010100) ₂ .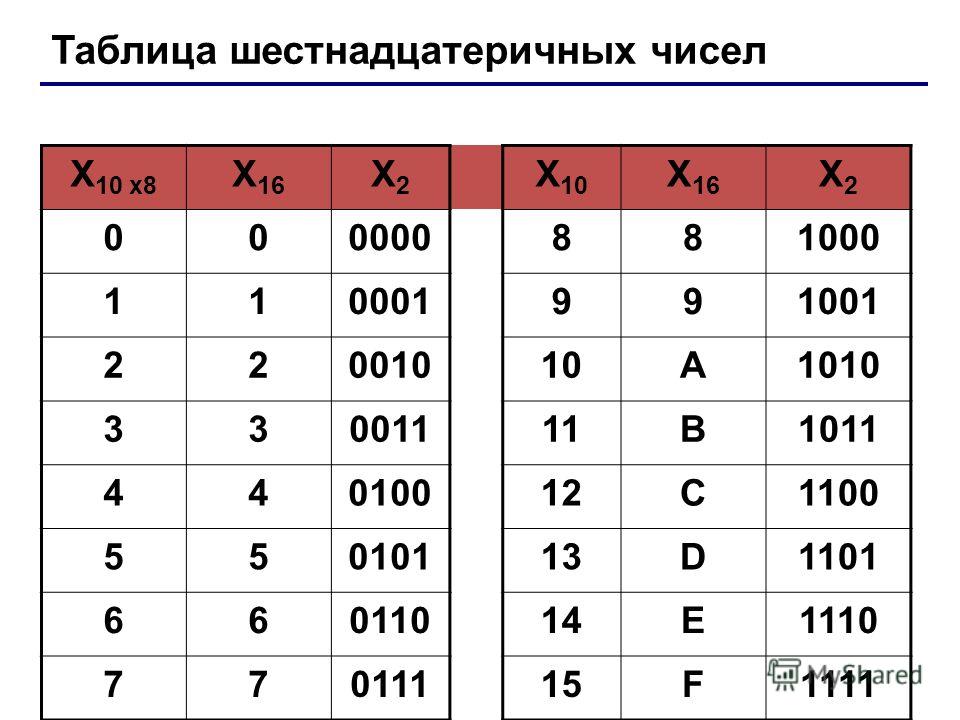

Следовательно, преобразование восьмеричного числа 916 ₈ это (1110010100) ₂ .

Пример 5: Преобразовать восьмеричное число (3246) ₈ в двоичное?

Sol:

Шаг 1: Сначала мы должны преобразовать данное число 3246 ₈ в десятичное число. Итак, давайте посмотрим, как преобразовать...

= 3 x 8 ³ + 2 x 8 ² + 4 x 8 ¹ + 6 x 8 ⁰

= + 1536 + 228 +

= 1702 ₁₀

Шаг 2: Теперь нам нужно преобразовать число (1702) ₁₀ в двоичное число. Let's convert…

Decimal No. ÷ by 2	Quotient	Remainder
1702 ÷ 2	815	0
815 ÷ 2	425	1
425 ÷ 2	212	1
212 ÷ 2	106	0
106 ÷ 2	53	0
53 ÷ 2	26	1
26 ÷ 2	13	0
13 ÷ 2	6	1
6 ÷ 2	3	0
3 ÷ 2	1	1
1 ÷ 2	0	1

Write all the remainder from Вниз к восходящему манеру

= 11010100110

Итак, наш ответ (11010100110) ₂

Следовательно, преобразование восьмиугольника 1702 ₈ - (110101100110110159 2 ₂ 0 2 60 260 2 (11010100110110) ₂ 0 2 0 2 0 260 - (11010110110110) ₈ .