3 в двоичной системе: Перевод чисел из десятичной системы в двоичную

Содержание

Быстрый перевод числа из десятичной системы счисления в двоичную

Чтобы быстро переводить числа из десятичной системы счисления в двоичную, нужно хорошо знать числа «2 в степени». Например, 2¹⁰=1024 и т.д. Это позволит решать некоторые примеры на перевод буквально за секунды. Одной из таких задач является задача A1 из демо ЕГЭ 2012 года. Можно, конечно, долго и нудно делить число на «2». Но лучше решать по-другому, экономя драгоценное время на экзамене.

Метод очень простой. Суть его такая: если число, которое нужно перевести из десятичной системы, равно числу «2 в степени», то это число в двоичной системе содержит количество нулей, равное степени. Впереди этих нулей добавляем «1».

Примеры:

Переведем число 2 из десятичной системы. 2=2¹. Поэтому в двоичной системе число содержит 1 нуль. Впереди ставим «1» и получаем 10₂.
Переведем 4 из десятичной системы. 4=2². Поэтому в двоичной системе число содержит 2 нуля. Впереди ставим «1» и получаем 100_2.
Переведем 8 из десятичной системы. 8=2³. Поэтому в двоичной системе число содержит 3 нуля. Впереди ставим «1» и получаем 1000_2.

На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.

Аналогичнои для других чисел «2 в степени».

Если число, которое нужно перевести, меньше числа «2 в степени» на 1, то в двоичной системе это число состоит только из единиц, количество которых равно степени.

Переведем 3 из десятичной системы. 3=2²-1. Поэтому в двоичной системе число содержит 2 единицы. Получаем 11_2.
Переведем 7 из десятичной системы. 7=2³-1. Поэтому в двоичной системе число содержит 3 единицы. Получаем 111_2.

На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.

Аналогиченперевод и для других чисел «2 в степени-1».

Понятно, что перевод чисел от 0 до 8 можно сделать быстро или делением, или просто знать наизусть их представление в двоичной системе. Я привела эти примеры, чтобы Вы поняли принцип данного метода и использовали его для перевода более «внушительных чисел», например, для перевода чисел 127,128, 255, 256, 511, 512 и т.д.

Можно встретить такие задачи, когда нужно перевести число, не равное числу «2 в степени», но близкое к нему. Оно может быть больше или меньше числа «2 в степени». Разница между переводимым числом и числом «2 в степени» должна быть небольшая. Например, до 3. Представление чисел от 0 до 3 в двоичной системе надо просто знать без перевода.

Если число больше, то решаем так:

Переводим сначала число «2 в степени» в двоичную систему. А потом прибавляем к нему разницу между числом «2 в степени» и переводимым числом.

Например, переведем 19 из десятичной системы. Оно больше числа «2 в степени» на 3.

19=16+3.

16=2⁴. 16₁₀=10000₂.

3₁₀=11₂.

19₁₀=10000₂+11₂=10011₂.

Если число меньше числа «2 в степени», то удобнее пользоваться числом «2 в степени-1». Решаем так:

Переводим сначала число «2 в степени-1» в двоичную систему. А потом вычитаем из него разницу между числом «2 в степени-1» и переводимым числом.

Например, переведем 29 из десятичной системы. Оно больше числа «2 в степени-1» на 2. 29=31-2.

31₁₀=11111₂.

2₁₀=10₂.

29₁₀=11111₂-10₂=11101₂

Если разница между переводимым числом и числом «2 в степени» больше трех, то можно разбить число на составляющие, перевести каждую часть в двоичную систему и сложить.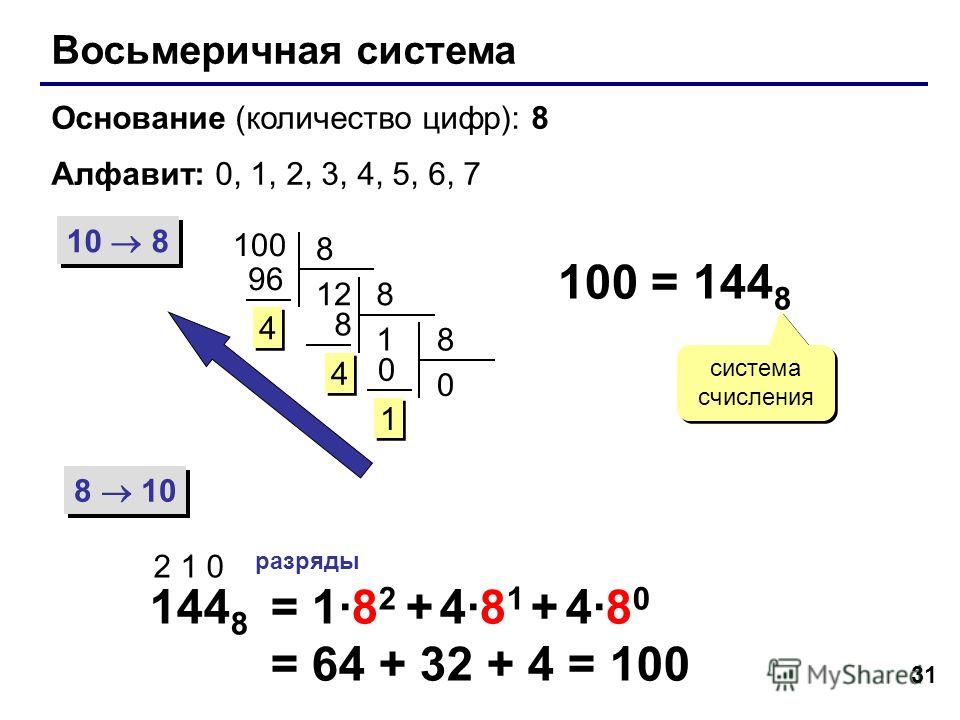

Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16.
512=2⁹. 512₁₀=1000000000₂.
16=2⁴. 16₁₀=10000₂.
Теперь сложим столбиком:

Данная методика позволяет тратить минимум времени на перевод чисел из десятичной системы в двоичную, но при условии, что Вы прекрасно знаете числа «2 в степени». Если это не так, то заучите эти числа. Тем более, что в задачах по информатике они активно используются.

Учить числа «2 в степени» удобно по этому материалу

Перейти к статьям:

«Как переводить числа между двоичной, восьмеричной и шестнадцатеричной системами счисления».

«Системы счисления: основные понятия».
«Решение задач демо ЕГЭ на системы счисления»
«Выполнение арифметических операций в двоичной системе счисления».

Двоичная система счисления

Содержание:
Что такое двоичная система счисления
Как перевести целое десятичное число в двоичную систему счисления
Как перевести десятичную дробь в двоичную систему счисления
Как перевести число из двоичной системы счисления в десятичную
Как перевести дробное двоичное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в двоичной системе счисления

Двоичная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа.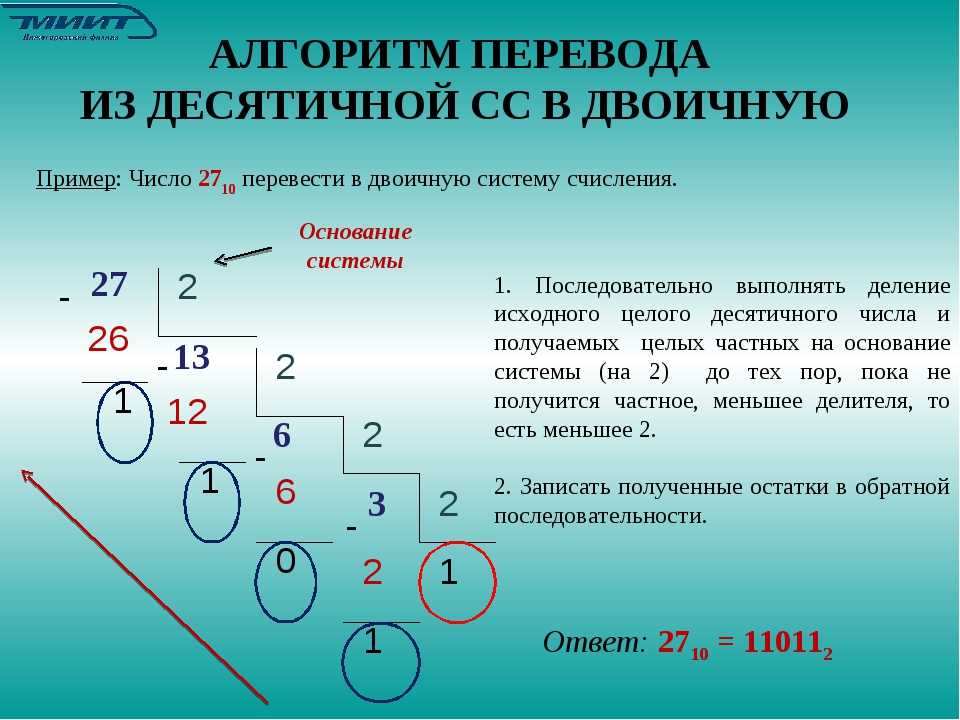

Для записи числа в двоичной системе счисления используется две цифры 0 и 1. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 1001₂ или 1000101₂

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в двоичную систему счисления

Для того, чтобы перевести целое десятичное число в двоичную систему счисления нужно десятичное число делить на 2 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 173₁₀ в двоичную систему счисления:

173 : 2 = 86 остаток: 1
86 : 2 = 43 остаток: 0
43 : 2 = 21 остаток: 1
21 : 2 = 10 остаток: 1
10 : 2 = 5 остаток: 0
5 : 2 = 2 остаток: 1
2 : 2 = 1 остаток: 0
1 : 2 = 0 остаток: 1

173₁₀ = 10101101₂

Как перевести десятичную дробь в двоичную систему счисления

Для того чтобы перевести десятичную дробь в двоичную систему счисления необходимо сначала перевести целую часть десятичной дроби в двоичную систему счисления, а затем дробную часть, последовательно умножать на 2, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой.

Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 5.74₁₀ в двоичную систему счисления:

Переведем целую часть

5 : 2 = 2 остаток: 1
2 : 2 = 1 остаток: 0
1 : 2 = 0 остаток: 1
5₁₀ = 101₂

Переведем дробную часть

0.74 · 2 = 1.48
0.48 · 2 = 0.96
0.96 · 2 = 1.92
0.92 · 2 = 1.84
0.84 · 2 = 1.68
0.68 · 2 = 1.36
0.36 · 2 = 0.72
0.72 · 2 = 1.44
0.44 · 2 = 0.88
0.88 · 2 = 1.76

0.74₁₀ = 0.1011110101₂
5.74₁₀ = 101.1011110101₂

Двоичные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной двоичной.

В данном примере получается бесконечная периодическая двоичная дробь, поэтому умножение на 2 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 5.74 не может быть точно представлена в двоичной системе счисления. К примеру, дробь 2.5₁₀ может быть представлена в двоичной системе счисления в виде конечной 2.5₁₀ = 10.1₂.

Как перевести число из двоичной системы счисления в десятичную

Для того, чтобы перевести число из двоичной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.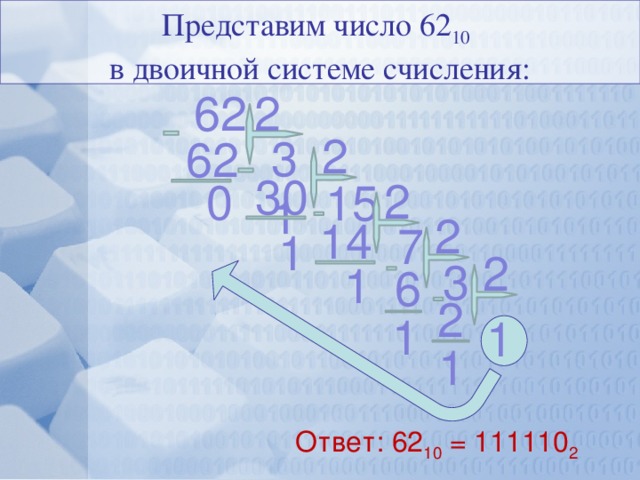

Например, переведем теперь обратно число 10101101₂ в десятичную систему счисления:

Позиция в числе	7	6	5	4	3	2	1	0
Число	1	0	1	0	1	1	0	1

10101101₂ = 1 ⋅ 2⁷ + 0 ⋅ 2⁶ + 1 ⋅ 2⁵ + 0 ⋅ 2⁴ + 1 ⋅ 2³ + 1 ⋅ 2² + 0 ⋅ 2¹ + 1 ⋅ 2⁰ = 173₁₀

Как перевести дробное двоичное число в десятичное

Для того, чтобы перевести дробное двоичное число в десятичное, необходимо записать дробное двоичное число, убрав точку и затем сверху расставить индексы. Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.

Каждая позиция цифры (индекс) будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное двоичное число 110.101 в десятичное:

Позиция в числе	2	1	0	-1	-2	-3
Число	1	1	0	1	0	1

110.101₂ = 1 ⋅ 2² + 1 ⋅ 2¹ + 0 ⋅ 2⁰ + 1 ⋅ 2^-1 + 0 ⋅ 2^-2 + 1 ⋅ 2^-3 = 6.625₁₀

Таблица значений десятичных чисел от 0 до 100 в двоичной системе счисления

Значение числа в десятичной системе счисления	Значение числа в двоичной системе счисления
0₁₀	0₂
1₁₀	1₂
2₁₀	10₂
3₁₀	11₂
4₁₀	100₂
5₁₀	101₂
6₁₀	110₂
7₁₀	111₂
8₁₀	1000₂
9₁₀	1001₂
10₁₀	1010₂
11₁₀	1011₂
12₁₀	1100₂
13₁₀	1101₂
14₁₀	1110₂
15₁₀	1111₂
16₁₀	10000₂
17₁₀	10001₂
18₁₀	10010₂
19₁₀	10011₂
20₁₀	10100₂
21₁₀	10101₂
22₁₀	10110₂
23₁₀	10111₂
24₁₀	11000₂
25₁₀	11001₂
26₁₀	11010₂
27₁₀	11011₂
28₁₀	11100₂
29₁₀	11101₂
30₁₀	11110₂
31₁₀	11111₂
32₁₀	100000₂
33₁₀	100001₂
34₁₀	100010₂
35₁₀	100011₂
36₁₀	100100₂
37₁₀	100101₂
38₁₀	100110₂
39₁₀	100111₂
40₁₀	101000₂
41₁₀	101001₂
42₁₀	101010₂
43₁₀	101011₂
44₁₀	101100₂
45₁₀	101101₂
46₁₀	101110₂
47₁₀	101111₂
48₁₀	110000₂
49₁₀	110001₂
50₁₀	110010₂

Значение числа в десятичной системе счисления	Значение числа в двоичной системе счисления
51₁₀	110011₂
52₁₀	110100₂
53₁₀	110101₂
54₁₀	110110₂
55₁₀	110111₂
56₁₀	111000₂
57₁₀	111001₂
58₁₀	111010₂
59₁₀	111011₂
60₁₀	111100₂
61₁₀	111101₂
62₁₀	111110₂
63₁₀	111111₂
64₁₀	1000000₂
65₁₀	1000001₂
66₁₀	1000010₂
67₁₀	1000011₂
68₁₀	1000100₂
69₁₀	1000101₂
70₁₀	1000110₂
71₁₀	1000111₂
72₁₀	1001000₂
73₁₀	1001001₂
74₁₀	1001010₂
75₁₀	1001011₂
76₁₀	1001100₂
77₁₀	1001101₂
78₁₀	1001110₂
79₁₀	1001111₂
80₁₀	1010000₂
81₁₀	1010001₂
82₁₀	1010010₂
83₁₀	1010011₂
84₁₀	1010100₂
85₁₀	1010101₂
86₁₀	1010110₂
87₁₀	1010111₂
88₁₀	1011000₂
89₁₀	1011001₂
90₁₀	1011010₂
91₁₀	1011011₂
92₁₀	1011100₂
93₁₀	1011101₂
94₁₀	1011110₂
95₁₀	1011111₂
96₁₀	1100000₂
97₁₀	1100001₂
98₁₀	1100010₂
99₁₀	1100011₂
100₁₀	1100100₂

3 в двоичном формате — Как преобразовать 3 из десятичного в двоичный?

3 в двоичном формате равно 11. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 2 бита для представления 3 в двоичном формате. В этой статье давайте узнаем, как преобразовать десятичное число 3 в двоичное.

Как преобразовать 3 в двоичный код?

Шаг 1: Разделите 3 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0,9.0006

Дивиденд	Остаток
3/2 = 1	1
1/2 = 0	1

Шаг 2: Запишите остаток снизу вверх, т.е. в обратном хронологическом порядке. Это даст двоичный эквивалент 3.

Следовательно, двоичный эквивалент десятичного числа 3 равен 11.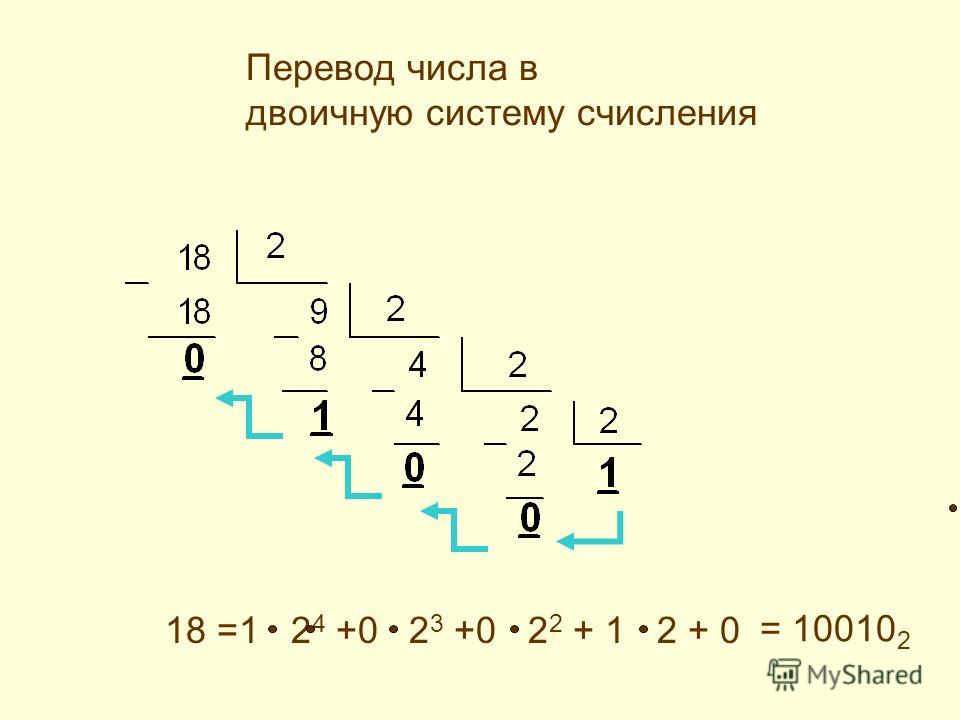

☛ Десятичный калькулятор для двоичных чисел

Давайте посмотрим на значение десятичного числа 3 в разных системах счисления.

3 в двоичном виде: 3₁₀ = 11₂
3 в восьмеричном: 3₁₀ = 3₈
3 в шестнадцатеричном формате: 3₁₀ = 3₁₆
11₂ в десятичном формате: 3₁₀

Описание проблемы:

Часто задаваемые вопросы о 3 в двоичном формате

Что такое 3 в двоичном формате?

3 в двоичном формате равно 11. Чтобы найти десятичный эквивалент в двоичном, разделите 3 последовательно на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.

☛ Двоичное преобразование в десятичное

Найдите значение 1 × 3 в двоичной форме.

Мы знаем, что 3 в двоичном формате равно 11, а 1 равно 1. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0 ; 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 11 × 1 = 11, что равно 3 в десятичной системе счисления. [3 × 1 = 3]

Каков двоичный эквивалент числа 3 + 83?

3 в двоичной системе счисления равно 11, а 83 равно 1010011. Мы можем сложить двоичный эквивалент 3 и 83, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (11)₂ + (1010011)₂ = (1010110)₂, что есть не что иное, как 86,9.0006

☛ Калькулятор двоично-десятичной системы счисления

Сколько бит имеет число 3 в двоичном формате?

Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 3 в двоичном формате, т. е. 11. Таким образом, мы использовали 2 бита для представления 3 в двоичном формате.

Как преобразовать 3 в двоичный эквивалент?

Мы можем разделить 3 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге.

3 mod 2 = 1 — LSB (младший значащий бит)
1 mod 2 = 1 — MSB (старший бит)

Записать остатки от MSB до LSB. Следовательно, десятичное число 3 в двоичном виде можно представить как 11.

☛ Также проверьте:

15 в двоичном виде — 1111
42 в двоичном формате — 101010
248 в двоичном формате — 11111000
134 в двоичном формате — 10000110
231 в двоичном формате — 11100111
18 в двоичном формате — 10010
90 в двоичном формате — 1011010

Рабочие листы по математике и
наглядный учебный план

Сколько значений можно представить тремя двоичными цифрами?

Система счисления — это система обработки чисел. Числовые форматы — это внутреннее представление числовых значений в архитектуре компьютера. Числовые значения хранятся в виде групп битов, таких как байты и слова. Существует четыре различных типа систем счисления, в основном используется десятичная система, а двоичная система используется компьютерами.

Четыре различных типа систем счисления,

1. Двоичная система счисления

В этой системе счисления используются только две цифры 0 и 1, за которыми следует основание 2. Двоичные цифры также известны как бит . Компьютеры понимают только двоичную систему.

2. Восьмеричная система счисления

Восьмеричная система счисления относится к основанию 8. Она содержит восемь символов, т.е. 0, 1, 2, 3, 4, 5, 6, 7.

3. Десятичная система счисления

Это система счисления, в которой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, за которыми следует основание 10. В математике обычно используется десятичная система.

4. Шестнадцатеричная система счисления

В шестнадцатеричной системе используются шестнадцать символов: 0,1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Бит в двоичном числе

Одна двоичная цифра называется битом.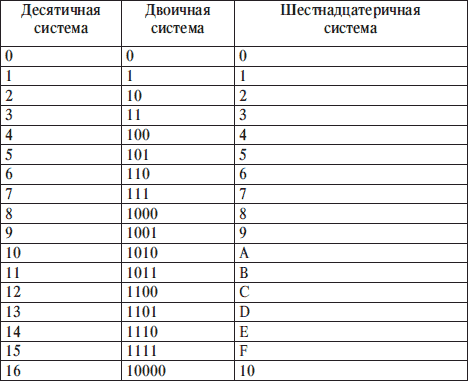 Двоичное число состоит только из 0 и 1. Это единственные две используемые цифры, и их комбинация по-разному используется для формирования разных значений/чисел.

Пример:

101 — трехбитное двоичное число

10100 — пятибитное двоичное число

Сколько значений может быть представлено трехзначным двоичным числом?

Трехзначный двоичный код просто означает расположение трех нулей и единиц всеми возможными способами для образования различных значений, например, 000, 001, 011, 100 и т. д. Поскольку цифр три, максимальное число способов их можно расположить так: 2 ³, что равно 8. Следовательно, это дает числа от 0 до 7. Ниже приведен способ определения числа на основе трехзначного двоичного числа, цифра единицы представляет 2 ⁰ x , the tens digit represents 2 ¹ x, the hundredth base represents 2 ² x, where x= 0 or 1.

Base 2 ² 2 ¹ 2 ⁰

Values  4 2 1

0 0 0 0

1 0 0 1

2 0 1 0

3 0 1 1

4 1 0 0

5 1 0 1

6 1 1 0

7 1 1 1

Максимальные значения представляют в 3 Дифунном бинарном.

Похожие вопросы

Вопрос 1. Сколько значений можно представить с помощью двузначного двоичного кода?

Решение:

Имеются 4 значения от 0 до 3, которые могут быть представлены двузначным двоичным кодом.

Base 2 ¹ 2 ⁰

Values  2 1

0 0 0

1 0 1

2 1 0

3 1 1

Вопрос 2: Сколько значений может быть представлено четырехзначным двоичным кодом?