Число 256, 0x000100, двести пятьдесят шесть
Энциклопедия чисел
Свойства натурального числа 256, 0x000100, 0x100:
Системы счисления Основные свойства Степени, корни
Тригонометрия Хэши, криптография Языки программирования
Дата и время Цвет по числу Интернет
Другие свойства
Рейтинг 9.1 из 10, оценок: 12.
Системы счисления, перевод в систему счисления
Десятичное число 256
- 256 в шестнадцатеричной системе счисления
- 100
- 256 в двоичной системе счисления
- 100000000
- 256 в восьмеричной системе счисления
- 400
Шестнадцатеричное число 100
- 100 в десятичной системе
- 256
- 100 в двоичной системе
- 100000000
- 100 в восьмеричной системе
- 400
Двоичное число 100000000
- 100000000 в десятичной системе
- 256
- 100000000 в шестнадцатеричной системе
- 100
- 100000000 в восьмеричной системе
- 400
Восьмеричное число 400
- 400 в десятичной системе
- 256
- 400 в шестнадцатеричной системе
- 100
- 400 в двоичной системе
- 100000000
Основные арифметические и алгебраические свойства
- Число 256 на русском языке, number in Russian, число 256 прописью:
- двести пятьдесят шесть
- Четность
- Четное число 256
- Разложение на множители, делители числа 256
- 2, 2, 2, 2, 2, 2, 2, 2, 1
- Простое или составное число
- Составное число 256
- Числа делящиеся на целое число 256
- 512, 768, 1024, 1280, 1536, 1792, 2048, 2304
- Число 256 умноженное на число два
- 512
- 256 деленное на число 2
- 128
- Список 8-ми простых чисел перед числом
- 251, 241, 239, 233, 229, 227, 223, 211
- Сумма десятичных цифр
- 13
- Количество цифр
- 3
- Десятичный логарифм 256
- 2.
 4082399653118
4082399653118
- Натуральный логарифм 256
- 5.5451774444796
- Это число Фибоначчи?
- Нет
- Число на 1 больше числа 256,
следующее число - число 257
- Число на 1 больше числа 256,
- Число на 1 меньше числа 256,
предыдущее число - 255
- Число на 1 меньше числа 256,
Степени числа, корни
- 256 во второй степени (в квадрате)
(функция x в степени 2 — x²) - 65536
- 256 во второй степени (в квадрате)
- В третьей степени (в кубе, 256 в степени 3, x³) равно
- 16777216
- Корень квадратный из 256
- 16
- Корень кубический из числа 256 =
- 6.3496042078728
Тригонометрические функции, тригонометрия
- Синус, sin 256 градусов, sin 256°
- -0.9702957263
- Косинус, cos 256 градусов, cos 256°
- -0.2419218956
- Тангенс, tg 256 градусов, tg 256°
- 4.
 0107809335
0107809335
- Синус, sin 256 радиан
- -0.99920803410706
- Косинус, cos 256 радиан
- -0.039790759931158
- Тангенс, tg 256 радиан равно
- 25.111559463448
- 256 градусов, 256° =
- 4.4680428851055 радиан
- 256 радиан =
- 14667.719555349 градуса, 14667.719555349°
Контрольные суммы, хэши, криптография
- MD-5 хэш(256)
- f718499c1c8cef6730f9fd03c8125cab
- CRC-32, CRC32(256)
- 3039150019
- SHA-256 hash, SHA256(256)
- 51e8ea280b44e16934d4d611901f3d3afc41789840acdff81942c2f65009cd52
- SHA1, SHA-1(256)
- dd7c1a3d9d5627da9aea5415e3d07202bfb5925e
- ГОСТ Р 34.11, GOST R 34.11-94, GOST(256)
- e7cdefcd759f89e6b7d9518b022d51eb256d1e2cc03082b8416f1304a89591be
- Base64
- MjU2
Языки программирования
- C++, CPP, C значение 256
- 0x000100, 0x100
- Delphi, Pascal значение числа 256
- $000100
Дата и время
- 256-й день года
- 13 сентября
- 256-й день високосного года
- 12 сентября
- Конвертация UNIX timestamp 256 в дату и время
- UTC
- в Москве, Россия
- в Лондоне, Великобритания
- в Нью-Йорке, США
Интернет
- Конвертация в IPv4 адрес Интернет
- 0.0.1.0
- 256 в Википедии:
- 256
Другие свойства числа
- Короткая ссылка на эту страницу, DEC
- https://bikubik.com/ru/256
- Короткая ссылка на эту страницу, HEX
- https://bikubik.com/ru/x100
- Номер телефона
- 2-56
- Телефонный код страны
- +256 Уганда
Цвет по числу 256, цветовая гамма
- html RGB цвет 256, 16-ричное значение
- #000100 — (0, 1, 0)
- HTML CSS код цвета #000100
- .
 color-mn { color: #000100; }
color-mn { color: #000100; }
.color-bg { background-color: #000100; }
Цвет для данного числа 256
Здесь вы можете изменить составляющую цвета для данного числа 256 или цвета 000100:
256 Из 10 в 8 систему счисления — ПК портал
Содержание
- Восьмеричная 256 во всех системах счисления
- О восьмеричной системе
- Предупреждение
- Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
- Перевод чисел из одной системы счисления в другую
- Перевод чисел из любой системы счисления в десятичную систему счисления
- Перевод чисел из десятичной системы счисления в другую систему счисления
Цифры в различных системах счисления
Шестнадцатеричная система — 100.
Двоичная система — 100000000.
Посмотрите так же как пишутся десятичные цифры 67, 15, 52, 206, 649, 235, 194, 410, 3264, 3166, 4257, 22412, 38348, 53558, 847368 в различных системах счисления.
Число 256 в других системах счисления:
2 — 100000000, 3 — 100111, 4 — 10000, 5 — 2011, 6 — 1104, 7 — 514, 8 — 400, 9 — 314, 10 — 256, 11 — 213, 12 — 194, 13 — 169, 14 — 144, 15 — 121, 16 — 100, 17 — f1, 18 — e4, 19 — d9, 20 — cg, 21 — c4, 22 — be, 23 — b3, 24 — ag, 25 — a6, 26 — 9m, 27 — 9d, 28 — 94, 29 — 8o, 30 — 8g, 31 — 88, 32 — 80.
Восьмеричная 256 во всех системах счисления
О восьмеричной системе
Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных.
Восьмеричная система применяется при выставлении прав доступа к файлам и прав исполнения для участников в Linux-системах.
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую.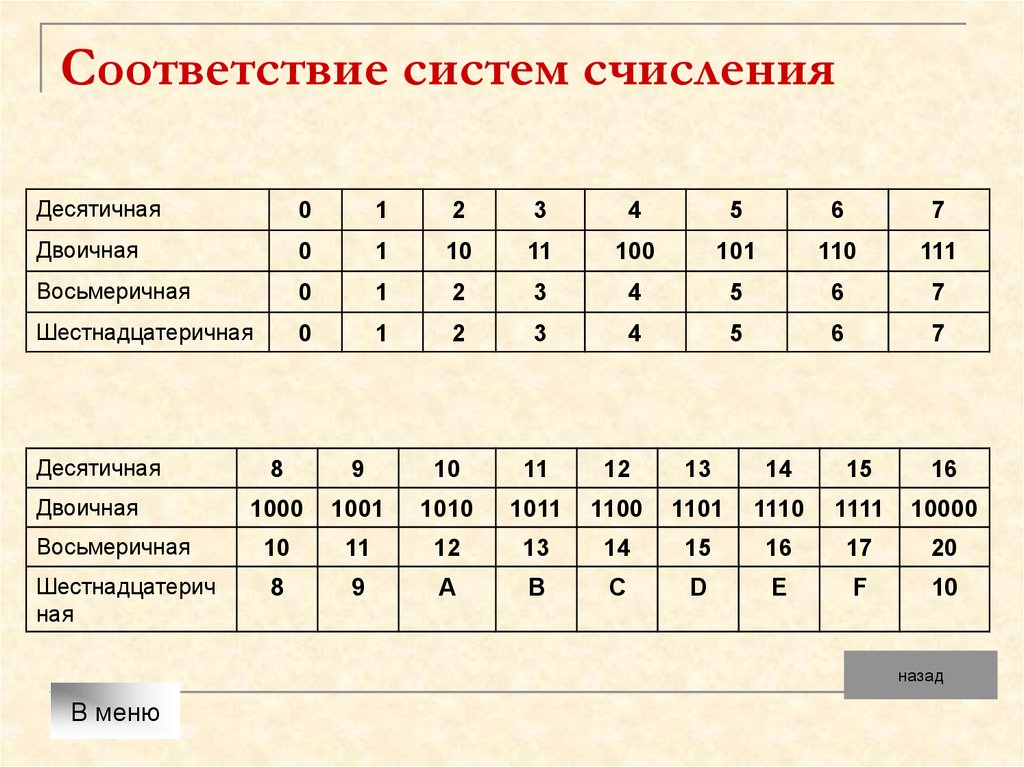 Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 | 0 |
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
где Цn-целое число в позиции n, Д-k— дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр <0,1,2,3,4,5,6,7,8,9>, в восьмеричной системе счисления — из множества цифр <0,1,2,3,4,5,6,7>, в двоичной системе счисления — из множества цифр <0,1>, в шестнадцатеричной системе счисления — из множества цифр <0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F>, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.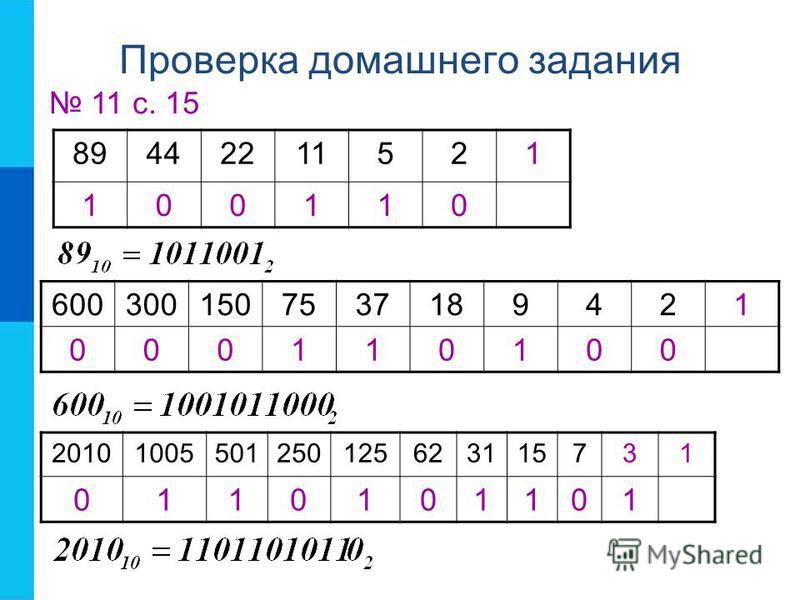
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.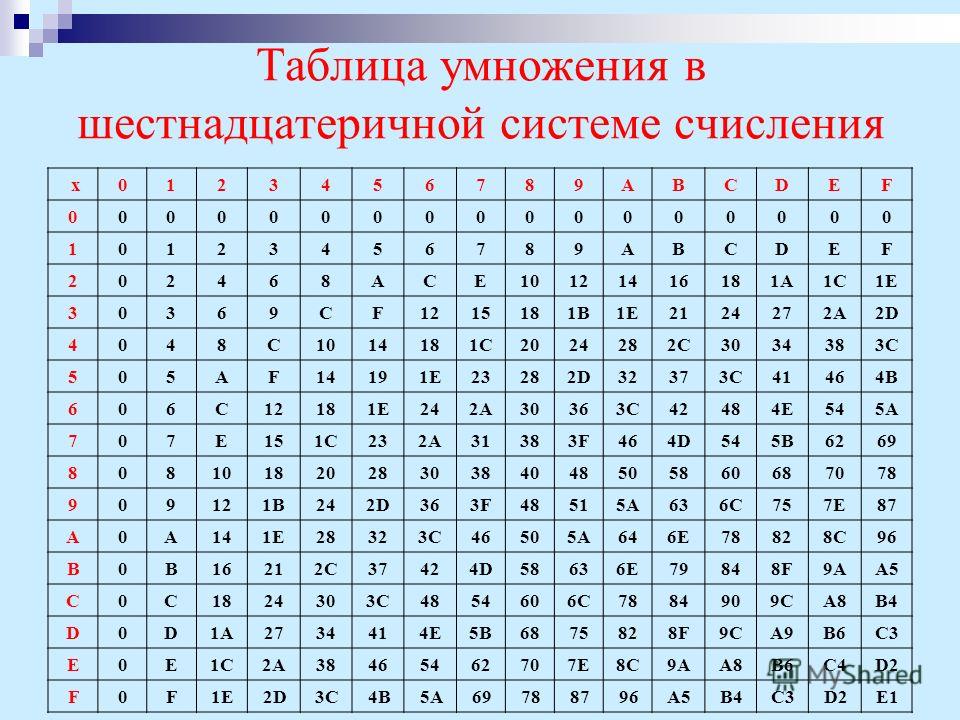
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1·2 6 + 0 ·2 5 + 1·2 4 + 1·2 3 + 1·2 2 + 0·2 1 + 1·2 0 + 0·2 -1 + 0·2 -2 + 1·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C- на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т. д.) до получения целого остатка, меньше, чем основание СС.
д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||
| 158 | 79 | 2 | |
| 1 | 78 | 39 | 2 |
| 1 | 38 | 19 | 2 |
| 1 | 18 | 9 | 2 |
| 1 | 8 | 4 | 2 |
| 1 | 4 | 2 | 2 |
| 0 | 2 | 1 | |
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов.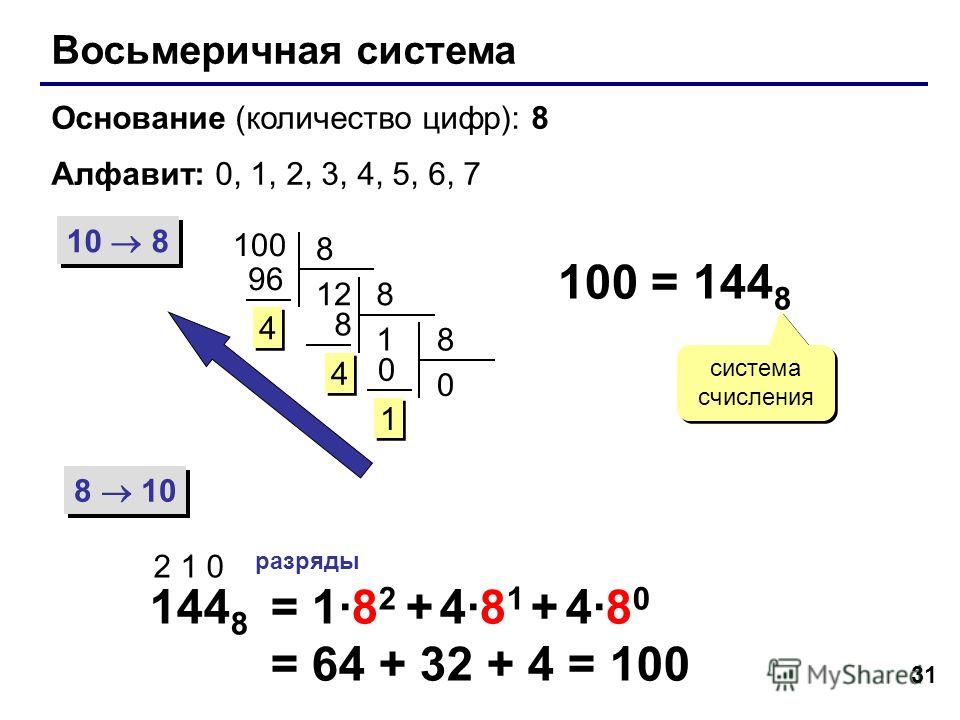 Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7. Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | |
| x | 2 |
| 0 | 0.428 |
| x | 2 |
| 0 | 0.856 |
| x | 2 |
| 1 | 0.712 |
| x | 2 |
| 1 | 0.424 |
| x | 2 |
| 0 | 0.848 |
| x | 2 |
| 1 | 0.696 |
| x | 2 |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0. 0011011.
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0. 0011011.
Следовательно можно записать:
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | |
| x | 2 |
| 0 | 0.25 |
| x | 2 |
| 0 | 0.5 |
| x | 2 |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
0. 214 214 | |
| x | 16 |
| 3 | 0.424 |
| x | 16 |
| 6 | 0.784 |
| x | 16 |
| 12 | 0.544 |
| x | 16 |
| 8 | 0.704 |
| x | 16 |
| 11 | 0.264 |
| x | 16 |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | |
| x | 8 |
| 4 | 0.096 |
| x | 8 |
| 0 | 0.768 |
| x | 8 |
| 6 | 0.144 |
| x | 8 |
| 1 | 0.152 |
| x | 8 |
| 1 | 0. 216 216 |
| x | 8 |
| 1 | 0.728 |
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
Способы перевода чисел из одной системы счисления в другую
Способы перевода чисел из одной системы счисления в другуюПроблема перевода из одной системы
счисления в другую очень часто встречается
при программировании. Например, при
определении адреса ячейки памяти, для
получения двоичного или
шестнадцатеричного эквивалентов
десятичного числа. Иногда встает проблема
увеличения скорости вычислений, и тогда
приходит на помощь двоичная система
счисления. В этой системе счисления очень
быстро производить операцию умножения
путем сдвига одного из операндов в двоичном
виде влево на такое число позиций, в которой
стоит единица во втором операнде.
В этой системе счисления очень
быстро производить операцию умножения
путем сдвига одного из операндов в двоичном
виде влево на такое число позиций, в которой
стоит единица во втором операнде.
Что касается применения шестнадцатеричной системы счисления, то здесь тоже большие возможности. Во-первых, некоторые стандартные процедуры Паскаля и Си требуют задачи параметров в шестнадцатеричной системе, а во-вторых, такая система счисления очень удобна для хранения информации, так как число в шестнадцатеричном виде занимает меньше объема диска, чем то же число в десятичном, а тем более в двоичном виде.
Таким образом мы убедились, что проблема перевода из двоичной системы счисления в десятичную, из шестнадцатеричной в десятичную и обратно очень актуальна.
Наиболее часто встречающиеся системы
счисления это двоичная, шестнадцатеричная
и десятичная. Итак, наша задача -
осуществить перевод из двоичной системы
счисления в десятичную и шестнадцатеричную,
из десятичной в двоичную и
шестнадцатеричную и из шестнадцатеричной в
двоичную и десятичную, т. е. взаимно
связать все эти три системы счисления.
е. взаимно
связать все эти три системы счисления.
Как же на практике осуществляется перевод
из одной системы счисления в другую?
Попробуем разобраться. Допустим, нам нужно
перевести число 567 десятичной системы в
двоичную систему. Делается это следующим
образом: отыскивается максимальная степень
двойки, чтобы два в этой степени было меньше
или равно исходному числу. В нашем случае
это 9, т.к. 29=512, а 210=1024, что больше
нашего начального числа. Таким образом, мы
получили число разрядов результата. Оно
равно 9+1=10. Значит результат будет иметь вид
1ххххххххх, где вместо х может стоять 1 или 0.
Найдем вторую цифру результата. Возведем
двойку в степень 9 и вычтем из исходного
числа: 567-29=55. Затем сравниваем с
числом 28=256. Так как 55 меньше 256, то
девятый разряд будет нулем, т.е. результат
уже примет вид 10хххххххх. Рассмотрим
восьмой разряд: 27=128 > 55, значит и
восьмой разряд будет нулем. Т.к. 26=64, то
седьмой разряд равен нулю. Таким образом мы
получили четыре старших разряда и число
примет вид 1000хххххх. Вычисляем 25=32 и
видим, что 32 < 55, значит шестой разряд равен
1 (результат 10001ххххх), остаток 55-32=23. 24=16
< 23 — пятый разряд 1 => 100011хххх. Остаток
23-16=7. 23=8 > 7 => 1000110ххх. 22=4 < 7
=> 10001101хх, остаток 3. 21=2 < 3 => 100011011х,
остаток 1. 20=1 => 1000110111. Мы получили
конечный результат.
Т.к. 26=64, то
седьмой разряд равен нулю. Таким образом мы
получили четыре старших разряда и число
примет вид 1000хххххх. Вычисляем 25=32 и
видим, что 32 < 55, значит шестой разряд равен
1 (результат 10001ххххх), остаток 55-32=23. 24=16
< 23 — пятый разряд 1 => 100011хххх. Остаток
23-16=7. 23=8 > 7 => 1000110ххх. 22=4 < 7
=> 10001101хх, остаток 3. 21=2 < 3 => 100011011х,
остаток 1. 20=1 => 1000110111. Мы получили
конечный результат.
При другом способом перевода из
десятичной системы в двоичную используется
деление в столбик. Рассмотрим то же самое
число 567. Разделив его на 2, получим частное
283 и остаток 1. Проведем ту же самую операцию
с числом 283. Получим частное 141, остаток 1.
Опять делим полученное частное на 2, и так до
тех пор, пока в качестве частного не получим
1. Теперь, для того чтобы получить число в
двоичной системе счисления, достаточно
записать последнее частное, то есть 1, и
приписать к нему в обратном порядке все
полученные в процессе деления остатки.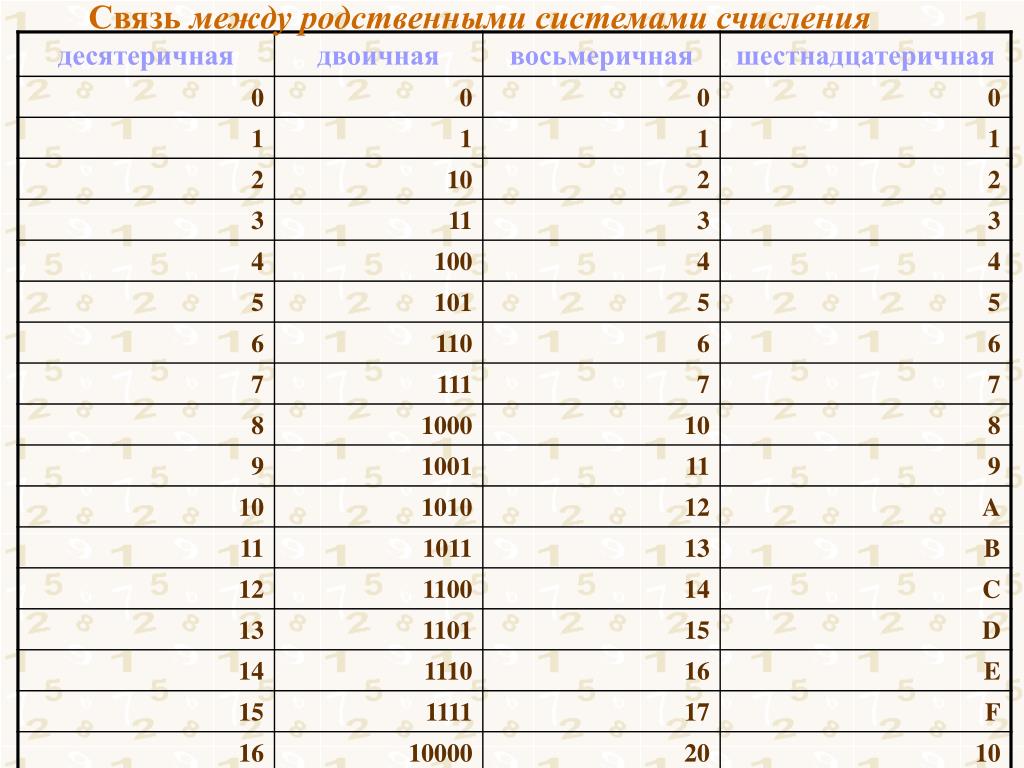
Таким образом, также получили, что 567 в двоичной системе счисления 1000110111.
Теперь попробуем перевести то же число 567,
но уже в шестнадцатеричную систему. Подход
примерно такой же. Определим максимальный
разряд. Так как 162=256 < 567, а 163=4096
> 567, то максимальный разряд 2+1=3. Определим
число, которое будет стоять в третьем
разряде. Ищется максимальный множитель в
пределах от 1 до 15, чтобы текущая степень
шестнадцати, умноженная на этот множитель,
была меньше или равнялась исходному числу (а
в дальнейшем — остатку). В нашем примере этот
множитель 2, т.к. 256*2=512 < 567, а 256*3=768 > 567.
Значит старший разряд нашего результата
будет равен 2, и результат примет вид 2хх, где
вместо х могут стоять любые цифры или буквы
из нижеперечисленных: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C,
D, E, F. Вычисляем остаток: 567-2*162=55. Определим, что будет стоять во втором
разряде. Так как 3*161=48 < 55, а 4*161=64
> 55, то во втором разряде будет стоять
цифра 3. Остаток = 55-3*161=7. Определяем
первый разряд: т.к. 160=1, то цифра
первого разряда равна остатку, т.е. 7. Таким
образом, мы получили число 237, но уже в
шестнадцатеричной системе счисления.
Определим, что будет стоять во втором
разряде. Так как 3*161=48 < 55, а 4*161=64
> 55, то во втором разряде будет стоять
цифра 3. Остаток = 55-3*161=7. Определяем
первый разряд: т.к. 160=1, то цифра
первого разряда равна остатку, т.е. 7. Таким
образом, мы получили число 237, но уже в
шестнадцатеричной системе счисления.
Здесь, так же, как и при переводе в двоичную систему, можно использовать деление в столбик, с той лишь разницей, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16. Конечно, не надо забывать и о том, что при записи числа в шестнадцатеричной системе счисления, надо будет заменить 10 на A, 11 на B и так далее.
Операция перевода в десятичную систему
выглядит гораздо проще, так как любое
десятичное число можно представить в виде x
= a0*pn + a1 * pn-1 + . .. + an-1*p1
+ an*p0, где a0 .. an — это
цифры данного числа в системе счисления с
основанием p.
.. + an-1*p1
+ an*p0, где a0 .. an — это
цифры данного числа в системе счисления с
основанием p.
Пример
Допустим нам нужно перевести число 4A3F в
десятичную систему.
Берем старший (4-й) разряд и возводим 16 в
степень 4-1=3, получаем 163=4096. Полученный
результат умножаем на значение четвертого
разряда, т.е. 4. Получается 4096*4=16384. Этот
результат мы заносим в сумму. Переходим к
следующему разряду: 162=256. 256 нужно
умножить на значение третьего разряда, т.е. A.
Как известно, в шестнадцатеричной системе
счисления буквы от A до F символизируют
числа от 10 до 15 ( A=10, B=11, C=12, D=13, E=14, F=15). Умножив
256 на 10, получим 2560, и этот результат
добавляем к сумме, в которой у нас пока было
16384. У нас получилось 18944. Переходим ко
второму разряду: 3*161=48, добавив это в
сумму получим 18992. И последний разряд: 15*160=15.
Конечная сумма равна 19007. Мы получили
результат в десятичной системе счисления.
И последний разряд: 15*160=15.
Конечная сумма равна 19007. Мы получили
результат в десятичной системе счисления.
Таким образом, мы рассмотрели, как осуществляется перевод чисел из двоичной, десятичной и шестнадцатеричной систем. Перевод из одних систем счисления и в другие осуществляется аналогичным способом.
Упражнение 1
Переведите в десятичную систему счисления:
100011102 = ?
123457 = ?
AA02D34B16 = ?
101010102 = ?
435267 = ?
CCCF2AFB16 = ?
110010112 = ?
535027 = ?
1010101016 = ?
Упражнение 2
Сравните два числа:
| 526379 | 526378 |
| 111112 | 111113 |
| 3627a16 | 6673bd18 |
| 10268 | 21616 |
Применительно к компьютерной информации
часто используются системы с основанием 2, 8
и 16. Рассмотрим таблицы, отражающие связь
между двоичной и восьмеричной и двоичной и
шестнадцатеричной системами.
Рассмотрим таблицы, отражающие связь
между двоичной и восьмеричной и двоичной и
шестнадцатеричной системами.
| 2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
|---|---|---|---|---|---|---|---|---|
| 16-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2-ная | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16-ная | 8 | 9 | A | B | C | D | E | F |
| 2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
|---|---|---|---|---|---|---|---|---|
| 8-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Содержание
Цвета | htmlbook.
 ru
ruДля задания цветов на веб-странице применяется три способа: первый использует обозначения цветов в шестнадцатеричном коде, второй — десятичном, а третий — по названию некоторых цветов. Преимущественно используется способ, основанный на шестнадцатеричной системе исчисления, как наиболее универсальный. Десятичная система, хотя и более привычна для представления, находит применение только с помощью CSS.
Шестнадцатеричные цвета
Для задания цветов в HTML используются числа в шестнадцатеричном коде. Шестнадцатеричная система, в отличие от десятичной системы, базируется, как следует из ее названия, на числе 16. Цифры будут следующие: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Цифры от 10 до 15 заменены латинскими буквами. В табл. 1 приведено соответствие десятичных и шестнадцатеричных чисел.
| Десятичные | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричные | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Числа больше 15 в шестнадцатеричной системе образуются объединением двух чисел
в одно. Например, числу 255 в десятичной системе соответствует число FF в шестнадцатеричной
(табл. 2).
Например, числу 255 в десятичной системе соответствует число FF в шестнадцатеричной
(табл. 2).
| Десятичные | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричные | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E | 1F |
Чтобы не возникало путаницы в определении системы счисления, перед шестнадцатеричным числом ставят символ решетки #, например #666999.
Типичный цвет, используемый в HTML, выглядит следующим образом.
<body bgcolor="#FA8E47">
Цвет фона задан как #FA8E47. Символ решетки # перед
числом означает, что оно шестнадцатеричное. Первые две цифры (FA) определяют
красную составляющую цвета, цифры с третьей по четвертую (8E) —
зеленую, а последние две цифры (47) — синюю. В итоге получится
такой цвет.
В итоге получится
такой цвет.
| FA | + | 8E | + | 47 | = | FA8E47 |
Каждый из трех цветов — красный, зеленый и синий — может принимать значения от 00 до FF, что в итоге образует 256 оттенков. Таким образом, в модели RGB количество цветом может быть 256 х 256 х 256 = 16.777.216 комбинаций.
Веб-цвета
Если установить качество цветопередачи монитора в 8 бит (256 цветов), то один
и тот же цвет может показываться в разных браузерах по-своему. Это связано со
способом отображения графики, когда браузер работает со своей собственной палитрой
и не может показать цвет, который у него в палитре отсутствует. В этом случае
цвет заменяется сочетанием пикселей других, близких к нему, цветов, имитирующих
заданный. Чтобы цвет оставался неизменным в разных браузерах, ввели палитру,
так называемых, веб-цветов. Веб-цветами называются такие цвета, для каждой составляющей которых — красной, зелёной и синей — устанавливается одно из шести значений —
0 (00), 51 (33), 102 (66), 153 (99), 204 (CC), 255 (FF). В скобках указано шестнадцатеричное
значение данной компоненты. Общее количество цветов из всех возможных сочетаний
дает 6х6х6 — 216 цветов. Пример веб-цвета — #33FF66.
В скобках указано шестнадцатеричное
значение данной компоненты. Общее количество цветов из всех возможных сочетаний
дает 6х6х6 — 216 цветов. Пример веб-цвета — #33FF66.
Основная особенность веб-цвета заключается в том, что он показывается одинаково во всех браузерах. В данный момент актуальность веб-цветов весьма мала из-за повышения качества мониторов и расширения их возможностей.
Названия цветов
Чтобы не запоминать совокупность цифр, вместо них можно использовать имена широко используемых цветов.
<body bgcolor="navy">
Ниже в таблице приведены 16 основных названий цветов, используемых во всех браузерах.
| Название | Цвет | Hex | Красный (R) | Зеленый (G) | Синий (B) |
|---|---|---|---|---|---|
| aqua | #00FFFF | 00 | 255 | 255 | |
| black | #000000 | 00 | 00 | 00 | |
| blue | #0000FF | 00 | 00 | 255 | |
| fuchsia | #FF00FF | 255 | 00 | 255 | |
| gray | #808080 | 128 | 128 | 128 | |
| green | #008000 | 00 | 128 | 00 | |
| lime | #00FF00 | 00 | 255 | 00 | |
| maroon | #800000 | 128 | 00 | 00 | |
| navy | #000080 | 00 | 00 | 128 | |
| olive | #808000 | 128 | 128 | 00 | |
| purple | #800080 | 128 | 00 | 128 | |
| red | #FF0000 | 255 | 00 | 00 | |
| silver | #C0C0C0 | 192 | 192 | 192 | |
| teal | #008080 | 00 | 128 | 128 | |
| white | #FFFFFF | 255 | 255 | 255 | |
| yellow | #FFFF00 | 255 | 255 | 00 |
цвет
Глава 15 Байты и шестнадцатеричные числа .
 Код. Тайный язык информатики
Код. Тайный язык информатикиДве усовершенствованные счетные машины, описанные в предыдущей главе, хорошо иллюстрируют концепцию потоков данных. Восьмибитные значения перемещаются по цепи от одного компонента к другому. Эти значения подаются на входы сумматоров, защелок и селекторов, а также появляются на выходах этих устройств. Кроме того, 8-битные значения задаются с помощью переключателей и отображаются рядом лампочек. Таким образом, поток данных в этих схемах имеет ширину восемь бит. Но почему? Почему не шесть, не семь, не девять и не десять?
Можно было бы ответить, что основой наших усовершенствованных счетных машин является исходный сумматор из главы 12, работающий с 8-битными значениями. Однако нет никаких особых причин конструировать эту машину именно так. Просто при ее создании мы сочли эту величину удобной. Как бы то ни было, признаю, что схитрил, поскольку с самого начала знал (возможно, и вы тоже), что восемь бит данных соответствуют одному байту.
Слово «байт» (byte) возникло в компании IBM примерно в 1956 году. Оно произошло от слова bite («кусок»), но его было решено писать через букву y, чтобы не путать со словом bit («бит»). В течение некоторого времени слово «байт» обозначало просто число битов в конкретном потоке данных. Однако в середине 1960-х, в связи с разработкой семейства компьютеров System/360 в компании IBM, это слово стало обозначать группу из восьми бит.
Как 8-разрядное число, байт может принимать значения в диапазоне от 00000000 до 11111111. Эти значения могут описывать положительные целые числа от 0 до 255, а при использовании дополнения до двойки для представления отрицательных чисел они могут отображать как положительные, так и отрицательные целые числа в диапазоне от ?128 до 127. Кроме того, конкретный байт может просто представлять одну из 28, или 256, разных вещей.
Число 8 оказалось весьма удобной величиной. Компания IBM отдала предпочтение 8-битным байтам в связи с простотой хранения чисел в формате BCD (о котором я расскажу в главе 23). Однако, как мы увидим далее, байт идеально подходит для хранения текста, поскольку большую часть языков мира (за исключением идеограмм, использующихся в китайском, японском и корейском) можно представить менее чем 256 символами. Кроме того, байт идеально подходит для представления оттенков серого на черно-белых фотографиях, поскольку человеческий глаз различает примерно 256 оттенков этого цвета. А там, где не хватает одного байта (например, для представления вышеупомянутых идеограмм китайского, японского и корейского языков), как правило, можно использовать два байта, которые позволяют выразить 216, или 65 536, различных элементов.
Однако, как мы увидим далее, байт идеально подходит для хранения текста, поскольку большую часть языков мира (за исключением идеограмм, использующихся в китайском, японском и корейском) можно представить менее чем 256 символами. Кроме того, байт идеально подходит для представления оттенков серого на черно-белых фотографиях, поскольку человеческий глаз различает примерно 256 оттенков этого цвета. А там, где не хватает одного байта (например, для представления вышеупомянутых идеограмм китайского, японского и корейского языков), как правило, можно использовать два байта, которые позволяют выразить 216, или 65 536, различных элементов.
Половина байта, то есть четыре бита, иногда называется тетрадой, однако это слово употребляется гораздо реже, чем «байт».
Поскольку байты часто используются при описании работы компьютеров, нам требуется как можно более лаконичный способ записи их значения. Например, запись числа, состоящего из восьми двоичных цифр 10110110, безусловно, является корректной, но едва ли лаконичной.
Разумеется, мы всегда можем обращаться к байтам, используя их десятичные эквиваленты, но это потребует преобразования двоичного числа в десятичное, что хоть и несложно, но весьма обременительно. В главе 8 я продемонстрировал один довольно простой подход. Поскольку каждая двоичная цифра соответствует степени 2, мы можем просто записать цифры двоичного числа, а под ними — степени 2, после чего перемножить числа в каждом столбце и сложить результаты. Далее представлен процесс преобразования числа 10110110.
Процесс преобразования десятичного числа в двоичное менее удобен и предполагает деление десятичного числа на убывающие степени двойки. Частное от каждого деления — двоичная цифра, а остаток делится на следующую в порядке убывания степень двойки. Вот как десятичное число 182 преобразуется в двоичное.
В главе 8 эта техника описана подробно. Тем не менее для преобразования двоичных чисел в десятичные и обратно обычно требуется бумага, карандаш и практика.
Мы уже узнали о восьмеричной системе счисления — системе счисления с основанием 8, где используются только цифры 0, 1, 2, 3, 4, 5, 6 и 7. Преобразовать восьмеричное число в двоичное легко. Все, что нужно, — это запомнить 3-битный эквивалент каждой восьмеричной цифры.
Двоичное число
Восьмеричное число
000
0
001
1
010
2
011
3
100
4
101
5
110
6
111
7
Если у вас есть двоичное число (например, 10110110), начинайте преобразование с правого края. Каждая группа из трех бит соответствует восьмеричной цифре.
Таким образом, байт 10110110 можно выразить в виде восьмеричного числа 266. Это выражение, безусловно, является более лаконичным, значит, восьмеричная система действительно подходит для представления байтов. Однако у нее есть небольшой недостаток.
Однако у нее есть небольшой недостаток.
В двоичной системе байты выражаются значениями в диапазоне от 00000000 до 11111111, в восьмеричной — значениями в диапазоне от 000 до 377. Как было показано в предыдущем примере, средней и крайней справа восьмеричным цифрам соответствуют группы из трех бит, однако крайней слева восьмеричной цифре соответствуют только два бита. Это означает, что восьмеричное представление 16-разрядного числа не совпадает с восьмеричными представлениями двух байтов, составляющих это 16-разрядное число.
Чтобы согласовать представления многобайтных значений с представлениями отдельных байтов, нужна система, в которой каждый байт делится на равное количество битов. Следовательно, нам требуется разделить каждый байт на четыре значения по два бита каждое (система счисления с основанием 4) или на два значения по четыре бита каждое (система счисления с основанием 16).
Систему счисления с основанием 16 мы еще не рассматривали, и на то есть причины. Система счисления с основанием 16 называется шестнадцатеричной[18], — даже название труднопроизносимо. В десятичной системе счисления считаем так:
Система счисления с основанием 16 называется шестнадцатеричной[18], — даже название труднопроизносимо. В десятичной системе счисления считаем так:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
В восьмеричной системе, как вы помните, не используются цифры 8 и 9:
0 1 2 3 4 5 6 7 10 11 12 …
В системе с основанием 4 не требуются цифры 4, 5, 6 и 7:
0 1 2 3 10 11 12 …
Наконец, в двоичной системе достаточно только 0 и 1:
0 1 10 11 100 …
Однако шестнадцатеричная система отличается тем, что в ней используется больше цифр, чем в десятичной. В шестнадцатеричной системе подсчет происходит примерно так:
0 1 2 3 4 5 6 7 8 9 ? ? ? ? ? ? 10 11 12 …
В данном случае 10 соответствует числу 16ДЕСЯТЬ. Вопросительные знаки говорят о том, что нам нужны еще шесть символов для представления шестнадцатеричных чисел. Что это за символы? Откуда их брать? Что ж, поскольку они не достались нам в наследство, подобно другим традиционным числовым символам, мы можем придумать их самостоятельно, например такие.
В отличие от символов, используемых для обозначения большинства чисел, у этих обозначений есть преимущество: они легко запоминаются и отождествляются с теми величинами, которые представляют. Существует так называемая десятигаллонная ковбойская шляпа, мяч для американского футбола (11 игроков в команде), дюжина пончиков (12 штук), черная кошка (с которой ассоциируется несчастливое число 13), полная луна (появляется на небе через 14 дней после новолуния) и кинжал (напоминающий об убийстве Юлия Цезаря в 15-й день марта). Каждый байт можно выразить в виде двух шестнадцатеричных цифр. Другими словами, шестнадцатеричная цифра эквивалентна четырем битам, или одной тетраде. В следующей таблице показаны соответствия двоичных, шестнадцатеричных и десятичных чисел.
Вот как можно представить двоичное число 10110110 в шестнадцатеричной системе.
И не важно, имеем ли мы дело с многобайтными числами.
Один байт всегда представляется парой шестнадцатеричных цифр.
К сожалению (а может быть, к счастью), мы не собираемся использовать футбольные мячи и пончики для записи шестнадцатеричных чисел, хотя они, безусловно, могли бы сгодиться для этой цели. Вместо них в шестнадцатеричной системе применяются обозначения, приводящие многих в замешательство. Дело в том, что шесть недостающих шестнадцатеричных цифр представляют шестью первыми буквами латинского алфавита:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 …
В следующей таблице показано реальное соответствие между двоичными, шестнадцатеричными и десятичными числами.
Двоичное число
Шестнадцатеричное число
Десятичное число
0000
0
0
0001
1
1
0010
2
2
0011
3
3
0100
4
4
0101
5
5
0110
6
6
0111
7
7
1000
8
8
1001
9
9
1010
A
10
1011
B
11
1100
C
12
1101
D
13
1110
E
14
1111
F
15
Таким образом, двоичное число 10110110 можно представить шестнадцатеричным числом B6, не рисуя футбольный мяч. Как вы помните, в предыдущих главах я указывал основание системы счисления с помощью нижнего индекса, например: 10110110ДВА — для двоичной системы; 2312ЧЕТЫРЕ — для четвертичной; 266ВОСЕМЬ — для восьмеричной; 182ДЕСЯТЬ — для десятичной.
Как вы помните, в предыдущих главах я указывал основание системы счисления с помощью нижнего индекса, например: 10110110ДВА — для двоичной системы; 2312ЧЕТЫРЕ — для четвертичной; 266ВОСЕМЬ — для восьмеричной; 182ДЕСЯТЬ — для десятичной.
По аналогии мы можем использовать обозначение B6ШЕСТНАДЦАТЬ для шестнадцатеричной системы.
Однако такое выражение чересчур громоздко. К счастью, для шестнадцатеричных чисел существуют и другие, более краткие, обозначения. Вы можете записать такое число следующим образом:
B6HEX.
В этой книге я буду использовать распространенный способ представления шестнадцатеричных чисел, предполагающий добавление к числу строчной латинской буквы h:
B6h.
В шестнадцатеричном числе положение каждой цифры соответствует степени числа 16.
Шестнадцатеричное число 9A48Ch можно представить так:
9A48Ch = 9 ? 10000h +
A ? 1000h +
4 ? 100h +
8 ? 10h +
C ? 1h.
Это выражение можно записать, используя степени числа 16:
9A48Ch = 9 ? 164 +
A ? 163 +
4 ? 162 +
8 ? 161 +
C ? 160.
Или десятичные эквиваленты этих степеней:
9A48Ch = 9 ? 65 536 +
A ? 4096 +
4 ? 256 +
8 ? 16 +
C ? 1.
Обратите внимание на отсутствие двусмысленности при записи отдельных цифр числа (9, А, 4, 8 и C) без нижнего индекса, обозначающего основание системы счисления. Девять — это 9, будь то десятичная или шестнадцатеричная система счисления. С другой стороны, А очевидно представляет шестнадцатеричный эквивалент десятичного числа 10.
По сути, преобразование всех цифр в десятичные числа позволяет выполнить расчет итогового значения:
9A48Ch = 9 ? 65 536 +
10 ? 4096 +
4 ? 256 +
8 ? 16 +
12 ? 1.
В итоге получается число 631 948.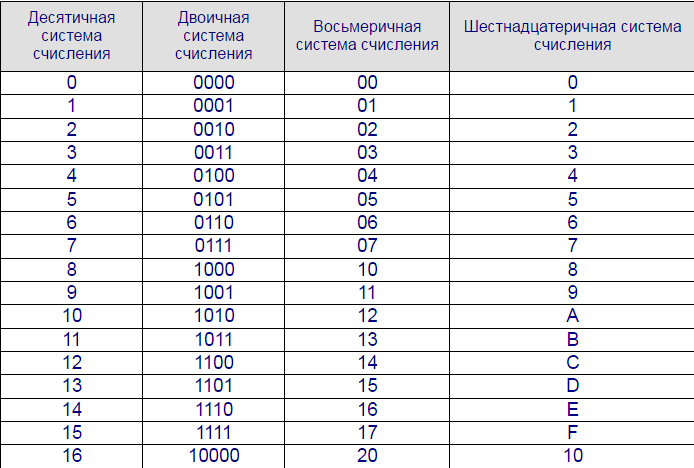 Таким образом шестнадцатеричные числа преобразуются в десятичные.
Таким образом шестнадцатеричные числа преобразуются в десятичные.
Шаблон для преобразования любого четырехзначного шестнадцатеричного числа в десятичное выглядит следующим образом.
В качестве примера преобразуем число 79ACh. Имейте в виду, что шестнадцатеричные цифры A и C эквивалентны десятичным числам 10 и 12.
Преобразование десятичных чисел в шестнадцатеричные обычно предполагает выполнение операций деления. Число меньшее или равное 255 можно представить одним байтом, состоящим из двух шестнадцатеричных цифр. Чтобы вычислить эти две цифры, нужно разделить число на 16, в результате чего получится частное и остаток. Вернемся к примеру с десятичным числом 182. Разделив 182 на 16, получим 11 (что соответствует цифре B в шестнадцатеричной системе) и 6 в остатке. Так, шестнадцатеричным эквивалентом десятичного числа 182 является B6h. Если десятичное число, которое вы хотите преобразовать, меньше 65 536, то шестнадцатеричный эквивалент будет состоять не более чем из четырех цифр. Шаблон для преобразования такого числа в шестнадцатеричное следующий.
Шаблон для преобразования такого числа в шестнадцатеричное следующий.
Сначала поместите десятичное число в верхний левый прямоугольник. Это наше первое делимое. Разделим число на 4096 (первый делитель). Частное впишем в прямоугольник, расположенный под делимым, а остаток — в прямоугольник справа от делимого. Этот остаток — новое делимое, которое мы разделим на 256. Вот как число 31 148 преобразуется в шестнадцатеричный формат.
Десятичные числа 10 и 12 соответствуют шестнадцатеричным цифрам A и C, поэтому результат равен 79ACh.
Одна из проблем этой техники заключается в том, что для деления вы, вероятно, решите использовать калькулятор, а калькуляторы не показывают остаток от деления. Если вы разделите 31 148 на 4096 на калькуляторе, то получите 7,6044921875. Чтобы рассчитать остаток, нужно умножить 4096 на 7 (получится 28 672) и вычесть это значение из 31 148. Или умножить 4096 на 0,6044921875 — дробную часть результата от деления. (Правда, некоторые калькуляторы предусматривают функцию преобразования десятичных чисел в шестнадцатеричные и обратно. )
)
Другой способ преобразования десятичных чисел от 0 до 65 535 в шестнадцатеричные предполагает разделение числа на два байта путем его деления на 256. Затем каждый байт делится на 16. Шаблон для этого следующий.
Начнем сверху. После каждой операции деления частное помещается в прямоугольник, расположенный слева от делителя, а остаток — в прямоугольник справа. Например, число 51 966 преобразуется таким образом.
Шестнадцатеричными эквивалентами чисел 12, 10, 15 и 14 являются буквы С, А, F и Е, поэтому результат скорее напоминает слово, чем число.
Далее представлена таблица сложения для шестнадцатеричной системы счисления.
Используя эту таблицу и обычные правила сложения в столбик, можно складывать шестнадцатеричные числа.
В главе 13 я упоминал, что для представления отрицательных чисел можно применять дополнение до двойки. Если вы имеете дело с 8-битными двоичными числами со знаком, то отрицательные числа начинаются с 1. В шестнадцатеричной системе счисления двузначные числа со знаком отрицательные, если они начинаются с цифр 8, 9, A, B, C, D, E или F, поскольку их двоичные эквиваленты начинаются с 1. Например, число 99h может соответствовать либо десятичному числу 153 (если вы знаете, что имеете дело с однобайтными числами без знака), либо десятичному числу –103 (если вы знаете, что это число со знаком).
В шестнадцатеричной системе счисления двузначные числа со знаком отрицательные, если они начинаются с цифр 8, 9, A, B, C, D, E или F, поскольку их двоичные эквиваленты начинаются с 1. Например, число 99h может соответствовать либо десятичному числу 153 (если вы знаете, что имеете дело с однобайтными числами без знака), либо десятичному числу –103 (если вы знаете, что это число со знаком).
Кроме того, байт 99h может соответствовать и десятичному числу 99. Это интересно, но, похоже, противоречит всему, о чем мы говорили до сих пор. В главе 23 объясню, как это работает, а теперь остановимся на памяти.
2.3.1. Целые числа без знака (unsigned)
Целые
числа без знака используются для
представления только положительных
чисел. Количество двоичных чисел,
которые могут быть представлены с
помощью n-разрядов
равно 2n.
Диапазон представления целых чисел без
знака определяется как 0 … 2n-1,
где n
– длина разрядой сетки.
Табл.2.14. Диапазон целых чисел без знака
Тип данных | Размер n, бит | Диапазон 0 … 2n-1 | |
Dec | Hex | ||
unsigned (short) char | 8 | 0 … 255 | 00 … FF |
unsigned int | 16 | 0 … 65535 | 0000 … FFFF |
unsigned long | 32 | 0 … 4294967295 | 00000000 … FFFFFFFF |
Пример:
Перевести целое десятичное число 12510 в двоичную систему счисления.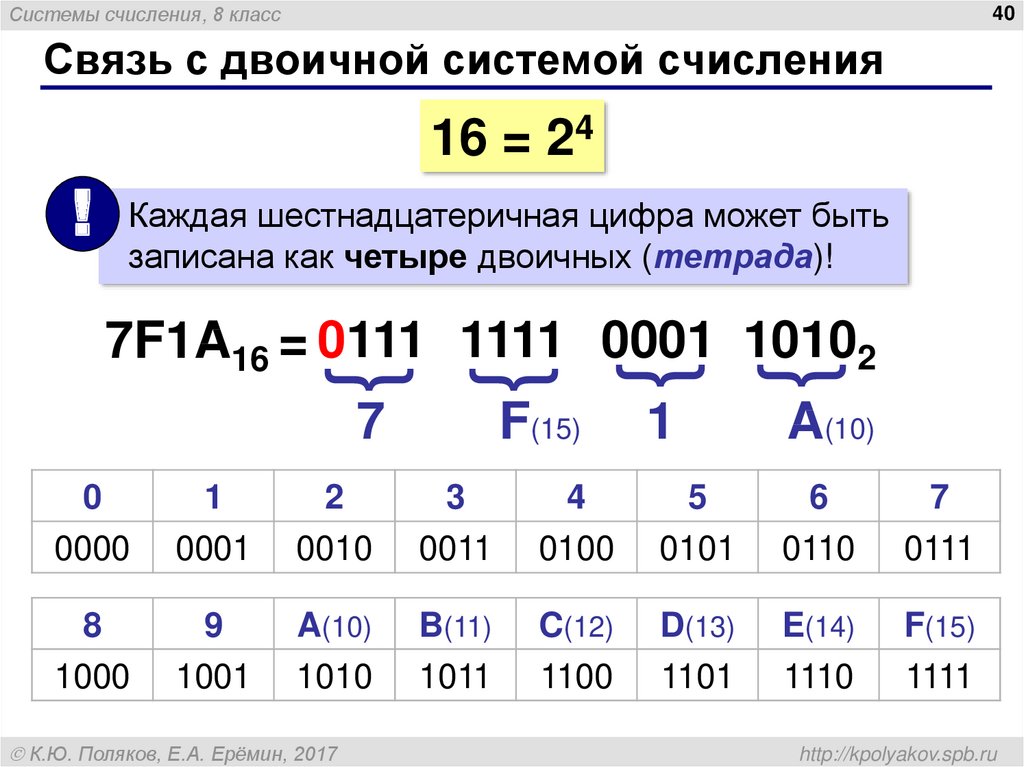 Двоичное
число записать восьмиразрядной и
шестнадцатиразрядной сетках.
Двоичное
число записать восьмиразрядной и
шестнадцатиразрядной сетках.
Перевод числа 12510 = 11111012.
Число 12510 входит в диапазон чисел 0 … 255 и 0 … 65535.
Ответ: 1. Для n=8 число 12510 = 0111 11012; 2. Для n=16 число 12510 = 0000 0000 0111 11012 (здесь и далее в записи двоичного числа используем пробел между тетрадами для контроля разрядности числа).
Пример: Перевести целое десятичное число 25610 в двоичную систему счисления. Двоичное число записать восьмиразрядной и шестнадцатиразрядной сетках.
Перевод числа: 25610 = 1 0000 00002.
Число 25610 не входит в диапазон чисел 0 … 255 и входит в диапазон чисел 0 … 65535.
Ответ:
1. Число 25610 нельзя представить в восьмиразрядной
сетке, т.к. оно не входит в диапазон 0 …
255; 2. Для n=16
число 25610 = 0000 0001 0000 00002.
Для n=16
число 25610 = 0000 0001 0000 00002.
Пример: Определить знак двоичного числа 10000000000000002.
Ответ: Двоичное число является положительным, так как в формате без знака все числа положительные.
Целые числа со знаком используются для представления как положительных, так и отрицательных чисел. Диапазон представления целых чисел со знаком определяется как 2n-1 … 2n-1-1, где n – количество разрядов сетки.
Табл.2.15. Диапазон целых чисел со знаком
Тип данных | Размер n, бит | Диапазон 2n-1 … 2n-1-1 | |
Dec | Hex | ||
signed (short) char | 8 | -128 … +127 | 00 … FF |
signed int | 16 | -32 768 … +32 767 | 0000 … FFFF |
signed long | 32 | -2 147 483 648 … +2 147 483 647 | 8000 0000 … 7FFF FFFF |
Для
изображения знака числа в разрядной
сетке используется старший (левый)
разряд, в котором 0 соответствует
положительному числу, 1
отрицательному. Для восьмиразрядной
сетки знаковым является седьмой разряд,
для шестнадцатиразрядной сетки знаковым
является пятнадцатый разряд.
Для восьмиразрядной
сетки знаковым является седьмой разряд,
для шестнадцатиразрядной сетки знаковым
является пятнадцатый разряд.
Табл. 2.15.1. Положительное двоичное восьмиразрядное число
7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Табл.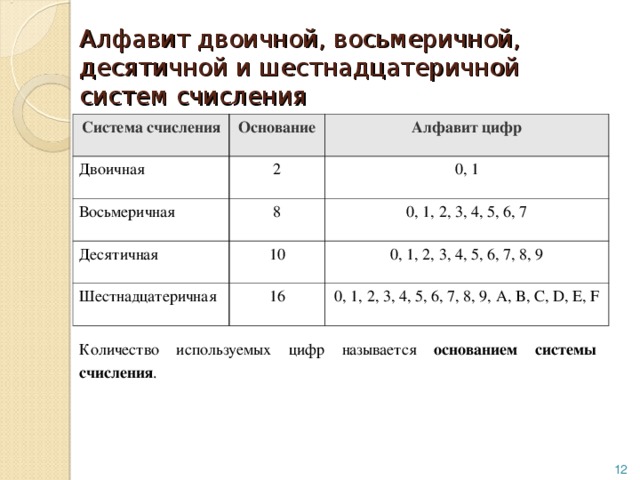 2.15.2. Отрицательное двоичное
восьмиразрядное число
2.15.2. Отрицательное двоичное
восьмиразрядное число
7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Для кодирования чисел со знаком в микропроцессорной технике применяется специальный двоичный дополнительный код, который обладает следующими свойствами:
Дополнительные коды положительных двоичных чисел формата signed определены в диапазоне 0 … 2n-1-1 и совпадают с двоичными кодами чисел формата unsigned, определенных в диапазоне 0 … 2n-1-1.
 Дополнительные коды положительных
двоичных чисел получаются делением на
2.
Дополнительные коды положительных
двоичных чисел получаются делением на
2.Дополнительный код отрицательного двоичного числа определяется двумя способами:
По формуле Х10 = [2n + Х10]2 , где Х10 – отрицательные десятичные числа в диапазоне от (-1) до (-2n/2).
По правилу изменения знака двоичного числа в дополнительном коде:
2.2.1. Записать двоичное число в заданной разрядной сетке.
2.2.2. Заменить в двоичном числе все нули на единицы, а единицы на нули (поразрядная инверсия).
2.2.3. Полученное число сложить с единицей по правилам двоичной арифметики.
Данное правило может применяться для перехода от положительных двоичных чисел к отрицательным числам, и наоборот.
Изменение знака шестнадцатеричного числа выполняется в следующей последовательности:
1.
Выполнить поразрядную инверсию каждого
символа по формуле [24 — 1 — Хi]16.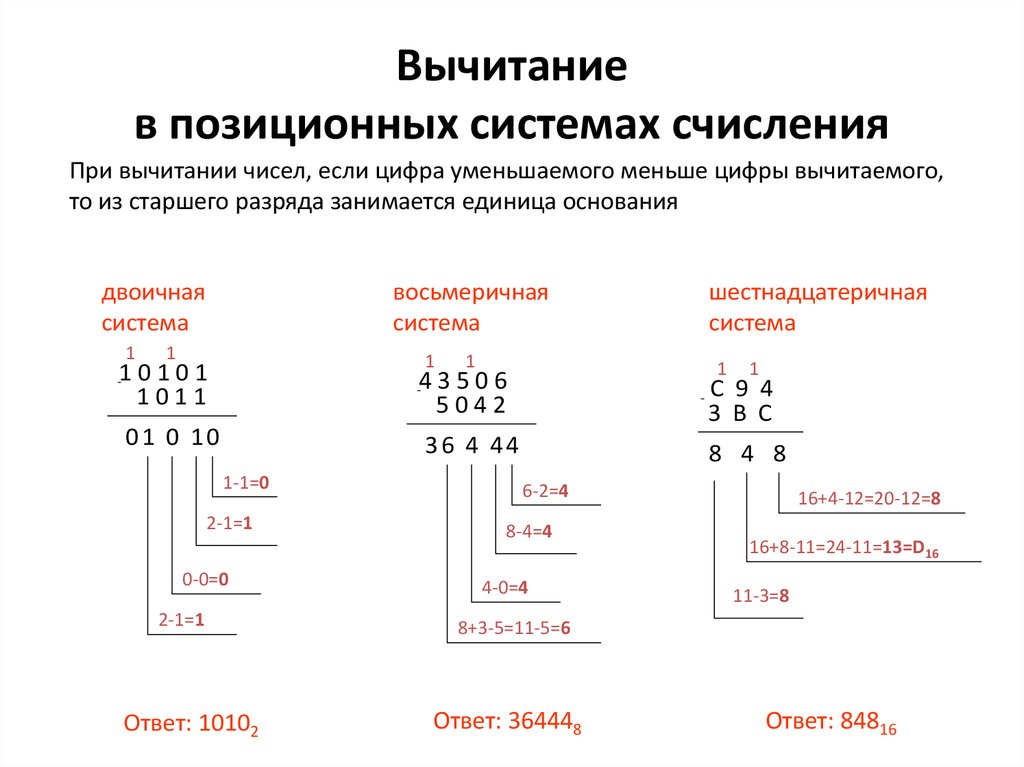
2. Полученное шестнадцатеричное число сложить с единицей по правилам двоичной арифметики .
Способ перевода двоичных чисел со знаком в десятичную систему счисления зависит от знака числа:
1. Целые положительные двоичные числа переводятся по формуле степенного ряда вида:
an-1рn-1 + an-2рn-2 + . . . + a1р1 + a0р0.
2. Целые отрицательные двоичные числа переводятся по формуле степенного ряда вида:
(-an-1)рn-1 + an-2рn-2 + . . . + a1р1 + a0р0, где (n-1) – старший разряд разрядной сетки.
Пример. Представить число +12510 в восьмиразрядной и шестнадцатиразрядной сетках.
Число +12510 входит в диапазон чисел (-128 … +127) и (-32768 … +32767).
Ответ:
1. Для n=8
число 12510 = 0111 11012;
2.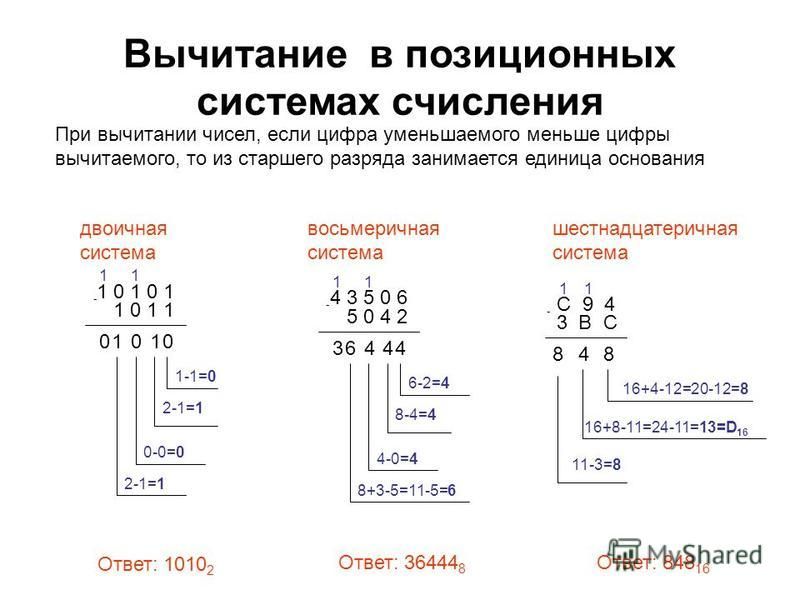 Для n=16
число 12510 = 0000 0000 0111 11012.
Для n=16
число 12510 = 0000 0000 0111 11012.
Пример: Определить знак двоичного числа 0111 11012 в восьмиразрядной сетке.
Число 0111 11012 записано в восьмиразрядной сетке.
Ответ: Число 0111 11012 положительное, т.к. в старшем 7-ом знаковом разряде записан ноль.
Пример: Определить знак двоичного числа 0000 0000 0111 11012 в шестнадцатиразрядной сетке.
Число 0000 0000 0111 11012 записано в шестнадцатиразрядной сетке.
Ответ: Число 0000 0000 0111 11012 положительное, т.к. в старшем 15-ом знаковом разряде записан ноль.
Пример. Представить число -12510 в восьмиразрядной и шестнадцатиразрядной сетках.
Число -12510 входит в диапазон чисел (-128 … +127) и –(32768 … +32767).
Для
n=8
d10 = -12510 =
[28 -12510]2 = [256 -12510]2 =[13110]2 = 100000112.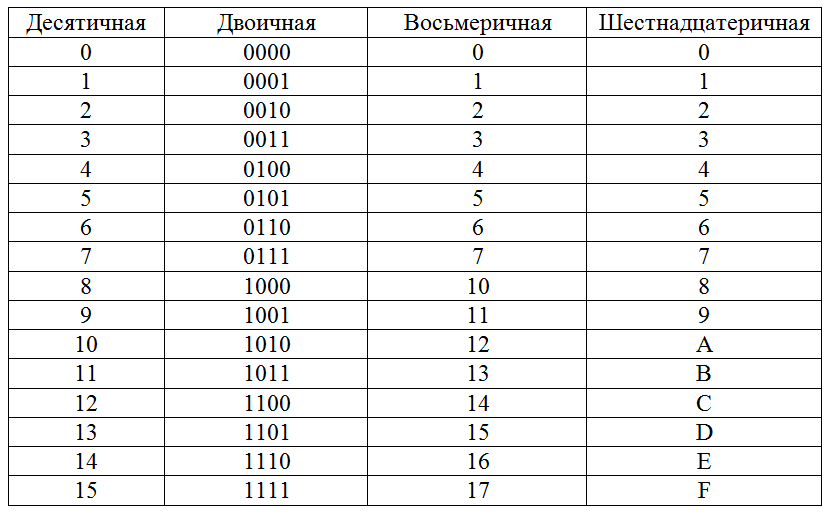
Для n=16 d10 = -12510 = [216 -12510]2 = [65536 -12510]2 =[6541110]2 = 1111 1111 1000 00112.
Ответ: для n=8 -12510 = 1000 00112 ; для n=16 -12510 = 1111 1111 1000 00112.
Пример: Представить двоичное число 0111 11012 в десятичной системе счисления.
Для положительного числа используем формулу:
a7р7 + a6р6 + a5р5 + a4р4 + a3р3 + a2р2 + a1р1 + a0р0 = 0+64+32+16+8+4+0+1 = 12510.
Ответ: число 0111 11012 = +12510.
Пример: Представить двоичное число 0111 11012 в шестнадцатеричной системе счисления.
Ответ: число 0111 11012 = 7D16.
Пример:
Определить знак шестнадцатеричного
числа 7D 16.
Ответ: числа 7D16 положительное, т.к. в старшем разряде числа 7D16 цифра 716 = 01112, старший бит тетрады равен 02, что соответствует знаку плюс.
Пример: Изменить знак двоичного числа 111 11012 и записать число в восьмиразрядной сетке.
1. Записываем 111 11012 число в восьмиразрядной сетке 0111 11012.
2. Число 0111 11012 положительное, т.к. в старшем 7-ом знаковом разряде записан ноль.
2. Выполняем поразрядную инверсию 1000 00102.
3. Складываем число с единицей 1000 00102 + 0000 00012 = 1000 00112.
Ответ: полученное число 1000 00112 является отрицательным, т.к. в старшем 7-ом знаковом разряде записана единица.
Пример: Определить знак двоичного числа 1111 11012 в восьмиразрядной сетке.
Число 1111 11012 записано в восьмиразрядной сетке.
Ответ:
Число 1111 11012 отрицательное, т. к. в старшем 7-ом знаковом
разряде записана единица.
к. в старшем 7-ом знаковом
разряде записана единица.
Пример: Определить знак двоичного числа 1000 0000 0111 11012 в шестнадцатиразрядной сетке.
Число 1000 0000 0111 11012 записано в шестнадцатиразрядной сетке.
Ответ: Число 1000 0000 0111 11012 отрицательное, т.к. в старшем 15-ом знаковом разряде записана единица.
Пример: Представить двоичное число 1000 00112 в десятичной системе счисления.
Для отрицательного числа используем формулу:
(-a7)р7 + a6р6 + a5р5 + a4р4 + a3р3 + a2р2 + a1р1 + a0р0 = -128+0+0+0+2+1 = -12510
Ответ: 1000 00112 = -12510.
Пример. Представить двоичное число 1000 00112 в шестнадцатеричной системе счисления.
Ответ:
1000 00112 = 8316.
Пример: Определить знак шестнадцатеричного числа 8316.
Ответ: число 8316 отрицательное, т.к. в старшем разряде числа 8316 цифра 816 = 10002, старший бит тетрады равен 12, что соответствует знаку минус.
Пример: Изменить знак двоичного числа 0111 11012 в шестнадцатиразрядной сетке.
1. Записываем 0111 11012 число в шестнадцатиразрядной сетке 0000 0000 0111 11012.
2. Выполняем поразрядную инверсию (заменяем все нули на единицы, а единицы — на нули) 1111 1111 1000 00102.
3. Складываем число с единицей
1111 1111 1000 00102 + 0000 0000 0000 00012 = 1111 1111 1000 00112.
Ответ: число 1111 1111 1000 00112.
Пример: Определить знак двоичного числа 1111 1111 1000 00112.
Двоичное число 1111 1111 1000 00112 записано в шестнадцатиразрядной сетке.
Ответ:
Число 1111 1111 1000 00112 отрицательное,
т.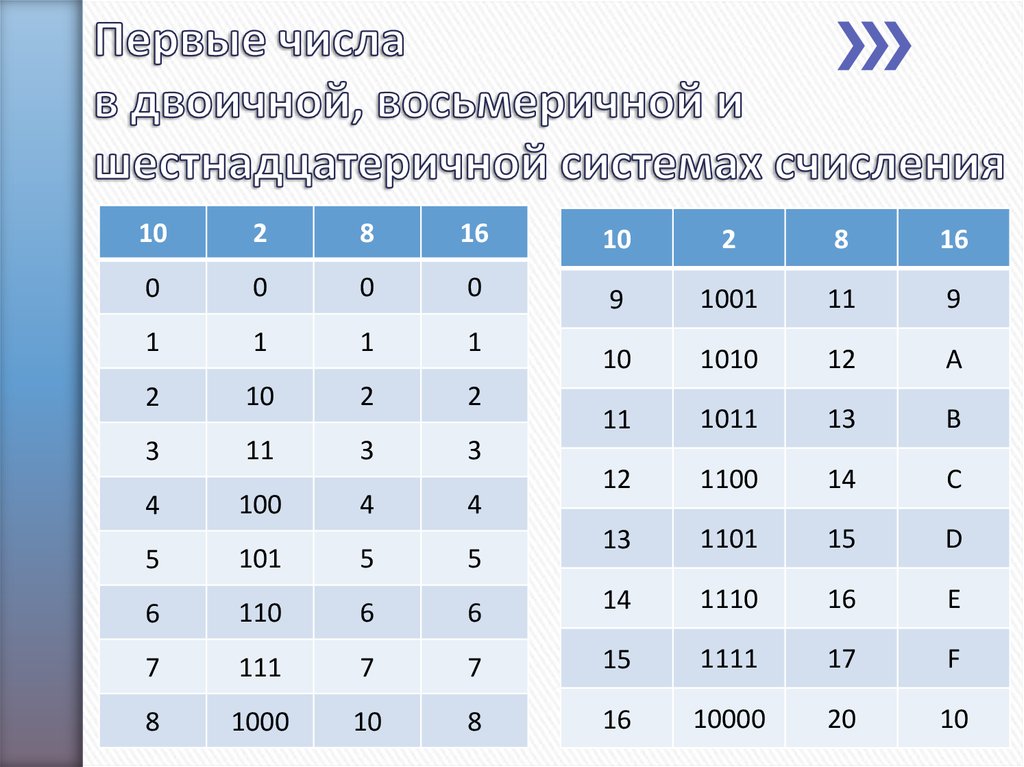 к. в старшем 15-ом знаковом разряде
записана единица.
к. в старшем 15-ом знаковом разряде
записана единица.
Пример: Представить двоичное число 1111 1111 1000 00112 в десятичной системе счисления.
Для отрицательного числа используем формулу:
(-a15)р15+a14р14+a13р13+a12р12+a11р11+a10р10+a9р9+a8р8+a7р7+a6р6+a5р5+a4р4+a3р3+a2р2
+a1р1+a0р0= = -32768+16384+8192+4096+2048+1024+512+256+128+0+0+0+2+1 = -12510
Ответ: 1111 1111 1000 00112 = -12510.
Пример: Представить двоичное число 1111 1111 1000 00112 в шестнадцатеричной системе счисления.
Ответ: 1111 1111 1000 00112 = FF8316
Пример:
Определить знак шестнадцатеричного
числа FF8316.
Ответ: числа FF8316 отрицательное, т.к. в старшем разряде символа F16 = 11112 старший бит тетрады равен 12.
Пример. Представить шестнадцатеричное число 7D16 в двоичной системе счисления.
Ответ: 7D16 = 0111 11012.
Пример. Представить шестнадцатеричное число 7D16 в десятичной системе счисления.
Число 7D 16 положительное, поэтому можно применить формулу степенного ряда: a1р1+a0р0.
7D 16 = (7)10 (13)10= 716р1+1316р0 = 112 +13 = 12510.
Ответ: 7D16 = +12510.
Пример. Представить шестнадцатеричное число 8316 в двоичной системе счисления.
Ответ: 7D16 = 1000 00112.
Пример. Представить шестнадцатеричное число 8316 в десятичной системе счисления.
Число
8316 отрицательное, поэтому сначала нужно
перевести в двоичную систему счисления
и перевести по формуле (-a7)р7 + a6р6 + a5р5 + a4р4 + a3р3 + a2р2 + a1р1 + a0р0.
8316 = 1000 00112 = -128 + 2 +1 = -12510.
Ответ: 8316 = -12510.
преобразовать десятичное число 256 в шестнадцатеричное
Как записать 256 в шестнадцатеричное (с основанием 16)?
256 равно 100 в шестнадцатеричной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать десятичное число 256 в шестнадцатеричное или преобразование десятичного числа в шестнадцатеричное.
| Декабрь | Шестнадцатеричный | Октябрь | Бункер |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | |
| 6 | 999999999999910|||
| 6 | 9999999999999999999999999999999999999999999999999999999910|||
| 6 | 99999999|||
| 6 | |||
| 6 | 9999|||
| 6 | 99110 | ||
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| 10 | A | 12 | 1010 |
| 11 | B | 13 | 1011 |
| 12 | C | 14 | 1100999 |
| 14 | 11009 | 110||
| 14 | 11009 9000 | ||
| 14 | 11009 | ||
| 0009 | D | 15 | 1101 |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| Dec | Hex | октября | Bin | |
|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | |
| 17 | 21 | 10001 | ||
| 21 | 10001 | |||
| 7 | 0009 | 12 | 22 | 10010 |
| 19 | 13 | 23 | 10011 | |
| 20 | 14 | 24 | 10100 | |
| 21 | 15 | 25 | 10101 | |
| 22 | 16 | 26 | 10110 | |
| 23 | 17 | 27 | 100009 | |
| 24 | 18 | 100009 | ||
| 24 | 18 | 100009 | ||
| 24 | 18 | 100009 | ||
| 24 | 18 | 0009 | 30 | 11000 |
| 25 | 19 | 31 | 11001 | |
| 26 | 1A | 32 | 11010 | |
| 27 | 1B | 33 | 11011 | |
| 28 | 1C | 34 | 11100 | |
| 29 | 1D | 35 | 11101 | |
| 30 | 1 EE | 369 | ||
| 30 0009 | 1E | 369 | ||
| 30 | 1E | |||
| 30 | 10009 | 11110 | ||
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | ||
|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | ||
| 33 | 21 | 41 | 100001 | ||
| 34 | 22 | 42 | 100010 | ||
| 35 | 23 | 1000109 | |||
| 35 | 23 | 0009 | 43 | 100011 | |
| 36 | 24 | 44 | 100100 | ||
| 37 | 25 | 45 | 100101 | ||
| 38 | 26 | 46 | 100110 | ||
| 39 | 27 | 47 | 100111 | ||
| 40 | 28 | 50 | 101000 | ||
| 41 | 29 2009 | 51 | |||
| 410009 | 29 | 51 | 101001 | ||
| 42 | 2A | 52 | 101010 | ||
| 43 | 2B | 53 | 101011 | ||
| 44 | 2C | 54 | 101100 | ||
| 45 | 2d | 55 | 101101 | ||
| 46 | 2E | 56 | 101110 | ||
| 47 | 2F | 57 | 11111192F | 57 | 101111111111111111111111111111111111111111111111111111111111111119. 0009 0009 |
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 48 | 30 | 60 | 110000 | |||
| 49 | 31 | 61 | 110001 | |||
| 50 | 32 | 62 | 110010 | |||
| 51 | 33 | 63 | 110011 | |||
| 52 | 34 | 64 | 9110100 | |||
| 53 | 35 | 65 | 110101 | |||
| 54 | 36 | 66 | 110110 | |||
| 55 | 37 | 67 | 110111 | |||
| 56 | 38 | 70 | 111000 | |||
| 57 | 39 | 71 | 111001 | |||
| 3A | 72 | 1110 | 3A | 72 | 1110111111110 | |
| 59 | 3B | 73 | 111011 | |||
| 60 | 3C | 74 | 111100 | |||
| 61 | 3D | 75 | 111101 | |||
| 62 | 3E | 76 | 111110 | |||
| 63 | 3F | 77 | 111111 |
 0070
0070| DEC | HEX | Октябрь | BIN | |
|---|---|---|---|---|
| 80999 | 50 9. 0009 0009 | 120 | 1010000 | |
| 81 | 51 | 121 | 1010001 | |
| 82 | 52 | 122 | 1010010 | |
| 83 | 53 | 123 | 1010011 | |
| 84 | 54 | 124 | 1010100 | |
| 85 | 55 | 125 | 1010101 | |
| 86 | 56 | 10009126 | 1010110 | |
| 87 | 57 | 127 | 1010111 | |
| 88 | 58 | 130 | 1011000 | |
| 89 | 59 | 131 | 1011001 | |
| 90 | 5A | 132 | 1011010 | |
| 91 | 5B | 133 | 1011011 | |
| 5C | 0009 | 134 | 1011100 | |
| 93 | 5D | 135 | 1011101 | |
| 94 | 5E | 136 | 1011110 | |
| 95 | 5F | 137 | 1011111 |
| DEC | HEX | Октябрь | BIN |
|---|---|---|---|
| 96 | 60 | 140 | |
| 0008 97 | 61 | 141 | 1100001 |
| 98 | 62 | 142 | 1100010 |
| 99 | 63 | 143 | 1100011 |
| 100 | 64 | 144 | 1100100 |
| 101 | 65 | 145 | 1100101 |
| 102 | 66 | 146 | 1100110 |
| 146 | 1100110 | ||
| 0008 103 | 67 | 147 | 1100111 |
| 104 | 68 | 150 | 1101000 |
| 105 | 69 | 151 | 1101001 |
| 106 | 6A | 152 | 1101010 |
| 107 | 6B | 153 | 1101011 |
| 108 | 6C | 154 | 1101100 | 154 | 1101100 | 0007 | 109 | 6D | 155 | 1101101 |
| 110 | 6E | 156 | 1101110 |
| 111 | 6F | 157 | 1101111 |
| Dec | HEX | октября | BIN |
|---|---|---|---|
| 112 | 70 | 160 | 1110000 |
| 113 | 71 | 161 | 1110001 |
| 114 | 72 | 162 | 1110010 |
| 115 | 73 | 163 | 1110011 |
| 116 | 74 | 164 | 1110100 |
| 117 | 75 | 165 | 1110101 |
| 118 | 76 | 166 | 1110110 |
| 119 | 167 | 0009 | 1110111 |
| 120 | 78 | 170 | 1111000 |
| 121 | 79 | 171 | 1111001 |
| 122 | 7A | 172 | 1111010 |
| 123 | 7B | 173 | 1111011 |
| 124 | 7C | 174 | 1111100 |
| 125 | 7D | 175 | 1111101 |
| 126 | 7E | 176 | 1111110 |
| 127 | 7F | 177 | 1111111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 128 | 80 | 200 | 10000000 | ||||
| 129 | 81 | 201 | 10000001 | ||||
| 130 | 10000001 | ||||||
| 130 | 000982 | 202 | 10000010 | ||||
| 131 | 83 | 203 | 10000011 | ||||
| 132 | 84 | 204 | 10000100 | ||||
| 133 | 85 | 205 | 10000101 | ||||
| 134 | 86 | 206 | 10000110 | ||||
| 135 | 207 | 10000119 | |||||
| 10000111 | |||||||
| 136 | 88 | 210 | 10001000 | ||||
| 137 | 89 | 211 | 10001001 | ||||
| 138 | 8A | 212 | 10001010 | ||||
| 139 | 8B | 213 | 10001011 | ||||
| 140 | 8C | 214 | 10001100 | ||||
| 141 | 8d | 215 | 10001101 | 215 | 10001101 | 0010 | |
| 142 | 8E | 216 | 10001110 | ||||
| 143 | 8F | 217 | 10001111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 144 | 90 | 220 | 10010000 | |
| 145 | 91 | 221 | 10010001 | |
| 146 | 9 | |||
| 1469 | 92 9000222 | 10010010 | ||
| 147 | 93 | 223 | 10010011 | |
| 148 | 94 | 224 | 10010100 | |
| 149 | 95 | 225 | 10010101 | |
| 150 | 96 | 226 | 10010110 | |
| 151 | 97 | 227 | 10010111 | |
| 152 | ||||
| 152 | 8 | 230 | 10011000 | |
| 153 | 99 | 231 | 10011001 | |
| 154 | 9A | 232 | 10011010 | |
| 155 | 9B | 233 | 10011011 | |
| 156 | 9C | 234 | 10011100 | |
| 157 | 9D | 235 | 10011101 | |
| 158 | 10011101 | |||
| 158 | 00099E | 236 | 10011110 | |
| 159 | 9F | 237 | 10011111 |
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 160 | A0 | 240 | 10100000 | |||
| 161 | A1 | 241 | 10100001 | |||
| 162 | A2 | 242 | 10100010 | 0009 | ||
| 163 | A3 | 243 | 10100011 | |||
| 164 | A4 | 244 | 10100100 | |||
| 165 | A5 | 245 | 10100101 | |||
| 166 | A6 | 246 | 10100110 | |||
| 167 | A7 | 247 | 10100111 | |||
| 168 | A8 | 250 | 168 | A8 | 250 | 0008 10101000 |
| 169 | A9 | 251 | 10101001 | |||
| 170 | AA | 252 | 10101010 | |||
| 171 | AB | 253 | 10101011 | |||
| 172 | AC | 254 | 10101100 | |||
| 173 | г. н.э.0009 н.э.0009 | 10101110 | ||||
| 175 | AF | 257 | 10101111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 176 | B0 | 260 | 10110000 | |
| 177 | B1 | 261 | 10110001 | |
| 178 | B2 | 262 | 10110010 | |
| 179 262 | ||||
| 179 | B3 | 263 | 10110011 | |
| 180 | B4 | 264 | 10110100 | |
| 181 | B5 | 265 | 10110101 | |
| 182 | B6 | 266 | 10110110 | |
| 183 | B7 | 267 | 10110111 | |
| 184 | B8 | 270 | 10111000 | 270 | 1011000 | 10111000 | 9000
| 185 | B9 | 271 | 10111001 | |
| 186 | BA | 272 | 10111010 | |
| 187 | BB | 273 | 10111011 | |
| 188 | BC | 274 | 10111100 | |
| 189 | BD | 275 | 10111101 | |
| 190 | BE | 276 | 10111110 | 0009 |
| 191 | BF | 277 | 10111111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 192 | C0 | 300 | 11000000 |
| 193 | C1 | 301 | 11000001 |
| 194 | C2 | 302 | 11000010 |
C310009 | 303 | 11000011 | |
| 196 | C4 | 304 | 11000100 |
| 197 | C5 | 305 | 11000101 |
| 198 | C6 | 306 | 11000110 |
| 199 | C7 | 307 | 11000111 |
| 200 | C8 | 310 | 11001000 |
| 201 | C9 | 311 | 11001001 |
| 202 | CA | 312 | 11001010 |
| 203 | CB | 313 | 11001011 |
| 204 | CC | 314 | 11001100 |
| 205 | CD | 315 | 11001101 |
| 206 | CE | 316 | 11001110 |
| 11001110 | |||
| 0008 207 | CF | 317 | 11001111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 208 | D0 | 320 | 11010000 |
| 209 | D1 | 321 | 11010001 |
| 210 | D2 | 322 | 11010010 |
| 211 | D3 | 323 | |
| 11010011 | |||
| 212 | D4 | 324 | 11010100 |
| 213 | D5 | 325 | 11010101 |
| 214 | D6 | 326 | 11010110 |
| 215 | D7 | 327 | 11010111 |
| 216 | D8 | 330 | 11011000 |
| 217 | D9 | ||
| 217 | D9 | 9000331 | 11011001 |
| 218 | DA | 332 | 11011010 |
| 219 | DB | 333 | 11011011 |
| 220 | DC | 334 | 11011100 |
| 221 | DD | 335 | 11011101 |
| 222 | DE | 336 | 1101110 |
| 223 | DF | ||
| 223 | DF | 0009337 | 11011111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 224 | E0 | 340 | 11100000 | ||||
| 225 | E1 | 341 | 11100001 | ||||
| 226 | E2 | 342 | 11100010 | ||||
| 227 | E3 | 343 | 1100011 | 343 | 1100011 | 9000||
| 228 | E4 | 344 | 11100100 | ||||
| 229 | E5 | 345 | 11100101 | ||||
| 230 | E6 | 346 | 11100110 | ||||
| 231 | E7 | 347 | 11100111 | ||||
| 232 | E8 | 350 | 11101000 | ||||
| 233 | 351 | 11101001 | 351 | 11101001 | 0009 | ||
| 234 | EA | 352 | 11101010 | ||||
| 235 | EB | 353 | 11101011 | ||||
| 236 | EC | 354 | 11101100 | ||||
| 237 | ED | 355 | 11101101 | ||||
| 238 | EE | 356 | 11101110 | ||||
| 239 | EF | 357 | 0008 11101111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 240 | F0 | 360 | 11110000 | ||||
| 241 | F1 | 361 | 11110001 | ||||
| 242 | F2 | 362 | 11110010 | ||||
| 243 | F3 | 363 | 11110011 | ||||
| 244 | F4 | 364 | 11110100 | ||||
| 245 | F5 | 365 | 11110101 | ||||
| 246 | F6 | 366 | 11110110 | ||||
| 247 | F7 | 367 | 11110111 | ||||
| 248 | F8 | 370 | 11111000 | ||||
| 249 | F9 | 371 | 11111001 | ||||
| 371 | 11111001 | ||||||
| 0008 250 | FA | 372 | 11111010 | ||||
| 251 | FB | 373 | 11111011 | ||||
| 252 | FC | 374 | 11111100 | ||||
| 253 | FD | 375 | 11111101 | ||||
| 254 | FE | 376 | 11111110 | ||||
| 255 | FF | 377 | 11111111199 | FF | 377 | 11111111111199 | 0010 |
Преобразователь базы чисел
Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- B400 hexadecimal to octal
- 100010 binary to decimal
- 162000 octal to hexadecimal
- 7C8 hexadecimal to octal
- decimal to hexadecimal
- 2024 decimal to octal
- 3340 octal to binary
- 7B7 hexadecimal до десятичной
- 2100 восьмеричное в шестнадцатеричное
десятичное 256 в шестнадцатеричном | работа, решение
Как написать 256 в шестнадцатеричном формате?
256 записывается как 100 в шестнадцатеричном формате
Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Десятичное число 256 в шестнадцатеричном формате | работа, решение или преобразование десятичного в шестнадцатеричное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.
Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.
С помощью этого конвертера вы можете получить ответы на такие вопросы, как:
- Что такое 256 в двоичном формате?
- Что такое 256 в шестнадцатеричном формате?
- Что такое восьмеричное число 256?
- Как преобразовать 256 в двоичный код?
- Как преобразовать 256 в двоичный код? И так далее.
Десятичная в двоичную диаграмму, включая шестнадцатеричную и восьмеричную0009
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 0008 2210010 | |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 17 | 27 | 10111 |
| 24 | 18 | 30 | |
| 0008 11000 | |||
| 25 | 19 | 31 | 11001 |
| 26 | 1A | 32 | 11010 |
| 27 | 1B | 33 | 11011 |
| 28 | 1C | 34 | 11100 |
| 29 | 1D | 35 | 11101 |
| 30 | 1E | 36 | 111110 |
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | 21 | 41 | 100001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | 22 | 42 | 100010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | 23 | 43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | 24 | 44 | 100100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | 25 | 45 | 100101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | 26 | 46 | 100110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | 27 | 47 | 100111 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | 28 | 50 | 101000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | 2951 | 101001 | 29 | 51 | 101001 | 51 | 101001 | 0009|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | 2A | 52 | 101010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | 2B | 53 | 101011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | 2C | 54 | 101100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | 2D | 55 | 101101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | 2E | 56 | 101110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | 2F | 57 | 101111 | 2F | 57 | 101111 | 0060
Образцы конверсии
 2858 2858
DisclaimerWhile every прилагаются усилия для обеспечения точности информации, представленной на этом веб-сайте, мы не даем никаких гарантий в отношении этой информации. Преобразование десятичного числа 256 в двоичное, восьмеричное, шестнадцатеричное
Hexadecimal
Страница 2 из 3 Не считаяСпособность считать в шестнадцатеричном формате — отличный способ понять, как работает система, но это не очень полезно, когда вы сталкиваетесь с таким сообщением, как . или Чтобы по-настоящему чувствовать себя с гексом как дома, вы должны понимать его немного по-другому. Вы, конечно, должны уметь преобразовывать шестнадцатеричные числа в десятичные и наоборот, но есть нечто более глубокое. Во-первых, как преобразовать шестнадцатеричное число в десятичное? Существует ряд стандартных алгоритмов, которые можно использовать для преобразования между различными системами счисления, но я должен признать, что предпочитаю более примитивный подход. Значения разрядов, используемые в шестнадцатеричном формате: .
, и вы можете использовать их, чтобы довольно легко вычислить эквивалентное десятичное значение. Например, AD45 это просто: , чтобы выразить это сочетанием шестнадцатеричных и десятичных чисел, или перейти полностью к десятичному: , что получается: Преобразование из десятичного числа в шестнадцатеричное немного сложнее, поскольку вам нужно выяснить, сколько частей 4096, 256 и 16 содержится в числе. Например, 44357 содержит 10 лотов 4096, потому что: Остаток, т.е. — это 3397, и это содержит 13 лотов по 256, потому что: и так далее, чтобы обнаружить, что остаток содержит 4 партии по 16 и 5 единиц. Запись 10 лотов по 4096, 13 лотов по 256, 4 лотов по 16 и 5 единиц в стандартном шестнадцатеричном формате дает AD45. К счастью, не часто приходится преобразовывать десятичные числа в шестнадцатеричные!
Чем полезен шестнадцатеричный код?До сих пор использование шестнадцатеричного числа выглядело так, как будто это какая-то интеллектуальная игра или что-то, что экзаменаторы могут использовать, чтобы задать хороший вопрос. Программисты как группа довольно ленивы, и можно поспорить, что они не стали бы использовать что-то, если бы это не упрощало жизнь. Есть два способа, которыми гексы облегчают жизнь. Во-первых, его можно использовать для записи очень больших целых чисел в компактной форме. Например, AD45 короче своего десятичного эквивалента 44357, и по мере увеличения значений разница в длине становится еще более заметной. Эта `короткая форма’ на самом деле является лишь незначительным преимуществом по сравнению со второй причиной, по которой мы используем шестнадцатеричный код. Шестнадцатеричные значения тесно связаны с двоичными значениями и степенями двойки. Например, 1 КБ памяти составляет 1024 байта в десятичном виде. Если вы адресуете каждую ячейку памяти в десятичном формате, диапазон адресов составляет от 0 до 1023. В шестнадцатеричном формате 1 КБ составляет 400 байт, а диапазон адресов составляет от 0 до 3FF. Это довольно интересно, но вы начинаете видеть отдачу, когда смотрите на проблему адресации, скажем, 64 КБ, что в десятичном виде равно 65536, а в шестнадцатеричном — просто 10000 байт. Эквивалентные диапазоны адресации: от 0 до 65535 в десятичном формате и от 0 до FFFF в шестнадцатеричном формате. В следующей таблице показано, насколько проще эти часто используемые значения и диапазоны выглядят в шестнадцатеричном формате: Размер памяти
Если вы посмотрите на эту таблицу, вы заметите, что 1 КБ выделяется, как больной палец, поскольку это не красивое шестнадцатеричное число. Практический шестигранникТеперь вы можете начать понимать, почему шестнадцатеричный формат так часто используется для передачи адресов и данных. В случае адреса шестнадцатеричная форма сразу сообщает вам, о какой области памяти идет речь. Например, если в сообщении об ошибке говорится о местоположении EF10, вы сможете понять, что это адрес в первых 64 КБ, где-то ближе к началу. Однако, чтобы действительно использовать такую информацию, вы должны иметь возможность использовать отладчик, чтобы просмотреть эту область памяти и пройтись по ней фрагмент за раз. Конечно, возможность сделать это иногда означает возможность выполнять шестнадцатеричные арифметические операции. Немногие умеют складывать и вычитать шестнадцатеричные числа, поэтому большинство отладчиков сделают это за вас, а калькулятор Windows имеет шестнадцатеричный режим. В старые времена у программистов, обычно программистов на ассемблере, часто были карманные шестнадцатеричные калькуляторы — да, настоящий калькулятор, который работал в шестнадцатеричном формате. Программисты на языке ассемблера думали в шестнадцатеричном формате. И да, я знал, что все зашло слишком далеко, когда понял, что только что выписал чек на $FB. << Предыдущая - Следующая >> Простая английская Википедия, бесплатная энциклопедия Шестнадцатеричная система счисления , часто сокращаемая до «hex» , представляет собой систему счисления, состоящую из 16 символов (основание 16). . Стандартная система счисления называется десятичной (основание 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. Люди в основном используют десятичную (с основанием 10) систему, в которой каждая цифра может иметь одно из десяти значений от нуля до десяти. Вероятно, это потому, что у людей десять пальцев на руках. Компьютеры обычно представляют числа в двоичном формате (с основанием 2). В двоичном формате каждая «двоичная цифра» называется битом и может иметь только одно из двух значений: единицу или ноль. Поскольку два возможных значения одного бита представляют одну пятую часть информации, потенциально передаваемой десятью возможными значениями десятичной цифры, для двоичных представлений целых значений может потребоваться гораздо больше (двоичных) битов, чем десятичных цифр. Например, трехзначное десятичное значение 219 требует, чтобы восемь битов были представлены в двоичном виде (11011011). Память компьютера организована в виде массива строк битов, называемых байтами. На современных компьютерах каждый байт обычно содержит восемь битов, которые удобно представить в виде двух шестнадцатеричных цифр. Инженеры и компьютерщики часто называют каждое из этих четырехбитных значений полубайтом (иногда пишется как nybble, см. компьютерный жаргон). Во избежание путаницы с десятичной, восьмеричной или другими системами счисления шестнадцатеричные числа иногда пишутся с «h» после или «0x» перед числом. Например, 63h и 0x63 означают 63 в шестнадцатеричном формате. Содержание
В отличие от современных компьютеров, многие ранние компьютеры имели шестибитные байты. Программисты этих систем обычно использовали альтернативную схему группировки битов, называемую восьмеричной. Каждая восьмеричная цифра эффективно представляет три бита, а шестибитный байт может быть представлен двумя восьмеричными цифрами. Три бита, каждый из которых может быть включен или выключен, могут представлять восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7. Шестнадцатеричная система счисления аналогична восьмеричной системе счисления (с основанием 8), поскольку каждую из них можно легко сравнить с двоичной системой счисления. Шестнадцатеричный использует четырехбитное двоичное кодирование. Это означает, что каждая цифра в шестнадцатеричном формате равна четырем цифрам в двоичном формате. В десятичной системе первая цифра — это разряд единицы, следующая цифра слева — это разряд десятков, следующая — разряд сотен и т. д. В шестнадцатеричной системе каждая цифра может иметь 16 значений , а не 10. Это означает, что цифры имеют занимает место, шестнадцать занимает место, а следующий 256 занимает место. Таким образом, 1h = 1 десятичный, 10h = 16 десятичный и 100h = 256 десятичный. Пример значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
Двоичный в шестнадцатеричный[изменить | изменить источник] При изменении числа с двоичного на шестнадцатеричное используется метод группировки.
Когда количество битов в двоичном числе не кратно 4, оно дополняется нулями, чтобы это было так.
Шестнадцатеричный код в десятичный[изменить | изменить источник]Чтобы преобразовать число из шестнадцатеричного в десятичное, есть два распространенных способа. Первый метод чаще используется при конвертации вручную:
Пример: 5Fh и 3425h в десятичном виде, метод 2
Десятичная 256 Шестнадцатеричная¿Cómo se escribe 256 шестнадцатеричная (основание 16)? 256 en el sistema numérico decimal es 100 en hexadecimal
| 101011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9000
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 176 | B0 | 260 | 10110000 | |||
| 177 | B1 | 261 | 10110001 | |||
| 178 | B2 | 262 | 10110010 | |||
| 179 | B3 | 263 | 10110011 | |||
| 180 | B4 | 264 | 10110100 | 264 | 10110100 | |
| 181 | B5 | 265 | 10110101 | |||
| 182 | B6 | 266 | 10110110 | |||
| 183 | B7 | 267 | 10110111 | |||
| 184 | B8 | 270 | 10111000 | |||
| 185 | B9 | 271 | 10111001 | |||
| 186 | BA | 272 | 0008 10111010 | |||
| 187 | BB | 273 | 10111011 | |||
| 188 | BC | 274 | 10111100 | |||
| 189 | BD | 275 | 10111101 | |||
| 190 | BE | 276 | 10111110 | |||
| 191 | BF | 277 | 1011119 |
| декабря |
|---|
| декаб0070 | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 192 | C0 | 300 | 11000000 | ||||
| 193 | C1 | 301 | 11000001 | ||||
| 194 | C2 | 302 | 11000010 | ||||
| 195 | C3 | 303 | 11000011 | ||||
| 196 | C4 | 304 | 11000100 | ||||
| 304 | 0008 197 | C5 | 305 | 11000101 | |||
| 198 | C6 | 306 | 11000110 | ||||
| 199 | C7 | 307 | 11000111 | ||||
| 200 | C8 | 310 | 11001000 | ||||
| 201 | C9 | 311 | 11001001 | ||||
| 202 | CA | 312 | 11001010999 | CA | 31211001010999 | 312 | 1100101099 | 0010
| 203 | CB | 313 | 11001011 | ||||
| 204 | CC | 314 | 11001100 | ||||
| 205 | CD | 315 | 11001101 | ||||
| 206 | CE | 316 | 11001110 | ||||
| 207 | CF | 317 | 110011119 |
| DEC |
|---|
| Bin | |||
|---|---|---|---|
| 208 | D0 | 320 | 11010000 |
| 209 | D1 | 321 | 11010001 |
| 210 | D2 | 322 | 11010010 |
| 211 | D3 | 323 | 11010011 |
| 212 | D4 | 324 | 11010100 |
| 213 | D5 9010 | 325 | 11010101 |
| 214 | D6 | 326 | 11010110 |
| 215 | D7 | 327 | 11010111 |
| 216 | D8 | 330 | 11011000 |
| 217 | D9 | 331 | 11011001 |
| 218 | DA | 332 | 11011010 |
| 219 | DB | 333 | 11011011 |
| 220 | DC | 334 | 11011100 |
| 221 | DD | 335 | 11011101 |
| 222 | DE | 336 | 11011110 |
| 223 | DF | 337 | 11011111 |
| DEC | HEX | октябрь | Bin | 0070 | ||
|---|---|---|---|---|---|---|
| 224 | E0 | 340 | 11100000 | |||
| 225 | E1 | 341 | 11100001 | |||
| 226 | E2 | 342 | 11100010 | |||
| 227 | E3 | 343 | 11100011 | |||
| 228 | E4 | 344 | 11100100 | |||
| 229 | E5 | 345 | 229 | 345 | 0008 11100101 | |
| 230 | E6 | 346 | 11100110 | |||
| 231 | E7 | 347 | 11100111 | |||
| 232 | E8 | 350 | 11101000 | |||
| 233 | E9 | 351 | 11101001 | |||
| 234 | EA | 352 | 11101010 | |||
| 235 | EB | 353 | 235 | 353 | 235 | 000911101011 |
| 236 | EC | 354 | 11101100 | |||
| 237 | ED | 355 | 11101101 | |||
| 238 | EE | 356 | 11101110 | |||
| 239 | EF | 357 | 11101111 |
| декабрь | HEX | октябрь | BIN |
|---|---|---|---|
| 2409 | . |
 4082399653118
4082399653118


 Причина в том, что 1 КБ — это странная единица памяти, на которую обращают внимание только потому, что она близка к 1000 десятичным числам, то есть 1024 байтам. Более естественно, что объем памяти удваивается на каждом шаге, потому что добавление дополнительной линии аппаратной адресации позволяет работать с удвоенным объемом памяти. Это причина того, что числа, которые продолжают встречаться, всегда являются степенями двойки, а шестнадцатеричный формат особенно хорош для представления степеней двойки в красивом аккуратном формате.
Причина в том, что 1 КБ — это странная единица памяти, на которую обращают внимание только потому, что она близка к 1000 десятичным числам, то есть 1024 байтам. Более естественно, что объем памяти удваивается на каждом шаге, потому что добавление дополнительной линии аппаратной адресации позволяет работать с удвоенным объемом памяти. Это причина того, что числа, которые продолжают встречаться, всегда являются степенями двойки, а шестнадцатеричный формат особенно хорош для представления степеней двойки в красивом аккуратном формате.
 Шестнадцатеричный использует десятичные числа и шесть дополнительных символов. Цифровых символов, представляющих значения больше девяти, не существует, поэтому используются буквы английского алфавита, в частности A, B, C, D, E и F. Шестнадцатеричный A = десятичный 10, а шестнадцатеричный F = десятичный 15.
Шестнадцатеричный использует десятичные числа и шесть дополнительных символов. Цифровых символов, представляющих значения больше девяти, не существует, поэтому используются буквы английского алфавита, в частности A, B, C, D, E и F. Шестнадцатеричный A = десятичный 10, а шестнадцатеричный F = десятичный 15.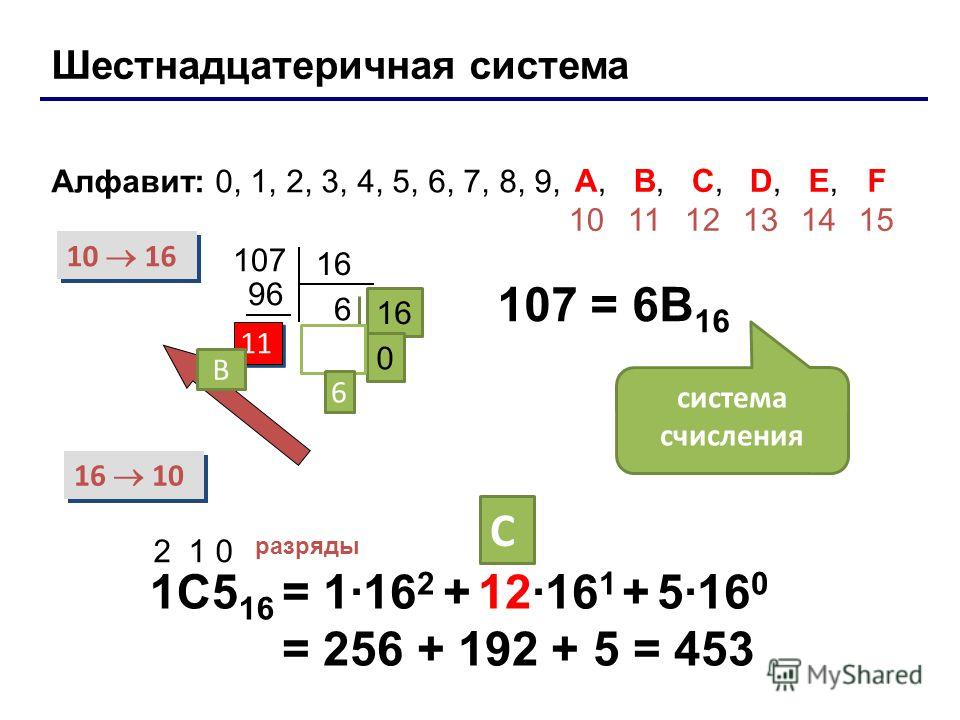 Людям неудобно читать, запоминать и печатать длинные цепочки битов. Шестнадцатеричный формат позволяет более удобно представлять группы из четырех битов одной «шестнадцатеричной» цифрой, поэтому восьмибитное двоичное значение 11011011 требует только двух шестнадцатеричных цифр «DB».
Людям неудобно читать, запоминать и печатать длинные цепочки битов. Шестнадцатеричный формат позволяет более удобно представлять группы из четырех битов одной «шестнадцатеричной» цифрой, поэтому восьмибитное двоичное значение 11011011 требует только двух шестнадцатеричных цифр «DB». 1 Двоичный код в шестнадцатеричный
1 Двоичный код в шестнадцатеричный Octal использует трехбитную двоичную систему.
Octal использует трехбитную двоичную систему. Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано в приведенной выше таблице для шестнадцатеричных чисел от 0 до F. Чтобы перейти от шестнадцатеричного, выполняется обратное. Каждая шестнадцатеричная цифра заменяется на двоичную, а группировка обычно удаляется.
Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано в приведенной выше таблице для шестнадцатеричных чисел от 0 до F. Чтобы перейти от шестнадцатеричного, выполняется обратное. Каждая шестнадцатеричная цифра заменяется на двоичную, а группировка обычно удаляется.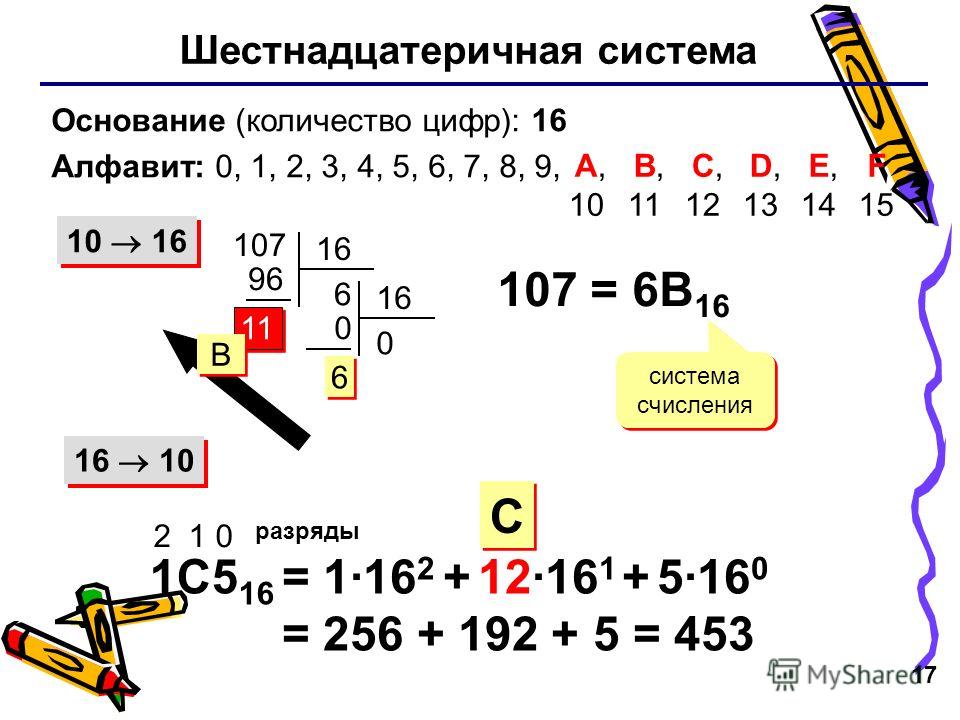 Примеры:
Примеры: Добавьте его к сумме.
Добавьте его к сумме.
 0009
0009 0009
0009