2 что такое основание системы счисления: Что называется основанием системы счисления?

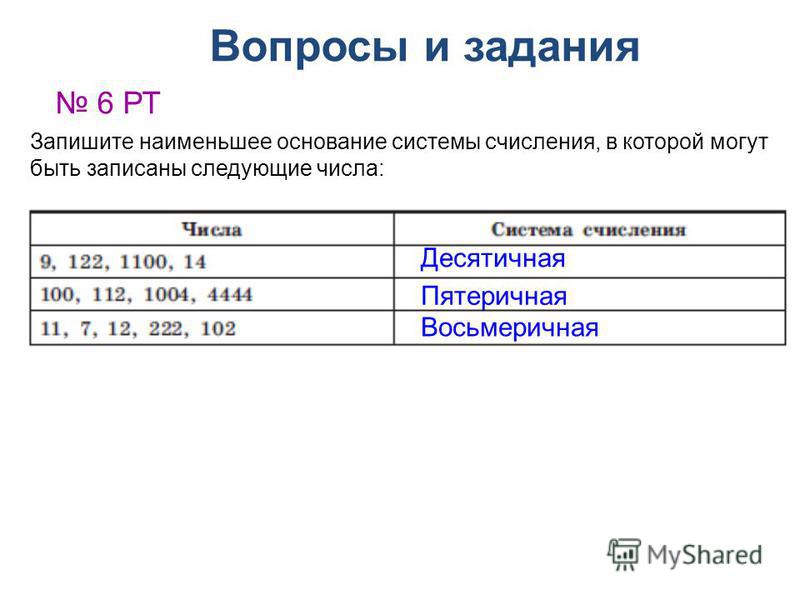
1.3. СИСТЕМЫ СЧИСЛЕНИЯ. — Основы информатики

1.3.1.ПОНЯТИЕ СИСТЕМЫ СЧИСЛЕНИЯ.

Все фантастические возможности вычислительной техники (ВТ) реализуются путем создания разнообразных комбинаций сигналов высокого и низкого уровней, которые условились называть «единицами» и «нулями».

Система счисления(СС) — это система записи чисел с помощью определенного набора цифр.CС называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе. Десятичная СС является позиционной: 999.Римская СС является непозиционной. Значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.Количество различных цифр, употребляемых в позиционной СС, называется основанием СС.

Развернутая форма числа — это запись, которая представляют собой сумму произведений цифр числа на значение позиций.

Например: 8527=8*10³+5*10²+2*10¹+7*10⁰

Развернутая форма записи чисел произвольной системы счисления имеет вид

, где

X — число;
a — основа системыисчисления;
i — индекс;
m — количество разрядов числа дробной части;
n — количество разрядов числа целой части.

Например: 327.46 n=3, m=2, q=10

Если основание используемой СС больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение.

Например: если 10=А, а 11=В, то число 7А.5В₁₂ можно расписать так:

7А.5В₁₂ = В·12^-2 + 5 ·2^-1 +А ·12⁰ + 7 ·12¹.

В шестнадцатеричной СС основа — это цифры 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 с соответствующими обозначениями 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Примеры чисел: 17D.ECH, F12AH.

ДвоичнаяСС— это система, в которой для записи чисел используются две цифры 0 и 1. Основанием двоичной системы счисления является число 2.

Двоичный код числа — запись этого числа в двоичной системе счисления. Например,

0=0₂
1=1₂
2=10₂
3=11₂ …
7=111₂
120=1111000₂.

В ВТ применяют позиционные СС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.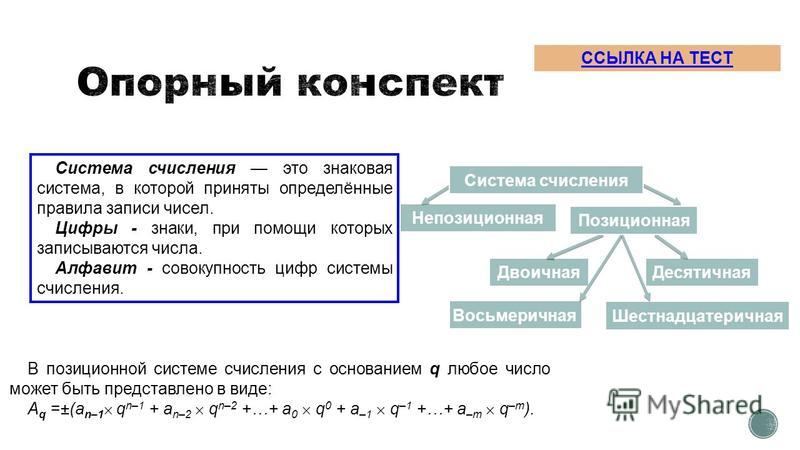 Для обозначения используемой СС число снабжают верхним или нижним индексом, в котором записывают основание СС. Другой способ – использование латинских букв после записи числа:

D – десятичная СС
В – двоичная СС
О – восьмеричная СС
Н – 16-ричная СС.

Несмотря на то, что 10-тичная СС имеет широкое распространение, цифровые ЭВМ строятся на двоичных элементах, т.к. реализовать элементы с 10 четко различимыми состояниями сложно. Историческое развитие ВТ сложилось таким образом, что ЭВМ строятся на базе двоичных цифровых устройств: триггеров, регистров, счетчиков, логических элементов и т.д.

16-ричная и 8-ричная СС используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов – команд, данных, адресов и операндов.

Задача перевода из одной СС в другую часто встречается при программировании, особенно, на языке Ассемблера. Например, при определении адреса ячейки памяти. Отдельные стандартные процедуры языков программирования Паскаль, Бейсик, Си, HTML требуют задания параметров в 16-ричной СС. Для непосредственного редактирования данных, записанных на жесткий диск, также необходимо умение работать с 16-ричными числами. Отыскать неисправность в ЭВМ невозможно без представлений о двоичной СС.

В таблице приведены некоторые числа, представленные в различных СС.

Двоичные числа	Восьмеричные числа	Десятичные числа	Шестнадцатеричные числа
0	0	0	0
1	1	1	1
10	2	2	2
11	3	3	3
100	4	4	4
101	5	5	5
110	6	6	6
111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

1.

3.2. ПЕРЕВОД ЧИСЕЛ ИЗ ПРОИЗВОЛЬНОЙ СС В ДЕСЯТИЧНУЮ И ОБРАТНО.

Перевод чисел из произвольной системы в десятичную. Для перевода числа из любой позиционной СС в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂=1*2³+1*2²+0*2¹+1*2⁰=13₁₀

17D.ECH=12·16^-2 + 14·16^-1 +13·16⁰ + 7·16¹ + 1·16²=381.921875

Перевод чисел из десятичной СС в заданную.

1) Для преобразования целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание СС, пока не получат нуль. Числа, которые возникают как остаток от деления на основание СС, представляют собой последовательную запись разрядов числа в выбранной СС от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

Например:

Читая остатки от деления снизу вверх, получим 111011011.

Проверка:

1*2⁸+1*2⁷+1*2⁶+0*2⁵+1*2⁴+1*2³+0*2 ²+1*2¹+1*2⁰=1+2+8+16+64+128+256=475₁₀.

2) Для преобразования десятичных дробей десятичной СС в число любой СС последовательно выполняют умножение на основание системы счисления , пока дробная часть произведения не станет равной нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например: перевести число 0.375 ₁₀ в двоичную СС.

Полученный результат — 0.011₂.

Необходимо отметить, что не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части, округляя последний разряд.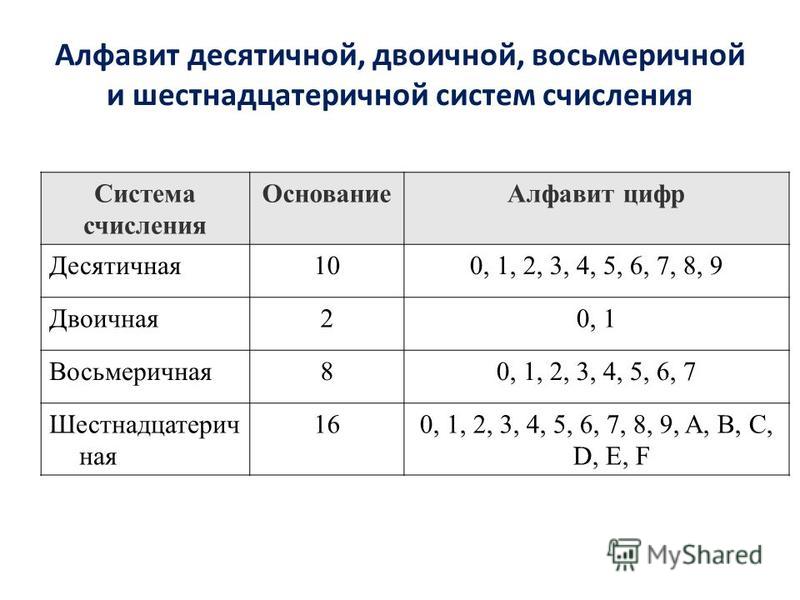

1.3.3. ПЕРЕВОД МЕЖДУ ОСНОВАНИЯМИ, СОСТАВЛЯЮЩИМИ СТЕПЕНЬ 2.

Для того, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

Например:

1234.777₈ = 001 010 011 100.111 111 111₂ = 1 010 011 100.111 111 111₂

1234567₈ = 001 010 011 100 101 110 111₂ = 1 010 011 100 101 110 111₂

Обратный перевод: каждая триада двоичных цифр заменяется восьмеричной цифрой, при этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Например:

1100111₂ = 001 100 111₂ = 147₈

11.1001₂ = 011.100 100₂ = 3.44₈

110.0111₂ = 110.011 100₂ = 6.34₈

При переводах между двоичной и шестнадцатеричной СС используются четверки цифр. При необходимости выравнивание выполняется до длины двоичного числа, кратной четырем.

Например:

1234.AB77₁₆ = 0001 0010 0011 0100.1010 1011 0111 0111₂ =1 0010 0011 0100.1010 1011 0111 0111₂

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂

0.1234AA₁₆ = 0.0001 0010 0011 0100 1010 1010₂

1100111₂ = 0110 0111₂ = 67₁₆

11.1001₂ = 0011.1001₂ = 3.9₁₆

110.0111001₂ = 0110.0111 0010₂ = 65.72₁₆

При переходе из восьмеричного счисления в шестнадцатеричное счисление и обратно используется вспомогательный двоичный код числа.

Например:

1234567₈ = 001 010 011 100 101 110 111₂ = 0101 0011 1001 0111 0111₂ = 53977₁₆

0.12034₈ = 0.001 010 000 011 100₂ = 0.0010 1000 0011 1000₂ = 0.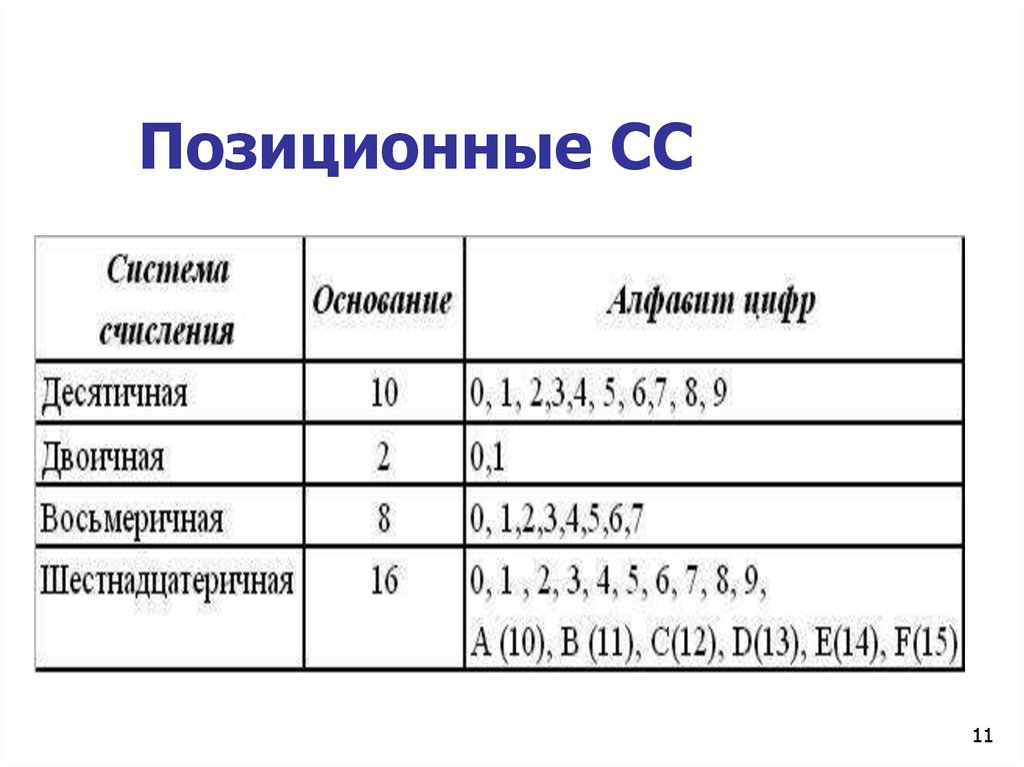 2838₁₆

120.34₈ = 001 010 000. 011 100₂ = 0101 0000.0111 0000₂ = 50.7₁₆

1234.AB77₁₆ = 0001 0010 0011 0100.1010 1011 0111 0111₂ =

= 001 001 000 110 100.101 010 110 111 011 100₂ = 11064.526734₈

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂ = 110 011 100 100 010 101 100 111₂ = 63442547₈

0.1234AA₁₆ =0.0001 0010 0011 0100 1010 1010₂ =0.000 100 100 011 010 010 101 010₂ =0.04432252₈

Раздел: Основные понятия информатики

Системы счисления – примеры, таблица, обозначение (9 класс, информатика)

4

Средняя оценка: 4

Всего получено оценок: 249.

4

Средняя оценка: 4

Всего получено оценок: 249.

Числа при письме заменяются специальными знаками. Метод представления числовых эквивалентов с помощью специальной знаковой системы называется системой счисления.

Системы счисления, как один из важных разделов теоретической информатики, подробно рассматриваются в курсе информатики 9 класса.

Что такое системы счисления

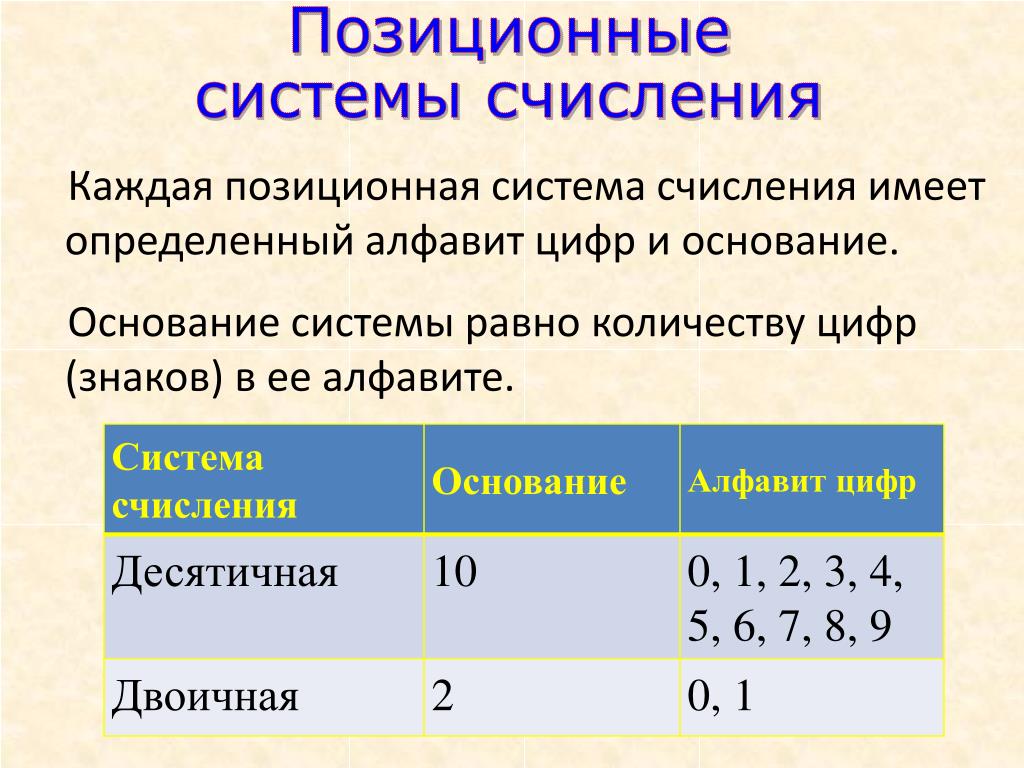
Системой счисления называется система записи чисел с помощью знаков по определенным правилам.

Символы, с помощью которых записываются числовые значения, обычно называют цифрами, а все вместе знаки системы счисления образуют алфавит. Количество знаков, используемых для обозначения чисел, называется основанием системы счисления.

Приведем примеры чисел систем счисления с различным основанием.

Основная десятичная система, привычная и общеупотребимая, имеет десять символов для обозначения всех чисел, то есть ее основание равно 10. Символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 представляют собой цифры. После цифры 9 в числовом ряду идет двузначное 10. При этом происходит сдвиг разрядной сетки числа влево на один разряд.

Десятичная система использует арабские цифры. Предположительно арабская система записи чисел возникла в Индии.

Индийскую систему записи чисел описал Аль Хорезми в своем трактате «Об индийском счете».

Рис. 1. Портрет Аль Хорезми.

Системы счисления в информатике не ограничиваются применением десятичных цифр, самыми распространенными системами являются двоичная, восьмеричная и шестнадцатеричная системы счисления.

В двоичной системе счисления все просто. Основание равно 2. Обозначение чисел выполняется только двумя символами 0 и 1.

И числовой ряд двоичных чисел выглядит так: 0, 1, 10, 11, 100, 101, 110, 111, 1000 и так далее.

Восьмеричная система использует 8 знаков для обозначения чисел: 0, 1, 2, 3, 4, 5, 6, 7. И числовой ряд восьмеричных чисел выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12 … Следует обратить внимание, что после 7 идет двузначное число 10, так как знаков всего восемь и происходит сдвиг разрядной сетки.

Шестнадцатеричная система имеет основание 16. Она применяет в качестве символов арабские цифры от 0 до 9 и затем буквы латинского алфавита A, B, C, D, E, F. В числовом ряду шестнадцатеричных чисел после 9 идет А, а после F идет 10.

Тогда возникает вопрос, как определить, в какой системе счисления, например число 107. Цифры 0, 1, 7 используются как в восьмеричной, так и в десятичной и шестнадцатеричной системе счисления. Для того чтобы различать системы, существует специальное обозначение систем счисления. Числа помечаются индексом с основанием системы. Так, 107₈ – это восьмеричное число, 107₁₀ – десятичное число, 107₁₆ – шестнадцатеричное число.

в истории существуют примеры использования и других систем счисления. Так, некоторые коренные культуры Африки и Австралии используют двоичные и троичные системы. Индейцы Юки пользуются четверичной системой счисления, пятеричная система счисления распространена больше (по количеству пальцев на руке), ее элементы встречаются у древних персов и ацтеков, у индейцев племени Таманакос. У древних Шумеров использовалась шестидесятеричная система счисления, разбивка часа на 60 минут и минуты на 60 секунд, вероятно, отголоски этой системы.

Позиционные системы счисления

Рассмотренные системы счисления относятся к классу позиционных систем. В них числовое значение каждой цифры зависит от положения в числе. Например, в десятичном числе 126 единица означает сотню, а в числе 216 единица уже на другом месте и обозначает десять.

Каждое число позиционной системы счисления можно представить как в свернутом виде, например, 126, так и в развернутом: 1*10² + 2*10¹ + 6*10⁰ , то есть 100 + 20 +6 =126.

Аналогично, двоичное число 111001 = 1*2⁵ + 1*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Восьмеричное число: 247 = 2*8² + 4*8¹ + 7*8⁰

Шестнадцатеричное число: 2A5F = 2*16³ + A*16² + 5*16¹ + F*16⁰

Используя развернутую форму, можно переводить числа из любой системы счисления в десятичную систему.

Непозиционные системы счисления

Кроме позиционных систем, существуют также непозиционные системы, в которых расположение цифры в числе не влияет на его числовое значение. Например, римская система цифр строится на основе символов I, V, X, L, C, D, M, которые означают соответственно 1, 5, 10, 50, 100, 500, 1000. Так, римское XVII означает 17. Получено путем суммирования 10 + 5 + 1 + 1.

Еще один пример: число 14 римскими цифрами записывается как XIV. Здесь использованы символы X, I, и V, которые обозначают 10, 1 и 5. Существует правило, согласно которому, меньшее число стоящее слева от большего следует вычитать из него. То есть I (1) меньше V (5), поэтому 5 – 1 = 4. И тогда число XIV получается как 10 + (5 – 1) = 14

Например, 1985 год в римской системе выглядит так MCMLXXXV: 1000 + (1000 – 100) + 50 + 10 + 10 + 10 + 5 = 1985

Рис. 2. Таблица римских цифр и их значений.

Самой первой системой счисления в истории человечества была унарная система, в которой использовался только один знак, или точнее один камень, палочка или засечка. Конечно, с помощью такой системы записать большие числа практически невозможно. Поэтому древние люди стали заменять группы палочек другим символом.

Рис. 3. Унарная система счисления.

Что мы узнали?

Числа для удобства записи представляются с помощью системы символов, которая называется системой счисления. Существуют позиционные и непозиционные системы счисления. В позиционных системах количество используемых знаков называется основанием. В информатике используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка статьи

4

Средняя оценка: 4

Всего получено оценок: 249.

---

А какая ваша оценка?

Тест с ответами: «Система счисления»

I вариант.

1. Что такое система счисления?
а) Правила выполнения операций над числами
б) Правила записи чисел
в) 1 и 2+
г) нет верного ответа

2. Название системы счисления, где в записи чисел могут быть использованы только цифры 0 1 2 3 4 5 6 7:
а) Двоичной
б) Семеричной
в) Восьмеричной+
г) Нет верного ответа

1. Выберите системы счисления, где может быть число 501:
а) Десятичная+
б) Двоичная
в) Восьмеричная+
г) Шестнадцатеричная+

5. Название системы счисления, где значение цифры зависит от занимаемой ею позиции в числе:
а) позиционная;
б) непозиционная;+
в) нет верного ответа;
г) перечисленное в п.1-2.

6. Вид числа 101, которое записали в двоичной системе счисления, после перевода в десятичную:
а) 3
б) 5+
в) 4
г) 6

7. Вид числа 10, которое записали в десятичной системе счисления, после перевода в двоичную:
а) 1010+
б) 1000
в) 1001
г) 1100

8. Произведите сравнение двух чисел 111(двоичное) и 5 (десятичное):
а) Числа равны
б) Первое число больше второго+
в) Первое число меньше второго

9. Возможна ли запись одного и того же числа в разных системах счисления?
а) Да+
б) Нет

10. Буду равным два числа: 11 в десятичной системе счисления и 11 в двоичной системе счисления?
а) Да
б) Нет+

11. Произведите сравнение двух чисел 1002 и 410 :
а) Первое число больше второго
б) Второе число больше первого
в) Равны+

12. Название системы счисления, где применяют только цифры 0,1,2:
а) двоичная
б) троичная+
в) семиричная
г) восьмиричная

13. Определите операцию, которая была применена к двоичным числам 1010 и 111, если в результате получено число 11?
а) деление
б) умножение
в) сложение
г) вычитание+

14. Система счисления, где кроме цифр используются буквы латинского алфавита:
а) двоичной
б) восьмеричной
в) десятичной
г) шестнадцатиричной+

15. Произведите перевод 295 из десятичной системы счисления в восьмеричную систему счисления:
а) 426
б) 447+
в) 744
г) 432

16. Произведите перевод 287 из десятичной системы счисления в шестнадцатеричную систему счисления:
а) 11F+
б) F11
в) 1511
г) 1115

17. Произведите перевод из восьмеричной системы счисления в двоичную число 1528:
а) 101010012
б) 1010100012
в) 11010102 +
г) 110110012

18. Произведите перевод из шестнадцатеричной системы счисления в двоичную число: 2ВС16
а) 1100101100102
б) 10101111002 +
в) 1011110000102
г) 001011100012

18. Что принято считать системой счисления?
а) алфавит;
б) способ представления чисел;
в) способ представления чисел и соответствующие ему правила действия над числами; +
г) набор чисел в определенной последовательности;

19. Системы счисления подразделяются на:
а) четные и нечетные;
б) позиционные и непозиционные;+
в) троичные, семеричные, десятичные;
г) двоичные, восьмеричные, шестнадцатеричные;

20. Какие символы есть в восьмеричной системе счисления?
а) 0, 1, 2, 3, 4, 5, 6, 7, 8;
б) 0, 1, 2, 3, 4, 5, 6, 7;+
в) 1, 2, 3, 4, 5, 6, 7, 8;
г) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F

21. Какие символы есть в шестнадцатеричной системе счисления?
а) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16;
б) 0, 1, 2, 3, 4, 5, 6, 7;
в) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F; +
г) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, А, В, С, D, E, F;

22. Какие символы есть в двоичной системе счисления:
а) 1, 2;
б) 0, 1;+
в) а, в;
в) все перечисленные

23. Подберите число, которое соответствует числу 100102 в десятичной системе:
а) 18;+
б) 17;
в) 100;
г) 36;

24. Подберите число, которое соответствует числу 1268 в десятичной системе счисления:
а) 15;
б) 86;+
в) 688;
г) 200;

25. Подберите число, которое соответствует числу 24310 в восьмеричной системе счисления:
а) 179;
б) 342;
в) 100110;
г) 363;

26. Подберите число, которое соответствует числу 82310 в шестнадцатеричной системе счисления:
а) 10011;
б) 337;+
в) АВ;
г) 12С;

27. К какому виду системы счисления относится римская система?
а) непозиционной системе;+
б) позиционной системе;
в) другой вариант;

28. К какому виду системы счисления относится десятичная система?
а) непозиционной системе;
б) позиционной системе; +
в) другой вариант;

29. Какое десятичное число соответствует числу МСХХIII?
а) 34;
б) 1117;
в) 1123;+
г) 73;

30. Подберите соответствующее римское число числу 1968:
а) нет правильного ответа;
б) MDCCCCLXIIIV;
в) MMLXVIII;
г) МСМLXVIII;+

31. Подберите соответствующее римское число числу CXIX:
а) 119;+
б) 129;
в) 69;
г) 59;

32. Система счисления, используемая жителями Древнего Египта при счете:
а) позиционную систему счисления;
б) непозиционную систему счисления;+

33. К какому виду системы относится единичная система счисления?
а) позиционной системе счисления;
б) непозиционной системе счисления;+

34. Какая из представленных систем является самой древней системой записи чисел:
а) древнеегипетская;
б) римская;
в) единичная;+
г) десятичная;

II вариант.

1. В какой системе счисления ЭВМ выполняет арифметические расчеты?
а) десятичной;
б) двоичной;+
в) единичной;
г) шестнадцатеричной;

2. Самой древней системой счисления является:
а) двоичная;
б) римская;
в) древнеегипетская;
г) единичная;+

3. В исчислении времени, в чередовании месяцев года сохранились остатки СС:
а) десятичной;
б) двенадцатеричной; +
в) двоичной;
г) восьмеричной.

4. Произведите перевод числа 37 из десятичной системы счисления в двоичную:
а) 100101;+
б) 10101;
в) 10011;
г) 10110

5. Произведите перевод числа 11010 2 из двоичной системы счисления в десятичную систему счисления:
а) 18;
б) 24;
в) 26;+
г) 14.

6. Системы счисления, не используемые специалистами для общения с ЭВМ?
а) десятичная;
б) троичная;+
в) двоичная;
г) шестнадцатеричная.

7. На берегу моря лежало 10 камней. Волной выбросило еще несколько. Их стало 1000. Сколько камней было выброшено волной?
а) 1000;
б) 1010;+
в) 1011;
г) 1110.

8. Основание системы счисления:
а) количество цифр, используемых для записи чисел;
б) отношение значений единиц соседних разрядов;+
в) арифметическая основа ЭВМ;
г) сумма всех цифр системы счисления.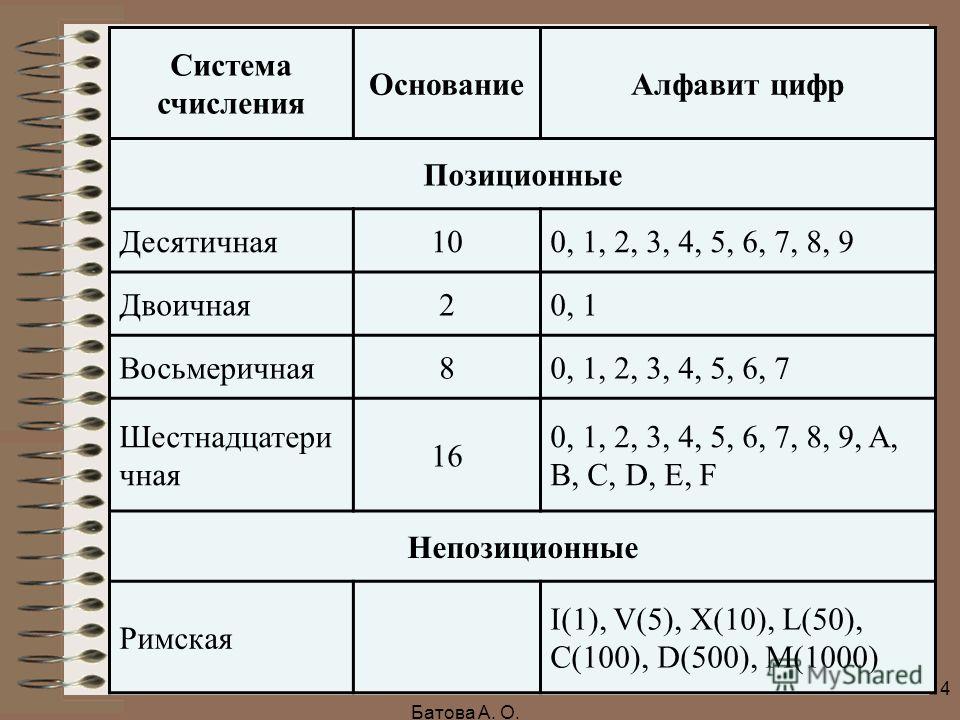

9. Произведите перевод числа 138 из десятичной системы счисления в двоичную:
а) 1001010;
б) 10001010;+
в) 10000110;
г) 1111110.

10. Произведите перевод числа 11011012 из двоичной системы счисления в десятичную систему счисления:
а) 109;+
б) 104;
в) 121;
г) 209.

11. При общении с ЭВМ профессионалы применяют …счисления.
а) двенадцатеричную;
б) троичную;
в) двоичную;+
г) пятеричную.

12. Греются на солнышке синицы. На нижней ветке сидело 110, а на верхней на 2 меньше. Сколько всего было синиц?
а) 1000;
б) 1001;
в) 1011;
г) 1010.+

13. Произведите перевод числа 243 из десятичной системы счисления в двоичную:
а) 11110011;+
б) 11001111;
в) 1110011;
г) 11011

14. Произведите перевод числа 11012 из двоичной системы счисления в десятичную систему счисления:
а) 11;
б) 13;+
в) 15;
г) 23.

15. Что такое числовой разряд?
а) цифра в изображении числа;
б) позиция цифры в числе;+
в) показатель степени основания;
г) алфавит системы счисления.

16. Младшая сестра учится в 101 классе. Старшая сестра на 11 старше. В каком классе учится старшая сестра?
а) 1000;+
в) 1111;
в) 1010;
г) 100

17. Количество цифр, которое используют в десятеричной системе счисления:
а) 9;
б) 10;+
в) 2;
г) бесконечное множество.

18. Произведите перевод числа 27 из десятичной системы счисления в двоичную:
а) 11011;+
б) 1011;
в) 1101;
г) 1111

19. Произведите перевод числа 11112 из двоичной системы счисления в десятичную систему счисления:
а) 16;
б) 15;
в)+ 7;
г) 14.

20. Выберите высказывание, касающееся позиционной системы счисления:
а) используются только арабские цифры;
б) количественное значение цифры не зависит от ее позиции в числе;
в) цифра умножается на основание системы счисления;
г) количественное значение цифры зависит от ее позиции в числе.+

21. В кабинетах русского и английского 1010 кактусов. В кабинете русского их 11. Сколько кактусов в кабинете английского языка?
а) 10;
б) 11;+
в) 1;

22. Основание системы позиционных систем счисления?
а) максимальное количество знаков, используемое для записи числа;+
б) цифры 1,2,3,4,5,6,7,8,9;
в) правила арифметических действий;
г) числовой разряд.

23. Произведите перевод числа 49 из десятичной системы счисления в двоичную:
а) 100011;
б) 10101;
в) 110001;+
г) 10110

24. Произведите перевод числа 1110112 из двоичной системы счисления в десятичную систему счисления:
а) 58;
б) 63;
в) 59;+
г) 14.

25. По какой причине в ЭВМ используется двоичная система счисления?
а) потому что составляющие технические устройства могут надежно сохранять и распознавать только два различных состояния;+
б) потому что за единицу измерения информации принят 1 байт;
в) потому что ЭВМ умеет считать только до двух;
г) потому что человеку проще общаться с компьютером на уровне двоичной системы счисления.

26. У второклассницы Маши 1111 палочек для счета. У Оли 10а) На сколько палочек у Маши больше, чем у Оли?
а) 1010;+
б) 100;
в) 1000;
г) 1001

27. Произведите перевод числа 11112 из двоичной системы счисления в восьмеричную:
а) 7;
б) 17;+
в) 15;
г) 33.

28. Произведите перевод числа А9 из шестнадцатеричной системы счисления в двоичную.
а) 10101001;+
б) 10011010;
в) 10101000;
г) 101010.

29. Произведение сложение чисел в двоичной системе счисления 101112 + 10112:
а) 11122;
б) 11010;
в) 10010;
г) 100010+.

30. Произведите перевод числа 10101010001110 из двоичной системы в восьмеричную:
а) 25216;+
б) 35217;
в) 25027;
г) 61252.

31. Произведите перевод числа А960В из шестнадцатеричной системы в двоичную:
а) 11111111011000001011;
б) 00000001011000001011;
в) 11111111111000001011;
г) 1010100101100000101+

32. Произведите перевод числа 1011112 из двоичной системы счисления в шестнадцатеричную:
а) 27;
б) 2F;+
в) 57;
г) В3.

33. Произведите перевод числа 71 из восьмеричной системы счисления в двоичную:
а) 111001;+
б) 1111;
в) 101010;
г) 10011

34. Произведение сложение чисел в двоичной системе счисления 1001 2 + 1112:
а) 10000+;
б) 10002;
в) 1000;
г) 11000.

Различные базы

Мы склонны думать, что совершенно естественно использовать 10 символы для записи чисел: 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Но единственная причина, по которой мы это делаем, заключается в том, что мы растем, считая на пальцах, которых у нас, оказывается, десять. Нет никакой реальной причины, почему десять лучше для математики, чем другое число, скажем 2 , 5 , 12 или же 16 .

С одной цифрой мы можем считать до 9 . Затем мы используем место значение писать большие числа. » 10 » означает один десяток и ноль единиц. Число 5723 действительно сокращение для:

5723 знак равно ( 5 × 1000 ) + ( 7 × 100 ) + ( 2 × 10 ) + ( 3 × 1 )

Места обозначают тысячи, сотни, десятки и единицы. Обратите внимание, что это все полномочия 10 :

5723 знак равно ( 5 × 10 3 ) + ( 7 × 10 2 ) + ( 2 × 10 1 ) + ( 3 × 10 0 )

Что, если бы мы ограничились только тремя цифрами, 0 , 1 , а также 2 , и использовали мощности 3 вместо полномочий 10 как значения места? Ниже мы считаем до 27 в базе 3 .

БАЗА 3	БАЗА 10
1	1
2	2
10	3
11	4
12	5
20	6
21	7
22	8
100	9
101	10
102	11
110	12
111	13
112	14
120	15
121	16
122	17
200	18
201	19
202	20
210	21
211	22
212	23
220	24
221	25
222	26
1000	27

Обратите внимание, что вместо разрядов «десятки», «сотни» и «тысячи» в левой колонке стоят разряды «тройки», «девятки» и «двадцать семь».

Это может показаться немного странным, но в base можно так же хорошо заниматься математикой. 3 как в базе 10 или любая другая база. Для иллюстрации решим задачу на сложение (в базе 3 слева, база 10 справа). Обратите внимание, что мы должны переносить, когда добавляем 1 + 2 !

1 1 0 1 + 1 2 _ 1 2 0 1 0 + 5 _ 1 5

Исторически так сложилось, что в большинстве, но не во всех культурах использовалась базовая 10 . Индейцы Юки в Калифорнии использовали базу 8 , потому что они считали промежутки между пальцами, а не сами пальцы. Вавилоняне использовали базу 60 , а майя использовали смесь базовых 20 а также 18 . Какая-то старая база 20 терминология проникла даже во французский и английский языки. Французы говорят «soixante et onze» для 71 , что буквально означает «три двадцатки и одиннадцать». Геттисбергская речь президента США Авраама Линкольна начиналась словами «Четыре десятка и семь», что означает 87 .

Наконец, в наше время база 2 ( бинарный ) и основание 16 ( шестнадцатеричный ) часто используются в информатике. (Если вы когда-либо играли с созданием веб-страницы, вы, возможно, знаете, что HTML использует 16 -цифровой шестнадцатеричный код для указания цвета. 16 цифры 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9, А , Б , С , Д , Е , Ф . Код для черного: » 000000 «; код для белого » FFFFFF «; » 9 Б20ДФ «это такой приятный мягкий фиолетовый цвет .)

Есть также некоторые люди, такие как Общество дюжины Америки, которые выступают за то, чтобы превратить весь мир в основу. 12 система. Они претендуют на базу 12 превосходит базу 10 потому что оно делится на большее количество чисел… так легче выучить таблицу умножения!

Числовая база | Названия основ счисления

Вы, наверное, выучили названия некоторых основ счисления в школе! Мы знаем, что десятичная — это основание 10, шестнадцатеричное — это основание 16, двоичное — основание 2, а восьмеричное — основание 8. Некоторые другие основания имеют более длинные и причудливые названия, в основном латинские. Основание 20, используемое майя, называется десятеричным, а основание 60, используемое древними месопотамцами, называется шестидесятеричным.

Ниже приведена таблица некоторых названий баз. Имена, выделенные жирным шрифтом, — это слова, которые вы могли бы найти в хорошем словаре. Поскольку не существует стандартного способа именования баз, этот веб-сайт изобрел другие, используя новую систему. Эта новая система пытается следовать тому, как были созданы другие имена, чтобы предоставить аналогичные имена для других баз. Нажмите здесь, чтобы узнать больше о новой системе!

Система базовых имен Lamadrid, применяемая на этом веб-сайте
Основания 1-10 1 унарный 2 двоичный 3 троичный 4 четвертичный 5 пятеричный 6 сенарий 7 семеричный 8 восьмеричный 9 нонарный 10 десятичный	Основания 11-20 11 десятичный 12 двенадцатеричный 13 трехзначный 14 четырехзначный 15 пятидесятеричный 16 шестнадцатеричный 17 шестнадцатеричный 18 восьмидесятеричный 19 шестнадцатеричный 20 десятеричный	21 недесятичная 22 двенадцатидесятичный 23 трехзначная 24 четырехдесятичный 25 пятидесятеричный … 30 тройничный 32 двенадцатиричный 36 шестигранный …	40 четырехзначный 50 пятидесятеричный 60 шестидесятеричный 70 семидесятеричный 80 восьмидесятеричный 90 недесятеричный 100 сотенных 120 сантовидесятичный 144 сентотетраквадратичное число 360 трецентошестидесятиричный

В отличие от названий химических элементов или самих чисел, основы не имеют общей системы названий. Что бы вы назвали основанием 14? Где взять детали, необходимые для создания такого имени? Конечно, мы всегда можем назвать это «основанием 14».

Если нам нужны формально звучащие имена, такие как «десятичный» для основания 10 или «шестнадцатеричный» для основания 16, мы можем попытаться использовать источники частей этих имен. Эти источники латинские и греческие.

Мы живем не в Древнем Риме и не в Греции, поэтому нам, возможно, не придется делать все то, что делают эти языки для выражения числа. Мы также можем смешивать латинский и греческий языки. Английский язык использует латинские и греческие слова для новых изобретений и научных терминов уже более пары столетий. Из-за этого многие части слов из этих языков довольно легко понять на английском языке. Часть греческого слова «теле» и часть латинского слова «видение» или часть греческого слова «телефон» легко понять. «Теле» означает «далеко», поэтому любое слово, в котором есть «теле-», имеет какое-то отношение к расстоянию. Телевидение и телефоны — это устройства, передающие изображения и звуки на расстоянии.

Мы используем часть греческого слова «гекса», чтобы передать идею шестичастности в английском языке. Мы знаем, что шестиугольник — это шестигранная фигура. Латинское слово «десятичный» имеет какое-то отношение к десяти. Когда мы складываем эти части вместе, мы получаем «шестнадцатеричное число», что означает основание 16. Таким образом, мы можем использовать греческие слова для единиц и латинские слова для десятков. Мы пишем их «назад», имея в виду сначала единицу, а затем декаду, потому что так устроены такие слова, как «шестнадцатеричный». Латинские единицы располагаются впереди десятилетий.

Нам не нужны совершенно хорошие латинские имена (или греческие) для систем счисления, потому что мы не пытаемся создавать латинские слова. Мы произносим новые английские слова, которые помогают нам говорить об основаниях счисления. Таким образом, нам не нужно делать все, что делают эти старые языки, чтобы создавать настоящие латинские или греческие имена чисел. Некоторые другие действия, которые латиница делает с числовыми именами, могли бы сбить с толку в английском языке, поэтому мы их не делаем!

Будет ли эта система работать на языках, отличных от английского? Это может. Нарушение правил латыни и греческого языка может повредить восприятию этой системы на других языках. Носители других языков могут задаться вопросом, почему мы не делаем того же, что и старые языки, что может показаться им странным и запутанным. Носители этих других языков должны будут придумать свои собственные названия основ; мы не будем пытаться их контролировать. На некоторых языках, таких как испанский, итальянский и французский, носители могут просто использовать настоящие латинские базовые имена. Это англоязычный веб-сайт; мы сосредоточимся на англоязычных решениях и позволим другим выбирать, как они хотят.

Итак, это система имен базовых чисел, используемая на этом веб-сайте. Умный молодой друг по имени Фернандо Мартинес Ламадрид из Мексики предложил систему для имен до основания 99; Я продолжил систему через тысячи. По этой причине эта система называется системой базовых имен Ламадрида. Похоже, это хорошая система, так что мы ее придерживаемся!

Эй! Посетите более подробное «радикологическое» объяснение названий числовых оснований здесь!

Числовые базы — Викиверситет

Взято из Викиверситета

Перейти к навигацииПерейти к поиску

Положительные целые числа в десятичной и двоичной системах счисления n -й степени двойки (2 ⁿ ).

• десятичный: основание десять (10)
• двоичный код: основание два (2 = 2 ¹ , первая степень двойки)
• четвертичный: основание четыре (4 = 2 ² , вторая степень двойки)
• восьмеричное: основание восемь (8 = 2 ³ , третья степень двойки)
• шестнадцатеричный: основание шестнадцать (16 = 2 ⁴ , четвертая степень двойки)
• двенадцатеричное число: основание тридцать два (32 = 2 ⁵ , пятая степень двойки)
• тетрашестидесятеричный: основание шестьдесят четыре (64 = 2 ⁶ , шестая степень числа два)
• цент-восьмидесятичный: основание 128 = 2 ⁷ (седьмая степень двойки)
• дучентогексапятидесятеричный: основание 256 = 2 ⁸ (восьмая степень двойки)
• quingentodudecimal: основание 512 = 2 ⁹ (девятая степень двойки)
• миллет, четверичная система счисления: основание 1024 = 2 ¹⁰ (десятая степень двойки)
• думиллоктоквадратичное число: основание 2048 = 2 ¹¹ (одиннадцатая степень двойки)
• квадрамильгексанадесятеричный: основание 4096 = 2 ¹² (двенадцатая степень двойки)

Обратите внимание, что числа с основанием 63 и выше включают произвольные символы для цифр (поскольку число индийско-арабских цифр плюс римские прописные и римские строчные буквы равно 62 персонажи). Base 64 представлен здесь с использованием двух дополнительных символов «-» (дефис) и «_» (подчеркивание) из «Алфавита Base-64, безопасного для URL и имен файлов» RFC 4648 Инженерной группы Интернета (IETF).

база 10	основание 2	база 4	база 8	база 16	основание 32	база 64
0	0	0	0	0	0	0
1	1	1	1	1	1	1
2	10	2	2	2	2	2
3	11	3	3	3	3	3
4	100	10	4	4	4	4
5	101	11	5	5	5	5
6	110	12	6	6	6	6
7	111	13	7	7	7	7
8	1000	20	10	8	8	8
9	1001	21	11	9	9	9
10	1010	22	12	А	А	А
11	1011	23	13	Б	Б	Б
12	1100	30	14	С	С	С
13	1101	31	15	Д	Д	Д
14	1110	32	16	Э	Э	Э
15	1111	33	17	Ф	Ф	Ф
16	10000	100	20	10	г	г
17	10001	101	21	11	Ч	Ч
18	10010	102	22	12	я	я
19	10011	103	23	13	Дж	Дж
20	10100	110	24	14	К	К
21	10101	111	25	15	л	л
22	10110	112	26	16	М	М
23	10111	113	27	17	Н	Н
24	11000	120	30	18	О	О
25	11001	121	31	19	П	П
26	11010	122	32	1А	В	В
27	11011	123	33	1Б	Р	Р
28	11100	130	34	1С	С	С
29	11101	131	35	1Д	Т	Т
30	11110	132	36	1Э	У	У
31	11111	133	37	1Э	В	В
32	100000	200	40	20	10	Вт
33	100001	201	41	21	11	Х
34	100010	202	42	22	12	Д
35	100011	203	43	23	13	З
36	100100	210	44	24	14	а
37	100101	211	45	25	15	б
38	100110	212	46	26	16	с
39	100111	213	47	27	17	д
40	101000	220	50	28	18	е
41	101001	221	51	29	19	ф
42	101010	222	52	2А	1А	г
43	101011	223	53	2Б	1Б	ч
44	101100	230	54	2С	1С	я
45	101101	231	55	2D	1Д	дж
46	101110	232	56	2Е	1Э	тыс.
47	101111	233	57	2F	1F	л
48	110000	300	60	30	1G	м
49	110001	301	61	31	1ч	н
50	110010	302	62	32	1И	о
51	110011	303	63	33	1Дж	р
52	110100	310	64	34	1К	q
53	110101	311	65	35	1л	р
54	110110	312	66	36	1М	с
55	110111	313	67	37	1Н	т
56	111000	320	70	38	1О	ты
57	111001	321	71	39	1П	В
58	111010	322	72	3А	1 кв.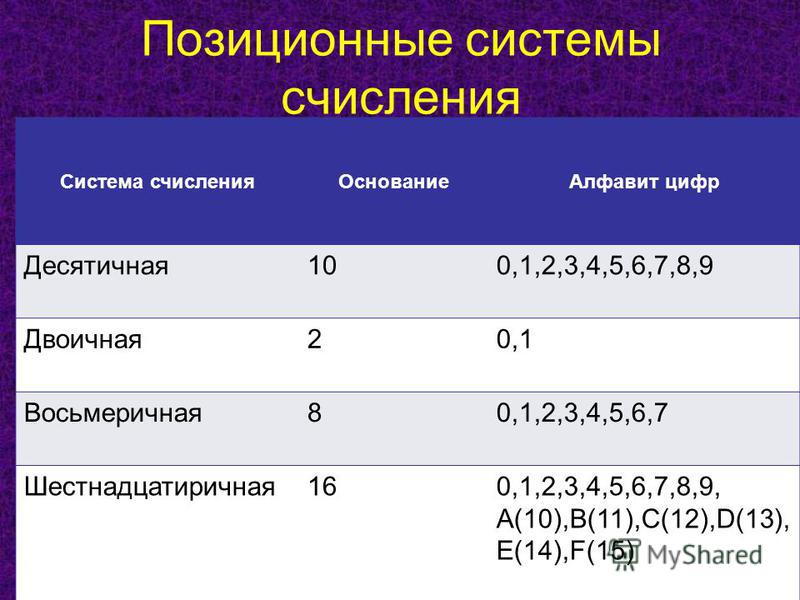	Вт
59	111011	323	73	3Б	1Р	х
60	111100	330	74	3С	1С	г.
61	111101	331	75	3Д	1T	г
62	111110	332	76	3Э	1U	—
63	111111	333	77	3F	1В	_
64	1000000	1000	100	40	20	10
65	1000001	1001	101	41	21	11
66	1000010	1002	102	42	22	12
67	1000011	1003	103	43	23	13
68	1000100	1010	104	44	24	14
69	1000101	1011	105	45	25	15
70	1000110	1012	106	46	26	16
71	1000111	1013	107	47	27	17
72	1001000	1020	110	48	28	18
73	1001001	1021	111	49	29	19
74	1001010	1022	112	4А	2А	1А
75	1001011	1023	113	4Б	2Б	1Б
76	1001100	1030	114	4С	2С	1С
77	1001101	1031	115	4Д	2D	1Д
78	1001110	1032	116	4Е	2Е	1Э
79	1001111	1033	117	4F	2F	1F
80	1010000	1100	120	50	2G	1G
81	1010001	1101	121	51	2ч	1ч
82	1010010	1102	122	52	2И	1И
83	1010011	1103	123	53	2Дж	1Дж
84	1010100	1110	124	54	2К	1К
85	1010101	1111	125	55	2л	1л
86	1010110	1112	126	56	2М	1М
87	1010111	1113	127	57	2Н	1Н
88	1011000	1120	130	58	2О	1О
89	1011001	1121	131	59	2П	1П
90	1011010	1122	132	5А	2 кв.	1 кв.
91	1011011	1123	133	5Б	2р	1Р
92	1011100	1130	134	5С	2С	1С
93	1011101	1131	135	5Д	2Т	1T
94	1011110	1132	136	5Э	2U	1U
95	1011111	1133	137	5F	2В	1В
96	1100000	1200	140	60	30	1 Вт
97	1100001	1201	141	61	31	1X
98	1100010	1202	142	62	32	1Г
99	1100011	1203	143	63	33	1Z
100	1100100	1210	144	64	34	1а
101	1100101	1211	145	65	35	1б
102	1100110	1212	146	66	36	1с
103	1100111	1213	147	67	37	1д
104	1101000	1220	150	68	38	1е
105	1101001	1221	151	69	39	1ф
106	1101010	1222	152	6А	3А	1 г
107	1101011	1223	153	6Б	3Б	1 час
108	1101100	1230	154	6С	3С	1и
109	1101101	1231	155	6D	3Д	1j
110	1101110	1232	156	6Е	3Э	1к
111	1101111	1233	157	6F	3F	1л
112	1110000	1300	160	70	3G	1м
113	1110001	1301	161	71	3ч	1н
114	1110010	1302	162	72	3И	1о
115	1110011	1303	163	73	3Дж	1 шт.
116	1110100	1310	164	74	3К	1 кв.
117	1110101	1311	165	75	3л	1р
118	1110110	1312	166	76	3М	1с
119	1110111	1313	167	77	3Н	1т
120	1111000	1320	170	78	3О	1у
121	1111001	1321	171	79	3П	1м
122	1111010	1322	172	7А	3 кв.	1 Вт
123	1111011	1323	173	7Б	3р	1x
124	1111100	1330	174	7С	3С	1 год
125	1111101	1331	175	7Д	3Т	1з
126	1111110	1332	176	7Э	3U	1-
127	1111111	1333	177	7Ф	3В	1_
128	10000000	2000	200	80	40	20
129	10000001	2001	201	81	41	21
130	10000010	2002 г.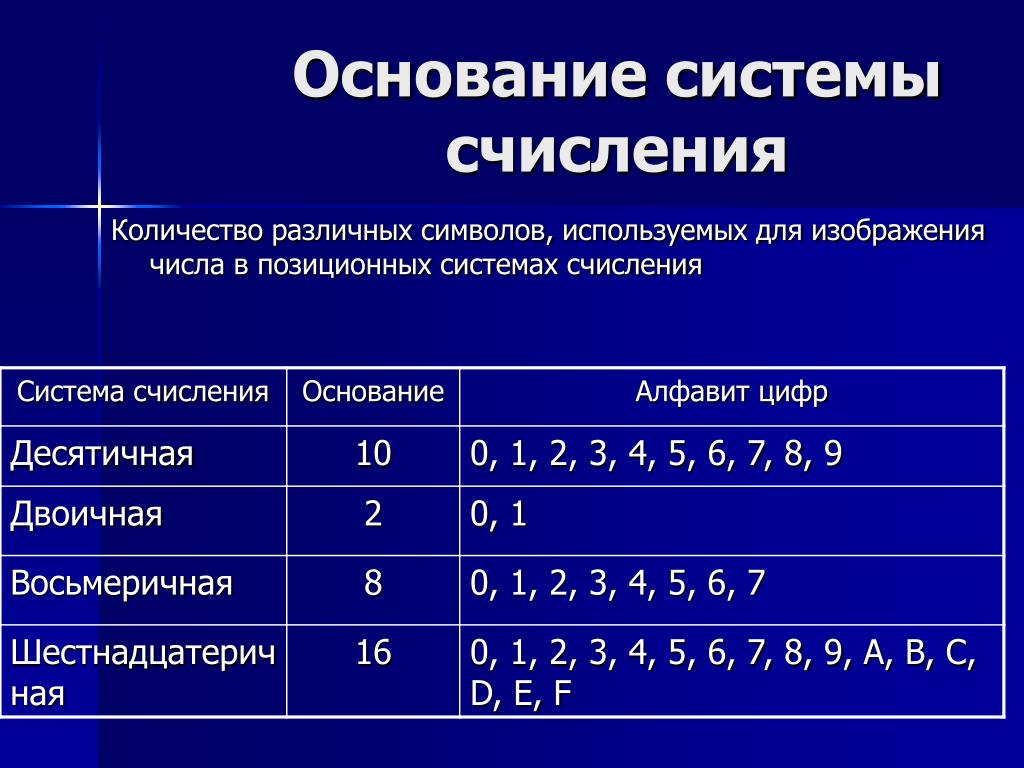	202	82	42	22
131	10000011	2003 г.	203	83	43	23
132	10000100	2010	204	84	44	24
133	10000101	2011	205	85	45	25
134	10000110	2012	206	86	46	26
135	10000111	2013	207	87	47	27
136	10001000	2020	210	88	48	28
137	10001001	2021	211	89	49	29
138	10001010	2022	212	8А	4А	2А
139	10001011	2023	213	8Б	4Б	2Б
140	10001100	2030	214	8С	4С	2С
141	10001101	2031	215	8Д	4Д	2D
142	10001110	2032	216	8Э	4Е	2Е
143	10001111	2033	217	8F	4F	2F
144	10010000	2100	220	90	4G	2G
145	10010001	2101	221	91	4Ч	2ч
146	10010010	2102	222	92	4И	2И
147	10010011	2103	223	93	4Дж	2Дж
148	10010100	2110	224	94	4К	2К
149	10010101	2111	225	95	4л	2л
150	10010110	2112	226	96	4М	2М
151	10010111	2113	227	97	4Н	2Н
152	10011000	2120	230	98	4О	2О
153	10011001	2121	231	99	4П	2П
154	10011010	2122	232	9А	4 кв.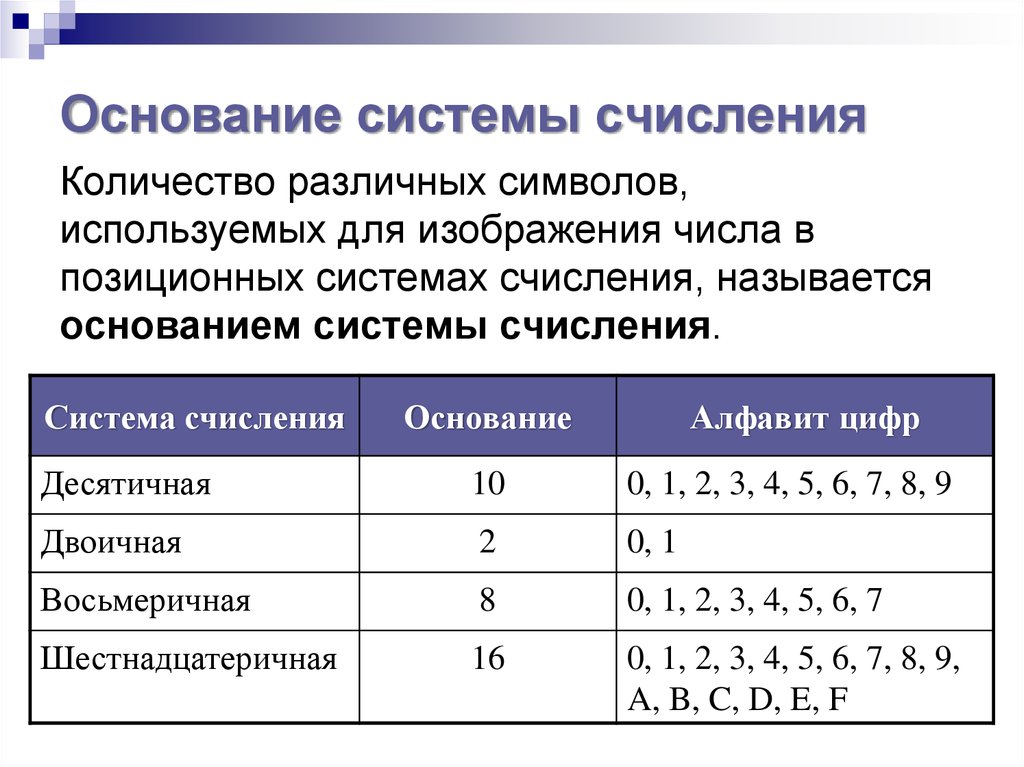	2 кв.
155	10011011	2123	233	9Б	4р	2р
156	10011100	2130	234	9С	4С	2С
157	10011101	2131	235	9Д	4Т	2Т
158	10011110	2132	236	9Е	4U	2U
159	10011111	2133	237	9Ф	4В	2В
160	10100000	2200	240	А0	50	2 Вт
161	10100001	2201	241	А1	51	2Х
162	10100010	2202	242	А2	52	2 года
163	10100011	2203	243	А3	53	2Z
164	10100100	2210	244	А4	54	2а
165	10100101	2211	245	А5	55	2б
166	10100110	2212	246	А6	56	2с
167	10100111	2213	247	А7	57	2д
168	10101000	2220	250	А8	58	2е
169	10101001	2221	251	А9	59	2ф
170	10101010	2222	252	АА	5А	2 г
171	10101011	2223	253	АБ	5Б	2 часа
172	10101100	2230	254	АС	5С	2и
173	10101101	2231	255	г. н.э.	5Д	2j
174	10101110	2232	256	АЭ	5Э	2к
175	10101111	2233	257	АФ	5F	2л
176	10110000	2300	260	Б0	5G	2 м
177	10110001	2301	261	Б1	5ч	2н
178	10110010	2302	262	Б2	5И	2о
179	10110011	2303	263	Б3	5Дж	2 шт.
180	10110100	2310	264	В4	5К	2к
181	10110101	2311	265	Б5	5л	2р
182	10110110	2312	266	В6	5М	2 с
183	10110111	2313	267	В7	5Н	2т
184	10111000	2320	270	В8	5О	2у
185	10111001	2321	271	В9	5П	2в
186	10111010	2322	272	БА	5Q	2 Вт
187	10111011	2323	273	ББ	5р	2x
188	10111100	2330	274	г. до н.э.	5С	2 года
189	10111101	2331	275	БД	5Т	2з
190	10111110	2332	276	БЭ	5У	2-
191	10111111	2333	277	БФ	5В	2_
192	11000000	3000	300	С0	60	30
193	11000001	3001	301	С1	61	31
194	11000010	3002	302	С2	62	32
195	11000011	3003	303	С3	63	33
196	11000100	3010	304	С4	64	34
197	11000101	3011	305	С5	65	35
198	11000110	3012	306	С6	66	36
199	11000111	3013	307	С7	67	37
200	11001000	3020	310	С8	68	38
201	11001001	3021	311	С9	69	39
202	11001010	3022	312	Калифорния	6А	3А
203	11001011	3023	313	КБ	6Б	3Б
204	11001100	3030	314	СС	6С	3С
205	11001101	3031	315	компакт-диск	6D	3Д
206	11001110	3032	316	СЕ	6Е	3Э
207	11001111	3033	317	КФ	6F	3F
208	11010000	3100	320	Д0	6G	3G
209	11010001	3101	321	Д1	6ч	3ч
210	11010010	3102	322	Д2	6И	3И
211	11010011	3103	323	Д3	6Дж	3Дж
212	11010100	3110	324	Д4	6К	3К
213	11010101	3111	325	Д5	6л	3л
214	11010110	3112	326	Д6	6М	3М
215	11010111	3113	327	Д7	6Н	3Н
216	11011000	3120	330	Д8	6О	3О
217	11011001	3121	331	Д9	6П	3П
218	11011010	3122	332	ДД	6Q	3 кв.
219	11011011	3123	333	ДБ	6Р	3р
220	11011100	3130	334	округ Колумбия	6С	3С
221	11011101	3131	335	ДД	6Т	3Т
222	11011110	3132	336	Германия	6У	3U
223	11011111	3133	337	ДФ	6В	3В
224	11100000	3200	340	Э0	70	3 Вт
225	11100001	3201	341	Е1	71	3X
226	11100010	3202	342	Е2	72	3 года
227	11100011	3203	343	Е3	73	3Z
228	11100100	3210	344	Е4	74	3а
229	11100101	3211	345	Е5	75	3б
230	11100110	3212	346	Е6	76	3с
231	11100111	3213	347	Е7	77	3д
232	11101000	3220	350	Е8	78	3е
233	11101001	3221	351	Е9	79	3ф
234	11101010	3222	352	шт.	7А	3g
235	11101011	3223	353	ЭБ	7Б	3 часа
236	11101100	3230	354	ЕС	7С	3i
237	11101101	3231	355	ЭД	7Д	3j
238	11101110	3232	356	ЕЕ	7Э	3k
239	11101111	3233	357	ЭФ	7Ф	3л
240	11110000	3300	360	Ф0	7G	3м
241	11110001	3301	361	Ф1	7ч	3н
242	11110010	3302	362	Ф2	7И	3о
243	11110011	3303	363	Ф3	7Дж	3р
244	11110100	3310	364	Ф4	7К	3к
245	11110101	3311	365	F5	7л	3р
246	11110110	3312	366	F6	7М	3 с
247	11110111	3313	367	F7	7Н	3т
248	11111000	3320	370	F8	7О	3у
249	11111001	3321	371	F9	7П	3в
250	11111010	3322	372	Ф. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт