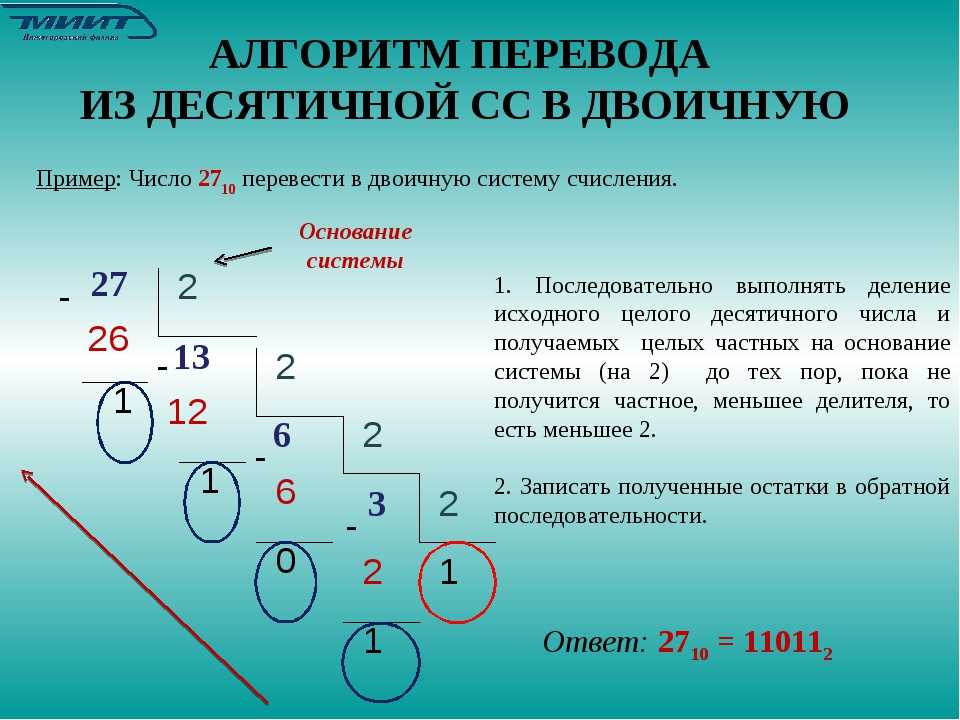
Система счисления — тест с ответами
Информатика в настоящее время является стремительно развивающийся наукой. Многие студенты постают в технические университеты, чтобы в будущем связать свою деятельность с IT или приближенными областями. Для проверки знаний по теме Система счисления предлагаем пройти тестирование на этой странице. Обращаем ваше внимание, что в тесте правильные ответы выделены символом [+].
Что такое система счисления?
[-] а) Правила выполнения операций над числами
[-] б) Правила записи чисел
[+] в) 1 и 2
[-] г) нет верного ответа
Название системы счисления, где в записи чисел могут быть использованы только цифры 0 1 2 3 4 5 6 7:
[-] а) Двоичной
[-] б) Семеричной
[+] в) Восьмеричной
[-] г) Нет верного ответа
Выберите системы счисления, где может быть число 501:
[+] а) Десятичная
[-] б) Двоичная
[+] в) Восьмеричная
[+] г) Шестнадцатеричная
Название системы счисления, где значение цифры зависит от занимаемой ею позиции в числе:
[-] а) позиционная;
[+] б) непозиционная;
[-] в) нет верного ответа;
[-] г) перечисленное в п. 1-
1-
Вид числа 101, которое записали в двоичной системе счисления, после перевода в десятичную:
[-] а) 3
[+] б) 5
[-] в) 4
[-] г) 6
Вид числа 10, которое записали в десятичной системе счисления, после перевода в двоичную:
[+] а) 1010
[-] б) 1000
[-] в) 1001
[-] г) 1100
Произведите сравнение двух чисел 111(двоичное) и 5 (десятичное):
[-] а) Числа равны
[+] б) Первое число больше второго
[-] в) Первое число меньше второго
Возможна ли запись одного и того же числа в разных системах счисления?
[+] а) Да
[-] б) Нет
Буду равным два числа: 11 в десятичной системе счисления и 11 в двоичной системе счисления?
[-] а) Да
[+] б) Нет
Произведите сравнение двух чисел 1002 и 410 :
[-] а) Первое число больше второго
[-] б) Второе число больше первого
[+] в) Равны
Название системы счисления, где применяют только цифры 0,1,2:
[-] а) двоичная
[+] б) троичная
[-] в) семиричная
[-] г) восьмиричная
Определите операцию, которая была применена к двоичным числам 1010 и 111, если в результате получено число 11?
[-] а) деление
[-] б) умножение
[-] в) сложение
[+] г) вычитание
Система счисления, где кроме цифр используются буквы латинского алфавита:
[-] а) двоичной
[-] б) восьмеричной
[-] в) десятичной
[+] г) шестнадцатиричной
Произведите перевод 295 из десятичной системы счисления в восьмеричную систему счисления:
[-] а) 426
[+] б) 447
[-] в) 744
[-] г) 432
Произведите перевод 287 из десятичной системы счисления в шестнадцатеричную систему счисления:
[+] а) 11F
[-] б) F11
[-] в) 1511
[-] г) 1115
Произведите перевод из восьмеричной системы счисления в двоичную число 1528:
[-] а) 101010012
[-] б) 1010100012
[+] в) 11010102
[-] г) 110110012
Произведите перевод из шестнадцатеричной системы счисления в двоичную число: 2ВС16
[-] а) 1100101100102
[+] б) 10101111002
[-] в) 1011110000102
[-] г) 001011100012
Что принято считать системой счисления?
[-] а) алфавит;
[-] б) способ представления чисел;
[+] в) способ представления чисел и соответствующие ему правила действия над числами;
[-] г) набор чисел в определенной последовательности;
Системы счисления подразделяются на:
[-] а) четные и нечетные;
[+] б) позиционные и непозиционные;
[-] в) троичные, семеричные, десятичные;
[-] г) двоичные, восьмеричные, шестнадцатеричные;
Какие символы есть в восьмеричной системе счисления?
[-] а) 0, 1, 2, 3, 4, 5, 6, 7, 8;
[+] б) 0, 1, 2, 3, 4, 5, 6, 7;
[-] в) 1, 2, 3, 4, 5, 6, 7, 8;
[-] г) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F
Какие символы есть в шестнадцатеричной системе счисления?
[-] а) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16;
[-] б) 0, 1, 2, 3, 4, 5, 6, 7;
[+] в) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F;
[-] г) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, А, В, С, D, E, F;
Какие символы есть в двоичной системе счисления:
[-] а) 1, 2;
[+] б) 0, 1;
[-] в) а, в;
[-] в) все перечисленные
Подберите число, которое соответствует числу 100102 в десятичной системе:
[+] а) 18;
[-] б) 17;
[-] в) 100;
[-] г) 36;
«Системы счисления» — Информатика, 10 класс
Результаты авторизованых пользователей
| Название теста | Дата | Результат | Пользователь |
|---|---|---|---|
| Философия / Мировоззрение | 02-07-2023 08:29:59 pm | 0/20 | tagir |
| Философия / Мировоззрение | 02-07-2023 08:27:42 pm | 0/20 | tagir |
| Философия / Мировоззрение | 02-07-2023 08:27:18 pm | 0/20 | tagir |
| Философия / Мировоззрение | 02-07-2023 08:27:01 pm | 0/20 | tagir |
| Философия / Мировоззрение | 02-07-2023 08:21:01 pm | 2/20 | tagir |
Все результаты
#1.
 Что такое система счисления
Что такое система счисленияA. Знаковая система, в которой числа записываются по определенным правилам с помощью символов (цифр) некоторого алфавита
A. Знаковая система, в которой числа записываются по определенным правилам с помощью символов (цифр) некоторого алфавитаB. Представление чисел с помощью букв
B. Представление чисел с помощью буквC. Произвольная последовательность символов
C. Произвольная последовательность символов#2. Какая из приведенных ниже систем счисления относится к позиционным
A. Славянская система счисления
A. Славянская система счисленияB. Двоичная система счисления
B. Двоичная система счисленияC. Римская система счисления
C. Римская система счисления#3. Какое число будет записано в свернутой форме 5*102+3*101+4*100+1*10-1+2*10-2
A. 53,12
53,12
B. 53412
B. 53412C. 534,12
C. 534,12#4. Переведите число 243 из десятичной системы счисления в двоичную
A. 11110011
A. 11110011B. 110111
B. 110111C. 11001111
C. 11001111#5. Переведите число 37 из десятичной системы счисления в двоичную
A. 36
A. 36B. 22
B. 22C. 26
C. 26#6. Какие системы счисления не используются специалистами для общения с ЭВМ
A. двоичная
A. двоичнаяB. троичная
B. троичнаяC. десятичная
C. десятичная#7.
 На берегу моря лежало 10 камешков. Набежавшая волна выбросила еще несколько. Их стало 1000. Сколько камешков было выброшено волной
На берегу моря лежало 10 камешков. Набежавшая волна выбросила еще несколько. Их стало 1000. Сколько камешков было выброшено волнойA. 1000
A. 1000B. 1011
B. 1011C. 1010
C. 1010#8. Что называется основанием системы счисления
A. отношение значений единиц соседних разрядов
A. отношение значений единиц соседних разрядовB. количество цифр, используемых для записи чисел
B. количество цифр, используемых для записи чиселC. арифметическая основа ЭВМ
C. арифметическая основа ЭВМ#9. Переведите число 138 из десятичной системы счисления в двоичную
A. 1001010
A. 1001010B. 10000110
B. 10000110 C.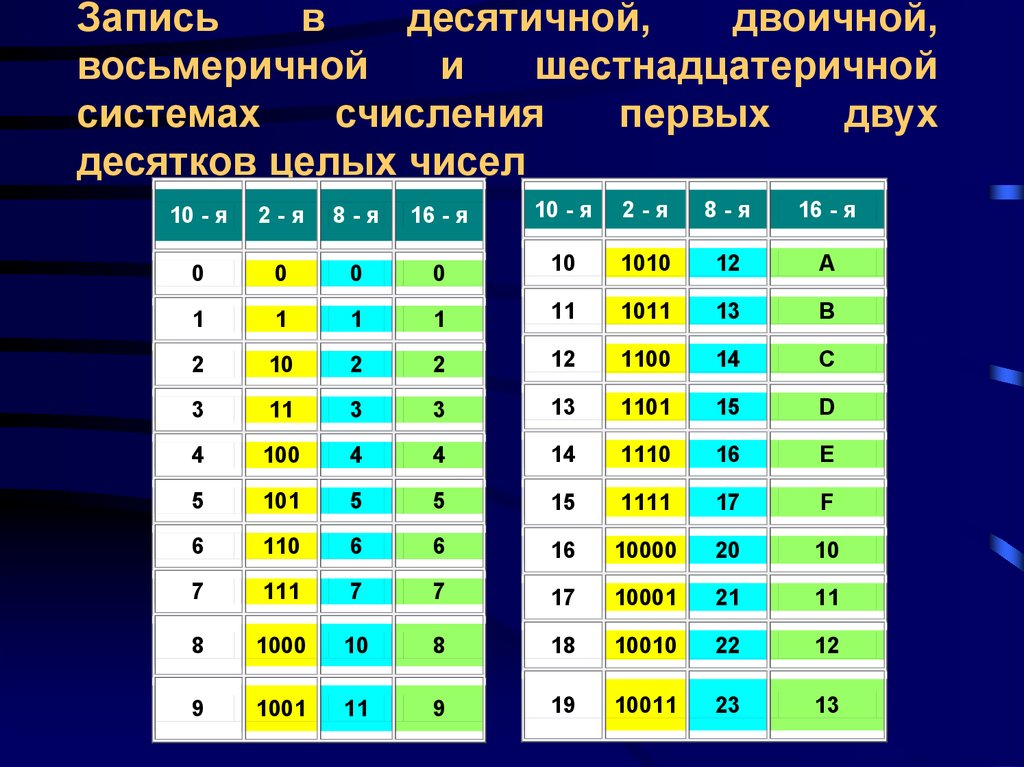 10001010
10001010
#10. Переведите число 11011012 из двоичной системы счисления в десятичную систему счисления
A. 209
A. 209B. 109
B. 109C. 104
C. 104#11. Какая система счисления используется специалистами для общения с ЭВМ
A. двоичная
A. двоичнаяB. пятеричная
B. пятеричнаяC. троичная
C. троичная#12. Греются на солнышке воробьи. На нижней ветке их было 110, а на верхней на 2 меньше. Сколько всего было воробьев
A. 1011
A. 1011B. 1010
B. 1010C. 1001
C. 1001#13. Все системы счисления делятся на две группы
A. позиционные и непозиционные
позиционные и непозиционные
B. римские и арабские
B. римские и арабскиеC. целые и дробные
C. целые и дробные#14. Переведите число 11012 из двоичной системы счисления в десятичную систему счисления
A. 12
A. 12B. 15
B. 15C. 13
C. 13#15. Числовой разряд
A. позиция цифры в числе
A. позиция цифры в числеB. цифра в изображении числа
B. цифра в изображении числаC. показатель степени основания
#16. Младший брат учится в 101 классе. Старший на 11 старше. В каком классе учится старший брат
A.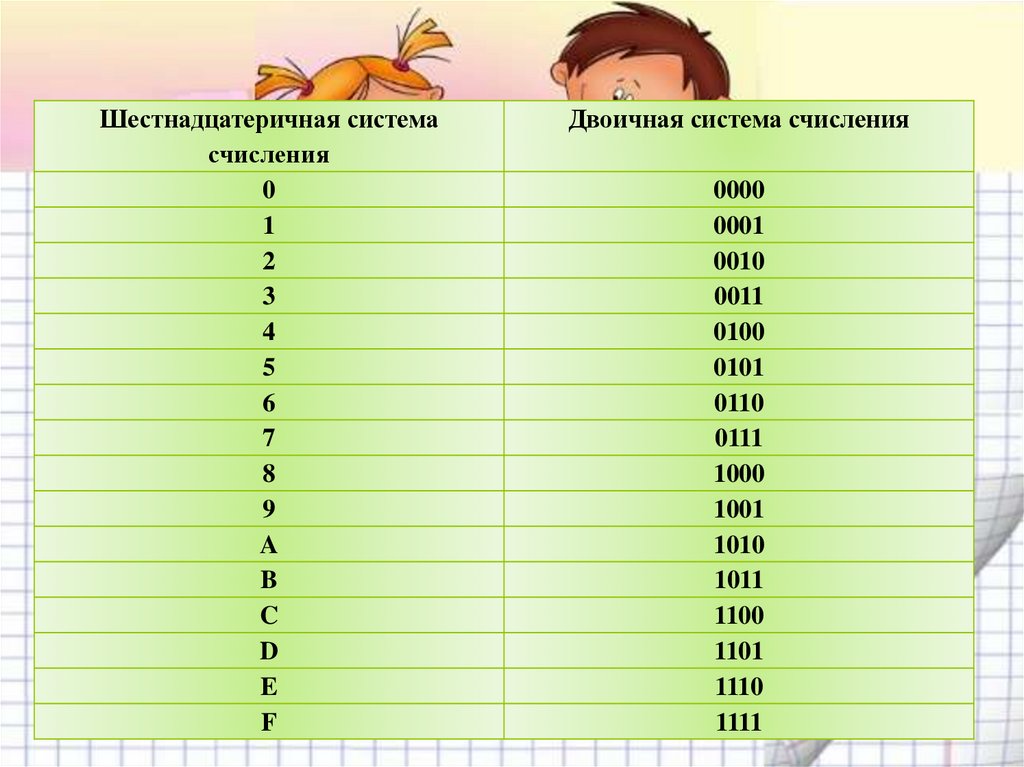 1010
1010
B. 1000
B. 1000C. 1111
C. 1111#17. Какое количество цифр используется в десятеричной системе счисления
A. 100
A. 100B. бесконечное количество
B. бесконечное количествоC. 10
C. 10#18. Переведите число 27 из десятичной системы счисления в двоичную
A. 11111
A. 11111B. 11011
B. 11011C. 1101
C. 1101#19. Переведите число 11112 из двоичной системы счисления в десятичную систему счисления
A. 21
A. 21B. 14
B. 14C. 7
C. 7#20. В позиционной системе счисления
A. цифра умножается на основание системы счисления
цифра умножается на основание системы счисления
B. количественное значение цифры зависит от ее позиции в числе
B. количественное значение цифры зависит от ее позиции в числеC. количественное значение цифры не зависит от ее позиции в числе
C. количественное значение цифры не зависит от ее позиции в числе#21. В кабинетах биологии и информатики 1010 кактусов. В биологии их 111. Сколько кактусов в кабинете информатики
A. 11
A. 11B. 21
B. 21C. 1110
C. 1110#22. В позиционных системах счисления основание системы
A. правила арифметических действий
A. правила арифметических действийB. максимальное количество знаков, используемое для записи числа
 максимальное количество знаков, используемое для записи числа
максимальное количество знаков, используемое для записи числаC. числовой разряд
C. числовой разряд#23. Переведите число 49 из десятичной системы счисления в двоичную
A. 100011
A. 100011B. 101101
B. 101101C. 110001
C. 110001#24. Переведите число 1110112 из двоичной системы счисления в десятичную систему счисления
A. 599
A. 599B. 59
B. 59C. 95
C. 95#25. Почему в ЭВМ используется двоичная система счисления
A. потому что человеку проще общаться с компьютером на уровне двоичной системы счисления
A. потому что человеку проще общаться с компьютером на уровне двоичной системы счисления B.
C. потому что составляющие технические устройства могут надежно сохранять и распознавать только два различных состояния
C. потому что составляющие технические устройства могут надежно сохранять и распознавать только два различных состояния#26. У первоклассника Паши 1111 палочек для счета. У Вани 101. На сколько палочек у Паши больше, чем у Вани
A. 1001
A. 1001B. 1010
B. 1010C. 1000
C. 1000#27. Переведите из двоичной системы счисления в восьмеричную число 11112
A. 17
A. 17B. 19
B. 19C. 23
C. 23#28. Сложите числа в двоичной системе счисления 101112 + 10112
A.
B. 10010
B. 10010C. 100010
C. 100010#29. Переведите число 10101010001110 из двоичной системы в восьмеричную
A. 25216
A. 25216B. 35217
B. 35217C. 61252
C. 61252#30. Переведите число 71 из восьмеричной системы счисления в двоичную
A. 1111
A. 1111B. 111001
B. 111001C. 100111
C. 100111Показать результаты
Оцените тест после прохождения!
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 1
Оценок пока нет. Поставьте оценку первым.
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
Помощь в написании работы
Десятичное число в двоичное — метод преобразования, примеры решения, викторина и часто задаваемые вопросы
Важно преобразовать значение из одной системы счисления в другую систему счисления. При этом мы сможем сказать, когда два разных значения будут представлять одинаковую сумму. При преобразовании десятичного числа в двоичное мы преобразуем числа с основанием 10 в числа с основанием 2, используя простую процедуру. Например, если десятичное число равно (11)₁₀, то его эквивалентное двоичное число будет (1011)₂. В этой статье мы обсудим преобразование десятичной системы счисления в двоичную с помощью примеров преобразования десятичной системы счисления в двоичную.
При этом мы сможем сказать, когда два разных значения будут представлять одинаковую сумму. При преобразовании десятичного числа в двоичное мы преобразуем числа с основанием 10 в числа с основанием 2, используя простую процедуру. Например, если десятичное число равно (11)₁₀, то его эквивалентное двоичное число будет (1011)₂. В этой статье мы обсудим преобразование десятичной системы счисления в двоичную с помощью примеров преобразования десятичной системы счисления в двоичную.
Пример преобразования десятичной системы счисления в двоичную
Здесь мы обсудим пример преобразования десятичной системы счисления в двоичную: —
Как мы знаем, десятичная система счисления имеет основание 10, а двоичная система счисления имеет основание 2. При преобразовании десятичных чисел в двоичные числа, основание десятичных чисел, т. е. 10, будет изменено на основание Конверсионной двоичной системы счисления, т. е. 2. Все десятичные числа сохраняют свои эквивалентные двоичные числа. Например, если мы хотим преобразовать (294)₁₀, то мы разделим это число на 2. У нас останется некоторый остаток и значение частного после деления данного числа на 2. Число будет делиться на 2 до тех пор, пока частное значение достигает нуля. Когда значение частного достигает 2, поместите оставшееся значение в последовательность младшего значащего бита (LSB) вверху и старшего значащего бита (MSB) внизу,
Например, если мы хотим преобразовать (294)₁₀, то мы разделим это число на 2. У нас останется некоторый остаток и значение частного после деления данного числа на 2. Число будет делиться на 2 до тех пор, пока частное значение достигает нуля. Когда значение частного достигает 2, поместите оставшееся значение в последовательность младшего значащего бита (LSB) вверху и старшего значащего бита (MSB) внизу,
Двоичные числа чаще всего используются компьютерами для целей кодирования и программирования, поскольку в двоичной системе счисления сохраняются 2 цифры 0 и 1, а компьютеры понимают только язык двоичной системы счисления. (изображение будет загружено в ближайшее время)
Как преобразовать десятичную систему счисления в двоичную систему счисления?
Чтобы преобразовать десятичные числа в двоичные, необходимо выполнить следующие шаги:-
Возьмите любое десятичное число и разделите его на «2». После деления вы получите некоторые результаты вместе с остатком.
Если выбранное вами десятичное число четное, то результатом будет целое число, а остаток даст 0.
Если выбранное вами десятичное число нечетное, то число не будет делиться полностью и вы получите остаток «1».
Продолжайте делить число, пока не получите частное 0
Теперь поместите все остатки в последовательности: младший бит (LSB) вверху и старший бит (MSB) внизу.
Основываясь на предыдущих шагах, давайте обсудим преобразование десятичных чисел в двоичные на примере.
Преобразуем десятичное число 244 в двоичное число.
Division of Decimal Number by 2 | Quotient | Remainder | Binary |
244/2 | 122 | 0 | 0 (младший бит) |
122/2 | 61 | 0 | 0 |
61/2 | 30 | 1 | 1 |
30/2 | 15 | 0 | 0 |
15/2 | 7 | 1 | 1 |
7/2 | 3 | 1 | 1 |
3/2 | 1 | 1 | 1 |
1/2 | 0 | 1 | 1 (MSB) |
Отсюда.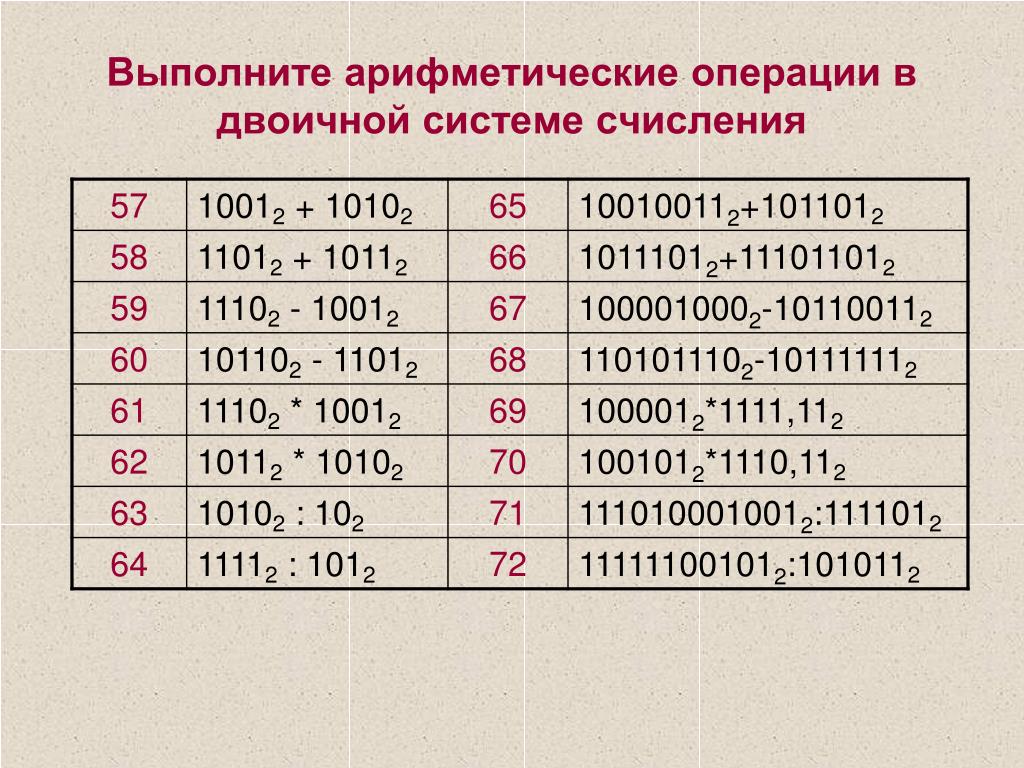 0005
0005
Вот некоторые из решенных примеров преобразования десятичной системы счисления в двоичную: —
1. Как преобразовать число 145 в двоичную систему счисления?
Solution:
Division of Decimal Number by 2 | Quotient | Remainder | Binary |
145/2 | 72 | 1 | 1 (LSB) |
72/2 | 36 | 0 | 0 |
36/2 | 18 | 0 | 0 |
18/2 | 9 | 0 | 0 |
9/8 | 4 | 1 | 1 |
4/2 | 2 | 0 | 0 |
2/2 | 1 | 0 | 0 |
1/2 | 0 | 1 | 1 (MSB) |
Hence, 145₁₀ = 10010001₂
2. Как преобразовать 112 в двоичную систему счисления?
Как преобразовать 112 в двоичную систему счисления?
Solution:
Division of Decimal Number by 2 | Quotient | Remainder | Binary |
112/2 | 56 | 0 | 0 |
56/2 | 28 | 0 | 0 |
28/2 | 14 | 0 | 0 |
14/2 | 7 | 0 | 0 |
7/2 | 3 | 1 | 1 |
3/2 | 1 | 1 | 1 |
1/2 | 0 | 1 | 1 |
Следовательно, 112₁₀ = 1110000₂
Задачи преобразования десятичных чисел в двоичные числа
Вот несколько вопросов, приведенных ниже относительно преобразования десятичных чисел в двоичные, которые должны решить учащиеся. Решение вопросов снова и снова поможет им быстро решить проблему. Благодаря этому они смогут точно решать вопросы и получать хорошие оценки на экзамене.
Решение вопросов снова и снова поможет им быстро решить проблему. Благодаря этому они смогут точно решать вопросы и получать хорошие оценки на экзамене.
Преобразование 112₁₀ в двоичную систему счисления
Преобразование 25673₁₀ в эквивалентное ему двоичное число.
Каким двоичным эквивалентом будет число 12999₁₀?
Преобразование 555₁₀ в двоичное число.
Интересные факты
Десятичная система счисления также известна как десятичная или двоичная система счисления.
Китайская система счетных стержней и индийско-арабская система счисления — единственные две позиционные десятичные системы в древней цивилизации.

Большинство компьютерных систем хранения, таких как компакт-диски DVD, используют двоичную систему счисления для представления больших файлов.
Набор из 8 двоичных цифр известен как бит
Иногда слово «точка» используется вместо «десятичный», чтобы указать точку, используемую для разделения позиции числа в десятичном числе. Система.
Время викторины
1. Сколько уникальных символов существует в двоичных системах счисления?
а. 15
б. 7
в. 2
д. 9
2. Какое наибольшее четырехзначное число можно составить из десятичных чисел?
а. 9999
б. 10000
в. 999
999
д. 1000
3. Какое наибольшее четырехзначное число можно составить из двоичных чисел?
а. 16
б. 13
в. 14
д. 15
4. Преобразуйте 100₁₀ в двоичную систему счисления.
а. 1100100
б. 1000100
в. 1111100
д. 1100101
Важность метода преобразования десятичных чисел в двоичные
Вы можете задаться вопросом, когда Интернет переполнен информацией о важности метода преобразования десятичных чисел в двоичные, тогда почему вы должны ссылаться только на веб-сайт Vedantu? Что ж, это очень правильный вопрос.
В Vedantu мы гарантируем, что весь предоставляемый вам контент подготовлен только экспертами, обладающими соответствующими знаниями в данной области. Они курируют информацию таким образом, чтобы она была удобна как для студентов, так и для новичков. Это поможет вам понять тему с самых основ, а позже вы сможете опираться на нее.
Это поможет вам понять тему с самых основ, а позже вы сможете опираться на нее.
Помимо надежности материалов, все это предоставляется вам абсолютно бесплатно. Никаких скрытых платежей не предусмотрено. Вам даже не нужно регистрироваться, так как они являются частью информации Vedantu с открытым исходным кодом и могут быть доступны любому.
Вывод:
Прочитав это, вы сможете распознать, является ли данное число двоичным или десятичным, вы узнаете определения обоих, вы узнаете, как их можно преобразовать друг в друга, необходимую формулу сделать это, и важность этого преобразования. Чтобы еще больше подогреть ваш энтузиазм, мы добавили забавные факты, которые вы можете прочитать и получить удовольствие от обучения. Помимо этого, в конце было предложено много вопросов, чтобы вы могли проверить свое понимание темы. Этот отчет был подготовлен очень целостно, чтобы вы могли понять и преуспеть на экзаменах.
3.
 3.4 Двоичная арифметика
3.4 Двоичная арифметикаИзучите
Двоичные дополнения
- В двоичной системе счисления или системе счисления с основанием 2 есть только две цифры,
0и1. - Это означает, что в отличие от десятичной системы счисления
1 + 1не равно2, это равно10. - Ознакомьтесь со следующими правилами, которые применяются при сложении двоичных чисел.
вместе:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (
0исодержат 1) - 1 + 1 + 1 = 11 (
1исодержат 1)
- Двоичное сложение можно выполнить с помощью сложения столбцов. Поскольку наибольшее значение, которое может иметь однозначное двоичное число, равно 1, что угодно превышающее это, должно быть перенесено в следующую колонку (2) в таблица значений мест с основанием 2:
| 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|
| 1 | ||||||
| + | 1 | |||||
| Ответить | 1 | 0 | ||||
Переносится | 1 |
- Посмотрите, как
0101и0111были сложены вместе с помощью столбца дополнение в примере ниже:
| 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | |||
| + | 0 | 1 | 1 | 1 | ||
| Ответить | 1 | 1 | 0 | 0 | ||
Переносится | 1 | 1 | 1 |
-
1 + 1 = 10и10 + 1 = 11поэтому: -
1 + 1 + 1 = 11
Ошибки переполнения
- Ошибка переполнения возникает при ответе на двоичное сложение
уравнение больше, чем ЦП способен обрабатывать.
- Например, процессор с разрядностью 8 бит может обрабатывать двоичные данные.
номера до
11111111. Однако, если добавить еще один бит, чтобы дать100000000, 9-битный ответ, ЦП проигнорирует1и выведет00000000, что неверно.
Объяснение двоичного сложения
- В следующем видео показано, как выполнить двоичное сложение.
Badge It
Silver — выполните следующие бинарные дополнения:
1
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | |
| + | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| Ответить | ||||||||
Переносится |
2
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | |
| + | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| Ответить | ||||||||
Переносится |
3
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | |
| + | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| Ответить | ||||||||
Переносится |
Загрузка в представление данных — двоичная арифметика: серебро на BourneToLearn
Learn It
Двоичные сдвиги
- В двоичной системе счисления или системе счисления с основанием 2 значение цифры изменяется
в степени двойки, когда его место в числе смещается влево
(умножение)или направо(разделенный) - В следующей таблице показано, как двоичные числа сдвигаются в степени из двух:
| Сдвиг влево | Сдвиг вправо | |
|---|---|---|
| Смена 1 место | Умножить на 2 | Разделить на 2 |
| Смена 2 места | Умножить на 4 | Разделить на 4 |
| Смена 3 места | Умножить на 8 | Разделить на 8 |
Сдвиг влево (умножение) двоичного числа)
- Если двоичное число сдвинуто влево, это эквивалентно
умножение числа на 2 для каждого сдвига влево.
- Например: Если мы сдвинем
на две позициивлево:
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
<—————————————————
- Это дает нам двоичное число:
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
- (Примечание: мы заполняем пустые бинарные позиции
нулямипо мере перехода к слева) - Исходное двоичное число имеет значение
15(т. е. 8 + 4 + 2 + 1 =
15).
е. 8 + 4 + 2 + 1 =
15). - После сдвига на две позиции влево получается
60(т.е. 32 + 16 + 8 + 2 + 1 = 15). Это умножается на4или 2 2
Сдвиг вправо (деление) двоичного числа)
- Если двоичное число сдвинуто вправо, это эквивалентно деление числа на 2 для каждого сдвига влево.
- Например: если мы сдвинем
на триразряда вправо:
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
—————————————————>
- Это дает нам двоичное число:
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
- Исходное двоичное число имеет значение
112(т. е. 64 + 32 + 16 =
112).
е. 64 + 32 + 16 =
112). - После сдвига на три позиции вправо значение равно
14(т.е. 8 + 4 + 2 = 14). Число было разделено на8и стало 2 3 - (Примечание: мы заполняем пустые бинарные позиции
нулямипо мере перехода к справа)
Badge It
Золото — Запишите результаты после следующих операций сдвига и запишите десятичные значения до и после сдвигов:
1. Двоичное число 11001100 сдвинуто на ДВА знака вправо. 2. Двоичное число 00011001 сдвинуто на ДВА знака влево. 3. Двоичное число 11001000 сдвинуто на ТРИ знака вправо. 4. Двоичное число 00000111 сдвинуто на ЧЕТЫРЕ разряда влево. 5. Двоичное число 10000000 сдвинуто на ПЯТЬ знаков вправо.
Загрузка в представление данных — двоичная арифметика: Золото на BourneToLearn
Точность двоичного сдвига с умножением/делением на степени 2
- Этот метод позволяет легко умножать и делить двоичные числа.