Перевод из десятичной в восьмеричную систему счисления, калькулятор
Реклама
- CALCUS.RU
- Перевод систем счисления
- Перевод из десятичной в восьмеричную
Исходное число
Направление перевода
2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
Сообщить об ошибке
В избранное
Виджет
Вы можете сохранять ваши расчеты и они будут отображаться здесь.
Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.
Для того, чтобы преобразовать число из десятичной системы счисления в восьмеричную, необходимо выполнить следующие действия.
- Делим десятичное число на 8 и записываем остаток от деления.
- Результат деления вновь делим на 8 и опять записываем остаток.
- Повторяем операцию до тех пор пока результат деления не будет равен нулю.
- Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 375
375 / 8 = 46 (остаток 7)
46 / 8 = 5 (остаток 6)
5 / 8 = 0 (остаток 5)
Записываем остатки в обратном порядке, получаем результат: 5678
Смотрите также
- Перевод из двоичной в десятичную
- Перевод из двоичной в восьмеричную
- Перевод из двоичной в шестнадцатеричную
- Перевод из десятичной в двоичную
- Перевод из десятичной в шестнадцатеричную
- Перевод из восьмеричной в двоичную
- Перевод из восьмеричной в десятичную
- Перевод из шестнадцатеричной в двоичную
- Перевод из шестнадцатеричной в десятичную
Восьмеричная система счисления
Тип урока: урок введения нового материала в 8 классе.
Дидактическая цель урока:
ознакомление учащихся с восьмеричной системой счисления, с переводом чисел из восьмеричной в десятичную систему счисления, и обратно, а так же с переводом из восьмеричной системы счисления в двоичную систему счисления и обратно. Отработка навыков перевода из одной системы счисления в другую.Развивающая цель урока: развитие умения рассуждать, сравнивать, делать выводы. Развитие памяти, внимательности, познавательного интереса к предмету с использованием соответствующих заданий.
Воспитательная: формирование самоконтроля у школьников.
Этапы урока:
- Организация начала урока – 2 мин.
- Проверка домашнего задания – 10 мин.
- Подготовка учащихся к усвоению новых знаний – 5 мин.
- Введение нового материала – 8 мин.
- Первичное закрепление нового материала – 5 мин.
- Контроль и самопроверка знаний – 10 мин.
- Информация о домашнем задании – 3 мин.
- Подведение итогов урока – 2 мин.
Структура урока:
- Проверка домашнего задания.
- Знакомство с записями восьмеричных чисел.
- Перевод целого числа из восьмеричной системы счисления в десятичную с проверкой.
- Перевод числа из восьмеричной системы счисления в двоичную и обратно.
- Информация о домашнем задании.
- Подведение итогов урока.
Средства обучения:
- Приложение операционной системы Windows XP-Калькулятор.
- Индивидуальная карточка учащегося.
- Алгоритм работы в приложении о.с. Windows XP-Калькулятор.
- Презентация.
- Карточка с заданием для перевода чисел из восьмеричной системы счисления в десятичную систему счисления.
- Карточка с заданиями для перевода из одной системы счисления в другую с помощью двоично-восьмеричной таблицы.
- Карточка с творческим заданием.
1 этап. Организация начала урока.
Цель этапа: подготовка учащихся к работе на занятиях.
Здравствуйте, ребята!
Сегодня на уроке мы с вами познакомимся с восьмеричной системой счисления и отработаем навыки перевода из одной системы счисления в другую.
Получают индивидуальные карточки, которые подписывают и куда будут вносить ответы заданий.
| Ф.И. | ||
| №1 | №2 | №3 |
Приложение 1
2 этап. Проверка выполнения домашнего задания.

Цель этапа: установление правильности и осознанности выполнения домашнего задания всеми учащимися, выявление пробелов и их коррекция.
Проверим выполнение домашнего задания с помощью стандартного приложения ОС Windows XP-Калькулятор.
Домашнее задание: переведите числа из двоичной системы счисления в десятичную и сделайте проверку.
Получают листы с алгоритмом работы в приложении Калькулятор, проверяют домашнее задание за ПК.
Приложение 2
Ответы проверим с помощью презентации к уроку.
- 102=210
- 112=310
- 1002=410
- 1012=510
- 1102=610
- 1112=710
3 этап. Введение нового материала.
Цель этапа: обеспечение восприятия, осмысления и первичного запоминания знаний и способов действий, связей и отношений в объекте изучения.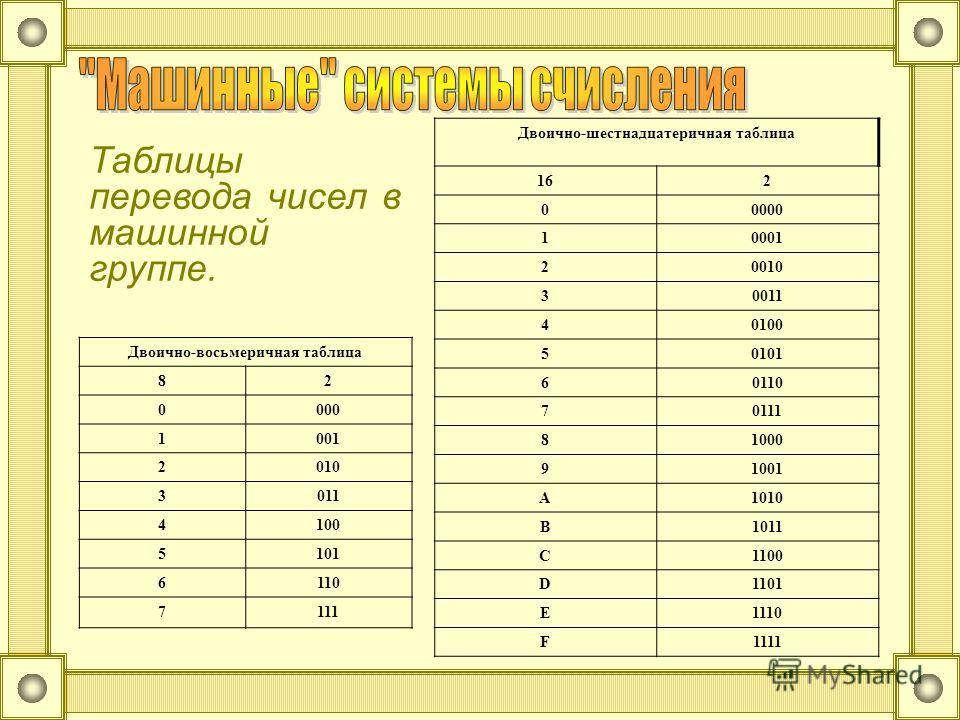
Запишите тему сегодняшнего урока: «Восьмеричная система счисления».
Основание: 8
Алфавит цифр: 0, 1, 2, 3, 4, 5, 6, 7
Рассмотрим перевод целого числа из восьмеричной системы счисления в десятичную и выполним проверку.
Алгоритм перевода целого числа из восьмеричной системы счисления в десятичную.
Записать восьмеричное число в развернутой форме и вычислить ее значение.
Пример 1.
10
218=2*81+1*80=16+1=1710
Выполним проверку.
Алгоритм перевода целого числа из десятичной системы счисления в восьмеричную.
- Последовательно выполнять деление исходного целого десятичного числа на 8 до получения результата строго меньше основания системы.
- Полученные остатки записать в обратной последовательности.
1710→А8
1710=218
Пример 2.
10
718=7*81+1*80=56+1=5710
4 этап. Первичное закрепление нового материала.
Цель этапа: установление правильности и осознанности усвоения нового учебного материала.
Задание №1 на первичное закрепление нового материала. Приложение 3
Перевести число из восьмеричной системы счисления в десятичную и выполнить проверку.
210
1148 =1*82+1*81+4*80=64+8+4=7610
Проверка:
7610=1148
Выбрать правильный ответ под соответствующей буквой и записать букву в индивидуальную карточку.
О) 8410
У) 7610
Е) 9710
5 этап. Контроль и самопроверка знаний.
Цель этапа: выявление качества и уровня овладения знаниями и способами действий.
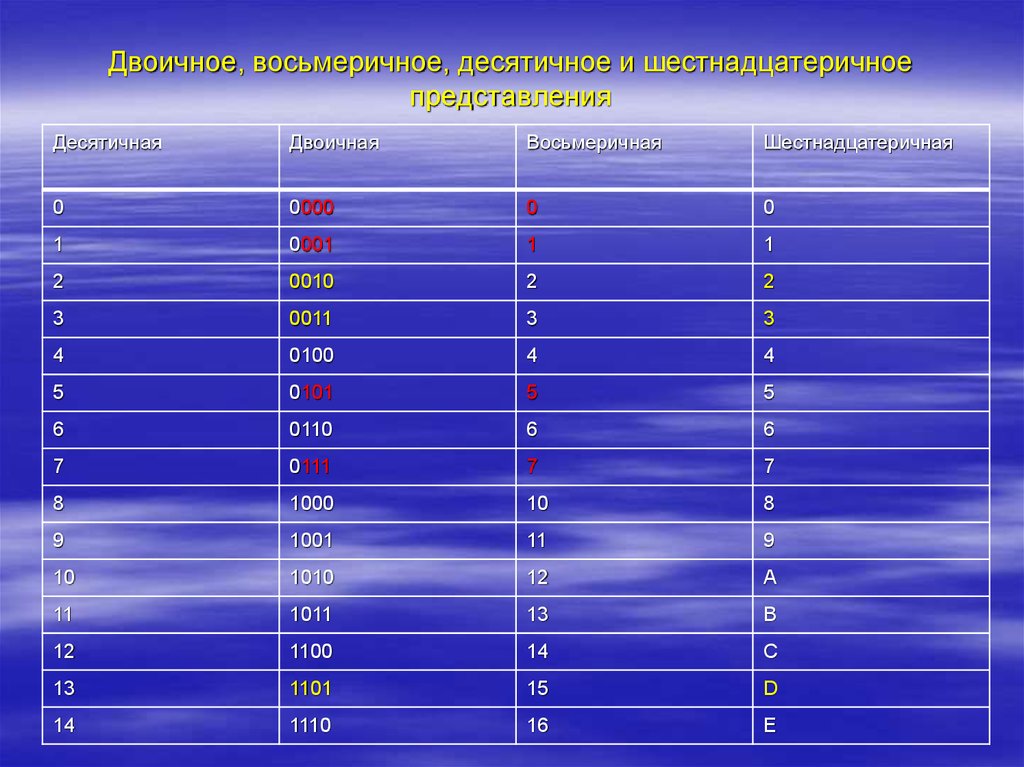
Мы научились переводить числа из одной системы в другую, а теперь рассмотрим способы переводов, которые не требуют от нас каких-либо вычислений. Для этого в тетради начертим таблицу, состоящую из двух столбцов. Число в 8-ой системе счисления соответствует тройке цифр двоичной системы счисления. Например, 08=0002, 18=0012, далее обратимся к проверяемому в начале урока домашнему заданию. Таблица легко заполняется.
Двоично-восьмеричная система счисления.
| 8 | 2 |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
При переводе восьмеричного числа в двоичное заменяют каждую восьмеричную цифру на соответствующую тройку цифр из таблицы.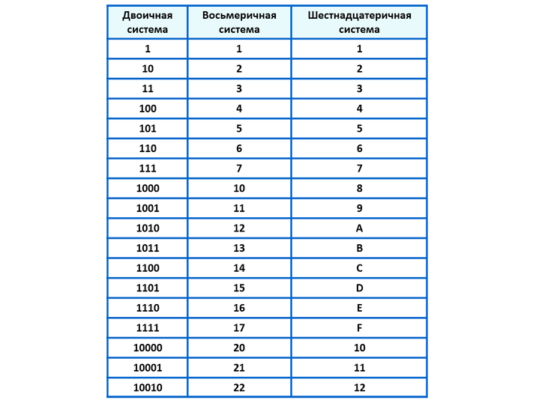 Для обратной операции, то есть для перевода из двоичной в восьмеричную систему, двоичное число разбивают на тройки цифр, потом заменяют каждую группу одной восьмеричной цифрой.
Для обратной операции, то есть для перевода из двоичной в восьмеричную систему, двоичное число разбивают на тройки цифр, потом заменяют каждую группу одной восьмеричной цифрой.
Например:
7148=111 001 1002
101 110 1002=5648.
Учащимся раздаются карточки с заданиями. После их решения, правильные ответы помещаются в индивидуальную карточку ученика.
Задания №2, №3 на контроль и самопроверку знаний. Приложение 4
Переведите числа из одной системы счисления в другую (с помощью двоично-восьмеричной таблицы).
2. Переведите число из восьмеричной системы счисления в двоичную систему счисления.
5328 =А2
ц) 11010012; р)101 011 0102; в) 1110011002;
3. Переведите из двоичной системы счисления в восьмеричную систему счисления.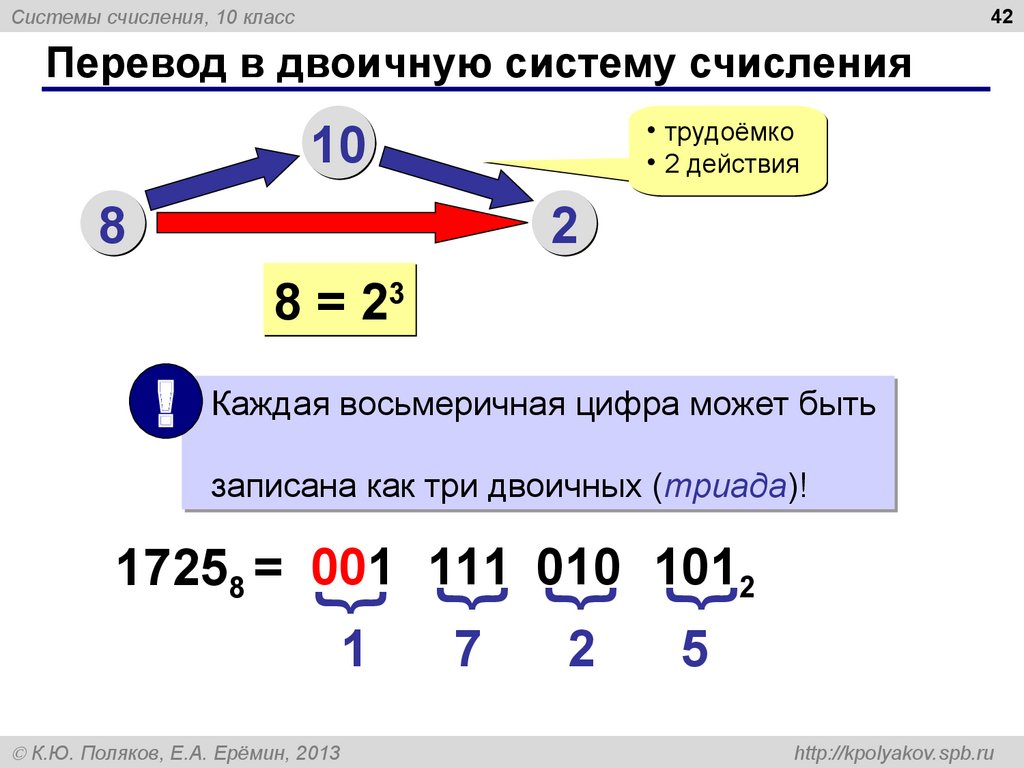
111 1112 =А8
а) 778; о) 648; в) 298;
Сдайте индивидуальные карточки и раздаточный материал. Проверим ответы с помощью слайда № 7 презентации к уроку.
Правильные ответы:
№2 р)101 011 0102
№3 а) 778
Индивидуальная карточка примет вид:
| Ф.И. | ||
| №1 | №2 | №3 |
| У | Р | А |
Ученики получают раздаточный материал с творческим заданием. Даны координаты точек в разных системах счисления.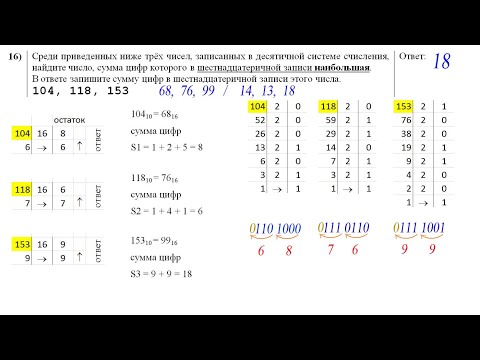 Необходимо выполнить перевод координат в десятичную систему счисления, отметить и соединить точки на координатной плоскости.
Необходимо выполнить перевод координат в десятичную систему счисления, отметить и соединить точки на координатной плоскости.
Творческое задание. Приложение 5
Даны координаты точек:
1(1002,12)
2(1002, 1102)
3(1002, 10002)
4(108,108)
5(68,78)
6(108,68)
Выполните перевод чисел в десятичную систему счисления и в координатной плоскости поставьте и соедините все точки.
Ответ (в десятичной системе счисления):
| 1 | 2 | 3 | 4 | 5 | 6 |
| (4,1) | (4,6) | (4,8) | (8,8) | (6,7) | (8,6) |
Рисунок 1
6 этап.
 Информация о домашнем задании.
Информация о домашнем задании.Цель этапа: обеспечение понимания цели, содержания и способов выполнения домашнего задания.
Переведите числа из восьмеричной системы счисления в двоичную, затем в десятичную систему счисления.
358 →А2→А10
658 → А2→А10
2158 → А2→А10
7 этап. Подведение итогов урока.
Цель этапа: дать анализ и оценку успешности достижения цели.
Если у вас в индивидуальной карте получилось слово: УРА, то вы получили «5».
Если справились с 2-мя заданиями, то оценка «4».
Если решили 1-о задание, то вы получили «3».
Сегодня на уроке мы познакомились с восьмеричной системой счисления, рассмотрели разные способы перевода чисел из одной системы счисления в другую. Одни из способов требовали от нас решать задачи математическими методами, другие с привлечением компьютера, третьи не требовали от нас каких-либо вычислений.
Спасибо за урок.
Преобразователь случайных чисел | Преобразование восьмеричной системы счисления с основанием 10 Конвертер длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность. Откуда: двоично-десятичный шестнадцатеричный base-2base-3base-4base-5base-6base-7base-8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base -23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base-23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 Уровень звукового давленияЗнаете ли вы, почему певцы не использовать измерительные микрофоны для записи в студии? Обзор Различные способы представления чисел Индо-арабские цифры Римские Системы в других культурах Унарная Позиционная система
Орден важен в римской системе, потому что большее число, за которым следует меньшее значение, которое нужно добавить, но меньшее число перед большим означает, что меньшее число вычитается из большего. Системы в других культурахЛюди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв. Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа. В некоторых культурах используются более простые представления, такие как вавилонская система, которая имеет только два клинописных символа: один (немного напоминающий букву «Т») и десять (немного похожий на букву «С»). Унарная система счисления. Метки подсчета в различных культурах Унарная Унарная система представляет каждое число с тем же количеством символов, что и его значение. Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства. Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему. Позиционная система Позиционная система работает с основанием.
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи. Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰ Двоичная система счисления Двоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2. Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Художественное представление двоичных чисел
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию. Например: 11111 (31) В этом случае, работая справа налево:
Итак, складывая это вместе, мы получаем 101010. Вычитание работает по тому же принципу, только вместо переноса единиц мы «заимствуем» единицы. Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например: 101 (5) Деление и расчет квадратных корней также очень похожи на основание-10. Классификация номеровВсе номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются. Долг — отрицательное число Отрицательные числаОтрицательные числа — это числа, представляющие отрицательное значение. Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число. Рациональные числа Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число. Натуральные числаНатуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456. Целые числаЦелые числа включают нули, отрицательные и положительные числа, которые не являются дробями. Примеры включают -65 и 11 223. Комплексные числаКомплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательного числа. Простые числа Простые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге. Интересные факты о числахКитайские цифры для защиты от мошенничества Числительные для защиты от мошенничестваДля предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать, добавив дополнительные штрихи. Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи. Современный счет в торговлеНекоторые языки в странах, где в настоящее время используется 10-кратная система счисления, свидетельствуют о том, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов. Группировка чисел И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. Несчастливые числаЛеонардо да Винчи. Последний ужин. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия. В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году. В России и многих странах бывшего СССР все четных чисел считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае число 7 также является несчастливым, потому что оно представляет собой духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов. В Японии другое несчастливое число — 9.0016 9 , что имеет то же произношение, что и «страдание». В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «я жил». 666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками. В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией. Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Список литературы Эта статья была написана Kateryna Yuri Преобразовать базу-36 в десятичное значение Преобразование шестнадцатеричного в десятичное значение Преобразование с основанием 4 в десятичное Преобразование десятичного в двоичное Преобразование десятичного в двоичное с основанием Преобразование шестнадцатеричного в двоичное Вас могут заинтересовать другие преобразователи в группе Общие преобразователи единиц:Длина и преобразователь расстояний массовый преобразователь Сухой объем и общие измерения приготовления Площадь преобразователя площади Объем и общий преобразователь измерения приготовления ТЕМПЕРАТУРА Давление, напряжение, модульный преобразователь модуля и рабочий преобразователь . Преобразователь мощности Преобразователь силы Преобразователь времени Преобразователь линейной скорости и скорости Преобразователь угла Конвертер топливной экономичности, расхода топлива и экономии топлива Конвертер единиц хранения информации и данных Конвертер метрических префиксов Конвертер передачи данных Курсы обмена валют Размеры мужской одежды и обуви 4 Размеры Компактный калькулятор Полный калькулятор Определения единиц измерения У вас возникли трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков. Общие конвертеры единиц измеренияДлина, масса, объем, площадь, температура, давление, энергия, мощность, скорость и другие популярные конвертеры единиц измерения. Преобразователь чисел Позиционное обозначение или разрядное обозначение — это метод представления или кодирования чисел. Основание 1 — Унарная система счисления. Это простейшая система счисления для представления натуральных чисел: для представления числа N произвольно выбранный символ, представляющий 1, повторяется N раз. Основание 2 — Двоичная система счисления. Это позиционная система с основанием 2, в которой числовые значения представлены двумя символами: 0 и 1. Основание 3 — Троичная (иногда называемая троичной) система счисления. Троичная цифра — это трит (троичная цифра). Он использует цифры 0, 1 и 2 для представления любого действительного числа. Эта система иногда используется в логике и вычислениях для подсчета трех состояний (низкое, высокое, неизвестное или открытое состояние). Основание 8 — восьмеричная система счисления — это система счисления с основанием 8, в которой используются цифры от 0 до 7. Она используется в цифровом оборудовании. Основание 10 — Десятичная система счисления (также называемая системой с основанием десять) представляет собой позиционную систему счисления, в основе которой лежит 10. Это числовая база, наиболее широко используемая современными цивилизациями. Основание 12 — двенадцатеричная система (также известная как основание 12 или дюжина) представляет собой позиционную систему счисления с основанием двенадцать. Основание 16 — Шестнадцатеричная система счисления (также называемая основанием 16 или шестнадцатеричной) — это позиционная система счисления с основанием 16. Она используется в современном цифровом оборудовании, информатике и математике. В системах с основанием менее 36 чаще всего символы 0–9 представляют значения от нуля до девяти, а латинские буквы от A до Z и альтернативно от a до z представляют значения от 10 до 36. Использование конвертера чиселЭтот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовать множество единиц измерения из одной системы в другую. Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах. 9», то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
Библиотека JavaScript BigInteger Мы усердно работаем над тем, чтобы результаты, представленные конвертерами и калькуляторами TranslatorsCafe.com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения. Если вы заметили ошибку в тексте или расчетах, или вам нужен другой конвертер, которого вы здесь не нашли, сообщите нам об этом! TranslatorsCafe.com Unit Converter Канал YouTube Десятичное число в восьмеричное — значение, шаги преобразования, десятичное число в восьмеричное с десятичным числом, примеры Преобразование десятичного числа в восьмеричное выполняется с учетом системы счисления. Система счисления — это форма представления чисел в виде цифр или символов. Существует 4 типа систем счисления — восьмеричная, двоичная, десятичная и шестнадцатеричная. Преобразование десятичного числа в восьмеричное можно выполнить, разделив десятичное число на восьмеричное основание.
Что такое десятичное преобразование в восьмеричное? Преобразование десятичного числа в восьмеричное происходит, когда нам нужно найти эквивалент любого числа. В этом случае нам нужно преобразовать десятичное число в эквивалентное ему восьмеричное число. В системе счисления каждый из типов имеет свое собственное базовое число, т.е. восьмеричное число имеет базовое число 8, а десятичное число имеет базовое число 10. Чтобы преобразовать десятичное число в восьмеричное, нам нужно разделить десятичное число на восьмеричное. Десятичная система счисленияЧисла с базовым числом 10 и использованием десяти цифр: 0,1,2,3,4,5,6,7,8 и 9 называются десятичной системой счисления. Десятичная система счисления используется для представления чисел в реальной жизни. Если какое-либо число представлено без основания, это означает, что его основание равно 10. Десятичные числа представляются как (a) 10 . Вот несколько примеров: \(23_{10}, 132_{10}, 257_{10}\) Восьмеричная система счисления Восьмеричная система счисления использует восемь цифр: 0,1,2,3,4 ,5,6 и 7 с основанием 8. Преимущество этой системы в том, что она имеет меньше цифр по сравнению с некоторыми другими системами, следовательно, будет меньше вычислительных ошибок. Цифры вроде 8 и 9не входят в восьмеричную систему счисления. Преобразование десятичного числа в восьмеричноеДля преобразования десятичного числа в восьмеричное существует два метода преобразования. Первый метод заключается в преобразовании десятичного числа в другую систему счисления, то есть в двоичную или шестнадцатеричную, и, наконец, в восьмеричную. Второй метод — это прямой метод, при котором мы напрямую преобразуем десятичные числа в восьмеричные. Давайте посмотрим оба метода: Метод 1: преобразование десятичного числа в двоичное в восьмеричное В этом методе десятичное число можно преобразовать в двоичное путем деления заданного числа на 2, пока мы не получим частное, равное 1. Числа записываются снизу вверх . Как только двоичное число получено, мы преобразуем его в восьмеричное число. Шаг 1: Сначала мы преобразуем десятичное число \((45)_{10}\) в двоичное число. Мы делим 45 на двоичное основание, то есть на 2, пока не получим частное 1. Следовательно, десятичное число \((45)_{10}\) = \((101101)_{2}\). Шаг 2: Как только мы получили двоичное число, мы можем преобразовать это число в восьмеричное, используя таблицу преобразования двоичного в восьмеричное. С помощью приведенной выше таблицы мы сначала записываем число в его 3-битное двоичное число, поскольку перед цифрами необходимо добавить ноль, чтобы сформировать 3-битное двоичное число. Следовательно, 3-битное двоичное число — это 101 и 101. Глядя на ту же таблицу выше, мы можем преобразовать эти двоичные числа в их восьмеричные числа, чтобы получить окончательное число. Следовательно, это числа 5 и 5. Следовательно, \((101101)_{2}\) = \((55)_{8}\). Шаг 3: Как только мы получили восьмеричное число, преобразование из десятичного числа в восьмеричное можно записать как: \((45)_{10}\) = \((55)_{8}\). Метод 2: преобразование десятичного числа в восьмеричноеВ этом методе десятичное число делится на 8 каждый раз, когда из предыдущей цифры получается напоминание. Первый полученный остаток представляет собой наименьшую значащую цифру (LSD), а последний остаток — старшую значащую цифру (MSD). Когда частное меньше 8, мы получаем восьмеричное число, записывая остаток в обратном порядке. Давайте разберемся с конверсией на примере. Преобразуйте десятичное число \((350)_{10}\) в восьмеричное число. Шаг 1: Проверьте, меньше ли десятичное число 8. Если да, восьмеричное число такое же. Если нет, то идите вперед. В данном случае 350 больше 8, поэтому переходим к шагу 2. Шаг 2: Разделите 350 на 8 (восьмеричное основание). Запишите частное и остаток в форме частное-остаток. Шаг 3: Как только мы получим частное меньше 8, мы прекращаем деление и получаем восьмеричное число. . Восьмеричное число считается путем чтения всех остатков и последнего частного снизу вверх. Следовательно, \((350)_{10}\) = \((536)_{8}\). Преобразование десятичного числа в восьмеричное с десятичной точкой Чтобы преобразовать десятичное число в восьмеричное с десятичной точкой, мы вычисляем десятичное число из двух частей. Во-первых, мы вычисляем целую часть десятичной точки путем деления восьмеричного основного числа, т.е. 8, до тех пор, пока частное не станет меньше 8. Вторая часть вычисляется на дробной части десятичного числа, где число умножается на основание числа 8. пока дробная часть не станет равной нулю. Здесь после умножения мы разделяем целую часть и дробную часть. Окончательное восьмеричное число вычисляется путем сложения как целого, так и дробного числа. Шаг 1: Разделите десятичное число на две части — целую и дробную. Итак, 29,45 = 29 + 0,45. Шаг 2: Сначала преобразуйте целую часть числа. Итак, сначала мы начнем с 29, разделив его на основание 8, пока частное не станет меньше 8. Частное | Остаток | 29/8 | 3 | 5 | 3/8 | 0 | 3 | Следовательно, 29 — это 35 в восьмеричном числе. Шаг 3: Как только целое восьмеричное число получено, мы переходим к дробной части. Итак, 0,45 умножается на 8 (восьмеричное основание числа), где результат снова делится на целую часть и дробную часть. Число умножается на 8, пока дробная часть не станет равной нулю.
Запишите всю целую часть сверху вниз, чтобы получить восьмеричное число дробного числа. Следовательно, 0,45 = 0,3463146. Шаг 4: Сложите вместе целую и дробную части, чтобы получить восьмеричное число. Следовательно, \((29,45)_{10}\) = \((35,3463146)_{8}\). Связанные темы Вот несколько тем, связанных с преобразованием десятичной дроби в восьмеричную, взгляните!
Часто задаваемые вопросы о преобразовании из десятичной в восьмеричнуюКак преобразовать десятичную систему в восьмеричную? Существует два метода преобразования десятичных чисел в восьмеричные. Первый — это прямое преобразование, когда десятичное число делится на восьмеричное основание, равное 8, до тех пор, пока частное не станет меньше 8. Окончательное восьмеричное число получается путем расположения остатка и последнего частного снизу вверх. Что такое преобразование десятичных чисел в восьмеричные?Преобразование десятичного числа в восьмеричное помогает определить эквивалент другого числа в системе счисления. Система счисления имеет четыре типа: двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Каждый из этих типов чисел имеет свои собственные базовые числа. Преобразование десятичного числа в восьмеричное основано на их основных числах.
Что такое десятичный эквивалент числа 12 в восьмеричной системе? Чтобы преобразовать десятичное число в восьмеричное, мы начнем с деления 12 на восьмеричное основание 8.
Следовательно, \((12)_{10}\) = \((14)_{8}\). Как преобразовать десятичное число в восьмеричное с десятичной точкой?Чтобы преобразовать десятичное число в восьмеричное с десятичной точкой, нам нужно разбить десятичное число на две части, т. е. целую часть и дробную часть. Преобразование начинается с целой части сначала путем деления числа на 8 до тех пор, пока частное не станет меньше 8. Отложите результат и перейдите к дробной части. Дробная часть будет умножаться на 8, пока результат не станет равным нулю. Здесь целая и дробная части снова будут храниться отдельно. Ответом будет целая часть, считая сверху вниз. Окончательное число получается путем сложения целой и дробной частей. Можно ли преобразовать \((21.4)_{10}\) из десятичного числа в восьмеричное?Чтобы преобразовать десятичное число 21,4 в восьмеричное, выполните следующие шаги: Шаг 1: Разбейте 21,4 на целую и дробную части, т. |
 Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
 Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.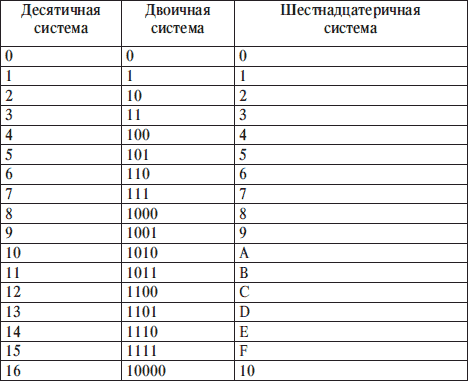 Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910).
Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910). Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа. Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати. Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике. Например, в базе 10 у нас есть следующее:
Например, в базе 10 у нас есть следующее: Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу: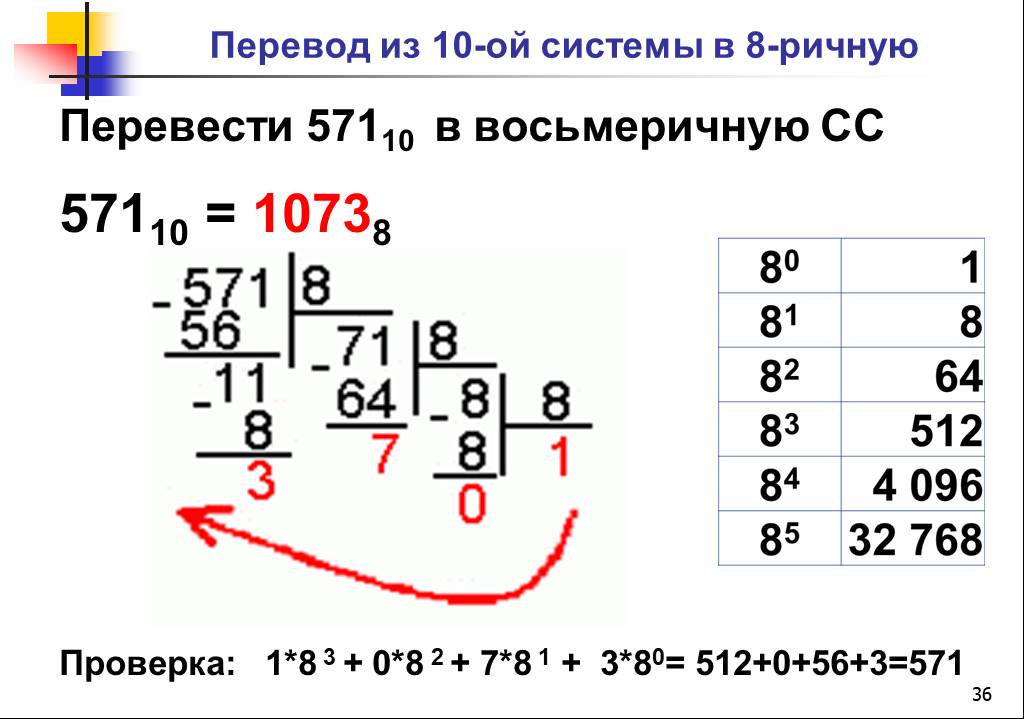
 Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.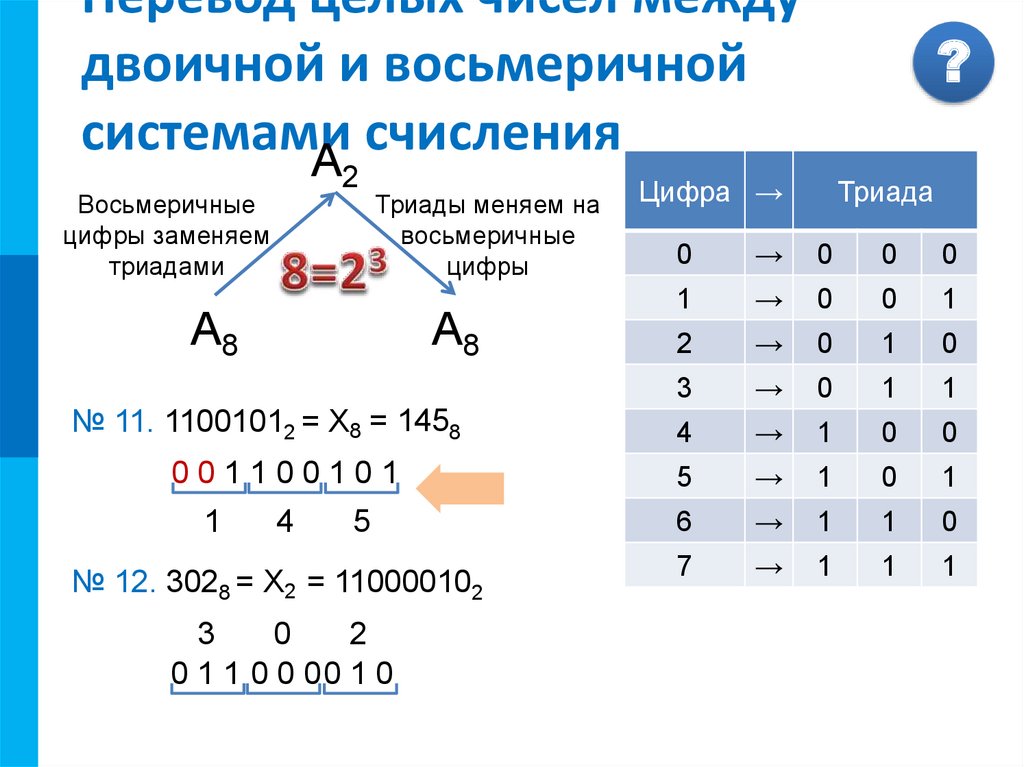
 В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны.
Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны. Это подразумевает, что жизнь окончена, и относится к смерти.
Это подразумевает, что жизнь окончена, и относится к смерти. Позиционное обозначение отличается от других обозначений (таких как римские цифры) использованием одного и того же символа для разных порядков величины (например, «разряд единиц», «разряд десятков», «разряд сотен»). В математических системах счисления основание или основание обычно представляет собой количество уникальных цифр, включая ноль, которые позиционная система счисления использует для представления чисел.
Позиционное обозначение отличается от других обозначений (таких как римские цифры) использованием одного и того же символа для разных порядков величины (например, «разряд единиц», «разряд десятков», «разряд сотен»). В математических системах счисления основание или основание обычно представляет собой количество уникальных цифр, включая ноль, которые позиционная система счисления использует для представления чисел.

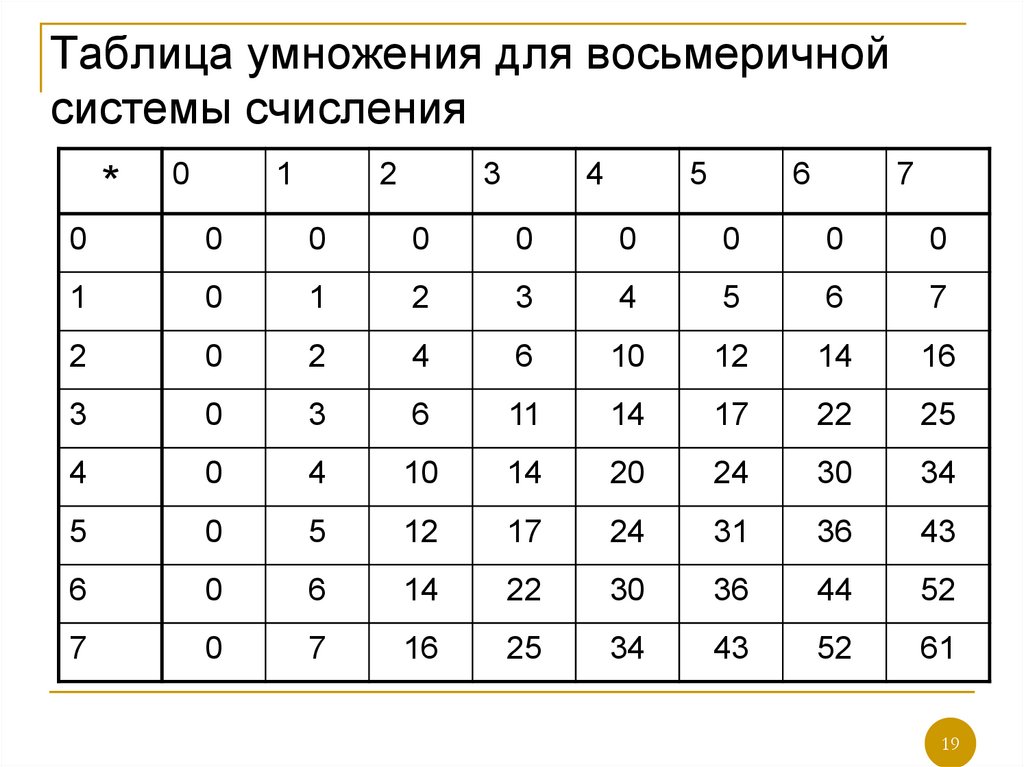 Давайте узнаем, как это сделать.
Давайте узнаем, как это сделать. по основанию 8 и запишите полученный остаток в обратном порядке, чтобы получить эквивалентное восьмеричное число. Перед преобразованием давайте узнаем о восьмеричной системе счисления и десятичной системе счисления.
по основанию 8 и запишите полученный остаток в обратном порядке, чтобы получить эквивалентное восьмеричное число. Перед преобразованием давайте узнаем о восьмеричной системе счисления и десятичной системе счисления. Восьмеричные числа представлены как (a) 8 . Каждый разряд в восьмеричном числе равен степени восьми. Например: \((151)_{8}\) = 1 x 8 2 + 5 x 8 1 + 1 x 8 0 .
Восьмеричные числа представлены как (a) 8 . Каждый разряд в восьмеричном числе равен степени восьми. Например: \((151)_{8}\) = 1 x 8 2 + 5 x 8 1 + 1 x 8 0 .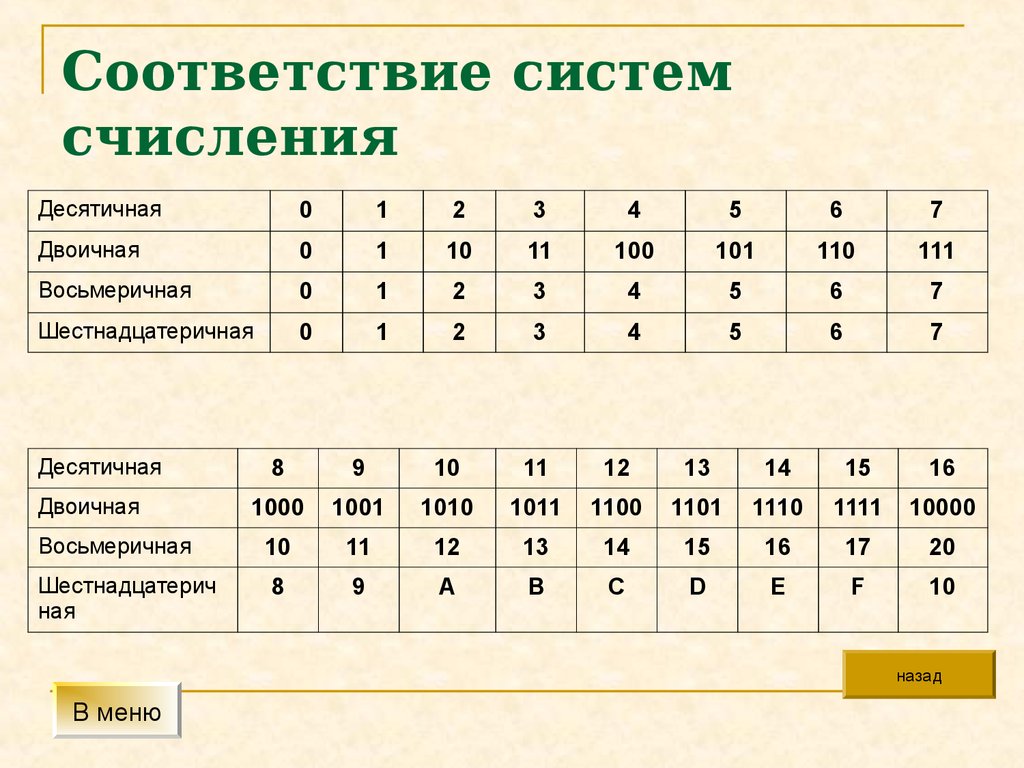 Давайте разберемся в этом на примере. Преобразуйте десятичное число \((45)_{10}\) в восьмеричное число.
Давайте разберемся в этом на примере. Преобразуйте десятичное число \((45)_{10}\) в восьмеричное число.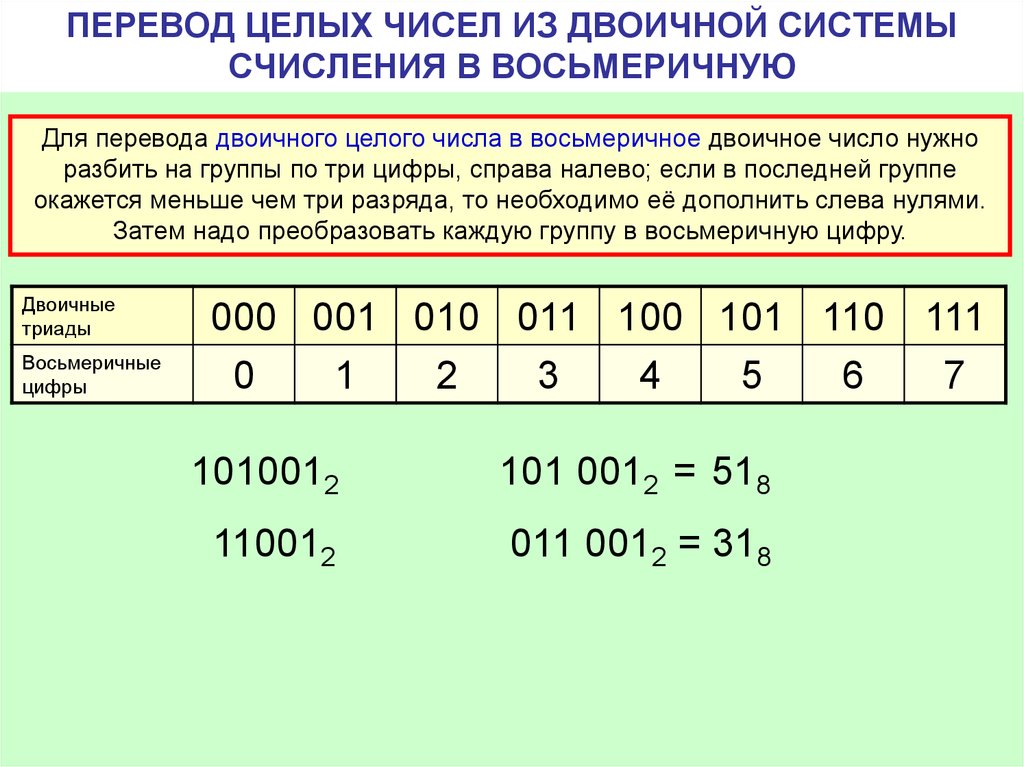
 Повторяйте этот процесс (снова деля частное на 8), пока частное не станет меньше 8.
Повторяйте этот процесс (снова деля частное на 8), пока частное не станет меньше 8. Давайте рассмотрим пример пошагово, чтобы лучше понять это. Преобразуйте десятичное число \((29.45)_{10}\) в восьмеричное число.
Давайте рассмотрим пример пошагово, чтобы лучше понять это. Преобразуйте десятичное число \((29.45)_{10}\) в восьмеричное число.
 Следовательно, 35 + 0,3463146 = 35,3463146.
Следовательно, 35 + 0,3463146 = 35,3463146. Второй метод преобразования десятичного числа в восьмеричное — это преобразование десятичного числа в другую систему счисления, то есть двоичную или шестнадцатеричную, а затем преобразование этого числа в восьмеричное число.
Второй метод преобразования десятичного числа в восьмеричное — это преобразование десятичного числа в другую систему счисления, то есть двоичную или шестнадцатеричную, а затем преобразование этого числа в восьмеричное число.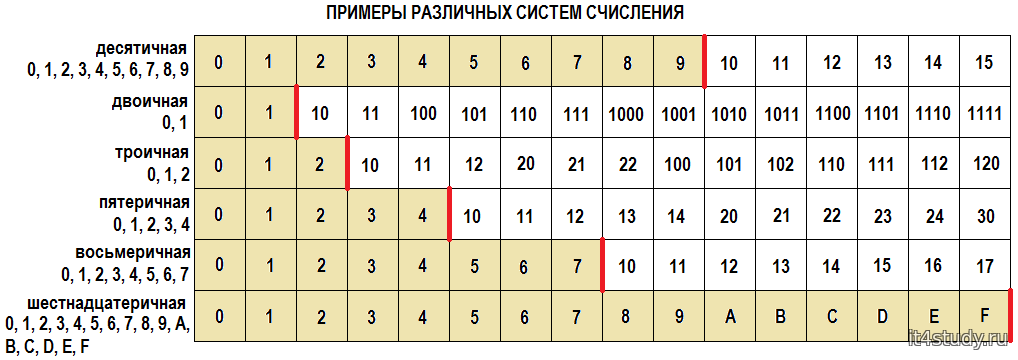 Вот шаги:
Вот шаги: