Разное

10 система счисления таблица: Таблица соответствия десятеричного от 1 до 255 (decimal), двоичного (binary) и шестнадцатеричного (hexadecimal) представлений чисел. Шестнадцатиричная система счисления, двоичное счисление.

Содержание

Семнадцатеричная система счисления

Содержание:
Что такое семнадцатеричная система счисления
Как перевести целое десятичное число в семнадцатеричную систему счисления
Как перевести десятичную дробь в семнадцатеричную систему счисления
Как перевести число из семнадцатеричной системы счисления в десятичную
Как перевести дробное семнадцатеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в семнадцатеричной системе счисления

семнадцатеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в семнадцатеричной системе счисления используется десять цифр и семь букв 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F и G. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием

системы счисления. Например, G4F2A17 или 3A7B17

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в семнадцатеричную систему счисления

Для того, чтобы перевести целое десятичное число в семнадцатеричную систему счисления нужно десятичное число делить на 17 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 7997410 в семнадцатеричную систему счисления:

79974 : 17 = 4704 остаток: 6
4704 : 17 = 276 остаток: 12, 12 = C
276 : 17 = 16 остаток: 4
16 : 17 = 0 остаток: 16, 16 = G

7997410 = G4C6

17

Как перевести десятичную дробь в семнадцатеричную систему счисления

Для того чтобы перевести десятичную дробь в семнадцатеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в семнадцатеричную систему счисления, а затем дробную часть, последовательно умножать на 17, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 78525.2916152910 в семнадцатеричную систему счисления:

Переведем целую часть

78525 : 17 = 4619 остаток: 2

4619 : 17 = 271 остаток: 12, 12 = C
271 : 17 = 15 остаток: 16, 16 = G
15 : 17 = 0 остаток: 15, 15 = F

7852510 = FGC217

Переведем дробную часть

0.29161529 · 17 = 4.95745993
0.95745993 · 17 = 16.27681881, 16 = G
0.27681881 · 17 = 4.70591977
0.70591977 · 17 = 12.00063609, 12 = C
0.00063609 · 17 = 0.01081353
0.01081353 · 17 = 0.18383001
0.18383001 · 17 = 3.12511017
0.12511017 · 17 = 2.12687289
0.12687289 · 17 = 2.15683913
0.15683913 · 17 = 2. 66626521

0.2916152910 = 0.4G4C00322217

78525.2916152910 = FGC2.4G4C00322217

Семнадцатеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной семнадцатеричной. В данном примере получается бесконечная семнадцатеричная дробь, поэтому умножение на 17 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 78525.29161529

10 не может быть точно представлена в семнадцатеричной системе счисления.

Как перевести число из семнадцатеричной системы счисления в десятичную

Для того, чтобы перевести число из семнадцатеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 17, так как система счисления 17-ичная. Необходимо последовательно умножить каждое число на 17 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем число 12A3GD17 в десятичную систему счисления:

Позиция в числе543210
Число12A3GD

A17 = 1010
D17 = 1310
G17 = 1610

12A3GD17 = 1 ⋅ 175 + 2 ⋅ 174 + 10 ⋅ 173 + 3 ⋅ 172 + 16 ⋅ 171 + 13 ⋅ 170 = 163718110

Как перевести дробное семнадцатеричное число в десятичное

Для того, чтобы перевести дробное семнадцатеричное число в десятичное, необходимо записать дробное семнадцатеричное число, убрав точку и затем сверху расставить индексы.

Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 17, так как система счисления 17-ичная. Необходимо последовательно умножить каждое число на 17 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное семнадцатеричное число G9A.3AF17 в десятичное:

Позиция в числе210-1-2-3
ЧислоG9A3AF

A17 = 1010
F17 = 1510
G17 = 1610

G9A.3AF17

= 16 ⋅ 172 + 9 ⋅ 171 + 10 ⋅ 170 + 3 ⋅ 17-1 + 10 ⋅ 17-2 + 15 ⋅ 17-3 = 4787. 214125788723794015876246693610

Таблица значений десятичных чисел от 0 до 100 в семнадцатеричной системе счисления

Значение числа в десятичной системе счисленияЗначение числа в семнадцатеричной системе счисления
010017
110117
210217
310
317
410417
510517
610617
710717
810817
910917
1010A17
1110
B17
1210C17
1310D17
1410E17
1510F17
1610G17
17101017
18101117
1910
1217
20101317
21101417
22101517
23101617
24101717
25101817
26101917
2710		1A17
28101B17
29101C17
30101D17
31101E17
32101F17
33101G17
34102017
35102117
36102217
37102317
38102417
39102517
40102617
41102717
42102817
43102917
44102A17
45102B17
46102C17
47102D17
48102E17
49102F17
50102G17

Значение числа в десятичной системе счисленияЗначение числа в семнадцатеричной системе счисления
51103017
52103117
53103217
54103317
55103417
56103517
57103617
58103717
59103817
60103917
61103A17
62103B17
63103C17
64103D17
65103E17
66103F17
67103G17
68104017
69104117
70104217
71104317
72104417
73104517
74104617
75104717
76104817
77104917
78104A17
79104B17
80104C17
81104D17
82104E17
83104F17
84104G17
85105017
86105117
87105217
88105317
89105417
90105517
91105617
92105717
93105817
94105917
95105A17
96105B17
97105C17
98105D17
99105E17
100105F17

Методы перевода десятичного числа в двоичное

 В одном из наших материалов мы рассмотрели определение двоичного числа. Оно имеет самый короткий алфавит. Только две цифры: 0 и 1. Примеры алфавитов позиционных систем счисления приведены в таблице.


  

Позиционные системы счисления

Название системы

Основание

Алфавит

Двоичная

2

0,1

Троичная

3

0,1,2

Четверичная

4

0,1,2,3

Пятеричная

5

0,1,2,3,4

Восьмеричная

8

0,1,2,3,4,5,6,7

Десятичная

10

0,1,2,3,4,5,6,7,8,9

Двенадцатеричная

12

0,1,2,3,4,5,6,7,8,9,А,В

Шестнадцатеричная

16

0,1,2,3,4,5,6,7,8,9,А,В,С,D,E,F

Тридцатишестиричная

36

0,1,2,3,4,5,6,7,8,9,А,В,С,D,E,F,G, H,I,J,K,L,M,N,O,P,R,S,T,U,V,X,Y,Z

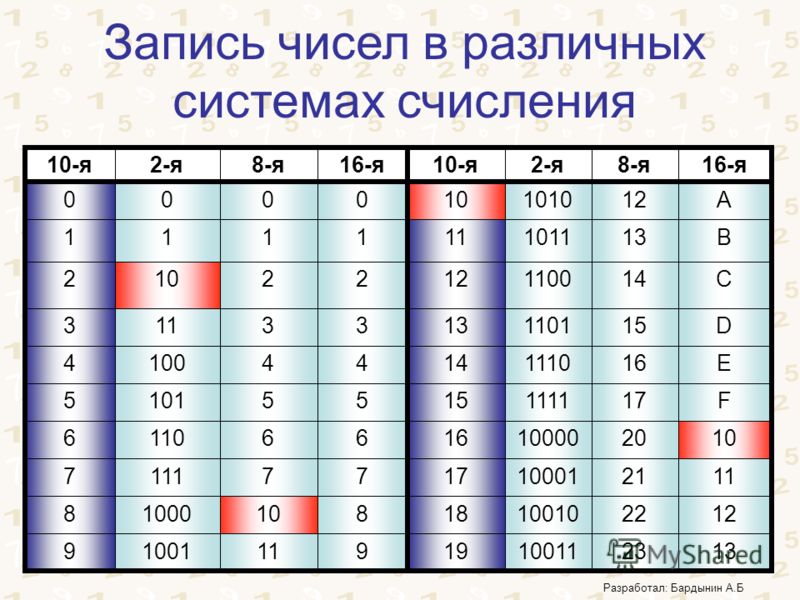
Для перевода небольшого числа из десятичного в двоичное, и обратно, лучше пользоваться следующей таблицей.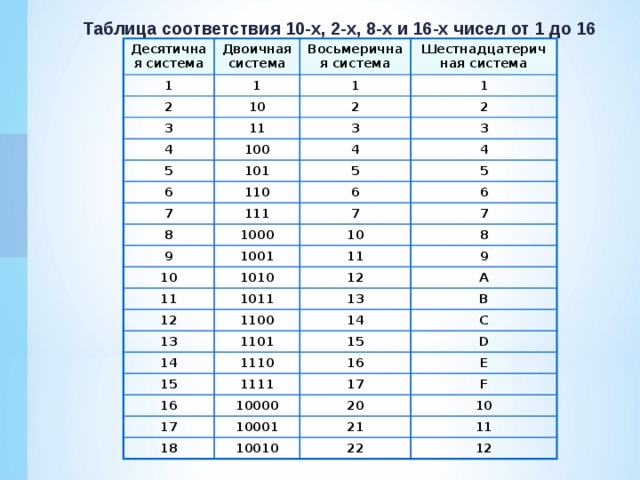


Таблица перевода десятичных чисел от 0 до 20 в двоичную систему счисления.

десятичное

число

двоичное число

десятичное

число

двоичное число

0

0000

11

1011

1

0001

12

1100

2

0010

13

1101

3

0011

14

1110

4

0100

15

1111

5

0101

16

10000

6

0110

17

10001

7

0111

18

10010

8

1000

19

10011

9

1001

20

10100

10

1010

и т. д.

 

Однако таблица получится огромной, если записать туда все числа. Искать среди них нужное число будет уже сложнее. Гораздо проще запомнить несколько алгоритмов перевода чисел из одной позиционной системы счисления в другую.

Как сделать перевод из одной системы счисления в другую? В информатике существует несколько простых способов перевода десятичных чисел в двоичные числа. Рассмотрим два из них.


Способ №1.

Допустим, требуется перевести число 637 десятичной системы в двоичную систему.

Делается это следующим образом: отыскивается максимальная степень двойки, чтобы два в этой степени было меньше или равно исходному числу.

В нашем случае это 9, т.к. 29=512, а 210=1024, что больше нашего начального числа. Таким образом, мы получили число разрядов результата. Оно равно 9+1=10.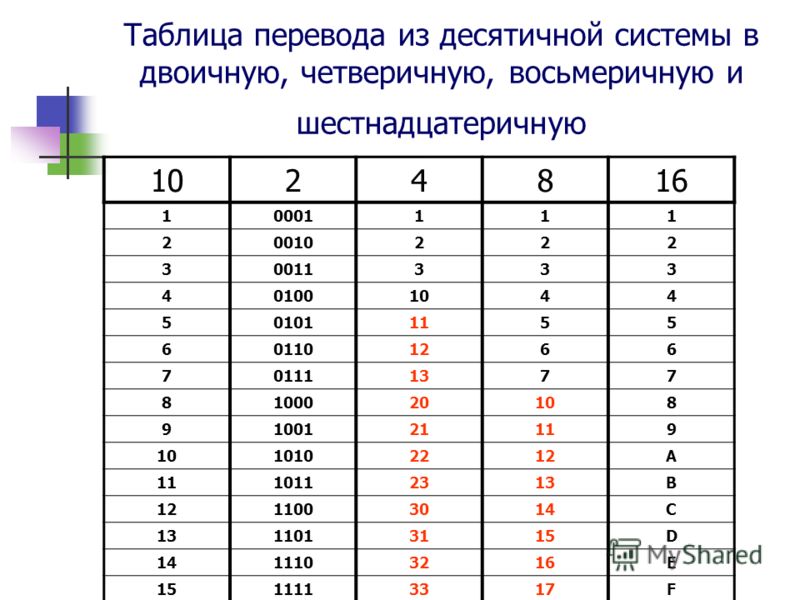 Значит, результат будет иметь вид 1ххххххххх, где вместо х может стоять 1 или 0.

Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 637-29=125. Затем сравниваем с числом 28=256. Так как 125 меньше 256, то девятый разряд будет 0, т.е. результат уже примет вид 10хххххххх.

27=128 > 125, значит и восьмой разряд будет нулём.

26=64, то седьмой разряд равен 1. 125-64=61 Таким образом, мы получили четыре старших разряда и число примет вид 10011ххххх.

25=32 и видим, что 32 < 61, значит шестой разряд равен 1 (результат 100111хххх), остаток 61-32=29.

24=16 < 29 — пятый разряд 1 => 1001111ххх. Остаток 29-16=13.

23=8 < 13 => 10011111хх. 13-8=5

22=4 < 5 => 10011111хх, остаток 5-4=1.

21=2 > 1 => 100111110х, остаток 2-1=1.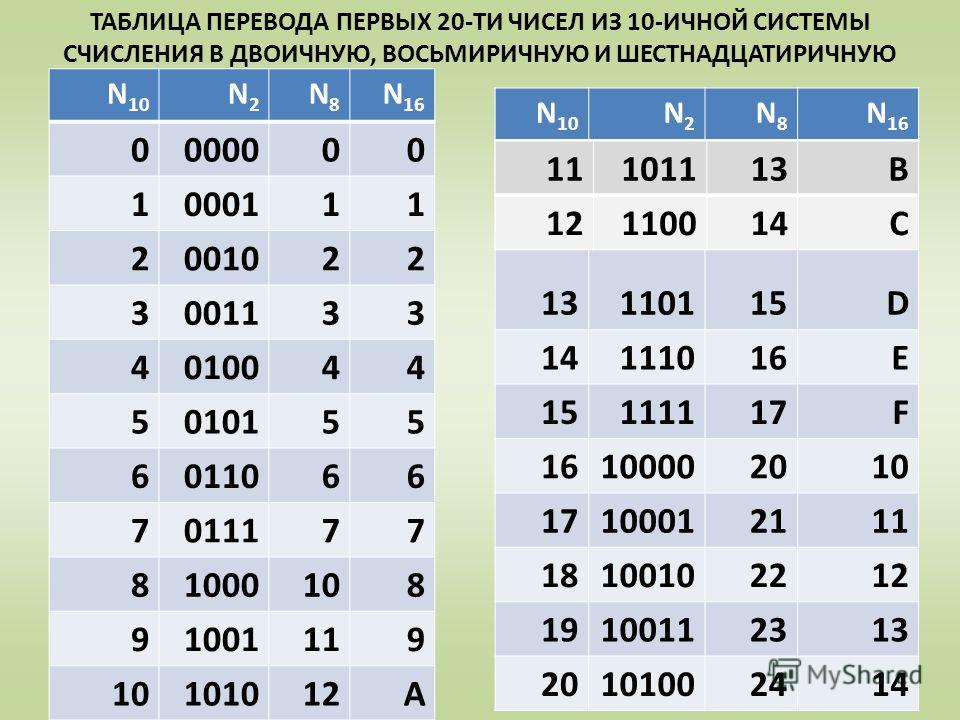

20=1 => 1001111101.

Это и будет конечный результат.


Способ №2.

Правило перевода целых десятичных чисел в двоичную систему счисления, гласит:


  1. Разделим an−1an−2…a1a0=an−1⋅2n−1+an−2⋅2n−2+…+a0⋅20 на 2.
  2. Частное будет равно an−1⋅2n−2+…+a1, а остаток будет равен
  3. Полученное частное опять разделим на 2, остаток от деления будет равен a1.
  4. Если продолжить этот процесс деления, то на n-м шаге получим набор цифр: a0,a1,a2,…,an−1, которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2.
  5. Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, которое будет равно нулю.

Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков. Записывать его начинаем с последнего найденного.

Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

Получили 1110=10112.


Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:


363

181

90

45

22

11

5

2

1

1

1

0

1

0

1

1

0

1

36310=1011010112



Двоичная система счисления Простыми словами о ядре Linux

Что такое число с основанием десять?

Что такое числа с основанием десять?

Основание системы счисления говорит нам, сколько уникальных цифр используется для формирования числа в этой системе.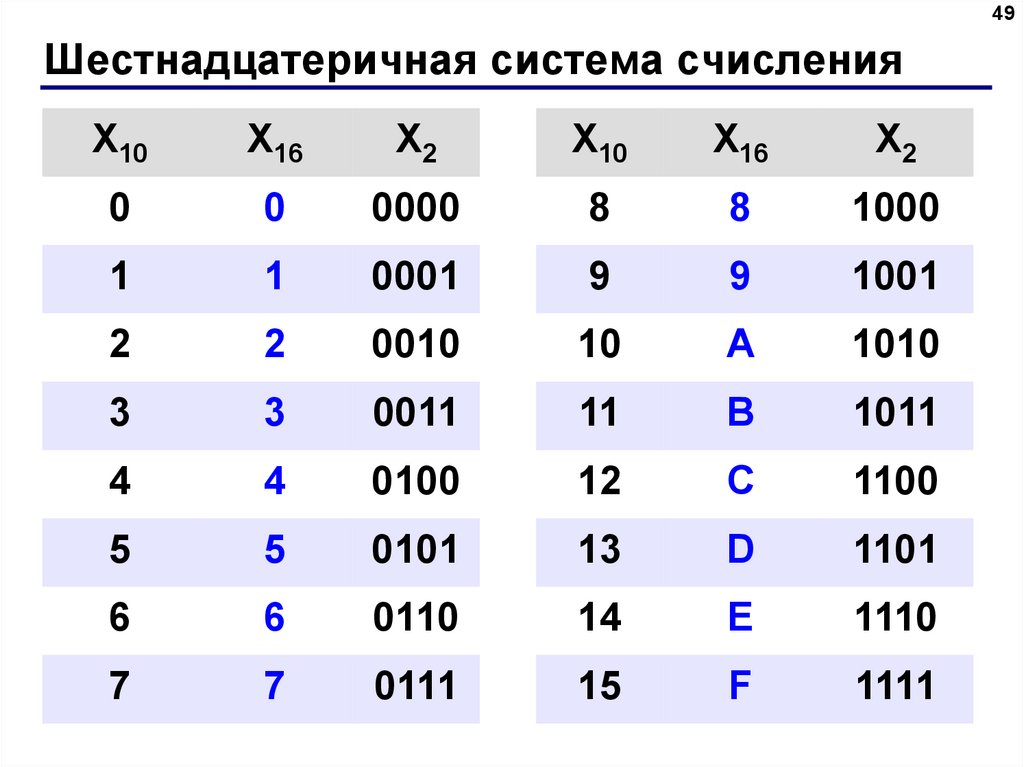 В десятичной системе десять уникальных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) используются для представления любого числа. Число — это арифметическое значение, которое мы используем для подсчета.

Десять цифр, используемых в системе счисления с основанием 10 для образования числа с основанием 10, следующие:

Родственные игры

Число с основанием десять Определение

Число с основанием десять записывается комбинацией цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, так что каждая позиция имеет значение в степенях десять.

Числа с основанием 10 Пример: 150 и «сто пятьдесят» являются числами с основанием 10. Первый записывается цифрами. Последний пишется в словесной форме.

Связанные рабочие листы

Таблица десятичных разрядов

Разрядность цифры говорит нам о значении этой цифры, основываясь на положении цифры в числе. Таблица или диаграмма стоимости места помогает назвать каждое значение места. Различные группы разрядных значений называются периодами. Периоды помогают нам легко определить значения мест. Таблица стоимости мест приведена ниже:

Рассмотрим число с основанием десять 5 219 037.

Поместив число в таблицу разрядных значений, мы получим 

. Мы читаем его, используя таблицу разрядных значений, как «Пять миллионов двести девятнадцать тысяч тридцать семь».

Как найти разрядное значение цифры?

Давайте найдем разрядное значение всех цифр в числе 345 162, используя следующие шаги.

  • Шаг 1: Расставьте цифры в таблице разрядов. В этом случае получаем:
  • Шаг 2: Найдите место, где находится каждая цифра.
  • Шаг 3: Умножьте цифру на соответствующий разряд.

Местное значение 2 равно 2 долларам x 1 = 2$

Местное значение 6 равно 6 долларам х 10 = 60$

Местное значение 1 равно 1 доллару х 100 = 100$ \times 1000 = 5000$

Значение 4 места равно 4$ \times 10000 = 40000$

Значение места 3 равно 3$ \times 100000 = 300000$

Расширенная форма

Расширенная форма числа — это способ выражения числа с использованием его разрядных значений.

Пример:

  1. Напишите развернутую форму числа 531 264.

Местное значение 4$ = 4$

Местное значение 6$ = 6 х 10 = 60$

Местное значение 2$ = 2 х 100 = 200$

Местное значение 1$ = 1 х 1000 = 1000 $

Разрядное значение $3 = 3 х 10000 = 30000$

Разрядное значение $5 = 5 х 100000 = 500000$

Расширенная форма $531,264 = 500000 + $30000 + 1000 + 20 20

  1. Число 4531 можно записать в развернутом виде как

4531 долл. США = 4000 + 500 + 30 + 1 долл. США

  1. Расширенная форма 2836 

2836$ = (2 х 1000) + (8 х 100) + (3 х 10) + (6 х 1)$

         $= 2000 + 800 + 30 + 6$

Разрядные значения в десятичных дробях

Десятичные числа — это числительные, целая и дробная части которых разделены десятичной точкой.

Пример 1. Рассмотрим десятичное число 125,473

Таблица разрядов показывает разряды различных цифр десятичной дроби.

Пример 2: Допустим, у нас есть десятичное число 345,27.

Разрядное значение 7 будет равно $7 \times \frac{1}{100} = \frac{7}{100}$

Разрядное значение 2 будет равно $2 \times \frac{1}{10} = \ frac{2}{10}$

Разрядное значение 5 будет равно $5 \times  1 = 5$

Разрядное значение 7 будет равно $4 \times 10 = 40$

Разрядное значение 7 будет равно $3 x 100 = 300$

Расширенная форма 345,27$ = 300 + 40 + 5 + \frac{2}{10} + \frac{7}{100}$

$= 3 \times 100 + 4 \times 10 + 5 \times 1 + 2 \times \frac{1}{10} + 7 \times \frac{1}{100}$

$= 3 \text {сотни} + 4 \text{десятки} + 5 \text{единицы} + 2 \text{десятые} + 7 \text{сотые}$

Интересный факт!

Десятичные числа составляют основу нашей системы счета и, следовательно, нашей денежной системы. Мы используем их в повседневной жизни для счета, измерений и расчетов.

Давайте сделаем это!

Вместо того, чтобы раздавать вашему ребенку рабочие листы с разрядным значением, попросите его использовать десятичные блоки для отображения разрядного значения. Это поможет им не только понять, как пишутся числительные с основанием десять, но и их позиционное значение.

Заключение

В этой статье мы узнали о десятичной системе счисления. Форма с основанием десять — это расширение числа с использованием разрядного значения. Чтобы прочитать больше таких информативных статей о других концепциях, посетите наш веб-сайт. Мы в SplashLearn стремимся сделать обучение интересным и интерактивным для всех учащихся.

Решаемые примеры

1. Запишите 4326.18 в расширенной форме.

Решение:

4326,18 $ = (4 \times 1000) + (3 \times 100) + (2 \times 10) + (6 \times 1) + (1 \times \frac{1}{10 }) + (8 \times \frac{1}{100})$

4326,189 $ = 4000 + 300 + 20 + 6 + 0,1 + 0,08 $

2. Каково место 6 в числе 75683?

Решение:

В данном числительном с основанием десять цифра 6 стоит на разряде сотен.

Разрядное значение 6 в $75683 = 6 х 100 = 600$

3. Укажите разрядные значения цифр 2 и 5 в числе 2 в $ 75,1824 = 2 х 0,001 = 0,002 $

Разрядное значение 5 в $75,1824 = 5 х 1 = 5$

4. Запишите разрядные значения цифры 9 в числе 948,319?

Solution: 

Hundreds Tens Ones DecimalPoint Tenths Hundredths Thousandths
9 4 8 . 3 1 9

Разрядность цифры 9 в разряде сотен$ = 9 \times 100 = 900$

Разрядность цифры 9 в разряде тысячных $= 9 \times 10000 =

$

5.90 Запишите числительное с основанием десять для данной расширенной формы.

$4 х ​​10000 + 5 х 1000 + 7 х 100 + 9 х 10 + 2 х 1 = $ ?

Решение: 

$4 \times 10000 + 5 \times 1000 + 7 \times 100 + 9 \times 10 + 2 \times 1$

$= 40000 + 5000 + 700 + 90 + 2$

$= 45792$

Практические задачи

1

Что из следующего является правильной расширенной формой для 432,987?

400$ + 30 + 2 + 9 + 8 + 0,007$

400$ + 30 + 2 + 0,9 + 8 + 0,007$

400$ + 3 + 2 + 0,9 + 0,8 + 0,007$ +

+ 3 9000$ 0,9 + 0,08 + 0,007$

Правильный ответ: 400$ + 30 + 2 + 0,9 + 0,08 + 0,007$
Правильная форма числа с основанием десять для $432,987 = 400 + 30 + 2 + 0,9+ 0,08 + 0,007$

2

Какое место занимает 0 в числе 7082?

100

1000

1

Правильный ответ: 0
0 лежит в разряде сотен.
Разрядное значение $0 = 0 \× 100 = 0$

3

Найдите разницу между разрядным значением 2 в 652,729.

0,98

1,8

1,98

2,02

Правильный ответ: 1,98
Разрядное значение $2 = 2$ и $0,02$
Разница $= 0,9$ $–$8$

4

Напишите число с основанием десять. 4 Сотни $+ 2 $ TENS+ 5 $ ONESE+ 6 $ DETHS $+ 7 $ СОТРЕТЫ $+ 1 $ КОНСТРУКЦИЯ

425.671

445671

42,5671

4256,71

Правильный ответ: 425,671

55555.71

. Правильный ответ: 425,671

555555,71

. Правильный ответ. + 2$ десятков $+ 5$ единиц $+ 6$ десятых $+ 7$ сотых $+ 1$ тысячных
$= 400 + 20 + 5 + 0,6 + 0,07 + 0,001$
$= 425,671$

5

Что число с основанием десять, представленное $ 9000 + 600 + 40 + 8 $?

96,48

9648

9.648

0,9648

Правильный ответ: 9648
$ 9000 + 600 + 40 + 8 = 9684 $

Часто задаваемые вопросы

33.

Двоичная система счисления — это просто система счисления с основанием 2, в которой для формирования всех чисел используются только 2 цифры (0 и 1).

Что такое десятичный блок в математике?

Блоки с основанием 10 — это просто визуальное представление десятичных разрядов, которые представляют различные разрядные значения (единицы, десятки, сотни и т. д.) с использованием блоков.

Как еще называется десятичная система счисления?

Система счисления с основанием десять также известна как десятичная система счисления, поскольку разрядность цифр определяется на основе их положения относительно десятичной точки.

Все ли числа используют десятичную систему счисления?

Да! Почти все страны мира используют десятичную систему счисления.

  • Разрядное значение
  • Номер
  • Система счисления

Base-10 Conversion Tool

Base Number

Base-10

[ base-10 ]

Base-10 эквивалентен десятичной дроби.

База-11

[база-11]

Десятичная (база-11) позиционная система счисления основана на числе одиннадцать. Для десятичной дроби требуется одиннадцать символов 0-9 и A.

Основание-12

[основание-12]

Двенадцатеричная система (также известная как основание-12 или дюжина) представляет собой позиционную систему счисления с основанием двенадцать. Для двенадцатеричной системы требуется двенадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A и B.

База-13

[база-13 ]

Трехдесятичная, треугольная, тринадцатеричная или с основанием 13 — это позиционная система счисления, основанная на тринадцати. Он использует 13 различных цифр для представления чисел. Цифры для основания 13 могут быть 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B и C. base-14) система позиционной записи основана на числе четырнадцать. Для тетрадесятичного числа требуется четырнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. , A, B, C, D.

Основание-15

[ основание-15 ]

Пятидесятеричная (основание-15) позиционная система счисления основана на числе пятнадцать. Для пятидесятичного числа требуется пятнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E.

Base-16

[ base-16 ]

База-16 эквивалентна шестнадцатеричной системе счисления.

Base-17

[ base-17 ]

Base 17 или семеричная система счисления является позиционной системой счисления с основанием 17. Символы, используемые в этой системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F и G.

Base-18

[ base-18 ]

Base 18 или восьмидесятеричный код основан на восемнадцати и требует 18 различных символов (0, 1, 2, 3 , 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G и H.

Base-19

[ base-19 ]

девятнадцать и требуют 19 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H и I.

Base-2

[ base-2 ]

Base-2 эквивалентен двоичному коду

Основание-20

[ основание-20 ]

Десятеричная система счисления, или система счисления с основанием 20, основана на двадцати. Двадцать используемых символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I и J.

Base-21

[ основание-21 ]

Основание 21 или недесятичная система счисления основана на двадцати одном. Используется двадцать один символ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J и K.

Основание-22

[ основание-22 ]

Основание 22 или двенадцатеричная система счисления основана на двадцати двух. Используются двадцать два символа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K и L.

Основание-23

[основание-23]

Основание 23 или триовидесятичная система счисления основана на двадцати- три. Двадцать три используемых символа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L и M.

Основание-24

[ основание-24 ]

Система счисления с основанием 24 — это система счисления с основанием 24. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , М и Н.

Основание-25

[ основание-25 ]

Система счисления с основанием 25 — это система счисления с основанием 25. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N и O.

Основание-26

[ основание-26 ]

Шестнадцатеричная система счисления имеет основание двадцать шесть. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N, O и P.

Base-27

[ base-27 ]

Семидесятичная система счисления имеет основание двадцать семь. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N, O, P и Q.

Base-28

[ base-28 ]

Система счисления с основанием 28 основана на двадцати восьми и использует 28 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q и R.)

База-29

[база-29]

База 29Система счисления основана на двадцати девяти и использует 29 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R и S.)

Base-3

[ base-3 ]

Терне или тринарная система счисления с основанием 3. Для троичной системы счисления требуется только три символа: 0, 1 и 2.

Основание-30

[ основание-30 ]

Тройная система счисления или основание 30 — это позиционная система счисления, использующая 30 в качестве основания. Цифры в этом основании могут быть представлены арабскими цифрами 0-9.и латинские буквы A-T.

Основание-31

[ основание-31 ]

Нетроичная система счисления или основание 31 — это позиционная система счисления, использующая 31 в качестве основания. Цифры в этом основании могут быть представлены с помощью арабских цифр 0-9 и латинских букв A-U.

Основание-32

[ основание-32 ]

Двенадцатеричное или основание-32 — это система счисления с основанием 32. Цифры в этой базе могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-V.

База-33

[ основание-33 ]

Система счисления с основанием 33 основана на 33 различных символах (цифры 0-9 и буквы A-W).

Base-34

[ base-34 ]

Система счисления с основанием 34 основана на 34 различных символах (числа 0-9 и буквы A-X).

Base-35

[ base-35 ]

Система счисления Base 35 основана на 35 различных символах (числа 0-9 и буквы A-Y).

Основание-36

[ основание-36 ]

Основание 36 или шестнадцатеричная система счисления — это позиционная система счисления, использующая 36 в качестве основания. Выбор 36 удобен тем, что цифры можно представить с помощью арабских цифр 0-9и латинские буквы A-Z.

Основание-4

[ основание-4 ]

Четвертичная система счисления с основанием 4. Он использует цифры 0, 1, 2 и 3 для представления любого действительного числа.

База-5

[база-5 ]

Пятикратная система счисления с основанием пять. Базовая пятерка начинается с 0-4.

Base-6

[ base-6 ]

Senary (base-6) — это система счисления с секс-символами (0, 1, 2, 3, 4, 5).

Основание-7

[основание-7]

Семеричная система счисления представляет собой систему счисления с основанием 7 и использует цифры 0-6.

Основание-8

[ основание-8 ]

Основание-8 эквивалентно восьмеричному.

Base-9

[ base-9 ]

Nonary — это система счисления с основанием 9, обычно использующая цифры 0-8.

Двоичный

[ по основанию 2 ]

Двоичная система счисления или система счисления с основанием 2 представляет числовые значения с помощью двух символов: 0 и 1.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *