Иллюстрированный самоучитель по MathCAD 12 › Линейная алгебра › Скалярное произведение. Векторное произведение. [страница — 131] | Самоучители по математическим пакетам
Скалярное произведение. Векторное произведение.
Скалярное произведение векторов (vector inner product) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов u и v равно uv=|u||v|cos0, где 0 – угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение (листинг 7.9).
Внимание!
Для обозначения скалярного произведения пользователю позволяется выбирать представление оператора умножения при помощи контекстного меню (подобно умножению скалярных величин). Однако никогда не применяйте для обозначения скалярного произведения символ х, который является общеупотребительным символом векторного произведения (см. разд. 7.2.3).
С осторожностью перемножайте несколько (более двух) векторов. По-разному расставленные скобки полностью изменяют результат умножения. Примеры такого умножения приведены в листинге 7.10.
Листинг 7.10. Скалярное произведение векторов, умноженное на третий вектор:
Векторное произведение
Векторное произведение (cross product) двух векторов u и v с углом 9 между ними равно вектору с модулем |u|-|v|sin0, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом х, который можно ввести нажатием кнопки Cross Product (Векторное произведение) в панели Matrix (Матрица) или сочетанием клавиш CTRL + 8. Пример приведен в листинге 7.11.
Листинг 7.11. Векторное произведение двух векторов:
samoychiteli.ru
Урок 21. Векторы и матрицы в Mathcad
С этими понятиями Вы могли сталкиваться, работая в Excel – столбец чисел называется вектор-столбцом, строка – вектор-строкой. Блок объектов является матрицей. Вычисления в Excel, по сути, являются операциями с векторами и матрицами. В этом уроке мы познакомимся с аналогичными вычислениями в Mathcad, и мы поймем, почему в Mathcad их проводить проще.
Введение
В предыдущих уроках наши векторы начинались с элемента с номером «0». В этом уроке для простоты сделаем номер первого элемента равным «1». Это можно сделать с помощью вкладки Расчет –> Параметры документа –> ORIGIN:
Это значение можно вывести прямо в документ, чтобы не забыть его и не запутаться:
Теперь рассмотрим несколько матриц:
Как видно, они могут включать в себя числа, символы и даже функции. Они также могут содержать текстовые элементы (строки).
Элемент матрицы можно вывести, используя подстрочные индексы:
Матрицы выше являются квадратными 2х2, но у них может быть любой размер по строкам и столбцам:

Запомните: первое число – номер строки (или их количество), второе – столбца.
Элементы, выделенные с помощью подстрочных индексов:
Для вектор-столбца второй индекс можно опустить, но не для вектор-строки:
Во вкладке Математика –> Операторы и символы –> Операторы –> Векторы и матрицы Вы найдете команды для выделения столбцов и строк:
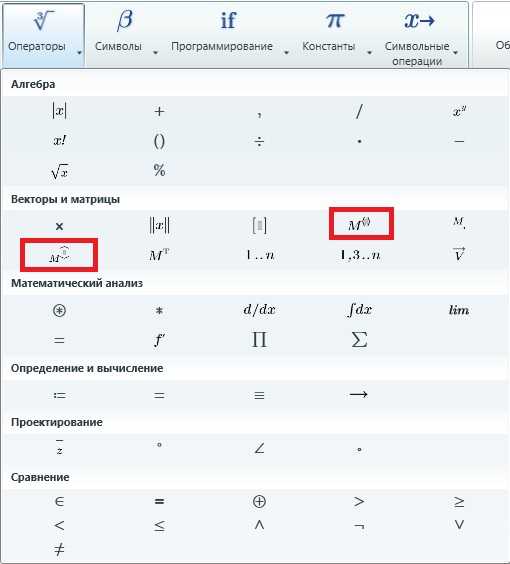
Многие операции для векторов и матриц аналогичны операциям для обычных чисел, переменных и функций: сложение, вычитание, некоторые виды умножения. Поиск обратной матрицы близко к операции деления. Вы можете записать эти операторы, используя имена векторов и матриц. В качестве примера рассмотрим векторное произведение матрицы и вектора:
Мы рассмотрим эту операцию подробнее позже. Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.
Применение векторов очень широко. Вспомните пиксели на экране монитора – их могут быть миллионы. Они обрабатываются с помощью операций с матрицами.
В Mathcad
Для создания вектора или матрицы откройте вкладку Матрицы/таблицы. Когда курсор находится в пустой области щелкните по самой левой кнопке «Вставить матрицу». Появится сетка с маленькими квадратами:
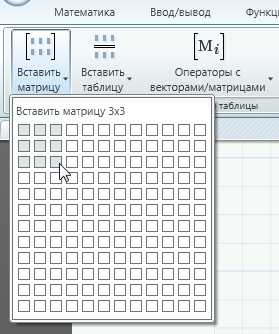
Перемести указатель на сетку, выберите желаемый размер матрицы, затем щелкните левой кнопкой мыши. Появится пустая матрица:
Матрице можно присвоить имя, щелкнув на левую скобку, нажав [:] для оператора присваивания и введя имя:
Вставку и удаление строк и столбцов легко осуществлять с помощью команд из меню «Операторы с векторами/матрицами» на вкладке Матрицы и таблицы:
Операции с матрицами
Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:
Транспонирование
Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:
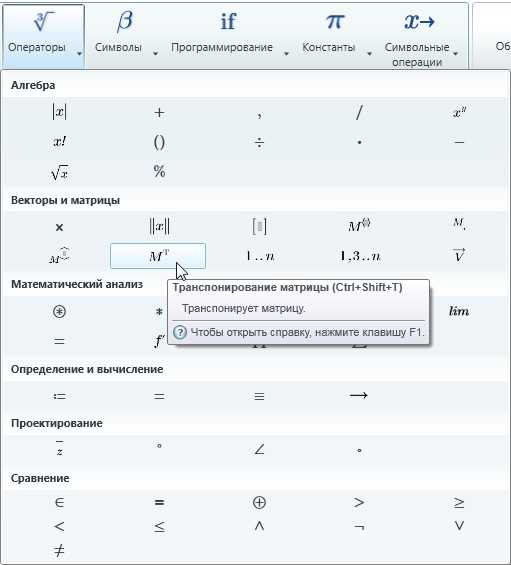
Щелкните по правой границе матрицы и примените оператор. Он работает как для символьных, так и для числовых матриц:
Поэлементные операции
Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:
Затем выберите все выражение и примените векторизацию:
Вычислите, чтобы посмотреть результат: первый элемент умножается на первый, второй – на второй, и т.д.:
Другие поэлементные операции:
Поэлементные операции применимы только к массивам одного размера.
Сложение и вычитание
Сложение и вычитание выполняется поэлементно:
Эта операция также применима лишь к массивам одного размера.
С помощью оператора суммирования можно найти сумму всех элементов вектора (не матрицы):
Скалярное произведение
Умножение на константу работает так:
При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:
Заметьте, что последовательность множителей играет роль:
Скалярное произведение не коммутативно, за исключением особых случаев:
Скалярное произведение двух векторов дает результат с комплексно-сопряженными числами (с чертой сверху). Для действительных чисел на это можно не обращать внимания:
Векторное произведение
Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:
Векторное произведение имеет широкое применение в механике, гидродинамике, электромагнетизме и в других областях.
Обратная матрица
Обратная матрица определяется только для квадратных матриц:
Произведение матрицы и ее обратной матрицы является единичной матрицей:
Произведение матрицы и единичной матрицы дает изначальную матрицу:
Определитель
Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:
Если определитель равен нулю, обратной матрицы не существует, а матрица является сингулярной. Вспомните деление на ноль в обычной алгебре. Mathcad сообщит, если матрица является сингулярной:
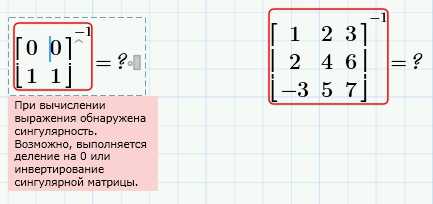
Для скаляра определитель равен его модулю:
Для вектора команда Определитель вычисляет длину вектора:
Резюме
В этом уроке мы рассмотрели векторы и матрицы (массивы).
- Элементы массива можно вывести с помощью подстрочного индекса – один индекс для вектор-столбца, два – для других массивов. Первое индекс – для строк, второй – для столбцов.
- Есть специальные команды для извлечения отдельных строк и столбцов.
- Векторы и матрицы создаются и редактируются с помощью команд со вкладки Матрицы/таблицы.
Операции над векторами и матрицами, которые мы рассмотрели:
- Транспонирование.
- Поэлементные операции.
- Сложение и вычитание.
- Скалярное произведение.
- Векторное произведение.
- Поиск обратной матрицы.
- Поиск определителя.
Другие интересные материалы
sapr-journal.ru
Иллюстрированный самоучитель по MathCAD 11 › Матричные вычисления › Векторное произведение. Сумма элементов вектора и след матрицы. [страница — 137] | Самоучители по математическим пакетам
Векторное произведение. Сумма элементов вектора и след матрицы.
Векторное произведение (cross product) двух векторов u и v с углом Q между ними равно вектору с модулем |u||v|sinQ, направленным перпендикулярно плоскости векторов и и v. Обозначают векторное произведение символом х, который можно ввести нажатием кнопки Cross Product (Векторное произведение) в панели Matrix (Матрица) или сочетанием клавиш CTRL + 8. Пример приведен в листинге 9.12.
Листинг 9.12. Векторное произведение:
Сумма элементов вектора и след матрицы
Иногда бывает нужно вычислить сумму всех элементов вектора. Для этого существует вспомогательный оператор (листинг 9.13, первая строка), задаваемый кнопкой Vector Sum (Сумма вектора) на панели Matrix (Матрица) или сочетанием клавиш CTRL + 4. Этот оператор чаще оказывается полезным не в векторной алгебре, а при организации циклов с индексированными переменными.
На том же листинге 9.13 (снизу) показано применение операции суммирования диагональных элементов квадратной матрицы. Эту сумму называют следом (trace) матрицы. Данная операция организована в виде встроенной функции tr:
- tr (A) – след квадратной матрицы А.
Листинг 9.13. Суммирование элементов вектора и диагонали матрицы:
samoychiteli.ru
Векторная алгебра
Векторы являются частным случаем матриц размерности Nх1, поэтому для них справедливы все те операции, что и для матриц, если ограничения особо не оговорены. Вместе с тем для векторов в линейной алгебре предусмотрен целый ряд специфических операций, и все они реализованы в системе Mathcad.
ВНИМАНИЕ!
Непосредственное проведение многих векторных операций над матрицами-строками, т. е. матрицами 1xN, невозможно; для того, чтобы превратить строку в вектор, ее нужно предварительно транспонировать.
Модуль вектора (vector magnitude)по определению равен квадратному корню из суммы квадратов его элементов.
ВНИМАНИЕ!
Не путайте модуль вектора и определитель матрицы, который обозначается тем же символом. Это характерный пример оператора, действующего по-разному на векторы и квадратные матрицы.
Модуль вектора
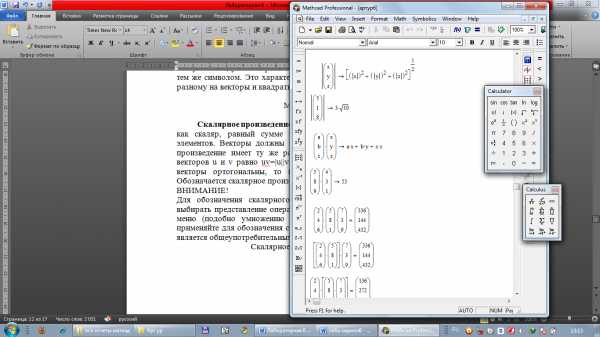
Скалярное произведение векторов(vector inner product) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов u и v равно uv=|u||v|cos0, где 0— угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение.
ВНИМАНИЕ!
Для обозначения скалярного произведения пользователю позволяется выбирать представление оператора умножения при помощи контекстного меню (подобно умножению скалярных величин). Однако никогда не применяйте для обозначения скалярного произведения символ х, который является общеупотребительным символом векторного произведения.
Скалярное произведение векторов
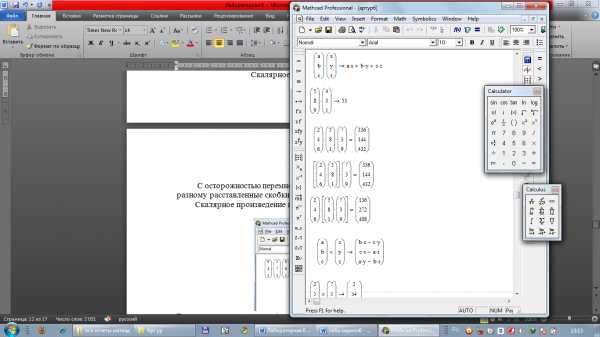
С осторожностью перемножайте несколько (более двух) векторов. По-разному расставленные скобки полностью изменяют результат умножения.
Скалярное произведение векторов, умноженное на третий вектор
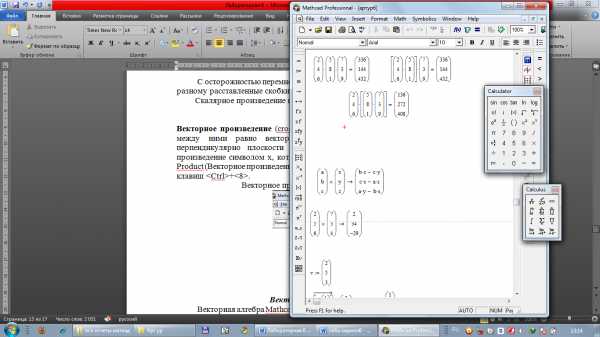
Векторное произведение(cross product) двух векторов u и v с углом ф между ними равно вектору с модулем |u|-|v|sin0, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом х, который можно ввести нажатием кнопки Cross Product (Векторное произведение) в панели Matrix (Матрица) или сочетанием клавиш <Ctrl>+<8>.
Векторное произведение двух векторов
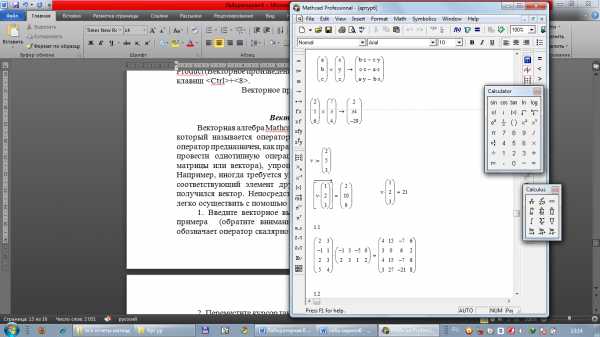
Векторизация массива
Векторная алгебра Mathcad включает несколько необычный оператор, который называется оператором векторизации (vectorize operator). Этот оператор предназначен, как правило, для работы с массивами. Он позволяет провести однотипную операцию над всеми элементами массива (т. е. матрицы или вектора), упрощая тем самым программирование циклов. Например, иногда требуется умножить каждый элемент одного вектора на соответствующий элемент другого вектора, чтобы в результате также получился вектор. Непосредственно такой операции в Mathcad нет, но ее легко осуществить с помощью векторизации. Для этого:
1. Введите векторное выражение, как показано во второй строчке примера (обратите внимание, что в таком виде символ умножения обозначает оператор скалярного произведения векторов).
2. Переместите курсор таким образом, чтобы линии ввода выделяли все выражение, которое требуется подвергнуть векторизации.
3. Введите оператор векторизации, нажав кнопку Vectorize (Векторизация) на панели Matrix (Матрица)), или сочетанием клавиш <Ctrl>+<->.
4. Введите <=>, чтобы получить результат.
Использование оператора векторизации для перемножения элементов вектора
Большинство неспецифических функций Mathcad не требуют векторизации для проведения одной и той же операции над всеми элементами вектора. Например, аргументом тригонометрических функций по определению является скаляр. Если попытаться вычислить экспоненту от векторной величины, Mathcad осуществит векторизацию по умолчанию, возведя в степень е каждый элемент и выдав в качестве результата соответствующий вектор.
Векторизация аргумента необязательна для большинства встроенных функций Mathcad
studfiles.net
Основы работы в MathCAD, страница 6
Пиктограмма | в панели инструментов Calculator (Калькулятор) в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «*» |
На Рис. 2.8 приведен пример умножения матриц.
Транспонирование матрицы
Транспонированием называется матричная операция, переводящая матрицу размером MxN в матрицу размером NxM, путем перестановки строк и столбцов с одинаковыми индексами.
Варианты ввода операции транспонирования.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Ctrl»+»1» |
На Рис. 2.9 приведен пример транспонирования матрицы.
Определитель матрицы
Варианты ввода операции расчета определителя матрицы.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Shift»+»|» |
На Рис. 2.9 приведен пример вычисления определителя матрицы.
Рис. 2.9. Операции умножения и сложения матриц
Модуль вектора
Модуль вектора равен квадратному корню из суммы квадратов его элементов
Варианты ввода операции модуля вектора.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Shift»+»|» |
На Рис. 2.9 приведен пример вычисления модуля вектора.
Обратная матрица
Матрица M-1 называется
обратной к матрице М, если
М*М-1=Е, где Е- единичная матрица.
Матрица имеет обратную только в том случае если она квадратная и ее определитель не равен нулю.
Варианты ввода операции обратной матрицы.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Shift»+»^» и ввести в показатель степени число -1 |
Функция | geninv(M), М – квадратная матрица с не нулевым определителем |
На Рис. 2.9 приведен пример вычисления обратной матрицы.
Рис. 2.10. Операции транспонирования, обратной матрицы и ее определителя и получения модуля вектора
Векторное произведение векторов
Векторным произведением называется вектор, длина которого равна произведению длин исходных векторов и синуса угла между ними, а направление его совпадает с направлением перпендикуляра к плоскости этих двух векторов (по правилу «буравчика»).
Варианты ввода операции векторного произведения векторов.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Shift»+»|» |
На Рис. 2.10 приведен пример векторного произведения векторов.
Скалярное произведение векторов
Скалярным произведением векторов называется число (или выражение), равное произведению длин перемножаемых векторов и косинуса угла между ними.
Варианты ввода операции скалярного произведения векторов.
Пиктограмма | в панели инструментов Calculator (Калькулятор) в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «*» |
На Рис. 2.10 приведен пример скалярного произведения векторов.
Суммирование элементов вектора
Варианты ввода операции суммирования элементов вектора.
Пиктограмма | в панели инструментов Matrix (Матрица) |
Клавиатура | клавиши «Ctrl»+»4» |
На Рис. 2.10 приведен пример суммирования элементов вектора.
Рис. 2.11. Операции векторного и скалярного умножения векторов и суммирование элементов вектора
3 Исследование систем линейных алгебраических уравнений в пакете MathCAD
Пример №1.
Задание. Показать, что столбцы и , составленные из коэффициентов уравнений
являются линейно независимыми.
______________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст «Пример №1» в правом верхнем углу листа.
Установить шрифт — MS Sans Serif сопроводительного текста, поддерживающий кириллицу. Для этого надо модифицировать текстовый стиль «Normal»:
vunivere.ru
в) скалярное произведение двух векторов.. ЭВМ с использованием математического пакета MathCad в среде Windows 98 для использования матричной алгебры в расчетах электротехнических систем
Похожие главы из других работ:
Лисп-реализация математических операций над комплексными числами
2.2.3 Произведение комплексных чисел
Произведение комплексных чисел z1=a+bi и z2=c+di называется комплексное число z =(ac-bd) + (ad + bc)i, z1z2 = (a + bi)(c + di) = (ac — bd) + (ad + bc)i. Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i2 на -1…
ЛИСП-реализация основных операций над нечеткими множествами
2.2.6 Произведение
Произведением нечётких множеств A и B называется нечёткое подмножество с функцией принадлежности:…
Модульное программирование
6.5 Произведение матриц
Напишите функцию, которая находит произведение двух прямоугольных матриц с согласованными размерами. Организовать тестирование функции. Прототип функции void MMult (float A [], float B [], float AB [], int m, int n…
Одномерные и двумерные массивы
2.1 Скалярное произведение
Напишите функцию, которая находит скалярное произведение двух векторов…
Основы диалога пользователя в MathCAD
4.2. Алгебра векторов. Преобразования векторов
Система MathCAD имеет ряд функций и операторов преобразования векторов. Они позволяют преобразовывать вектор и выполнять действия над его элементами. Основные функции приведены в таблице: 4…
Построение аналитических моделей алгоритмов и оценка их сложности
3.2 Протоколы работы машины Тьюринга (на двух словах языка и двух словах, не принадлежащих языку)
Пример работы алгоритма на слове “01”, которое не является словом исходного языка приведен в таблице 3.1. Таблица 3…
Построение аналитических моделей алгоритмов и оценка их сложности
3.4 Протоколы работы машины Тьюринга, построенные программно (на двух словах языка и двух словах, не принадлежащих языку)
Протоколы работы машины Тьюринга, построенные программно, приведены в приложении В. Стрелкой в них выделено положение УУ. Символом “~” обозначен пустой символ…
Построение синтезированных 3D изображений местности по цифровой карте
5.1.2 Расчет векторов нормали
Поскольку нормали являются перпендикулярами к поверхности, можно начать поиск нормали в конкретной точке с нахождения плоскости, которая касается поверхности только в одной этой точке. Нормаль — это вектор перпендикулярный к этой плоскости…
Применение технологии «Nvidia CUDA» для неграфических вычислений
3.2 Сложение векторов
Для подтверждения преимущества проведения неграфических вычислений на GPUс применением технологии CUDA, выполним сложение векторов. Для проверки скорости вычислений на CPU и GPU, будут использованы программы, производящие идентичные вычисления…
Программирование на языке высокого уровня
2.2.3 Произведение комплексных чисел
Произведение комплексных чисел z1=a+bi и z2=c+di называется комплексное число z =(ac-bd) + (ad + bc)i, z1z2 = (a + bi)(c + di) = (ac — bd) + (ad + bc)i. Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i2 на -1…
Программная реализация метода шифрования цифровых изображений
2.1 Декартово произведение множеств, бинарные отношения
Декартовым произведением множеств U и V называется множество упорядоченных пар, первый элемент которых принадлежит U, а второй — V . (1) Бинарное отношение R (из множества U в множество V) называется подмножество декартова произведения множеств U и V…
Разработка программного обеспечения для реализации арифметических операций над комплексными числами
2.2.3 Произведение комплексных чисел
Произведение комплексных чисел z1=a+bi и z2=c+di называется комплексное число z =(ac-bd) + (ad + bc)i, z1z2 = (a + bi)(c + di) = (ac — bd) + (ad + bc)i. Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i2 на -1…
ЭВМ с использованием математического пакета MathCad в среде Windows 98 для использования матричной алгебры в расчетах электротехнических систем
а) умножение матрицы на скалярное число
Произведение матрицы А на число (или числа на матрицу А) называется матрица С того же размера, что и А, элементы которой равны произведению соответствующих элементов матрицы А на число…
ЭВМ с использованием математического пакета MathCad в среде Windows 98 для использования матричной алгебры в расчетах электротехнических систем
б) умножение вектора на скалярное число
…
ЭВМ с использованием математического пакета MathCad в среде Windows 98 для использования матричной алгебры в расчетах электротехнических систем
д) деление матрицы на скалярное число
…
prog.bobrodobro.ru