Mathcad

Solve mathcad: Решение уравнений и систем уравнений в Mathcad

Решение уравнений и систем уравнений в Mathcad

Уравнение и системы уравнений в математическом пакете Mathcad  в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:

Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню  Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “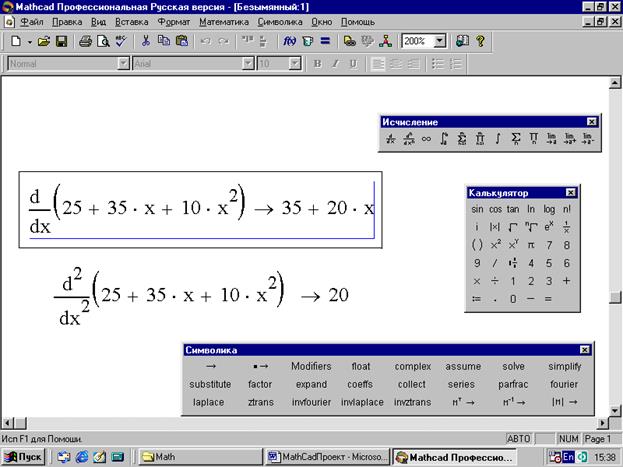

This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения

solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера.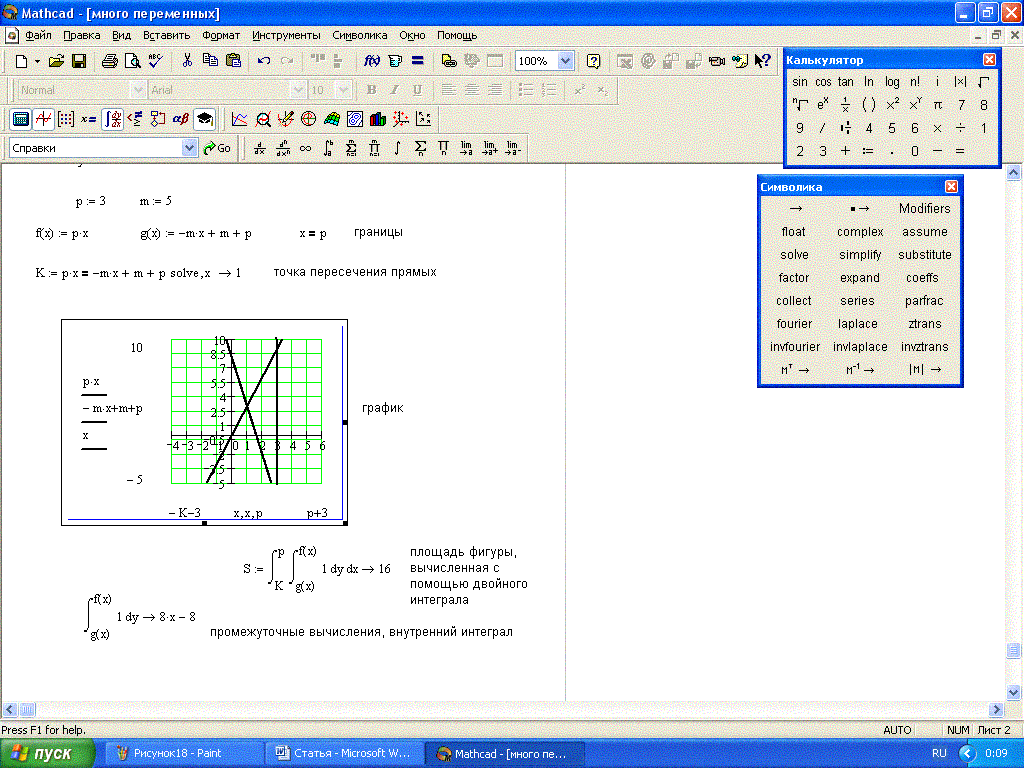 Например:

Пример использования блока given…find для решения системы уравнений:

Иллюстрированный самоучитель по MathCAD 7 › Работа с символьным процессором › Решение уравнения относительно заданной переменной (Solve) [страница — 138] | Самоучители по математическим пакетам

Решение уравнения относительно заданной переменной (Solve)

Если задано некоторое выражение F(x) и отмечена переменная х, то операция Solve (Решить) возвращает символьные значения указанной переменной х, при которых F(x)==0. Это очень удобно для решения алгебраических уравнений, например квадратных и кубических, или для вычисления корней полинома. Рис. 8.13 содержит примеры решения квадратного уравнения и нахождения комплексных корней полинома четвертой степени.


Рис. 8.13. Примеры решения уравнений

Ранее отмечалось, что усложнение уравнения, например переход от квадратного уравнения к кубическому, может вызвать и существенное усложнение результата.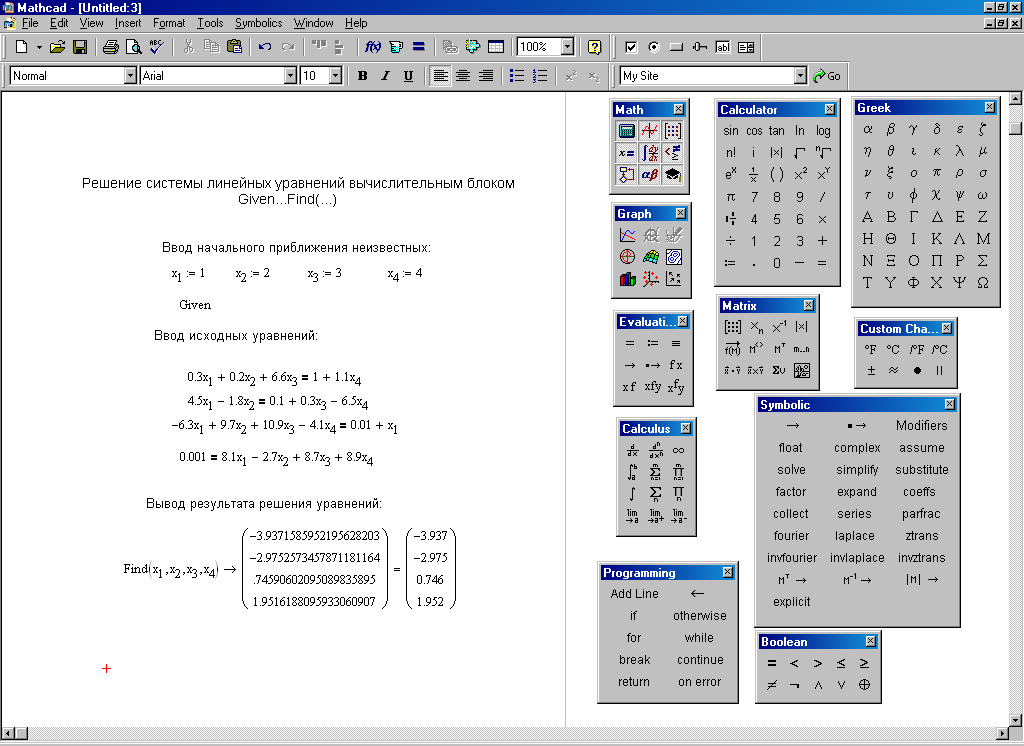 Тогда система представляет решение в более компактном виде (но без общепринятой математической символики) и предлагает занести его в буфер обмена.

С помощью операции Paste (Вставить) в позиции Edit (Правка) главного меню можно перенести решение в основное окно системы, но оно имеет уже тип текстового комментария, а не математического выражения, пригодного для дальнейших преобразований. Впрочем, часть его можно (опять-таки с помощью буфера обмена) ввести в формульные блоки для последующих преобразований и вычислений.

Более того, форма представления результата в таком случае отличается от принятой в системе MathCAD (например, в качестве знака деления используется косая черта, для возведения в степень – составной знак

** и т. д.). Это сделано ради компактности представления результатов вычислений. Рис. 8.14 показывает результат решения кубического уравнения в символьном виде.


Рис. 8.14. Решение кубического уравнения в символьном виде

Последний пример наглядно иллюстрирует проблему «разбухания» результатов.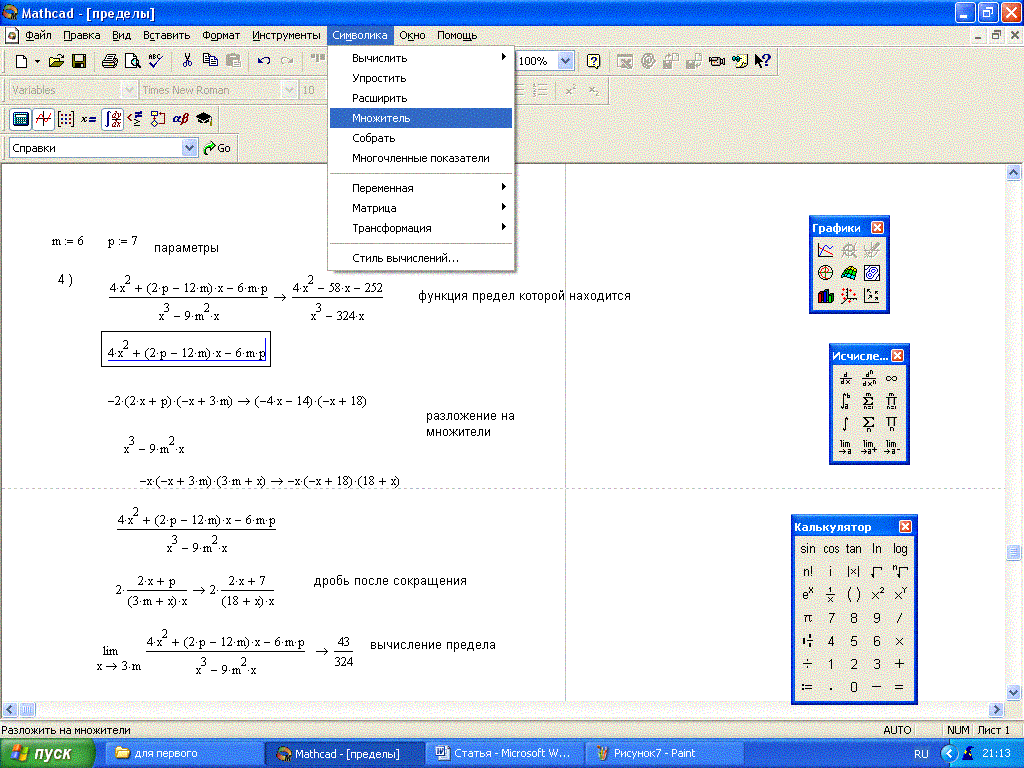 Если при решении квадратного уравнения получены простые выражения, известные даже школьникам (рис. 8.13 – первый пример), то при увеличении порядка уравнения всего на единицу результат оказался представленным весьма громоздкими и малопригодными для анализа формулами. Хорошо еще, что существующими!

В случаях, подобных приведенному, пользователю надо реально оценить свои силы в упрощении решения. Это придется сделать вручную. При технических расчетах специалист нередко знает, какие из параметров решения несущественны и может отбросить их. Однако для строгих математических расчетов это не всегда возможно, поэтому даже громоздкий результат может быть весьма полезным с познавательной точки зрения.

mathcad — Translation into Russian — examples English

These examples may contain rude words based on your search.

These examples may contain colloquial words based on your search.

Here for a comparison outcomes of a package MathCad.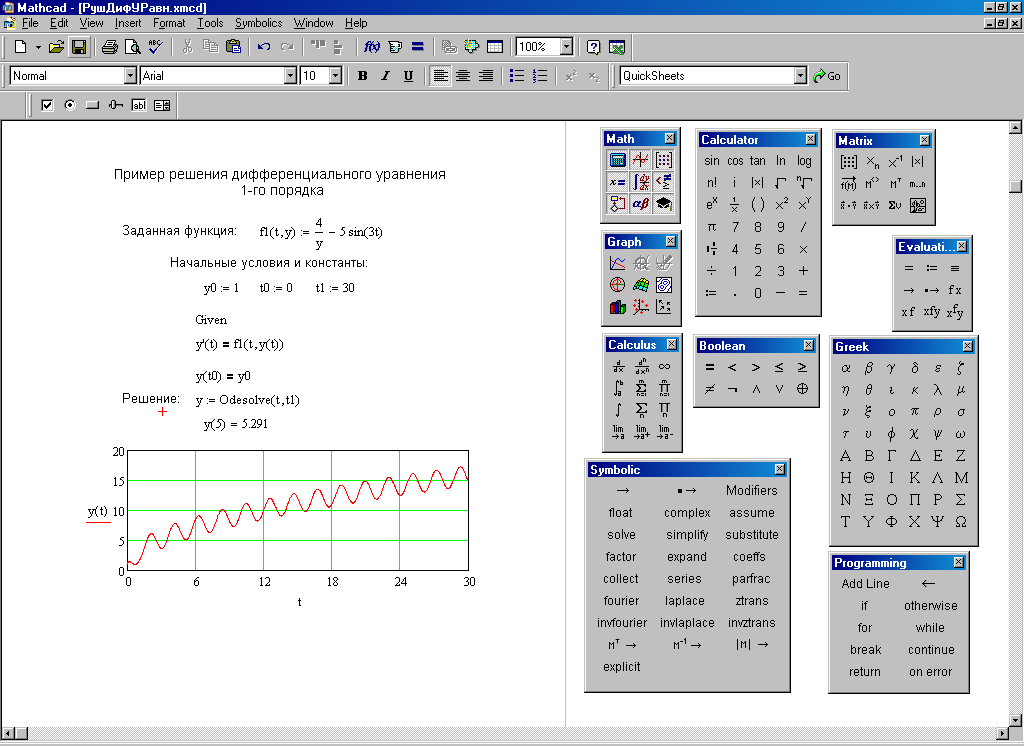

Вот для сравнения результаты пакета MathCad.

The idea of calculation is very easy and the same with Mathcad.

Mathcad is used to solve, analyze, and share engineering calculations.

Mathcad достаточно удобно использовать для обучения, вычислений и инженерных расчетов.

The company became most famous for its Mathcad software, a powerful application for solving and visualizing mathematical problems.

Компания стала знаменитой благодаря разработке программы Mathcad, мощного приложения для решения и визуализации математических задач.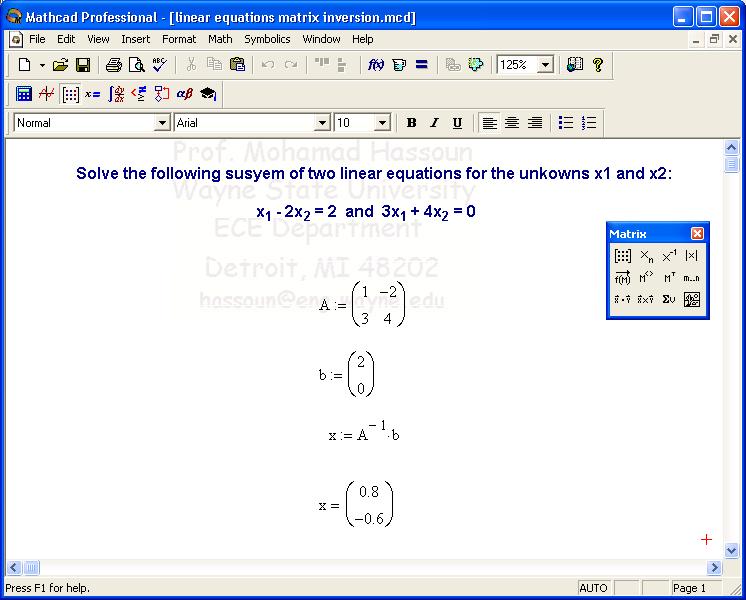

Mathsoft Engineering & Education continued to develop and sell its flagship Mathcad product as well as the Mathcad Calculation Server, an enterprise server for sharing technical calculations.

Mathsoft Engineering & Education продолжает разрабатывать и продавать свой флагманский продукт Mathcad, а также Mathcad Calculation Server, корпоративный сервер для разделения технических вычислений.

MathCAD — это просто! Часть 17. Снова символьные вычисления

Уже третью статью подряд мы с вами будем заниматься символьными вычислениями. Среда MathCAD, как вы сами уже имели возможность убедиться, имеет очень гибкие и мощные средства организации подобного рода вычислений. И вычисления эти в математике бывают важны и используются очень часто — именно поэтому мы с вами говорим о них столь подробно. Сегодня мы познакомимся с некоторыми новыми аспектами организации символьных вычислений в MathCAD’е, которые наверняка пригодятся вам при последующей работе с этой мощной математической средой.

Разложение на дроби

Мы уже говорили с вами о работе с дробями — точнее, о приведении суммы нескольких маленьких дробей к одной, но большой дроби. Теперь пришло время поговорить о процессе, диаметрально противоположном этому — о разложении одной дроби на сумму нескольких. Для решения этой задачи в MathCAD’е есть специальный оператор, который называется parfrac (от английского partial fraction — частные дроби). Использование этого оператора чрезвычайно простое, как, впрочем, и всех остальных операторов, которые можно найти на панели Symbolic. Достаточно, записав дробь, которую вы хотите разложить на сумму простых, затем выбрать на этой панели кнопку parfrac и указать имя переменной, для которой будет проводиться разложение. Когда вы добавите оператор parfrac, то перед ним автоматически добавится и оператор convert. Можете попробовать использовать их раздельно — уже на первой же дроби вы сможете собственноручно убедиться, что ничего ни хорошего, ни плохого из этого не выйдет — MathCAD просто не приемлет эти два оператора по отдельности.

Тот же самый результат, не используя оператор parfrac, можно получить, выбрав в меню Symbolics пункт Variable, а в нем — Convert to Partial Fraction. В этом случае, правда, если что-то нужно будет изменить в исходном выражении, операцию придется повторить, поэтому лучше все же использовать оператор parfrac.

Оператор collect

Мы уже говорили о работе со скобками в различных выражениях. Оператор collect является еще одним весьма и весьма полезным оператором, помогающим в работе со скобками — если конкретнее, то для вынесения из-за скобок общих множителей для полиномиальных выражений. Думаю, вы оцените все преимущества использования этого простого, но крайне эффективного оператора, если вам когда-нибудь будет нужно в реальных расчетах заниматься подобными вещами в практических целях.
В общем-то, конечно, кто-то может сказать (и будет, пожалуй, прав), что поиск и вынесение за скобки общего множителя — не самая трудоемкая задача, а потому особой нужды в том, чтобы напрягать для ее решения MathCAD, пожалуй, что и нет. Однако на самом деле гибкость оператора collect позволяет проводить поиск даже самых замысловатых общих множителей, что вручную все-таки бывает не всегда удобно. Способ применения оператора collect действительно предельно прост. Мы, как обычно, записываем выражение, которое нужно преобразовать, а затем ищем на привычной уже нам панели Symbolic нужный нам оператор. После запятой в качестве параметра указывается имя переменной, которую мы будем выносить за скобки. Можно указывать не отдельную переменную, а какую-то функцию либо выражение — например, синус или логарифм. Правда, вынесение общих множителей реализовано довольно своеобразно — программа работает только с одной степенью переменной. То есть, если у вас будет запись вида x2+x, то она останется неизменной после применения оператора collect по переменной x.

Коэффициенты многочленов

Иногда бывает полезно вынести коэффициенты многочлена в специальный столбец для того, чтобы потом ими оперировать. Конечно, для большинства распространенных задач полиномы не превышают третьей степени, и сделать это не так уж и сложно вручную. Однако зачем выполнять вручную то, что можно сделать одним оператором? Я думаю, вы согласитесь с тем, что это будет не слишком рациональным использованием времени, а потому имеет смысл применить оператор coeffs для того, чтобы получить готовый столбец коэффициентов. В общем-то, я думаю, вы уже догадались, как применять этот оператор. Нужно записать многочлен, а затем воспользоваться панелью Symbolic (еще раз напомню, что название оператора, который нужно в данном случае использовать, coeffs). Обращу ваше внимание на то, что столбец записывается снизу вверх от высших степеней многочлена к высшим. Также, конечно же, можно использовать именованные функции или другие выражения, которые возведены в различные степени.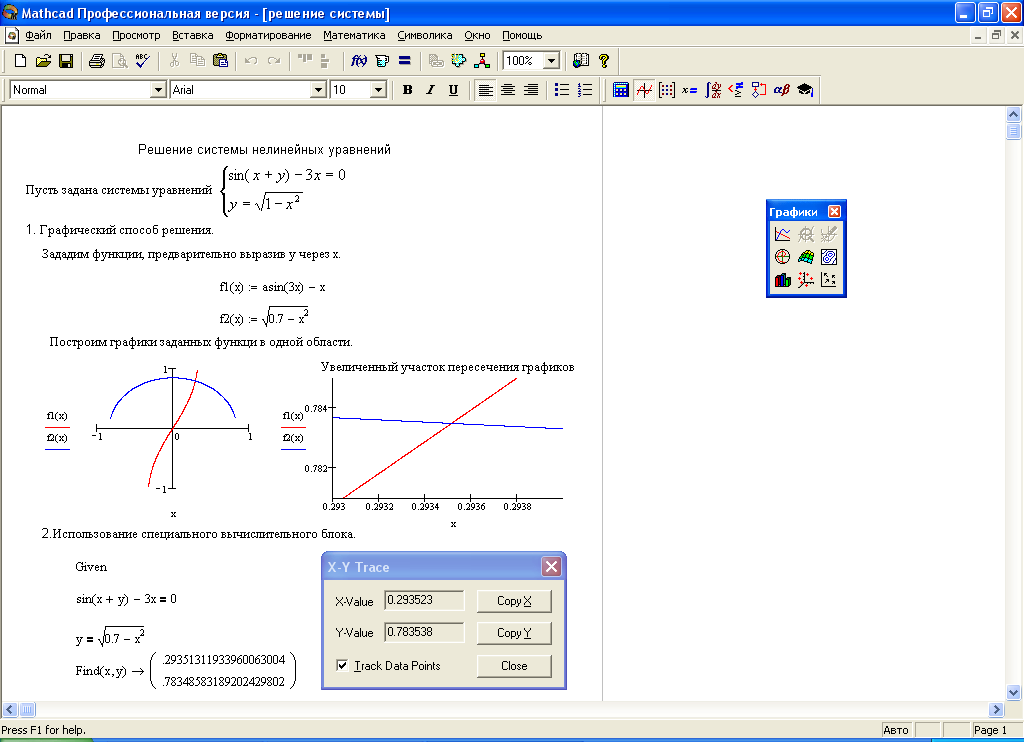

Ограничения на переменные в вычислениях

Иногда при использовании символьных вычислений есть необходимость выставить определенные ограничения в вычислениях, которые могут коренным образом упростить итоговое выражение. Действительно, весьма и весьма часто при решении прикладных задач по условиям этих самых задач на переменные накладываются определенные ограничения — например, очень часто переменные можно считать неотрицательными или даже строго больше нуля. Как рассказать MathCAD’у, что переменные ограничены определенным диапазоном значений? Естественно, для этого в этом мощном математическом пакете существует специальный оператор. И имя ему — assume. Оператор assume используется вместе с остальными операторами (особенно часто в сочетании с оператором simplify). Я уже рассказывал в прошлый раз о том, как изменяется внешний вид операторов символьных вычислений в MathCAD, а потому это не должно стать для вас сюрпризом.В качестве ограничений, накладываемых на переменные, могут выступать не только минимальное и максимальное значения этой самой переменной.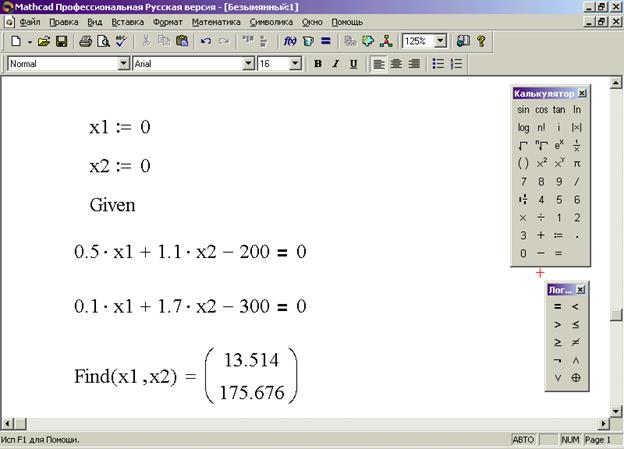 Для того, чтобы увидеть полный список всех возможных ограничений, нажмите на панели Symbolic кнопку Modifiers. Она, в отличие от большинства других кнопок на этой панели, не добавляет никаких новых операторов в рабочий лист MathCAD, а всего лишь показывает или прячет панель с модификаторами (modifiers) — эта панель как раз и пригодится нам для выставления различных ограничений на переменные при упрощении выражений и других символьных операциях.Как видите, модификаторов в панели не так уж много, а потому мы поговорим о каждом из них. Первый — это, как вы можете заметить, уже довольно неплохо знакомый нам с вами assume. Не буду повторяться — о его использовании я рассказывал всего парой абзацев выше. Второй по счету модификатор — это real. Поскольку MathCAD может оперировать и комплексными числами (об этой полезной возможности мы с вами еще обязательно поговорим), то местами в подобных вычислениях полезно наложить на переменную ограничение и определить ее как действительную. RealRange — третий по счету модификатор на панели Modifiers — это двустороннее ограничение на действительную переменную на определенном отрезке (то есть, обратите внимание, концы этого отрезка также попадут в область значений нашей переменной). 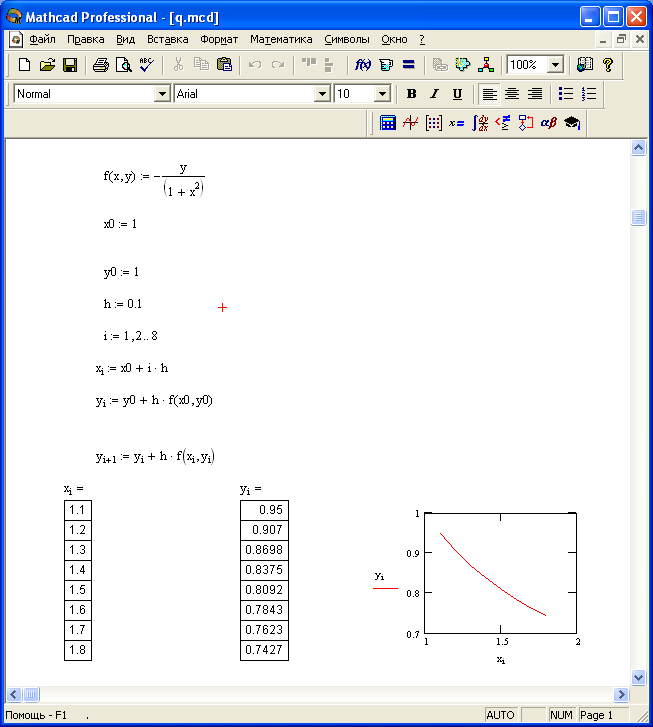Четвертый модификатор имеет название trig, и он обозначает переменную как тригонометрическую величину. Этот модификатор используется по сравнению с остальными совсем не часто, поскольку при работе с тригонометрическими функциями все же предпочтительнее использовать их общепринятые обозначения, которые, будучи совсем не длинными, сильно упрощают чтение проекта и уменьшают вероятность в нем запутаться. Последний модификатор, который можно найти на панели, — это модификатор integer. Он используется для задания целочисленных переменных. Используются модификаторы для указания выражений в операторе assume. То есть, например, если мы хотим указать при вычислении какого-либо символьного выражения, что переменная n у нас будет целочисленной, то мы должны записать после оператора assume следующее: n = integer. Совершенно аналогично и для всех остальных модификаторов, которые были описаны выше. Кстати, при преобразовании выражений наподобие того, что приведено на иллюстрации чуть выше, совершенно не обязательно использовать assume вместе с simplify. Если вы уберете оператор simplify, то сможете сами убедиться в том, что без него выражение будет вычислено ничуть не хуже. Правда, если пойти дальше и убрать еще и assume, оставив при этом n = integer, то MathCAD выдаст ошибку с сообщением о неверном синтаксисе команды.

Оператор float

Напоследок мы с вами поговорим о еще одном весьма полезном операторе, который, будучи оператором символьных вычислений, используется для получения конкретного результата в виде числа. Оператор float используется тогда, когда нужно получить результат символьных вычислений не в виде формулы, а в виде числа. Вполне понятно, что применять его можно исключительно в тех случаях, когда все числа в выражении заданы не в общем виде (т.е. не какими-то именованными константами), а конкретными значениями. В противном случае MathCAD ошибки не выдаст, однако использование оператора float будет напрочь лишено смысла. Для того, чтобы проиллюстрировать использование этого оператора, обратимся к примеру кубического уравнения, который рассматривался в предыдущей части нашей серии статей по MathCAD’у.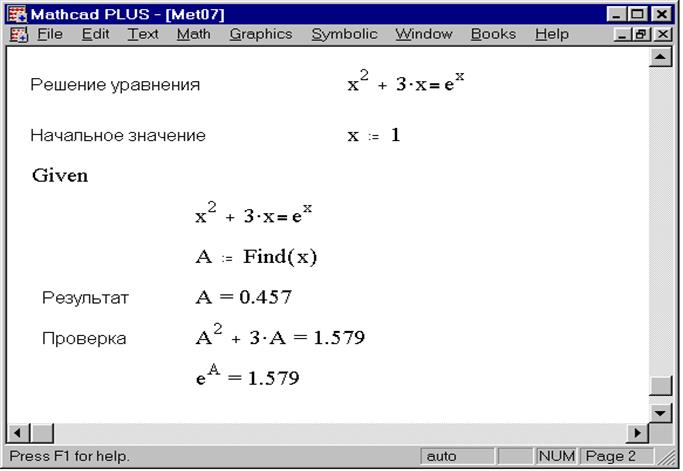 Решения кубических уравнений в виде формул занимают очень много места и отличаются громоздкостью, а потому их целесообразно упрощать с помощью оператора float. Можете сравнить формульные результаты, полученные нами в прошлый раз, с тем, как они записываются с помощью этого оператора: разница, как говорится, налицо.

Думаю, синтаксис использования этого оператора вполне понятен из примера: в качестве первого параметра (до оператора) — выражение, которое нужно вычислить (в приведенном примере его, конечно, лучше опускать, потому что иначе это приводит, как показано на иллюстрации, к дублированию результата), а в качестве второго (после оператора) — точность, т.е. количество значимых цифр после запятой, остающихся после вычислений. Что ж, пока что, я так думаю, хватит на этот раз — нехорошо было бы перегружать вас, уважаемые читатели, информацией, тем более, что тема символьных вычислений в MathCAD’е явно не относится к тем, которые можно обсуждать практически бесконечно за чашкой чая или кофе. Я думаю, что те операторы, которые мы сегодня рассмотрели, наверняка пригодятся вам в повседневных буднях вычислений в MathCAD’е, и вы еще не раз будете добрым словом поминать разработчиков этого всесторонне замечательного математического пакета, предусмотревших для вас все эти возможности.

SF, [email protected]

Компьютерная газета. Статья была опубликована в номере 30 за 2008 год в рубрике soft

Решение в MathCAD


float
Численное вычисление

complex
Комплексное вычисление

assume
Символьное вычисление с некоторыми предположениями

solve
Решение уравнения (системы уравнений) относительно переменной (переменных)

simplify
Упрощение выражений

substitute
Замена переменной

factor
Разложение на множители

expand
Перемножение степеней и произведений

coeffs
Определение коэффициентов полинома

collect
Группировка слагаемых по степеням переменной

series
Разложение в ряд Тейлора или Лорана

parfac
Разложение на элементарные дроби

fourier
Преобразование Фурье

invfourier
Обратное преобразование Фурье

lарlасе
Преобразование Лапласа

invlaplace
Обратное преобразование Лапласа

ztrans
Z-преобразование

invztrans
Обратное Z-преобразование

MT
Транспонирование матрицы

M-1
Нахождение обратной матрицы

|M|
Нахождение определителя матрицы

Ключевые слова допустимо набирать только строчными буквами (кроме Modifier — первая буква в этом слове должна быть прописной).
Блоки системы SmartMath имеют следующие отличительные свойства:
дают хорошее визуальное представление операций;
имеют шаблоны для задания параметров и опций;
обеспечивают работу с функциями пользователя;
обеспечивают передачу данных от формулы к формуле;
допускают расширение, позволяющее использовать сразу несколько директив;
имеют конструкцию, схожую с конструкцией программных блоков.
Как нетрудно заметить, директива упрощения simplify не имеет параметров. Директива разложения в ряд Тейлора series требует указания двух параметров: задания начального значения переменной х и указания числа членов ряда. Директивы преобразования Лапласа laplace и решения уравнений solve требуют одного параметра — указания имени переменной (в нашем случае х). С помощью директивы solve можно решать и системы уравнений — тогда ее параметр будет вектором неизвестных.
Выполнение матричных операций в символьной форме особой специфики не имеет.

Операции с выделенными переменными.

Следующая группа символьных операций выполняется с выражениями, требующими указания переменной, по отношению к которой выполняется операция.

Решение уравнений и наборов уравнений в Mathcad

В математическом пакете Mathcad уравнения и наборы уравнений в символьном представлении решаются с помощью специального оператора символьного вычисления resolve в сочетании со знаком равенства символов, который также может быть введен с панели управления «» Символы ». Например:

Те же операции для решения уравнений в Mathcad можно выполнить с помощью меню « Symbols ».Во-первых, вам нужно ввести вычисляемое выражение. Во-вторых, необходимо удалить переменную, составляющую центр уравнения, затем войти в меню « Symbols, Variable, Compute ». Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [ = ]. Например:

При решении некоторых уравнений результат содержит большое количество символов. Mathcad сохраняет его в буфере, а на дисплее отображается следующее: « В этом массиве больше элементов, чем может быть отображено за один раз.Попробуйте использовать функцию «подматрица ». В этом случае рекомендуется применить расчетное решение. Или, если требуется, символьное решение можно вывести и отобразить на дисплее.

Решение символов может быть получено с помощью блока given… find. В этом случае, пока вводится уравнение, используется логическое равенство « = » на панели инструментов Логическое значение используется для объединения правой и левой частей уравнения.Например:

Наборы уравнений в символьном представлении решаются аналогичным образом. Ниже вы можете увидеть примеры решения систем уравнений в символьном представлении различными методами. Когда оператор решения символа решить используется вместе со знаком равенства символов, набор уравнений может быть введен в векторной форме, которая вводится вместо левого маркера оператора решения , в то время как список переменные системы уравнений вводятся вместо правого маркера. Например:

Пример … найти для используемых наборов уравнений показан ниже:

Mathcad Function — обзор

Встроенные функции

Встроенные функции варьируются от очень простых до очень сложных. Вот некоторые простые встроенные функции PTC Mathcad: sin () , cos () , ln () и max () . Все функции PTC Mathcad настраиваются аналогичным образом.Дается имя функции, за которым следует пара круглых скобок. Информация, указанная в круглых скобках, называется аргументом. У каждой функции есть имя и аргумент. Функция берет информацию из аргумента (содержащегося в круглых скобках), обрабатывает информацию на основе правил, определенных для конкретной функции, а затем возвращает результат.

Вкладка Functions на ленте содержит все встроенные функции PTC Mathcad. Функции организованы по категориям. Все категории не отображаются на вкладке Функции . Чтобы просмотреть список всех встроенных функций PTC Mathcad, выберите элемент управления ALL Functions .

Если щелкнуть элемент управления All Functions , в левой части рабочего листа PTC Mathcad появится список, в котором показаны все встроенные функции PTC Mathcad. По умолчанию функции группируются по категориям. См. Рисунок 4.1. Выберите треугольник слева от категории, чтобы увидеть функции в этой категории.Если вы хотите просмотреть алфавитный список всех функций PTC Mathcad по имени, нажмите кнопку вверху списка функций. См. Рисунок 4.2.

РИСУНОК 4.1. Функции по категориям

РИСУНОК 4.2. Функции по имени

Если вы наведете курсор на имя функции, появится информационное окно с указанием имени функции и ее аргументов в круглых скобках. Он сообщает вам, что делает функция, и перечисляет любые ограничения для аргументов (например, должен ли аргумент быть в радианах или должен быть целым числом).

Некоторые функции ожидают только одного аргумента. Другие функции ожидают двух аргументов. Некоторые функции требуют нескольких аргументов или имеют необязательные аргументы. Некоторые функции могут иметь переменное количество аргументов. Они будут обозначены тремя точками после перечисленных аргументов. На рис. 4.3 показаны четыре функции, каждая с разным числом аргументов.

РИСУНОК 4.3. Аргументы функций

Найдите минутку, чтобы просмотреть полный список встроенных функций PTC Mathcad из списка Function .В следующих главах мы обсудим выбранные функции. Если вас интересует конкретная функция, см. Справку PTC Mathcad. На рис. 4.4 показаны примеры использования четырех различных функций PTC Mathcad, требующих различной длины аргументов.

РИСУНОК 4.4. Примеры использования различных типов аргументов

В выражение PTC Mathcad может входить неограниченное количество функций. Чтобы вставить функцию в выражение, просто выберите место в выражении, в котором должна быть функция, а затем щелкните имя функции на вкладке Функции . Если вы знакомы с именем функции и ее аргументами, вы можете просто ввести имя функции и заключить необходимые аргументы в круглые скобки. Помните, что имена функций PTC Mathcad чувствительны к регистру. Если вы вводите имя функции, а PTC Mathcad не распознает его, используйте список Function , чтобы узнать, является ли первая буква прописной или строчной. На рис. 4.5 показано выражение, использующее несколько встроенных функций.

РИСУНОК 4.5. Пример использования встроенных функций в выражении

Использование Mathcad для решения систем дифференциальных уравнений Чарльз…

Использование Mathcad для решения систем из < strong> Дифференциальные Уравнения Чарльз Нипперт. Начало работы. Системы дифференциальных уравнений довольно распространены при динамическом моделировании. .Решение системы дифференциальных уравнений несколько отличается от решения одного обыкновенного дифференциального уравнения. Процедура решения требует небольшого предварительного планирования. Система дифференциальных уравнений должна быть сначала помещена в в «стандартную форму», показанную ниже: y ‘= F t, y, y Ly y’ M y ‘yy M 1 1 2 2 n (t 0) (t) 0 1 = F (1 2 n) (t, y, y Ly) 2 = F n (t 0) = C n (t, y, y Ly) = C 1 = C yn Обычно это преобразование можно выполнить, однако для этого могут потребоваться некоторые манипуляции.Пример преобразования системы дифференциальных уравнений . Рассмотрим систему из дифференциальных уравнений и условий начального значения, показанных ниже y » = y — 3y yy 1 y ‘2 2 1 0 (0) = 2 (0) = 1 (0) = 3 1 y 2 Для генерации решения , определите новую переменную y 3 = y 1 ‘и переставьте , чтобы получить следующую систему. ‘y’ = yy ‘y’ yy 1 1 2 2 3 1 2 1 = y ‘+ y’ = y 1 3 = y 1 1 2 (0) = 2 (0) = 3 (0) = 1 2 — y 3 — 3y y3 В образце этих заметок вы получите численное решение следующей системы дифференциальных уравнений. Вы будете использовать решение для создания как обычного параметрического графика, так и графика фазовой плоскости. 2 2 n n

Основы MathCAD

Основы MathCAD

ВВЕДЕНИЕ В MathCAD

MathCAD — одна из нескольких конкурирующих программ, используемых в качестве инструмента автоматизированного проектирования для ученых, инженеров, инженеров-технологов и инженеров.Некоторые из этих конкурирующих программ включают Mathmatica, Matlab, TK Problem Solver и Maple. Некоторые могут рассматривать в качестве конкурентов электронные таблицы, такие как Excel, StarCalc или Gnumeric. Однако позже в этом курсе мы увидим, что MathCAD довольно хорошо работает с компонентами электронных таблиц, особенно с MS Excel. Фактически, часть этого курса посвящена совместному использованию MathCAD и Excel, обеспечивая очень мощный инструмент для проектирования / расчета.

Подобно портативному калькулятору, MathCAD НЕ является инструментом, который сделает вашу работу за вас; и это не инструмент, который заменит плохие математические навыки.Последний момент особенно важен. Чтобы эффективно применять MathCAD, необходимо разбираться в математике в целом, а также в специфике своей дисциплины. Можно даже утверждать, что дальнейшее использование MathCAD на других курсах и на работе значительно улучшит математические навыки.

MathCAD избавит вас от утомительного выполнения многих математических операций. Благодаря встроенному символьному механизму это включает символьную алгебру и символьное исчисление.Например, хотя решение двух уравнений с двумя неизвестными посредством ручного вычисления является очень простым процессом, использование блока «Решить» в MathCAD позволяет выполнить такое решение за секунды.

Как и любое другое программное обеспечение, MathCAD прост в использовании, если вы его знаете. Однако в нем есть свои нюансы, с которыми вам необходимо ознакомиться. Таким образом, для его эффективного и действенного использования требуется практика. Но ни один курс не может научить вас всем аспектам MathCAD или любой другой важной части программного обеспечения в этом отношении.Несомненно, наиболее важным аспектом любого программного обеспечения для изучения является его справочная / учебная утилита. MathCAD имеет исключительную справочную функцию.

Использование справки MathCAD

MathCAD предоставляет широкий набор функций справки. К ним относятся:

  • Справка MathCAD
    Это стандартный диалог справки Windows, который вы найдете в любом программном пакете. Этот диалог включает вкладки «Содержание», «Указатель» и «Поиск».Откройте диалоговое окно справки, нажав клавишу « F1 » или выбрав «Справка»> «Справка MathCAD» в строке меню.

  • Содержание Вкладка представляет информационные темы в виде Оглавления, как в любой книге.
  • Указатель Вкладка организована в виде указателя, который можно найти в конце любой книги.
  • Search позволяет искать тему на основе ввода ключевого слова.

В конце концов, все три метода поиска информации заканчиваются одним и тем же результатом. То, что вы используете, — это скорее вопрос предпочтений.

Доступ к учебным пособиям из пункта меню «Справка». Все темы учебника будут вам полезны в течение всего квартала. Но в первую неделю вам следует ознакомиться с «Учебниками по началу работы» (за исключением символических праймеров). Эти учебники охватывают большую часть того, чем мы занимаемся в первую неделю занятий.

Функция quicksheet — одна из самых приятных функций в арсенале вспомогательных инструментов MathCAD.Короче говоря, это живые рабочие листы MathCAD, содержащие примеры функций MathCAD, возможностей построения графиков и программирования. Вы также можете изменить или добавить в Quicksheet. Хотя вы не можете сохранить эти изменения в исходном файле Quicksheet, вы можете сохранить файл под другим именем. Вы также можете скопировать / вставить уравнения из быстрой таблицы на свой рабочий лист.

Еще одна уникальная особенность MathCAD — наличие справочных таблиц. Это просто таблицы различных физических свойств, таких как удельный вес выбранных жидкостей, фундаментальные константы и т. Д.Хотя это ни в коем случае не исчерпывающий ресурс, они исключительно подходят для ряда приложений.

Еще одна особенность MathCAD — электронная книга или электронная книга. MathCAD поставляется с несколькими электронными книгами, которые установлены по умолчанию. Дополнительные электронные книги доступны на веб-сайте MathCAD. Большинство из них бесплатны, но некоторые необходимо покупать. Электронные книги, как правило, посвящены определенной теме. Например, одна из установленных по умолчанию электронных книг — «Механика материалов». Это электронное приложение к популярному тексту материалов, написанному Гиром и Тимошенко.


  • Сотрудничество MathCAD (Форум пользователей)
Сотрудничество — это форум пользователей в сети. Это отличный способ получить помощь опытных людей. Сотрудничество разделено на предметные области, такие как машиностроение, гражданское строительство и финансы, и это лишь некоторые из них. Также доступны пожертвованные листы по множеству тем.

Структура рабочего листа

Фраза «Блокнот инженера» часто используется для описания MathCAD.Это подходящее описание. MathCAD позволяет вам писать уравнения, фактически, для разработки полных решений проблем, как если бы вы это делали на бумаге. По большей части вы можете размещать уравнения, определения переменных, графики и текст в любом месте на странице, где захотите. Вот почему я часто называю MathCAD «электронной таблицей произвольной формы». Однако существует минимальный набор правил относительно такого размещения и есть синтаксис, который необходимо понимать в отношении математических операций.

Основные математические операции

От базовой арифметики до уравнений в частных производных MathCAD использует стандартную номенклатуру для всех математических операций. MathCAD также следует стандартной иерархии операций. А пока давайте сосредоточимся на арифметических операциях и определениях переменных.

  • Круглые скобки — используйте открывающие / закрывающие круглые скобки (Shift-9 и Shift-0) для круглых скобок. Не пытайтесь использовать квадратные или фигурные скобки. MathCAD при необходимости изменит скобки, если вы используете вложенные наборы.
  • Возведение в степень — используйте символ пряника (Shift-6) для возведения в степень
  • Умножение — используйте звездочку (Shift-8) в качестве оператора умножения.Оператор отображается в виде выпуклой точки. (например: вводится как 5 * 6 =)
  • Деление — используйте косую черту в качестве оператора деления. Оператор отображается в виде стандартной дроби. (например: вводится как 5/6 =)
  • Дополнение — Вы можете использовать знак плюса на цифровой клавиатуре или в верхнем ряду клавиш (Shift- =)
  • Вычитание — вы можете использовать знак минус на цифровой клавиатуре или в верхнем ряду клавиш.

Примечание. Во многих случаях нет необходимости явно нажимать клавишу умножения при вводе уравнения, включающего умножение.Например, при вводе выражения 5x множитель вводится автоматически. Однако, по моему опыту, при определенных условиях это вызывает проблемы. Другими словами, в некоторых ситуациях множитель не вводится автоматически, когда он должен быть. Поэтому я рекомендую вам ВСЕГДА явно нажимать клавишу умножения (Shift-8) при вводе формулы, включающей умножение.

Переменные, присвоение переменных и вычисление уравнений.

Конечно, чтобы в полной мере использовать MathCAD, нужно уметь определять переменную, использовать ее в уравнении или функции, а затем оценивать эту функцию.Очевидно, это делается со знаком равенства, но существует шесть различных форм знака равенства в зависимости от того, определяете ли вы переменную или оцениваете функцию. Ниже объясняется каждая из этих форм.

Присвоение равно (:) — Используйте эту версию знака равенства, чтобы присвоить значение локальной переменной или определить уравнение или функцию. Используйте ключ с двоеточием. Например, нажатие клавиш для присвоения значения пяти переменной «x» будет x: 5. Значение «x» доступно только для функций, следующих за объявлением.



Глобальное присвоение равно (~) — Используйте эту версию знака равенства, чтобы присвоить значение глобальной переменной. Для этого используйте клавишу тильды (~). Эта клавиша обычно находится сразу под клавишей Escape. Эта версия знака равенства позволяет назначенной переменной быть доступной для всех уравнений на рабочем листе, даже если объявление переменной происходит после объявления уравнения. Хотя это звучит неплохо, это может затруднить устранение неполадок на сложном листе.Я рекомендую вам использовать этот метод объявления переменных только для объявления констант. Клавиши, используемые для присвоения значения 13 переменной ‘y’, имеют вид y ~ 13.



Вычислить равно (=) — Эта форма знака равенства используется для фактического вычисления уравнения или функции. Он НЕ используется для присвоения значения. Оператор оценки равенства — это просто стандартный знак равенства на клавиатуре. Например, предположим, что переменная «z» представляет собой сумму переменных «x» и «y», обе из которых были определены выше.. Мы можем ввести это, нажав клавиши z: x + y, что приведет к уравнению:



Чтобы оценить результат, просто введите z =
.


Логическое равенство (Ctl- =) — Логическое равенство фактически является логическим оператором. Он не используется для присвоения значений и не используется для оценки функции. Он используется как оператор сравнения и задает вопрос: «Равна ли переменная ‘x’ ‘y’?». Если выражение истинно, оно возвращает единицу, если выражение ложно, оно возвращает ноль.Логический оператор равенства используется в основном в программировании, но мы также будем использовать его при решении систем уравнений. Сочетание клавиш для логического оператора равенства — Ctl- =. Например, мы ранее присвоили значение пять переменной x и значение 13 переменной y. Очевидно, мы знаем, что «x» не равно «y». В терминах логического выражения мы можем записать и оценить следующим образом:



Вышеприведенное выражение просто сравнивает значение «x» со значением «y», определяет, что они не равны, таким образом возвращает значение нуля (ложь).

Локальное присвоение ({) — Эта версия знака равенства идентична двоеточию равенства, за исключением того, что она используется в рамках программы MathCAD. Имеет вид:



Локальное назначение не имеет абсолютно никакой цели вне рамок программирования. Мы обсудим это в следующей лекции по программированию MathCAD.

Символьное вычисление (Ctl-.) — В то время как описанный выше знак равенства дает приблизительное решение, символьное вычисление дает точное решение с использованием символьного механизма MathCAD.Чаще всего он используется для вычисления выражений символьного исчисления. В качестве примера оцените частное 17/51 приблизительно и точно следующим образом:

Приближенное решение с использованием оценки равно.

Точное решение с использованием символьной оценки

На первый взгляд кажется, что символическая оценка просто уменьшает дробь. В случае простой арифметики это, по сути, верно. Но на самом деле символический двигатель делает гораздо больше. Чтобы не усложнять задачу, символьный движок предоставляет точное решение, сохраняя все числа в их рациональной форме (то есть: 1/3 вместо 0.3333) или выразив решение с помощью символа (например: p вместо 3,14159). Например, натуральный логарифм 5 — это иррациональное число. Его нельзя выразить рациональной дробью, приблизительное и точное решение:

Приблизительное решение
Точное решение

Определение переменных

При определении переменных важно не переопределять встроенную переменную или переопределять ранее определенную пользовательскую переменную. Еще одна важная проблема, связанная с переменными, заключается в том, что MathCAD чувствителен к регистру.Следующие переменные, хотя они могут показаться вам и мне одинаковыми, уникальны для MathCAD просто из-за использования заглавных букв.





Обратите внимание на зеленую волнистую линию под последним определением. Это указывает на переопределение переменной. В этом случае «галлоны в минуту» в нижнем регистре — это единица измерения MathCAD галлонов в минуту. НИКОГДА не переопределяйте переменную MathCAD или модуль , если вы точно не знаете, что делаете и каковы последствия вашего действия.Как мы обсудим позже, это, вероятно, приведет к переопределению ряда других модулей, что приведет к ошибочным результатам, которые трудно устранить. Обратите внимание на эту маленькую закорючку. Это сэкономит ваше время.

Встроенные константы

MathCAD имеет ряд встроенных констант. Это:

Infinity (Ctl-Shift-z) — При алгебраическом использовании бесконечность имеет значение 1×10 307 и -1×10 307 .
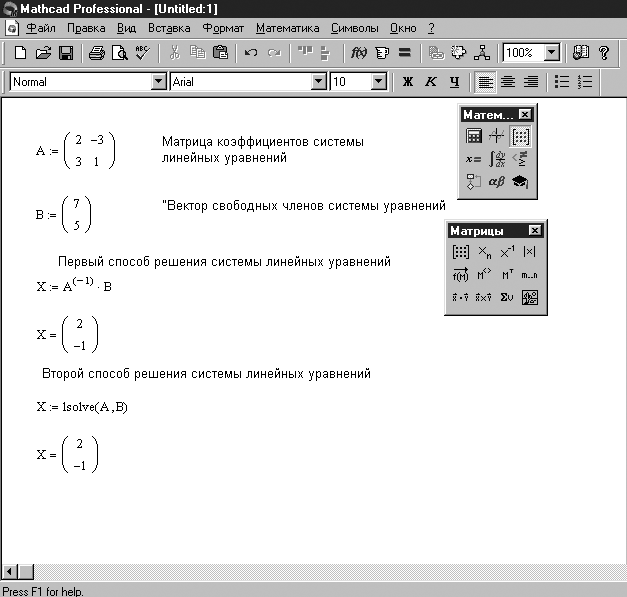
При символическом использовании это трактуется как истинная бесконечность.

или же Алгебраическое определение
или же Символическое определение

Пи (Ctl-Shift-p) —
Ускорение свободного падения (g) — Хотя MathCAD действительно определяет ускорение свободного падения, он не определяет гравитационную постоянную. В системе единиц СИ гравитационная постоянная равна единице. Однако в английской системе единиц гравитационная постоянная g c равна
. 32.174 (фут-фунт м ) / (фунт f -сек 2 ).

База Напериана (д) — Это значение «е», используемое при работе с натуральными логарифмами.

Процент (%) — Процент всегда является десятичным числом. Таким образом, символ процента фактически умножает предыдущее число на 0,01. Например,
Speed ​​of Light (c) — Маленькая буква c обозначает скорость света в вакууме

Комплексные числа (i) — Квадратный корень из отрицательного числа обозначается буквой «i» или буквой «j». Я рекомендую вам выбрать наиболее удобную для вас номенклатуру и придерживаться ее. Чтобы ввести комплексное число, просто введите коэффициент, за которым следует буква «i» или «j» (в зависимости от того, что вы предпочитаете).

ВАЖНО: введенные строчные буквы «i» или «j» НЕ представляют собой квадратный корень из отрицательного числа. Вы ДОЛЖНЫ ставить перед буквой «i» или «j» цифру один. Например, приведенные ниже выражения — это два разных числа, несмотря на то, что они имеют одинаковый внешний вид.

Корень квадратный из отрицательного
Переменной i присвоено значение три

Греческие буквы

Как мы все знаем, использование греческих букв в технике довольно распространено. Греческие буквы доступны через палитру «Греческий», которая, в свою очередь, доступна из палитры «Математика». Если ваша математическая палитра не отображается, включите ее в строке меню, выбрав «Вид»> «Панели инструментов»> «Математика». Если вы знаете взаимосвязь между греческим алфавитом и набором римских символов, вы можете просто ввести латинскую букву, а затем нажать Ctrl-G, чтобы преобразовать ее в соответствующую греческую букву.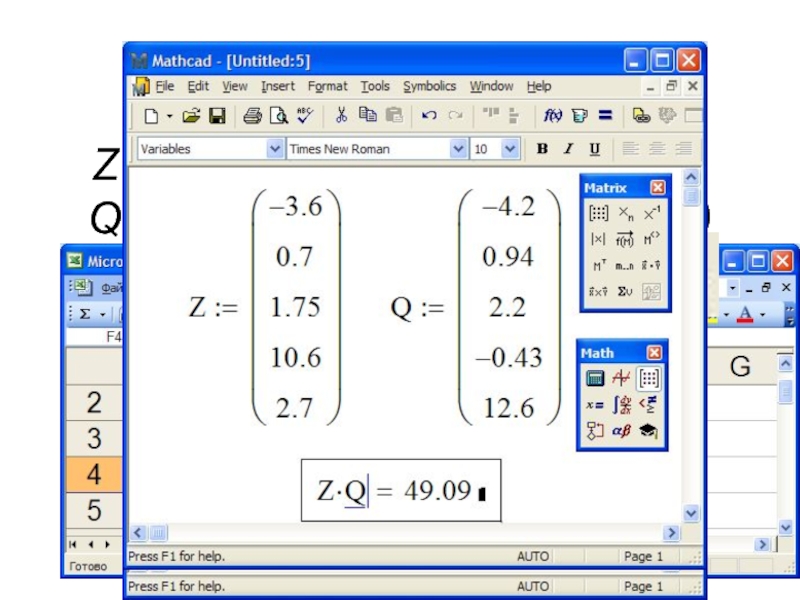

Будьте очень осторожны при использовании заглавных греческих букв, которые выглядят как заглавные латинские буквы. Например, заглавная буква «А» и заглавная буква альфа показаны ниже.

Заглавная буква римская ‘А’
Заглавная буква греческого альфа

Хотя они выглядят практически одинаково, это две разные переменные. Это может вызвать значительные трудности при устранении неполадок или даже при простом использовании рабочего листа. Также обратите внимание, что заглавная римская буква «A» помечена как ранее определенная переменная (помните зеленую волнистую линию?).В этом случае MathCAD использует его в качестве инженерной единицы для усилителя. Вероятно, использовать A в качестве переменной — не лучшая идея. С другой стороны, вместо этого можно было бы использовать заглавную альфа, но вам нужно помнить, что символ, который выглядит как заглавная римская буква «А», на самом деле является заглавной греческой альфой. Думаю, вы видите проблему.

Написание собственных уравнений и функций

Прежде чем писать уравнения и функции, давайте обсудим еще два пункта. Первый касается использования индексов при определении переменных.MathCAD использует два разных типа индексов: литеральные индексы и индексы массива. Литеральный нижний индекс очень полезен для различения похожих переменных. Вы можете указать нижний индекс, просто нажав клавишу точки (.) При определении переменной. Например, давайте определим переменную ex sub see (x c ) и установим ее равной 10. Нажатие клавиш при этом будет x.c: 10.


Индексы массивов будут рассмотрены через пару недель, когда мы обратимся к матрицам и векторам.

Последний пункт — использование клавиши пробела. Пробел полезен для управления синим курсором, окружающим разработку уравнения. Несомненно, наиболее частое использование — это перемещение курсора из знаменателя дроби или из экспоненты. Например, предположим, что вы хотите написать формулу, умножив десять на одну треть, а затем прибавив 20. 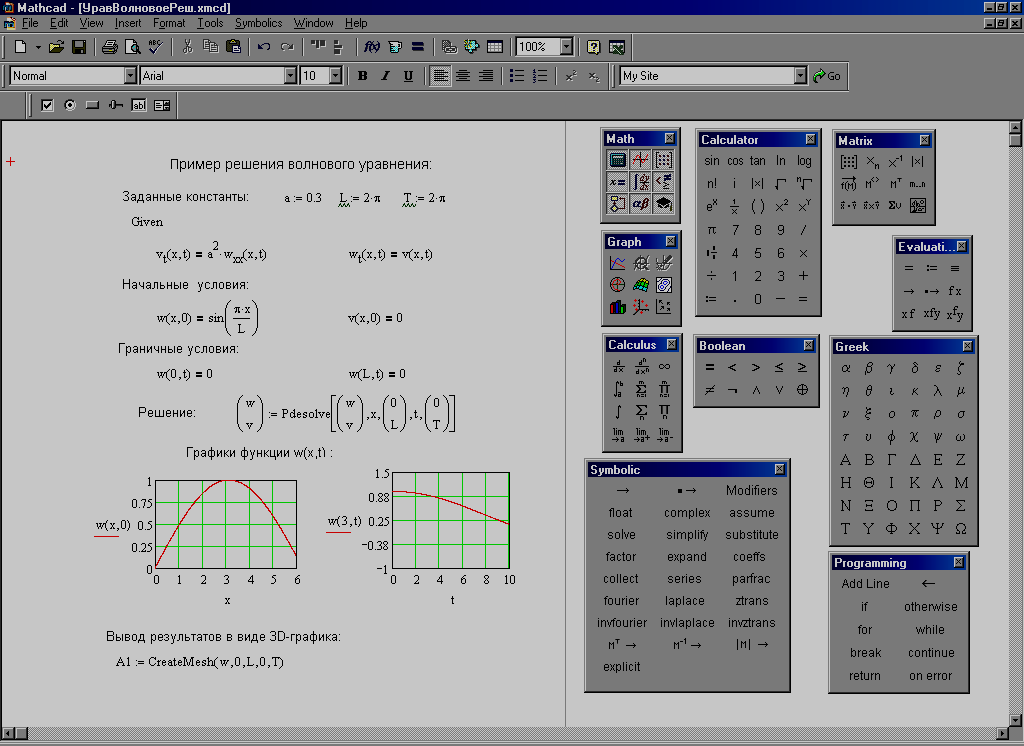Дробь, одна треть, вводится нажатием клавиш 1/3. Однако, прежде чем нажимать клавиши +20, вы должны вывести курсор из знаменателя, иначе +20 окажется в знаменателе дроби, а не в качестве независимого члена, который вам нужен.Введите уравнение, нажав следующие клавиши: 1/3 {sp} + 20 = где {sp} обозначает пробел. Следует также отметить, что повторное нажатие клавиши пробела циклически перемещает синий курсор Math по рассматриваемому уравнению.



Теперь давайте применим наши навыки на практике. Заимствуя из курса статики, продублируйте определение следующих переменных и следующее выражение.






Попытайтесь воспроизвести приведенное выше уравнение в стороне.Обратите внимание, что символ квадратного корня можно найти на палитре калькулятора или воспользоваться сочетанием клавиш, косой чертой (\). Если ваше заполненное уравнение станет красным, это означает, что произошла ошибка. При нажатии на уравнение появится всплывающая всплывающая подсказка, сообщающая вам, в чем проблема. 0.5 {sp} * (R.3)

Примечание. {Sp} — это пробел
. Ctl-g — это последовательность клавиш, в которой удерживается клавиша управления при одновременном нажатии и отпускании клавиши «g».

Часто более желательно определить уравнение как функцию. Пользовательские функции определяются так же просто, как уравнение. Например, уравнение параболы можно определить как:

Поскольку переменная ‘b’ не определена, уравнение генерирует ошибку. Но если бы кто-то определил его как функцию ‘f’ в переменной ‘b’, мы бы записали его следующим образом:

Теперь мы можем оценить функцию в дискретных точках, просто подставив число или определенную переменную в качестве аргумента функции.

Функции также могут быть определены в нескольких переменных.

Обратите внимание, что переменная ‘c’ помечена как предопределенная переменная; снова обратите внимание на зеленую волнистую линию. Маленькая буква «c» зарезервирована MathCAD как скорость света.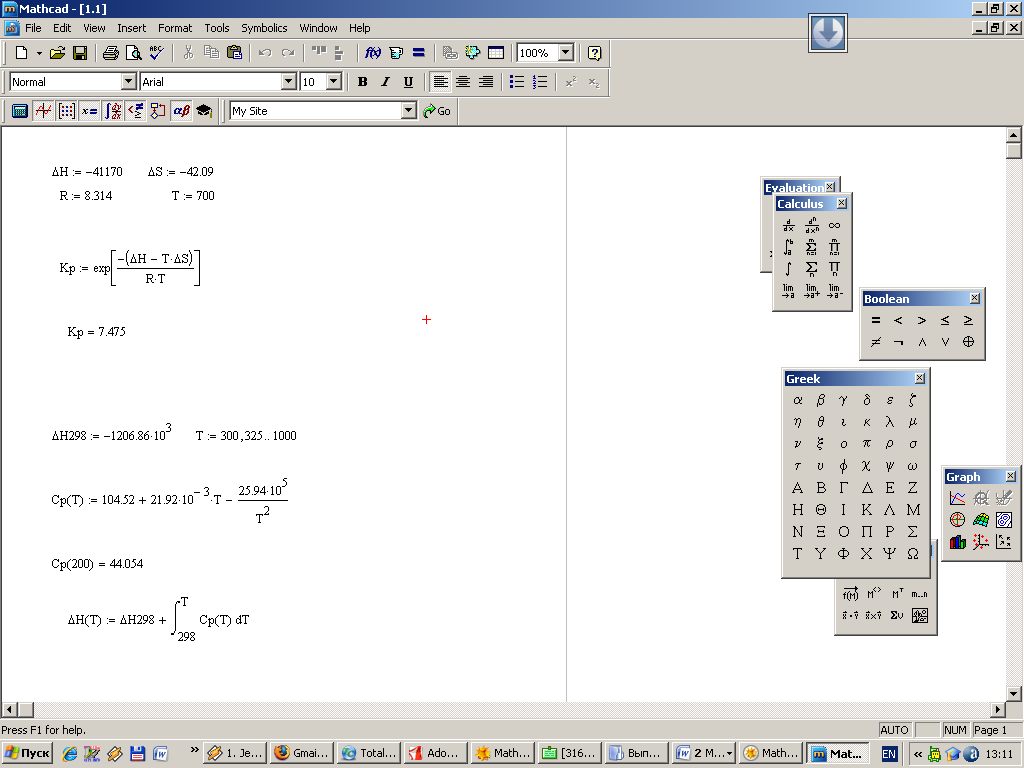 Если ваши расчеты прямо или косвенно не включают скорость света, вероятно, можно использовать эту переменную. Но поймите, что у вас больше нет доступа к этой константе для оставшейся части рабочего листа.

Встроенные функции

MathCAD имеет множество встроенных функций, больше, чем кто-либо, вероятно, когда-либо воспользуется.Определенно больше, чем у нас есть время для обсуждения. Вот почему функция справки MathCAD так важна. Если вам нужно что-то сделать, воспользуйтесь служебными программами помощи, чтобы узнать, как это сделать.

Доступ к функциям можно получить, щелкнув значок f (x) в строке меню. В появившемся диалоговом окне на правой панели отображается полный список функций. Не пугайтесь существующих функций. Эта программа предназначена для использования в самых разных дисциплинах.Мы будем использовать только небольшое подмножество доступных функций.

Функции, которые нам нужно решить сегодня, включают тригонометрические функции, логарифмические функции и функции округления / усечения. Имея дело с тригонометрическими функциями, важно понимать, что MathCAD ожидает углы в радианах. Все функции arc возвращают углы в радианах. Если мы хотим использовать градусное измерение, мы должны явно указать это как таковое. Например, синтаксис функции синуса — sin (x), где x — угловое измерение в радианах.Чтобы использовать градусные меры, умножьте аргумент на единицу измерения «градус». Ниже приведены некоторые примеры.

При использовании функций дуги результатом является угловая величина в радианах.

Если вы нажмете на указанное выше выражение, вы увидите заполнитель, маленький черный квадрат, сразу справа от результата. В этот заполнитель вы вводите единицу измерения. Если вы хотите отображать указанное выше в градусах, введите «градус» в поле-заполнитель.

Логарифмические функции включают в себя функции с основанием Напериана, основанием 10 и основанием «n».

Функции пола и потолка работают очень хорошо, если нужно определить целое число объектов.Например, при проектировании бетонной балки выполняется расчет для определения количества арматурных хомутов. Очевидно, что количество хомутов должно быть целым, но расчет дает десятичное число. Использование функции потолка позволяет MathCAD возвращать целое число хомутов, которое затем можно использовать в последующих вычислениях для определения расстояния хомутов.

Базовые единицы

Единицы можно рассматривать как переменную и применяются как таковые. Другими словами, если кто-то хочет объявить значение ‘x’ равным пяти футам, можно определить это, используя нажатия клавиш x: 5 * ft.

MathCAD может обрабатывать преобразование единиц измерения без явного указания коэффициента преобразования.Например, определите переменную t как 10 секунд, а переменную v как частное от x и t.

В приведенном выше примере отображаются футы в секунду. Если кто-то желает получить решение в разных единицах, можно заменить любую эквивалентную единицу таким же образом, как мы преобразовали радианы в градусы (как обсуждалось выше).

MathCAD неплохо справляется с отображением результирующих единиц вычисления.Однако бывают случаи, когда полученные единицы сводятся к чему-то более фундаментальному. В этих обстоятельствах вам нужно будет заменить желаемое устройство. Например, в термодинамике базовый расчет теплопередачи утверждает, что энергия равна массе объекта, умноженной на удельную теплоемкость этого объекта, умноженную на изменение температуры. Предположим, что объект имеет массу 30 слизней, удельную теплоемкость 12 британских тепловых единиц / (фунт R) с изменением температуры на 30 градусов по Ренкину.Результирующее энергосодержание должно быть в БТЕ.

Обратите внимание, что результат не отображается в BTU. Результат отображается в наборе единиц, размерно эквивалентных BTU. Чтобы отобразить правильную единицу, щелкните результат и вручную вставьте единицу BTU в заполнитель.

Примечание о температуре в MathCAD

MathCAD не может обрабатывать температуры, выраженные в градусах Фаренгейта или в градусах Цельсия.Вы можете использовать только температуры, выраженные в градусах Ренкина (R) или в Кельвинах (K). Это связано с тем, что преобразование из Ренкина в Фаренгейта и из Кельвина в Цельсия связано с дополнительным компонентом.

Ренкин = Фаренгейт + 459,69
Кельвинов = Цельсия + 273,17
Фаренгейт = 1,8 (Цельсия) +32

Однако преобразование между Рэнкином и Кельвином является мультипликативным, поэтому преобразование единиц измерения выполняется легко.

Ренкина = 1,8 Кельвина

Однако все это не проблема.В дисциплинах термодинамики и теплопередачи большинство расчетов связано с разницей температур. Поскольку шкала Ренкина и шкала Фаренгейта на самом деле являются одними и теми же шкалами, только обозначены по-разному, разница температур в один градус, выраженная в шкале Ренкина, представляет собой разность температур в один градус, выраженную в Фаренгейте. Это также верно для шкал Кельвина и Цельсия. Самая распространенная проблема, с которой сталкивается учащийся при работе с температурой, — это понимание этой концепции. Предположим, у вас есть тело, которое начинается при температуре 120 F и заканчивается при температуре 150 F.Очевидно, это изменение температуры на 150–120 = 30 градусов по Фаренгейту. Но каково изменение температуры в градусах Ренкина? Просто преобразуйте температуру Фаренгейта в температуру Ренкина, добавив 460, а затем вычтите две температуры следующим образом.

(150 + 460) — (120 + 460) = 610 — 580 = 30
рэндов
Изменение температуры по шкале Фаренгейта такое же, как и по шкале Ренкина. Опять же, в этом есть смысл. Это одинаковые весы с разными надписями.

Те расчеты, которые учитывают текущую температуру тела, а не изменение температуры, всегда основаны на абсолютной температуре, выраженной в единицах Ренкина или Кельвина.Таким образом, проблема, связанная с Farenheit или Celcius, не имеет значения.

Заметка о единицах массы и силы в MathCAD

Нет ничего особенного в использовании единиц массы и силы в MathCAD. Однако использование соответствующих единиц для массы и силы кажется проблемой для многих студентов, особенно в английской системе. Типичные единицы массы и силы в английской системе и системе СИ показаны под
.
Английский SI

Масса пули кг (кг-масса)
фунт (фунт-масса)

Сила фунт-сила (фунт-сила) Н (Ньютон)
кгс (килограмм-сила)

К настоящему времени мы все знаем закон Ньютона, сила — это продукт массы и ускорения.Применение закона Ньютона довольно просто при использовании системы единиц СИ. Многие не знают, как применять закон Ньютона в английской системе единиц, когда масса выражается в единицах массы или фунта.

Например, в системе СИ закон Нетвона требует, чтобы масса выражалась в килограммах, ускорение свободного падения составляет 9,807 м / с 2 , а результирующая сила выражается в ньютонах.

В системе дюйм-фунт закон Ньютона требует, чтобы масса выражалась в слагах.Слизняк — это старая английская единица массы. Он равен (фунт f с 2 ) / фут. Результирующая сила измеряется в фунтах силы. В MathCAD фунт-сила выражается в фунтах-силах. Следует отметить, что обе единицы массы. фунт-масса и снаряд до сих пор используются в машиностроении и инженерных технологиях. Нужно знать и то, и другое.

Однако более распространенной единицей массы в системе дюйм-фунт является фунт-масса.В MathCAD единицей фунта-массы является просто фунт. Но чтобы использовать фунт-массу в законе Ньютона, нужно немного изменить закон Ньютона, введя гравитационную постоянную. Многие люди не осознают, что ускорение свободного падения НЕ является постоянной величиной. На самом деле он немного варьируется по поверхности земли. Однако гравитационная постоянная — постоянная величина. Он присваивается переменной g c и имеет значение 32,174 (фут-фунт м ) / (фунт f -с 2 ).Таким образом, закон Ньютона модифицируется, как показано, и результирующая сила выражается в фунтах силы.

Хотя все это верно и очень важно понимать, многое из этого становится неактуальным при работе в MathCAD.Это потому, что MathCAD выполняет все преобразования единиц измерения за вас. Например, можно показать, что одна пуля равна 32,174 фунтам массы. Поскольку MathCAD выполняет все преобразования единиц измерения, нет необходимости явно писать закон Ньютона с использованием гравитационной постоянной при работе с массой в фунтах-массах. Рассмотрим следующий пример.

При использовании единиц измерения в MathCAD программа всегда будет поддерживать целостность размеров, даже если вы ошиблись при указании единицы измерения.Это часто приводит к появлению каких-то странных (бессмысленных?) Дисплеев устройств. Например, рассмотрим следующее уравнение для определения выходной мощности двигателя с учетом развиваемого крутящего момента и скорости вращения. В показанном уравнении крутящий момент выражается в единицах силы фут-фунт, а число оборотов в минуту выражается в единицах в минуту (1 / мин). Единицей измерения мощности в MathCAD является л.с. С точки зрения размеров, лошадиные силы — это сила на фунт-фут в единицу времени. Найдите выходную мощность двигателя, если развиваемый крутящий момент составляет 1000 фут-фунт-сила, а скорость вращения составляет 3600 об / мин.

Просто определите переменные крутящего момента и оборотов, как показано

Напишите уравнение для мощности

Покажите решение.Выглядит правильно, не так ли?

Повторно отобразите решение и введите единицу измерения «hp» в поле единицы измерения. Обратите внимание на результат. Что именно это означает? Короче говоря, это значит, что кто-то ошибся. В этом конкретном случае причина, по которой единица отображается так, как показано, заключается в том, что мы неправильно определили крутящий момент.Обратите внимание, что крутящий момент был неправильно определен в единицах массы фут-фунт. Предполагается, что крутящий момент определяется как сила на фунт-фут. Эта ошибка в сочетании с тем фактом, что хорспауэр — это сила в фут-фунт в единицу времени, вынуждает MathCAD вставлять «корректирующую» единицу для сохранения целостности размеров относительно того, как были определены исходные данные. Это легко исправить. Просто определите крутящий момент с правильной единицей измерения фут-фунт-сила.

Если такая ситуация возникает, когда вы делаете домашнее задание, интерпретируйте ее так, какова она есть, ВЫ ЧТО-ТО ДЕЛАЛИ НЕПРАВИЛЬНО.Таким образом, исправьте ошибку, прежде чем сдавать задание. Я не вижу смысла в отправке заведомо неверного задания.

Это произошло по двум причинам. Первая причина, как объяснено выше, заключается в использовании неправильных единиц измерения. Вторая причина — [случайно] переопределение встроенного модуля. Например, многие люди любят использовать переменную m для определения массы в уравнении. Однако MathCAD использует переменную m для определения единицы измерения. Поскольку метр также является частью единицы силы Ньютона, такое переопределение вызовет значительные проблемы.Два способа определить, безопасно ли использовать конкретную переменную (т. Е. Вы не переопределяете ее случайно).

Введите переменную, а затем оценку равно (например: m =). Если единица измерения определена, вы получите что-то, как показано слева. Это очевидное свидетельство того, что переменная является встроенной единицей или была ранее определена вами.

С другой стороны, если переменная не используется, то ее ввод (например: n =) приведет к ошибке. Обычно MathCAD не может найти определение переменной. Поскольку MathCAD не может найти определение, он предполагает, что вы пытаетесь его определить, и заменяет знак равенства оценки двоеточием.

Второй способ — это фактическое определение переменной.Если под переменной появляется зеленая волнистая линия, переменная уже используется. В зависимости от того, является ли переменная встроенной переменной MathCAD или пользовательской переменной, вы должны принять решение о выборе новой переменной или переопределении существующей. Почти всегда можно переопределить пользовательскую переменную. Очень редко вы хотите переопределить встроенную переменную или единицу MathCAD. Это может иметь негативные последствия, которые ОЧЕНЬ сложно устранить.

ВНИМАНИЕ: Следует понимать, что способность MathCAD определять переопределение переменной является новой, начиная с первого обновления пакета обновления для MathCAD 11.В исходном выпуске версии 11 и во всех предыдущих версиях MathCAD не извивался :). Кроме того, этот параметр может быть отключен пользователем (Инструменты> Настройки> Предупреждения). В этом случае не полагайтесь на эту функцию, если вы не знаете, что она доступна (то есть: правильная версия MathCAD и функция включена).

Структура рабочего листа

Рабочий лист MathCAD состоит из трех областей: математической, текстовой и графической.Как можно понять из названий, математическая область содержит только математические формулы, текстовая область содержит только текст, а область графика содержит только график.

По умолчанию, когда вы начинаете вводить текст на листе, MathCAD автоматически создает математическую область. Ниже приведены некоторые примеры.

Если первый вводимый вами символ является альфа-символом, MathCAD предполагает, что вы вводите имя переменной.

Если первый вводимый вами символ — это число, MathCAD интерпретирует его как число.

Если первый вводимый вами символ — это число, за которым следует строка буквенных символов, MathCAD интерпретирует это как число, умноженное на переменную. Знак умножения не очевиден, но подразумевается.Щелкните запись, чтобы увидеть подразумеваемый знак умножения.

ПРИМЕЧАНИЕ. Я рекомендую НИКОГДА не вводить подобное выражение. Известно, что это вызывает трудности. В некоторых случаях подразумеваемого умножения не происходит. Это часто случается при работе с символической математикой.

Текстовая область — это область, содержащая чистый текст.Весь текст, который вы читали, находится в текстовой области. Самый простой способ начать текстовую область — просто начать печатать. Как только вы начнете печатать, MathCAD создаст математическую область. Но как только вы нажимаете клавишу пробела, регион преобразуется в текстовую область. Однако с этим неявным методом создания текстовой области возникают некоторые трудности. Большинство знаков препинания — это сочетания клавиш в MathCAD для ввода определенных функций. Таким образом, если вы начинаете текстовую область с числа или знака препинания (например, апострофов) или если вы должны ввести знак препинания перед нажатием клавиши пробела, MathCAD интерпретирует нажатие клавиши как желание ввести какой-либо тип функции. или формула.В таких случаях ЗАПУСТИТЕ текстовую область, нажав клавишу двойных кавычек.

Вы можете отличить математическую область от текстовой двумя способами. Самым надежным считается внешний вид курсора. В математической области курсор имеет синий цвет и окружает математическую запись или ее часть с двух сторон от нее. Текстовый курсор представляет собой вертикальную красную линию.

Второй способ — распознать разницу в стиле и размере шрифта между математической областью и текстовой областью. Однако пользователь может изменять стили и размеры шрифтов как для математических, так и для текстовых областей.Другими словами, шрифты в обоих регионах могут быть идентичными. Однако по умолчанию это не так.

Все числа и формулы, вводимые в текстовой области, являются текстовыми строками. Это не живые формулы. Однако MathCAD позволяет вводить математическую область внутри текстовой области. Фактически, этот метод широко используется в этом листе, а также в других листах лекций, используемых в оставшейся части этого курса. Чтобы ввести математическую область внутри текстовой области, перейдите в пункт меню «Вставка»> «Математическая область».Например, я могу определить переменную:



и формула:



Обратите внимание, что и «x», и «y» доступны, даже если они определены внутри текстовой области. Это отличная функция, позволяющая писать хорошо работающие отчеты. Другими словами, вам не нужно делать непонятную ссылку на переменную или функцию в тексте, который вы пишете, а затем разбивать текст, чтобы ввести переменную или формулу в отдельной области Math.Вы можете просто ввести математическую область внутри текстовой области. У вас будет много возможностей попрактиковаться в этом при выполнении первого домашнего задания.

Область графика — это просто область, в которую вводится график.Графики вводятся из меню вставки. MathCAD позволяет создавать графики различных типов. Однако мы сосредоточимся только на создании стандартного графика X-Y. График также можно ввести, нажав клавишу @ (Shift-2). Простой график создается путем простой вставки графика, ввода функции в местозаполнитель центральной оси Y и последующего помещения зависимой переменной в местозаполнитель центральной оси x. Остальные четыре заполнителя предназначены для определения пределов осей x и y.Если вы их не заполните, MathCAD построит график функции для значения x от -10 до 10. Мы обсудим построение графиков более подробно в следующей лекции. А пока давайте определим и построим график функции:

Макет страницы

К настоящему времени очевидно, что MathCAD имеет возможности обработки текстов. Хотя эти возможности не такие широкие, как у MS Word и др. др., их более чем достаточно для создания красивого документа. Я позволю вам самостоятельно изучить возможности форматирования текста и абзацев.Поговорим о форматировании страниц.

В MathCAD единственные параметры форматирования страницы, которые у вас есть, — это ширина поля, ориентация страницы, размер страницы и разрывы страниц. Для правильной документации (например, домашнего задания) вам необходимо знать это, чтобы ваша статья выглядела профессионально.

Чтобы установить поля, размер бумаги и ориентацию страницы, перейдите в пункт меню «Файл»> «Параметры страницы». Установите параметры по своему усмотрению.

Как и в MS Word, разрывы страниц бывают двух видов: жесткие и мягкие.Непосредственно над этим текстом находится горизонтальная сплошная линия (не отображается, если вы читаете это на распечатке или в виде HTML-страницы). Чуть выше, над графиком, находится горизонтальная пунктирная линия (также не видна на распечатке или странице HTML). Пунктирная линия представляет собой мягкий разрыв страницы. За исключением возможности изменять поля страницы, вы не можете перемещать или каким-либо иным образом контролировать расположение мягкого разрыва страницы. Однако вы можете вставить, удалить или переместить жесткий разрыв страницы. Сплошная линия непосредственно выше — это такой разрыв страницы.Чтобы вставить разрыв, поместите курсор в то место, где вы хотите разрыв, и выберите «Разрыв страницы» в меню «Вставить». Чтобы переместить или удалить разрыв страницы, используйте мышь и щелкните разрыв, удерживая нажатой клавишу «Shift». Разрыв будет выделен парой пунктирных линий. Используйте мышь, чтобы перетащить разрыв. Чтобы удалить, щелкните разрыв, удерживая клавишу Shift, и выберите «Вырезать» в меню редактирования. Выполняя домашнее задание, убедитесь, что вы правильно используете разрывы страниц, чтобы домашнее задание отображалось логично. Нет причин, чтобы разрыв страницы пересекал уравнение! Вам будут выставлены оценки за представление домашнего задания.

При вычислении рабочего листа MathCAD чувствителен к относительному расположению формул и переменных. Как и в случае с электронной таблицей, MathCAD выполняет вычисления слева направо и сверху вниз. Это означает, что вы должны убедиться, что ваши формулы и определения переменных правильно расположены. Обычно это просто перетаскивание соответствующей математической области в соответствующее место. С другой стороны, бывают случаи, когда вы хотите, чтобы формулы выстраивались либо по горизонтали, либо по вертикали. Для этого используйте две кнопки выравнивания на панели значков.MathCAD предупредит вас, если выравниваемые области перекрываются. Если они это сделают, вам, возможно, придется внести некоторые незначительные изменения в расположение регионов перед автоматическим выравниванием.

Вы также можете вставить «Область» MathCAD. Просто выберите «Вставить»> «Область» в меню «Вставка». Такая область чрезвычайно полезна для сокрытия расчетов. При желании зону можно свернуть и заблокировать. С помощью мыши щелкните правой кнопкой мыши стрелку вверху и слева. Контекстное меню позволяет свернуть область (если она развернута) или развернуть область (если она свернута).Также позволяет заблокировать
область с паролем. НЕ ПОТЕРЯЙТЕ ПАРОЛЬ. Невозможно разблокировать область, если пароль утерян.

ПРИМЕЧАНИЕ. Эта область не отображается при просмотре как HTML-страница; он будет отображаться как обычный абзац. Разграничение области печатается на распечатке, но при желании может быть скрыто.


Выполнение инженерных расчетов с использованием Mathcad

Инженерные расчеты с использованием Mathcad

Краткое содержание курса

1.Цель обучения
2. Курс Введение
3. Курс Содержание
4. Курс Резюме
5. Связанные Ссылки

Этот курс включает в себя викторину с несколькими вариантами ответов в конце.

Цель обучения

В заключение из этого курса студент:

  • Be знаком с интерфейсом, графикой, текстом и вычислительными возможностями Mathcad
  • Be возможность выполнять

    инженерных расчетов с использованием Mathcad

Курс Введение

Математика везде и в все.От мостов до высоток, от американских горок до космических челноков, математика имеет решающее значение для современного высокотехнологичного общества. Mathcad от PTC делает математику простой и доступной для пользователей из средней школы студентов инженерам, которые находятся на переднем крае некоторых из самых важных и требовательная техническая среда в мире.

Содержание курса

Mathcad — это ценный технический компьютер инструмент для инженеров и архитекторов. Вы можете рассматривать Mathcad как комбинацию

  • мощного технического вычислительная среда, основанная на вещественной математической нотации, и
  • а гибкий, полнофункциональный технический текстовый редактор.

Mathcad обеспечивает комплексное решение проблем среда, которая предоставляет вам широкий спектр инструментов для анализа и визуализации. В отличие от других технических программ, Mathcad выполняет математические вычисления так же, как и вы. Что потому что он выглядит и работает как блокнот и карандаш. На экране Mathcad интерфейс представляет собой пустой рабочий лист, на котором вы можете вводить уравнения, графические данные или функций, а также добавлять текстовые аннотации в любом месте рабочего листа.

Некоторые важные вычислительные возможности Mathcad для инженерных приложений находятся:

  • Встроенный единицы измерения и проверки размеров.
  • Встроенный решатель одновременных уравнений и неравенств.
  • Суммы, продукты и итерация.
  • Тригонометрические, гиперболические, экспоненциальные функции и функции Бесселя.
  • Быстрое одномерное и двумерное преобразование Фурье.
  • Пользовательские функции.
  • Векторы и матрицы, включая операцию умножения матриц, матрица обратное, транспонирование, определитель, скалярное произведение и векторное произведение.
Математические выражения в Mathcad выглядят так, как вы их видите в учебнике или справочник.Единственное отличие состоит в том, что уравнения и графики Mathcad живы, что означает, что Mathcad пересчитывает математику и перерисовывает графики каждые когда вы изменяете какие-либо данные, переменную или уравнение на листе. Эта функция в Mathcad называется «Интерфейс живого документа».

В дополнение к интерфейсу Live Document Interface, еще одна важная функция, которая устанавливает Mathcad, помимо других технических вычислительных инструментов, имеет встроенную поддержку единицы измерения. Mathcad может автоматически преобразовывать единицы измерения на листе.

Таким образом, техническая документация, подготовленная с помощью Mathcad, может быть легко понятна. и проверено другими. Кроме того, использование Mathcad в вашей работе может облегчить избавьтесь от утомительных и повторяющихся расчетов конструкции, исключите арифметические ошибки, и произвести качественные проектные расчеты.

На этом уроке вы изучите основные особенности Mathcad и двух приложений Mathcad в реальной инженерной сфере анализ.

Чтобы изучить основные функции Mathcad, вам необходимо приобрести копию Mathcad. из Mathcad.com. После установки программного обеспечения, вам необходимо изучить Mathcad встроенный учебник (файл PDF, 688 КБ, 51 страница). Кроме того, вам необходимо посмотреть следующие видео-уроки:

1. Демонстрация Mathcad для начинающих (12:42 видео)
2. Mathcad Prime 1.0 Demo (11:26 видео)
3. Веб-семинар по Mathcad Prime 2.0 (1:00:15 видео)
4. Анализ бетонных балок с использованием таблицы Mathcad (15:17 видео)

В частности, вам необходимо научиться:

  1. введите текст
  2. построение математических выражений
  3. определение переменных
  4. определение функций
  5. определение переменных диапазона
  6. создание графиков
  7. определение единиц измерения

Mathcad Веб-библиотека содержит множество примеров приложений Mathcad в различных дисциплины.В этом уроке вам необходимо скачать и изучить следующие два Файлы приложения Mathcad, так как вам будет предложено решить некоторые простые проблемы с лучом. при прохождении викторины.

  1. Упругий изгиб балок прямоугольного сечения (bending.mcd -бесплатно, Mathcad 2000i, 24 kb)
  2. Диаграммы сдвига и моментов для любых балок с опорой или нависанием (ssbeam.mcd-free скачать, Mathcad 7 Prof., 508 kb) К. Хаук
Гибкая среда расчетов и документации Mathcad развивается как единое целое самых популярных платформ для отраслевых решений, в том числе Электронные книги Mathcad, пакеты расширений Mathcad, динамически связанные библиотеки (DLL, т.е., пользовательские библиотеки C ++) и совместимость с другими приложениями. например, программное обеспечение для работы с электронными таблицами.

Краткое содержание курса

Этот курс охватывает некоторые из основных функций Mathcad, который включает функции интерфейса, графические функции, вычислительные функции, а также функции текста и документов. Через этот онлайн-курс студент должен уметь использовать Mathcad для решения некоторых рутинных задач проектирования в его / ее дизайнерская практика. Для более сложных тем о приложениях Mathcad, таких как как электронные книги и анимацию, вы можете посетить Mathsoft.ком Веб-сайт.

Ссылки по теме

Для дополнительную техническую информацию по этой теме, пожалуйста, посетите следующие веб-сайты или веб-страницы:

Руководство пользователя MathCAD 2000
Mathcad — Википедия

Как только вы закончите изучение вышеперечисленного Файлы документов и приложений Mathcad, которые необходимо взять с собой викторина для получения кредитов PDH.

***


ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ: Материалы, содержащиеся в онлайн-курсе, не предназначены для демонстрации или гарантии со стороны PDHonline.org или любое другое лицо / организацию по имени здесь. Материалы предназначены только для общего ознакомления. Они не заменяют за грамотную профессиональную консультацию. Применение этой информации к конкретному Проект должен быть рассмотрен зарегистрированным профессиональным инженером. Кто-нибудь делает использование информации, изложенной в настоящем документе, делает это на свой страх и риск и предполагает любую вытекающую из этого ответственность.

Ваша работа станет проще с PTC Mathcad © 4.0

{«items»: [«5f60b64cb3cbd

f5a598″, «5f60b64cb3cbd

f5a599″, «5f60b64cb3cbd

f5a596″, «gallery», 5f60b64cb3cbd

f5a596dcd5f05122d1dd5f2605dd1d5f05702dd1dd5f560564dd1 «,» groupSize «: 1,» showArrows «: true,» cubeImages «: true,» cubeType «:» fill «,» cubeRatio «:» 100% / 100% «,» isVertical «: false,» gallerySize «: 30, «Плотность коллажа»: 0.8, «groupTypes»: «1», «oneRow»: true, «imageMargin»: 0, «galleryMargin»: 0, «scatter»: 0, «rotatingScatter»: «», «chooseBestGroup»: true, «smartCrop» : false, «hasThumbnails»: false, «enableScroll»: true, «isGrid»: false, «isSlider»: false, «isColumns»: false, «isSlideshow»: true, «cropOnlyFill»: false, «fixedColumns»: 1 , «enableInfiniteScroll»: true, «isRTL»: false, «minItemSize»: 120, «rotatingGroupTypes»: «», «rotatingCropRatios»: «», «columnWidths»: «», «gallerySliderImageRatio»: 1.7777777777777777, «numberOfImages»: 3, «numberOfImagesPerCol»: 1, «groupsPerStrip»: 0, «borderRadius»: 0, «boxShadow»: 0, «gridStyle»: 0, «mobilePanorama»: false, «placeGroupsLtr»: false, «viewMode»: «предварительный просмотр. «,» thumbnailSpacings «: 4,» galleryThumbnailsAlignment «:» bottom «,» isMasonry «: false,» isAutoSlideshow «: true,» slideshowLoop «: false,» autoSlideshowInterval «: 3,» bottomInfoHeight «: 0,» titlePlacement «: «SHOW_ON_HOVER», «galleryTextAlign»: «center», «scrollSnap»: true, «itemClick»: «ничего», «fullscreen»: true, «videoPlay»: «hover», «scrollAnimation»: «NO_EFFECT», «slideAnimation» «:» S CROLL «,» scrollDirection «: 1,» scrollDuration «: 400,» overlayAnimation «:» FADE_IN «,» arrowPosition «: 0,» arrowSize «: 18,» watermarkOpacity «: 40,» watermarkSize «: 40,» useWatermark » : true, «watermarkDock»: {«top»: «auto», «left»: «auto», «right»: 0, «bottom»: 0, «transform»: «translate3d (0,0,0)» }, «loadMoreAmount»: «все», «defaultShowInfoExpand»: 1, «allowLinkExpand»: true, «expandInfoPosition»: 0, «allowFullscreenExpand»: true, «fullscreenLoop»: false, «galleryAlignExpand»: «left», «addToCartBorderWidth» «: 1,» addToCartButtonText «:» «,» slideshowInfoSize «: 160,» playButtonForAutoSlideShow «: false,» allowSlideshowCounter «: false,» hoveringBehaviour «:» NEVER_SHOW «,» thumbnailSize «: 1Seed» magic: imageHoverAnimation «:» NO_EFFECT «,» imagePlacementAnimation «:» NO_EFFECT «,» calculateTextBoxWidthMode «:» PERCENT «,» textBoxHeight «: 0,» textBoxWidth «: 200,» textBoxWidthPercent «: 50,» textImageSpace «: 50,» textImageSpace » : 0, «textBoxBorderWidth»: 0, «loadMoreButtonText»: «», «loadMoreButtonBorderWidth»: 1, «loadMoreButtonBorderRadius»: 0, «imageInfoType»: » ATTACHED_BACKGROUND »,« itemBorderWidth »: 0,« itemBorderRadius »: 0,« itemEnableShadow »: false,« itemShadowBlur »: 20,« itemShadowDirection »: 135,« itemShadowSize »: 10,« imageLoadingMode »:« BLURimation »,« imageLoadingMode »:« BLURimation », : «NO_EFFECT», «imageQuality»: 90, «usmToggle»: false, «usm_a»: 0, «usm_r»: 0, «usm_t»: 0, «videoSound»: false, «videoSpeed»: «1», » videoLoop «: true,» jsonStyleParams «:» «,» gallerySizeType «:» px «,» gallerySizePx «: 220,» allowTitle «: true,» allowContextMenu «: true, «textHorizontalPadding»: — 30, «showVideoPlayButton»: true , «galleryLayout»: 5, «targetItemSize»: 220, «selectedLayout»: «5 | bottom | 1 | fill | false | 1 | true», «layoutsVersion»: 2, «selectedLayoutV2»: 5, «isSlideshowFont»: true , «externalInfoHeight»: 0, «externalInfoWidth»: 0}, «container»: {«width»: 220, «height»: 284, «galleryWidth»: 220, «galleryHeight»: 123, «scrollBase»: 0}}

MACAW | Food4Rhino


Macaw обеспечивает взаимодействие с MathCAD.MathCAD — это программа расчета WYSIWYG для математики. Одним из основных преимуществ MathCAD является возможность писать математические выражения в истинной математической форме, а также возможность использования единиц в вычислениях любого типа. Возможность использования единиц измерения позволяет пользователю бесконечно смешивать и сопоставлять единицы измерения и позволяет самопроверку математических выражений и вычислений, поскольку результаты должны возвращаться в правильных единицах. MathCAD доступен в полнофункциональной версии и бесплатной экспресс-версии, которая включает в себя хороший набор функций, включая матричную алгебру, запрос набора данных с использованием таблиц данных, 2D-графические графики и другие функции.

Чтобы бесплатно загрузить MathCAD Prime express, перейдите сюда:

http://www.ptc.com/engineering-math-software/mathcad/free-download

MathCAD отличается от программ типа электронных таблиц, таких как excel, тем, что обеспечивает простоту использования и удобство использования ноутбука — в сочетании с живыми математическими обозначениями, интеллектуальными единицами измерения и мощными вычислительными возможностями. Это программное обеспечение для инженерной математики позволяет вам представлять свои расчеты с помощью графиков, текстов и изображений в одном документе.

MACAW позволяет пользователю напрямую связываться с MathCAD, позволяя пользователю изменять данные и переменные в MathCAD и / или считывать данные и переменные прямо из MathCAD в кузнечик.

Способность работать с единицами измерения позволяет проектировщику / инженеру работать с любыми единицами и одновременно смешивать британские и метрические единицы с автоматической проверкой и преобразованием единиц.

Возможности

MathCAD включают:

  1. Система управления объектами-
    2. Функции
  2. — сотни встроенных функций, включая подгонку и сглаживание кривых, доступ к файлам
  3. Матричная алгебра
  4. Анализ набора данных с использованием объектов таблиц Mathcad
  5. Построение и построение графиков, включая 2D и 3D графики
  6. Решение, включая дифференциальные уравнения
  7. Функции данных для работы с файлами Excel, CSV, txt, jog и bmp
  8. Программирование, пользователь определяет свои собственные пользовательские функции и процедуры с помощью графического интерфейса пользователя MathCAD

Обновление 1.1 19 марта 2017

Обновлений:

  1. Удалено предупреждение о приоритетной нагрузке при работе
  2. Включает новый компонент для пользователя, позволяющий назначить библиотеку функций MathCAD входному значению
  3. Параметр транспонирования при создании матрицы
  4. Параметры автоматической приостановки и перезапуска вычислений mathcad при записи входных значений в Mathcad — улучшает производительность в реальном времени
  5. Параметр «Регулярное выражение» для фильтрации значений, возвращаемых из Mathcad для входных и выходных значений для получения компонента.

.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *