Система уравнений в mathcad: функция Find MathCAD 12 руководство

2. Решение систем уравнений и неравенств в пакете Mathcad

2.1 Решение систем линейных алгебраических уравнений (слау)

СЛАУ – это  система уравнений вида:

Здесь m – количество уравнений, а n – количество неизвестных. x₁, x₂, …, x_n— неизвестные, которые надо определить.a₁₁, a₁₂, …, a_mn— коэффициенты системы — и b₁, b₂, … b_m— свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.

Рассмотрим в этой работе решение способами: матричным методом, с применением функции lsolve, методом Крамера и при помощи решающего блокаGivenи функцииFind.

Способ 1. Решение СЛАУ матричным методом

Решение этим методом заключается в решении матричного уравнения вида R:=M^-1*V. Для этого необходимо:

• сформировать матрицу коэффициентов системы линейных уравнений – М;

• сформировать вектор-столбец свободных членов системы линейных уравнений – V;

• н

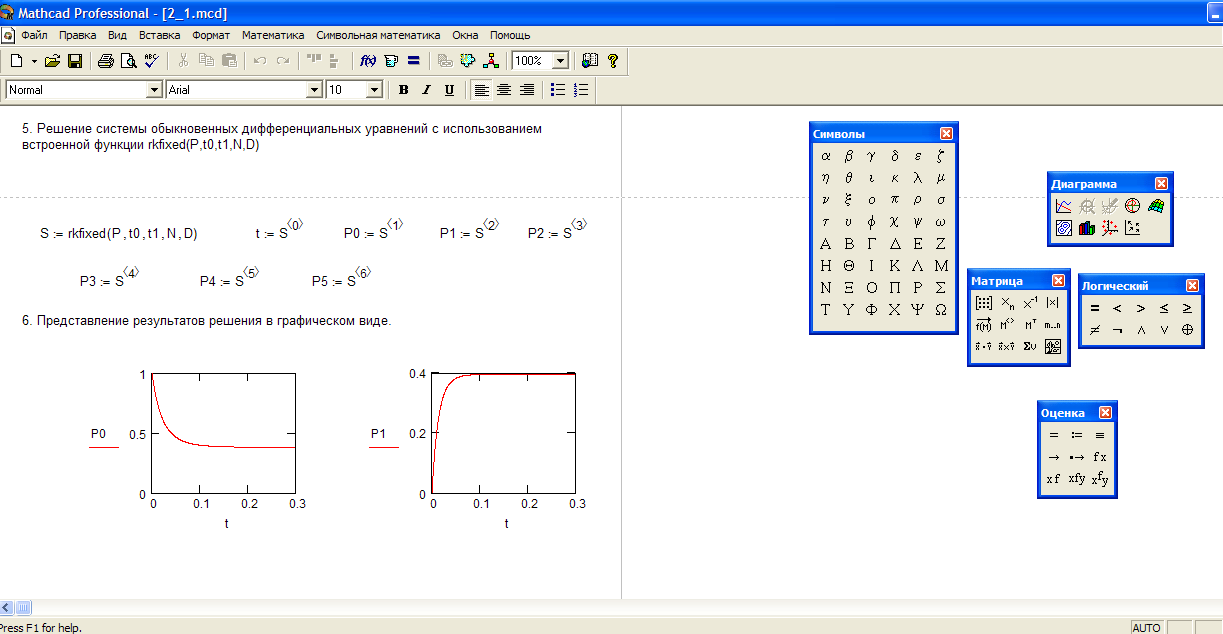
  Рисунок 6– Решение СЛАУ матричным методом

  айти искомые параметры с помощью матричного уравнения.

Пусть задана система:

Решение матричным методом показано на рис.6.

С

Рисунок 7– Решение СЛАУ с применением функцииlsolve

пособ 2. Решение СЛАУ с применением функцииlsolve

Для решения этим способом нужно:

• сформировать матрицу коэффициентов системы линейных уравнений – М;

• сформировать вектор-столбец свободных членов системы линейных уравнений – V;

• вызвать с помощью мастера функций функцию lsolveс параметрамиMиVкак показано на рис.  7.

Способ 3. Решение СЛАУ методом Крамера

Д

Рисунок 8– Решение СЛАУ методом Крамера

ля решения этим способом нужно:

• сформировать матрицу коэффициентов системы линейных уравнений – М;

• сформировать вектор-столбец свободных членов системы линейных уравнений – V;

• найти определитель матрицы М;

• сформировать матрицы по количеству неизвестных системы из коэффициентов СЛАУ, в каждом из которых заменить один из столбцов на столбец вектора свободных членов V;

• найти определители сформированных матриц;

• частное от деления определителей этих матриц на определитель матрицы М – решение СЛАУ (рис.8).

Способ 4. Решение СЛАУ при помощи решающего блока Given и функции Find

К

Рисунок 9– Решение СЛАУ при помощи решающего блока Given и функции Find

ак уже говорилось ранее в описании решения уравнения с помощью решающего блокаGivenи функцииFind, первоначально определяются нулевые приближения, затем после указания зарезервированного словаGivenдаются уравнения системы, причем равенство берется с панели «Булева алгебра». Решение приведено на рис.9.

2.2 Решение систем нелинейных уравнений (сну)

С

Рисунок 10– Решение СНУ при помощи решающего блока Given и функции Find	Рисунок 11– Решение системы неравенств

истема нелинейных уравнений – система, содержащая трансцендентные уравнения. Трансцендентное уравнение – уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции. ВMathcadтакие системы решаются при помощи решающего блока Given и функции Find. Пример такого решения приведен на рис. 10.

MathCAD — это просто! Часть 4.

Системы линейных алгебраических уравнений

Итак, мы с вами продолжаем изучать MathCAD — самую дружелюбную к пользователю математическую среду из существующих в настоящее время. Пока мы занимались тем, что изучали способы решения уравнений — трансцендентных и алгебраических, и теперь вы знаете, как их решать с помощью MathCAD’а в общем виде или численно. Как вы могли убедиться из материала третьей части, численное решение уравнений — не такая простая задача, как может показаться с первого взгляда, однако и не такая сложная, если построить график уравнения. Но просто уравнения — это, согласитесь, довольно скучно, потому что в жизни, как правило, уравнения по одиночке не встречаются. Поэтому сегодня мы перейдем к более сложной, а значит, и более интересной, теме — попробуем решать системы уравнений. Я сказал «попробуем»? Простите, пожалуйста — я, наверное, оговорился. Конечно, не попробуем, а научимся — потому что благодаря MathCAD’у можно быть уверенным в том, что подобные попытки увенчаются успехом.

Готовы? Ну что же, тогда вперед.

Решение систем с помощью функции lsolve

Системы уравнений многие просто-таки ненавидят еще со школы — прямо как русскую литературу. Что ж, школа может привить отвращение ко многим вещам, которые без нее могли бы оказаться гораздо более интересными. Как и любая обязаловка, она убивает романтику изучения чего-то нового. Но теперь, когда вас никто не заставляет изучать решение систем уравнений, вы можете взглянуть на них с совершенно новой для себя стороны. И поможет в этом, конечно же, MathCAD.

Для обозначения систем линейных алгебраических уравнений у математиков есть своя аббревиатура — СЛАУ. Ее используют намного чаще, чем полное название, что, в общем-то, вполне естественно — эта аббревиатура и произносима легко, и не перекрывается с другими математическими аббревиатурами. Так что и мы с вами тоже будем ее применять. СЛАУ называется система уравнений следующего вида:
k11x1 + k12x2 + … + k1nxn + l1 = 0
k12x1 + k22x2 + … + k2nxn + l2 = 0
…
kn1x1 + kn2x2 + … + knnxn + ln = 0

Здесь kij и li — какие-то числовые константы, называемые, соответственно, коэффициентами и свободными членами уравнений, а xj — переменные.

Такие уравнения обычно записывают также с помощью матриц:
KX + L = 0

Здесь K — матрица (kij), составленная из коэффициентов при переменных величинах, где i — номер строки матрицы, а j — номер столбца. X и L — это, соответственно, векторы, составленные из переменных и свободных членов. Собственно, при решении СЛАУ с помощью MathCAD мы будем записывать СЛАУ именно в таком виде, потому что решение СЛАУ в MathCAD реализовано именно с помощью матричных методов. Возможно, вы что-нибудь слышали о методах решения СЛАУ Гаусса и Крамера, но даже если и нет, ничего страшного в этом нет — MathCAD тем и удобен, что с его помощью можно решать уравнения, не задумываясь над тем, каким именно алгоритмом пользуется математическая система при их решении.

Итак, для начала давайте посмотрим, каким именно образом в MathCAD’е нужно задавать матрицы. Для этого на панели инструментов Matrix нажмите кнопку Matrix or Vector, а в появившемся окне задайте количество столбцов и строк в матрице. Мы с вами попробуем решать для начала СЛАУ из четырех уравнений, и, соответственно, нам нужна будет матрица размером четыре на четыре элемента. Только, поскольку мы будем присваивать значение, записанное в этой матрице, переменной, обозначающей матрицу коэффициентов, то сначала лучше записать «K_:=», а потом уже вставлять матрицу. Обратите внимание на то, что мы будем обозначать матрицу не просто буквой К, а еще добавлять подчеркивание. Делается это специально для того, чтобы не переобозначать встроенные переменные среды MathCAD. Аналогичным образом теперь нужно задать вектор свободных членов — только его размер уже будет не 4х4, а 1х4. Для решения СЛАУ после того, как мы ввели коэффициенты (вы можете ввести их произвольно, а можете

воспользоваться теми, которые приведены на скриншоте — с ними цифры в ответе получаются довольно ровными и красивыми), нужно для решения СЛАУ использовать функцию lsolve. У нее есть два параметра: первый — это матрица коэффициентов уравнений, а второй — вектор свободных членов. То есть для получения результата нам нужно написать:
lsolve(K_, L_) =

Ну, а после знака равенства MathCAD нам уже нарисует результат.

С помощью функции lsolve можно получать и аналитические решения СЛАУ. Давайте попробуем заменить одно из чисел в матрице коэффициентов на букву — например, «а». Функция lsolve сразу выдаст ошибку, но не нужно этого пугаться — нужно просто заменить знак равенства на стрелку (ее можно найти на панели инструментов Symbolic или же записать комбинацией клавиш Ctrl + .). Дело в том, что знак «равно» в MathCAD’е используется для численных вычислений, а стрелка — для символьных, то есть при решении систем уравнений в общем виде нужно применять именно стрелку.

Решение с помощью solve

В общем-то, решать такую систему можно было бы и используя уже знакомый нам с вами оператор solve. Для этого достаточно записать уравнения в виде матрицы, а затем применить к ней оператор solve точно так же, как если бы мы с вами решали не целую систему, а всего лишь одно- единственное уравнение.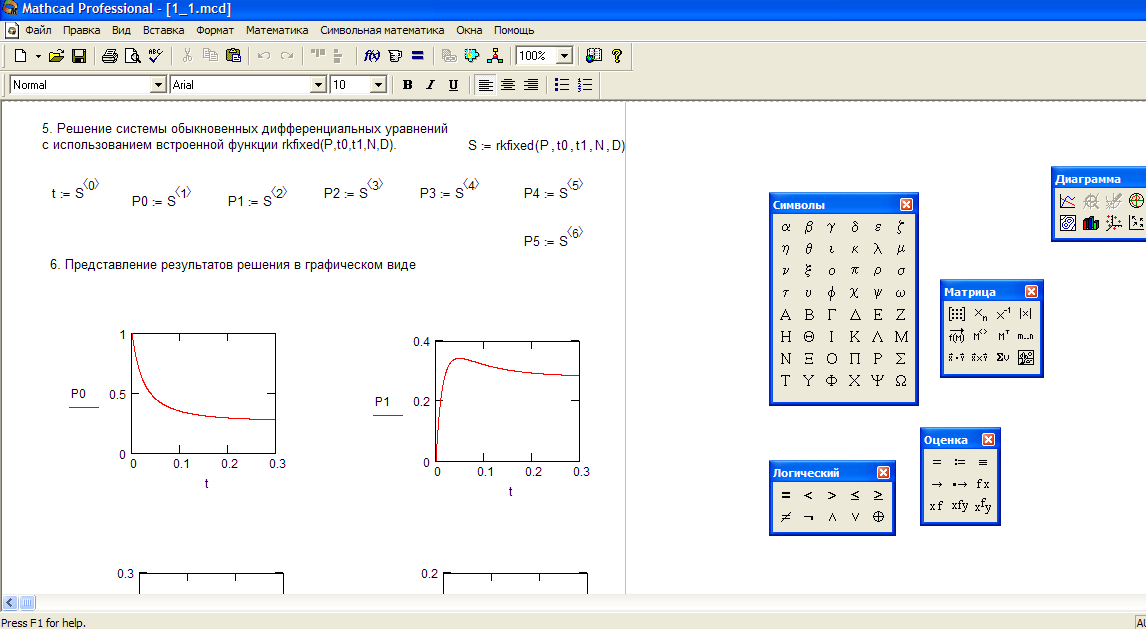 «Записать уравнения в виде матрицы» в данном случае означает не запись матричного уравнения KX + L = 0, а просто запись в каждой строке одностолбцовой матрицы (т.е. вектор-столбца) одного уравнения из системы. Напомню на всякий случай, что оператор solve находится на панели Symbolic, а для записи знака равенства нужно использовать не просто клавишу «=», а ее комбинацию с клавишей Ctrl. Еще хочу добавить, что в данном случае, как, впрочем, и во многих других, которые мы с вами уже обговорили, это может вполне успешно использоваться для получения не только символьных, но и для численных решений.

Решение СЛАУ с помощью solve поначалу кажется не таким уж привлекательным, однако, по сути, оно ничем не отличается от использования функции lsolve. Например, если вы замените какой-нибудь из числовых коэффициентов в одном из уравнений на букву, чтобы получить аналитическое решение, solve справится с этим точно так же быстро и хорошо, как и функция lsolve. Так что, в общем-то, выбор при решении СЛАУ в пользу функции lsolve или в пользу оператора solve — дело скорее вкуса, причем вкуса в плане записи самой системы уравнений, а не оператора или функции, у которых, в общем-то, даже названия очень и очень похожи. Пожалуй, один из немногих случаев, когда все же предпочтительнее использовать именно оператор solve — это когда уравнений у нас больше, чем неизвестных, содержащихся в них. В этом случае матрица системы будет выглядеть не так, как хотелось бы, а вот с solve все будет нормально. Даже если решение найти не удастся, solve любезно об этом сообщит. Аналогичным образом можно попытаться решить СЛАУ и в том случае, когда соотношение между уравнениями и неизвестными, напротив, не в пользу уравнений (правда, как говорится, не с разгромным счетом, а то решение заведомо найти не удастся). Но даже в случае, когда мы пытаемся решить систему с тремя уравнениями и четырьмя неизвестными, оставив после solve только две из них, у нас это далеко не всегда может получиться — в этом вы можете убедиться воочию.

Численное решение СЛАУ

Что ж, давайте теперь посмотрим, как решать СЛАУ с использованием численных методов их решения. Это тоже вовсе не так сложно, как может с самого начала показаться, поскольку MathCAD имеет в своем арсенале ряд средств и на этот случай. Как и в случае с одиночными уравнениями, сначала нужно задать начальное приближение (на то оно и начальное, чтобы задавать его сначала). Только, поскольку переменная у нас теперь не одна, а их несколько, то и начальное приближение необходимо будет задать для каждой из них. В тех случаях, когда переменных в СЛАУ много, это будет совсем не просто. После того, как вы задали начальные приближения для каждой из нужных переменных, запишите сами уравнения — только сделайте это так, чтобы их и начальные приближения разделяло специальное слово «Given» (оно, конечно же, в рабочей области MathCAD’а должно быть записано безо всяких кавычек). После того, как вы записали начальные приближения, слово «Given» и сами уравнения, можно смело воспользоваться функцией find, которая найдет точные значения решений системы. Поскольку в СЛАУ каждая из переменных в итоге будет иметь только одно значение, над подбором максимально точного начального приближения можно особо и не страдать — в конечном итоге в случае СЛАУ оно скорее просто формальность, нежели реальная необходимость, и, как вы сами имели возможность убедиться, есть методы, которые прекрасно решают СЛАУ и без него.

Теперь, когда вы знаете уже столько разных способов решения СЛАУ, вполне логично было бы задаться вопросом: а какой из них лучше при прочих равных условиях? В литературе, как правило, рекомендуется использовать функции lsolve или find, дающие точность до 15 знаков после запятой — однако на самом деле, учитывая тот факт, что такая точность бывает нужна не так уж часто, данным советом можно пренебречь, потому что точность решения системы намного больше зависит от нее самой, нежели от используемого метода ее решения в MathCAD’е. Так что используйте пока что смело тот, который показался вам наиболее удобным, а о погрешностях при решении СЛАУ мы с вами еще поговорим, но только, пожалуй, немного попозже.

SF, [email protected]

Компьютерная газета. Статья была опубликована в номере 16 за 2008 год в рубрике soft

Системы уравнений » MathCadHelp.com » Номер 1 в MathCad Задания

Mathcad позволяет решить систему из пятидесяти одновременных уравнений с пятьюдесятью неизвестными. В первой части этого раздела описывается процедура. Остальная часть содержит несколько примеров, а также обсуждение некоторых распространенных ошибок. Приведенный здесь метод всегда будет возвращать числа для неизвестных переменных. Чтобы увидеть неизвестные в терминах других переменных и констант, используйте блоки символьного решения, описанные в разделе «Символическое решение уравнений»

Решение системы одновременных уравнений состоит из четырех шагов. Это:

• Предоставьте начальное предположение для всех неизвестных, которые вы собираетесь решать. Mathcad решает уравнения, делая ряд предположений, которые в конечном итоге сходятся к правильному ответу. Первоначальные предположения, которые вы даете, дают Mathcad возможность начать поиск решений.

• Введите слово «Дано». Это говорит Mathcad, что далее следует система уравнений. Вы можете набирать Given любым сочетанием прописных и строчных букв и любым шрифтом. Просто убедитесь, что вы не вводите его в текстовой области или абзаце.

• Теперь введите уравнения и неравенства в любом порядке после слова «Дано». Убедитесь, что вы используете символ «=» для разделения левой и правой частей уравнения. Блоки Press Solve не могут быть вложены друг в друга. В каждом блоке решения может быть только одно заданное и одно найденное. Однако вы можете определить функцию вроде f(x) := Find(x) в конце одного блока решения и использовать эту же функцию в другом блоке решения. Это также обсуждается в разделе «Эффективное использование решателя» на странице 325.

Как правило, никогда не следует использовать операторы присваивания (такие как x : = 1) внутри блока решения. Mathcad помечает операторы присваивания внутри блоков решения соответствующим сообщением об ошибке.

На рис. 15-6 показан блок решения с несколькими типами ограничений. Есть два уравнения и два неизвестных. В результате функция Find содержит два аргумента, x и y, и возвращает вектор с двумя компонентами.

Блок решения с уравнениями и неравенствами.

Что делать, если решатель не достигает решения

Если решатель не может внести дальнейшие улучшения в решение, но не все ограничения удовлетворены, то решатель останавливается и помечает поиск сообщением об ошибке, указывающим, что он не смог найти решение.

Если у вас возникли трудности с поиском решения, часто бывает полезно построить кривую или кривые, о которых идет речь. График может обеспечить графическое представление о том, где может быть решение. Это поможет вам выбрать подходящие начальные предположения для переменных.

На рис. 15-11 показана проблема, для которой Mathcad не смог найти решение.

Проблема, решение которой не удалось найти решателю.

Решатель отказывается от попыток решить систему уравнений всякий раз, когда разница между последовательными приближениями к решению превышает TOL и:

• Решатель достигает точки, в которой он не может больше уменьшать ошибку.

• Решатель достигает точки, из которой нет предпочтительного направления. Из-за этого у решателя нет основы для дальнейших итераций.

• Решатель достигает предела своей точности. Ошибки округления делают маловероятным, что дальнейшие вычисления повысят точность решения. Это часто происходит, если вы установили значение TOL ниже 10–15.
Следующие проблемы могут вызвать такой сбой:

• Решения может и не быть.

• Возможно, вы дали реальные предположения для уравнения, не имеющего реального решения. Если решение для переменной сложное, решатель не найдет его, если начальное значение этой переменной также не является сложным. На рис. 15-11 показан пример.

• Решатель мог застрять в локальном минимуме значений ошибки. Метод решения, который использует Mathcad, иногда достигает точки, после которой он больше не может минимизировать ошибки. Чтобы найти действительное решение, попробуйте использовать другие начальные значения или добавьте неравенство, чтобы Mathcad не попал в ловушку локального минимума.

• Решатель мог застрять в точке, которая не является локальным минимумом, но из которой он не может определить, куда двигаться дальше. Стратегии обхода этой проблемы такие же, как и обхода локального минимума: изменить исходные догадки или добавить неравенство, чтобы избежать нежелательной точки остановки.

• Может оказаться невозможным решить ограничения в пределах желаемого допуска. Если значение TOL относительно невелико, Mathcad может достичь чего-то очень близкого к решению, но по-прежнему не сможет решить все ограничения с ошибкой меньше, чем TOL. Попробуйте определить TOL с большим значением где-нибудь над блоком решения. Увеличение допуска изменяет то, что Mathcad считает достаточно близким, чтобы назвать решение.

Что делать, если ограничений слишком мало

Если ограничений меньше, чем переменных, Mathcad вообще не может запустить решатель. Затем Mathcad помечает поиск соответствующим сообщением об ошибке.

Проблема, подобная показанной на рис. 15-12, недоопределена. Ограничения не дают достаточно информации для поиска решения. Поскольку в функции Найти пять аргументов, Mathcad считает, что вы хотите решить два уравнения с пятью неизвестными. В общем случае такая задача имеет бесконечное число решений.

Чтобы использовать решатель в Mathcad, вы должны предоставить как минимум столько уравнений, сколько есть переменных для решения. Если вы укажете значение некоторых переменных, возможно, вы сможете решить для остальных переменных. На Рисунке 15-13 показано, как решить проблему, показанную на Рисунке 15-12. Поскольку функция Find содержит только аргументы z и w,
Mathcad знает, что вы хотите, чтобы x, y и v оставались постоянными на уровне 10, 50 и 0 соответственно. Блок решения с двумя уравнениями становится законным, потому что теперь есть только два неизвестных, z и w.

Пять аргументов в поиске заставляют решатель думать, что вы хотите

Задача может быть решена с меньшим числом переменных в качестве аргументов Prime, вы можете решать линейные, нелинейные и дифференциальные системы уравнений.

В PTC Mathcad есть несколько методов, которые мы можем использовать:

• Функция lsolve.
• Конструкция блока решения.
• Символьное решение.

lsolve

Для решения линейных систем уравнений мы используем встроенную решающую функцию lsolve , чтобы быстро найти решение.

 

Блок решения

Для решения как линейных, так и нелинейных систем уравнений мы используем функцию блока решения, которая является чрезвычайно мощной и гибкой конструкцией.

Блок решения находится на вкладке «Математика» и содержит три разных раздела:

• Предполагаемые значения: в этом разделе вы инициализируете переменные, которые хотите решить, используя оператор определения для присвоения значения. Если вы не знаете, что использовать, используйте значение 1.
• Ограничения: В этом разделе вы пишете свою систему уравнений. Примечание: для знака равенства вы используете оператор сравнения, а не оператор оценки.
• Решатель: Здесь вы создаете вектор для переменных, которые хотите решить. Затем используйте оператор определения, чтобы назначить функцию поиска для тех же переменных.

Затем за пределами блока решения оцените вектор или отдельные переменные, чтобы увидеть решения.

Блок решения — это специальная структура в Mathcad. Помимо решения систем уравнений, его можно использовать для выполнения оптимизаций — нахождения минимума или максимума для функции и дифференциальных уравнений.
Кроме того, это отличная возможность для использования в отчетах, так как читатель может легко следить за ходом вычислений, и ему предоставляется полная картина вычислений.

Другой пример:
Нелинейная система уравнений представлена ​​на графике в приведенном ниже примере, где мы можем видеть точки пересечения.
В этом примере мы вставили блок решения с вкладки «Математика» и ввели начальные значения вместе с ограничениями, которые являются пределами того, что мы хотим вычислить.

Как только вы поймете структуру блока решения, вы почувствуете уверенность в применении задач инженерного проектирования блоков решения, например, при решении минимального диаметра трубы для создания заданного расхода.