Rkfixed в mathcad: 28. Тема 7. Решение дифференциальных уравнений и систем в MathCad. Краткие теоретические сведения

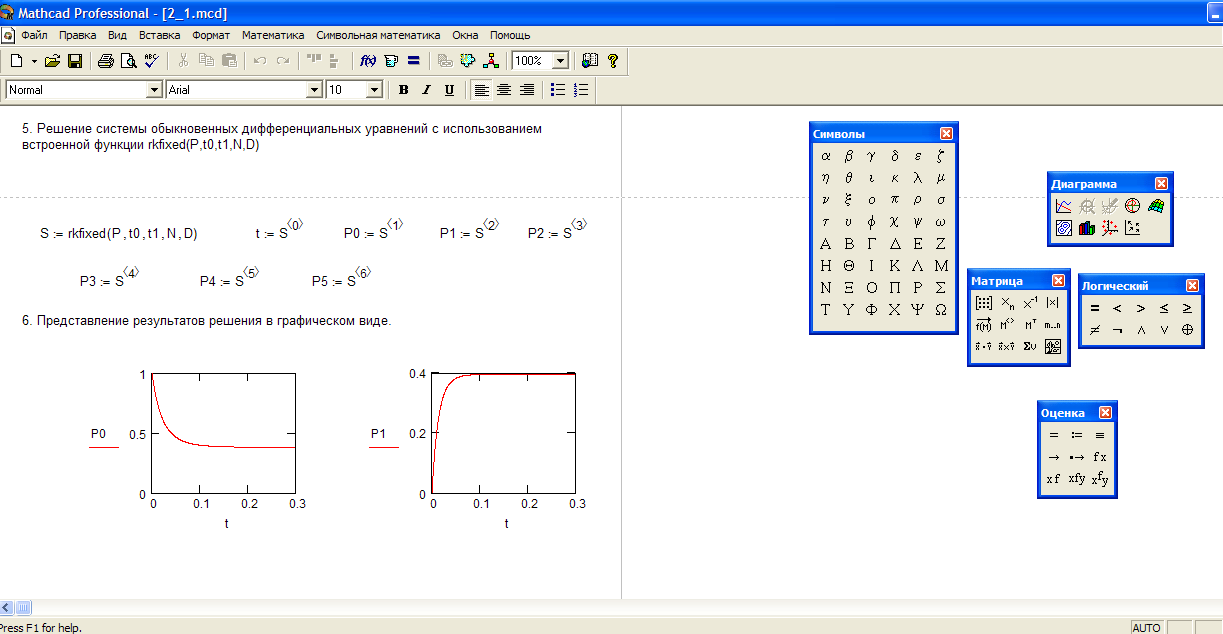
Использование встроенных функций rkfixed( ), Rkadapt( ), Bulstoer( )

Альтернативным методом решения ОДУ является использование встроенных функций rkfixed( ), Rkadapt( ) или Bulstoer( ). Этот метод несколько проигрывает первому и в простоте, и в наглядности, однако иногда приходится решать ОДУ с помощью альтернативного метода, например, при следующих обстоятельствах:

— ОДУ решается в контексте с более сложными задачами, в которые входят системы дифференциальных уравнений (для которых вычислительный блок неприменим) — в этом случае может потребоваться единый стиль программирования;

— ответ предпочтительнее получить в виде матрицы, а не функции;

— в старых версиях Mathcad’a не было вычислительного блока, а у пользователя имеется много документов, созданных с помощью альтернативного метода.

Приведем пример использования функции rkfixed( ) для решения той же самой задачи Коши для ОДУ первого порядка у’ =у-у².

Здесь необходимо явно задать начальное значение y:=0.01, описать первую производную D(t,y):=y-y² и указать количество точек интегрирования m=100. Результат получаем в виде матрицы y размерностью (m+1) x 2. В первом столбце содержатся значения аргумента t в интервале от 0 до 10, во втором столбце — значения искомой функции y(t), рис. 5.2.

Рис. 5.2. Решение задачи Коши для ОДУ первого порядка вторым способом

Это не лучший стиль решения задачи Коши. В самом деле, сначала переменной у присвоено значение скаляра у=0.01, а затем этой же переменной присвоено матричное значение (результат решения ОДУ). Нужно избегать такого стиля, когда один и тот же идентификатор используется при разных типах данных. Неплохим решением было бы назвать результат по-другому, например u.

Рассмотренный пример взят из области математической экологии и описывает динамику популяций с внутривидовой конкуренцией. Сначала происходит рост численности популяции, близкий к экспоненциальному, а затем осуществляется выход на стационарное состояние.

Обыкновенное дифференциальное уравнение с неизвестной функцией y(t), в которое входят производные этой функции вплоть до y⁽ⁿ⁾(t), называется ОДУ n-го порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши кроме самого уравнения требуется задать n начальных условий на саму функцию y(t) и ее производные от первого до (n -1) го порядка включительно. В Mathcad’e можно решать ОДУ высших порядков как с помощью вычислительного блока Given-Odesolve( ), так и альтернативным методом с использованием функций типа rkfixed().

Внутри вычислительного блока Given-Odesolve( ):

— ОДУ должно быть линейно относительно старшей производной;

— начальные условия должны иметь форму y(t0)=b или y⁽ⁿ⁾(t0)=b;

В остальном, решение ОДУ высших порядков ничем не отличается от решения уравнений первого порядка.

На рис. 5.3 показано решение дифференциального уравнения второго порядка затухающего гармонического осциллятора, которое описывает, например, колебания маятника. Для модели маятника функция y(t) описывает изменения угла его отклонения от вертикали, y'(t) — угловую скорость маятника, y»(t) — ускорение, а начальные условия, соответственно, начальное отклонение маятника у (0) =0.1 (в радианах) и начальную скорость у'(0)= 0.

Рис. 5.3. Решение дифференциального уравнения второго порядка

Альтернативный метод решения ОДУ высшего порядка реализуется с помощью трех встроенных функций, которые позволяют решать поставленную задачу в форме Коши различными численными методами:

— rkfixed(y, t0, t1, m, D) — метод Рунге-Кутта с фиксированным шагом;

— Rkadapt(y, t0, t1, m, D) — метод Рунге-Кутта с переменным шагом;

— Bulstoer(y, t0, t1, m, D) — метод Bulirsch-Stoer;

— у — вектор начальных значений в точке t0 размерностью n x1;

— t0 — начальная точка интервала;

— t1 — конечная точка интервала;

— m — число шагов, на которых численный метод находит решение;

— D — векторная функция дифференциальных уравнений размером n x1 от двух аргументов — скалярного t, по которому взяты производные и векторного у, элементы которого являются младшими производными искомой функции.

Покажем на примере дифференциального уравнения третьего порядка

методику формирования векторной функции D(t,y). Для этой цели нужно разрешить уравнение относительно старшей производной

Затем следует в этом уравнении выполнить замену производных компонентами вектораy:

Врезультате замены получим:

После этого можно записать векторную функцию D(t,y):

Векторная функцияD(t,y) имеет количество компонентов, равное порядку дифференциального уравнения. Поскольку младших производных нет, то вместо уравнений записываются их обозначения (y₁ и y₂). Вместо старшей производной записывается правая часть y₃. Начальные условия должны задаваться для искомой функции и каждой младшей производной, например:

Каждая из приведенных функций выдает решение в виде матрицы размером (m+1) х (n+1).

В ее левом столбце находятся значения аргумента t, делящие интервал на равномерные шаги, а в остальных n столбцах — значения искомых функций y₀(t) ,y₁(t), y₂(t)…, рассчитанные для этих значений аргумента. Поскольку всего точек (помимо начальной) m, то строк в матрице решения будет всего m+1.

В подавляющем большинстве случаев достаточно использовать функцию rkfixed( ), как это показано на рис. 5.4 на примере решения системы ОДУ модели осциллятора с затуханием:

Рис. 4.4. Решение системы ОДУ второго порядка

Система ОДУ на рис. 5.4 задается с помощью векторной функции D(t,y), составленной по описанной выше методике. Такой же размер имеет вектор начальных значений у. Число шагов, на которых определяется решение, задано параметром m=100. Решение системы ОДУ осуществляется на интервале (0, 50). Просмотреть все компоненты матрицы можно с помощью вертикальной полосы прокрутки.

Решения обыкновенных дифференциальных уравнений часто удобнее изображать не в функции от аргумента t, а в фазовом пространстве. Фазовый портрет системы — это кривая на фазовой плоскости, построенная в координатах y’(t) и y(t), рис. 5.5.

Фазовый портрет, как правило, имеет одну стационарную точку (аттрактор), на которую «накручивается» решение. В теории динамических систем аттрактор такого типа называется фокусом.

В общем случае, если система состоит из n ОДУ, то фазовое пространство является n-мерным. При n>3 наглядность теряется, и для визуализации фазового портрета приходится строить различные его проекции.

Метод Рунге-Кутта четвертого порядка обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем. Поэтому в большинстве случаев стоит применять функцию rkfixed( ). Если по различным причинам время расчетов становится критичным или точность неудовлетворительна, стоит попробовать вместо rkfixed( ) другие функции.

Рис. 5.5. Фазовый портрет решения системы ОДУ

Функция Rkadapt( ) может быть полезна в случае, когда известно, что решение на рассматриваемом интервале меняется слабо, либо существуют участки медленных и быстрых его изменений. Метод Рунге-Кутта с переменным шагом разбивает интервал не на равномерные шаги, а более оптимальным способом. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений — частыми. В результате, для достижения одинаковой точности требуется меньшее число шагов, чем для rkfixed( ). Метод Bulirsch-Stoer часто оказывается более эффективным для поиска гладких решений.

MathCAD — это просто! Часть 22. Другие методы численного решения дифференциальных уравнений

В прошлый раз мы с вами обсуждали вопросы решения дифференциальных уравнений в мощнейшей из математических сред (то есть в MathCAD) с помощью встроенной функции Odesolve. Функция эта, как мы с вами успели выяснить, в общем-то, всем хороша, однако, как я уже успел в прошлый раз обмолвиться, она предлагает не единственный из всех возможных путей численного решения дифференциальных уравнений в MathCAD. Для того, чтобы чувствовать себя в MathCAD’е как рыба в воде, нужно в совершенстве овладеть всеми способами решения дифференциальных уравнений. Ну, а для начала, наверное, стоит познакомиться с этими самыми способами с помощью вот этой статьи. Кроме того, мы с вами разберемся с такими вопросами, как решение систем «диффуров», поскольку системы дифференциальных уравнений встречаются едва ли не чаще, чем уравнения одиночные. В общем, планы, как видите, прямо-таки наполеоновские, а потому не буду затягивать вступления, а перейду к самому рассказу о работе с дифференциальными уравнениями в MathCAD’е.

Выбор метода интегрирования

Если вы еще помните наш с вами разговор о численном интегрировании в среде MathCAD, то должны помнить и о том, что можно выбирать разные методы интегрирования в зависимости от задачи. В общем-то, поскольку решение дифференциальных уравнений — это, по большому счету, то же самое интегрирование, разумно было бы ожидать, что и при решении ДУ можно будет выбирать метод интегрирования. И действительно, MathCAD (как, впрочем, и всегда) не обманывает наших ожиданий: выбирать способ вычисления решения дифференциального уравнения при использовании функции Odesolve и можно, и нужно.

Хитрости в изменении метода интегрирования для Odesolve никакой нет. Достаточно кликнуть правой кнопкой мыши по названию функции и выбрать в появившемся меню один из трех вариантов: Fixed, Adaptive или Stiff. Думаю, имеет смысл все же сделать некоторые пояснения по поводу того, чем различаются данные способы интегрирования дифференциальных уравнений. Fixed использует фиксированный шаг интегрирования, а Adaptive, как можно понять уже из его названия, — адаптивный (то есть изменяющийся). Если вы не очень хорошо представляете себе, что это все означает, и как они друг от друга отличаются, то имеет смысл вернуться к той статье про численное интегрирование в MathCAD’е, в которой я довольно подробно об этом всем рассказывал. Что касается метода Stiff, то он довольно специфичен и используется для так называемых жестких систем. Если вы работаете с ними, то вы сами знаете, что они жесткие, и вам следует устанавливать флажок именно напротив этого пункта меню. Если же, скажем так, в жесткости системы возникают сомнения, то лучше всего использовать метод Adaptive, потому что он гарантирует более высокую точность решения и избавляет пользователя от хлопот, связанных с подбором правильного шага интегрирования.

Использование функции rkfixed

Как я уже говорил во вступлении к статье, функция Odesolve является не единственным возможным вариантом применяемой для решения дифференциальных уравнений функции. Сейчас мы с вами рассмотрим функцию rkfixed, которая также может быть успешно использована для их решения. Вы можете спросить, зачем нужна еще одна функция для численного решения дифференциальных уравнений, если Odesolve и так самым что ни на есть замечательным образом справляется со своими прямыми обязанностями.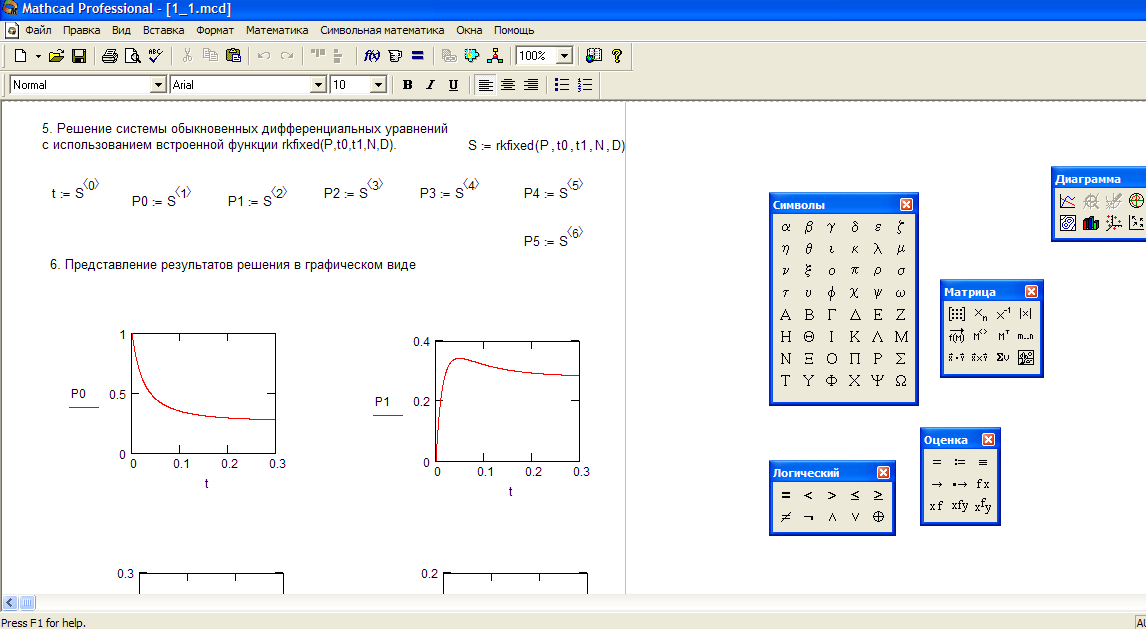 Что ж, вопрос резонный, но на самом деле хронологически Odesolve появилась в MathCAD’е позже, чем некоторые другие функции для решения дифференциальных уравнений (в том числе rkfixed). В общем-то, пожалуй, можно было бы и не говорить о более старых функциях, поскольку Odesolve более проста для пользователя в силу своей универсальности, однако бывают случаи, когда приходится сталкиваться и со старыми функциями, которые в новых версиях MathCAD оставлены, в основном, из соображений обратной совместимости со старыми версиями этой математической среды. Поэтому, если вам придется столкнуться с документами, сделанными в старых версиях MathCAD’а, в которых используется для решения дифференциальных уравнений функция rkfixed, то вы не будете пребывать в растерянности, а сможете разобраться, что именно хотел вычислить автор данного документа.

Итак, rkfixed. Пользоваться этой функцией, по сути дела, нужно точно так же, как и Odesolve. То есть сначала должны идти начальные условия для уравнения, а также само уравнение, оформленное в виде функции двух переменных (т.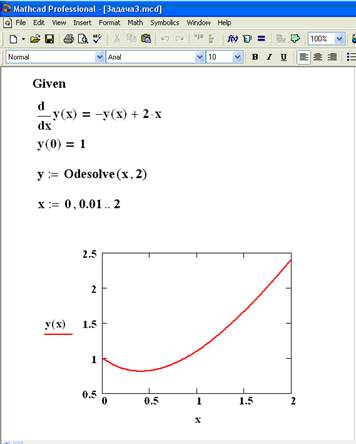 е. dy/dx = f(x, y)). К сожалению, функция rkfixed позволяет решать уравнения исключительно такого вида, а потому, например, работать с уравнением второго порядка вам придется с ее помощью уже как с системой двух дифференциальных уравнений. Помимо этого, нужно указать количество шагов интегрирования, для которых будут рассчитываться значения решения нашего дифференциального уравнения. Использования функции rkfixed вы можете на соответствующей иллюстрации к статье. Из нее, кстати, несложно понять, какие аргументы мы передаем в функцию для решения ДУ. Первый параметр — это начальное значение аргумента, по которому берется производная; второй и третий — это, соответственно, начало и конец того отрезка, на котором будет производиться интегрирование; четвертый параметр — это количество шагов интегрирования, ну, а последний — собственно сама функция f(x, y) для нашего уравнения dy/dx = f(x, y).

Как видите, использовать Odesolve действительно проще и удобнее. Помимо rkfixed, в MathCAD’е есть и другие функции, которые позволяют решать ДУ не с использованием фиксированного шага, а с адаптивным методом интегрирования или со специальными методами решения некоторых видов уравнений. Найти их в справке MathCAD’а не представит никакой сложности, кроме того, мы еще поговорим немного ниже о них. Однако их, как и rkfixed, рекомендуется по возможности не применять, заменяя на Odesolve.

Решение систем дифференциальных уравнений

Что ж, с одиночными дифференциальными уравнениями мы с вами, в общем-то, можно считать, практически разобрались. Конечно, было бы интересно узнать, как работают алгоритмы, лежащие в основе методов численного решения ДУ в MathCAD’е. Возможно, в следующий раз нам с вами и удастся об этом поговорить. Пока же на очереди вопрос более насущный и важный — решение систем дифференциальных уравнений. Поспешу вас обрадовать: мы с вами уже почти умеем решать системы дифференциальных уравнений — недаром же мы с вами останавливались на вопросах использования такой, казалось бы, устаревшей и не сильно для нас с вами полезной функции, как rkfixed. Оказывается, именно она поможет нам решать системы дифференциальных уравнений, с которыми, к сожалению, функция Odesolve никаких дел иметь не хочет.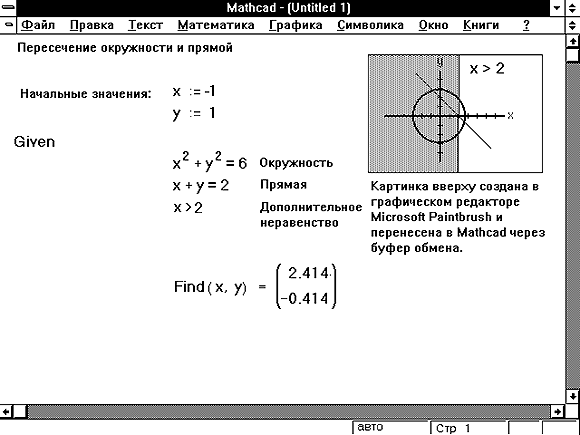 Использование функции rkfixed (и некоторых других) для решения систем ДУ имеет самые что ни на есть минимальные отличия от ее же использования в случае одиночных уравнений. По сути дела, для самого MathCAD’а отличий и вовсе никаких нет — просто скалярные переменные в этой функции заменяются на векторные, с которыми она работает точно так же, как и со скалярными. При этом, правда, действует все то же ограничение на вид уравнений, входящих в систему: они должны быть линейными и не содержать производных выше первой. Впрочем, как я уже говорил, ограничение, связанное с производными высших порядков, довольно просто обходится.

Вы легко обнаружите на иллюстрации к статье, демонстрирующей решение системы уравнений с помощью rkfixed, что совсем не так уж много отличий между решением системы и решением одиночного дифференциального уравнения. Кстати, если внимательно присмотреться к решенной на иллюстрации системе, то можно обнаружить, что она как раз и относится к тому «хитрому» способу решения дифференциальных уравнений второго порядка, к которому приходится прибегать при использовании для решения функции rkfixed.

Теперь, пожалуй, стоит рассказать немного о других функциях, аналогичных по сути rkfixed, но работающих несколько иначе. Функция rkfixed (как видно из ее названия) использует для интегрирования фиксированный шаг, что, с одной стороны, обеспечивает приемлемую точность интегрирования, а с другой — его высокую скорость. Но иногда этой точности бывает недостаточно, и тогда имеет смысл применить функцию rkadapt. В отличие от rkfixed, она имеет изменяющийся соответственно скорости изменения интегрируемой функции шаг интегрирования, а потому в случае быстро изменяющихся функций имеет смысл применять именно ее. Впрочем, ее лучше привыкнуть применять всегда, поскольку адаптивный шаг интегрирования позволяет добиться большей точности результатов вычисления решения дифференциального уравнения. Еще одна функция, которая может применяться в процессе решения — Bulstoer. Она позволяет достигать еще большей точности интегрирования, однако применять ее можно только тогда, когда интегрируемая функция будет достаточно гладкой и достаточно медленно изменяющейся.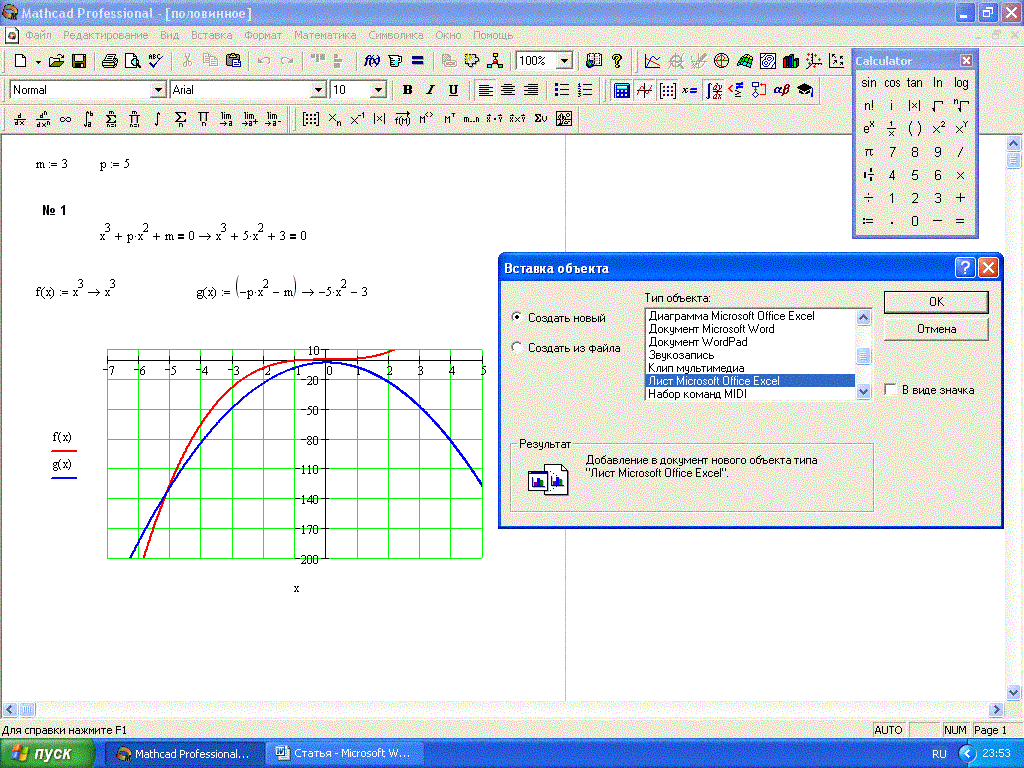 Насколько именно гладкой и медленно изменяющейся должна быть функция, можно попробовать установить экспериментально, сравнив результаты решения с применением каждой из этих трех функций. Как вы понимаете, все они имеют одинаковые параметры, и, поскольку мы уже разобрали параметры rkfixed, то для двух остальных функций мы их разбирать не будем.

Подведем итоги

Что ж, сказано всего в этот раз о численном решении дифференциальных уравнений и их систем было, как всегда, немало, и настало время по традиции подвести итоги. Как видите, решать системы дифференциальных уравнений в MathCAD уже не так просто, как одиночные уравнения, но, в принципе, это все было вполне ожидаемо, и ничего такого особенно трагичного в этом, как мне кажется, нет. Если не бояться их решать, то решать совсем не так уж и сложно — в любом случае, куда как проще, чем с помощью ручки и бумаги. Впрочем, как видите, решение дифференциальных уравнений и их систем сопряжено с рядом довольно-таки тонких моментов, например, касательно того, какой метод интегрирования выбрать. Для того, чтобы не допустить досадной ошибки, отрицательно влияющей на результат, мало просто быть знакомым с разными методами интегрирования — надо еще хорошо представлять себе особенности решаемой с помощью MathCAD задачи и применяемых в ней функций. То есть, несмотря на всю свою мощь, MathCAD все-таки не может освободить вас от знаний высшей математики, потому что это не компьютерный решатель задач, а всего лишь мощный «навороченный» калькулятор. И успехов при работе с MathCAD можно достичь только если подходить к нему именно как к помощнику, а не как к универсальному математическому решателю.

SF, [email protected]

Компьютерная газета. Статья была опубликована в номере 36 за 2008 год в рубрике soft

Оценка скорости реакции металл-вода IWTS (отчет Fauske and Associates 99-26) (технический отчет)

Оценка скорости реакции металл-вода IWTS (отчет Fauske and Associates 99-26) (технический отчет) | ОСТИ.GOV

перейти к основному содержанию

• Полная запись
• Другое связанное исследование

В отчете представлен анализ термической стабильности частично металлических частиц в двух компонентах IWTS, отстойнике и отстойниках. Частицы в выбивном стакане термически стабильны для комбинаций среднего размера частиц и массовой доли металла, которые кажутся реалистичными. Твердые частицы в отстойниках термически стабильны, если учитывать реалистичный учет реакций частиц с течением времени, фракцию металла и распределение по размерам.

Авторов:

ДУНКАН, Д. Р.

Дата публикации:

1999-07-29

Исследовательская организация:

NHC (США)

Организация-спонсор:

ЭКОЛОГИЧЕСКИЙ МЕНЕДЖМЕНТ (США)

Идентификатор ОСТИ:

797538

Номер(а) отчета:

SNF-4266, Ред. 0
РНН: US0202017

Номер контракта с Министерством энергетики:  

АК06-96РЛ13200

Тип ресурса:

Технический отчет

Отношение ресурсов:

Прочая информация: PBD: 29 июля 1999 г.

Страна публикации:

США

Язык:

Английский

Тема:

21 СПЕЦИАЛЬНЫЕ ЯДЕРНЫЕ РЕАКТОРЫ И СОПУТСТВУЮЩИЕ УСТАНОВКИ; РАСПРЕДЕЛЕНИЕ; ОЦЕНКА; РЕАКЦИИ РАСПЛАВЛЕННЫЙ МЕТАЛЛ-ВОДА; РАЗМЕР ЧАСТИЦЫ; ЧАСТИЦЫ; СТАБИЛЬНОСТЬ

---

Форматы цитирования

• MLA
• АПА
• Чикаго
• БибТекс

DUNCAN, DR. IWTS оценка скорости реакции металл-вода (отчет Fauske and Associates 99-26) . США: Н. П., 1999. Веб. дои: 10.2172/797538.

Копировать в буфер обмена

DUNCAN, DR. IWTS, оценка скорости реакции металл-вода (отчет Fauske and Associates 9).9-26) . Соединенные Штаты. https://doi.org/10.2172/797538

Копировать в буфер обмена

ДУНКАН, Д. Р. 1999. «Оценка скорости реакции металл-вода IWTS (отчет Fauske and Associates 99-26)». Соединенные Штаты. https://doi.org/10.2172/797538. https://www.osti.gov/servlets/purl/797538.

Копировать в буфер обмена

@статья{ости_797538,
title = {Оценка скорости реакции металл-вода IWTS (отчет Fauske and Associates 99-26)},
автор = {ДАНКАН, Д. Р.},
abstractNote = {В отчете представлен анализ термической стабильности частично металлических частиц в двух компонентах IWTS, отстойнике и отстойниках. Частицы в выбивном стакане термически стабильны для комбинаций среднего размера частиц и массовой доли металла, которые кажутся реалистичными. Твердые частицы в отстойниках термически стабильны, если учитывать реалистичный учет реакций частиц с течением времени, фракцию металла и распределение по размерам.},
дои = {10.2172/797538},
URL-адрес = {https://www.osti.gov/biblio/797538}, журнал = {},
номер =,
объем = ,
место = {США},
год = {1999},
месяц = ​​{7}
}

Копировать в буфер обмена

---

Посмотреть технический отчет (2,51 МБ)

https://doi.org/10.2172/797538

---

Экспорт метаданных

Сохранить в моей библиотеке

Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.