5. Решение дифференциальных уравнений с помощью встроенных функций MathCad
72
Обыкновенное дифференциальное уравнение первого порядка, по определению, содержит, помимо самой искомой функции у(t), только ее первую производную y'(t). В подавляющем большинстве случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши), разрешенное относительно старшей производной:
у'(t)=f(y(t),t)
Только с такой формой умеет работать вычислительный процессор Mathcad. Правильная с математической точки зрения постановка соответствующей задачи Коши для ОДУ первого порядка должна, помимо самого уравнения, содержать одно начальное условие — значение функции y(t0) в некоторой точке t0. Требуется явно определить функцию y(t) на интервале от t0 до tx. По характеру постановки задачи Коши называют еще задачами с начальными условиями (initial value problem), в отличие от краевых задач.
Для
численного интегрирования одного ОДУ
у пользователя Mathcad имеется выбор — либо
использовать вычислительный блок Given
– Odesolve(
), либо встроенные
функции.
Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутта, состоит из трех частей:
— Given — ключевое слово;
— ОДУ и начальное условие, записанное с помощью Булевых операторов, причем начальное условие должно быть в форме у(t0) = b;
— Odesolve(t, t1) — встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1).
Допустимо, и даже часто
предпочтительнее, задание функции
Odesolve
(t, t1, step) с тремя
параметрами, где step
– необязательный внутренний параметр
численного метода, определяющий
количество шагов, в которых по методу
Рунге-Кутта будет получено решение
дифференциального уравнения. Чем больше
step,
тем с лучшей точностью будет получен
результат, но тем больше времени будет
затрачено на его решение.
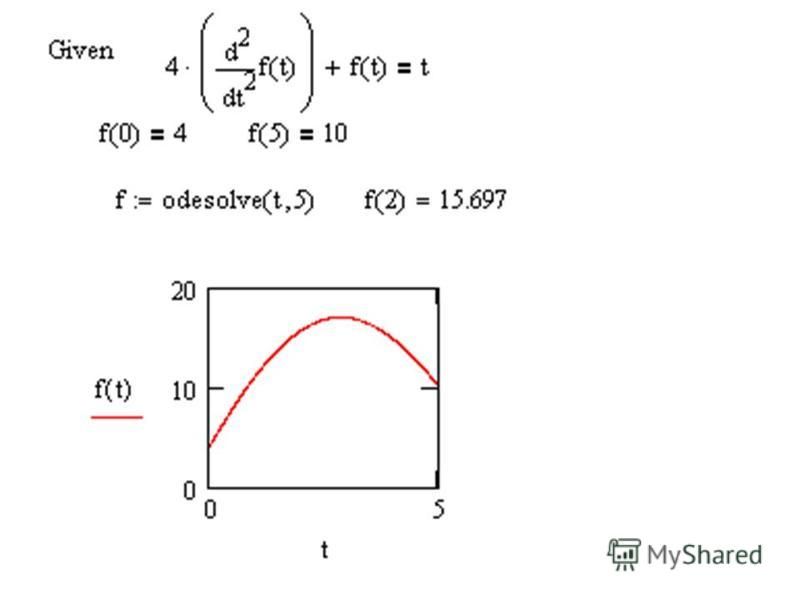
Пример решения задачи Коши для ОДУ первого порядка у’=у-у2 посредством вычислительного блока Given – Odesolve( ) приведен на рис. 5.1. Вставлять логические операторы нужно при помощи панели инструментов Boolean (Булевы операторы). При вводе с клавиатуры логического знака равенства нужно использовать сочетание клавиш Ctrl =. Символ производной можно ввести как средствами панели Calculus (Вычисления), как это сделано на рис. 5.1, так и в виде штриха (‘), набрав его с помощью сочетания клавиш Ctrl +F7.
Рис.5.1. Решение задачи Коши для ОДУ первого порядка
Mathcad требует, чтобы конечная
точка интегрирования ОДУ лежала правее
начальной (t0<t1),
иначе будет выдано сообщение об ошибке.
Функция Odesolve(
) возвращает функцию
y(t),
определенную на интервале (t0,t1).
Пользователь имеет возможность выбирать между двумя модификациями численного метода Рунге-Кутта. Для смены метода необходимо нажать ПКМ на область функции Odesolve( ), вызвать контекстное меню и выбрать в нем один из двух пунктов: Fixed (Фиксированный шаг) или Adaptive (Адаптивный). По умолчанию применяется первый из них, т. е. метод Рунге — Кутта с фиксированным шагом.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ:Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов. Интересное: Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 7Следующая ⇒
При решении ОДУ его следует привести к нормальной форме (к виду разрешенному относительно производнойисходного ОДУ) ДляОДУ с разделяющимися переменными исходное уравнение можно привести к виду , тогда выражение задает решение задачи Коши с начальными условиями как функцию y от переменной х.
Пример 2.4-22. Решить ОДУ вида . Найдем частное решение данного ОДУ с использованием средств Mathcad, сначала методом разделения переменных, а затем с использованием функции odesolve(x, xk, n), где х – имя переменной, относительно которой решается уравнение, xk – конец интервала интегрирования, n – количество шагов, на которых вычисляется решениеОДУ. Результаты подтверждают правильность преобразований.
Аналитическое выражение для решений ОДУ удается получить достаточно редко, поэтому широкое распространение при решении ОДУ получили численные методы.
Пример 2.4-23. Решить ОДУ на отрезке [0;3] методами Рунге-Кутты с постоянным шагом h=0,6. В приведенном ниже документе решение, полученное методом Эйлера, обозначено как y1, методом Рунге-Кутты 2-го порядка – y2, а 4-го порядка – y4.
В Mathcad нет средств символьного решения ОДУ, но достаточно широко представлены методы численного решения задачи Коши. Для этого предназначена, например, функция rkfixed(y, x0, xend, N, D), где y– первоначально равно y0, x0 и xend– начальное и конечное значения аргумента, N – количество проводимых вычислений решения, а переменной D(x,y) должно быть присвоено выражение для вычисления правой части уравнения. Результатом вычислений функции rkfixe( ) служит матрица, в первом столбце которой содержатся координаты узлов x0 … xend, а во втором – значения приближенного решения в соответствующих узлах. В функции rkfixed( ) вместо метода Рунге-Кутты используется метод Булирша-Штера. Ниже приведены решения и их графическая иллюстрация, полученные с шагом 0.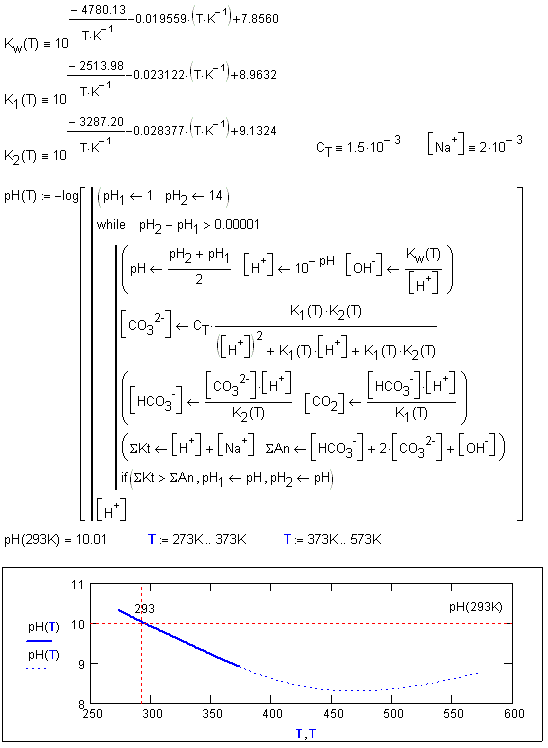 6 и 0.15. 6 и 0.15.
Пример 2.4-24. Решить ОДУ у’=
Решение ОДУ 2-го порядка вида у”=F(x, y, z), где z=y’ также может быть получено методом Рунге-Кутты 4-го порядка. Ниже приведены формулы для решения ОДУ:
Система Mathcad имеет специальную встроенную функцию для решения дифференциальных уравнений. Она имеет вид:Odesolve( x , b [ , steps ] ). Для решения задачи Коши необходимы так называемые начальные условия и указание конца интервала. Эти данные вместе с самим уравнением записываются в блок функции Given, и лишь затем применяется сама функция odesolve( ). Функция имеет ряд особенностей. Если указано число шагов step, то решение выполняется с фиксированным шагом, иначе — адаптивным методом. Пример 2.4-25. Решить дифференциальное уравнение.
⇐ Предыдущая1234567Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
[PDF] Документ — Скачать PDF бесплатно
MathCAD
Краевая задача Дифференциальное уравнение второго порядка
y f x, y, y имеют два начальных значения. Их можно разместить в разных точках. y A для x a y B для x b B
A
a
b
Краевая задача Другой тип граничных условий
y A для x a x
A
a
b
Краевая задача Применяется
к дифференциальным уравнениям второго порядка или системам дифференциальных уравнений первого порядка Начальные условия задаются на противоположных границах области решения Численные методы (обычно) требуют начальных значений, сфокусированных в одной точке (одной из границ)
Краевая задача Исходная условия, необходимые для начала процедуры интегрирования
y A для x a y tg для x a a
b
Краевая задача Нам нужно угадать недостающее начальное условие в точке, где мы начинаем вычисления
Приведенные условия
Условие для угадывания
yA, yB
y’A или y’B
yA, y’B
y’A или yB
900 0 y’0, 0 BКраевая задача В
химическая и технологическая техника: Смещенные
параметры: тепломассоперенос
перенос Противоточные теплообменники Массообмен с сопровождающей химической реакцией
Краевая задача КАК УГАДАТЬ??! ! 1. Предположим, что в начальной точке отсутствуют начальные значения. 2. Выполните расчет до конечной точки диапазона независимой переменной. 3. Проверить разницу между рассчитанным граничным условием и заданным в конечной точке. 4. Если разница (ошибка) слишком велика, изменить принятые значения и вернуться к пункту 2.
Предположим, что в начальной точке отсутствуют начальные значения. 2. Выполните расчет до конечной точки диапазона независимой переменной. 3. Проверить разницу между рассчитанным граничным условием и заданным в конечной точке. 4. Если разница (ошибка) слишком велика, изменить принятые значения и вернуться к пункту 2.
Краевая задача Пример: Даны начальные условия системы двух дифференциальных уравнений dy1 dx f x, y1 , y2 dy2 f x, y , y 1 2 dx (диапазон ) : y , y 1a
1b
Для начала вычислений требуется значение y2a 1. 2. 3.
4.
Предположим, что y2a Вычислить значения y1, y2 до достижения точки b Вычислить разницу (ошибку ) e = |y1b(расчетное)-y1b,(данное)| Если e>emax, измените y2a и перейдите к с. 2
Краевая задача Что необходимо для решения краевой задачи? 1. Система уравнений 2. Концы диапазона независимой переменной (границы диапазона) 3. Известные значения начальных точек 4. Значения начальных точек, подлежащие угадыванию 5. Расчет погрешности значений функций на противоположной (начальной) стороне диапазон
Расчет погрешности значений функций на противоположной (начальной) стороне диапазон
Краевая задача →
Для поиска отсутствующих начальных значений в MathCAD можно использовать процедуру sbval. СИНТАКСИС: sbval(v, a, b, D, S, B)
v – вектор догадок искомых начальных значений в начальной точке a (стр. 4) a, b – конечные точки диапазона, на котором вычисляется дифференциальное уравнение (п. 2) D – вектор-функция независимой переменной и вектора зависимой переменной, состоит из правых частей уравнений. Зависимые переменные в уравнениях ДОЛЖНЫ БЫТЬ векторными! (стр. 1) S – векторная функция начальной точки, известной и искомой (v) определяющая начальные условия в начальной точке (стр. 3 и 4) B – функция (может быть векторного типа) для вычисления ошибки в конечной точке (b) (p 5) Результат: вектор искомых начальных условий.
Краевая задача
Краевая задача
Odesolve Общая процедура решения ОДУ
Odesolve
Возвращает функцию(и) независимой переменной, которая является решением одного обыкновенного дифференциального уравнения или системы ОДУ Решение задачи с начальными условиями а также краевую задачу Может решать одиночное ОДУ и систему ОДУ Результатом является неявная функция
Одесское решение Синтаксис Ключевое слово
Дано Дифференциальное(ые) уравнение(я) с использованием логического равенства(ий) (жирный шрифт =). Производные символы `, нажав [ctrl][F7] или конструкции типа d n из панели исчисления. dx n Начальное/граничное(ые) условие(я) (для производных только символы `). Булево равно. function_name:=Odesolve([v],x,b,[initvls])
Производные символы `, нажав [ctrl][F7] или конструкции типа d n из панели исчисления. dx n Начальное/граничное(ые) условие(я) (для производных только символы `). Булево равно. function_name:=Odesolve([v],x,b,[initvls])
Odesolve Дополнительная
информация:
– вектор имен функций — только для системы ОДУ b – конечная точка интегрирования Initvls – количество интервалов дискретизации (по умолч. 1000) функции должны быть определены явно (y (x) не только y) Принимаются алгебраические ограничения. v
Odesolve Один
ODE второго порядка
Odesolve Система
из
два ODE первого порядка
Odesolve Числовой
методы:
Adams/BDF
вызовы:
Метод Адамса-Бэшфорда для нежестких систем ОДУ Метод BDF для жестких систем ОДУ
– вызывает rkfixed Adaptive – вызывает Rkadapt Radau – вызывает метод – используется с алгебраическими ограничениями Фиксированный
Символьные операции MathCAD
Выбранные символьные операции, доступные в MathCAD
Простая символьная обработка: алгебраические выражения, вывод, интегрирование, матричные операции, вычисление пределов и т. д. Символический с ключевым словом : замена, расширение, упрощение, преобразование, парфракция, серия, решение и т. д.
д. Символический с ключевым словом : замена, расширение, упрощение, преобразование, парфракция, серия, решение и т. д.
Символьные операции MathCAD
Символьные операции доступны из панели символов или с помощью клавиш:
Чтобы получить символьный результат, переменным, используемым в выражениях, нельзя присваивать НИКАКОЕ ЗНАЧЕНИЕ!!
Символьные операции MathCAD
→
простые операции →
Символьное интегрирование →
→
Символьный вывод
Неопределенный оператор интегрирования (символ), выражение, [ctrl]+[.] Производный оператор, выражение, [ctrl]+[.]
Расчет пределов, суммы
Символьные операции MathCAD
Substitute — замена всех вхождений переменной на другую переменную, выражение или число
expand — расширяет все степени и произведения сумм в выбранном выражении
выражение [ctrl][shift ][.] замена, уравнение подстановки (используйте полужирный символ =)
выражение [ctrl][shift][. ] расширить, переменная
] расширить, переменная
Упростить — выполнить базовое алгебраическое упрощение, отменив общие множители и применить тождества тригонометрических и обратных функций
выражение [ctrl][shift][.] упростить
Символьные операции MathCAD
Фактор – преобразует выражение (или число) в произведение (простых чисел)
выражение [ctrl][shift][.] фактор
неполная дробь, тип:
→
выражение, [ctrl][shift][.] convert,parfrac, переменная ][shift][.] ряд, переменная = центральная точка разложения, порядок аппроксимации
Для решения одного уравнения
выражение [ctrl][shift][.] решить, переменная
Предполагается, что выражение равно 0
Символьные операции MathCAD К
решить систему уравнений
Введите
Дано Введите уравнения (используя [ctrl]+[=]) find(var1, var2,..) [ctrl][.]
Единицы в MathCAD
Система SI
единиц измерения, доступных в MathCAD:
— основные единицы измерения: метры (м), килограммы (кг), секунды (с), ампер (А), кельвины (К), канделлы (кд), моли (моль ). MKS — основные единицы: метры (м), килограммы (kg), секунды (sec), кулоны (coul), кельвины (K) CGS — основные единицы: сантиметры (cm), граммы (gm), секунды (sec) , кулоны (coul), кельвины (K) США — основные единицы: футы (ft), фунты (lb), секунды (sec), кулоны (coul), кельвины (K)
MKS — основные единицы: метры (м), килограммы (kg), секунды (sec), кулоны (coul), кельвины (K) CGS — основные единицы: сантиметры (cm), граммы (gm), секунды (sec) , кулоны (coul), кельвины (K) США — основные единицы: футы (ft), фунты (lb), секунды (sec), кулоны (coul), кельвины (K)
К
добавьте единицу измерения: введите единицу измерения после числа (MathCAD добавит знак умножения между числом и единицами измерения) MathCAD преобразует единицы измерения между системами единиц измерения и между основными и производными единицами измерения. Пользователь может определить новые производные единицы как парные: производная_единица:=множитель*основная_единица, например: кПа:=1000*Па
Независимо от
единиц, используемых в данных, результаты приводятся в основных единицах фактической системы единиц. Результат
единица измерения может быть изменена!!
После оценки появляется заполнитель. В этих заполнителях введите желаемую единицу измерения
Расчеты с единицами измерения.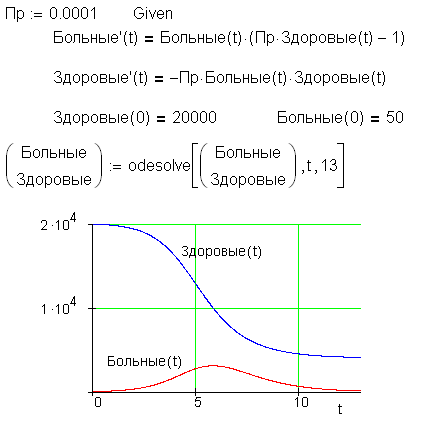
Вычислить объем прямоугольной призмы размером фут
Задача с единицами Параметры
с единицами измерения нельзя использовать в определении векторной функции системы дифференциальных уравнений (особенно при преобразовании ОДУ второго порядка в систему ОДУ первого порядка) Решение: Умножить
каждого элемента суммы в определении векторной функции на инверсию ее единицы
Оглавление контрольного номера Библиотеки Конгресса 2011928800
Оглавление контрольного номера Библиотеки Конгресса 2011928800
Библиографическая запись и ссылки на соответствующую информацию из каталога Библиотеки Конгресса
Информация из электронных данных, предоставленных издателем. Может быть неполным или содержать другую кодировку.
Предисловие Глава 1. Формально-кинетическое описание одно- и двухстадийных реакций 1.1 Основные понятия химической кинетики 1.2 Кинетика простых реакций 1.3 Реакции, включающие две элементарные стадии 1.
 3.1 Обратимые (двусторонние) реакции
1.3.2 Последовательные реакции
1.3.3 Параллельные реакции
1.3.4 Простейшая самокаталитическая реакция
Глава 2. Многошаговые реакции: методы аналитического решения прямой задачи
2.1 Разработка математической модели реакции
2.2. Классический матричный метод решения прямой кинетической задачи
2.3 Преобразование Лапласа в кинетических расчетах
2.3.1 Краткие примечания из операционного исчисления
2.3.2 Вывод кинетических уравнений для линейных последовательностей реакций первого порядка
2.3.3 Переходный режим в системе проточных реакторов
2.3.4 Кинетические модели в виде уравнений, содержащих кусочно-непрерывные функции
2.4. Приближенные методы химической кинетики
2.4.1 Метод стационарной концентрации
2.4.2. Квазиравновесное приближение. Кинетика ферментативной реакции
Глава 3. Численное решение прямой задачи химической кинетики
3.1 Решатель Given/Odesolve в системе Mathcad
3.2 Встроенные интеграторы Mathcad
3.3 Команды системы Maple dsolve, odeplot в численных расчетах
3.
3.1 Обратимые (двусторонние) реакции
1.3.2 Последовательные реакции
1.3.3 Параллельные реакции
1.3.4 Простейшая самокаталитическая реакция
Глава 2. Многошаговые реакции: методы аналитического решения прямой задачи
2.1 Разработка математической модели реакции
2.2. Классический матричный метод решения прямой кинетической задачи
2.3 Преобразование Лапласа в кинетических расчетах
2.3.1 Краткие примечания из операционного исчисления
2.3.2 Вывод кинетических уравнений для линейных последовательностей реакций первого порядка
2.3.3 Переходный режим в системе проточных реакторов
2.3.4 Кинетические модели в виде уравнений, содержащих кусочно-непрерывные функции
2.4. Приближенные методы химической кинетики
2.4.1 Метод стационарной концентрации
2.4.2. Квазиравновесное приближение. Кинетика ферментативной реакции
Глава 3. Численное решение прямой задачи химической кинетики
3.1 Решатель Given/Odesolve в системе Mathcad
3.2 Встроенные интеграторы Mathcad
3.3 Команды системы Maple dsolve, odeplot в численных расчетах
3. 4 Моделирование колебательных процессов
3.5 Некоторые вопросы неизотермической кинетики
Глава 4. Обратная задача химической кинетики
4.1 Особенности обратной задачи
4.2 Определение кинетических параметров с помощью линеаризации данных
4.2.1 Гидролиз метилацетата в кислой среде
4.2.2 Димеризация бутадиена: определение порядка реакции и константы скорости
4.2.3 Исключение времени как независимой переменной
4.2.4. Линеаризация с численным интегрированием кинетических данных. Основной гидролиз диэтиладипата 4.2.5. Оценка доверительных интервалов для рассчитанных констант
4.2.6 Кинетика изомеризации α-пинена
4.3 Обратная задача и специальные методы минимизации
4.3.1 Получение параметров для эмпирического уравнения скорости синтеза фосгена
4.3.2 Кинетика изомеризации трансстильбена
4.3.3. Кинетика ступенчатого обмена лигандов в комплексах хрома
4.4 Вычисление кинетических параметров с использованием инструментов нелинейной аппроксимации
4.5. Универсальные подходы к обратной задаче химической кинетики.
4 Моделирование колебательных процессов
3.5 Некоторые вопросы неизотермической кинетики
Глава 4. Обратная задача химической кинетики
4.1 Особенности обратной задачи
4.2 Определение кинетических параметров с помощью линеаризации данных
4.2.1 Гидролиз метилацетата в кислой среде
4.2.2 Димеризация бутадиена: определение порядка реакции и константы скорости
4.2.3 Исключение времени как независимой переменной
4.2.4. Линеаризация с численным интегрированием кинетических данных. Основной гидролиз диэтиладипата 4.2.5. Оценка доверительных интервалов для рассчитанных констант
4.2.6 Кинетика изомеризации α-пинена
4.3 Обратная задача и специальные методы минимизации
4.3.1 Получение параметров для эмпирического уравнения скорости синтеза фосгена
4.3.2 Кинетика изомеризации трансстильбена
4.3.3. Кинетика ступенчатого обмена лигандов в комплексах хрома
4.4 Вычисление кинетических параметров с использованием инструментов нелинейной аппроксимации
4.5. Универсальные подходы к обратной задаче химической кинетики. 4.5.1 Обратимая реакция с димеризацией промежуточного соединения
4.5.2 Термическое разложение дисилана
Глава 5. Введение в электрохимическую кинетику
5.1 Общие черты электродных процессов
5.2. Кинетика медленного разрядно-ионизационного этапа
5.3. Электрохимические реакции со ступенчатым переносом электрона
5.4. Электродные процессы в условиях медленной диффузии
5.4.1 Связь между скоростью и потенциалом при стационарной диффузии
5.4.2. Нестационарная линейная диффузия к плоскому электроду в электростатических условиях.
5.4.3. Нестационарная диффузия к сферическому электроду в потенциостатических условиях.
5.4.4. Нестационарная диффузия в гальваностатических условиях.
Глава 6. Интерфейс Mathcad 15 и Mathcad Prime
6.1 Ввод/отображение данных
6.2 VFO (оператор переменной функции)
6.2.1 Функция и оператор
6.2.2 Имя переменной
6.2.3 Невидимая переменная
Пример 1. Невидимое дополнение
Пример 2. Величина нулевой размерности
Пример 3. Римская арифметика
Пример 4. Разреженная матрица
Пример 5.
4.5.1 Обратимая реакция с димеризацией промежуточного соединения
4.5.2 Термическое разложение дисилана
Глава 5. Введение в электрохимическую кинетику
5.1 Общие черты электродных процессов
5.2. Кинетика медленного разрядно-ионизационного этапа
5.3. Электрохимические реакции со ступенчатым переносом электрона
5.4. Электродные процессы в условиях медленной диффузии
5.4.1 Связь между скоростью и потенциалом при стационарной диффузии
5.4.2. Нестационарная линейная диффузия к плоскому электроду в электростатических условиях.
5.4.3. Нестационарная диффузия к сферическому электроду в потенциостатических условиях.
5.4.4. Нестационарная диффузия в гальваностатических условиях.
Глава 6. Интерфейс Mathcad 15 и Mathcad Prime
6.1 Ввод/отображение данных
6.2 VFO (оператор переменной функции)
6.2.1 Функция и оператор
6.2.2 Имя переменной
6.2.3 Невидимая переменная
Пример 1. Невидимое дополнение
Пример 2. Величина нулевой размерности
Пример 3. Римская арифметика
Пример 4. Разреженная матрица
Пример 5.
 ..
..

 ..
..