Обработка векторов и матриц в MathCad, примеры
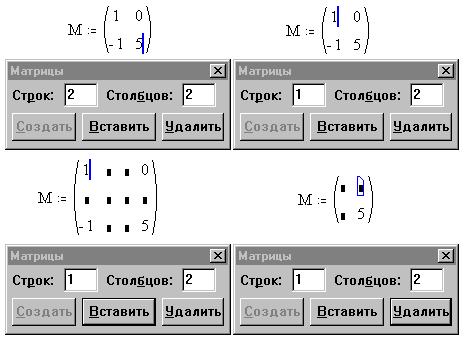
Создать матрицу можно с помощью шаблона командой Вставка — Матрица, щелчком на кнопке панели векторов и матриц. В появившемся окне задать размерность массива, нажать ОК, а затем ввести элементы массива;
Обращение к элементам матрицы M, вектора V:
элементам массива | столбцам матрицы | строкам матрицы |
V<номер элемента> M<номер строки, номер столбца> | M<номер строки, индекс столбца>, |
Работа с массивами
выполняется с помощью инструментов
панели Матрица.
Создание программных фрагментов в MathCad, примеры
Для создания программного фрагмента используется панель программирования, кнопки которой имеют следующее назначение:
Add Line — создание и расширение программного фрагмента;
¬ — оператор внутреннего локального присваивания.
if — оператор условия.
for — оператор цикла с заданным числом повторений.
while – оператор цикла с предусловием.
оtherwise — оператор «иначе», обычно используется совместно с if для выполнения действий в случаи невыполнения условия.
Переменные,
определенные в программном фрагменте,
являются локальными и их значения не
могут использоваться в документе вне
этого фрагмента.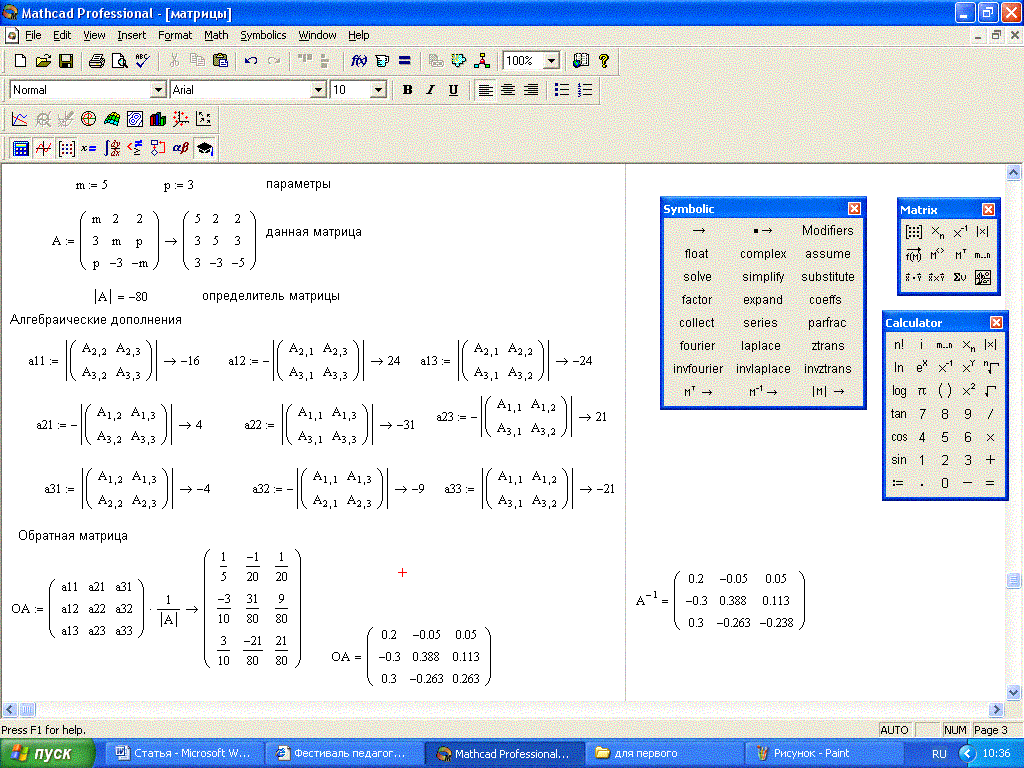
В программном фрагменте могут использоваться переменные, значения которых определены до программного фрагмента.
Создание двумерных графиков в MathCad, графики кусочно-непрерывных функций
Редактирование и форматирование графиков в MathCad
Для построения графиков используется палитра графиков, вид которой приведен ниже. Перечень возможных типов графиков приведен в основном меню Insert – Graph
При построении двумерных графиков после нажатия соответствующей кнопки на панели графических инструментов появляется шаблон вида:
Функция
Аргумент
При форматировании линий графика выбирается закладка Traces в окне форматирования.
Обработка внешних файлов в Mathcad
Можно использовать функции READ и READPRN
После импорта
данных Mathcad отображает их так же, как
если бы это были данные, созданные в
Mathcad.13. Символьные вычисления в MathCad
Если вы хотите получить не число в результате преобразования какого-либо выражения либо решения уравнения, а аналитическую формулу, то это и называется символьными вычислениями. Именно таким родом вычислений и занимается символьный процессор.
Далеко
не всегда символьный процессор способен
выдавать результат именно в том виде,
в каком его ожидаете увидеть вы. И даже
более того: сам по себе результат в каком
бы то ни было виде тоже далеко не всегда
может быть найден. Дело здесь, в общем-то,
не столько в каких-то внутренних дефектах
или ограничениях символьного процессора
MathCAD’а, сколько в том, что компьютерам,
вообще говоря, не слишком свойственно
креативное мышление, которое и является
залогом успешного решения любой
математической задачи. Очень часто
компьютер может элементарно «не
догадываться» о тех или иных приемах,
которые представляются элементарными
знакомому с математикой человеку, и
глупо на него за это обижаться.
MathCAD — это просто! Часть 11. Продолжаем работать с матрицами
Матрицы — вещь важная, а потому было бы просто непростительно отводить на них всего одну статью из нашего цикла о работе в среде MathCAD. Узнав о том, как можно транспонировать матрицы, вычислять определители, обратные матрицы, а также перемножать и складывать их, сегодня мы с вами продолжим издевательства над этими важными в математике объектами. Думаю, что изложенные ниже сведения будут полезны и в практических вычислениях, производимых в среде MathCAD, ведь матрицы очень часто встречаются в реальных задачах.
Еще о вспомогательных функциях
В прошлый раз мы немного поговорили о специальных MathCAD’овских функциях, позволяющих разрезать матрицы на составные части или же склеивать их.
Это не единственные из вспомогательных функций, действующих над матрицами, которые могут пригодиться в практике повседневной работы. Пришло время познакомиться с некоторыми другими функциями, которые также имеют неплохой шанс оказаться весьма и весьма полезными. Особую роль в матричном исчислении играют единичные матрицы. На всякий случай напомню, что единичной называется такая матрица, у которой все недиагональные элементы равны нулю, а элементы, расположенные на главной диагонали (от верхнего левого угла к нижнему правому), равны единице. Единичные матрицы могут иметь самые разные размеры. Чтобы пользователь не тратил свое время на вбивание нулей и единиц в строки и столбцы такой матрицы, в MathCAD’е имеется специальная функция Identity, создающая единичную матрицу заданного размера. У этой функции есть единственный аргумент, задающий размерность матрицы.
Еще она по своему действию довольно близкая к Identity функция называется Diag. Она создает не матрицы, а векторы, состоящие из диагональных элементов квадратных матриц (т.
е. из тех элементов, которые стоят на ее главной диагонали). Стоит при этом отметить, что размер вектора, получаемого на выходе, автоматически определяется размером входной матрицы.
Для определения размера матриц можно использовать функции Rows и Cols. Каждая из них имеет один-единственный входной параметр, которым является сама матрица, а на выходе выдают значения числа строк и столбцов соответственно. Для определения размера вектора можно использовать функцию length, которая работает аналогично указанным для матриц функциям.
Интересной также является предоставляемая MathCAD’ом функция для сортировки элементов векторов. Называется она просто и незатейливо — Sort. В качестве входного параметра этой функции нужно передать вектор, сортировкой которого мы будем заниматься, и на выходе получим почти такой же вектор, только его элементы будут упорядочены по возрастанию. Для сортировки строк и столбцов матрицы можно воспользоваться соответственно функциями Rsort и Csort, которым нужно передать в качестве параметров саму матрицу и номер того столбца или строки, которые должны быть отсортированы.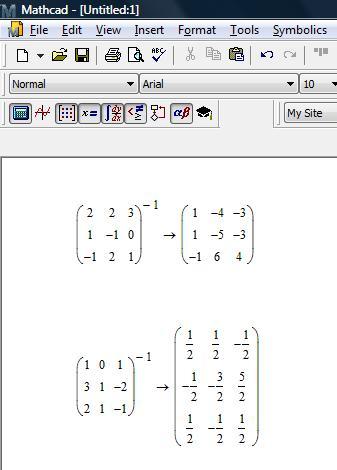
Ранг и норма матрицы
Два фундаментальных понятия, играющих очень важную роль в линейной алгебре — это ранг и норма матрицы. MathCAD позволяет пользователю вычислять эти характеристики матриц без лишних усилий, и сейчас я расскажу, как именно это делается.
Минором матрицы порядка k называется определитель, вычисленный для матрицы, образованной из k столбцов и k строк данной матрицы. Главным минором называется минор, для которого номера выбранных столбцов совпадают с номерами выбранных строк. Понимаю, это определение звучит несколько громоздко, но я думаю, если вы прочитаете его внимательно еще раз, то все станет просто и понятно.
Норма матрицы — понятие более расплывчатое, чем ранг. Для полного определения нормы матрицы используется система ограничений, которым должен подчиняться строящийся по определенным правилам функционал. Вы можете найти подробное определение нормы матрицы в любом учебнике по линейной алгебре. Мы же сейчас удовлетворимся знанием того, что норма матрицы — это некоторый аналог величины, который для векторов называют длиной (норма вектора как раз и есть его длина). Впрочем, в отличие от длины вектора, где все понятно и определенно, норма матрицы может вычисляться несколькими разными способами, и в зависимости от способа вычисления ее величина может быть различной.
Собственные вектора и собственные значения матриц
Собственным вектором x и собственным значением ? матрицы X называются такие вектор и число соответственно, которые удовлетворяют соотношению xX = ?x. Обычно матрица имеет несколько собственных векторов и соответствующих им собственных значений, а потому мы будем рассматривать именно этот случай. Конечно, в MathCAD’е не слишком сложно с помощью некоторых преобразований рассчитать необходимые числа и вектора самостоятельно, однако можно еще больше упростить себе жизнь, воспользовавшись встроенными в эту среду функциями.
Функция Eigenvecs принимает в качестве входного параметра некоторую матрицу, а возвращает другую, содержащую собственные вектора исходной. При интерпретации результатов работы этой функции необходимо помнить, что в MathCAD’е вектора записываются в виде столбцов, так что и в этой матрице каждый из столбцов является собственным вектором первоначальной матрицы. Другая функция, Eigenvals, также принимает на вход некоторую матрицу, однако выдает для нее уже не собственные вектора, а собственные значения. Записываются они также в виде столбика. В этом столбце они идут в том же порядке, что и столбцы в матрице, возвращаемые первой функцией. То есть i-му столбцу матрицы, получаемой на выходе функцией Eigenvecs, соответствует i-е собственное значение в векторе. Впрочем, проследить соответствие собственных векторов и собственных значений для матрицы можно и более наглядным образом. Для этого существует специальная функция Eigenvec (не путайте с Eigenvecs), которой на вход передаются матрица и одно из ее собственных значений, а она уже вычисляет соответствующий этому собственному значению собственный вектор.
Скалярное и векторное произведение векторов
Напоследок поговорим о вещах довольно простых, но очень распространенных в практике решения задач, а потому особенно важных. Сейчас мы рассмотрим, как с помощью MathCAD’а вычислять скалярное и векторное произведение векторов. Напомню, что скалярным произведением x.y называется число, равное x0y0 + x1y1 + x2y2 + … + xnyn, а вот с векторным все несколько сложнее. Оно определяется только для трехмерных векторов и вычисляется как определитель матрицы, составленной из базисных векторов (i, j и k) и элементов тех векторов, для которых вычисляется векторное произведение. Традиционно в математике векторное произведение обозначают c помощью крестика, который ставится между двумя перемножаемыми векторами.
Для вычисления скалярного и векторного произведения векторов обратимся снова к панели матричных вычислений, неоднократно выручавшей нас в наших упражнениях с MathCAD’ом. Скалярное произведение называется на ней Dot Product и обозначается как точка между двумя векторами, а векторное — Cross Product и обозначается крестиком, как я уже говорил выше.
Чтобы перемножить два вектора, вы можете сначала обозначить их с помощью каких- либо символьных обозначений, а можете сразу записывать произведения между столбцами чисел.
Теперь, пожалуй, о матрицах самое основное и важное сказано. Как видите, в плане работы с векторами и матрицами MathCAD ничуть не менее мощный, чем во всем остальном. Поэтому использовать эту среду для матричных вычислений можно и нужно. Ну а как это делать, вы теперь уже знаете.
Компьютерная газета. Статья была опубликована в номере 24 за 2008 год в рубрике soft
Векторные и матричные функции » MathCadHelp.com » Номер 1 в MathCad Assignments
Mathcad включает в себя функции для работы с массивами способами, распространенными в линейной алгебре. Эти функции предназначены для использования с векторами и матрицами. Если функция явно не настроена на прием векторного или матричного аргумента, неуместно предоставлять ее в качестве аргумента.
Обратите внимание, что функции, которые ожидают векторы, всегда ожидают векторы-столбцы, а не векторы-строки. Чтобы преобразовать вектор-строку в вектор-столбец, используйте оператор транспонирования [Ctrl]l.
В следующих таблицах перечислены векторные и матричные функции Mathcad. В этих таблицах
• A и B являются массивами, либо векторными, либо матричными.
• v — вектор.
• M и N — квадратные матрицы.
• z — скалярное выражение.
• Имена, начинающиеся с m, n, i или j, являются целыми числами.
Размер и область действия массива
Mathcad предоставляет несколько функций, которые возвращают информацию о размере массива и его элементов. На рис. 10-10 показано, как используются эти функции.
Рисунок 10-10:
Специальные типы матриц
Следующие функции можно использовать для получения из массива или скаляра специального типа или формы матрицы. Некоторые из этих функций доступны только в Mathcad Professional.
Векторные и матричные функции
Функции преобразования массивов.
Особые характеристики матрицы
Вы можете использовать функции в следующей таблице, чтобы найти трассировку, ранг, нормы и числа обусловленности матрицы. Большинство этих функций доступны только в Mathcad Professional.
Специальные характеристики матрицы
Формирование новых матриц
Mathcad предоставляет две функции для соединения матриц вместе, либо рядом, либо друг над другом. Mathcad также предоставляет функцию для заполнения матрицы значениями предопределенной функции и функцию для извлечения меньшей матрицы из большей. На Рисунке 10-12 и Рисунке 10-13 показаны некоторые примеры.
Формирование новых матриц
Соединение матриц вместе со стеком и функциями расширения.
Извлечение подматрицы из матрицы с помощью функции подматрицы
.
Собственные значения и собственные векторы
Mathcad предоставляет функции для работы с собственными значениями и собственными векторами матрицы.
Функция собственных векторов, доступная в Mathcad Professional, одновременно получает все собственные векторы. Если вы используете Mathcad Professional, у вас также будет доступ к genvals и
genvecs для нахождения обобщенных собственных значений и собственных векторов. На рис. 10–14 показано, как используются некоторые из этих функций.
Собственные значения и собственные векторы
Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям вектора v, возвращаемого функцией genvais. N-й столбец этой матрицы — это собственный вектор x, удовлетворяющий обобщенной задаче на собственные значения M . Икс знак равно V п . Н . Икс . Матрицы M и N являются квадратными матрицами с действительными значениями, имеющими одинаковое количество столбцов.
Нахождение собственных значений и собственных векторов
Использование собственных векторов для одновременного нахождения всех собственных векторов
Декомпозиция
Mathcad Professional предлагает некоторые дополнительные функции для выполнения декомпозиции Холецкого, QR-декомпозиции, LU-декомпозиции и сингулярной декомпозиции матрицы.
Некоторые из этих функций возвращают две или три матрицы, объединенные вместе в одну большую матрицу. Используйте подматрицу, чтобы извлечь эти две или три меньшие матрицы. На рис. 10-16 показан пример.
Разложение
Использование функции подматрицы для извлечения результатов функции qr. Аналогичным образом используйте подматрицу для извлечения результатов из функций lu и svd
Решение линейной системы уравнений
В Mathcad Professional вы сможете использовать функцию lsolve для решения линейной системы уравнений. На рис. 10-17 показан пример. Обратите внимание, что аргумент M для lsolve должен быть матрицей, которая не является ни сингулярной, ни почти сингулярной. Матрица является вырожденной, если ее определитель равен нулю. Матрица почти сингулярна, если она имеет высокое число обусловленности. Вы можете использовать одну из функций, описанных в разделе «Специальные характеристики матрицы» на стр. 19.8, чтобы найти число обусловленности матрицы.
Решение системы линейных уравнений
Кроме того, вы можете решить систему линейных уравнений, используя обращение матриц, как показано в правом нижнем углу Рисунка 10-9. Чтобы узнать о других методах численного решения в Mathcad, см. главу 15, «Решение уравнений». Для символьных решений систем уравнений см. главу 17, «Символические вычисления».
Использование Isolve для решения двух уравнений с двумя неизвестными
14.3: Ссылки на части матриц
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15001
- Трой Симерс
- Военный институт Вирджинии через APEX Calculus
Иногда вам может понадобиться использовать часть матрицы: запись, строку, столбец или подматрицу внутри другой матрицы.
Вы должны быть очень осторожны при обращении к частям матрицы, так как по умолчанию начальный индекс равен нулю! Это означает, что на «первую» строку матрицы ссылаются, как если бы она была «нулевой строкой». Начальный индекс хранится в переменной с именем 9.0013 ORIGIN и может быть изменен для листа двумя способами: либо с помощью Tools > Worksheet Options (и изменив ORIGIN ), либо введя ORIGIN:=1 в верхней части листа.
- Ссылка на одну запись в матрице
Чтобы выбрать одно число из существующей матрицы, можно использовать оператор «нижний индекс» на панели инструментов матрицы (кнопка x n ) или с помощью клавиши [. Здесь мы выбираем запись во 2-й строке и 2-м столбце, сбросив ORIGIN в 1 и определение b из матрицы a .
Обратите внимание: если матрица имеет только один столбец («вектор-столбец») или одну строку («вектор-строка»), то необходим только один нижний индекс.
- Для ссылки на один столбец в матрице
Чтобы выбрать один столбец из существующей матрицы, можно использовать оператор «Столбец» на панели инструментов матрицы ( M <>), или сочетанием клавиш Ctrl +6. Здесь мы выбираем 2-й столбец, сбрасывая ORIGIN на 1 и определяя b из матрицы a .
- Для ссылки на одну строку в матрице
Выбрать одну строку из существующей матрицы сложнее. Необходимо использовать комбинацию оператора «Транспонирование» (который переключает строки и столбцы) вместе с оператором «Столбец». Операция транспонирования на панели инструментов матрицы — это кнопка MT, а также ее можно создать с помощью сочетания клавиш Ctrl +1. Здесь мы выбираем 2-ю строку, сбрасывая ORIGIN на 1 и определяя b из матрицы a. Вводить это немного сложно. Точная последовательность клавиш
b : a (Ctrl + 1) (Ctrl + 6) 2 (пробел) (Ctrl + 1) =
- Для ссылки на подматрицу
Выбор подматрицы из существующей матрицы осуществляется только через команду подматрицы.