Mathcad значение должно быть массивом: ОЭБ «Оренбуржья»: Недопустимый идентификатор

Урок 7. Переменные-диапазоны и графики в Mathcad

Павел Демидов 11.06.2014 Уроки Mathcad 0

Рассмотрим простую функцию:

Вы можете построить график этой функции, вычислив значения y для различных значений переменой x. Для этой и многих других операций в Mathcad используются переменные-диапазоны.

Переменные-диапазоны

Переменные-диапазоны имеют множество значений. На рисунке Вы видите определение и вывод двух переменных-диапазонов.

Для первой переменной начальное значение равно 0, конечное – 3, а шаг равен 1. Для второй переменной первое значение определено 3, второе – 6, а верхняя граница равна 13. Первая переменная-диапазон i создана как математическая область с помощью оператора [..]:

Для ввода этого выражения наберите [i:0..3].

Вторая переменная j определяется в два шага:

1. Введите [j:3,], и после запятой появится местозаполнитель

2. Введите второе значение и верхнюю границу:

Первый тип переменной-диапазона, с шагом 1, наиболее часто используем. При необходимости, эту переменную можно изменить:

Можно использовать параметры в определении переменной-диапазона. В следующем примере с помощью параметра можно изменять длину переменной-диапазона:

Второй метод определения более гибок. В местозаполнитель, который появляется после запятой, вводится второе значение переменной-диапазона (не шаг увеличения). Во второй местозаполнитель вводится верхняя граница: значения переменной-диапазона закончатся на этой границе или до нее:

Если переменная-диапазон используется в качестве индекса массива, то ее элементы должны быть натуральными числами или нулем.

Элемент переменной-диапазона нельзя получить по индексу – при попытке сделать это появится сообщение об ошибке «Значение должно быть вектором»:

Понятие «вектор» мы обсудим позднее в наших уроках.

Наша функция

Мы вычислим нашу функцию для шести значений переменной-диапазона:

(Ряд 0, 1, 2, 3, 4, 5 включает в себя шесть значений. ) Определим шесть значений переменной x (подстрочный индекс – с помощью [):

С помощью подстрочных индексов можно проверить значения:

Теперь определим и проверим значения функции:

Для проверки всех значений наберите [x=] и [y=]:

Это векторы – мы их подробно обсудим в уроке 22.

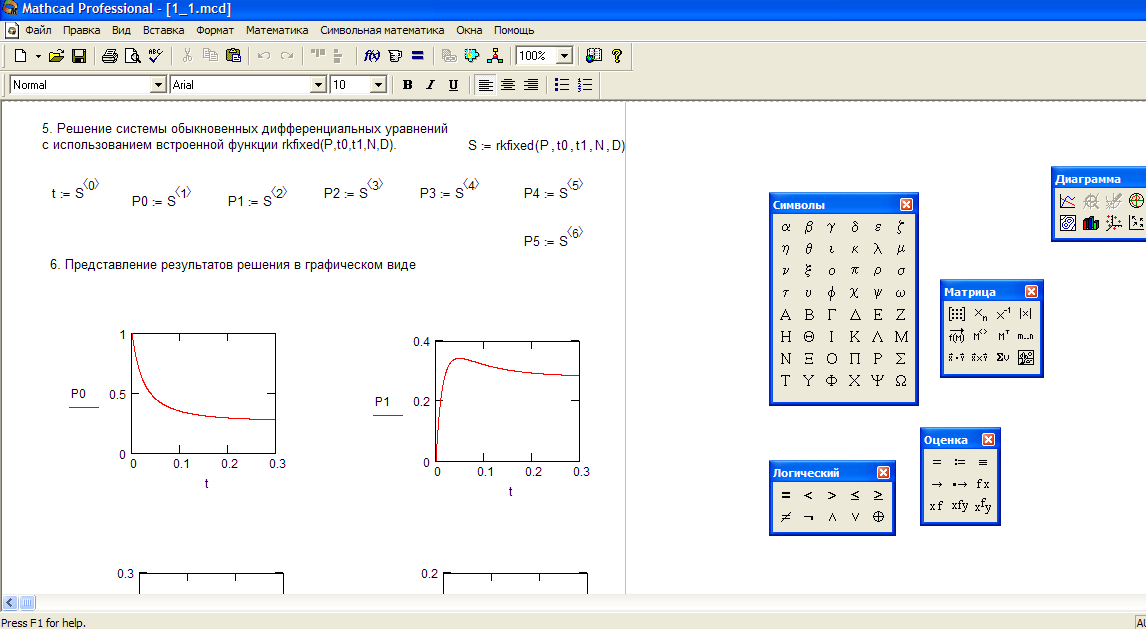
Первый график

Теперь значения x и y можно вывести на график. Нажмите Графики –> Вставить график –> График XY

Появятся оси. В местозаполнитель введите y:

Щелкните по местозаполнителю внизу, введите [x] и нажмите [Enter]. Появится график:

Элементы графика

Элементы графика показаны на рисунке внизу. Этими элементами являются:

1. Две оси: ось X и ось Y.
2. Легенды осей X и Y.
3. Фон графика.
4. Линия графика.
5. Метки на осях.
6. Значения на метках.

Выберите созданный график щелчком с зажатой клавишей [Ctrl]. Подведите курсор к правому нижнему углу – он изменится на двойную стрелку. Щелкните мышью и перемещайте курсор для изменения размеров области. Установите такой размер, который Вам больше подходит. Теперь подведите курсор на горизонтальную ось X. С помощью двойной стрелки Вы можете перемещать ее вверх и вниз. Вертикальную ось Y можно перемещать аналогичным образом в горизонтальном направлении. Фон графика можно изменить с помощью вкладки График –> Фон графика. Выберите тип фона Прозрачный.

Мы посчитали и вывели на график лишь несколько точек, поэтому график получился несглаженным. Возможно, лучше вывести на график только точки. Выберите Графики –> Стили –> Символ и выберите круг – третий символ в списке. На линии появятся символы:

Выберите Стиль линии –> (нет), и линия исчезнет. Поскольку символы малы, увеличьте толщину кривой (размер символов также увеличится). Измените также цвет кривой на красный:

Теперь обратите внимание на метки и значения возле них. Медленно проведите указатель мыши по меткам вдоль оси Y. Значения на первой, второй и последней метки увеличатся при наведении на них указателя. Их можно изменить. Первое и последнее значение определяют границы вывода графика. С помощью второго значения можно изменять число меток на оси. Измените значение на второй метке на оси Y на 5 вместо 2.5, а на оси X – на 1 вместо 0.5:

Выберите график, затем щелкните по вкладке График –> Оси –> Выражения оси. При щелчке вне графика легенда исчезнет (она появится, если Вы щелкните по графику). На рисунке вместо легенды размещены две маленькие математические области с

y и x:

Полученный в результате график, возможно, выглядит лучше, чем изначальный, но это дело вкуса.

Быстрое построение графика

Есть способ построить график быстрее, если Вы хотите увидеть лишь поведение функции. Перед тем, как сделать это, удалите предыдущие значения переменной x с помощью команды clear(x):

Функция, график которой нужно построить:

Вставьте график XY. Введите [y(x] в первый местозаполнитель и [x] во второй. Затем щелкните вне графика. Диапазон x обычно выставляется от -10 до 10. Диапазон по y выбирается автоматически:

Резюме

Переменные-диапазоны:

1. Переменная-диапазон – это набор значений. Переменные-диапазоны, используемые для индексов массива, должны принимать значения положительных целых чисел или нуля.
2. Переменные-диапазоны имеют начальное значение, шаг и верхнюю границу.
3. Переменные-диапазоны с шагом увеличения 1 вводятся набором имени переменной, оператором присваивания и двумя точками. Первый местозаполнитель содержит начальное значение, второй – верхняя граница (она же – последнее значение).
4. Диапазоны с иным шагом увеличения вводятся с помощью запятой после ввода первого значения. Два местозаполнителя должны содержать второе значение и верхнюю границу.

График набора точек

1. Выберите число точек, которое Вы хотите вывести на график.
2. Создайте переменную-диапазон от нуля до выбранного значения.
3. Определите необходимые значения x, используя имя переменной-диапазона в качестве подстрочного индекса.
4. Вычислите соответствующие значения функции.
5. Вставьте график XY с помощью Графики –> Вставить график –> График XY.
6. Введите имена переменных (в нашем случае – x и y) в местозаполнители.
7. Щелкните вне области, чтобы построить график.

Чтобы быстро построить график заданной функции y(x):

1. Вставьте график XYс помощью Графики –> Вставить график –> График XY.
2. Ведите имя функции (здесь y(x)) в первый местозаполнитель, имя переменной (здесь x) – во второй.
3. Щелкните вне области, чтобы построить график.

About Павел Демидов

Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.

View all posts by Павел Демидов →

Mathcad

Урок 6. Редактирование выражений в Mathcad

Урок 8. 2D-графики функций в Mathcad

Простейшие вычисления MathCAD

Во внутреннем представлении символы даны целыми числами. Конвертировать массив символов в числовую матрицу позволяет команда double. Обратная операция совершается по команде char. Печатаемые символы из стандартного набора ASCII представлены числами от 32 до 255. Объединить текстовые строки можно, просто заключив их в квадратные скобки или при помощи команды strcat. Приведем примеры для данных команд. Вначале введем строку:
>> s = \’Привет\’
s =
Привет
Отметим, что для ввода русских букв следует выбрать в меню File/ Preferences/ Command Windows Font шрифт с русской кодировкой. Теперь найдём коды введённых символов:
>> v = double(s)
v =
207 240 232 226 229 242
Объединим две строки:
>> h = [v + \’ от MATLAB\’]

v =
Привет от MATLAB
Тот же результат получится, если вместо переменной v использовать строковую переменную s. В завершение попробуем применить команду strcat. Для перевода численных данных в строковые переменные имеется ряд команд преобразования. В табл. 1. приведены некоторые команды для этих и обратных операций, а полных список можно получить по команде help strfun.
Таблица 1. Логические операции.
Имя команды

Действие
num2str

Перевод числа в строку
int2str

Перевод целого числа в строку
mat2str

Преобразование матрицы в строку
str2mat

Объединение строк в матрицу
str2num

Преобразование строки в число
strcat

Объединение строк

Приведём пример:
>> z=1.2e3; strcat(\’z=\’,num2str(z))
ans =
z=1200
Многомерные массивы

Массивы с числом размерностей более двух считаются многомерными. Такие массивы могут быть считаны из файла или созданы при помощи команд, таких как zeros, ones, rand. Число параметров при обращении к этим командам должно соответствовать размерности вводимого массива. Например, трёхмерный массив 2х4х2 из нулей будет организован по команде
>> S=zeros(2,4,2)
S(:,:,1) =
0 0 0 0
0 0 0 0
S(:,:,2) =
0 0 0 0
0 0 0 0
Обращение к элементам многомерного массива производятся по обычным правилам работы с массивами, так что действуют двоеточия для указания диапазона, а end обозначает максимальное значение данной размерности.

<< Назад   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 Вперед >>

Переменные диапазона » MathCadHelp.

com » Номер 1 в назначениях MathCad

Переменная диапазона — это переменная, которая принимает диапазон значений каждый раз, когда вы ее используете. В этой главе описываются переменные диапазона и показано, как использовать их для выполнения итерационных вычислений, отображения таблиц чисел и упрощения ввода многих значений данных в таблицу.

Данная глава состоит из следующих разделов.

Переменные диапазона
Как пройти через диапазон чисел путем определения диапазона

переменная.
Таблицы вывода
Как отобразить таблицу чисел.

Ввод таблицы чисел
Как использовать переменные диапазона для ввода таблицы чисел.

Итерационные вычисления
Как выполнить итерацию с одной или двумя переменными диапазона.

Итерация с заполнением
Как выполнить итерацию, когда значения на одном шаге зависят от значений на предыдущем шаге.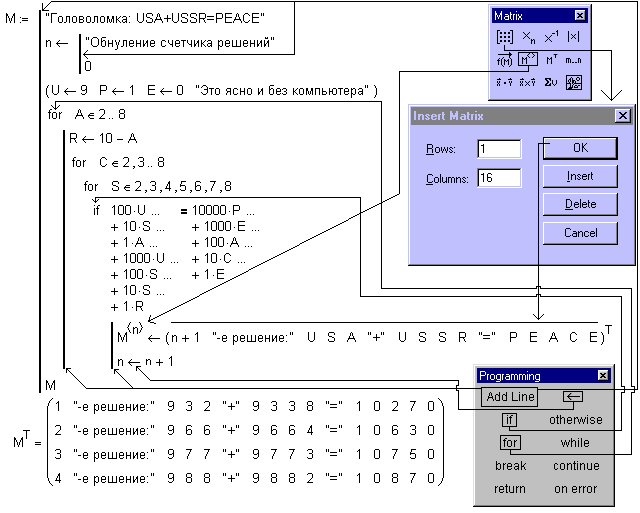 Подобные рекурсивные методы обеспечивают основу для решения разностных уравнений в Mathcad.
Нотация вектора или индекса
Когда использовать оператор «векторизации», а не индексы.

Переменные диапазона

Итерационные процессы в рабочих листах Mathcad зависят от переменных диапазона. За исключением способа определения, переменная диапазона выглядит так же, как обычная переменная. Разница в том, что обычная переменная принимает только одно значение. С другой стороны, переменная диапазона принимает диапазон значений, разделенных одинаковыми шагами. Например, вы можете определить переменную диапазона так, чтобы она изменялась от -4 до 4 с шагом 2. Если теперь вы используете эту переменную диапазона в выражении, Mathcad вычисляет это выражение пять раз, по одному разу для каждого значения, принимаемого переменной диапазона.

Переменные диапазона имеют решающее значение для максимально полного использования возможностей Mathcad.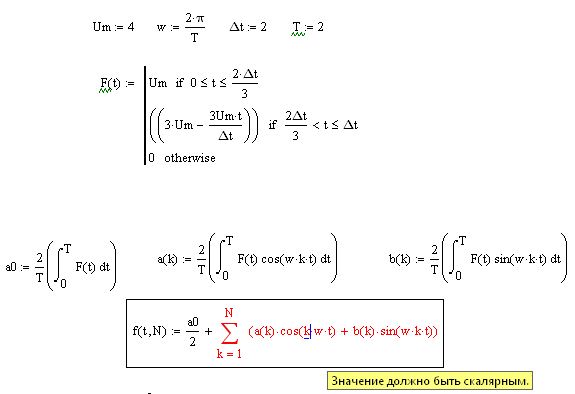 В этом разделе показано, как определить и использовать переменные диапазона для выполнения итерации. Чтобы получить описание
более сложных итерационных операций, которые стали возможными благодаря операторам программирования в Mathcad Professional, обратитесь к Главе 18, «Программирование».

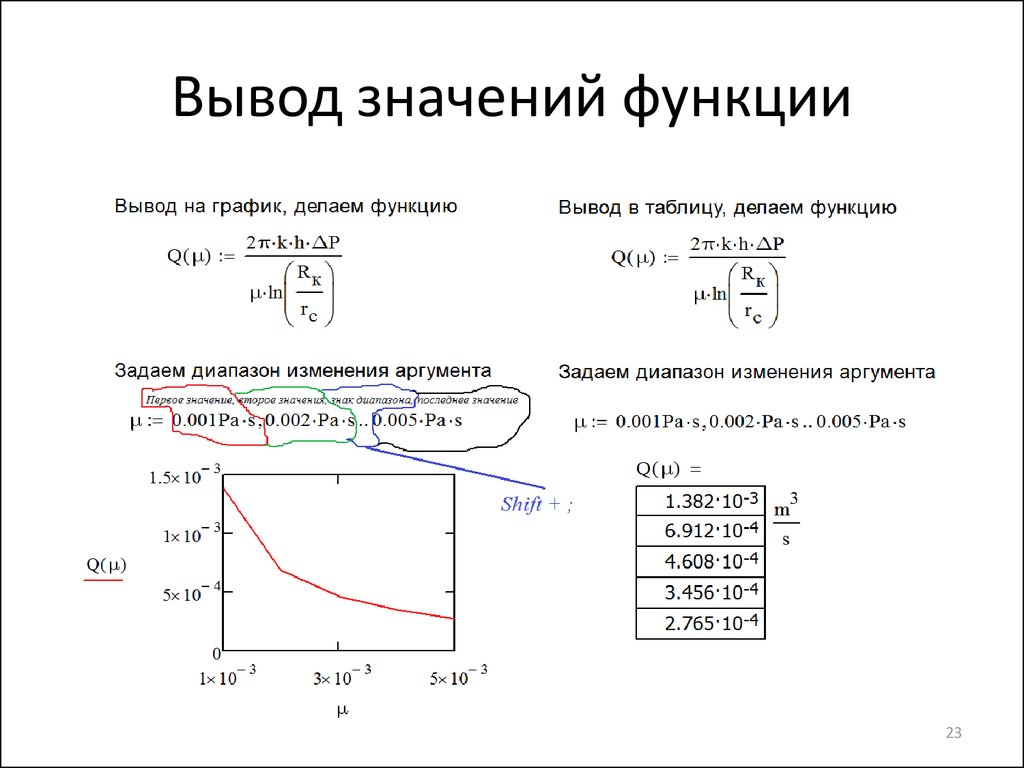
Определение и использование переменных диапазона

Чтобы определить переменную диапазона, введите имя переменной, затем двоеточие и диапазон значений. Например, вот как определить переменную} в диапазоне от 0 до 15

• Введите j, а затем нажмите клавишу двоеточия. Пустой заполнитель указывает, что mathcad ожидает определения для j. В этот момент mathcad не знает, должна ли j быть обычной переменной или переменной диапазона

Определение и использование переменных диапазона 1

Это определение указывает, что} теперь принимает значения 0,1,2 … 15. Чтобы определить переменную диапазона
, которая изменяется с шагом, отличным от 1, см. раздел «Типы диапазонов» на странице 216.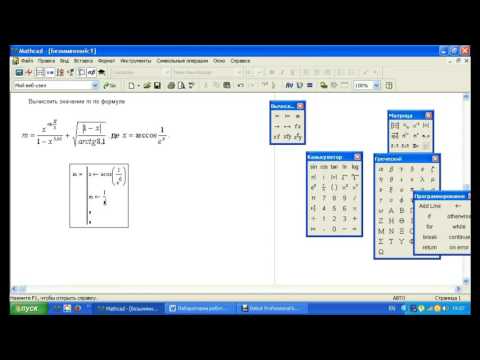

После определения переменная диапазона, она принимает полный диапазон значений каждый раз, когда вы ее используете. Например, если вы используете переменную диапазона в уравнении, Mathcad должен вычислить это уравнение один раз для каждого значения переменной диапазона.

Вы должны определить переменную диапазона точно так, как показано выше. Должны быть:

• имя переменной слева,
• либо «:=», либо «=» посередине и
• допустимый диапазон справа.

В частности, нельзя определить переменную в терминах переменной диапазона. Например, если после определения}, как показано, вы теперь определяете i=i + 1 , Mathcad предполагает, что вы пытаетесь установить скалярную переменную равной переменной диапазона, и помечает уравнение соответствующим сообщением об ошибке.

Одним из применений переменных диапазона является заполнение элементов вектора или матрицы. Вы можете определить векторные элементы, используя переменную диапазона в качестве нижнего индекса.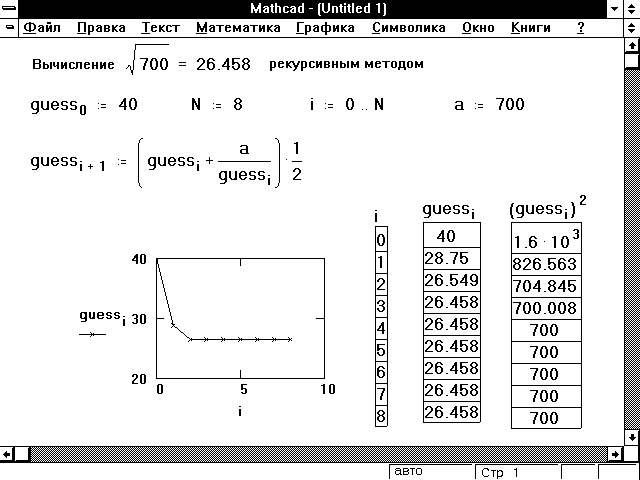 Например, чтобы определить Xj для каждого значения}:

• Введите x [ j : j A2[Пробел]+1.

Определение и использование переменных диапазона 2

На рис. 11-1 показан вектор значений, рассчитанный по этому уравнению. Поскольку} – это переменная диапазона, все уравнение оценивается один раз для каждого значения}. Это определяет Xj для каждого значения} от 0 до 15. Эффект точно такой же, как если бы вы набрали

Определение и использование переменных диапазона 3

Использование переменной диапазона для определения значений вектора x.

Чтобы понять, как Mathcad выполняет вычисления с переменными диапазона, помните об этом фундаментальном принципе:

Если вы используете переменную диапазона в выражении, Mathcad вычисляет выражение один раз для каждого значения переменной диапазона.

Этот принцип суммирует разницу между выражениями с переменными диапазона и без них. Выражения, не включающие переменные диапазона, имеют только одно значение.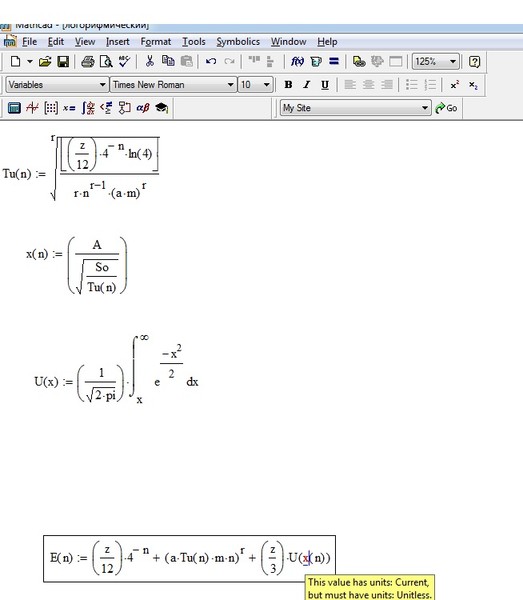 Выражения, включающие переменные диапазона, принимают множество значений, по одному для каждого значения каждой переменной диапазона.

Если вы используете две или более переменных диапазона в уравнении, Mathcad вычисляет уравнение один раз для каждого значения каждой переменной диапазона. В разделе «Итеративные расчеты» на странице 222 это обсуждается более подробно.

Mathcad требует больше времени для вычисления уравнений с диапазонными выражениями, так как для каждого уравнения выполняется много вычислений. Во время вычислений Mathcad указатель мыши меняет свой вид. Чтобы узнать, как прервать выполняемые вычисления, см. раздел «Прерывание вычислений» на странице 146.

Типы диапазонов

Определение j в предыдущем разделе, в диапазоне от 0 до 15, является самым простым типом определения диапазона. Mathcad допускает переменные диапазона со значениями в диапазоне от любого значения до любого другого значения, используя любое постоянное увеличение или уменьшение.

Чтобы определить переменную произвольного диапазона, введите уравнение следующего вида:

k:1,1.1;2

Это отображается в окне вашего документа как

K= 1, 1,1 .. 2

В этом определении диапазона :

• Переменная k — это имя самой переменной диапазона. Это должно быть простое имя. Никакие индексы или определения функций не допускаются.
• Число 1 — это первое значение, принимаемое переменной диапазона k.
• Число 1,1 является вторым значением в диапазоне. Обратите внимание, что это не размер шага. Размер шага в этом примере равен 0,1, это разница между 1,1 и 1. Если вы опустите запятую и 1,1, Mathcad примет размер шага, равный единице, в любом подходящем направлении (вверх или вниз).
• Число 2 является последним значением в диапазоне. В этом примере значения диапазона постоянно увеличиваются. Если вместо этого вы определили k := 10 .. 1 , тогда k будет отсчитывать от 10 до 1. Даже если третье число в определении диапазона не является четным числом приращений от начального значения, диапазон не выйдет за пределы это. Например, если вы определите k := 10, 20 .. 65, будут принимать значения 10, 20, 30 … 60.

Вместо 1, 1,1 и 2 можно использовать произвольные скалярные выражения. Однако эти значения всегда должны быть действительными числами. Комплексные числа не имеют смысла в определениях переменных диапазона, потому что для двух комплексных чисел существует бесконечное количество путей, соединяющих их. На рис. 11-2 показаны результаты различных определений переменных диапазона.

Некоторые допустимые определения для переменных диапазона.

Обратите внимание: если вы используете дробное приращение для переменной диапазона, вы не сможете использовать эту переменную диапазона в качестве нижнего индекса. Это связано с тем, что индексы должны быть целыми числами.

Массивы, даты и логические значения

Текстовые значения

Блок-значения могут быть текстом, как в обычных электронных таблицах (называемых строками в большинстве языков программирования).

Ввод текстовых значений

В ячейку электронной таблицы

Ввод текста в электронную таблицу или стол ячейке, просто введите текст.

Если ваш текст начинается со знака равенства, используйте апостроф в начале текста.

Это помечает ввод ячейки как текст, а не как формулу. Апостроф не будет включен в текстовое значение.

В формуле

Чтобы ввести текст в формулу, используйте кавычки в начале и в конце вводимого текста.

Допускаются как двойные, так и одинарные кавычки (апостроф).

Текстовые значения, указанные таким образом, можно использовать непосредственно в середине уравнений, или вы можете использовать их для определения именованных значений, которые затем можно использовать в уравнениях.

Экранирующие символы

Поскольку кавычки обозначают начало и конец текста, вы не можете использовать такой же знак внутри самого текста.

Например, 'Не пытайтесь' выдаст ошибку, потому что апострофы определяют текстовое значение, а один используется внутри текста.

Вместо этого вам нужно либо использовать обычные кавычки, чтобы указать текст (потому что они отличаются от апострофа, используемого внутри), или используйте escape-символ \ . Управляющий символ сообщает Blockpad, что следующий за ним символ следует интерпретировать как текст, а не как что-либо еще.

В качестве другого примера, для текста Он сказал: «Давайте сделаем это!» , escape-символ должен использоваться в любом стиле кавычек, используемом для указания текста.

Если вам нужно использовать символ \ в самом текстовом значении, то введите его дважды. Один раз как escape-символ, а затем еще раз как текст, который вы хотите использовать.

Управление текстовыми значениями

Конкатенация

Знак + работает как оператор конкатенации. Используйте его для объединения текстовых значений.

Текстовые функции

Для других текстовых манипуляций используйте текстовые функции. Вы можете найти список в текстовой функции раздел функций глубокое погружение.

В качестве примера ниже используются некоторые основные текстовые функции.

Арифметика даты и времени

Значения даты и расчеты поддерживаются в формулах Blockpad.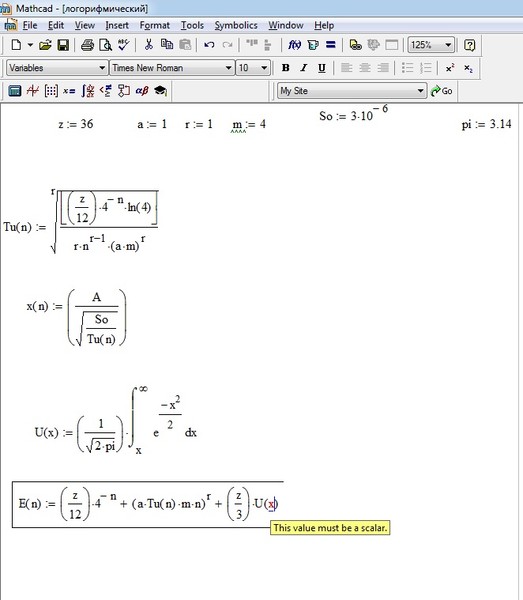

Введите дату

Основной синтаксис для ввода даты в формулу — гггг.мм.дд. Однако месяц или день можно ввести одной цифрой.

Например, дата 3 января 1892 года вводится как 1892.01.03. Вы также можете ввести дату, используя функцию Date(). Наш пример выше будет Date(1892,1,3).

Введите дату и время суток

Вы можете ввести дату и время, где гггг.мм.дд.чч.мм.сс — это синтаксис. При этом военное время необходимо использовать для п.м. раз.

Секунды, минуты или часы можно не указывать в конце, но необходимо указать год, месяц и дату. В противном случае Blockpad увидит обычное число с десятичной запятой.

Расчет даты и времени

Вы можете выполнять базовые вычисления со значениями даты и числами с единицами измерения времени. Таким образом, значение даты, вычтенное из значения даты, дает число времени.

Кроме того, число времени, добавляемое к значению даты или вычитаемое из него, дает значение даты.

Логические и логические значения

Логические тесты и функции в Blockpad аналогичны логическим операциям в обычных электронных таблицах.

Основное различие между обычными электронными таблицами заключается в том, что для проверки равенства используются два знака равенства. Кроме этого, это то же самое.

• == равно
• != не равно
• <> не равно (эквивалентно !=)
• < меньше
• > больше
• <= меньше/равно
• >= больше/равно

Вы можете изменить настройки математического макета чтобы эти операторы выглядели более традиционно при отображении в математической записи (например, ≠, ≤ и ≥). Обратите внимание, что операторы в формуле всегда те, что показаны выше, но вы можете изменить способ их отображения.

Вы можете использовать If() для выполнения логических вычислений if/then. If() в Blockpad работает так же, как If() в обычных электронных таблицах, но отображается в виде логической таблицы.

Вы также можете вводить логические значения (true или false) непосредственно в формулу.

Если несколько тестов используются подряд, то все они должны быть истинными по отдельности, чтобы получить истину.

Это то же самое, что использовать функцию And() для каждого теста отдельно.

Матрицы и массивы

Динамические уравнения Blockpad поддерживают массивы и матрицы. Многие встроенные функции также совместимы с матрицами.

Введите массив или матрицу

Для создания массива в формуле используются скобки. Скобки ([ ]) указывают начало и конец массива. Запятые (,) разделяют элементы одной строки на столбцы, а точка с запятой (;) указывает конец строки. Например, [11, 22, 33; 22, 33, 11; 33, 11, 22], введенные в формулу, дают приведенную ниже матрицу.

В Blockpad массивы и ссылки на группы ячеек обрабатываются одинаково. Итак, массивы можно создавать, ссылаясь на группу ячеек из электронной таблицы или таблицы. В этом случае массив будет обновляться вместе с таблицей.

Имена массивов

Значения массива могут иметь имена, как обычные числовые и текстовые значения.

Матричные расчеты

Для сложения, вычитания, деления и умножения матриц используются обычные операторы (+, -, /, *). 9-1) или используйте обратную функцию.

Если расчет матрицы не может быть завершен, вы получите сообщение об ошибке.

Матрицы также поддерживают единицы измерения и их отслеживание.

Функции работают и с массивами. Некоторые рассматривают массив как группу ячеек электронной таблицы.

А некоторые рассматривают массив как матрицу.

Массивы — больше, чем просто числа

Массивы могут иметь значения любого типа: текст, числа, массивы даже больше. все, что может быть в ячейке электронной таблицы и немного больше.

Полезным приложением является использование функций поиска с массивами, точно так же, как их использование с электронной таблицей.

Формулы массива в электронных таблицах

Массивы также могут отображаться в электронной таблице.

Создайте формулу массива:

1. Введите формулу, которая приведет к массиву.
2. Нажмите ctrl+shift+enter вместо ввода, чтобы завершить формулу.

Теперь, когда вы пытаетесь изменить любую ячейку в массиве, вам будет предложено изменить формулу массива. Однако вы по-прежнему можете ссылаться на ячейки, как обычно.

Если есть непустые ячейки, которые формула массива пытается заполнить, то формула все еще выполняется, но появляется красная линия, чтобы вы знали, что она не заполнила все ячейки.

Поиск скобок массива

Вы можете ссылаться на значения внутри массива, используя круглые скобки после имени массива. Базовый синтаксис — ArrayName(RowNumber, ColumnNumber).

Если вы дадите только одно число в скобках, то оно указывает строку. Вы можете указать столбец, набрав звездочку для строки. Это также работает, чтобы указать только строку, просто поставьте звездочку для столбца.

Расширенные функции массива

Есть ряд полезных функций для работы с массивами, большинство из них в библиотеке скриптов (Library.Scripts), который не включается автоматически в файлы Blockpad. Для доступа к ним необходимо использовать полное имя библиотеки, создать ярлык, или включить библиотеку в файл.

В этих примерах библиотека скриптов включена в файл, поэтому ниже приведены инструкции, как это сделать.

Включить библиотеку сценариев:

1. На панели инструментов выберите Библиотека > Включить библиотеки .
2. Нажмите Добавить в появившемся окне.
3. Выберите Скрипты .
4. Нажмите «ОК».
5. Щелкните Закрыть, чтобы выйти из окна включения библиотек.

Ниже мы рассмотрим следующие функции:

LinearSeries()	Создает одномерный массив с заданными началом, концом и интервалом.
Личность()	Возвращает матрицу идентификации с заданным размером.
Каждый()	Выполняет функцию для каждого элемента массива.
Каждая строка()	Выполняет функцию для каждой строки массива.
Каждая колонка()	Выполняет функцию для каждого столбца в массиве.
Где()	Возвращает одномерный массив элементов, соответствующих заданным критериям.
Первый()	Возвращает первый элемент массива, соответствующий указанным критериям.
Последний()	Возвращает первый элемент массива, соответствующий указанным критериям.
ConcatRows()	Объединяет массивы вертикальной укладкой.
ConcatColumns()	Объединяет массивы по горизонтали.
ConcatItems()	Объединяет массивы в одномерный массив.

Использование LinearSeries() и Identity()

Функция LinearSeries() относительно проста. Укажите начало массива, конец массива и интервал шагов между ними.

Identity() еще проще. Просто укажите размер (n) матрицы, и функция создаст единичную матрицу размера n x n.

Использование функции Every().

Функция Every() выполняет указанную функцию для каждого элемента в массиве, а затем возвращает его как новый массив. Выглядит так: Каждый( Массив , Встроенная функция для выполнения ) .

В приведенном выше примере каждый элемент массива A_4 возведен в квадрат. Обратите внимание на встроенную функцию. Для Each() (и многих других формул массива) встроенная функция следует этой форме nameForItem => формула с использованием nameForItem . Обратите внимание, что вы называете nameForItem , поэтому пример ниже работает так же, как пример выше.

Ниже приведен еще один пример. Обратите внимание, что в функции могут использоваться внешние значения, в данном случае давление.

EachRow() и EachColumn() похожи на функцию Every(), но они работают со строками и столбцами, а не с отдельными элементами. Настройка такая же, включая использование встроенных функций, но встроенная функция работает с одномерным массивом (строкой или столбцом).

Обратите внимание, что поскольку EveryRow() и EachColumn() действуют на строки/столбцы как на массивы, вывод может быть массивом массивов, как в примере ниже.

Использование функций Where(), First() и Last().

Where(), First() и Last() используются для поиска определенных значений в массиве, и все они следуют одному и тому же шаблону. Сначала рассмотрим функцию Where(), наиболее общую.

Where() находит все элементы в массиве, соответствующие критериям, и возвращает их в виде одномерного массива. Выглядит это так: Где( Массив , Функция критериев ) .

Функция критериев обычно состоит только из логического оператора (==, >, <, <= или >=) и значения.

На самом деле это сокращение для встроенной функции (о чем говорилось выше). Вы также можете указать критерии, используя формулу формы nameForItem => , используя nameForItem . Где формула имеет логический результат. Примеры ниже делают то же самое, что и выше.

В большинстве случаев вам это не нужно, но это дает больше возможностей. В приведенном ниже примере функция Where() используется для фильтрации недлинных единиц.

Функции First() и Last() аналогичны функции Where(), но возвращают одно значение вместо массива. Это как если бы вы выполнили функцию Where(), а затем сохранили только первое (или последнее) значение из массива.

Вы также можете использовать First() и Last() без критериев.