Mathcad разложение в ряд фурье: Разложение функции в гармонический ряд фурье mathcad. Ряды MathCAD

2.7.2. Разложение в ряд Тейлора в системе Mathcad

В системе Mathcad разложение в отрезок ряда Тейлора возможно в режиме символьных вычислений, как в командном режиме, так и с помощью символьной функции series. Шаблон этой функции имеет три места ввода — для разлагаемого выражения, для имени переменной, по которой ведется разложение, и для числа возможных членов ряда n. Он также содержит оператор символьного ввода .

П ример 2.31. Вычислить разложение в отрезки ряда Маклорена (в окрестности точки x=0) следующих выражений sin(x), exp(x) и 2^x:

О

.

братите внимание на то, что некоторые из возможных членов ряда могут отсутствовать, но они входят в число n. Например, ряд для синуса содержит только члены с нечетными номерами.

.

Пример 2.32. Вычислить разложение в отрезок ряда Тейлора выражения ln(x) в окрестности точки

x=1:

О братите внимание на то, что в этом случае вместо x надо записывать x=1, используя жирный знак равенства.

Пример 2.33. Самостоятельно постройте график функции sin(x) и графики трех разложений синуса в окрестности точки x=0 для n=3, 5 и 7. Убедитесь в том, что разложение приближается к исходной функции только при малых отклонениях от точки разложения и очень сильно отклоняется от нее вдали от нее.

К фундаментальным положениям математики относится возможность представления периодических (а при определенных условиях и непериодических) функций и сигналов совокупностью их синусоидальных (гармонических) составляющих в виде так называемого ряда Фурье. Эта возможность используется во множестве прикладных областей, достаточно отметить, что на ее основе реализуется передача через каналы связи практически любой информации, например речи или музыки, и ее эффективная

фильтрация (выделение нужной информации и отсев шумов) [16].

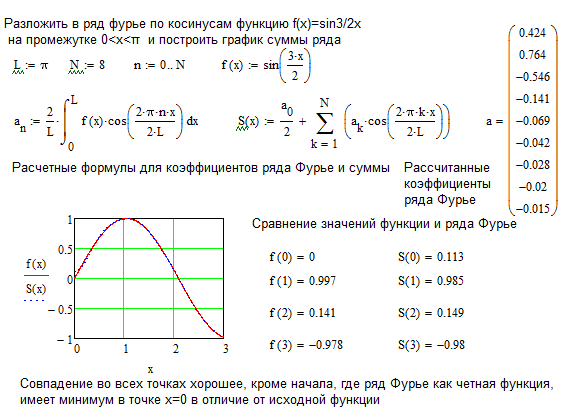
Рядом Фурье для интегрируемой на отрезке [-, ] функции y(x), удовлетворяющей известным условиям Дирихле (конечное число разрывов и непрерывность функции между ними), называют следующий ряд:

.

Коэффициенты Фурье этого ряда находятся по формулам Эйлера-Фурье:

.

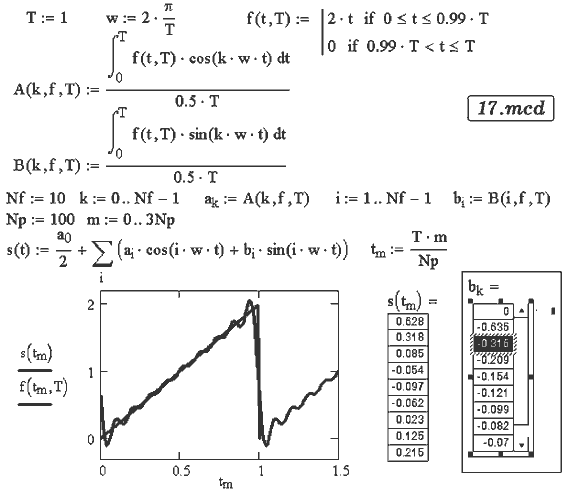
Важными сферами применения рядов Фурье являются радиотехнические расчеты. В них периодические сигналы обычно представляют как функции времени y(t) на отрезке [0, T] с периодом T = 1/f₁, где f₁ — частота первой гармоники периодического сигнала. В этом случае ряд Фурье после несложных преобразований записывается в виде

.

Здесь коэффициенты выглядят следующим образом:

.

В этом случае коэффициенты a_k и b_k описывают косинусную и синусную составляющие k-й гармоники сигнала с периодом T и частотой повторения f₁ = 1/T. Часто используется иная форма ряда Фурье, упрощающая его синтез:

.

Здесь A_k — амплитуда k-й гармоники периодического сигнала, j_k — фаза k-й гармоники. Они вычисляются по формулам:

.

Разложение функции на гармонические составляющие, то есть вычисление коэффициентов Фурье, принято назвать спектральным анализом. А воссоздание приближения функции рядом Фурье, то есть получение ее тригонометрического представления, называют спектральным синтезом.

Гармонику с k = 1 называют основной, или первой гармоникой сигнала. Она задает его частоту повторения f₁. Остальные гармоники называют высшими, их частоты равны f_k = k·f₁, где k = 2, 3, … . Таким образом, спектр периодических сигналов дискретный — он содержит набор фиксированных частот f_k, где k = 1, 2, 3, … . У непериодических сигналов спектр будет сплошным, и вместо амплитуды гармоник он характеризуется спектральной плотностью сигнала.

3.5.1. Разложение в ряд при помощи меню MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1216 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• MathCAD 12

• Дифференцирование
• 3.1. Аналитическое дифференцирование
  • 3.1.1. Аналитическое дифференцирование функции
  • 3.1.2. Вычисление производной функции в точке
  • 3.1.3. Определение функций пользователя через оператор дифференцирования
  • 3.1.4. Дифференцирование при помощи меню
• 3.2. Численное дифференцирование
  • 3.2.1. Дифференцирование в точке
  • 3.2.2. Об алгоритме дифференцирования
• 3.3. Производные высших порядков
• 3.4. Частные производные
  • 3.4.1. Частные производные
  • 3.4.2. Примеры: градиент, дивергенция и ротор
  • 3.4.3. Пример: якобиан
• 3.5. Разложение функции в ряд Тейлора
  • 3.5.1. Разложение в ряд при помощи меню
  • 3.5.2. Оператор разложения в ряд

Чтобы разложить некоторое выражение в ряд:

1. Введите выражение.

2. Выделите значение переменной, по которой требуется получить разложение в ряд.

3. Выполните команду Symbolics / Variable / Expand to Series (Символика / Переменная / Разложить в ряд) (рис. 3.12).

Рис. 3.12. Аналитическое разложение выражения в ряд по переменной х

4. В появившемся диалоговом окне Expand to Series (Разложить в ряд) введите желаемый порядок аппроксимации (Order of Approximation) и нажмите кнопку ОК.

Результат разложения появится под выражением (он показан на рис. 3.12, внизу).

ПРИМЕЧАНИЕ

Не забывайте, что разложение строится только в точке х=0. Чтобы получить разложение в другой точке х=а, можно, к примеру, подставить вместо переменной х значение х-а.

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9981 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6993 0

Глава 2 Работа с файлами Mathcad 11

12567 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.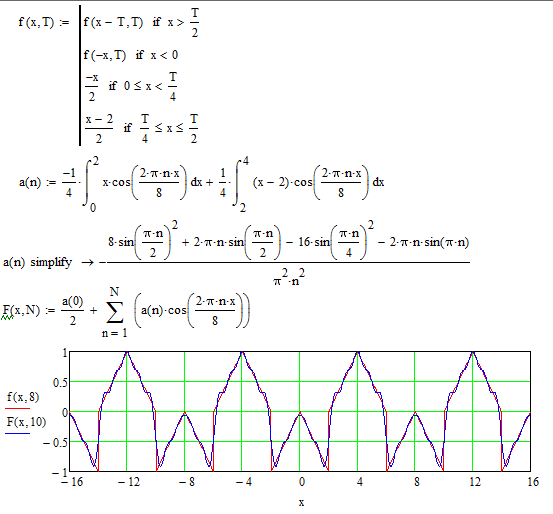

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2377 s

Введение в ряды Фурье

Введение в ряды Фурье

НЕПРЕРЫВНЫЙ РЯД ФУРЬЕ   ПРЕДВАРИТЕЛЬНЫЕ ТРЕБОВАНИЯ И ЗАДАЧИ Предпосылки для непрерывного Фурье Серия [PDF] [ДОК] Цели непрерывного Фурье Ряд [PDF] [ДОК] ГЛАВА УЧЕБНИКА Глава учебника по непрерывному Ряд Фурье [PDF] [ДОК] jpg»> ЦИФРОВОЕ АУДИОВИЗУАЛЬНОЕ ЛЕКЦИИ   Непрерывный ряд Фурье: часть 1 из 2 [ЮТУБ 9:41] Непрерывный ряд Фурье: часть 2 из 2 [ЮТУБ 7:40] Непрерывный ряд Фурье: Пример: Часть 1 из 2 [ЮТУБ 9:33] Непрерывный ряд Фурье: Пример: Часть 2 из 2 [ЮТУБ 9:06] Комплексная форма ряда Фурье: Часть 1 из 2 [ЮТУБ 15:05] Комплексная форма ряда Фурье. Часть 2 из 2 [ЮТУБ 13:42] ПРЕЗЕНТАЦИИ Презентация непрерывных рядов Фурье в PowerPoint [PDF] [ППТ] РАБОЧИЕ ЛИСТЫ Рабочий лист непрерывного Фурье Серия   [MATLAB] [МАТКАД] [МАТЕМАТИКА] МНОЖЕСТВЕННЫЙ ТЕСТ Проверьте свои знания о непрерывном Фурье Ряд [HTML] [ВСПЫШКА] [PDF] [ДОК] АНЕКДОТЫ Промышленный инжиниринг — прогнозирование сезонного спроса [PDF] [ДОК] jpg»> СВЯЗАННЫЕ ТЕМЫ Введение в ряд Фурье Пара быстрого преобразования Дискретные преобразования Фурье Неформальная разработка пары быстрых преобразований > Дом > Быстрый Преобразование Фурье

АУДИТОРИЯ | НАГРАДЫ | ЛЮДИ | ТРЕК | РАСПРОСТРАНЕНИЕ | ПУБЛИКАЦИИ
Авторские права: Университет Южной Флориды, 4202 E Fowler Ave, Tampa, FL 33620-5350. Все права защищены. Вопросы, предложения или комментарии, контакт [email protected] Этот материал основан на работе, поддержанной Национальным научным фондом. по гранту # 0126793, 0341468, 0717624 , 0836981, 0836916 , 0836805, 1322586. Любые мнения, выводы и заключения или рекомендации, изложенные в этом материале, являются рекомендациями автор(ы) и не обязательно отражают взгляды Национального научного фонда. Другой спонсоры включают Maple, MathCAD, USF, FAMU и MSOE. На основе работы в http://mathforcollege.com/nm. Целостные численные методы лицензированы под Лицензия Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported.		АНАЛИТИКА

Введение в ряды Фурье

Введение в ряды Фурье

Целостные численные методы Трансформация Численные методы Educa для STEM Бакалавриат
МООК | МОБИЛЬНЫЙ | ВИДЕО | БЛОГ | ЮТУБ | Твиттер | КОММЕНТАРИИ | АНАЛИТИКА | О КОМПАНИИ | КОНТАКТЫ | САЙТЫ КУРСОВ | КНИГИ | МАТЕМАТИКА ДЛЯ КОЛЛЕДЖА

ВВЕДЕНИЕ В СЕРИИ ФУРЬЕ ПРЕДВАРИТЕЛЬНЫЕ ТРЕБОВАНИЯ И ЗАДАЧИ Предпосылки для знакомства с Ряд Фурье [PDF] [ДОК] Цели введения в Фурье Ряд [PDF] [ДОК] УЧЕБНИК ГЛАВА Глава учебника по введению в Ряд Фурье [PDF] [ДОК] jpg»> ЦИФРОВОЕ АУДИОВИЗУАЛЬНОЕ ЛЕКЦИИ   Введение в ряды Фурье: Часть 1 из 2 [ЮТУБ 10:36] Введение в ряды Фурье: часть 2 из 2 [ЮТУБ 8:32] ПРЕЗЕНТАЦИИ Презентация PowerPoint «Введение в ряды Фурье» [PDF] [ППТ] СВЯЗАННЫЕ ТЕМЫ Непрерывный ряд Фурье Пара быстрого преобразования Дискретные преобразования Фурье Неформальная разработка пары быстрого преобразования > Дом > Быстрый Преобразование Фурье

АУДИТОРИЯ | НАГРАДЫ | ЛЮДИ | ТРЕК | РАСПРОСТРАНЕНИЕ | ПУБЛИКАЦИИ

Авторские права: Университет Южной Флориды, 4202 E Fowler Ave, Tampa, FL 33620-5350. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт