Реферат на тему «Программирование в MathCAD»
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ
ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М. Е. ЕВСЕВЬЕВА»
Физико-математический факультет
Кафедра информатики и вычислительной техники
Реферат
Программирование в MathCAD
Автор работы __________________________________________ М. С. Юрьева
Направление подготовки 44.03.05 Педагогическое образование
Профиль Информатика. Математика
Проверила________________________________________Т. В. Кормилицына
Оценка ________
Саранск 2020
Содержание
Введение 3
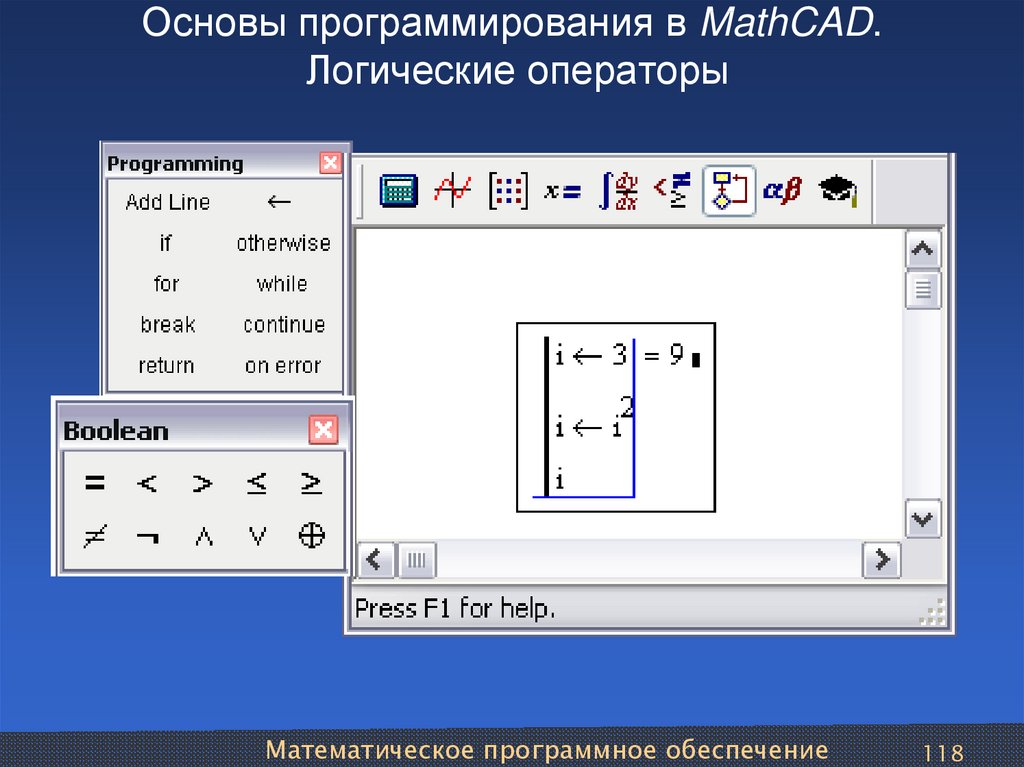
Основы программирования в MathCAD 4
Условные конструкции в MathCAD 8
Циклические конструкции в MathCAD 10
Операторы break и continue 13
Оператор return (возврат значения) 15
Обработка ошибок 16
Заключение 18
Список использованных источников 19
Введение
MathCAD – это система, ориентированная на пользователя, который не обязан знать абсолютно ничего о программировании. Создатели MathCAD изначально поставили перед собой такую задачу, чтобы дать возможность профессионалам – математикам, физикам и инженерам самостоятельно проводить сложные расчеты, не обращаясь за помощью к программистам. Несмотря на блестящее воплощение этих замыслов, выяснилось, что совсем без программирования MathCAD серьезно теряет в своей силе, в основном, из-за недовольства пользователей, знакомых с техникой создания программ.
Создатели MathCAD изначально поставили перед собой такую задачу, чтобы дать возможность профессионалам – математикам, физикам и инженерам самостоятельно проводить сложные расчеты, не обращаясь за помощью к программистам. Несмотря на блестящее воплощение этих замыслов, выяснилось, что совсем без программирования MathCAD серьезно теряет в своей силе, в основном, из-за недовольства пользователей, знакомых с техникой создания программ.
В очень ранних версиях MathCAD встроенного языка программирования не было. Чтобы применять привычные операции проверки условий и организовывать циклы, приходилось изобретать причудливую смесь из встроенных функций if и until, а также комбинаций ранжированных переменных. Но надо отметить, что использование ранжированных переменных – мощный аппарат MathCAD, похожий на применение циклов в программировании. В подавляющем большинстве случаев намного удобнее организовать циклы с помощью ранжированных, чем заниматься для этого программированием.
И тем не менее встроенный язык программирования MathCAD позволяет решать самые различные, в том числе и довольно сложные, задачи и является серьезным подспорьем для расчетов. Поэтому последние версии MathCAD имеют не очень мощный, но весьма элегантный собственный язык программирования.
Основы программирования в MathCAD
Для вставки программного кода в документы MathCAD имеется специальная панель инструментов. Большинство кнопок этой панели выполнено в виде текстового представления операторов программирования, поэтому их смысл легко понятен. Операторы программирования могут быть введены только с этой панели, но никак не с клавиатуры (можно еще их вводить с помощью сочетаний клавиш, которые приведены в тексте всплывающей подсказки).
Создание программного блока начинается с команды . Нажатие этой клавиши приведет к тому, что в рабочей области документа появится вертикальная черта, а справа от нее – два пустые поля ввода .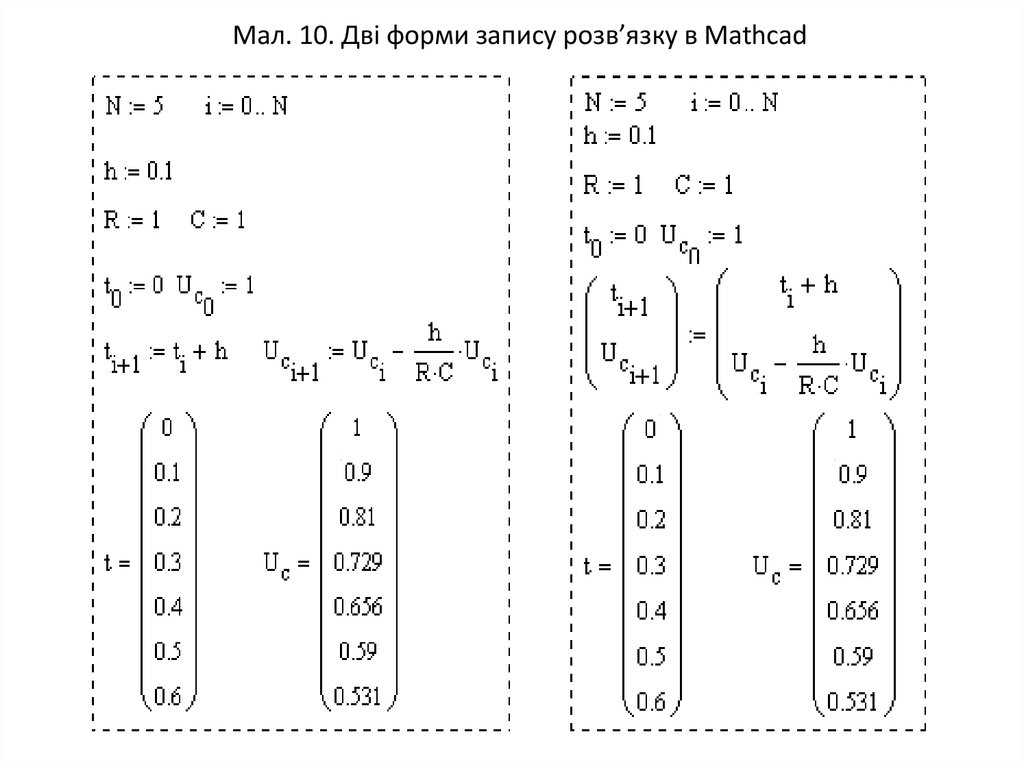 Вертикальная черта означает, что строки, находящиеся справа от нее, образуют линейную программную последовательность операций. Эта черта является особенностью программ MathCAD. В полях ввода можно ввести две первые строки программы, а если требуется большее число строк, то необходимо нажимать клавишу столько раз, сколько необходимо строк. Не стоит забывать, что программа является полноценным выражением MathCAD. Это выражение может быть использовано для присвоения значения скалярной или векторной переменной или определения функции, или даже в составе другого выражения, в том числе и другой программы.
Вертикальная черта означает, что строки, находящиеся справа от нее, образуют линейную программную последовательность операций. Эта черта является особенностью программ MathCAD. В полях ввода можно ввести две первые строки программы, а если требуется большее число строк, то необходимо нажимать клавишу столько раз, сколько необходимо строк. Не стоит забывать, что программа является полноценным выражением MathCAD. Это выражение может быть использовано для присвоения значения скалярной или векторной переменной или определения функции, или даже в составе другого выражения, в том числе и другой программы.
Для определения функции это будет выглядеть следующим образом:
Внутри программы можно использовать глобальные переменные документа, но изменить их значение внутри программы никак нельзя. Можно создать в программе другие переменные, доступ к которым может осуществляться только из самой программы. Эти переменные называются локальными переменными. Локальные переменные «не видны» извне. Локальная переменная создается с помощью знака локального присвоения с панели Programming. Для оператора локального присваивания, так же как и для операторов обычного и глобального присваивания, можно изменить внешний вид так, чтобы он выглядел как обычный знак равенства. Для этого достаточно вызвать контекстное меню этого оператора и в нем выбрать команду View Definition As/Equal.
Эти переменные называются локальными переменными. Локальные переменные «не видны» извне. Локальная переменная создается с помощью знака локального присвоения с панели Programming. Для оператора локального присваивания, так же как и для операторов обычного и глобального присваивания, можно изменить внешний вид так, чтобы он выглядел как обычный знак равенства. Для этого достаточно вызвать контекстное меню этого оператора и в нем выбрать команду View Definition As/Equal.
Последняя строка любой программы не должна содержать никаких управляющих операторов. Эта строка задает значение, возвращаемое программой. В качестве этого значения может быть скаляр (число или переменная), вектор или матрица. Таким образом, последняя строка программы может содержать имя локальной переменной либо некоторое математическое выражение, куда входят как локальные, так и глобальные переменные, либо вектор или матрицу.
Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки Add Line. Для этого следует поместить на нужное место внутри программы линии ввода.
Для этого следует поместить на нужное место внутри программы линии ввода.
Если вертикальная линия ввода находится в начале текущей строки, то нажатие кнопки приведет к появлению новой строки перед текущей строкой, если вертикальная линия ввода находится в конце строки, то нажатие кнопки приведет к появлению новой строки после текущей. Можно выделить только часть текущей строки, что повлияет на положение новой строки в программе (например, если необходимо для некоторого условия выполнить не одно действие, а несколько). Таким образом, основной принцип создания программных модулей заключается в правильном расположении строк кода. Ориентироваться в их действии довольно легко, т.к. фрагменты кода одного уровня сгруппированы в программе с помощью вертикальных черт.
Условные конструкции в MathCAD
Программы в MathCAD могут быть не только линейными, но и разветвленными. Одним из вариантов ветвления в программах является проверка условия. Условия могут проверять значения как локальных, так и глобальных переменных, а также выражений, содержащих эти переменные.
Одним из вариантов ветвления в программах является проверка условия. Условия могут проверять значения как локальных, так и глобальных переменных, а также выражений, содержащих эти переменные.
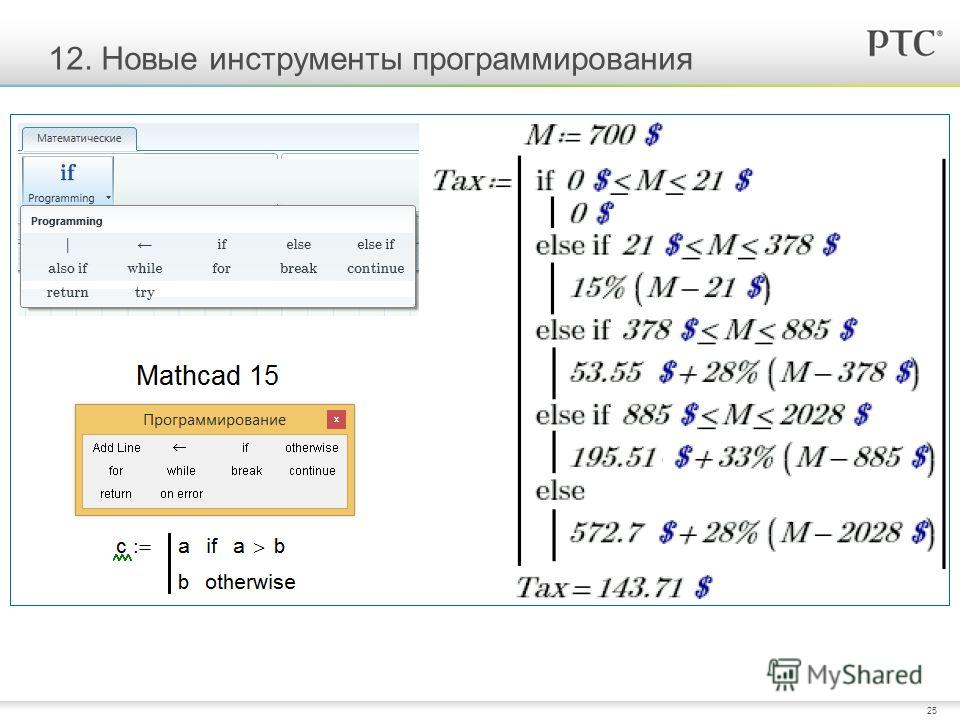
Для проверки условий в программах MathCAD служит оператор if . В поле ввода справа нужно ввести условие. Для ввода условий служит панель Boolean. На этой панели есть кнопки, предназначенные для проверки условий , а также кнопки, предназначенные для вставки логических операций (логическое отрицание, операция «и», операция «или», операция «исключающее или»). Вторые позволяют создавать сложные условия. В поле ввода слева нужно ввести строку программы, которая должна выполняться, если введенное условие истинно.
Если для условия «истинно» необходимо выполнение нескольких строк программы, надо воспользоваться кнопкой .
Если невыполнение условия должно привести к выполнению какого-либо иного программного кода, можно в строке, следующей за оператором if, вставить оператор . В поле ввода слева от этого оператора необходимо ввести строку программы, которая будет выполняться только в том случае, если не выполнилось условие, заданное в операторе if.
В поле ввода слева от этого оператора необходимо ввести строку программы, которая будет выполняться только в том случае, если не выполнилось условие, заданное в операторе if.
Следует помнить, что если в программе введено подряд несколько строк с оператором if , то выражение слева от оператора otherwise будет выполнено только в том случае, если не выполняются условия, заданные во всех операторах if.
Примеры:
Циклические конструкции в MathCAD
Другим очень важным элементом при создании нелинейных программ являются циклы. Циклы позволяют повторять несколько раз выполнение одного и того же программного блока. Для создания циклов в MathCAD предусмотрено два оператора for и while.
Цикл for – цикл со счетчиком.
В таких циклах создается некоторая переменная-счетчик, значение которой изменяется после каждого выполнения тела цикла. Выход из цикла происходит при достижении этой переменной заданного значения. Этот оператор вводится с панели Programming клавишей for . В поле ввода после слова for следует указать имя переменной – счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения. В поле ввода после знака следует указать диапазон значений переменной-счетчика. Вводить диапазон в данном случае следует так же, как и при создании ранжированной переменной. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В этом случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Возможность перебора элементов массива не может быть реализована с помощью цикла while, поэтому именно в таких случаях цикл for и является незаменимым. В поле ввода под словом for следует ввести тело цикла.
Выход из цикла происходит при достижении этой переменной заданного значения. Этот оператор вводится с панели Programming клавишей for . В поле ввода после слова for следует указать имя переменной – счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения. В поле ввода после знака следует указать диапазон значений переменной-счетчика. Вводить диапазон в данном случае следует так же, как и при создании ранжированной переменной. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В этом случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Возможность перебора элементов массива не может быть реализована с помощью цикла while, поэтому именно в таких случаях цикл for и является незаменимым. В поле ввода под словом for следует ввести тело цикла.
Пример. Заполнить вектор числами от xнач до xкон с шагом h. Затем определить сумму элементов этого вектора и найти их среднее арифметическое значение.
Цикл while – цикл, который выполняется до тех пор, пока выполняется определенное условие.
В поле ввода справа от слова while следует ввести условие. Это условие строится по тем же правилам, что и в операторе if. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится. В поле ввода ниже слова while следует ввести тело цикла (напомним, что для ввода нескольких строк в теле цикла надо воспользоваться кнопкой Add Line).
Пример 1. Вычислить сумму с точностью е.
Пример 2. Найти первый элемент, превышающий определенный порог.
Операторы break и continue
Иногда возникает необходимость повлиять на выполнение цикла некоторым образом, например, прервать его выполнение по какому-либо условию или выполнять некоторые итерации не так, как другие. Для этого и служат операторы break и continue.
Для этого и служат операторы break и continue.
Оператор break, если он расположен внутри цикла, означает немедленное прекращение выполнения текущей итерации и выход из цикла. Если есть необходимость прекратить выполнение цикла по какому-либо условию, то следует использовать конструкцию следующего вида break if (условие).
Пример. Выделить из массива все элементы от начала и до первого вхождения в него заданного числа.
Оператор continue используется для того, чтобы немедленно перейти в начало цикла и начать следующую итерацию. Этот оператор также обычно используется в составе конструкции вида continue if (условие). Оператор continue используется в случаях, когда необходимо чтобы некоторые вычисления производились для одних итераций и не производились для других.
Пример. Требуется заполнить элементы квадратной матрицы в шахматном порядке.
Оператор return (возврат значения)
Как мы уже указывали, результат выполнения программного модуля помещается, как правило, в последней его строке. Но можно прервать выполнение программы в любой ее точке (например, с помощью условного оператора) и выдать некоторое значение, применив оператор return. В этом случае при выполнении указанного условия значение, введенное в поле ввода после return, возвращается в качестве результата, и никакой другой код больше не выполняется. Вставляется в программу оператор return с помощью одноименной кнопки панели Programming.
Но можно прервать выполнение программы в любой ее точке (например, с помощью условного оператора) и выдать некоторое значение, применив оператор return. В этом случае при выполнении указанного условия значение, введенное в поле ввода после return, возвращается в качестве результата, и никакой другой код больше не выполняется. Вставляется в программу оператор return с помощью одноименной кнопки панели Programming.
Пример.
Обработка ошибок
Система MathCAD предоставляет пользователю некоторый контроль над ошибками, которые могут возникнуть при вычислении выражений или при выполнении программ. Для этой цели служит оператор on error, который можно вставить с помощью одноименной кнопки панели Programming. В поле ввода справа следует ввести выражение или программу, которые необходимо вычислить (известно, что это выражение может содержать ошибку при определенных значениях входных параметров).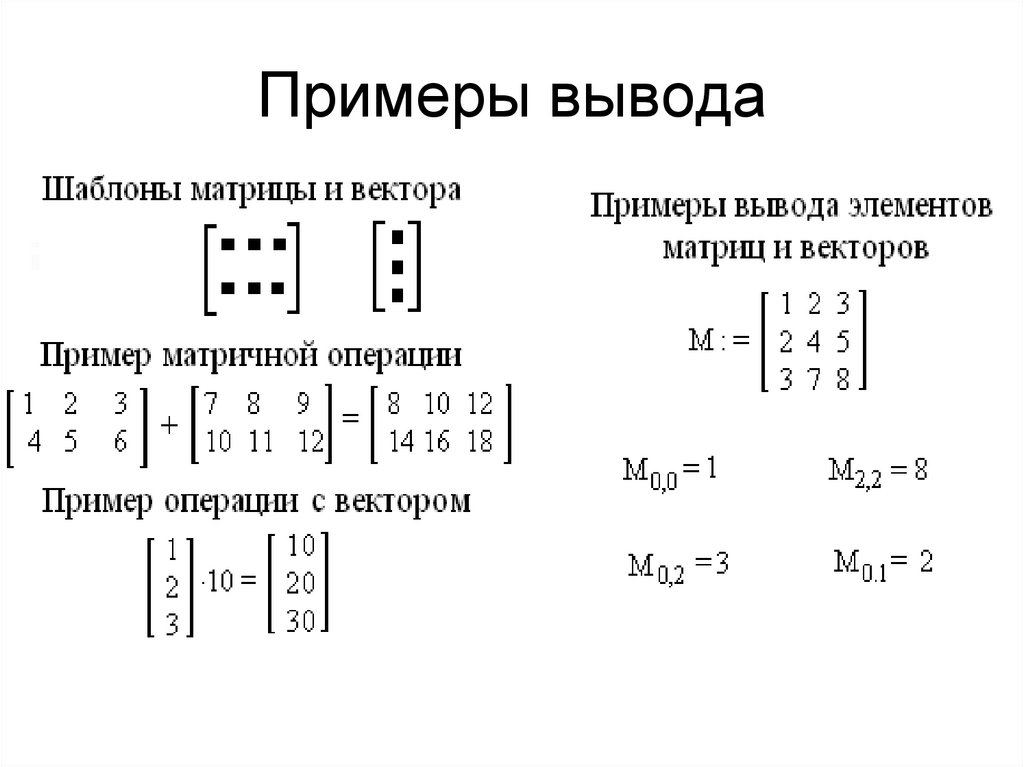 В поле ввода слева следует ввести выражение, которое будет выполнено вместо правого выражения, если при выполнении последнего возникнет ошибка.
В поле ввода слева следует ввести выражение, которое будет выполнено вместо правого выражения, если при выполнении последнего возникнет ошибка.
Пример. Если аргументу функции присвоено нулевое значение, то в программе возникает ошибка – деление на нуль. Но за счет оператора on error сообщение не выводится, а функции в этой точке присваивается значение, указанное слева от оператора on error – значение машинной бесконечности.
В поле ввода слева может быть введено текстовое выражение, сообщающее об ошибке
Конечно, если программа содержит только простейшие математические операции, то никаких ошибок, кроме деления на нуль или превышения наибольшего допустимого числа в ней возникнуть не может. В таких программах оператор on error используется редко. Но для более сложных программ, которые содержат функции решения дифференциальных уравнений, аппроксимации или другие сложные функции MathCAD, использование on error может избавить от многих трудностей.
Иногда может возникнуть ситуация обратная той, которая была описана выше, т.е. необходимо, чтобы при определенных условиях результатом выражения было сообщение об ошибке, хотя в действительности при этом не возникает ни одной стандартной ошибки MathCAD. Для таких случаев в MathCAD предусмотрена встроенная функция error. В качестве аргумента этой функции нужно в кавычках указать текст сообщения об ошибке, который должен быть выведен. Таким образом, если необходимо, чтобы программа возвращала ошибку при определенном условии, то следует использовать конструкцию вида: error («текст ошибки») if (условие).
Пример.
Для того, чтобы иметь возможность нормально вводить текст на русском языке в аргумент функции error (а также во все другие функции со строками), следует изменить шрифт, который используется во встроенном стиле Constant. Для того чтобы этот стиль правильно отображал русские буквы, установите курсор на любом числе или строковом выражении в формульном блоке. При этом в поле на панели инструментов Formatting, отображающем текущий стиль, должно быть написано – Constant. Теперь выберите из раскрывающегося списка шрифтов шрифт, поддерживающий кириллицу.
При этом в поле на панели инструментов Formatting, отображающем текущий стиль, должно быть написано – Constant. Теперь выберите из раскрывающегося списка шрифтов шрифт, поддерживающий кириллицу.
Заключение
MathCAD является главной математической системой для большинства пользователей. Ее отличает простота, удобный пользовательский интерфейс и тщательно продуманные, отобранные и ориентированные на нужды большинства пользователей математические возможности, а также отсутствие избыточных функций. Оставаясь по-прежнему мощной системой для численных расчетов, MathCAD позволяет выполнять и большинство символьных операций, т.е. стала полноценной системой компьютерной алгебры. Для этого по лицензии фирмы Maple в систему MathCAD было введено несколько урезанное ядро символьных операций от системы Maple. Число таких операций тщательно оптимизировалось, и было ограничено тем разумным минимумом, который необходим массовому пользователю. Тем не менее, символьные и другие возможности системы расширялись и расширяются от версии к версии.
Тем не менее, символьные и другие возможности системы расширялись и расширяются от версии к версии.
Список использованных источников
Макаров Е.Г. Инженерные расчеты в Mathcad 15. Учебный курс [Текст] / Макаров Е.Г. М: Питер, 2011. — 400 стр. ISBN 978-5-459-00357-4.
Охорзин В.А. Прикладная математика в системе Mathcad [Текст] / Охорзин В.А. — М: Лань, 2009. — 352 стр. ISBN 978-5-8114-0814-6.
Шушкевич Г.Ч., Шушкевич С.В. Компьютерные технологии в математике. Система Mathcad 14. В 2 частях. [Текст] / Шушкевич Г.Ч., Шушкевич С.В. — М: Издательство Гревцова, 2010. — 288 стр. ISBN 978-985-6826-81-1, 978-985-6826-86-6.
Моделирование задач линейного программирования в MathCad
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМ. М.Е.ЕВСЕВЬЕВА»
М.Е.ЕВСЕВЬЕВА»
Факультет физико-математический
Кафедра информатики и вычислительной техники
Реферат
Моделирование решения задач линейного программирования в MathCad
Выполнила: студентка группы МДИ-117
Федюшкина В. А.
Проверила: Кормилицына Т. В.
Саранск 2020
Содержание
Введение 3
1 Задачи линейного программирования в MathCad 4
1.1 Общая постановка задачи линейного программирования 4
1.2 Алгоритм решения задач линейного программирования в MathCad 5
2 Примеры решения задач линейного программирования в MathCad 7
2.1 Решение задачи линейного программирования 7
2.2 Решение транспортной задачи 8
2.3 Решение задачи о назначениях 10
Список использованной литературы 12
Введение
Линейное программирование – наука о методах исследования и нахождения наибольшего или наименьшего значений линейной (целевой) функции при наличии линейных ограничений. Термин «программирование» понимается в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации.
Термин «программирование» понимается в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации.
Развитие компьютерной техники, совершенствование информационных технологий, распространение пакетов прикладных программ позволили сделать доступными и наглядными современные методы решения математических задач широкому кругу пользователей, освободив от проведения трудоемких расчетов.
Опыт преподавания показывает необходимость использования в рамках дисциплины исследования операций табличного процессора MS Excel и систем компьютерной математики, в частности системы MathCad, главными достоинствами которой является то, что она проста в изучении и использовании, позволяет одновременно с расчетами создавать документы в общепринятом виде.
Задачи линейного программирования в MathCad
Общая постановка задачи линейного программирования
Линейное программирование это один из первых и более углубленно изученных разделов математического программирования. Не что иное, как линейное программирование стало тем разделом, с помощью которого и начала развиваться дисциплина «математическое программирование».
Не что иное, как линейное программирование стало тем разделом, с помощью которого и начала развиваться дисциплина «математическое программирование».
Линейное программирование используется при построении математических моделей процессов, в основе которых положена гипотеза линейного представления мира: финансовых задач, оптимального расположения оборудования, а также задач управления и планирования и т.д.
К задачам линейного программирования можно отнести такие задачи, в которых целевая функция и ограничения в виде равенств и неравенств являются линейными. Для примера задачу линейного программирования можно задать следующим образом: необходимо найти вектор значений переменных, которые доставляют экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств.
Как было сказано ранее линейное программирование является часто используемым методом оптимизации. К задачам линейного программирования относят задачи:
а) рационального расхода материалов и сырья;
б) производственной программы какой-либо компании;
в) наилучшего размещения и концентрации производства;
г) создание наиболее прибыльного плана перевозок, работы транспорта;
д) управление производственными запасами;
е) и множество других задач, которые принадлежат к этой сфере.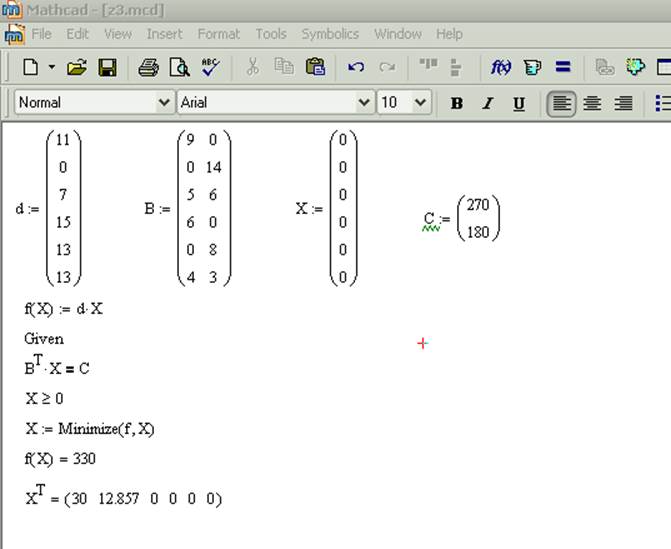
Если судить по оценкам американских экспертов, то около 75% от всего числа используемых методов оптимизации приходится на линейное программирование. Больше половины машинного времени, которое было потрачено за последние годы на проведение некоторых научных испытаний, отвели решению задач линейного программирования.
Таким образом, линейным программированием называется наука, изучающая исследования и поиск наибольших и наименьших значений линейной функции, на неизвестное которой наложены ограничения. Следовательно, задачи линейного программирования принадлежат к задачам на условный экстремум функции.
1.2 Алгоритм решения задач линейного программирования в MathCad
Система MathCad позволяет упростить решения задач линейного программирования, используя при этом основные функции Maximize и Minimize.
Рассмотрим порядок выполнения решения задачи линейного программирования в системе MathCad с системой ограничений двух или трех переменных.
1. Установить режим автоматических вычислений.
2. Определить целевую функцию как функцию трех переменных.
3. Задать начальные приближения для всех переменных.
4. Ввести ключевое слово Given.
5. Ввести выражения из системы ограничений и условия неотрицательности переменных. Для ввода знаков , Булевый.
6. Задать вектор-столбец, элементы которого переменные х1, х2, х3. Ввести знак присваивания и функцию Maximize (f, x1,x2,x3) для решения задачи линейного программирования на максимум, или Minimize (f, x1,x2,x3) для решения задачи линейного программирования на минимум.
7. Еще раз ввести вектор-столбец с переменными x1, x2, x3, нажать знак равенства и будет получено оптимальное решение.
8. Вычислить значение целевой функции в точке экстремума.
9. Оформить документ и сохранить его в файле.
2 Примеры решения задач линейного программирования в MathCad
2.1 Решение задачи линейного программирования
Задача 1. Найти максимальное значение функции
при заданных ограничениях:
Решение:
1) Специальной переменной ORIGIN присваиваем значение 1. Значением ORIGIN является номер первого элемента строки или столбца в матрице. По умолчанию ORIGIN=0.
В меню Math выбрать строку Options или
2) Вводим исходные данные задачи в матричной форме.
3) Вводим линейную целевую функцию.
4) Задаем начальные значения переменным задачи.
5) Вводим ограничения задачи в матричной форме.
6) Определяют оптимальное решение задачи с помощью встроенной функции Maximize (в случае поиска максимума функции) или Minimize (в случае поиска минимума функции).
2.2 Решение транспортной задачи
Задача 2. Имеются n пунктов производства и т пунктов распределения продукции. Стоимость перевозки единицы продукции с і-го пункта производства в j-й центр распределения приведена в таблице, где под строкой понимается пункт производства, а под столбцом — пункт распределения. Кроме того, в этой таблице в i-й строке указан объем производства в і-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения.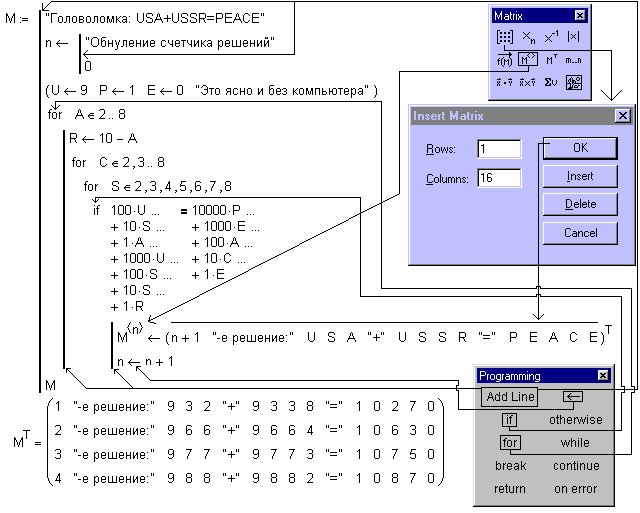 Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.
Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.
Стоимость перевозки единицы продукции | Объем производства | |||
1 | 3 | 4 | 5 | 20 |
5 | 2 | 10 | 3 | 30 |
3 | 2 | 1 | 4 | 50 |
6 | 4 | 2 | 6 | 20 |
42 | 40 | 80 | 38 | |
Объем потребления
Решение:
Ввели исходные данные в матричной форме.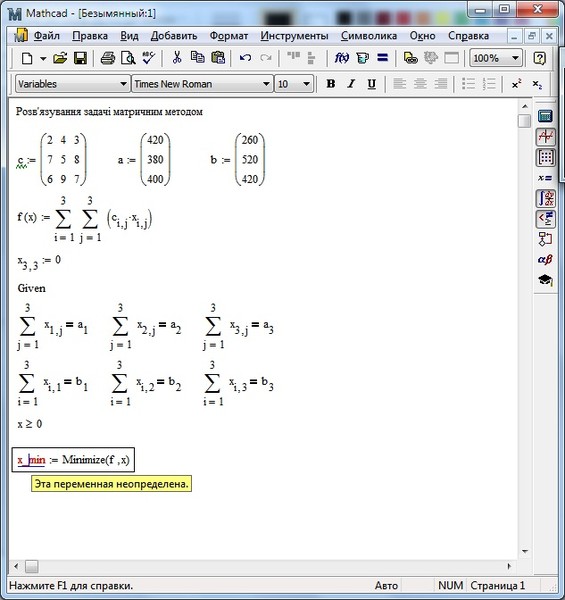
Ввели линейную целевую функцию.
Задали начальные значения переменных:
Ввели ограничения задачи в матричной форме.
Определили оптимальное решение задачи с помощью встроенной функции Minimize:
2.3 Решение задачи о назначениях
Задача 3. Имеются n рабочих и т видов работ. Стоимость выполнения і-и работником j-й работы приведена в таблице, где рабочему соответствует строка, а работе – столбец. Необходимо составить план работ так, чтобы все работы были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость выполнения всех работ была минимальной.
Стоимость выполнения работ
Виды работ | ||||
Рабочие | 14 | 21 | 14 | 22 |
12 | 12 | 23 | 31 | |
13 | 17 | 45 | 33 | |
14 | 15 | 75 | 34 | |
Решение задачи средствами MathCad:
Ввели исходные данные в матричной форме.
Ввели линейную целевую функцию.
Задали начальные значения переменных:
Ввели ограничения задачи в матричной форме.
Определили оптимальное решение задачи с помощью встроенной функции Minimize:
Заключение
MathCad – система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Математическую систему MathCad достаточно удобно использовать для обучения, вычислений и инженерных расчетов. Она славится универсальностью своего пакета, который может быть использован для решения самых разнообразных инженерных, экономических, статистических и других научных задач. Программирование на общепринятом математическом языке позволяет преодолеть языковой барьер между машиной и пользователем, что делает его востребованным среди студентов и академиков. А совместное применение текстового редактора, формульного транслятора и графического процессора позволяет пользователю в ходе вычислений получить готовый документ.
Программирование на общепринятом математическом языке позволяет преодолеть языковой барьер между машиной и пользователем, что делает его востребованным среди студентов и академиков. А совместное применение текстового редактора, формульного транслятора и графического процессора позволяет пользователю в ходе вычислений получить готовый документ.
Опыт работы с системой MathCad позволяет сделать вывод, что студенты, аспиранты, инженеры и ученые получили превосходный инструмент для повседневной работы.
Список использованной литературы
Аверьянова С.Ю., Растеряев Н.В. Содержательные задачи линейного программирования и их решение с помощью ЭТ MS EXCEL и пакета MATHCAD: учебное пособие/ Южный федеральный университет. – Ростов-на-Дону: Издательство ЮФУ, 2014. – 132 с.
Гольштейн Е. Г., Юдин Д.Б. Задачи линейного программирования транспортного типа. — М.: Наука, 1969. – 382 с.
Капустин Е.И. Решение некоторых классов математических задач в программе Excel. URL://exponenta.ru/educat/systemat/kapustin/003.asp/.
URL://exponenta.ru/educat/systemat/kapustin/003.asp/.
Карманов В.Г. Математическое программирование: Учеб. Пособие. М.: Физматлит, 2001. 263 с.
Кудрявцев Е.М. MathCad-2000. М.: ДМК Пресс, 2001. С. 576.
Кузнецова Л.Г. Системы компьютерной математики / Учебное пособие. Омск, 2003. С. 108.
Растеряев, Н.В., Герасименко Ю.Я. Решение оптимизационных задач в среде MATHCAD и EXCEL: Учеб. пособие – Новочеркасск: Южно-российский гос. тех. ун-т (НПИ), 2004.- 100 с.
Mathcad Prime — математическое программное обеспечение
перейти к содержаниюMathcad PrimeNick Exposito2023-04-25T17:16:58-07:00
PTC Mathcad Prime — это самый передовой и всеобъемлющий математический инструмент для самых сложных расчетов.
Бесплатная пробная версия
Сравнить
Что такое
PTC Mathcad Prime ? Mathcad Prime позволяет решать, анализировать, документировать и делиться своими инженерными расчетами. Вам нужно комплексное, но интуитивно понятное приложение, которое выполняет точные расчеты, обеспечивает отслеживаемость, защищает интеллектуальную собственность и позволяет вам демонстрировать свою работу.
Вам нужно комплексное, но интуитивно понятное приложение, которое выполняет точные расчеты, обеспечивает отслеживаемость, защищает интеллектуальную собственность и позволяет вам демонстрировать свою работу.
Записывайте свои расчеты в инженерную тетрадь с естественными математическими обозначениями и единицами измерения. Покажите свою работу, используя широкие возможности форматирования, а также графики, текст и изображения в одном профессионально отформатированном документе.
Выберите PTC Mathcad Prime , потому что электронные таблицы просто не могут конкурировать с . Mathcad Prime визуально представляет математику интуитивно понятным способом, упрощая определение, понимание и управление инженерными расчетами с помощью пользовательского интерфейса, похожего на доску.
Оживите свои инженерные расчеты.
Загрузить пробную версию
Mathcad Datasheet
Загрузить техническое описание Mathcad Prime 9
Что нового в Mathcad Prime 9?
PTC Mathcad Prime — это отраслевой стандарт программного обеспечения для инженерной математики, позволяющий решать самые сложные задачи и обмениваться инженерными расчетами.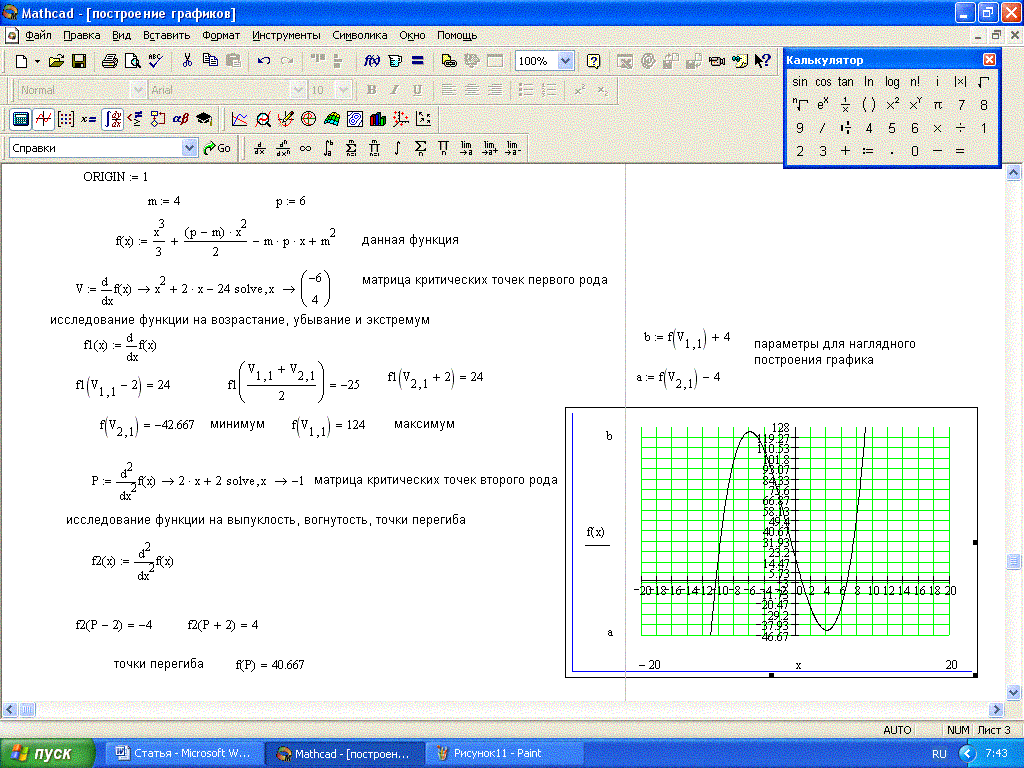 И с PTC Mathcad Prime 9, инженерные расчеты стали лучше. В этом выпуске представлены ключевые приложения, символьный движок, числовой движок и улучшения удобства использования, включая:
И с PTC Mathcad Prime 9, инженерные расчеты стали лучше. В этом выпуске представлены ключевые приложения, символьный движок, числовой движок и улучшения удобства использования, включая:
-
Оператор градиента
-
Символьное решение с блоком решения
- 9 0004 Символьное решение обыкновенных дифференциальных уравнений
См. Что нового в Mathcad Prime 9!
Использование Excel для инженерных расчетов? Подумайте еще раз.
Excel изначально был разработан для составления таблиц основных бухгалтерских и финансовых показателей и расчетов с использованием строк и столбцов. С тех пор он со временем развивался, добавляя математические функции, но оставался верным своему исходному формату сетки.
Инженерам для управления проектами требуется больше, чем просто электронная таблица. «А как насчет Экселя?» ты говоришь! Ну да… если это все, что у нас было в те дни, когда компьютеры были маленькими и медленными, то в наши дни все делается на ноутбуках или смартфонах с инженерами, питающимися кофеином! Теперь благодаря технологическим достижениям, таким как Mathcad Prime , вы можете предоставить возможности Excel инженерам-проектировщикам, которые работают за пределами традиционных офисов и сред (и не хотят, чтобы скучные старые электронные таблицы мешали вам выполнять самые важные расчеты).
Так зачем же использовать что-то устаревшее, когда для вашей организации доступны более совершенные обновленные варианты?
Большая разница между Mathcad и Excel
Инженерная математика в Excel
Вот как может выглядеть типичная инженерная математика в Excel. Ваши надежды на передачу инженерных знаний легко теряются в хаосе ссылок на ячейки и скобок. Математика электронных таблиц подвержена ошибкам, и очень сложно проверить и подтвердить вашу работу. В Excel также нет инженерных единиц, поэтому читатели даже не знают, для чего нужна эта формула.
Инженерная математика в PTC Mathcad
PTC Mathcad был разработан для удовлетворения потребностей инженеров. Это тот же пример уравнения, что и в Excel, но естественная математическая запись Mathcad представляет его так, как будто оно взято из учебника по математике. Любой инженер может посмотреть и проверить формулу. Кроме того, Mathcad полностью интегрируется с Excel, при этом он отслеживает единицы измерения, что позволяет понять, что это формула для механической энергии.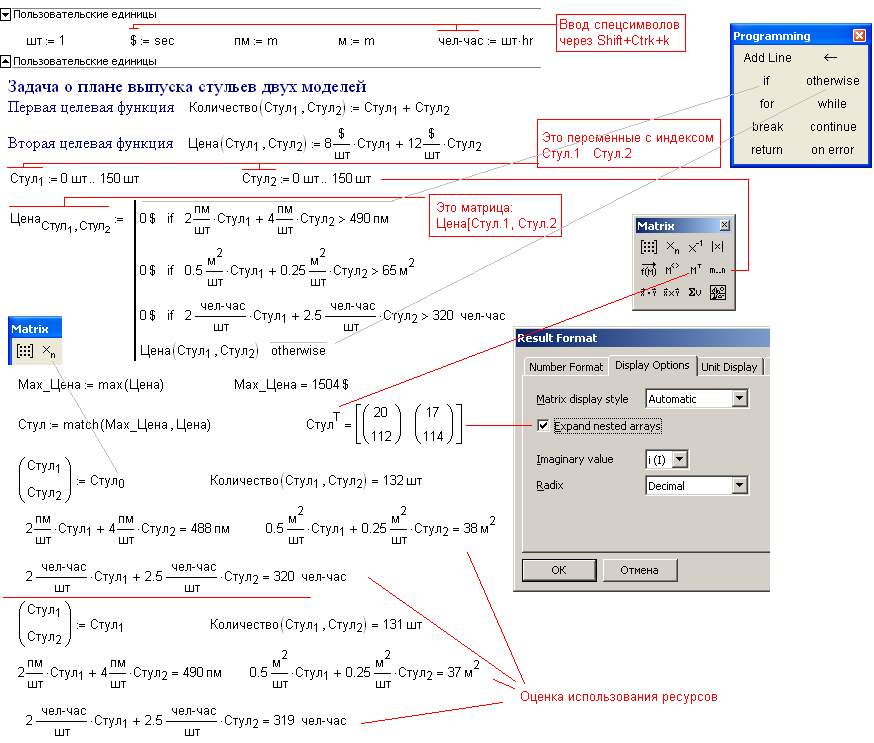
Лучшее из двух миров: совместное использование Mathcad Prime и Excel
Вам не нужно отказываться от своих надежных электронных таблиц Excel в пользу Mathcad Prime. Используйте лучшие возможности обеих программ и получайте максимальные преимущества! Наслаждайтесь хранением данных из Excel, а также расчетами и документами из Mathcad — все интегрировано для бесперебойной работы.
Легко переключайтесь между двумя приложениями, так как изменения, которые вы делаете в любой из сторон, автоматически обновляются в каждой программе соответственно. С помощью PTC Mathcad Prime и Excel вы можете оптимизировать рабочие процессы проектирования, объединив мощь двух замечательных инструментов!
Узнать ценуУзнать цену
Бесплатная пробная версияБесплатная пробная версия
Ищете что-то конкретное?
Вот еще несколько ресурсов, рекомендуемых для вас ниже:
Связанные документы
Связанные ресурсы
-
PTC Обзор Mathcad Prime 9.
 0
0 -
Обзор PTC Mathcad Prime 8.0
ПОСЛЕДНИЕ НОВОСТИ MATHCAD НА TRISTAR
alejanic2023-01-31T16:04:38-07:0031 января 2023 г.|Блог, Mathcad|
В PTC Mathcad Prime существует пять вариантов форматирования результатов: общий, десятичный, научный, инженерный и процентный. В этом сообщении блога быстро объясняется, как форматировать числовые результаты с помощью раздела «Результаты» на вкладке «Математическое форматирование» на ленте, и, в частности, как отображать десятичный ответ в виде дроби.
alejanic2023-02-23T12:32:39-07:0012 октября 2022 г.|Блог, Mathcad|
Если вы инженер, скорее всего, вы использовали (или, по крайней мере, слышали) две самые популярные математические программы: Maple и Mathcad. У обоих есть свои плюсы и минусы, но когда дело доходит до дела, есть только один явный победитель инженерных расчетов!
alejanic2023-02-23T12:44:42-07:004 сентября 2022 г. |Блог, Mathcad|
|Блог, Mathcad|
Инженерам, ученым и математикам требуется специальное программное обеспечение для расчетов. Альтернативы требуют слишком много времени и подвержены риску использования в сегодняшней гиперконкурентной среде. Узнайте 6 основных ошибок, которых следует избегать, и как сделать правильный выбор!
Поговорите с главным представителем PTC Mathcad!
Узнать цену
Бесплатная пробная версия
Ссылка для загрузки страницы Перейти к началуРисунок 1 из книги «От C++ к Mathcad: преподавание вводного курса программирования на нетрадиционном языке программирования»
- ings{Brannan1998FromCT,
title={От C++ до Mathcad: введение в курс программирования на нетрадиционном языке программирования},
автор = {Кеннет П. Браннан и Джон Олден Мерден},
год = {1998}
}
- К. Браннан, Дж. Мерден
- Опубликовано 28 июня 1998 г.
- Информатика
Mathcad заменил C++ в качестве языка вводного курса программирования, преподаваемого на факультете гражданского и экологического проектирования в Цитадели.
 В статье обсуждаются преимущества и недостатки, связанные с переключателем. Проведено сравнение между курсом программирования на основе Mathcad и предыдущими версиями курса, преподаваемыми с использованием традиционных языков программирования. Включена оценка использования Mathcad учащимися через год после завершения курса на основе Mathcad…
В статье обсуждаются преимущества и недостатки, связанные с переключателем. Проведено сравнение между курсом программирования на основе Mathcad и предыдущими версиями курса, преподаваемыми с использованием традиционных языков программирования. Включена оценка использования Mathcad учащимися через год после завершения курса на основе Mathcad… Посмотреть через издателя
peer.asee.orgДесять лет спустя: преподавание Mathcad как нетрадиционного языка программирования
- Дж. Мерден, К. Браннан
Образование
- 2006
Предоставлены доказательства того, что студенты, прошедшие курс компьютерных приложений на основе Mathcad, приобретают широкий спектр компьютерных инструментов и совершенствуют навыки, которые пригодятся им на протяжении всей их академической карьеры, и эта тенденция сохраняется более десяти лет.
Пакеты программирования высокого уровня для бакалавриата по машиностроению
- Ян Х.

Информатика
- 2004
В начале учебного года 2003-04 года Mathcad и Matlab были выбраны для вводного курса программирования в факультет машиностроения, и каждый пакет имеет свои сильные стороны и свою роль в обучении инженеров бакалавриата.
Влияет ли выбор языка программирования на понимание учащимися концепций программирования на первом курсе инженерного курса
- Benjamin D. McPheron, Stephanie M. Gratiano, W. Palm
Информатика
- 2015
Результаты показывают, что выбор языка программирования, скорее всего, не имеет значения для понимания студентами концепций программирования и преподавателя курса с должны свободно выбирать язык программирования на основе других факторов, таких как рыночный спрос, стоимость или наличие педагогических ресурсов.
Программирование для дошкольного образования с использованием Squeak Smalltalk
- Кэтрин Н.
 Родхаус, Бенджамин Купер, С. Уоткинс
Родхаус, Бенджамин Купер, С. Уоткинс Информатика
- 2010
В рамках этого проекта была разработана интегрированная серия учебных пособий по программированию, позволяющая всем, независимо от их текущих навыков программирования , изучить прикладное программирование методы и избегать простых манипуляций с кодом без понимания основных концепций Squeak Smalltalk.
Преподавание и изучение проектирования преобразователя постоянного тока с использованием MathCAD
- Taufik
Информатика
SoD ’07
- 2007
В этой статье представлен подход к обучению проектированию преобразователей постоянного тока с использованием MathCAD и представлен пример дизайна с использованием Excel, который затем сравнивается с тот же пример с использованием MathCAD.
Преподавание и изучение проектирования преобразователя постоянного тока в постоянный с использованием
- MathCAD, Taufik
Инженерное дело
- 2011
проектирование преобразователя постоянного тока с использованием MathCAD.
 MathCAD предоставляет преимущества, которые значительно улучшают процесс преподавания и обучения, особенно когда он долгий и…
MathCAD предоставляет преимущества, которые значительно улучшают процесс преподавания и обучения, особенно когда он долгий и…Использование Интернета для облегчения проверки знаний учащихся
- Дж. Мерден, К. Браннан
Образование
- 1999
Время, сэкономленное при выставлении оценок веб-тесты и оценка успеваемости учащихся были значительными и привели к чистое уменьшение преподавательского времени для случая, представленного в этой статье.
Интеграция профессиональной и этической ответственности в курс компьютерных приложений
- Дж. Мерден, К. Браннан
Образование
- 2005
Описывается модуль по профессиональной и этической ответственности для второкурсников Класс компьютерных приложений и оценивается влияние на мнение учащихся. Модуль сосредоточился на принципах…
2006-1549: ОБУЧЕНИЕ ЧИСЛЕННЫМ МЕТОДАМ В ИНЖИНИРИНГЕ С MATHCAD
- П.