Mathcad метод простых итераций: ВОЗМОЖНОСТИ МАТЕМАТИЧЕСКОГО ПАКЕТА MATHCAD. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ УРАВНЕНИЙ И ИХ СИСТЕМ

Решение нелинейных уравнений и их систем

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

 

Учреждение образования «Гомельский государственный университет

имени Франциска Скорины»

 

Математический  факультет

 

Кафедра вычислительной математики и  программирования

 

 

 

 

 

 

 

ПРОГРАММИРОВАНИЕ В ПАКЕТЕ MATHCAD:

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И  ИХ СИСТЕМ

 

 

 

К У Р С О В А Я   Р А Б О Т А

 

 

 

 

 

 

 

 

 

 

Исполнитель студент группы ####	##########
Научный руководитель к.ф.–м.н., доцент	###########

 

 

Гомель 2012

 

Реферат

 

Курсовая работа 40 страниц, 23 рисунка, 10 источников.

 

Ключевые слова: системы нелинейных уравнений, программирование, простые итерации, рекурсивные вычисления, исследование функции

 

Объект исследования: объектом исследования является система компьютерной математики Mathcad на примере работы решения систем нелинейных уравнений.

 

Цель курсовой работы: получение практических навыков работы в системе компьютерной математики Mathcad на примерах работы решения нелинейных систем уравнений.

 

Выводы: в ходе выполнения данной курсовой работы были получены навыки работы в системе компьютерной математики Mathcad на примерах  решения систем нелинейных уравнений.

 

 

Содержание

 

Введение 4

1 Решение уравнений с одной переменной 6

1.1Постановка задачи 6

1.2Отделение корней 7

1.3Метод половинного деления 7

1.4Метод простой итерации 10

1.5Оценка погрешности метода простой итерации 12

1.6Преобразование уравнения к итерационному виду 13

1. 7Решение уравнений методом простой итерации в пакете mathcad 13

1.8Метод хорд 15

1.9Метод касательных 18

2 Методы решения систем нелинейных уравнений 21

2.1Векторная запись нелинейных систем. Метод простых итераций 21

2.2Метод Ньютона решения систем нелинейных уравнений 24

2.3Решение нелинейных систем методами спуска 29

Заключение 36

Список используемых источников 40

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

Система Mathcad изначально была задумана как система для численных вычислений. Но версия Mathcad 2001 стала настолько «интеллектуальной», что блестяще справляется со множеством аналитических (символьных) вычислений.

Mathcad – это многофункциональная  интерактивная вычислительная 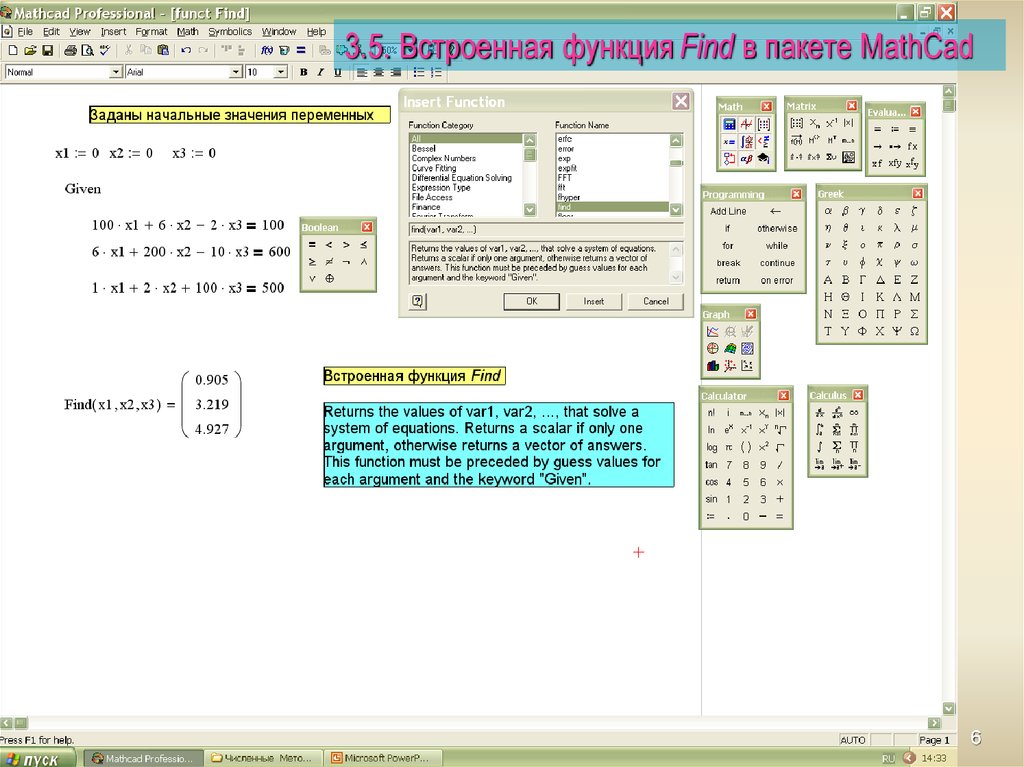система,  позволяющая, благодаря встроенным  алгоритмам, решать аналитически  и численно большое количество  математических задач. Рабочий документ Mathcad – электронная книга с живыми формулами, вычисления в которой производятся автоматически в том порядке, в котором записаны выражения. Отличается простым и удобным интерфейсом, написанием выражений стандартными математическими символами, хорошей двух – и трехмерной графикой, возможностью подключения к распространенным офисным и конструкторским программам, а также к Internet.

Программирование занимает особое место в Mathcad. Для начального обучения изучать его совершенно не обязательно. Возможности Mathcad позволяют решить подавляющее количество задач без  всякого программирования, да к тому же, как правило, несколькими способами. Однако есть класс задач, при решении  которых без программирования не обойтись. Это задачи, в которых  часть документа из нескольких или многих операторов надо выполнить многократно. В таких случаях документ должен состоять из отдельных подпрограмм, объединенных в единую «головную» программу. И в этом случае программирования можно было бы избежать, если бы создатели Mathcad предусмотрели оператор перехода к метке, который есть (был) во многих языках программирования, в частности в FORTRAN.

Mathcad позволяет вводить программы  любой сложности. Образцом достаточно  сложной программы является программа  решения плоской упругопластической  задачи методом конечных элементов.

Программирование в Mathcad чрезвычайно  наглядно и понятно, так как программа  представляет собой последовательность формул. Основные операторы программирования расположены на панели Programming (Программирование), вызываемой щелчком на кнопке Programming Toolbar (Панель программирования) математической панели. Далее программами будем называть не все документы Mathcad, а только те из них, которые написаны с использованием панели программирования.

К важным достоинствам Mathcad относятся  настройка под любой маломальски  известный тип печатающих устройств, богатый набор шрифтов, возможность  использования всех инструментов Windows, прекрасная графика и современный  многооконный интерфейс.

Многие задачи, решаемые с помощью  математических пакетов, сводятся к  решению уравнений – алгебраических, степенных, тригонометрических, к поиску значений неизвестных, превращающих эти уравнения в тождества строго или приближенно.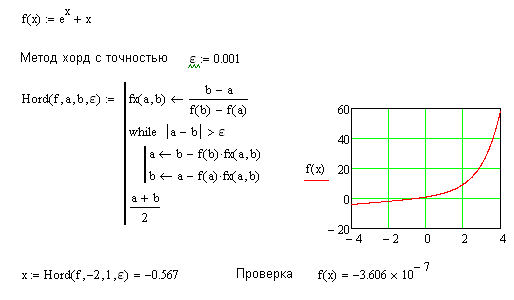

Успех в решении подобных задач зависит не только от мощности соответствующих инструментов, встроенных в Mathcad, но и от знания пользователем их особенностей, нюансов, сильных и слабых сторон.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Решение уравнений с одной переменной

 

Уравнения можно решать различными методами, такими как: метод половинного деления, метод простой итерации, метод хорд, метод касательных. В этой главе рассмотрим подробнее вышеперечисленные методы.

 

1. Постановка задачи

 

Наиболее общий вид нелинейного  уравнения:

                                                 (1.

1)

где функция  определена и непрерывна на конечном или бесконечном интервале .

Определение 1.1. Всякое число обращающее функцию F(x) в нуль, называется корнем уравнения (1.1).

Определение 1.2. Число , называется корнем – ой кратности, если при вместе с функцией равны нулю ее производные до –го порядка включительно:

                           (1.2)

Определение 1.3. Однократный корень называется простым.

Определение 1.4. Уравнения и называются равносильными (эквивалентными), если множества решений данных уравнений совпадают.

Нелинейные  уравнения с одной переменной подразделяются на алгебраические и трансцендентные.

Определение 1.5. Уравнение (1.1) называется алгебраическим, если функция является алгебраической.

Путем алгебраических преобразований из всякого алгебраического уравнения  можно получить уравнение в канонической форме:

                            (1.3)

где – действительные коэффициенты уравнения; – неизвестное.

Из алгебры  известно, что всякое алгебраическое уравнение имеет, по крайней мере, один вещественный или два комплексно сопряженных корня.

Определение 1.6. Уравнение (1.1) называется трансцендентным, если функция не является алгебраической.

Определение 1.7. Решить уравнение (1.1) означает следующее:

– установить имеет ли уравнение корни;

– определить число корней уравнения;

– найти значения корней уравнения с заданной точностью.

2. Отделение корней

 

Определение 1.8. Отделение корней – процедура нахождения отрезков, на которых уравнение (1.1) имеет только одно решение.

В большинстве случаев отделение  корней можно провести графически. Для этого достаточно построить  график функции  и определить отрезки, на которых функция имеет только одну точку пересечения с осью абсцисс.

В сомнительных случаях графическое  отделение корней необходимо подкреплять вычислениями. При этом можно использовать следующие очевидные положения: если непрерывная функция принимает на концах отрезка значения разных знаков (т.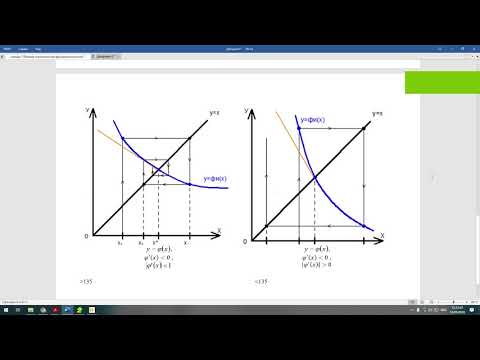 е. ), то уравнение (1.1) имеет на этом отрезке по меньшей мере один корень;

если  функция к тому же и строго монотонна, то корень на отрезке единственный.

 

3. Метод половинного деления

 

Пусть уравнение (1.1) имеет на отрезке единственный корень, причем функция на данном отрезке непрерывна (рисунок 1.1).

Разделим  отрезок пополам точкой . Если , то возможны два случая:

– функция меняет знак на отрезке ;

– функция меняет знак на отрезке .

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и, продолжая процесс половинного  деления дальше, можно дойти до сколь угодно малого отрезка, содержащего  корень уравнения.

 

Рисунок 1.1 – К объяснению метода половинного деления

 

Пример 1.1

Решение в пакете Mathcad методом половинного  деления уравнения

 

1. Задание функции:

 

2. Построение графика функции (Рисунок 1. 2).

Рисунок 1.2 – График функции

 

3. Задание функции, реализующей метод половинного деления (Рисунок 1.3). Здесь аргументы функции: – имя функции, – левая и правая координаты концов отрезка; – точность вычисления корня.

 

4. Вычисление значения корня уравнения:

5. Проверка найденного значения корня:

Для рассмотрения процесса нахождения корня уравнения в динамке  необходимо сохранить значение корня  на каждом шаге вычислительной процедуры и построить зависимость значения корня от номера шага. Функция, возвращающая значение корня на каждом шаге метода половинного деления, представлена на рисунке 1.4. Аргументы функции: – имя функции,– левая и правая координаты концов отрезка, –точность вычисления корня.

Рисунок 1.3 – Функция, реализующая метод половинного деления

Рисунок 1. 4 – Функция, реализующая метод половинного деления и возвращающая значение корня уравнения на каждом шаге процесса вычислений

 

После создания функции необходимо дополнить описанный выше документ следующей последовательностью  команд.

1. Вычисление матрицы, первый столбец которой содержит номер итерации, второй – значение корня:

2. Визуализация зависимости значения корня от номера шага вычислительной процедуры (рисунок 1.5).

 

Рисунок 1.5 – Зависимость значения корня от номера шага вычислительной процедуры

 

4. Метод простой итерации

 

Заменим уравнение (1.1) равносильным уравнением

.                                                     (1.4)

Пусть – корень уравнения (1.4), а , полученное каким–либо способом нулевое приближение к корню . Подставляя в правую часть уравнения (1.4) , получим некоторое число . Повторим данную процедуру с и получим . Повторяя описанную процедуру, получим последовательность

                                                 (1.5)

называемую  итерационной последовательностью.

Итерационная последовательность, вообще говоря, может быть как сходящейся, так и расходящейся, что определяется видом функции .

Теорема 1.1. Если функция непрерывна, а последовательность (1.5) сходится, то предел последовательности (1.5) является корнем уравнения (1.4).

Действительно, пусть . Перейдем к пределу в равенстве

  .          (1.6)

Условие сходимости итерационного  процесса определяется теоремой о достаточном условии сходимости итерационного процесса.

 

Геометрическая  интерпретация данного алгоритма представлена на рисунке 1

 

Рисунок 1.6 – К объяснению метода простой итерации

 

Теорема 1.2. Пусть уравнение имеет единственный корень на отрезке и выполнены условия:

1. определена и дифференцируема на .
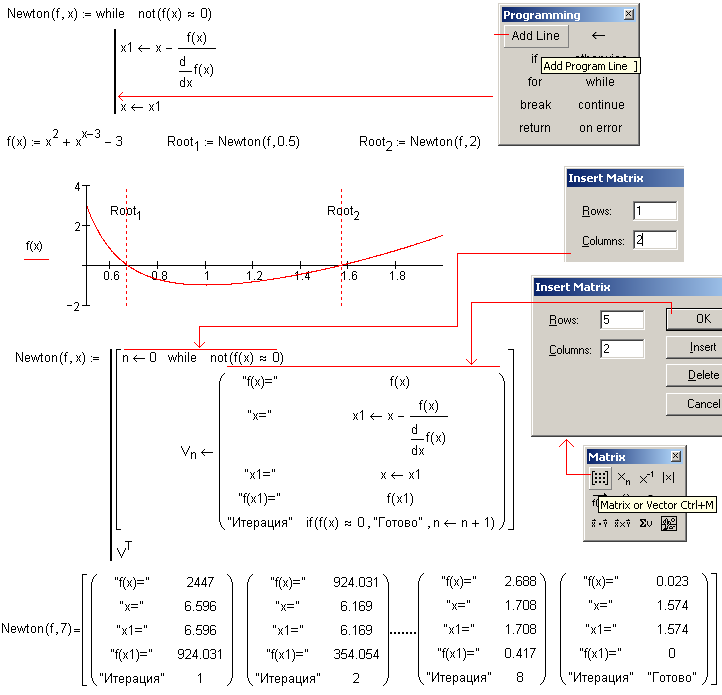
2. для всех .
3. Существует такое вещественное , что для всех .

Тогда итерационная последовательность сходится при любом начальном приближении

Доказательство. Построим итерационную последовательность вида (1.5) с любым начальным значением . В силу условия 2 теоремы 1.2 все

члены последовательности находятся в отрезке .

Метод итераций онлайн

Метод итераций онлайн

Построить график функции Точки разрыва функции Построение графика методом дифференциального исчисления Упростить выражение

Примеры решенийМетод Зейделя Метод Ньютона Метод хорд Решение уравненийМетод LU-разложения Метод Гаусса Матрица Гессе Градиент функции Экстремум функции

Назначение сервиса. Онлайн-калькулятор предназначен для отыскания корней уравнения методом итераций.

• Решение онлайн
• Видеоинструкция

F(x) =

Искать в интервале от до . (2/3)

Одним из наиболее эффективных способов численного решения уравнений является метод итерации. Сущность этого метода заключается в следующем. Пусть дано уравнение f(x)=0.
Заменим его равносильным уравнением

x=φ(x). (1)

Выберем начальное приближение корня x₀ и подставим его в правую часть уравнения (1). Тогда получим некоторое число

x₁=φ(x₀). (2)

Подставляя теперь в правую часть (2) вместо x₀ число x₁ получим число x₂=φ(x₁). Повторяя этот процесс, будем иметь последовательность чисел

x_n=φ(x_n-1) (n=1,2..). (3)

Если эта последовательность сходящаяся, то есть существует предел , то переходя к пределу в равенстве (3) и предполагая функцию φ(x) непрерывной найдем или ξ=φ(ξ).
Таким образом, предел ξ является корнем уравнения (1) и может быть вычислен по формуле (3) с любой степенью точности. Рис. 1а Рис. 1б
Рис. 2. |φ′(x)|>1 — расходящийся процесс

На рис.1а, 1б в окрестности корня |φ′(x)|<1 и процесс итерации сходится. Однако, если рассмотреть случай |φ′(x)|>1, то процесс итерации может быть расходящимся (см. рис.2).

Достаточные условия сходимости метода итерации

Теорема 7. Пусть функция φ(x) определена и дифференцируема на отрезке [a,b], причем все ее значения φ(x)∈[a,b] и пусть |φ′(x)|≤q<1 при x∈[a,b]. Тогда процесс итерации x_n = φ(x_n-1)  сходится независимо от начального значения x₀∈[a,b] и предельное значение является единственным корнем уравнения x= φ(x) на отрезке [a,b].
Доказательство: Рассмотрим два последовательных приближения x_n = φ(x_n-1) и x_n+1= φ(x_n) и возьмем их разность x_n+1-x_n=φ(x_n)-φ(x_n-1). По теореме Лагранжа правая часть может быть представлена как

φ′(x_n)(x_n-x_n-1)

где x_n∈[a,b]
Тогда получим

|x_n+1-x_n|≤φ′(x_n)|x_n-x_n-1|≤q|x_n-x_n-1|

Полагая n=1,2,…

|x₂-x₁|≤q|x₁-x₀|
|x₃-x₂|≤q|x₂-x₁|≤q²|x₁-x₀|
|x_n+1-x_n≤qⁿ|x₁-x₀| (4)

Из (4) в силу условия q<1 видно, что последовательность {x_n} сходится к некоторому числу ξ, то есть , и следовательно,
 (в силу непрерывности функции φ(x))
или ξ= φ(ξ) ч.т.д.
Для погрешности корня ξ можно получить следующую формулу.
Имеем x_n=φ(x_n-1).
Далее ξ-x_n=ξ-φ(x_n-1) = φ(ξ)-φ(x_n-1) →
Теперь φ(x_n-1)=φ(x_n)-φ′(c)(x_n-x_n-1) →
φ(ξ)-φ(x_n)+φ′(c)(x_n-x_n-1)
В результате получим

ξ-x_n = φ′(c₁)(ξ-x_n-1)+φ′(c)(x_n-x_n-1)
или
|ξ-x_n|≤q|ξ-x_n|+q|x_n-x_n-1|

Отсюда

, (5)

откуда видно, что при q близком к 1 разность |ξ -x_n| может быть очень большой несмотря на то что |x_n-x_n-1|<ε, где ε-заданная величина. Для того, чтобы вычислить ξ с точностью ε необходимо обеспечить

. (6)

Тогда подставляя (6) в (5), получим |ξ -x_n|<ε.
Если q очень мало, то вместо (6) можно использовать

|x_n-x_n-1|<ε

Сходимость метода итерации линейная с коэффициентом сходимости α=q. Действительно, имеем
ξ-x_n=φ(ξ)-φ_n-1 = φ′(c)·(ξ-x_n-1), отсюда |ξ-x_n|≤q·|ξ-x_n-1|.

Замечание. Пусть в некоторой окрестности корня ξ∈(a,b) уравнения x= φ(x) производная φ’(x) сохраняет постоянный знак и выполнено неравенство |φ’(x)|≤q<1. Тогда, если φ’(x) положительна, то последовательные приближения x_n = φ(x_n-1) сходятся к корню монотонно.
Если же φ’(x) отрицательна, то последовательные приближения колеблются около корня.
Рассмотрим способ представления уравнения f(x)=0 в форме x= φ(x).
Функцию φ(x) необходимо задать такую, чтобы |φ’(x)| была малой величиной в окрестности корня.
Пусть известно m₁ и M₁ — наименьшее и наибольшее значения производной f’(x)
0<m₁≤f’(x) ≤M₁ (7)
Заменим уравнение f(x)=0 эквивалентным ему уравнением
x = x — λf(x).
Положим φ(x) = x- λf(x). Подберем параметр λ таким образом, чтобы в окрестности корня ξ выполнялось неравенство

0≤|φ′(x)|=|1-λ·f′(x)|≤q≤1

Отсюда на основании (7) получаем

0≤|1-λM₁|≤|1-λm₁|≤q

Тогда выбирая λ = 1/M₁,  получим
q = 1-m₁/M₁ < 1.
Если λ =1/f’(x), то итерационная формула  x_n = φ(x_n-1) переходит в формулу Ньютона

x_n = x_n-1 – f(x_n)/f’(x).

Метод итераций в Excel

В ячейку B2 заносим начало интервала a, в ячейку B3 заносим конец интервала b. Строку 4 отводим под заголовок таблицы. Сам процесс итераций организуем в ячейках A5:D5.

Процесс нахождения нулей функции методом итераций состоит из следующих этапов:

1. Получить шаблон с омощью этого сервиса.
2. Уточнить интервалы в ячейках B2, B3.
3. Копировать строки итераций до требуемой точности (столбец D).

Примечание: столбец A — номер итерации, столбец B — корень уравнения X, столбец C — значение функции F(X), столбец D — точность eps.

Пример. Найти корень уравнения e^-x-x=0, x=∈[0,1], ε=0.001 (8)
Решение.
Представим уравнение (8) в форме x=x-λ(e-x-x)
Найдем максимальное значение производной от функции f(x)= e^—x-x.
max f′(x)=max(-(e^-x+1)) ≈ -1.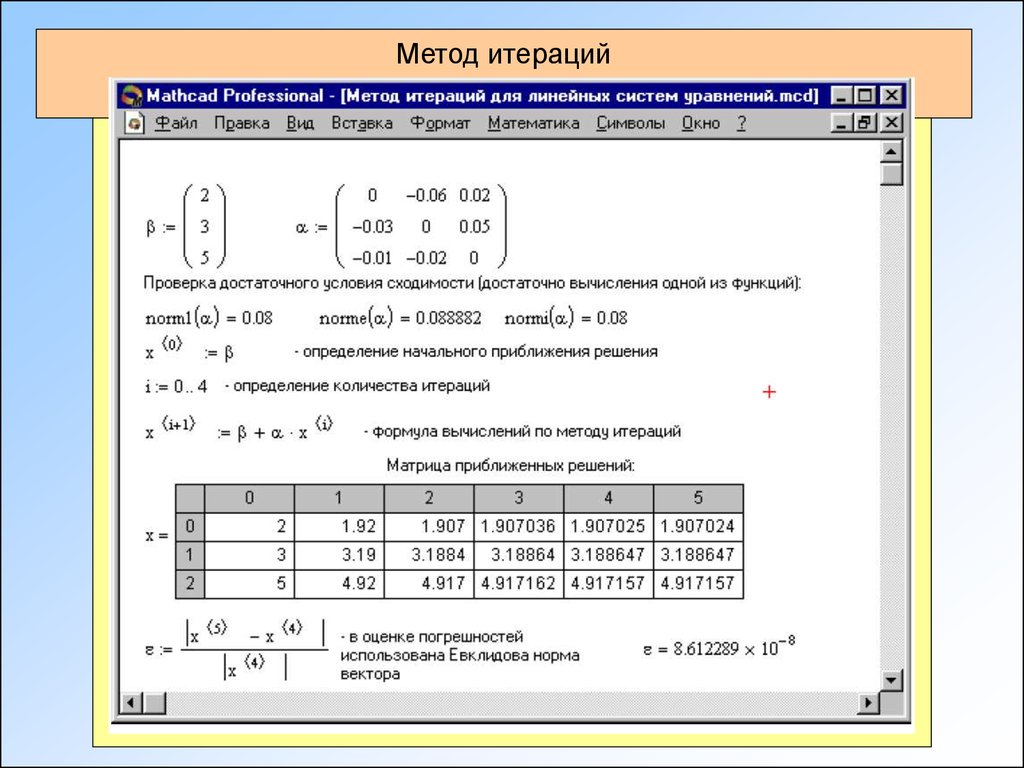 37. Значение . Таким образом, решаем следующее уравнение
x=x+0,73(e^—x-x)
Значения последовательных приближений даны в таблице.

n	xi	f(xi)
1	0.0	1.0
2	0.73	-0.2481
3	0.5489	0.0287
4	0.5698	-0.0042
5	0.5668	0.0006

• Помощь в решении
• Поиск
• Поддержать проект

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Итерационные вычисления » MathCadHelp.com » Номер 1 в назначениях MathCad

В этом разделе показано, как использовать переменные диапазона для выполнения итерации

Итерация в диапазоне

Простейший вид итерации в Mathcad — это просто обобщение скалярных вычислений . Любой расчет, который вы можете выполнить один раз, вы можете выполнить для диапазона значений.

Например, предположим, что вы хотите создать список значений x и y для точек на полярной кривой r = cos(8) + 1 . Основная идея заключается в следующем:

• 8 должно принимать значения от 0 до 2
• Для каждой 8 соответствующий r определяется как r = cos (8) + 1 .
• Для каждого ранда 8 существуют соответствующие x и y, заданные как x = r-cos(8)-и y = r·sin (8) .

Стратегия решения этой проблемы проста: создайте переменную диапазона i и затем вычислите e, r, x и y для каждого значения i. Формула для ei определяет, что e изменяется от 0 до 21t с шагом 21t/N. Чтобы создать другие формулы, просто поставьте нижний индекс i перед каждой переменной в формуле. Рисунок 11-6 показывает результат.

Использование итерации для создания аполярной кривой с использованием графика X-Y.

Обратите внимание, что в этом примере i, а не e, определяется как переменная диапазона. Поскольку i принимает только целые числа, это допустимый индекс. С другой стороны, e принимает дробные значения. Поэтому его нельзя использовать в качестве индекса. Во многих случаях вы можете избежать этого дополнительного шага, используя функции вместо векторов. На рис. 11-7 показано, как сгенерировать кардиоиду, показанную на рис. 11-6, с помощью функций вместо векторов.

Использование функции для выполнения того же действия, что и на рис. 11-6.

Используя векторную запись и оператор векторизации, вы можете исключить использование нижнего индекса в последних трех уравнениях на рис. 11-6. На рис. 11-8 показан пример того, как это сделать.

Использование оператора векторизации для создания полярного графика.

Уравнения, использующие векторную запись вместо индексов, обычно вычисляются гораздо быстрее. Дополнительные сведения см. в главе 10 «Векторы и матрицы».

Несколько переменных диапазона и двойные индексы

Если вы используете в уравнении две переменные диапазона, Mathcad просматривает каждое значение каждой переменной диапазона. Это полезно для определения матриц. Например, чтобы определить матрицу 5 x 5, i,j-й элемент которой равен i +j , введите следующие уравнения:

i:O;4
j:O;4
x[i,j:i+j

Примечание что вам не нужно набирать [Пробел], чтобы оставить индекс в этом случае. Ввод: оставляет нижний индекс и создает символ определения

На рис. 11-9 показан результат ввода приведенных выше уравнений. Обычно лучше всего отображать матрицу в форме, показанной на рис. 11-9. Если вместо x= ввести x [i, j =, Mathcad отобразит одну длинную выходную таблицу с 25 числами. Такую таблицу часто трудно интерпретировать. Аналогичная проблема возникает, когда вы используете пару переменных диапазона на графике.

Определение матрицы

Уравнение Xi,j оценивается для каждого значения каждой переменной диапазона, всего 25 оценок. Результатом является матрица, показанная внизу, с 5 строками и 5 столбцами. Элемент в i-й строке и j-м столбце этой матрицы равен i +j .

Обратите внимание, что если две переменные диапазона имеют значения m и n соответственно, то уравнение, использующее обе переменные диапазона, будет вычислять m . результаты. Если вы попытаетесь использовать две переменные диапазона в выходной таблице, Mathcad отобразит эти m . n приводит к длинной таблице с одной записью для каждого результата. Если вы используете две переменные диапазона на графике, Mathcad нанесет одну точку для каждой из m . n results

Итеративные вычисления » MathCadHelp.com » Номер 1 в MathCad Assignments

Mathcad может выполнять повторяющиеся или итерационные вычисления так же легко, как и отдельные вычисления. Mathcad использует специальную переменную, называемую переменной диапазона, для выполнения итерации. Переменные диапазона принимают диапазон значений, например все целые числа от 0 до 10. Всякий раз, когда переменная диапазона появляется в уравнении Mathcad, Mathcad вычисляет уравнение не только один раз, но и по одному разу для каждого значения переменной диапазона. В этом разделе описывается, как использовать переменные диапазона для выполнения итерационных вычислений.

Создание переменной диапазона

Чтобы вычислить уравнения для диапазона значений, сначала создайте переменную диапазона. Например, в задаче, показанной на рис. 1-5, вы можете вычислить результаты для диапазона значений t от 10 до 20 с шагом 1. Для этого выполните следующие шаги:
• Сначала замените t на диапазон переменная II I, редактирующая ее определение. Нажмите на 10 в -=t =:==l.Q]= _ уравнение t := 10. Точка вставки должна быть рядом с 10, как показано справа.
• Введите, 11. Это сообщает Mathcad, что следующим числом в диапазоне будет 11. ” Введите; 20. Это сообщает Mathcad, что последним числом в диапазоне будет 20. Mathcad отображает точку с запятой в виде пары точек.
• Теперь щелкните вне уравнения для t. Mathcad начинает вычисления с t, заданным как переменная диапазона. Поскольку теперь t принимает одиннадцать различных значений, должно быть также одиннадцать различных ответов. Они показаны в таблице, показанной на рис. 1-6. Возможно, вам придется изменить размер окна или прокрутить вниз, чтобы увидеть всю таблицу.

7

Определение функции

{Вы можете получить дополнительную гибкость, определяя функции. Вот как добавить определение функции на лист:
• Сначала удалите таблицу. Для этого щелкните в любом месте таблицы
и нажимайте [Пробел], пока не заключите все между двумя строками редактирования.
• Теперь определите функцию d(t), введя d(t) :
• Завершите определение, введя следующее выражение: 1600+acc/ 2[Space)*tA2[.J] -490 Только что введенное определение определяет функция. Имя функции — d, а аргумент функции — t. Вы можете использовать эту функцию для вычисления приведенного выше выражения для различных значений t. Для этого просто замените t на соответствующее число. Например:

• Чтобы оценить функцию при значении 3,5, я набираю d (3,5) =. Mathcad возвращает правильное значение d (3.5) = 939,975 rect, как показано справа.
• Чтобы вычислить функцию один раз для каждого значения t, которое вы определили ранее, щелкните под другими уравнениями и введите d (t). Mathcad отобразит таблицу значений (рис. 1-7). Первые два значения, 1.11. 103 и 1.007. 103 , представлены в экспоненциальном (степень 10) представлении.

8

Форматирование результата

Вы можете установить формат отображения для любого числа, которое Mathcad рассчитывает и отображает.