Mathcad given: Given/Odesolve — Mathcad

Решение уравнений и систем уравнений

 

 

Вычисление корней численными методами включает два основных этапа:

·      отделение корней;

·      уточнение корней до заданной точности.

Рассмотрим эти два этапа подробно.

 

Отделение корней нелинейного уравнения

 

Учитывая легкость построения графиков функций в MathCAD, в дальнейшем будет использоваться графический метод отделения корней.

Пример. Дано алгебраическое уравнение

.

Определить интервалы локализации корней этого уравнения.

 

 

Пример. Дано алгебраическое уравнение

.

Определить интервалы локализации корней этого уравнения.

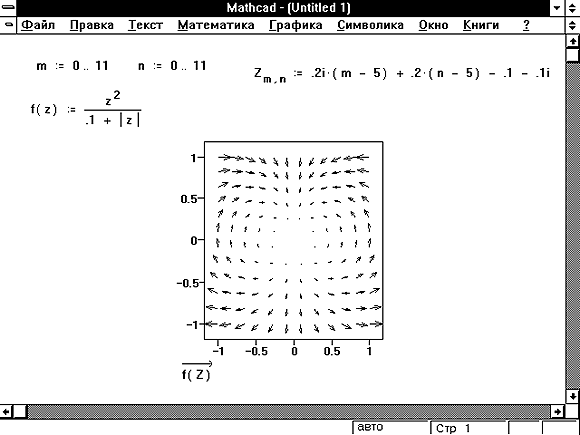
На рисунке приведен график функции , построенный в MathCAD. Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨

 

Уточнение корней нелинейного уравнения

 

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

Функция root. В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root, которая может иметь два или четыре аргумента, т.е.  или , где  – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению,  – скалярная переменная, относительно которой решается уравнение,  – границы интервала локализации корня.

Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.

 

 

Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨

 

Функция root с двумя аргументами требует задания (до обращения к функции) переменной  начального значения корня из интервала локализации.

 

Пример 8.1.5. Используя функцию root, вычислить изменения корня нелинейного уравнения   при изменении коэффициента а от 1 до 10 с шагом 1.

 

 

 

Функция polyroots. Для вычисления всех корней алгебраического уравнения порядка  (не выше 5) рекомендуется использовать функцию polyroots. Обращение к этой функции имеет вид polyroots(v), где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.

Пример. Используя функцию polyroots, найти все три корня уравнения , включая и два комплексных

 

 

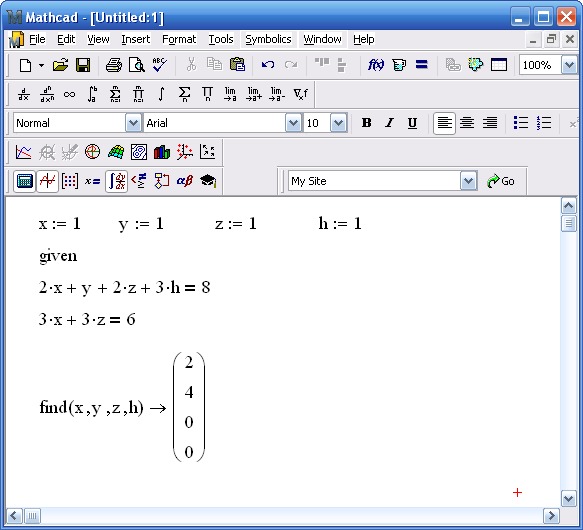
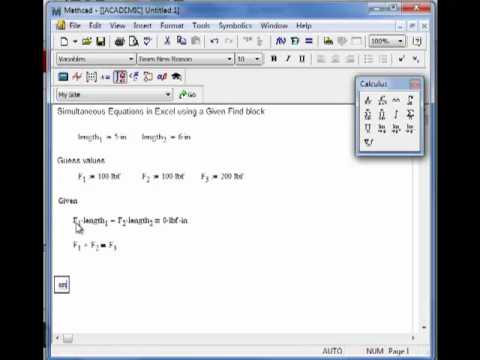
Блок Given.  При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given, имеющий следующую структуру:

 

 

Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры ЛОГИЧЕС­КИЙ.

Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

 

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find(x), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr(x), которая возвращает приближенное значение корня.

 

Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find(x) и в появившемся контекстном меню (см.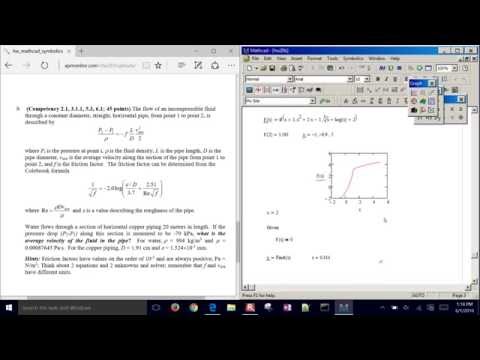 рисунок) выбрать подходящий алгоритм.

 

Аналогично можно задать алгоритм решения и для функции   Minerr(x).

 

Использование численных методов в функциях Find(x), Minerr(x) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.

 

Пример. Используя блок Given, вычислите корень уравнения  в интервале отделения .

 

 

 

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

·      алгебраические системы уравнений;

·      трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

 

Системы линейных алгебраических уравнений

 

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

 

В матричном виде систему можно записать как

 

,

где  – матрица размерности ,  – вектор с  проекциями.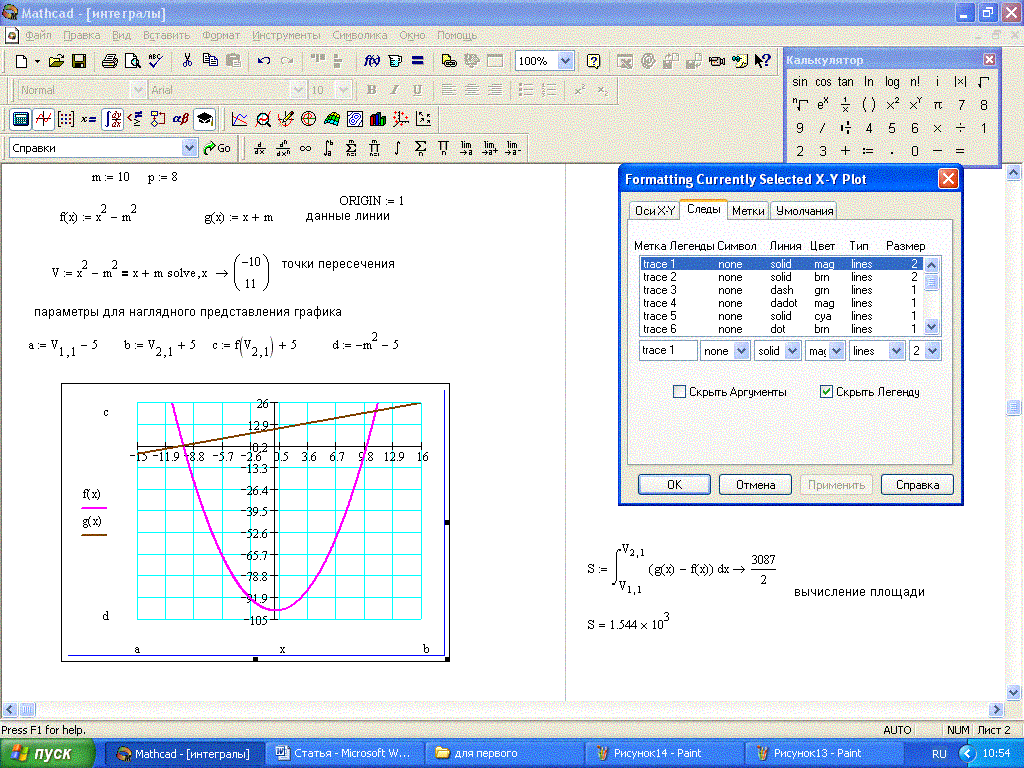

 

Для вычисления решения СЛАУ следует использовать функцию lsolve, обращение к которой имеет вид: lsolve(А,b), где А – матрица системы,  – вектор правой части.

Решение систем нелинейных уравнений

 

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD2001i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

 

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

Пример. Дана система уравнений:

Определить начальные приближения для решений этой системы.

 

 

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20).  ¨

Вычисление решения системы уравнений с заданной точностью. Для этого используется уже известный вычислительный блок Given.

 

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find(x), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке < Начальные условия >. Число аргументов функции должно быть равно числу неизвестных.

 

Следующие выражения недопустимы внутри блока решения:

·      ограничения со знаком ¹;

·      дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

·      блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr).

 

Пример. Используя блок Given, вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

 

 

Пример. Используя функцию , вычислите решение системы уравнений

 

 

Организация решения задач исследования операций в MATHCAD

Библиографическое описание:

Имомов, А. И. Организация решения задач исследования операций в MATHCAD / А. И. Имомов, Б. С. Эргашев. — Текст : непосредственный // Молодой ученый. — 2015. — № 8 (88). — С. 5-10. — URL: https://moluch.ru/archive/88/17276/ (дата обращения: 03.03.2023).

Основная цель работы — показать, как решаются основные задачи исследования операций, такие как задача линейного программирования, транспортная задача, задача о назначении, задача о коммивояжере, матричная игра в MathCAD.

Ключевые слова: исследование операций, задача линейного программирования, транспортная задача, задача о назначении, задача о коммивояжере, матричная игра, решения задач в MathCAD.

 

1. Управление и планирование являются наиболее сложными функциями в работе предприятий, фирм, служб администраций всех уровней. Долгое время они являлись монополией человека с соответствующей подготовкой и опытом работы [1–3].

Создание компьютеров и программных средств создало огромные возможности для развития науки, совершенствования методов планирования и управления производством. Однако без строгих формулировок задач, без математического описания процессов современный уровень управления и планирования не может быть достигнут. В последнее время появились математические системы- математические программы, позволяющие решить многие задачи без составления компьютерных программ, такие как MathCAD, Maple, Mathematica и т. д. [3–5].

Задачи управления и планирования обычно сводятся к выбору некоторой системы параметров и функций, которые приводят к экстремальным задачам следующего вида.

Требуется найти максимум или минимум функции

                                                                             (1)

при условиях:

                                                                                                       (2)

.                                                                                           (3)

где ,  — функции,  — параметры управления [1–3].

Выражение (1) называется функцией цели. Условия (2),(3) представляют собой ограничения поставленной задачи. Условия (3) справедливы для многих задач, особенно экономических, когда параметры управления  по своему физическому смыслу не могут быть отрицательными. Среди условий задачи могут быть равенства.

Математическая дисциплина, занимающаяся изучением экстремальных (максимальных или минимальных) задач управления, планирования и разработкой методов их решения, получила название исследования операций.

2. Решение задачи линейного программирования в MathCAD.

В задаче линейного программирования целевая функция и ограничения линейны:

,                                                                               (4)

.                                  (5)

Здесь в неравенствах возможны знаки . Когда все ограничения заданы равенствами, то говорят о канонической задаче линейного программирования, в остальных случаях — об общей задаче линейного программирования. Вводя матрицу , и векторы , ограничения можно задавать в векторно-матричном виде .

Каноническая задача линейного программирования решается с помощью хорошо известного симплекс метода [1–3]. Здесь мы покажем, как можно решить задачу линейного программирования с помощью математической системы MathCAD.

Решим задачу ([1],21.1). После знака // записываем замечание-смысл команд MathCAD.

ORIGIN: =1 m: =2 n: =4 i: =1..m j: =1..n // ввод конечных значений индексов

 // целевая функция

 // матрица и вектор ограничений

Given   // обращение к внутренней функции

 // вывод результатов

Переменная введена для экономии места. Здесь и дальше в блоке Given …Minimize знаки равенств и неравенств жирные. Они набираются в панели MathCAD булево.

3. Решение транспортной задачи в MathCAD. Задачи о назначении и коммивояжере.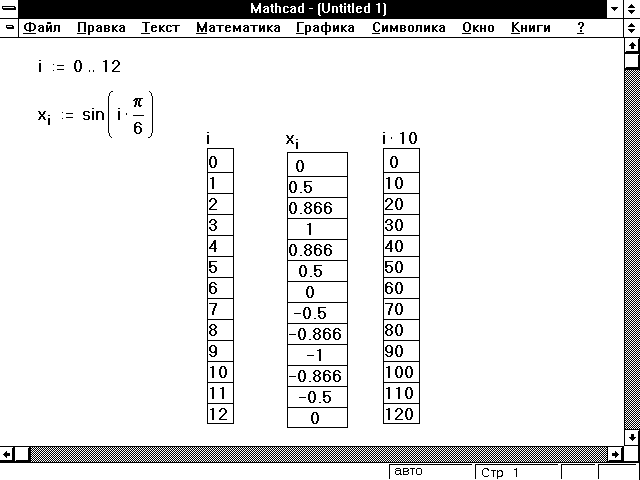

В организации перевозок некоторого продукта (груза) между пунктами его производства , , и пунктами потребления , , возникает транспортная задача. Каждый пункт производства  характеризуется запасом продукта  . Каждый пункт потребления  характеризуется потребностью в продукте , . Сеть дорог, соединяющая систему рассматриваемых пунктов, моделируется с помощью матрицы . Элемент  представляет собой нормы затрат на перевозку единицы груза из пункта производства  в пункт потребления . Через  обозначим количество продукта, перевозимого из пункта  в пункт . Тогда план перевозок груза представляется в виде матрицы:

.

Транспортная задача ставиться так:

,                                                                                       (6)

,                                                                                                   (7)

.                                                                                                   (8)

.                                                                                         (9)

Для решения закрытой транспортной задачи, т.  е. для случая , хорошо известным методом является метод потенциалов [1–3].

С транспортной задачей связаны задачи о назначении и о коммивояжере.

Задача о назначении формулируется таким образом: для реализации производственного процесса необходимо выполнить  операций. Имеется  рабочих, которые способны осуществить их, и время (затраты) выполнения каждым рабочим любой из  операций. Требуется определить: кто и какую операцию должен выполнить, чтобы суммарное время (затраты) выполнения всего производственного процесса было минимально. Возможны и другие постановки.

Формализация задачи. Введём матрицу, , где  при  и  при . Тогда каждый рабочий может выполнить лишь одну операцию и справедливо ограничение:

.                                                                                                      (10)

Каждая операция может выполняться лишь одним рабочим и справедливо ограничение:

.                                                                                                     (11)

Матрица системы (10,11) имеет ранг , т.  е. из  неизвестных  являются свободными.

Если обозначить себестоимость выполнения операции рабочим через , то суммарная себестоимость выполнения всех работ будет:

.                                                                                                   (12)

Задача о назначении заключается в минимизации сумму (12) при выполнении ограничений (10), (11) и . Для решения задачи о назначении разработан венгерский метод [1–3]. В решении задачи в матрице , в главной диагонали могут стоять либо 1 либо 0, но в каждой строке и столбце могуть стоять только по одной 1. Матрица С есть матрица себестоимости выполнения соответствующих операций.

Задача о коммивояжере формулируется таким образом: имеется  городов, выезжая из исходного города , коммивояжер должен побывать в каждом городе  по одному разу и должен вернуться в город . Задача заключается в определении последовательности городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время в пути, суммарное расстояние и т.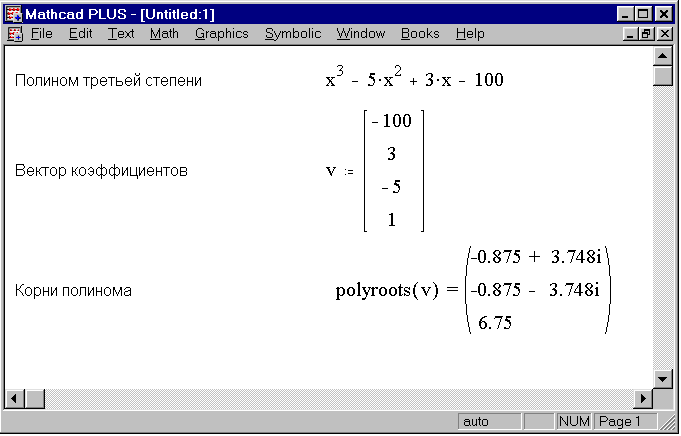

 д.

Задача о коммивояжере формализуется как задача о назначении, но только в матрице решений , в главной диагонали всегда должна стоять 0. Кроме того, в матрице С в главной диогонали должны стоять большие числа.

Здесь мы покажем, как можно решить транспортную задачу, задачи о назначении и о коммивояжере с помощью математической системы MathCAD. Ясно, что задачи о назначении и о коммивояжере являются частными случаями транспортной задачи.

Решим сначала транспортную задачу ([1],23.1).

ORIGIN: =1 m:=3 n: =4 i: =1..m j: =1..n // ввод конечных значений индексов

  // матрица и вектор ограничений

 //начальный план перевозок

 // целевая функция

Given  // обращение к внутренней функции

  // вывод результатов

Решим теперь задачу о назначении ([1], 26.1).

 //индексы

 //матрица и вектор ограничений

 // начальное приближение

 // целевая функция

Given  // внутренняя функция

  // вывод результатов

Given  // внутренняя функция

  // вывод результатов

Решим теперь задача о коммивояжере [5].

 // индексы

  // платёжная матрица

 // векторы ограничений

  // целевая функция

Given

   // внутренняя функция

  // вывод результатов

4. Решение матричных игр в MathCAD.

Матричные игры задаются платёжной матрицей , .

В матричной игре участвуют два игрока. Строки являются чистыми стратегиями первого игрока, а столбцы являются чистыми стратегиями второго игрока. Гарантированный выигрыш первого игрока, применяющего ю стратегию равен . Число

называется нижним значением игры, и называется максиминной стратегией первого игрока. Аналогично, число

называется верхним значением игры. Всегда . Если , то игра имеет седловую точку в чистых стратегиях, а число  называется значением (ценой) игры. Если игра имеет седловую точку, то существует элемент матрицы такой, что

.                                                                                                             (13)

Если игра не имеет седловую точку в чистых стратегиях, то по теореме Фона Неймана, игра имеет седловую точку в смешанных стратегиях. Для этого определяем вероятности

, .                                                      (14)

Смысл этих вероятностей заключаются в следующем. Первый игрок выбирает свою ю чистую стратегию с вероятностью , а второй игрок выбирает своюю чистую стратегию с вероятностью . Если первый игрок выбирает свою ю чистую стратегию с вероятностью , а второй игрок выбирает своюю чистую стратегию с вероятностью , то средний выигрыш первого игрока равен

.                                                                                               (15)

Выигрыш называется функцией игры. Пара смешанных стратегий называется седловой точкой функции , если

.                                                                                      (16)

Задача максимизации гарантированного выигрыша первого игрока и задача минимизации гарантированного проигрыша второго игрока сводятся к паре двойственных задач линейного программирования:

Задача первого игрока заключается в следующем

.                                  (17)

Задача второго игрока заключается в следующем

.                                 (18)

Процесс решения задач упрощается, если перейти к переменным

; .

Это возможно, если . Если так, то имеем:

Задача первого игрока принимает вид

.                                            (19)

Задача второго игрока принимает вид

.                                         (20)

Оптимальные стратегии игроков не изменится, если матрицу игры заменить матрицей . Так как, при этом цена игры увеличивается на .

Решим задачу ([1],31.3)

ORIGIN: =1 // начальное значение индексов

 // платёжная матрица

 // целевая функция

Given  // внутренняя функция

 // вывод результатов

 // целевая функция

Given  // внутренняя функция

 // внутренняя функция

 // вывод результатов

 

Литература:

 

1.         Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании: Учеб.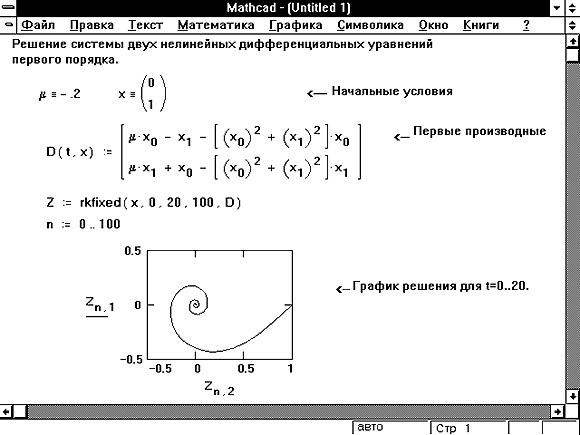  — 2-е изд., испр. — М.: Дело, 2001. — 688 с.

2.         Таха Х. А. Введение в исследование операций, 7-е издание.: Пер. с англ. — М.: Издательский дом «Вильямс», 2005. — 912 с: ил. — Парал. тит. англ.

3.         Охорзин В. А. Прикладная математика в системе MathCAD. -СПб, Лань.2008.-352 с.

4.         Имомов А «Организация приближённого решения интегральных уравнений в MathCAD». Молодой учёный, № 14(73), сентябрь 1, 2014 г.-с.6–15.

5.         Мусатенко К. Е., Раводин О. М. Компьютерная модель для лабораторной работы «Выбор оптимальной траектории движения транспортного робота с использованием задачи о коммивояжере». Молодой учёный, 12 (59), 2013 г.-с.71–75.

Основные термины (генерируются автоматически): задача, линейное программирование, транспортная задача, внутренняя функция, вывод результатов, целевая функция, ORIGIN, вектор ограничений, коммивояжер, чистая стратегия.

11.10: Решение линейных уравнений с помощью Mathcad

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

135018

• Франк Риу
• Колледж Святого Бенедикта/Университет Святого Иоанна

Численные методы : Система уравнений решается численно с помощью блока решения «Дано/Найти». Mathcad требует начальных значений для каждой переменной числового метода.

Исходные значения: x :=1 y :=1 z :=1

Дано: \(5 \cdot x + 2 \cdot y + z = 36\) \(x + 7 \cdot y + 3 \cdot z = 63\) \(2 \cdot x + 3 \cdot y + 8 \cdotz = 81\)

Найти (x, y, z) = \( \begin{pmatrix}
3,6\\
5,4\\
7.2
\end{pmatrix}\)

Можно использовать другие блоки решения Give/Find.

Дано \(\begin{pmatrix}
5 \cdot x + 2 \cdot y + z = 36\\
x + 7 \cdot y + 3 \cdot z = 63\\
2 \cdot x + 3 \cdot y + 8 \cdot z = 81
\end{pmatrix}
= \begin{pmatrix}
36\\
63\\
81
\end{pmatrix}\) Find(x, y, z) = \( \begin{pmatrix}
3.6\\
5.4\\
7.2
\end{pmatrix}\)

Дано \(\begin{pmatrix}
5 & 2 & 1\\
1 & 7 & 3\\
2 & 3 & 8
\end{pmatrix} \cdot \begin{pmatrix}
x\\
y\\
z
\end{pmatrix } = \begin{pmatrix}
36\\
63\\
81
\end{pmatrix}\) Find(x, y, z) = \( \begin{pmatrix}
3. 6\\
5.4\\
7.2
\end{pmatrix}\)

Матричные методы : Уравнения также можно решать с помощью матричной алгебры, как показано ниже. В матричной форме уравнения записываются как MX = C. Вектор решения находится путем умножения матрицы на обратную M.

M:= \(\begin{pmatrix}
5 & 2 & 1\\
1 & 7 & 3\\
2 & 3 & 8
\end{pmatrix}\) C:= \(\begin{pmatrix }
36\\
63\\
81
\end{pmatrix}\) X := M ^-1 \(\cdot\) C X = \(\begin{pmatrix}
3.6\\
5.4\\
7.2
\end{pmatrix}\)

Подтвердить, что решение найдено:

М \( \cdot\) X = \( \begin{pmatrix}
36\\
63\\
81
\end{pmatrix}\)

Альтернативное решение матрицы с помощью команды lsolve.

X := lsolve(M,C) X = \( \begin{pmatrix}
3.6\\
5.4\\
7.2
\end{pmatrix}\) M \( \cdot\) X = \( \begin {pmatrix}
36\\
63\\
81
\end{pmatrix}\)

Метод символов в реальном времени : Для использования метода символов в реальном времени в этом документе Mathcad требуются рекурсивные определения, четкие предыдущие значения x, y и z.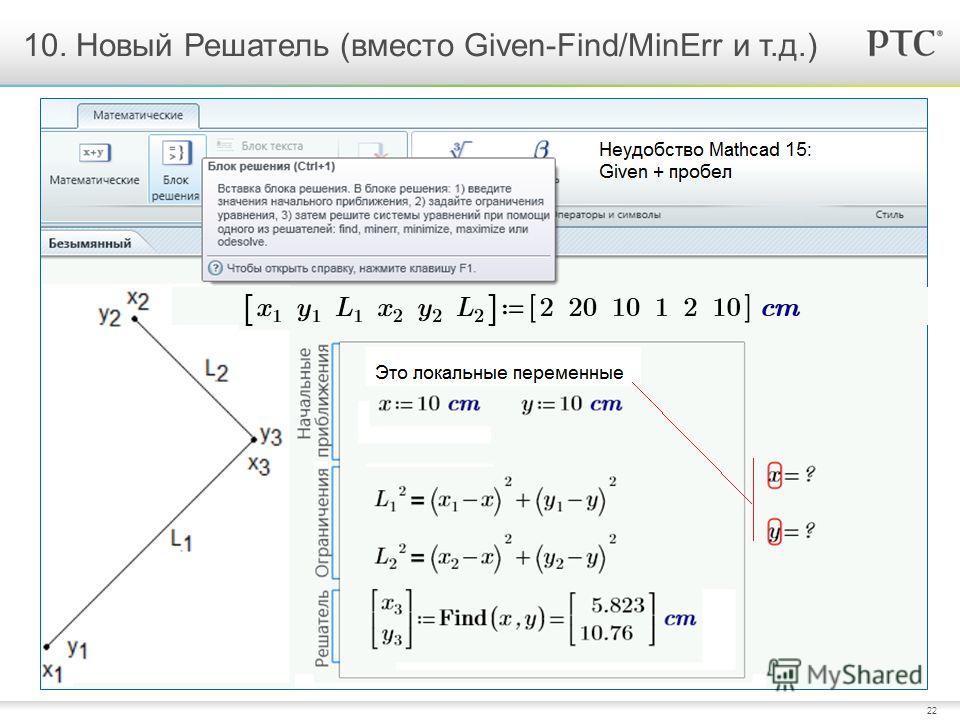 В этом не было бы необходимости, если бы x, y и z не были определены ранее.

х := х у := у z := z

\(\begin{pmatrix}
5 \cdot x + 2 \cdot y + z = 36\\
x + 7 \cdot y + 3 \cdot z = 63\\
2 \cdot x + 3 \cdot y + 8 \cdot z = 81
\end{pmatrix}
решить, \begin{pmatrix}
x\\
y\\
z
\end{pmatrix} \rightarrow \begin{pmatrix}
\frac{18} {5} & \frac{27}{5} & \frac{36}{5}
\end{pmatrix} = \begin{pmatrix}
3.6 & 5.4 & 7.2
\end{pmatrix}\)

---

Эта страница под названием 11.10: Решение линейных уравнений с помощью Mathcad распространяется под лицензией CC BY 4.0 и была создана, переработана и/или курирована Фрэнком Риу через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Франк Риу

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   № на стр.

2. Теги

   1. источник@https://faculty.csbsju.edu/frioux/workinprogress.html

Mathcad PLUS 6.0 Professional Edition — Socket 3

28 сентября 2019 г. 23 ноября 2019 г.

Для простого сложения или извлечения квадратного корня из числа всегда было достаточно калькулятора в Windows. Если вы хотите сделать что-то более сложное, требующее поверхностного графика или использования векторов, вам нужно что-то более специализированное. Некоторые могут попытаться использовать Excel или вытащить свой графический калькулятор. В качестве альтернативы есть Mathcad.

Mathcad на самом деле не для обычного пользователя; те, у кого есть опыт работы в области науки, статистики или инженерии, с большей вероятностью найдут его полезным.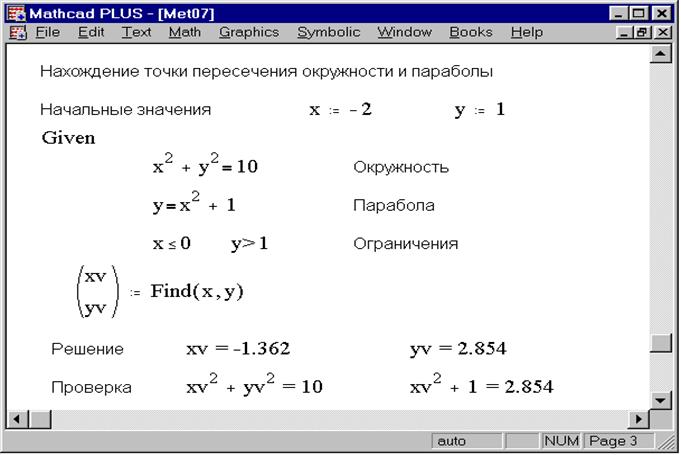 Это давно работающее приложение, которое началось в DOS в 1986 году и было разработано компанией MathSoft Incorporated из Массачусетса. Программное обеспечение все еще существует по сей день, однако теперь известно как PTC Mathcad после того, как Parametric Technology Corporation приобрела Mathsoft в 2006 году. Редакция PLUS позволяет прикреплять функциональные пакеты к целевым областям, а также предоставляет более полные возможности в области символьной математики.

Минимальные требования к ПК на базе 386, в идеале с математическим сопроцессором, 8 МБ ОЗУ и 20 МБ свободного места на диске. Было указано дополнительно 12 МБ из виртуальной памяти. Как и ожидалось, учитывая характер программного обеспечения, был рекомендован процессор 486. Версия 6.0 была последней для Windows 3.1, кроме того, для нее требовались надстройки Microsoft Win32s и Video for Windows. Видео для Windows предназначено для воспроизведения клипов AVI в рамках учебных пособий и позволяет экспортировать ваши рабочие листы в виде анимации. Windows NT 3.5 и Windows 95 официально поддерживались, а также был выпущен отдельный выпуск для System 7.x на Macintosh.

В начале установки предоставляется возможность добавить путь к Lotus Notes. Требовался как минимум клиент Notes 3.0 и сервер Notes, чтобы хранить вашу работу в базе данных. Это должно было разрешить контроль версий рабочих листов.

Установка Mathcad PLUS 6.0 в Windows 3.1.

Я не из тех, кто обычно использует такие программы, как Mathcad, но, к счастью, прилагаемые учебные пособия достаточно полны, чтобы помочь мне в этом. Как показано ниже, я создал простой график x-y на основе предоставленной формулы и внес коррективы в рисунки. Без учебника я не был уверен, как сопоставить формулу с пустым графиком, ожидая необходимости где-то указать формулу, как если бы вы связывали ячейки в электронной таблице с гистограммой. Это было так же просто, как ввести алгебраические буквы «x» и «f (x)» напротив оси в соответствии с формулой.

Приложение, подобное этому Я ожидал более тесного взаимодействия с Excel 5.