MATHCAD 14: Основные сервисы и технологии
Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 4
Упражнение 1:
Номер 1
Какая из приведенных функций не может быть использования для решения уравнений
Ответ:
 (1) root() 
 (2) lsolve() 
 (3) Find() 
 (4) CreateMesh() 
Номер 2
Какая переменная отвечает за точность вычислений корней уравнения функцией root() ?Ответ:
 (1) ORIGIN 
 (2) TOL 
 (3) начальное приближение 
 (4) аргумент функции 
Номер 3
Для численного решения уравнения с использованием функции root() необходимо задать:Ответ:
 (1) границы отрезка, где находится корень  
  (2) начальное приближение корня 
 (3) ничего не требуется 
 (4) максимальное значение функции уравнения 
Упражнение 2:
Номер 1
Решение системы уравнений с помощью блока given find дает решение:
Ответ:
 (1) приближенное 
 (2) минимальное  
 (3) точное  
 (4) максимальное 
Номер 2
Какой знак равенства в уравнениях используется в блоке решения Given Find:
Ответ:
 (1) := 
 (2) == 
 
 (4)  
Номер 3
Решение системы уравнений с помощью блока given minerr дает решение:
Ответ:
 (1) точное 
 (2) приближенное  
 (3) минимальное  
 (4) максимальное 
Упражнение 3:
Номер 1
Сколько корней имеет уравнение
Ответ:
 (1) 1 
 (2) 2 
 (3) 3 
 (4) 4 
Номер 2
Какими способами можно получить решение уравнения :
Ответ:
 (1) используя root()  
 (2) используя given Find())  
 (3) используя функцию lsolver()  
 (4) используя оператор solver 
Номер 3
Выбрать правильное решение уравнения :
Ответ:
 (2) (5.
01; 10.8) 
 (3) (3.05;13) 
 (4) (0,1;12) 
Упражнение 4:
Номер 1
При численном нахождении корней полинома n степени с помощью функции Polyroots(): аргументом функции являетсяОтвет:
 (1) вектор коэффициентов длиной n  
 (2) вектор коэффициентов длиной n+1 
 (3)
вектор коэффициентов длинойn-1  (4) начальное приближение 
Номер 2
Какими способами можно получить решение уравнения :
Ответ:
 (1) +используя функцию root()  
 (2) +используя блок given Find())  
 (3) +используя функцию Polyroots() 
 (4) используя функцию lsolver() 
 (5) +используя оператор solver 
Номер 3
Выбрать действительный корень уравнения :
Ответ:
 (1) (-0.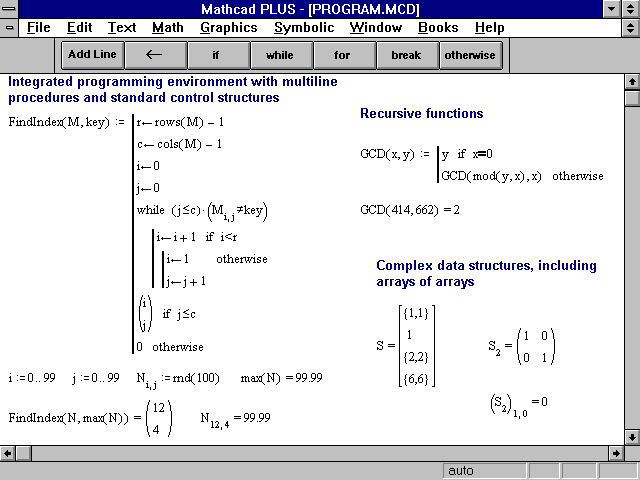
819) 
 (2) (-1.819) 
 (3) (0.819) 
 (4) (2.819) 
Упражнение 5:
Номер 1
Система уравнений имеет вид Сколько корней имеет система.
Ответ:
 (1) 1 
 (2) 2 
  (3) 3 
 (4) 4 
Номер 2
Какими способами можно получить решение системы уравнений
Ответ:
 (1) используя функцию root()  
 (2) используя блок given Find())  
 (3) используя функцию Polyroots() 
 (4) используя функцию lsolver() 
Какие решения являются корнями системы уравнений?
Ответ:
 (1) (-0,53; 0.
26) 
 (2) (1,89; 2.1) 
 (3) (1.71; 0.78) 
 (4) (6.53; 8.73) 
Упражнение 6:
Номер 1
Система уравнений имеет вид Сколько корней имеет система.
Ответ:
 (1) 1 
 (2) 2 
 (3) 3 
 (4) 4 
Номер 2
Какими способами можно получить решение системы уравнений:
Ответ:
 (1) используя функцию root()  
 (2) используя блок given Find())  
 (3) используя функцию Polyroots() 
 (4) используя функцию lsolver() 
Номер 3
Какие решения являются корнями системы уравнений?
Ответ:
 
70) 
 (2) (1,56; 4.91) 
 (3) (5.53; 10.26) 
 (4) (0.15; 1.02) 
Упражнение 7:
Номер 1
Решение систем линейных алгебраических уравнений в матричном виде методом обратной матрицы осуществляется с помощью формулы:
Ответ:
 (1)  
 (2)  
 (3)  
 (4)  
Номер 2
Сколько способов существует в MathCad для решения системы линейных алгебраических уравнений
Ответ:
 (1) 1 
 (2) 2 
 (3) 3 
 (4) 4 
Номер 3
Матрица A имеет вид , матрица .Выбрать правильное решение уравнения
Выбрать правильное решение уравнения Ответ:
 (1) (4; 2.93; 2.71) 
 (2) (3; 1.93; 1.71) 
 (3) (2; 0.93; 0.71) 
 (4) (1; -0.93;- 0.71) 
Упражнение 8:
Номер 1
Для решения задач оптимизации используются блоки:
Ответ:
 (1) given maximize 
 (2) given miniimize 
 (3) given find 
 (4) given solver 
Номер 2
В задаче оптимизации начальные значения неизвестных параметров вводятся с использованием знака:
Ответ:
 (1) := 
 (2) = 
 (3) = 
 (4)  
Номер 3
В задаче оптимизации оптимизируемая функция вводится с использованием знака:
Ответ:
 (1) := 
 (2) = 
 (3) = 
 (4)  
Упражнение 9:
Номер 1
Решение задачи оптимизации MathCad представляет в виде:
Ответ:
 (1) вектора 
 (2) числа (чисел) 
 (3) функции 
 (4) экстремального значения функции 
Номер 2
Максимальное значение функции при условии равно
Ответ:
 (1) 40 
 (2) 60 
 (3) 50 
 (4) 70 
Номер 3
Значения x и y, для которых функция имеет максимум при условии , равны
Ответ:
 (1) (1 ; 0.
4) 
 (2) (0.9 ; 3) 
 (3) (0.9 ;0.4) 
 (4) (0.7 ; 0.5) 
Упражнение 10:
Номер 1
Задачи оптимизации решаются методами :
Ответ:
 (1) математической статистики 
 (2) линейного программирования 
 (3) математического анализа 
 (4) решения дифференциальных уравнений  
Номер 2
Для решения задач оптимизации необходимо задать:
Ответ:
 (1) начальные значения неизвестных параметров  
 (2) начальное значение оптимизируемой функции  
 (3) ограничения для неизвестных параметров 
 (4) вид оптимизируемой функции  
Номер 3
Для решения задач оптимизации можно использовать встроенные функции MathCad:
Ответ:
 (1) maximize 
 (2) miniimize 
 (3) root() 
 (4) lsolver() 
Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 4
Маткад
МаткадНазначение
Чтобы присвоить значение переменной, которой не было присвоено значение, введите имя переменной, за которым следует знак равенства.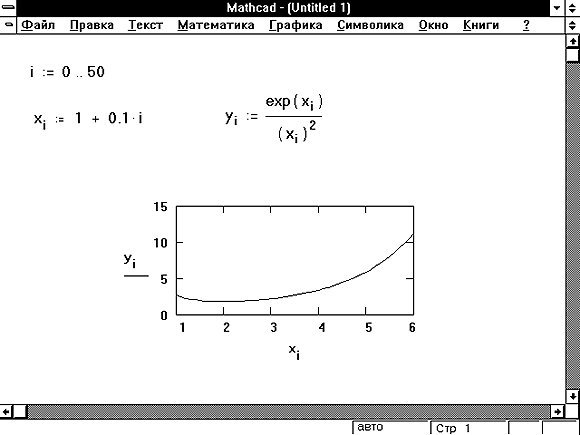
Если нет
значение было присвоено переменной, то вы увидите :=
и почерневший квадрат. Поместите новое значение переменной в квадрат.Если переменная имеет уже присвоено значение, чтобы увидеть, что это значение просто введите имя переменной и знак равенства.
Чтобы присвоить новое значение переменной, просто введите имя переменной, за которым следует двоеточие.
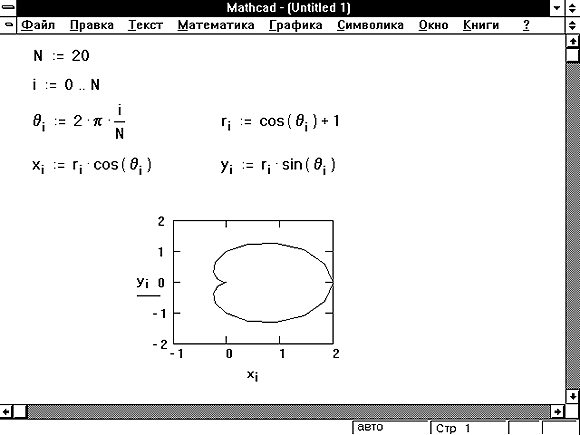
Графики рисования
Одной из приятных особенностей Mathcad является что он позволяет легко рисовать графики функций. Чтобы нарисовать график функции f(x), необходимо сначала указать, что диапазон значений, которые должна принимать переменная x. Затем определите функция. Например, нарисуем график sin(x) на интервал (0,90). Как и большинство языков программирования, Mathcad ожидает вам ввести значения в радианах в функцию sin, поэтому мы должны сделать преобразование. Чтобы ввести диапазон значений для переменной x, введите x с последующим двоеточием. Затем введите минимальное значение в диапазоне, за которым следует точкой с запятой, а затем максимальное значение в диапазоне.
Теперь, чтобы нарисовать график, перейдите в палитру графиков и выберите график xy.
В ящике слева ф(х). Вверху и внизу экрана появится зачерненный квадрат. прямоугольник. Это пределы y-диапазона.
После помещения f(x) в зачерненный квадрат на слева и наложение ограничений на диапазон y, если вы оставите область графика, Mathcad примет независимую переменную и x и выберите подходящий диапазон.
СИМВОЛИЧЕСКАЯ ДИФФЕРЕНЦИАЦИЯ И ИНТЕГРАЦИЯ
Кому символически дифференцировать, сначала введите вопросительный знак, а затем заполните в почерневших квадратах.
Символически дифференцировать, введите CTRL . а затем введите
Кому символически интегрировать, сначала нажмите CTRL I, а затем заполните почерневшие квадраты.
Кому символически интегрировать, введите CTRL . а затем войти.
ПРОГРАММИРОВАНИЕ В MATHCAD
Mathcad дает вам возможность писать и выполнение программ.
Есть три специальности
задачи, которые могут вам понадобиться при написании программы. Вы должны быть
способный выполнять условно, зацикливать и вызывать функции и подпрограммы.
Разберем простую программу.Приведенная выше программа найдет максимум два числа. Обратите внимание, что эта программа на самом деле функция. Цель функции — найти максимум два числа. Обратите внимание, что нам нужен условный оператор if. Ты можете найти это на вашей палитре программирования. Когда вы пишете программу, не вводите слово if. Последнее указанное значение будет вывод функции. Это значение локальной переменной z это то, что будет возвращено функцией max(x,y). Чтобы запустить программы, просто введите имя функции и дайте ему два метров в круглых скобках, а затем введите =.
Рассмотрим несколько более сложный
функция. Предположим, мы хотим найти наибольший общий делитель
два положительных целых числа. Мы используем алгоритм Евклида.
следующая функция реализует алгоритм Евклида.
Предположим, мы хотим узнать значения всех частные, а также НОД. Мы можем использовать матрицу возможности Mathcad.
Расчет и моделирование ваших идей
Главная › Продукты › Математика и моделирование › Mathcad › Расчет и моделирование ваших идей
Mathcad предоставляет сотни операторов и встроенных функций для решения технических задач. Используйте Mathcad для выполнения числовых расчетов или поиска символьных решений. Он работает с широким спектром числовых типов и типов данных, работает со скалярами, векторами и матрицами, а также автоматически отслеживает и преобразует единицы измерения.
Математические функции Mathcad включают:
- Блоки решения уравнений в частных производных для параболических (тепло) и гиперболических (волн) уравнений в одном измерении
- Комплексные аргументы и дробный порядок для функций Бесселя и новые функции Ганкеля
- Процедуры подбора для общего и экспоненциального подбора
- Функция трассировки ошибок для отслеживания источников ошибок в сложных листах
- Поддержка сложных аргументов для floor, ceil, round и trunc
- Новая функция sinc
Вычислительные возможности Mathcad включают:
- Числовые операторы выполняют суммирование, произведение, производные, интегралы и логические операции.
- Числовые функции применяют тригонометрические, экспоненциальные, гиперболические и другие функции и преобразования.
- Символика упрощает, дифференцирует, интегрирует и преобразует выражения алгебраически. Запатентованная технология Mathcad в режиме реального времени автоматически пересчитывает алгебраические решения.
- Векторы и матрицы управляют массивами и выполняют различные операции линейной алгебры, такие как поиск собственных значений и собственных векторов и поиск значений в массивах.
- Статистика и анализ данных генерируют случайные числа или гистограммы, подгоняют данные под встроенные и общие функции, интерполируют данные и строят модели распределения вероятностей. Решатели дифференциальных уравнений
- поддерживают обыкновенные дифференциальные уравнения, системы дифференциальных уравнений и краевые задачи как в командной строке, так и в блоках решения, которые используют естественные обозначения для задания DiffEQ и ограничений.
