Mathcad дифференциальные уравнения: Урок 25. Дифференциальные уравнения в Mathcad

Урок 25. Дифференциальные уравнения в Mathcad

Павел Демидов 10.12.2014 Уроки Mathcad 0

Дифференциальные уравнения очень часто применяются для описания изменяющихся процессов. Для начала рассмотрим обыкновенное дифференциальное уравнение (ОДУ):

Аналитическое решение этого уравнения:

Аналитическое решение является точным, и оно быстро дает результат. К сожалению, многие практические дифференциальные уравнения не могут быть решены аналитически. Поэтому нам нужны численные методы.

Метод Эйлера

Наиболее простой метод решения дифференциальных уравнений – метод Эйлера. Это старый метод, легкий для понимания и программирования.

Вычисляем изменения, шаг за шагом:

Сравнение результата и точного решения:

Заметьте, что решение методом Эйлера немного отличается от точного решения, и с ростом аргумента эта разница увеличивается. Уменьшить ошибку можно, если увеличить число шагов.

Блок решения ОДУ

Mathcad содержит все главные решатели дифференциальных уравнений. Их можно найти в меню Функции –> Дифференциальные уравнения. В этом уроке мы рассмотрим самый важный из них. Он прост в использовании и точен. Такой метод сочетает использование блока решения и функцию odesolve(). Перед решением определим:

Все вхождения зависимой переменной c в блоке решения записываются как функции независимой переменной, т.е. как c(t). Есть только одно исключение – запись слева от команды odesolve().

Решение этим методом и аналитическое решение близки. Этот же результат можно получить, записав производную через штрих с помощью [Ctrl+’]:

Пример: сердце и артерии

Работа сердца похожа на работу поршневого насоса: оба они расширяются и сжимаются, клапаны на входе и выходе позволяют течь только в одном направлении.

Впускной клапан открывается, когда камера расширяется и позволяет крови попасть в сердце из вены. При сжатии камеры впускной клапан закрывается, и кровь выбрасывается в артерию. Выпускной клапан закрывается, когда камера начинает расширяться.

Пульсация потока уменьшается расширением и сжатием эластичных стенок артерий.

Перепады давления возле легких низки: примем, что избыточное давление в точках A и B равно нулю. Центральным элементом являются артерии, изменение объема которых определяются разницей входного и выходного потоков:

Предположим, что объем сердца изменяется во времени по синусоидальному закону, но кровь выпускается только в течение положительной полуволны:

График для восьми ударов:

Средний поток – это интеграл объема в течение одного удара, деленный на время удара:

Расширение артерий зависит от эластичности стенок и их геометрии, но мы не будем анализировать это здесь. Предположим, что объем линейно зависит от избытка давления:

Чем эластичнее стенки, тем больше значение k.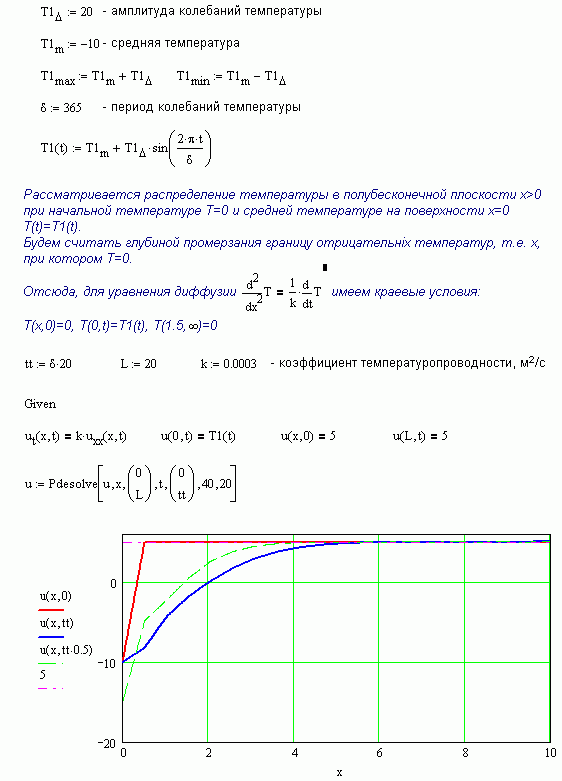 Определим три значения:

Сопротивление тела:

Разность давлений следует из:

Баланс объемов артерий:

Из

получаем дифференциальное уравнение для давления:

Решим его таким же образом, как и предыдущее, с той разницей, что k передадим в блок решения как параметр:

Выведем решения:

Максимумы давления зависят от эластичности артерий – чем больше эластичность, тем меньше давление:

Здесь мы использовали для примера одно дифференциальное уравнение первого порядка, но Mathcad этим не ограничивается.

Резюме

1. Обыкновенное дифференциальное уравнение содержит два вида переменных: зависимые (y(x)) и независимые (x).

 

2. Решение можно получить с помощью блока решения и функции odesolve().
3. Используйте оператор дифференцирования или штрих в записи дифференциального уравнения. Штрих вводится с помощью [Ctrl+’].
4. Введите необходимые граничные условия (они могут содержать запись производной через штрих).
5. Функция odesolve() содержит зависимую переменную и независимую переменную.
6. Зависимые переменные записываются как функции от независимых.
7. В завершение присвойте выходной переменной функцию odesolve(). Выходная переменная не записывается как функция от независимой переменной.
8. Однако, при использовании вывода нужно записывать его как функцию независимой переменной.

About Павел Демидов

Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.

View all posts by Павел Демидов →

Как узнать свободный объем сборки в Autodesk Inventor

Как еще можно использовать блоки в AutoCAD

MathCAD — это просто! Часть 21. Продолжаем борьбу с дифференциальными уравнениями

Итак, в прошлый раз, если вы помните, мы с вами поговорили об аналитическом решении дифференциальных уравнений. Процесс это, как мы убедились, совершенно несложный, однако имеющий один существенный и неоспоримый минус — совсем не факт, что мы сможем аналитически получить решение дифференциального уравнения даже тогда, когда наверняка знаем, что оно существует.

Мы с вами уже говорили когда-то о символьном процессоре MathCAD, и я рассказывал вам, что он, мягко говоря, далеко не всемогущ, и уж точно не настолько всемогущ, чтобы решать абсолютно все, что ему подсунет пользователь. В общем-то, причина этого вполне понятна: решение многих математических задач требует творческого подхода — откровенно говоря, лишь в очень малом числе задач оно лежит достаточно близко к поверхности, чтобы его сходу мог найти математический процессор MathCAD’а. Хотя алгоритмы, лежащие в его основе, чрезвычайно сложны (в отличие, кстати, от тех, на которых построены численные способы решения), они вовсе не безупречны и даже близко не приближают компьютер по мыслительным и аналитическим способностям к человеку. Когда речь идет о дифференциальных уравнениях, все сказанное не просто верно, а верно в квадрате.

Дифференциальные уравнения сами по себе довольно сложны и коварны, и потому не зря, как я говорил в прошлый раз, вызывают трепет у студентов, имеющих «удовольствие» их изучать. Конечно, существуют выработанные многими поколениями математиков способы решения основных типов дифференциальных уравнений, однако в реальных задачах (особенно физических и технических) иногда возникают уравнения, которые сложно решить с помощью классических формул. И символьный процессор MathCAD’а тоже опускает руки. Как быть в этом случае? Сдаться и признать такое уравнение нерешаемым? Думаю, вряд ли это такая уж хорошая идея. Гораздо эффективнее вооружиться тем инструментом, который придуман специально для решения того, что невозможно решить аналитически — численными методами. Изначально MathCAD проектировался и создавался именно как средство численного решения математических задач, а потому это удается ему особенно хорошо. Решать дифференциальные уравнения в этой мощной математической среде численно ничуть не сложнее, чем аналитически, и сейчас вы сможете в этом воочию убедиться.

Небольшое отступление

Чтобы лучше понимать суть численного решения дифференциальных уравнений, стоит сначала напомнить, что именно представляют собой решения дифференциальных уравнений. Для простоты остановимся на простейшем (простите за тавтологию, но здесь она неизбежна) случае — обыкновенном дифференциальном уравнении с одной переменной первого порядка (т.е. только с первыми производными). Давайте вспомним, что именно мы ищем, решая дифференциальное уравнение? Ищем мы некоторую функцию, которая будет удовлетворять данному уравнению — то есть при подстановке в него превращать его в тождество (верное числовое равенство). Такая функция может существовать, а может и нет. Будем считать, что она существует — ведь в противном случае получается, что дифференциальное уравнение, которое мы пытаемся решить, на самом-то деле нерешаемо. Как мы помним, любое дифференциальное уравнение должно включать в себя хоть одну производную искомой величины — иначе оно не будет дифференциальным, и решать его нужно будет с помощью методов, применяемых к обычным уравнениям.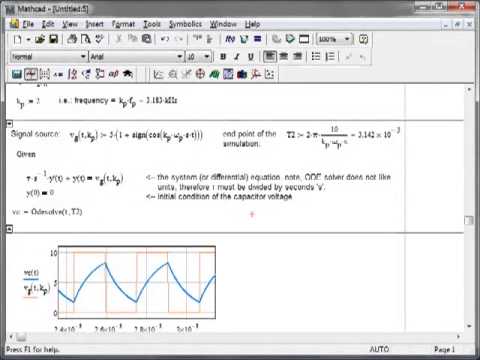

Но, поскольку уравнение содержит производные — значит, его решение верно с точностью до константы. То есть, вообще говоря, решений бесконечное множество, и каждое отличается от другого каким-то постоянным членом. Ведь при дифференцировании любая постоянная обращается в ноль, и, значит, решение с любой константой будет верным.

Если интерпретировать геометрически решения дифференциального уравнения, мы получим семейство кривых, проходящих через все точки плоскости. Для того, чтобы выделить из этих всех кривых какую-то одну, на уравнение накладывают дополнительные ограничения. Формулироваться эти ограничения могут либо в виде задачи Коши, либо в виде граничной задачи. Задача Коши определяет заданную кривую с помощью задания значений самой искомой функции и ее производных (для уравнений высших порядков) в какой-то определенной точке. Граничная же задача формулируется как задание значений функции на границах искомого отрезка. Физическая интерпретация этих двух ограничений такова: задача Коши определяет решение временной задачи, задавая значения переменных в начальный момент времени.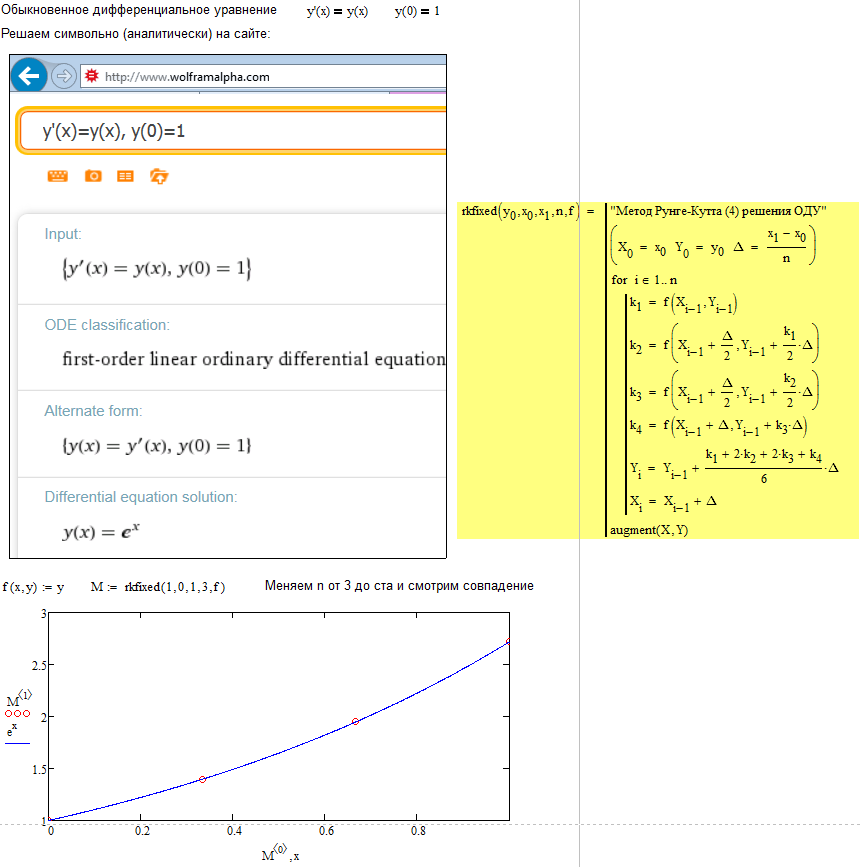

Граничная же задача (она также часто называется краевой) нужна для решения пространственных задач: она определяет начальные значения переменных в рамках какой-то пространственной области. Решение этих двух типов задач численно в MathCAD’е отличается, и вы сами сможете убедиться в том, что отличия эти порой довольно-таки существенны. Поэтому мы пойдем, как водится, от простого к сложному и начнем решение дифференциальных уравнений с рассмотрения задачи Коши.

Задача Коши для обыкновенных дифференциальных уравнений

Давайте посмотрим, как можно решать задачу Коши для обыкновенного дифференциального уравнения. В качестве уравнения возьмем простое до ужаса dX(t)/dt + X(t) = 0. Думаю, вы сможете сразу сказать, что за выражение будет решением данного уравнения. Конечно же, это экспонента с показателем минус t. Тем не менее, для того, чтобы удостовериться, что MathCAD правильно решает дифференциальные уравнения численными методами, мы подсунем это простейшее уравнение ему и посмотрим, как он с ним справится.

Для того, чтобы показать MathCAD’у, где начинается условие нашей задачи Коши, мы должны воспользоваться ключевым словом MathCAD’а — Given (обязательно писать его с большой буквы, поскольку, как вы помните, среда MathCAD чувствительна к регистру букв в именах переменных, функций и ключевых слов). После того, как записано это слово, мы должны записать начальные условие. Поскольку у нас уравнение первого порядка, то оно у нас будет всего одно — например, можно написать X(0) = 1. Далее (то есть под начальным условием) мы должны записать само дифференциальное уравнение, решением которого мы нагрузим MathCAD. Ну, а для поиска решений мы применим функцию Odesolve. У функции этой предусмотрено два (в нашем случае) параметра. Первый — это имя переменной, по которой будет проводиться интегрирование уравнения (в нашем случае, сами понимаете, выбирать, собственно говоря, не из чего — это будет t), а второй параметр — конечное значение интегрирования, задающее верхнюю границу того интервала, для которого MathCAD будет искать решение нашего уравнения. Собственно, после функции Odesolve уже можно ничего и не писать — если уравнение имеет решения, то оно обязательно будет решено.

Не писать-то, конечно, можно, только это не лучший вариант. Как проверить решение уравнения? Исходя из того, что у нас сейчас простейший одномерный случай, проще всего построить график этого решения. По нему отлично видно, что MathCAD самым что ни на есть замечательным образом справился с поставленной перед ним задачей и решил уравнение именно так, как оно и должно решаться: перед нами — не что иное, как график экспоненциальной функции с отрицательным показателем.

Здесь, правда, возможны некоторые накладки. Совсем недавно мы с вами, если помните, говорили об использовании комплексных чисел в MathCAD’е. При решении дифференциальных уравнений MathCAD также по умолчанию оперирует именно комплексными числами, и это отнюдь не случайно: ведь комплексные решения получаются в дифференциальных уравнениях гораздо чаще, чем действительные. И если у вашего уравнения будут комплексные корни, то MathCAD не сможет построить его график, и тогда нужны будут другие способы знакомства с решением — можно будет, скажем, построить таблицу решения в определенных ключевых точках и посмотреть, какие они имеют значения.

Краевая задача для обыкновенных дифференциальных уравнений

Давайте теперь еще коротко поговорим о решении граничной задачи для обыкновенных дифференциальных уравнений. С помощью функции Odesolve, в общем-то, решать ее нужно будет точно так же, как и задачу Коши — с той только, конечно, разницей, что вместо начального условия нужно записать граничные. В качестве простой иллюстрации рассмотрим дифференциальное уравнение d2X(t)/dt2 + dX(t)/dt + X(t) = 0. Граничные условия будут такими: X(0) = 10, X(10) = 0. Конечно, теперь уже такую простую аналитическую формулу решения, как для первого уравнения, нам подобрать не удастся, однако в этом нет ничего страшного, потому что MathCAD сможет ничуть не хуже построить график решения нашего обыкновенного дифференциального уравнения.

Конечно, использование функции Odesolve — не единственный метод решения обыкновенных дифференциальных уравнений в среде MathCAD, однако он достаточно удобен в силу своей простоты. В следующий раз мы с вами, конечно, познакомимся и с другими способами их решения, которые предлагает пользователю эту мощная математическая среда, но пока что достаточно — нехорошо перегружать читателя информацией, особенно по такому сложному предмету, как дифференциальные уравнения. Пусть даже MathCAD и облегчает их решение, все равно лучше не торопиться с тем, чтобы в них въехать.

Подведем итоги

Что ж, давайте подытожим все то, о чем мы с вами успели сейчас поговорить. Как обычно, итоги будут простыми и жизнеутверждающими. Численное решение дифференциальных уравнений — гораздо более универсальный способ их решения, чем аналитическое решение, поскольку численные методы как раз и создавались для тех случаев, когда искать аналитическое решение не слишком удобно или попросту абсурдно. Правда, конечно, в результате численного решения мы не получим простую и красивую формулу (хотя, когда речь идет о дифференциальных уравнениях, весьма наивно ожидать ее получение и в результате аналитического решения). Зато мы получим хоть какой-то результат — а это, согласитесь, гораздо лучше, чем отсутствие вообще любого результата. То есть, как говорит мудрая пословица, лучше синица в руках, чем журавль в небе. Это как раз таки именно тот самый случай. Решать численно дифференциальные уравнения в MathCAD, как вы могли убедиться, совсем не сложно, однако, естественно, везде есть свои тонкости, и численные методы совсем не панацея. Немного об этом рассказано в справке самого MathCAD’а, и именно ее чтением вы можете заняться, чтобы не терять время зря в ожидании следующей статьи из серии «MathCAD — это просто».

SF, [email protected]

Компьютерная газета. Статья была опубликована в номере 35 за 2008 год в рубрике soft

Решение дифференциальных уравнений » MathCadHelp.

com » Номер 1 в заданиях MathCad

В этой главе описывается, как решать обыкновенные дифференциальные уравнения и уравнения в частных производных, имеющие решения с действительными значениями. Mathcad Standard поставляется с функцией rkfixed, решателем Рунге-Кутты общего назначения, который можно использовать для дифференциальных уравнений n-го порядка с начальными условиями или для систем дифференциальных уравнений. Mathcad Professional включает множество дополнительных, более специализированных функций для решения дифференциальных уравнений. Некоторые из них используют свойства дифференциального уравнения для повышения скорости и точности. Другие полезны, когда вы собираетесь построить решение, а не просто оценивать его в конечной точке.

Данную главу составляют следующие разделы:

Решение обыкновенных дифференциальных уравнений
Использование функции rkfixed для решения обыкновенного дифференциального уравнения n-го порядка с начальными условиями. Этот раздел является обязательным для всех остальных разделов этого .

Системы дифференциальных уравнений
Как адаптировать функцию rkfixed для решения систем дифференциальных уравнений с начальными условиями.

Специализированные программы для решения дифференциальных уравнений
Описание дополнительных функций решения дифференциальных уравнений и случаев, когда вы можете их использовать.

Краевые задачи
Как решать краевые задачи с многомерными функциями.

Решение обыкновенных дифференциальных уравнений

В дифференциальном уравнении вы решаете неизвестную функцию, а не просто число. Для обыкновенных дифференциальных уравнений неизвестная функция является функцией одной переменной. Уравнения с частными производными — это дифференциальные уравнения, в которых неизвестное является функцией двух или более переменных.

Mathcad имеет множество функций для возврата решения обыкновенного дифференциального уравнения. Каждая из этих функций численно решает дифференциальные уравнения. Вы всегда будете получать матрицу, содержащую значения функции, оцененные по набору точек. Эти функции отличаются конкретным алгоритмом, который каждая из них использует для решения дифференциальных уравнений. Однако, несмотря на эти различия, для каждой из этих функций необходимо указать как минимум три вещи:

• Начальные условия.
• Диапазон точек, по которым вы хотите оценить решение.
• Само дифференциальное уравнение, записанное в конкретной форме, описанной в этом документе.

В этом разделе показано, как решить одно обыкновенное дифференциальное уравнение с помощью функции rkfixed. Он начинается с примера решения простого дифференциального уравнения первого порядка, а затем показывает, как решать дифференциальные уравнения более высокого порядка.

Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка — это уравнение, в котором производная старшего порядка неизвестной функции является первой производной. На рис. 16-1 показан пример решения относительно простого дифференциального уравнения. :

• В левом столбце указаны точки, в которых оценивается решение дифференциального уравнения.

• Правый столбец содержит соответствующие значения решения.

Решение дифференциального уравнения первого порядка.

Уравнения высшего порядка

Процедура решения дифференциальных уравнений высшего порядка является расширением той, которая используется для дифференциальных уравнений второго порядка. Основное отличие состоит в том, что:

• Функция D теперь представляет собой вектор из n элементов

Уравнения высшего порядка

Решение дифференциального уравнения высшего порядка.

 

решение системы дифференциальных уравнений в mathcad

спросил 10 лет, 6 месяцев назад

Изменено 10 лет, 6 месяцев назад

Просмотрено 5к раз

$\begingroup$

Я хочу научиться решать систему дифференциальных уравнений в MathCad вот так:

 dI(t)/dt = коэфф * I(t) * S(t)
dS(t)/dt = -коэфф * I(t) * S(t)
N = S (t) + I (t)
 

где ‘N’ и ‘коэффициент’ — заданные пользователем коэффициенты

В MathCad я сделал:

 ( коэфф * у0 * у1 )
D(t, у) := ( )
            (-коэфф * у0 * у1)
      ( 1 )
ик := ( )
      ( 9 )
 

Но :

 S := rkfixed (ic, 0, 10, 100, D)
 

возвращает: D — здесь нельзя использовать эту функцию.

И я не знаю как и куда вставлять N=S(t) + I(t) уравнение 🙁

• обыкновенные-дифференциальные-уравнения

$\endgroup$

5

$\begingroup$

Могу дать ответ по вышеуказанной системе (2 ОДУ). Для вашей системы уравнение 3 может быть получено из уравнений 1,2, поскольку: $$\frac{dI(t)}{dt}=coeff\cdot S(t)\cdot I(t) \hspace{0,5cm} (1 )$$ $$\frac{dS(t)}{dt}=-коэфф\cdot S(t)\cdot I(t) \hspace{0,5 см} (2)$$

Сложив $(1)$ и $(2)$, вы получите:

$$\frac{dI(t)}{dt}+\frac{dS(t)}{dt}=0 \Leftrightarrow I (t)+S(t)=c \\forall\t\geq0$$, где $c$ — константа. Итак, определяя IC, вы также определяете $N=c=I(0)+S(0)$, и поэтому уравнение $(3)$ бесполезно. Что касается Mathcad, поскольку вы пытаетесь двигаться вперед во времени, вы правильно решили использовать rkfixed. Вот код mathcad, который я использовал для примера задачи:

Как видите, сумма $S(t)+I(t)$ постоянна для каждого t и равна 1,1, как определено начальным условием.