Матричные функции в Mathcad
Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.
Среди функций, предназначенных для создания матриц, следует выделить функцию matrix(L,N,f), где L – число строк матрицы, N – число столбцов матрицы, f – функция f(l,n) при . Другая функция из этой группы identity(n). Функция предназначена для создания единичной матрицы размерности n. Следующая функция geninv(M) позволяет осуществить обращение матрицы M
Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.
Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.
Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).
Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу.
Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.
Простейшие вычисления MathCAD
Слияние матриц
Для того чтобы составить из двух или более матриц одну, в MathCAD предусмотрены две матричные функции:
— augment (А, B, C,…) — матрица, сформированная слиянием матриц-аргументов слева направо;
— stack (А, B, C,…) — матрица, сформированная слиянием матриц-аргументов сверху вниз;
3. Вывод размера матриц
Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции:
— rows (A) — число строк;
— cols (A) — число столбцов;
— length (v) — число элементов вектора;
— last (v) — индекс последнего элемента вектора;
4.
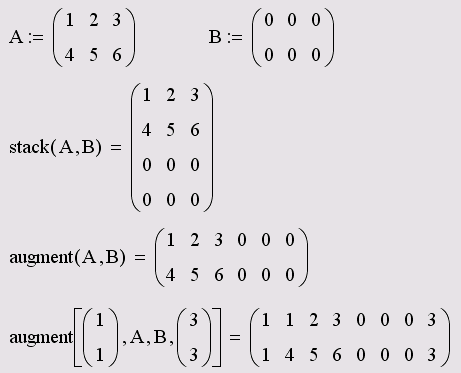Сортировка матриц
Часто бывает нужно переставить элементы матрицы или вектора, расположив их в определенной строке или столбце в порядке возрастания или убывания. Для этого имеются несколько встроенных функций, которые позволяют гибко управлять сортировкой матриц:
— csort(A, i) — сортировка строк матрицы выстраиванием элементов i-го столбца в порядке возрастания;
— rsort(A, i) — сортировка столбцов матрицы выстраиванием элементов i-й строки в порядке возрастания;
— reverse (v) — перестановка элементов вектора в обратном порядке;
Ранг матрицы
Рангом (rank) матрицы называют наибольшее натуральное число k, для которого существует не равный нулю определитель k-ro порядка подматрицы,составленной из любого пересечения k столбцов и k строк матрицы.
Для вычисления ранга в MathCAD предназначена функция rank.- rank (A) — ранг матрицы; А — матрица.
Построение графиков.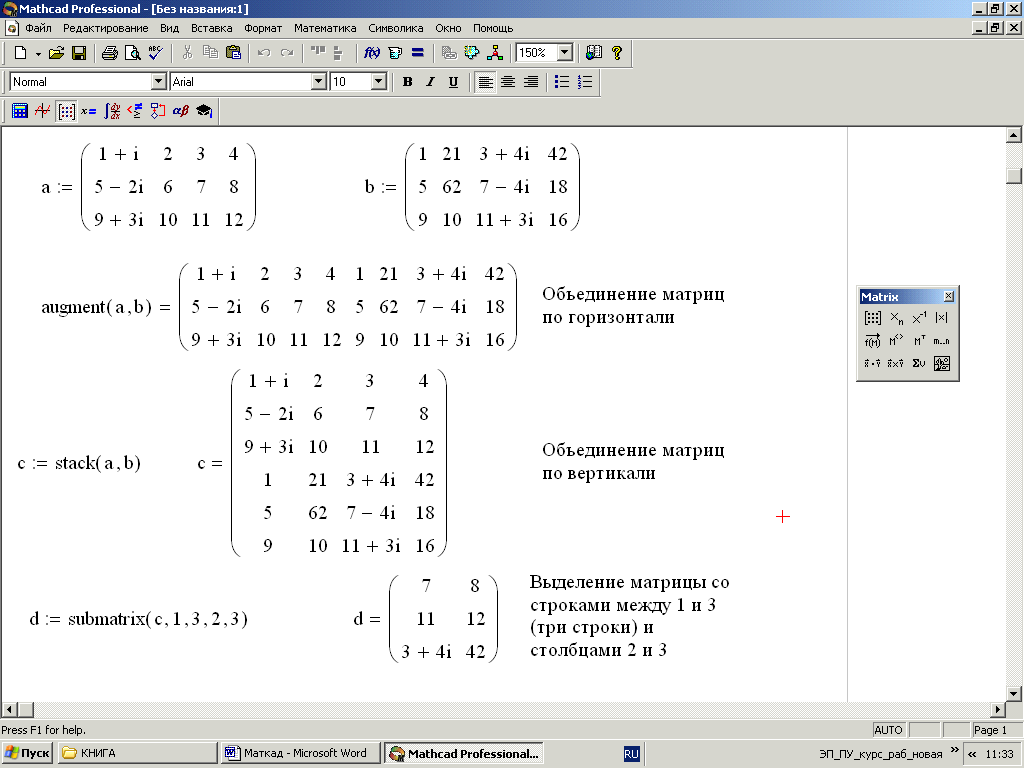
Существует два основных способа построения графиков функций в Mathcad.
1. Задать интервал изменения аргумента в формате
x:=начальное значение[,начальное значение+шаг]..конечное значение
в скобках указан необязательный параметр, если его нет, шаг, по умолчанию, равен 1
После чего можно определить функцию от этого аргумента, например:
2.
НОУ ИНТУИТ | Лекция | Нечеткие множества
Аннотация: В лекции представлены методы моделирования экономических задач с использованием нечетких множеств в среде Mathcad. Введены основные понятия теории нечетких множеств. На примерах показаны операции над множествами, расчет свойств. Рассмотрены оригинальные задачи, в которых применен нечетко-множественный подход в процессе принятия решения. Техника моделирования реализована с помощью матриц программы Mathcad.
Цель лекции. Познакомить с нечеткими множествами. Научить ставить задачу для построения нечетко-множественной модели.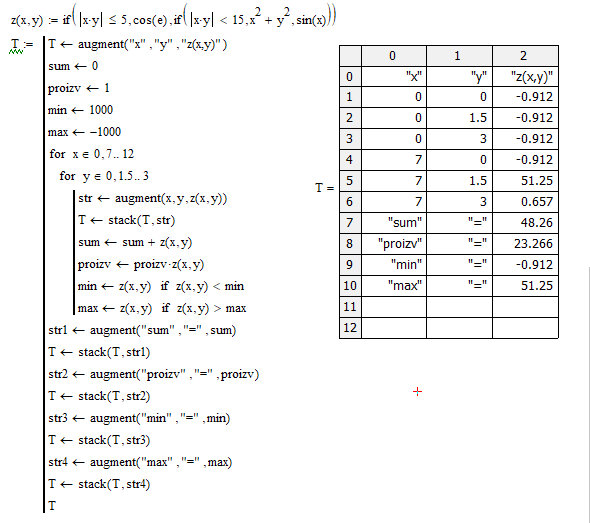
Показать, как строить нечеткие множества и производить действия над ними в Mathcad. Представить методы решения нечетко-множественной модели в процессе решения задач.
6.1 Нечетко-множественное моделирование
При моделировании широкого класса реальных объектов возникают необходимость принимать решения в условиях неполной нечеткой информации. Современным перспективным направлением моделирования различного вида неопределенностей является теория нечетких множеств. В рамках теории нечетких множеств разработаны методы формализации и моделирования рассуждений человека, таких понятий как «более или менее высокий уровень инфляции», «устойчивое положение на рынке», «более ценный» и т.д.
Впервые понятие нечетких множеств предложил американский ученый Л.А.Заде (1965 г ). Его идеи послужили развитию нечеткой логики . В отличие от стандартной логики с двумя бинарными состояниями (1/0, Да/Нет, Истина/Ложь), нечеткая логика позволяет определять промежуточные значения между стандартными оценками.
Примерами таких оценок являются: «скорее да, чем нет», «наверное да», «немного вправо», «резко влево» в отличие от стандартных: «вправо» или «влево», «да». В теории нечетких множеств введены нечеткие числа как нечеткие подмножества специализированного вида, соответствующих высказываниям типа «значение переменной примерно равно а». В качестве примера рассмотрим треугольное нечеткое число, где выделяются три точки: минимально возможное, наиболее ожидаемое и максимально возможное значение фактора. Треугольные числа – это самый часто используемый на практике тип нечетких чисел, причем, чаще всего их используют в качестве прогнозных значений параметра. Например, ожидаемое значение инфляции на следующий год. Пусть наиболее вероятное значение – 10%, минимально возможное – 5%, а максимально возможное – 20%, тогда все эти значения могут быть сведены к виду нечеткого подмножества или нечеткого числа A: А: (5, 10, 20)
С введением нечетких чисел оказалось возможным прогнозировать будущие значения параметров, которые меняются в установленном расчетном диапазоне.
Вводится набор операций над нечеткими числами, которые сводятся к алгебраическим операциям с обычными числами при задании определенного интервала достоверности (уровня принадлежности). Применение нечетких чисел позволяет задавать расчетный коридор значений прогнозируемых параметров. Тогда ожидаемый эффект оценивается экспертом также как нечеткое число со своим расчетным разбросом (степенью нечеткости).
Нечеткая логика, как модель человеческих мыслительных процессов, встроена в системы искусственного интеллекта и в автоматизированные средства поддержки принятия решений (в частности, в системы управления технологическими процессами).
6.2 Основные понятия теории нечетких множеств
Множество — неопределяемое понятие математики. Георг Кантор (1845 – 1918) – немецкий математик, чьи работы лежат в основе современной теории множеств, дает такое понятие: «…множество — это многое, мыслимое как единое».
Множество, включающее в себя все объекты, рассматриваемые в задаче, называют универсальным множеством. Универсальное множество принято обозначать буквой . Универсальное множество является максимальным множеством в том смысле, что все объекты являются его элементами, т.е. утверждение в рамках задачи всегда истинно. Минимальным множеством является пустое множество – , которое не содержит ни одного элемента. Все остальные множества в рассматриваемой задаче являются подмножествами множества . Напомним, что множество называют подмножеством множества , если все элементы являются также элементами . Задание множества — это правило, позволяющее относительно любого элемента универсального множества однозначно установить, принадлежит множеству или не принадлежит. Другими словами, это правило, позволяющее определить, какое из двух высказываний, или , является истинным, а какое ложным. Одним из способов задания множеств является задание с помощью характеристической функции.
Характеристической функцией множества называют функцию , заданную на универсальном множестве и принимающую значение единица на тех элементах множества , которые принадлежат , и значение нуль на тех элементах, которые не принадлежат :
| ( 6.1) |
В качестве примера рассмотрим универсальное множество и два его подмножества: — множество чисел, меньших 7, и — множество чисел, немного меньших 7. Характеристическая функция множества имеет вид
| ( 6.2) |
intuit.ru/2010/edi»>Множество в данном примере является обычным множеством.Записать характеристическую функцию множества , используя лишь 0 и 1, невозможно. Например, включать ли в числа 1 и 2? «намного» или «ненамного» число 3 меньше 7? Ответы на эти и подобные им вопросы могут быть получены в зависимости от условий задачи, в которой используются множества и , а также от субъективного взгляда того, кто решает эту задачу. Множество называется нечетким множеством. При составлении характеристической функции нечеткого множества решающий задачу (эксперт) может высказать свое мнение относительно того, в какой степени каждое из чисел множества принадлежит множеству . В качестве степени принадлежности можно выбрать любое число с отрезка . При этом означает полную уверенность эксперта в том, что — столь же полную уверенность, что говорит о том, что эксперт затрудняется в ответе на вопрос, принадлежит ли множеству или не принадлежит. Если , то эксперт склонен отнести к множеству , если же , то не склонен.
Функцией принадлежности нечеткого множества называют функцию , которая
- устанавливает значения степени принадлежности нечеткому множеству каждого из элементов универсального множества и принимает значения на отрезке .
- позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству .
Такую функцию называют функцией принадлежности нечеткому множеству . — Максимальное значение функции принадлежности , присутствующее в множестве — верхняя грань — называется супремум. Функция принадлежности отражает субъективный взгляд специалиста на задачу, вносит индивидуальность в ее решение.
Характеристическую функцию обычного множества можно рассматривать как функцию принадлежности этому множеству, но в отличие от нечеткого множества, принимает лишь два значения: 0 или 1.
Нечетким множеством называют пару , где — универсальное множество, — функция принадлежности нечеткого множества .
Несущим множеством или носителем нечеткого множества называют подмножество множества , состоящее из элементов, на которых .
Точкой перехода нечеткого множества называют элемент множества , на котором .
В рассматриваемом примере, где , — множество чисел, меньших 7, — множество чисел, немного меньших 7, субъективно выбираем значения для множества , которые будут составлять функцию принадлежности . В таблице 6.1 представлены функции принадлежности и для и .
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0,5 | 0,6 | 0,8 | 0,9 | 0 | 0 | 0 | 0 |
intuit.ru/2010/edi»>Часто используется более компактная запись конечных или счетных нечетких множеств. Так, вместо приведенного выше табличного представления подмножеств и , эти подмножества можно записать следующим образом:В приведенных равенствах указаны значения функции принадлежности для соответствующих элементов множества , знак "+" означает объединение одноэлементных подмножеств , для которых значения функции принадлежности больше нуля. Такое объединение называют несущим множеством или носителем соответствующего нечеткого множества. Так, несущее множество для состоит из чисел: .
Нечеткое множество записывают в виде (1.2), если , и в виде (1.3), если непрерывно.
Общая форма записи нечеткого подмножества для случаев, когда U дискретно имеет вид:
(
6. 3) |
В общем случае нечеткое множество B с непрерывным носителем U обозначается
| ( 6.4) |
В выражениях (6.3) и (6.4), как правило, указываются лишь элементы несущего множества. Использование символа интеграла не означает интегрирования, но предполагает, объединение по всем элементам несущего множества . Знак интеграла показывает, что несущее множество является частью числовой оси.
Элемент множества , на котором значение функции принадлежности равно 0.5, называют точкой перехода. Точкой перехода для множества в рассмотренном выше примере является .
Точка перехода – это точка, о которой мнение эксперта можно выразить словами "неизвестно", "не определено" и т.п. Если функция принадлежности нечеткого множества достигает 1, то множество называют нормальным, если не достигает — субнормальным. Поскольку в разобранном примере ни одно из значений не достигло своего возможного максимального значения – 1, то – нечеткое субнормальное множество. Субнормальное множество можно нормировать, разделив все значения функции принадлежности на ее наибольшее значение. Множество после нормирования примет следующий вид: .
Удобно представление нечетких множеств в виде графиков функций принадлежности (рис.6.1).
Рис. 6.1. Функции принадлежности обычного множества и нечеткого множества B
Матричных функций в Mathcad
Mathсad имеет в себе более 50 функций , которые выполняют операции с векторами и матрицами.
Все функции можно разделить на группы в зависимости от их функциональности. Например: функции, которые создают матрицы общего и специального вида, функции для редактирования и преобразования матриц, функции, определяющие параметры матрицы и т. Д. Давайте изучим функции, которые имеют основное прикладное значение.
Среди функций, которые используются для создания матриц, важно отметить функцию matrix (L, N, f) , где L — количество строк матрицы, N — количество столбцов матрицы, f — функция f (l, n) . Другая функция той же группы — identity (n) . Он используется для создания функции единицы размерности n . Следующая функция geninv (M) позволяет произвести инверсию матрицы M , аналогичную операции M -1 .
Для определения размерности матрицы Mathcad предлагает функцию строк (M) , которая определяет количество строк матрицы M , и функцию cols (M) , которая определяет количество столбцов матрицы M .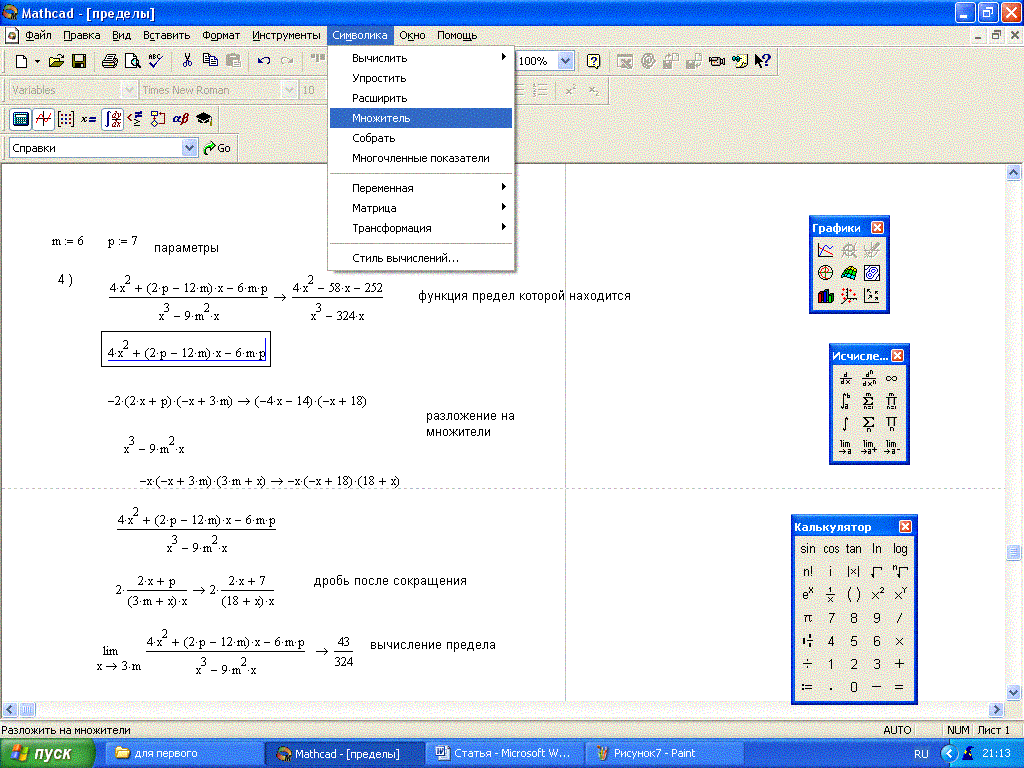
Сортировку составляющих матрицы выполняют две функции: csort (M, i) , rsort (M, j) . Функция csort (M, i) выполняет сортировку по возрастанию компонентов столбца i путем перестановки строк, а функция rsort (M, j) выполняет сортировку по возрастанию j компонентов строки путем перестановки столбцов. .
Для определения минимальной и максимальной составляющих матрицы используются две функции min (M) и max (M) .
Вы можете выбрать случайную подматрицу из матрицы М в Mathcad, применив функцию submatrix (M, r1, r2, c1, c2) , где М — заданная функция, r1 и r2 — номера нижней и верхней строк матрицы М , которые затем становятся согласованными элементами конечной подматрицы, а с 1 и с 2 — номера нижнего и верхнего столбца матрицы М , которые затем становятся непротиворечивыми элементами итоговой подматрицы.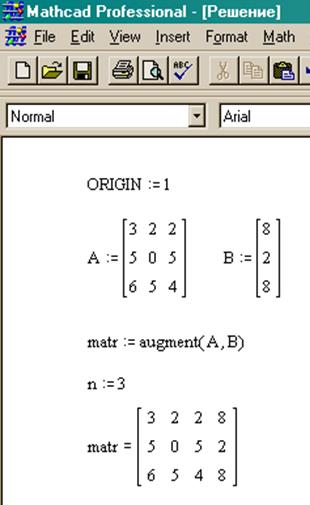
Дополнение матриц может быть выполнено с помощью функций augment (A, B,…) и stack (A, B,…) . Функция augment (A, B,…) — применяется для объединения матриц À , Â и т. Д. Слева направо, количество строк в матрицах должно быть одинаковым. Другая функция stack (A, B,…) применяется для объединения матриц сверху вниз. Количество столбцов в матрицах также должно быть таким же. Обсуждаемые функции могут быть применены и к векторам.В листинге программы показан пример использования обсуждаемых матричных функций.
Векторные и матричные функции »MathCadHelp.com» Номер 1 в MathCad Assignments
Mathcad включает функции для управления массивами способами, которые являются общими в линейной алгебре. Эти функции предназначены для использования с векторами и матрицами. Если функция не настроена явно для получения аргумента вектора или матрицы, нецелесообразно указывать его в качестве аргумента.
Обратите внимание, что функции, которые ожидают векторы, всегда ожидают векторы-столбцы, а не векторы-строки.Чтобы преобразовать вектор-строку в вектор-столбец, используйте оператор транспонирования [Ctrl] l.
В следующих таблицах перечислены векторные и матричные функции Mathcad. В этих таблицах
• A и B — массивы, векторные или матричные.
• v — вектор.
• M и N — квадратные матрицы.
• z — скалярное выражение.
• Имена, начинающиеся с m, n, i или j, являются целыми числами.
Размер и объем массива
Mathcad предоставляет несколько функций, возвращающих информацию о размере массива и его элементов.На рис. 10-10 показано, как используются эти функции.
Рисунок 10-10:
Специальные типы матриц
Вы можете использовать следующие функции, чтобы получить из массива или скаляра особый тип или форму матрицы. Некоторые из этих функций доступны только в Mathcad Professional.
Векторные и матричные функции
Функции преобразования массивов.
Особые характеристики матрицы
Вы можете использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа состояния матрицы.Большинство этих функций доступны только в Mathcad Professional.
Особые характеристики матрицы
Формирование новых матриц
Mathcad предоставляет две функции для объединения матриц, расположенных рядом или одна поверх другой. Mathcad также предоставляет функцию для заполнения матрицы значениями предопределенной функции и функцию для извлечения меньшей матрицы из большей. На рисунках 10-12 и 10-13 показаны некоторые примеры.
Формирование новых матриц
Объединение матриц вместе с функциями стека и увеличения.
Извлечение подматрицы из матрицы с помощью функции подматрицы
.
Собственные значения и собственные векторы
Mathcad предоставляет функции для работы с собственными значениями и собственными векторами матрицы.
Функция eigenvecs, доступная в Mathcad Professional, получает все собственные векторы сразу. Если вы используете Mathcad Professional, у вас также будет доступ к genval и
genvecs для поиска обобщенных собственных значений и собственных векторов.На рис. 10-14 показано, как используются некоторые из этих функций.
Собственные значения и собственные векторы
Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям в v, векторе, возвращенном genvais. N-й столбец этой матрицы — это собственный вектор x, удовлетворяющий обобщенной задаче на собственные значения M. х = V н. N. Икс . Матрицы M и N представляют собой квадратные матрицы с действительным знаком, имеющие одинаковое количество столбцов.
Нахождение собственных значений и собственных векторов
Использование eigenvecs для нахождения всех собственных векторов сразу
Разложение
Mathcad Professional предлагает некоторые дополнительные функции для выполнения разложения Холецкого, QR-разложения, LU-разложения и разложения матрицы по сингулярным числам.
Некоторые из этих функций возвращают две или три матрицы, объединенные в одну большую матрицу. Используйте подматрицу для извлечения этих двух или трех меньших матриц. На рис. 10-16 показан пример.
Разложение
Использование функции подматрицы для извлечения результатов из функции qr. Аналогичным образом используйте подматрицу для извлечения результатов из функций lu и svd
Решение линейной системы уравнений
В Mathcad Professional вы сможете использовать функцию lsolve для решения линейной системы уравнений.На рис. 10-17 показан пример. Обратите внимание, что аргумент M для lsolve должен быть матрицей, которая не является ни сингулярной, ни почти сингулярной. Матрица сингулярна, если ее определитель равен нулю. Матрица почти сингулярна, если у нее высокое число обусловленности. Вы можете использовать одну из функций, описанных в разделе «Особый характер, эристика матрицы» на стр. 198, чтобы найти число обусловленности матрицы.
Решение линейной системы уравнений
В качестве альтернативы вы можете решить систему линейных уравнений, используя обращение матрицы, как показано в правом нижнем углу рисунка 10-9.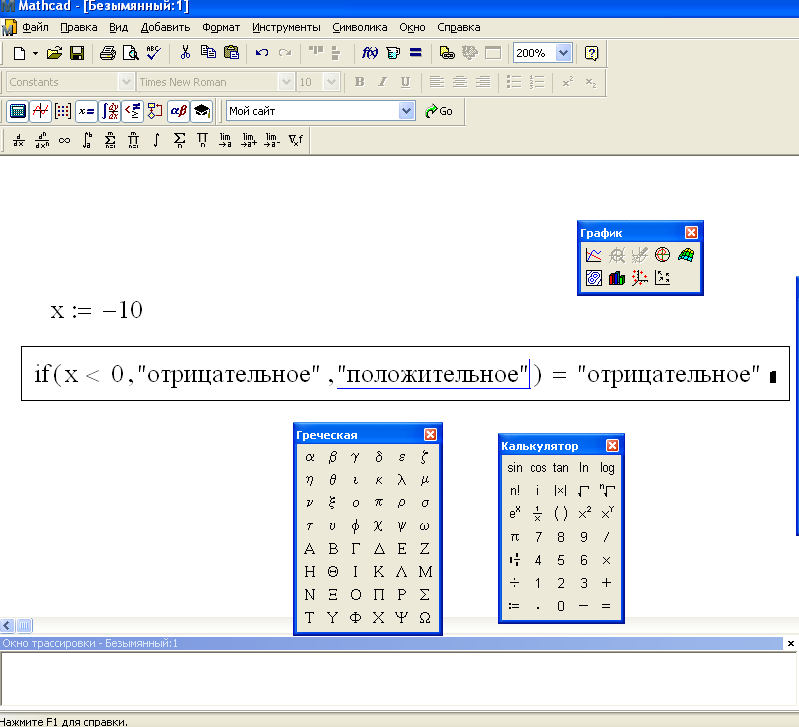
О других методах численного решения в Mathcad см. Главу 15 «Решение уравнений». Символьные решения систем уравнений см. В главе 17 «Символьные вычисления».
Использование Isolve для решения двух уравнений с двумя неизвестными
Четыре функции, которые необходимо использовать в PTC Mathcad | PTC
PTC Mathcad содержит множество функций для инженеров, специалистов по обработке данных, математиков и деловых людей. Каждый найдет что-то для себя, независимо от его дисциплины; но вот четыре функции, которыми должен овладеть каждый, чтобы добиться максимальной производительности и эффективности.
Чтение файлов
Мы работаем не в вакууме; большинство из нас работают в командах, которым требуется высокая степень сотрудничества с другими отделами, поставщиками и клиентами. Нам придется обменяться с ними данными. Microsoft Excel является стандартом де-факто для электронных таблиц, но вы также можете получать данные в виде значений, разделенных запятыми (CSV), или в текстовых файлах.
PTC Mathcad может импортировать эти и другие форматы, используя как встроенные функции, так и диалоговые окна, которые помогут вам. Вы также можете создавать компоненты Excel прямо на листе с настраиваемыми входами и выходами.
Начало работы: перейдите на вкладку Ввод / вывод . Затем выберите один из значков в группе Data Import / Export . Также ознакомьтесь с функциями > Чтение и запись файлов в PTC Mathcad Справка или ознакомьтесь с рабочими таблицами ввода / вывода (требуется учетная запись сообщества PTC.com/PTC).
Матричные и векторные операции
После ввода файла Excel, CSV или текстового файла часто возникает необходимость в обработке его данных. Это включает в себя манипулирование ячейками с помощью операторов и функций.Векторные и матричные операторы позволяют извлекать столбцы, строки и отдельные элементы из импортированных данных.
PTC Mathcad содержит более 50 стандартных функций для определения минимальных и максимальных значений, извлечения подматриц, поиска совпадающих значений и поиска значений.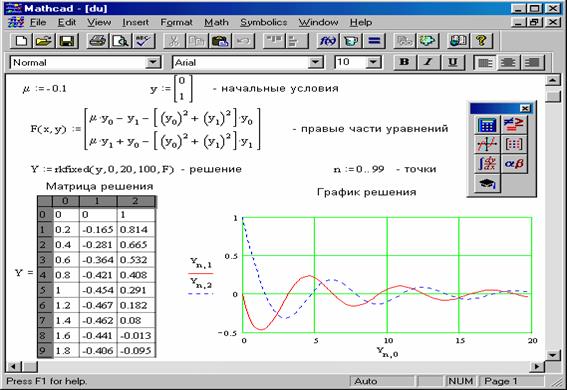
И, конечно же, у вас есть стандартная матричная математика, такая как перекрестные произведения, определители и собственные значения. Вы даже можете создавать новые матрицы из существующих векторов и матриц.
Начало работы: перейдите на вкладку Matrices / Tables и выберите из Vector / Matrix Operators и Vector / Matrix Functions значки.Также ознакомьтесь с рабочими таблицами векторов и матриц (требуется учетная запись сообщества PTC.com/PTC). Или изучите Вектор, матрицы и таблицы и Функции > Вектор и матрица > Характеристики массива > О функциях характеристик массива в справке PTC Mathcad .
Пользовательские функции и программы
PTC Mathcad содержит более 400 встроенных функций, таких как вышеупомянутые векторные и матричные функции.Другие мощные группы функций, предоставляемые PTC Mathcad, включают такие области, как статистика, дифференциальные уравнения, анализ данных, но этого недостаточно.
Людям нужна возможность создавать свои собственные определяемые пользователем функции для своих приложений, формируя сложные выражения, включающие константы, переменные, предварительно определенные функции и математические выражения, включая исчисления. Пользовательские функции позволяют вам указывать входные данные, которые могут быть числами, текстом, переменными и матрицами, а затем выполнять эти вычисления для значений, которые вы отправляете в функцию.
Программы выводят определяемые пользователем функции на новый уровень за счет включения циклов и условных выражений. Циклы, подобные традиционному компьютерному программированию для и , а конструкции позволяют повторять действия несколько раз. Условные выражения позволяют вам решать, какие действия предпринимать, в зависимости от того, является ли что-то истинным или ложным. Эти возможности дополняют ваши инженерные расчеты дополнительным уровнем интеллекта и контроля.
Начало работы: в справке PTC Mathcad изучите Учебники > Задача 3-4: Определение и оценка функций и Пользовательские функции .
Или просмотрите рабочие листы функций и программирования (требуется учетная запись сообщества PTC.com/PTC).
Построение и построение графиков
Как говорится, картинка стоит десяти тысяч слов. Мы все очень спешим, поэтому хотим усваивать информацию как можно быстрее. Человеческая природа — пропускать уравнения, достоверные данные и текстовые пояснения, чтобы сразу перейти к визуальной инкапсуляции ответа. Неважно, насколько хороши ваши данные и уравнения, если вы не можете донести правильные выводы до заинтересованных сторон и аудитории.Вот почему черчение и построение графиков — такие важные навыки, которые нужно освоить.
Стандартные функции построения графиков позволяют создавать двумерные графики X-Y, контурные графики и трехмерные графики. Эти графики могут содержать несколько трассировок различных источников данных, и вы можете управлять цветами, осями и делениями для форматирования результатов.
С помощью компонента диаграммы, представленного в PTC Mathcad Prime 5.
0, вы можете создавать полнофункциональные, богато форматированные 2D-графики. Компонент диаграммы также предоставляет возможность для дополнительной оси Y, которая имеет собственный масштаб, параметры конфигурации и параметры форматирования.Графики, созданные с помощью компонента диаграммы, могут быть дополнены заголовками, легендами, метками осей, линиями сетки и границами, каждая из которых имеет собственное форматирование, поэтому они готовы к публикации в отчетах, статьях и веб-страницах.
Начало работы: в справке PTC Mathcad изучите Учебники > Упражнение 5 и Диаграммы . Кроме того, после создания графика на листе дважды щелкните область графика, чтобы открыть приложение PTC Mathcad Chart и дополнительно настроить график.Или ознакомьтесь с рабочими таблицами 2D- и 3D-печати (требуется учетная запись сообщества PTC.com/PTC).
Навигация на расстоянии одного клика
Если вы расширите свой личный набор навыков, включив в него чтение файлов, матричные операции, определяемые пользователем функции и программы, а также построение графиков, тогда вы научитесь создавать и документировать свои инженерные расчеты.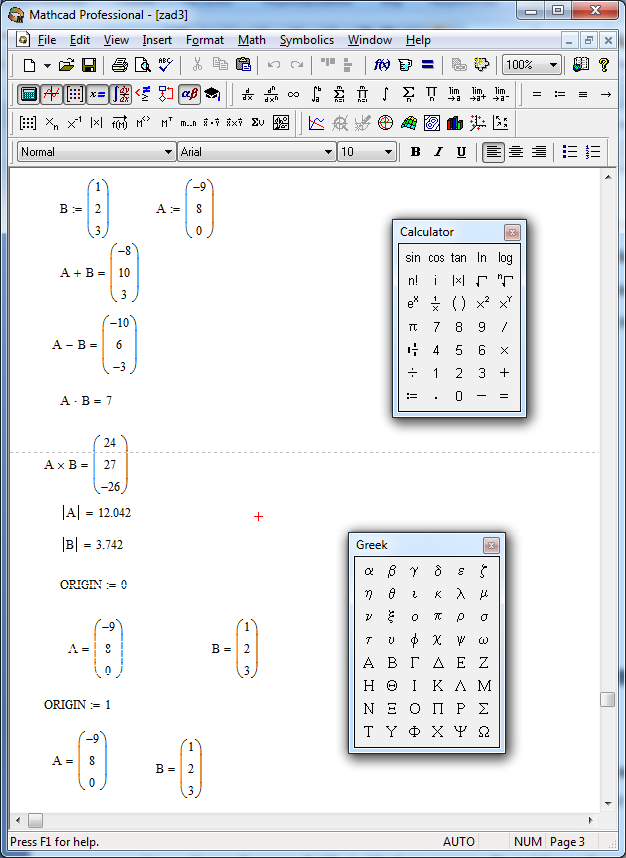
Для получения дополнительной справки просто нажмите функциональную клавишу F1 в PTC Mathcad Prime, чтобы узнать больше.
Об авторе
Дэйв Мартин — бывший инструктор и консультант Creo, Windchill и Mathcad.После ухода из PTC он был специалистом по Creo в Amazon; и инженер-механик, администратор Creo и администратор Windchill для Amazon Prime Air. Он получил степень в области машиностроения в Массачусетском технологическом институте и в настоящее время работает инженером по авионике в Blue Origin.
Мартин является автором книг «Планирование дизайна в Creo Parametric» и «Дизайн сверху вниз в Creo Parametric», которые доступны на сайте www.amazon.com. С ним можно связаться по адресу [email protected].
Создание более сложных 2D-графиков с помощью Mathcad Prime 5.
0PTC Mathcad Prime обеспечивает мощное управление инженерными расчетами, помогающее прогнозировать поведение проекта, определять критические параметры и размеры и улучшать визуализацию данных с помощью 2D-построения. Поскольку было много отзывов от пользователей о необходимости улучшения функций построения графиков в предыдущих выпусках Mathcad, Mathcad Prime 5.0 почти полностью сосредоточен на улучшении двухмерных графиков.
Новые возможности Mathcad Prime 5.0
Новые возможности значительно улучшают возможности пользователей настраивать внешний вид и макет своих диаграмм и графиков, чтобы лучше передавать информацию заинтересованным сторонам.Prime 5.0 добавляет новую кнопку под вкладкой Math, которая называется «Компонент диаграммы». Вкладка графиков будет выглядеть так же, как и в предыдущих версиях Mathcad, потому что ничего не было удалено, а только расширено для добавления нового компонента диаграммы.
Это изображение показывает пользователям, где они могут найти новый компонент построения диаграмм в Mathcad Prime 5.
0.
До выхода новой версии пользователи не могли полностью управлять заголовком, условными обозначениями, линиями сетки, второй осью Y или настраиваемым форматированием при создании графика графика на вкладке графиков.Эти возможности теперь доступны в Mathcad Prime 5.0!
Использование нового «компонента диаграммы» в Mathcad
Вставьте компонент диаграммы под вкладкой математики — это вставит пустой встроенный объект диаграммы. Если вы дважды щелкните по нему, вы можете активировать приложение для построения графиков.
Это изображение показывает пользователям активированное графическое приложение после двойного щелчка по встроенному объекту.Теперь пользователь может получить доступ ко всем функциям приложения, которые помогают настроить диаграмму на вкладке графика, на вкладке x и на вкладке y, например заголовок, граница, линии сетки, легенда, шрифт и цвета.
Как только вы закроете эту вкладку, вы снова увидите свой документ и заметите, что над компонентом диаграммы есть область с надписью «Входные данные».
Здесь вы определяете данные или функцию, которые необходимы для построения диаграммы. Вы можете определить функции или переменные, которые хранят данные. Если вы нажмете на этот раздел, вы увидите раскрывающееся меню с различными вариантами, в котором вы можете выбрать «Вставить выражение оси X» или «Вставить выражение оси Y».
После ввода данных осей x и y вы можете дважды щелкнуть график еще раз, чтобы получить доступ к предварительному просмотру графика и настроить детали графика.
Чтобы узнать, что еще можно делать с Mathcad Prime 5.0, посмотрите, как Анжи Себерино из PTC демонстрирует расширенные параметры диаграмм, доступные пользователям, нажав на видео ниже.
Как это:
Нравится Загрузка …
Сопутствующие товарыДомашняя страница интерактивной линейной алгебры
Домашняя страница интерактивной линейной алгебрыЭта книга больше не издается; однако он доступен в Интернете по адресу http: // www. math.upenn.edu/~gjporter/ila Для «чтения» книги требуется Mathcad версии 13 или выше. | |
| Джеральд Дж. Портер, Дэвид Р. Холм |
Интерактивная линейная алгебра — это новый тип текст — интерактивный. Взаимодействие происходит посредством используя числовые, графические, символьные и текстовые возможности Mathcad. Весь текст представлен на компьютер в Mathcad.
Курс преподается в лабораторные условия, с дополнительными лекциями или без них.Благодаря этому подходу, ориентированному на технологии, математика становится экспериментальной наукой.
Студенты становятся активными участниками обучения процесс, который приводит к более глубокому пониманию концепции. В то же время этот подход развивает уверенность в способности ученика читать, использовать и напиши о линейной алгебре.
Электронный текст помогает студентам
линейная алгебра и ее приложения с тщательно
запланированная серия компьютерных дискуссий, примеры,
вопросы и проекты.
С его графикой, символикой,
числовые данные и возможности редактирования, Mathcad предоставляет
инструменты, необходимые для разработки, визуализации, подключения,
и применяя понятия линейной алгебры.
Джерри Портер ([email protected]) является профессором математики Университета Пенсильвания в Филадельфии, штат Пенсильвания.
Он работает на факультете Пенсильвании с 1965 г. Заместитель декана по вычислительной технике в Школе искусств и Наук с 1980 по 1990 год.
Портер имеет A.Б. из Принстонского университета, где он написал кандидатскую диссертацию с использованием оригинала фон Неймана. компьютер. Его доктор философии. по математике из Корнелла.
Его исследования были в области теории гомотопии, области Алгебраическая топология и учебное использование вычисления. Он использовал компьютеры в бакалавриате. инструкция с 1968.
Портер был первым председателем комитета МАА по
Компьютеры в обучении математике и был директором
проекта «Интерактивный математический текст», многолетний
проект, предназначенный для поощрения использования и создания
интерактивные математические тексты.
IMTP финансировался
IBM и NSF. Он был редактором и сотрудником
Вычислительная техника и математика, Использование вычислений в
инструкция по математике для студентов, MAA Notes, Number
9, (1988).
Портер был казначеем
Математическая ассоциация Америки с 1990 по 2001 год и в настоящее время
служит на многих
своего
комитеты.
Дэйв Хилл ([email protected] ) — профессор математики в Темплском университете. в Филадельфии, штат Пенсильвания. Он работает на факультете с 1973 г. и занимал должность директора бакалавриата. программа по математике 1982-86 гг.
Хилл получил степень бакалавра в Университете штата Индиана в Пенсильвании. и докторскую степень по математике в Университете г. Питтсбург.
Его математические области представляют собой линейную алгебру,
численный анализ и обучающие вычисления. холм
использовал программное обеспечение как лекцию, лабораторию и
инструмент для решения проблем со студентами за последние два года
десятилетия на уровне бакалавриата и магистратуры
и много публиковал и читал лекции по использованию
ПО в инструкции.
Он был ведущим в
ATLAST (Расширение обучения линейной алгебре через
использование программных средств) в 1992-1995 гг.
спонсируется Национальным научным фондом
Хилл принимал активное участие в математической Ассоциации Америки и занимал пост президента Отделение MAA в Восточной Пенсильвании и Делавэре.
Автор экспериментов по вычислительной матрице, 1988; co
автор Численных методов: Учебное пособие (для
актуарная наука), 1992, Вводная линейная алгебра.
с приложениями, 1993, и лабораторное руководство Linear
LABS по алгебре с MATLAB, 1994.
[PDF] Введение в MathCAD
Загрузить Введение в MathCAD …
Введение в MathCADАнимация, интерполяция и другие красивые картинки
Пример анимации Пример
из нашей схемы LCR
MathCAD # 7 dpl 2001
2
Анимация # 2 Основы Автоматическое использование переменной FRAME
FRAME устанавливается mathCAD для каждого кадра анимации Выберите «Вид | Анимация…», чтобы открыть диалоговое окно анимации.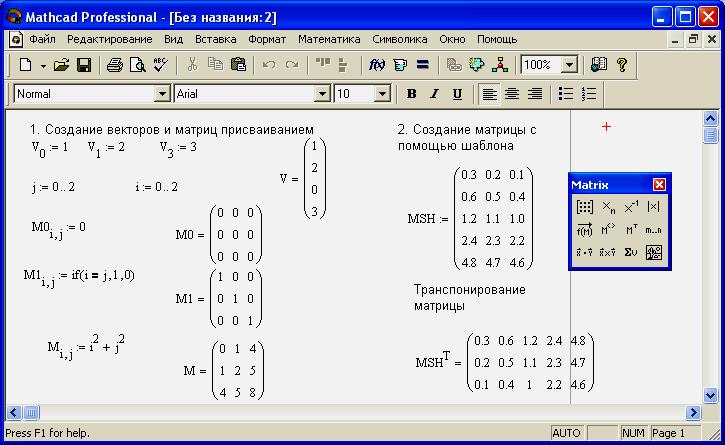
Задайте начальные и конечные значения для КАДРА. Выберите область для анимации. Выберите «Анимация» для создания «Сохранить как…» для создания.avi файл
MathCAD # 7 dpl 2001
3
Анимация # 3 Подсказки «Ошибка
инициализация видеопотока» => Ничего не выбрано Может потребоваться масштабирование КАДР Анимация может: — На создание требуется много времени — Создание больших файлов Видеопроигрыватель Windows
позволяет перемещать ползунок вперед и назад
MathCAD # 7 dpl 2001
4
Анимация # 4 Дополнительные советы Исправить масштаб
на графиках Не нужно включать вычисления в анимации Echo FRAME = в кадре Если масштабируется, переменная масштабируется по эхо Для графиков частот масштабируйте FRAME следующим образом: P t sP erDecad e 5
FR AME
Pts PerDecade
10
MathCAD # 7 dpl 2001
5
Графики векторных полей # 1 График
, матрица комплексных чисел Каждая точка показана в виде вектора lot График масштабирован так, чтобы наибольший вектор был промежутком между точками Полезно для: — — — —
Электрические поля Магнитные поля Динамические потоки График ting Градиент функций
MathCAD # 7 dpl 2001
6
Графики векторных полей # 2 x
0 19
Mx y
y
0 19
i x 0 .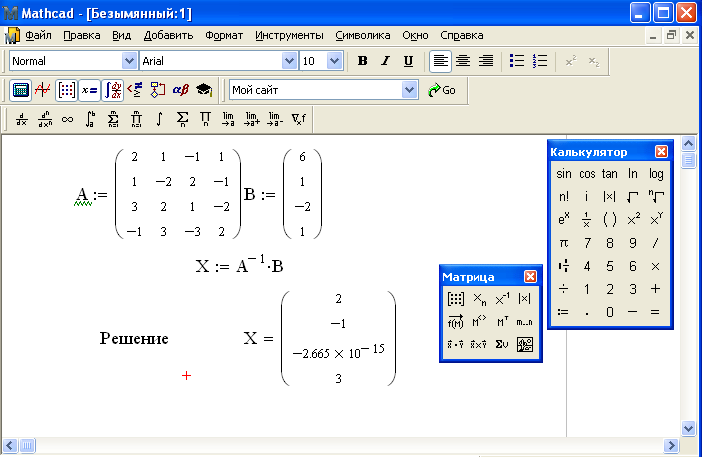
3
y e
M
MathCAD # 7 dpl 2001
7
Data Analysis # 1 Получение данных из файла Считывание данных
из файла данных Используйте либо: — Insert | Component | File Read or Запишите и следуйте указаниям мастера — READPRN («имя файла») Считывает данные
из файла в вектор или матрицу Компонент чтения файлов предлагает гораздо больше типов файлов
MathCAD # 7 dpl 2001
8
Data Analysis # 2 Выбрать данные, которые мы хотим Используйте матричные функции
для выбора данных, которые нас интересуют Строки (M) и Столбцы (M), чтобы получить размер массива данных Подматрица (M, rs, rf, cs, cf) для выбора прямоугольного фрагмента M для выбора столбца Csort для сортировки массива Увеличение и стек для создания массивов
MathCAD # 7 dpl 2001
9
Data Analysis # 3 Smoothing Data
medsmooth (vy, n) возвращает vy, сглаженный при запуске медианы
s сглаженные
s 50
medsmooth (данные s)
8 00 90 005
6 00
s 4 00 сглаженный i
2 00
0 6 00
6 10
6 20
6 30
6 40
6 50
i
Math # 7 dpl 2001
10
Анализ данных # 4 Линейная регрессия Наклон
и функции пересечения принимают векторы значений X и Y 8 00
6 00
Y
4 00
2 00
0
0
20
40
60
80
1 00
X
точка пересечения (X Y) 4.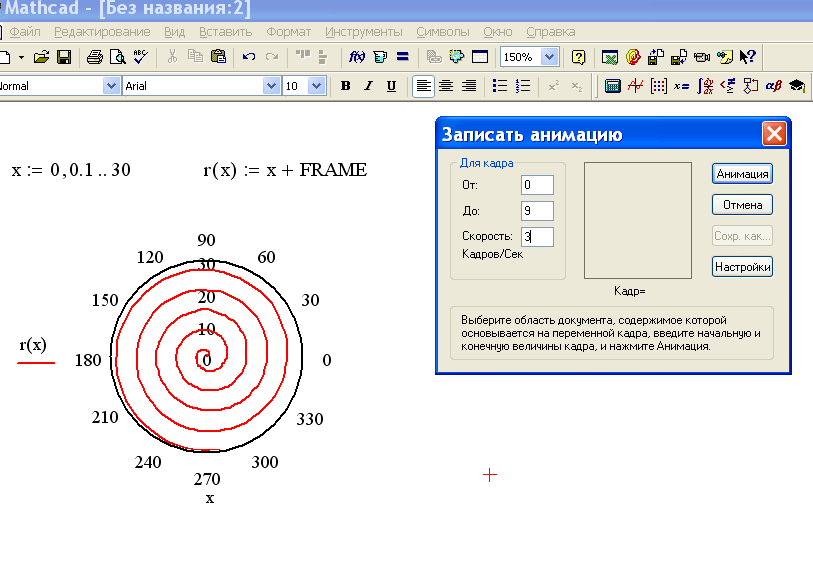
914 slope (X Y) 6.955
MathCAD # 7 dpl 2001
11
Data Analysis # 5 Interpolation 2
stage process
— Fit polynomial through points cspline — Cubic spline Bspline — B-spline — B-spline
— интерполировать с использованием полинома, полученного на этапе 1
interp
MathCAD # 7 dpl 2001
12
Подгонка кубическим сплайном и интерполированная подгонка 9 0,69 3 00 3
Посадка Y (z)
0. 4 62 3 02 min (X)
1
X z
Данные XY Кубическая сплайн-интерполяция
MathCAD # 7 dpl 2001
max (X)
1
13
Функция Fitting
Cspline& Bspline подгоняет плавную кривую через точки данных При физическом моделировании мы знаем форму функции, которую нужно подобрать, просто нужны параметры Пример: — Отклик детектора счета фотонов
MathCAD # 7 dpl 2001
14
Функция Пример установки # 1 5 1 1 0
4 1 1 0
3 1 1 0
1 Данные
100
10
1
0.
1 7 1 1 0
Подгонка к устройству
1 1 0
1 1 0
6
f (x) a x e
Определить
5
1 1 0
1 1 0 0 Данные 4
3
0,01
0,1
1
b x
параметры a & b
MathCAD # 7 dpl 2001
15
Функция Пример № 2 Перепишитеf (x) и производные Замените a, b на u0, u1… Найдите частные производные от f (x) Создайте вектор функции & pds f (x) a x eu 0 x e F (x u)
b x
u x 1
d
x exp u 1 x
da
2 u 0 x exp u 1 x
d db
a x e
b x
a x e
b x
MathCAD # 7 dpl 2001
x exp (b x)
2 a x exp (b x)
16
Пример подгонки функции № 3 Создать
вектор значений предположения
5 10
5
предположение
7
Для решения вызовите
genfit Определите функцию, используя параметры параметров f (x)
0 1 g enfit D ata D ata g uess F
F (x p arams) 0
MathCAD # 7 dpl 2001
17
Пример подгонки функции № 4 График
f (x) против данных
5 1 1 0 4 0 2.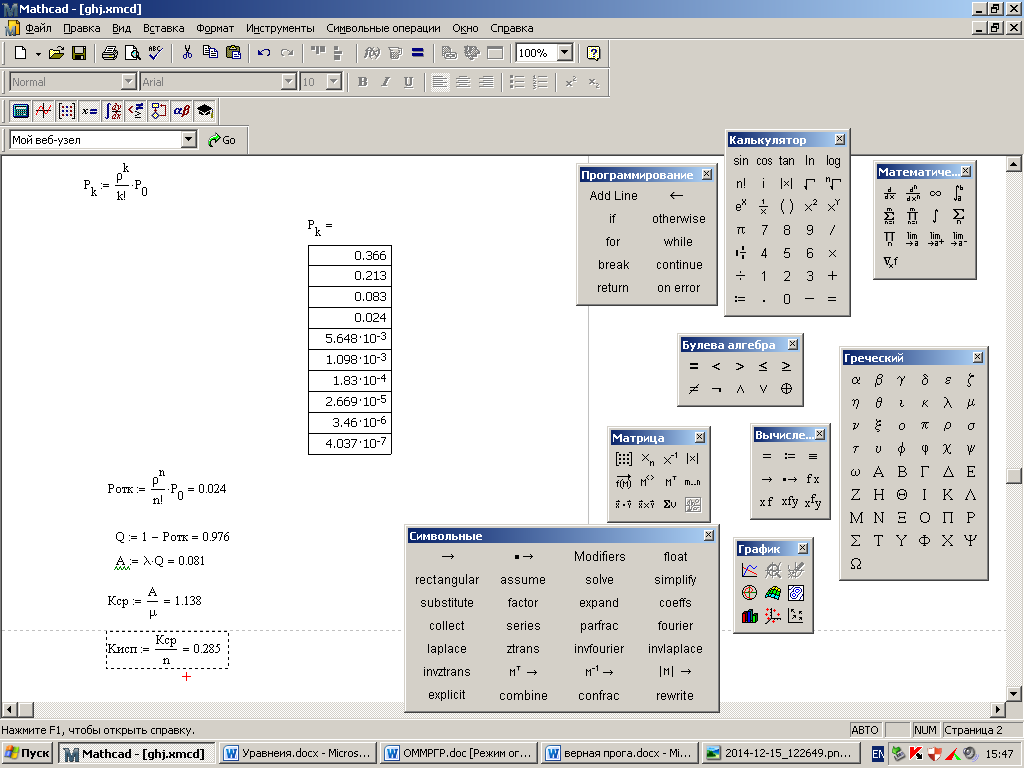
4 5 11 4 1 1 0
3 1 1 0
1 Данные 0 f Данные
100
10
1
0 .1
0 .0 6 6 0 .0 1 7 6 1 1 0 1 1 0 0 7 1 .5 4 21
1 1 0
5
1 1 0
4 0 Data
1 1 0
3
MathCAD # 7 dpl 2001
0 .0 1
0 .1
1 0 .3 5
18
Creo AR | Виртуальная реальность Creo
Дополненная реальность (AR), это прямое или косвенное изображение физической, реальной среды, элементы которой дополняются компьютерным сенсорным вводом, например звуком, видео, графикой или данных. Creo AR, совершенно новая функциональность, добавленная в Creo 4, обеспечивает захватывающий сдвиг парадигмы в том, как мы рассматриваем трехмерную компьютерную геометрию, в данном случае объекты Creo Parametric. Представьте, что вы проектируете оборудование и можете увидеть его в реальной среде, в которой оно будет использоваться; это то, что предоставляет функция Creo AR.
Возможно, вы разработали новое оборудование для своих производственных предприятий. Используя видео вашего смартфона в реальном времени о том, где будет установлено оборудование, приложение Creo AR для телефона наложит 3D-модель Creo Parametric на сцену, и это будет выглядеть так, как если бы модель действительно была там.Чтобы увидеть заднюю сторону, просто обойдите ее, держа телефон направленным к ней. Как это круто!
Другое применение — проверка дизайна. Сколько раз в обзоре дизайна один человек хочет увидеть одно изображение, проецируемое на экран, а другой — другое. Используя Creo AR, каждый человек имеет собственное AR-представление объекта и может смотреть на него как угодно.
Итак, как работает Creo AR?
В процессе используется графическое изображение ThinkMark, как показано ниже; По сути, это персональный штрих-код, принадлежащий пользователю Creo.Образ ThinkMark — это то, что связывает 3D-геометрию Creo со средой AR.
В Creo Parametric есть три простых шага для создания опыта дополненной реальности.
Первый — разместить ThingMark где-нибудь в пределах своей модели. Это может быть поверхность детали или базовая плоскость. Предположим, что он размещен на базовой плоскости под сборкой, как показано ниже.
Модель, будет ли затем опубликована отдельная деталь или сборка вместе с ThingMark на сервере PTC AR в облаке.
Наконец, вы можете отправить электронное письмо людям, чтобы они могли просмотреть вашу модель AR. В электронном письме будет содержаться ThingMark в качестве вложения и ссылки на то, где приложения для телефона могут быть загружены и установлены на вашем смартфоне.
Чтобы фактически просмотреть объект AR, вы просто распечатываете графику ThingMark, включенную в электронное письмо, на листе бумаги и кладете распечатанное изображение на пол или, возможно, на столешницу. Используя приложение View на смартфоне, вы просто наводите камеру телефона на изображение.После того, как приложение распознает графику ThingMark, на экране телефона появится трехмерная геометрия модели, расположенная относительно того места, где ThingMark был расположен в модели Creo, и масштабируется соответствующим образом.