Как построить спектр сигнала в mathcad: 14.1.1. Фурье-спектр действительных данных MathCAD 12 руководство

14.1.1. Фурье-спектр действительных данных MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1471 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• org/Breadcrumb»>MathCAD 12

• Спектральный анализ
• 14.1. Фурье-спектр
  • 14.1.1. Фурье-спектр действительных данных
  • 14.1.2. Обратное преобразование Фурье
  • 14.1.3. Преобразование Фурье комплексных данных
  • 14.1.4. Пример: артефакты дискретного Фурье-преобразования
  • 14.1.5. Пример: спектр модели сигнал/шум
  • 14.1.6. Двумерный спектр Фурье
• 14.2. Вейвлет-спектры
  • 14.2.1. Встроенная функция вейвлет-преобразования
  • 14.2.2. Программирование вейвлет-преобразований
• 14.3. Сглаживание и фильтрация
  • 14.3.1. Встроенные функции для сглаживания: ВЧ-фильтр
  • 14.3.2. Скользящее усреднение: ВЧ-фильтр
  • 14.3.3. Устранение тренда: НЧ-фильтр
  • 14.3.4. Полосовая фильтрация
  • 14.3.5. Спектральная фильтрация
  • 14.3.6. Пример: вычисление спектра мощности

Преобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм, называемый БПФ (быстрое преобразование Фурье). Рассмотрим сначала наиболее типичную для физического эксперимента ситуацию расчета Фурье-спектра действительного сигнала, для которой алгоритм БПФ реализован в нескольких встроенных функциях Mathcad, различающихся нормировками:

•  fft (у) — вектор прямого преобразования Фурье;
•  FFT (у) — вектор прямого преобразования Фурье в другой нормировке:

•  у — вектор действительных данных, взятых через равные промежутки значений аргумента.

ВНИМАНИЕ!

Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно 2

n элементов (n— целое число). Результатом является вектор с 1+2^n-1 элементами. Если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями, иначе вместо решения появится сообщение об ошибке.

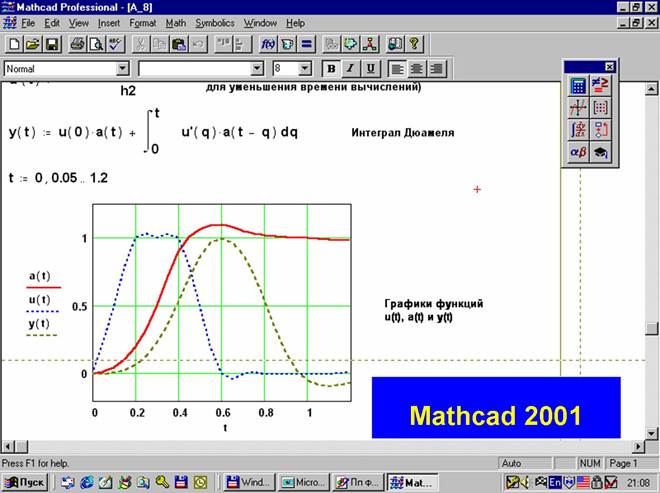
Рис. 14.1. Исходные модельные данные (продолжение листинга 14.1)

Чтобы смысл преобразования Фурье был более понятен, используем в качестве модельных данных дискретизацию детерминированного сигнала,, равного сумме трех синусоид (рис.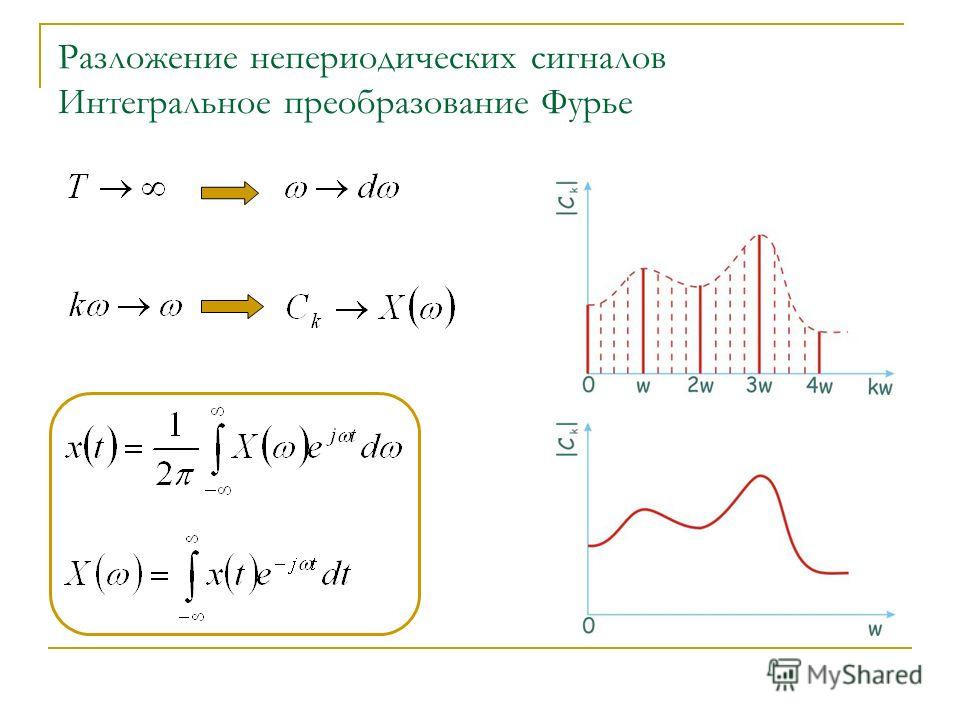 14.1). Листинг 14.1 демонстрирует расчет Фурье-спектра по N=128 точкам, причем предполагается, что интервал дискретизации данных y_i равен Δ. В середине листинга применяется встроенная функция fft, а его оставшаяся часть предназначена для корректного пересчета соответствующих значений частот Ω_{i(они вычисляются в последней строке листинга). Обратите внимание, что результаты расчета представляются в виде модуля Фурье-спектра (рис. 14.2), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра (рис. 14.3) с определением синусоид в листинге 14.1.}

Листинг 14.1. Быстрое преобразование Фурье

Рис. 14.2. Матрица-результат вычисления Фурье-спектра данных (продолжение листинга 14.1)

Исключительно важными представляются два параметра, заданные в предпоследней строке листинга 14.1, называемые соответственно граничной частотой и частотой Найквиста. Граничная частота Ω₀ определяет нижнюю, а частота Найквиста Ω_N — верхнюю границу аргумента вычисленного спектра, как показано маркерами на рис. 14.3. Кроме того, важно, что интервал дискретизации Фурье-спектра также равен Ω₀, а общее число вычисляемых точек спектра составляет N/2 (в нашем примере N/2=64). Последние утверждения иллюстрируются маркерами на рис. 14.4, изображающем график Фурье-спектра вблизи нижней границы частот.

Рис. 14.3. График Фурье-спектра данных (продолжение листинга 14.1)

Рис. 14.4. Низкочастотная область Фурье-спектра (продолжение листинга 14.1)

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

10045 0

Глава 10 Работа с информационными ресурсами Mathcad 11

7036 0

Глава 2 Работа с файлами Mathcad 11

12737 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.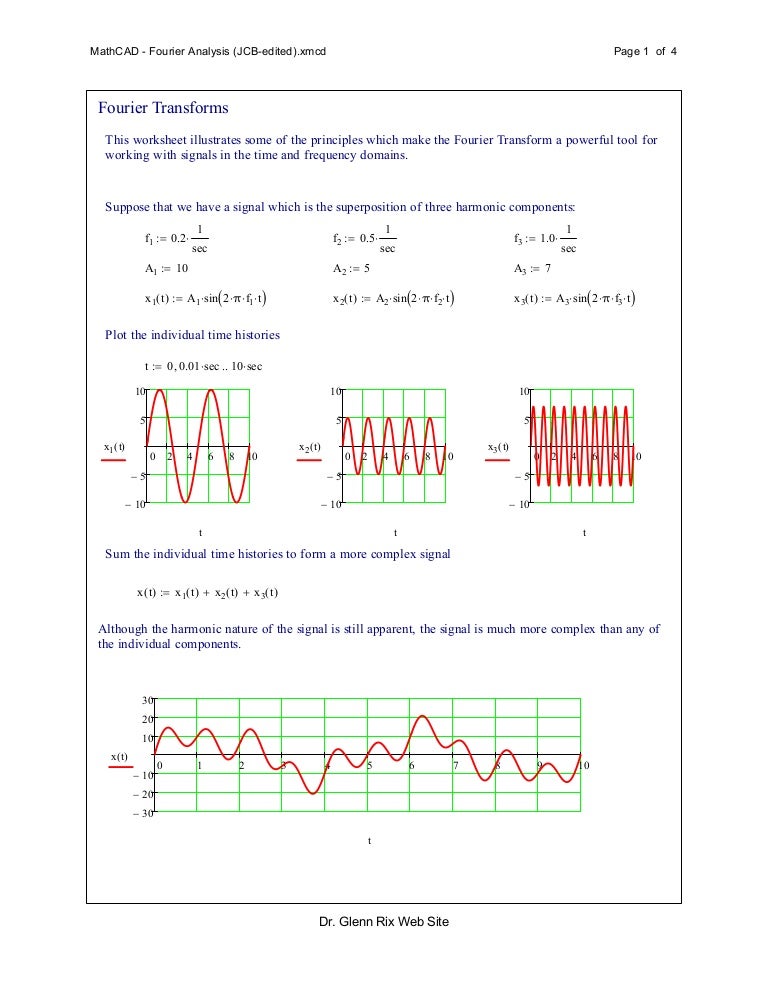

ru обязательна. 0.2128 s

Разработка моделей первичных сигналов в программной среде MathCAD

В статье рассматривается методика разработки моделей первичных сигналов в программной среде MathCAD для их дальнейшего использования в системах схемотехнического моделирования радиоэлектронных устройств. Материал может оказаться полезным разработчикам аналоговой аппаратуры, а также студентам, аспирантам и преподавателям, специализирующимся в области проектирования и моделирования радиоэлектронных устройств, предназначенных для обработки аналоговых сигналов.

При проектировании и моделировании радиоэлектронных устройств с помощью систем схемотехнического моделирования (ССМ), таких как OrCAD, Microcap DesignLab [1], и других, часто приходится использовать различные источники сигналов для проверки проектируемой схемы на предмет безыскаженной передачи (преобразования) первичного сигнала. При этом имеющиеся в подобного рода программах источники сигналов не всегда в полной мере удовлетворяют запросам разработчиков.

Для исследования характеристик схем в условиях воздействия реальных сигналов и помех часто приходится разрабатывать собственную модель сигнала, а затем использовать ее при моделировании схемы в ССМ. В связи с этим весьма полезным является освоение принципов построения моделей сигналов, используемых в радиоэлектронных устройствах. Настоящая публикация знакомит читателя с методикой разработки моделей первичных сигналов с использованием программной среды MathCAD [2] и последующего их использования в качестве источников сигналов из внешнего файла в ССМ радиоэлектронных устройств DesignLAB.

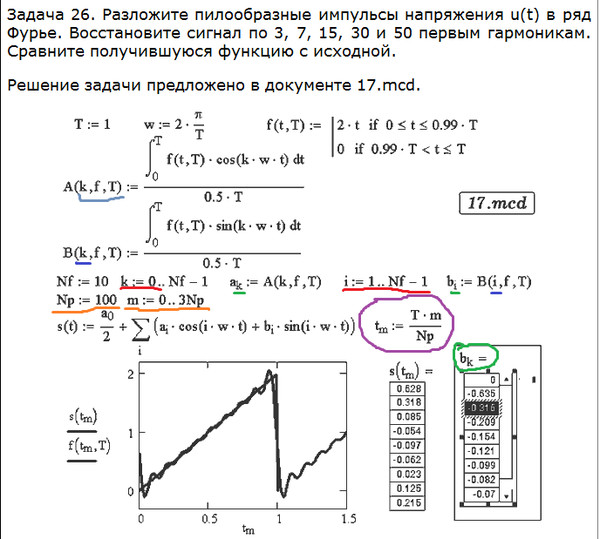
К первичным (модулирующим) сигналам обычно относят сумму нескольких гармонических составляющих (телефонное сообщение) и различные импульсные последовательности [3]. При этом основными представлениями сигналов являются временное (зависимость амплитуды сигнала от времени) и спектральное (зависимость амплитуды или фазы гармонических составляющих сигнала от частоты). Задача заключается в разработке моделей сигналов, которые позволили бы получить их временное представление в виде массивов значений (отсчетов), а спектральные характеристики (комплексный спектр сигнала) можно будет получить с использованием быстрого преобразования Фурье [3] с помощью выражения:

где S(t) — массив временных значений сигнала. Для реализации этого преобразования в системе MathCAD воспользуемся встроенным быстрым Фурье-преобразованием в виде функции Сfft (S(t)) [2].

Рассмотрим методику построения модели телефонного сообщения в виде суммы нескольких гармонических составляющих, аппроксимирующих спектр реального телефонного сообщения (ТЛФС) и имеющих регулируемые случайные пределы отклонения амплитуд, частот и начальных фаз:

где F_k, U_mk — частоты и их амплитуды, аппроксимирующие спектр реального ТЛФС; dU_k, dF_k — случайные отклонения амплитуд и частот гармонических составляющих; φ_k — начальные фазовые сдвиги частот; N_г — количество гармонических составляющих сигнала. Покажем, каким образом наша аналитическая модель (2) преобразуется в программный код MathCAD (рис. 1).

Рис. 1. Программный код модели телефонного сообщения

Поясним введенные идентификаторы и программный код модели. В строках 1–4 задаем амплитуды и частоты тринадцати гармонических составляющих телефонного сообщения, в строке 5 формируем отсчеты индексной переменной j — управляющей переменной, которую будем использовать для индексации массивов, необходимых в модели, а также формируем отсчеты времени

t_j и частоты ƒ_j . В строке 6 задаем количество гармонических составляющих и индексную переменную k. В строке 7 формируем начальные фазовые сдвиги, отклонения амплитуд и частот, причем, если установить маркер в какоелибо из этих полей (выражений), то каждый раз при моделировании будут генерироваться новые значения параметров и это отразится на выходном сигнале. В строке 8 пересчитываем значения частот и амплитуд с учетом сгенерированных случайных сдвигов. В строке 9 формируем временное представление сигнала и выполняем его нормировку. В строке 10 рассчитываем комплексный спектр сигнала SwТ, его модуль vT и выполняем нормировку амплитудно-частотного спектра (АЧС) результирующего сигнала, используя переменную r. Результат присваиваем идентификатору bT и строим график полученного массива от отсчетов частоты ƒ_j. На рис. 2 показаны форма и спектр телефонного сигнала, полученные с помощью модели (2).

Рис. 2. Форма и спектр телефонного сигнала

Итак, мы построили простую и удобную для управления параметрами модель первичного сигнала в виде суммы нескольких гармонических составляющих. Мы можем изменять амплитуды, частоты и начальные фазы каждой составляющей сигнала и видеть результаты изменений этих параметров на временном и спектральном представлении их суммы. Единственное, что осталось сделать — это записать в файл результат формирования временного представления сигнала для его использования в качестве входного сигнала в системе схемотехнического моделирования РЭУ. В ССМ DesignLAB предусмотрен источник сигнала из файла, при этом данные в файле необходимо представить в следующем формате:

Для того чтобы наш сигнал выглядел в файле подобным образом, добавим в модель следующий программный код:

Поясним введенные обозначения. Мы сформировали массив всего из двух значений (0 и 1) для индексной переменной i, которая будет участвовать в формировании двумерного массива sig по правилу: если i = 0, то в j-элемент массива записываем отсчет времени t_j, если не равен нулю (равен 1) — то записываем отсчет сигнала st_j . Затем формируем файл с именем sig.dat, он будет размещаться в том же каталоге, что и наш файл с моделью. Следует также сказать о том, что для правильной записи результатов моделирования в файл, необходимо в программе MathCAD установить следующие значения системных параметров PRN File Settings: Precision (точность отображения) = 10, Column Width (ширина столбца) = 20.

Покажем теперь, как выполнить ввод и моделирование испытательной схемы для проверки модели сигнала в DesignLAB 8.0. Введем схему, показанную на рис. 3.

Рис. 3. Испытательная схема с источником сигнала из файла

В качестве источника сигнала воспользуемся компонентом VPWL_FILE (источник напряжения, заданный в файле) и установим значение его атрибута File=sig. dat. Сохраним собранную схему, поместив в папку со схемой файл sig.dat, зададим параметры директивы временного анализа и выполним моделирование. В окне программы Probe системы DesignLAB мы увидим точно такой же сигнал, который первоначально был создан нами с помощью программы MathCAD (рис. 4).

Рис. 4. Результаты моделирования источника сигнала в системе DesignLAB

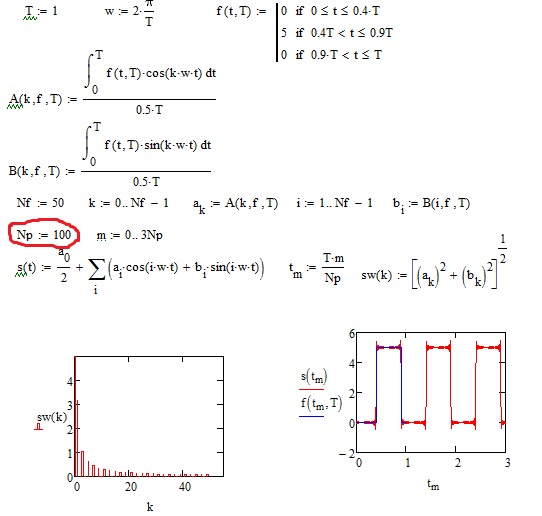
Разработаем модель первичного сигнала в виде последовательности прямоугольных импульсов с управляющими параметрами длительности импульса, периода следования импульсов и числа импульсов в моделируемом фрагменте. Хотя подобного рода сигналы можно сгенерировать и с помощью имеющихся в ССМ источников сигналов, модель такого сигнала понадобится нам для создания источников сигналов с дискретной модуляцией, которых, к сожалению, в системе DesignLAB нет. Алгоритм формирования последовательности импульсов N_и с заданной длительностью t_и и периодом следования Т аналитически можно записать с помощью условной функции вида:

где с1, с2 — значения переменной х, определяющие границы условия; d1 — значение, принимаемое функцией при выполнении условия; d2 — значение, принимаемое функцией при невыполнении условия. Тогда, представив импульсную последовательность в виде суммы одиночных импульсов, смещенных друг относительно друга по оси времени на длительность импульса и периода их следования t_u×n+T×n, получим алгоритм формирования последовательности импульсов с заданной скважностью и длительностью импульсов:

где t_з — длительность интервала задержки последовательности относительно момента времени t_i = 0; N_и — количество импульсов в последовательности: t_и , Т — длительность и период следования импульсов для заданной скважности q = T/t_и. В выражении (4) формируется массив значений I1, в котором для каждого i-го отсчета определено значение, откладываемое по оси ординат: 1 — если отсчет времени t_i находится в пределах длительности импульса (удовлетворяется условие), и 0 — во всех остальных случаях (условие не удовлетворяется). Просуммировав полученные таким способом одиночные импульсы, смещенные по оси времени на интервал Tn, получим требуемую последовательность импульсов с варьируемыми значениями длительности и периодом следования.

На языке MathCAD выражение (3) можно ввести с помощью условной функции if(arg,y1,y2) [2]. Тогда программа для формирования временного представления импульсной последовательности может быть записана следующим образом. Задаем начальные значения параметров ti — длительность импульса, T — период следования импульсов, ni — количество импульсов в пачке:

Формируем массивы управляющей переменной j, отсчетов времени t_j и частоты ƒ_j , отсчетов импульсной последовательности a_j в соответствии с выражением (4):

Для генерирования дискретных сигналов с кодовым формированием импульсов воспользуемся все тем же принципом суммирования элементарных импульсов, но сдвинутых друг относительно друга по оси времени на длительность единичной посылки T_n/N_u×n. Для этого сформируем кодовый массив M = (m₀, m₁, m₂…mN_u–1), в котором число элементов равно числу единичных импульсов.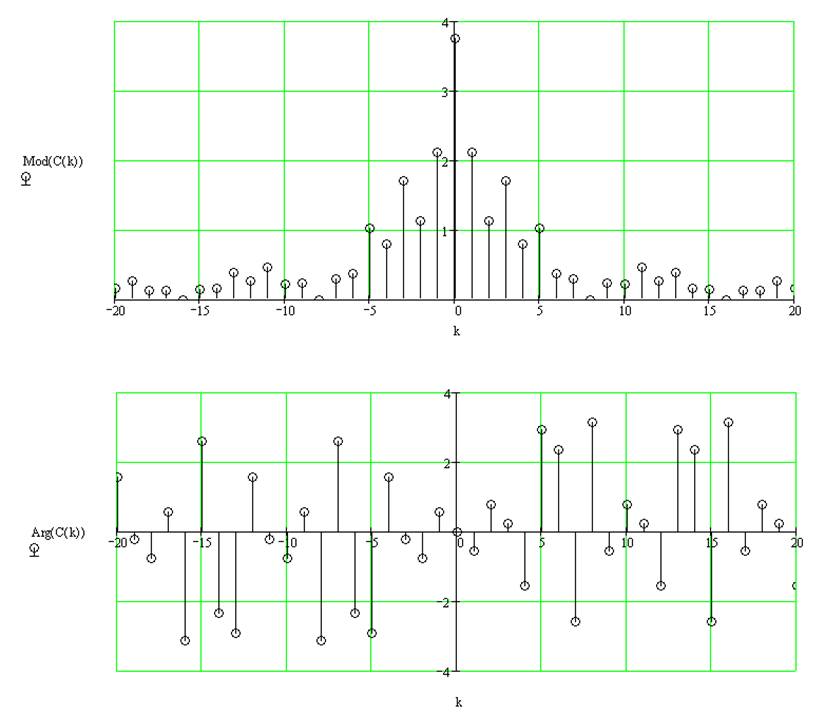 Так, например, для семиэлементного произвольного кода массив можно представить в виде М = [1 1 1 0 0 1 0]. Тогда алгоритм формирования кодовой посылки импульсов с использованием (4) запишется в виде выражения (5), где t_з — длительность интервала задержки кодовой посылки относительно момента времени t_i = 0; N_и — количество импульсов в посылке; Т_п — длительность кодовой посылки.

Для получения последовательности, состоящей из нескольких посылок, разделенных временными промежутками, просуммируем сдвинутые по времени посылки на длительности элементарного импульса и периода повторения посылки T_n /N_u×n + P×k. Тогда алгоритм (5) следует записать в виде (6), где t_з — длительность интервала задержки кодовой посылки относительно момента времени t_i = 0; N_и — количество импульсов в посылке; Т_п — длительность кодовой посылки; N_п — количество посылок в последовательности; Р — период повторения посылок.

Приступим к созданию модели первичного сигнала в виде импульсной последовательности с кодовым формированием единичных посылок. Задаем начальные значения параметров Тс — длительность пачки импульсов, Per — период следования пачек импульсов, Кс — количество импульсов в пачке и m_k — значения единичных посылок:

• длительность пачки импульсов
• период следования пачки импульсов/количество пачек
• кодовая последовательность

Формируем массивы управляющей переменной j, отсчетов времени t_j и частоты f_j, отсчетов импульсной последовательности a_j в соответствии с выражением (6), отсчетов одиночного импульса a1_j длительностью Тс и отсчетов одиночного импульса a2_j длительностью Тс/Кс, которые являются вспомогательными при анализе спектра последовательности:

В результате получим график временного представления импульсной последовательности с кодовым формированием единичных посылок, показанный на рис.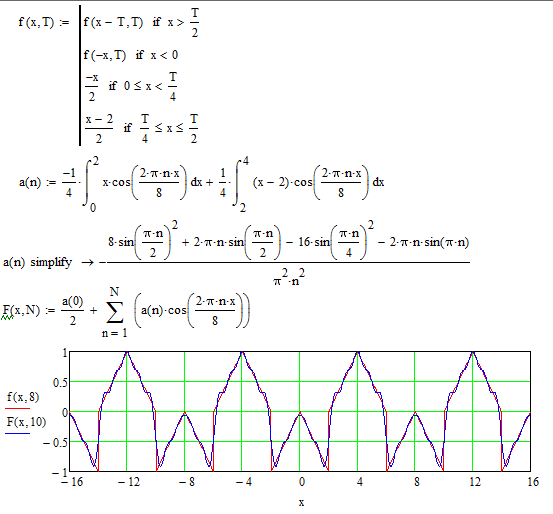 5.

Рис. 5. Временное представление импульсной последовательности с кодовым формированием единичных посылок

Спектры импульсной последовательности b_j с кодовым формированием единичных посылок, одиночных импульсов b1_j и b2_j с длительностями Тс и Тс/Кс соответственно показаны на рис. 6.

Рис. 6. Спектры одиночных импульсов и последовательности с кодовым формированием единичных посылок

Используя рассмотренную методику разработки моделей сигналов в программной среде MathCAD, читатель самостоятельно сможет создать источники первичных сигналов для моделирования с их помощью различных радиоэлектронных устройств.

В следующих статьях будет показано, каким образом можно с использованием рассмотренного подхода разработать модели сигналов с аналоговой и дискретной модуляцией, а также модели некоторых сложных сигналов.

1. Разевиг В. Д. Система сквозного проектирования электронных устройств DesignLab 8. 0. М.: Солон, 1999.
2. Saffe R. C. Random Signals for Engineers using MATLAB and MathCAD. Springer — Verlag. 2000.
3. Гоноровский И. С. Радиотехнические цепи и сигналы. М.: Радио и связь, 1986.

Иджис делает волны в радиоспутниковом проекте

Иджис делает волны в радиоспутниковом проекте

История вопроса

Aegis Systems Limited, консалтинговая компания по разработке спектра, основанная в 1988 году, изучает поведение радиочастотного спектра: то, как действуют и взаимодействуют радиоволны. После пробного запуска нескольких программных пакетов Aegis решила использовать программное обеспечение Mathsoft для управления расчетами Mathcad (теперь PTC Mathcad) в сочетании с Fortran и C++ в качестве общекорпоративного инструмента. PTC Mathcad был протестирован в сравнении с конкурентами, такими как Maplesoft (Maple) и Wolfram Research (Mathematica), и был выбран Aegis благодаря интуитивно понятному и удобному интерфейсу.

Почему PTC Mathcad?

PTC Mathcad часто используется компанией Aegis для проектов моделирования в тех случаях, когда требуется быстрое вычисление, выполнение которого на языке программирования заняло бы слишком много времени. В настоящее время в Aegis работают шесть инженеров, а гонорары довольно равномерно распределяются между работой в государственном и частном секторах. Например, инженеры выполнили проект, чтобы выяснить, как два спутника на разных орбитах будут пересекаться и взаимодействовать. Они написали симуляцию с использованием PTC Mathcad, которая выполнялась в течение двух дней.

Aegis хранит справочную библиотеку рабочих листов PTC Mathcad для каждого проекта, за который она берется. Это тщательное управление расчетами означает, что младшие инженеры могут получить доступ к большому количеству накопленной информации для справки, а старшие инженеры тратят меньше времени на объяснение фундаментальных расчетов. Еще одним преимуществом ведения таких записей является то, что если коллега уходит, его или ее знания могут быть сохранены в интересах компании.

Ричард Радд, главный инженер-консультант компании Aegis, сказал: «PTC Mathcad установил стандарт нашей работы, помогая нам более эффективно управлять своим временем, что повлияло на производительность бизнеса, поскольку целое.»

Проект

Схема S@TCOM Британского национального космического центра (BNSC) действует уже три года, и проекты и исследования в рамках этой схемы проводились экспертами в данной области (МСП), такими как Aegis, а также крупными такие организации, как Roke Manor Research и Astrium. S@TCOM был разработан, чтобы помочь британским компаниям развивать опыт и знания на спутниковом рынке.

В начале сентября 2003 г. перед компанией Aegis была поставлена ​​задача собрать статистические данные, измеряющие влияние застроенной среды на широкополосные радиосигналы, чтобы помочь схеме S@TCOM.

С этой целью он использовал воздушный шар с гелием, чтобы смоделировать пути спутников в нескольких населенных пунктах на юго-востоке Англии. Результаты были загружены в PTC Mathcad, и были созданы трехмерные представления отклика радиоканала.

Результаты

Результаты исследования представляют особый интерес для космической отрасли Великобритании, часть которой собирается принять участие в европейской версии американской системы глобального позиционирования (GPS). Это связано с тем, что исследование Aegis было разработано для измерения того, как здания повлияют на мощность каждой радиоволны, которая имеет фундаментальное значение для технологий позиционирования, а также других технологий, таких как сотовые телефоны и радары.

«Благодаря скорости, с которой PTC Mathcad может обрабатывать данные и представлять их визуально, мы смогли представить цифры, относящиеся к экспериментам, в BNSC всего за два дня», — прокомментировал Радд.

Британские компании, которые хотят воспользоваться коммерческими преимуществами спутников, будут использовать результаты Aegis, включая такие рынки, как телекоммуникации, радиовещание, наблюдение Земли и навигация, которым необходимо знать, как большие города повлияют на них и их технологии.

Моделирование вариаций спутников

Чтобы измерить, как здания будут изменять радиосигналы, инженерам Aegis пришлось смоделировать возможные изменения угла места спутников при передаче и приеме радиосигналов. Изначально для моделирования искали вертолет; однако этот метод оказался непригодным из-за бюджетных и экологических ограничений.

В конце концов команда решила использовать в качестве альтернативы большой воздушный шар, наполненный гелием. Передатчик был прикреплен к воздушному шару, а приемник расположен в разных местах внутри каждого здания.

Ответы радиоканала собирались примерно один раз в секунду в течение 100 секунд. Получатель пересылал результаты непосредственно на ноутбук, и необработанные данные были собраны. Затем данные были загружены в PTC Mathcad, и были созданы двумерные и трехмерные диаграммы, демонстрирующие различные отклики каналов.

Образец, показывающий, что вместо одного однородного пика, который можно было бы ожидать в «идеальном» канале, за прямым сигналом с моделируемого спутника следует несколько меньших сигналов с уменьшающейся амплитудой.

Эта картина показывает, что здания, местность и другие помехи мешают работе радиоканала, вызывая, как и ожидалось, запаздывающие отражения. Компания Aegis также смогла оценить размер задержки в различных местах и ​​сделать соответствующие выводы. Исследование также показало, что для исследованных мест статистика радиоканала не показала зависимости от высоты «спутника».

О компании Aegis

Компания Aegis Systems Limited, основанная в 1988 году, предоставляет полный спектр услуг по проектированию спектра и управлению использованием частот на основе всесторонних знаний теории и практики проектирования радиосистем. В настоящее время компания Aegis признана одним из ведущих европейских поставщиков консалтинговых услуг в этой области, предлагающим подробные знания в области регулирования, а также практические знания в области анализа помех и моделирования распространения. Эта основная возможность поддерживается и расширяется за счет опыта в разработке программного обеспечения на заказ.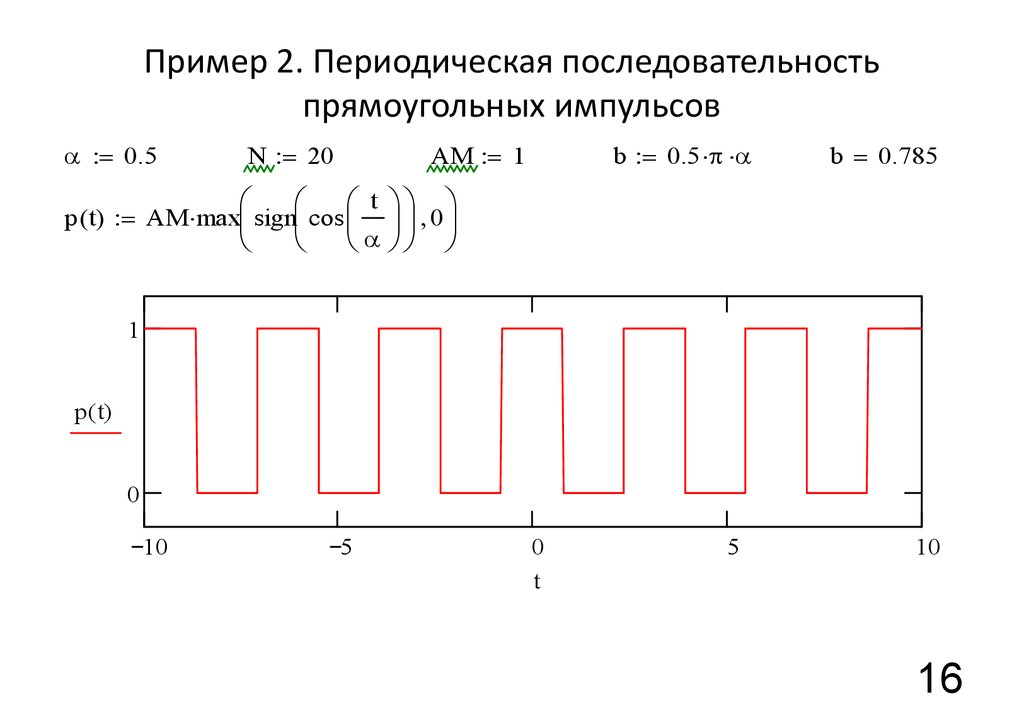 Имея большой опыт в области проектирования спектра, Aegis предлагает своим клиентам быстрые, точные и практичные решения практических и теоретических проблем в области проектирования спектра.

Получите 30-дневную бесплатную пробную версию Mathcad Prime уже сегодня!

Как и Aegis, вы тоже можете использовать преимущества скорости и производительности PTC Mathcad Prime. Попробуйте последнюю версию Mathcad Prime для себя и сравните с тем, как вы сейчас выполняете инженерные расчеты.

Скачать сейчас / / /

Страница не найдена или в настоящее время переводится на запрошенный вами язык. Если вы хотите перенаправить на английский язык, нажмите Да

(PDF) Спектр йода — ДОКУМЕНТЫ.

СОВЕТЫ

Спектр йода Джордж Лонг Кафедра химии и Индианский университет Пенсильвании Индиана, Пенсильвания 15705 [email protected] Тереза ​​Юлия Зелински Департамент Химия, медицинские технологии и физика Западный университет Монмута Лонг-Бранч, Нью-Джерси 07764 [электронная почта защищена]

Copyright 1998 Отдел химического образования, Inc., Американское химическое общество. Все права защищены. Для использования в классе учителей, один экземпляр на каждого учащегося в классе может быть сделан бесплатно заряжать. Напишите в JCE Online, [email protected], чтобы разрешение разместить документ бесплатно в классе Интранет.

Предпосылки: Этот рабочий лист подходит для использования в Занятия по физической химии для младших и старших классов. Чтобы использовать документ у вас должен был быть хотя бы год исчисления и физики. В Кроме того, рекомендуется, чтобы вы изучили приложение уравнения Шредингера к гармоническому осциллятору и жесткому ротор. Этот документ является одним из пяти, остальные MorsePotential. mcd, BirgeSponer.mcd, FranckCondonBackground.mcd и FranckCondonComputation.mcd. Каждый документ можно использовать отдельно, но вы получите наибольшую извлекает выгоду из ваших исследований, используя их вместе. Маткад документы в этом наборе требуют Mathcad 6.0+. Цель: цель этот документ должен представить систематическое развитие Связь между спектроскопическими экспериментами и определение длин молекулярных связей в основном состоянии и электронные возбужденные состояния для двухатомных молекул. Введение: Определение спектра йода является классическим экспериментом в физике. Химия. Этот легко получаемый спектр демонстрирует ряд важные принципы спектроскопии. Изучение экспериментального спектра ясно показывает связь между колебательными и электронных энергетических уровней, введя понятие вибронного переход, демонстрирующий ангармонизм колебательной энергии уровни и обеспечение диссоциативного предела для вибронного переходы. При некотором дополнительном анализе данных также возможно для расчета параметров функции потенциальной энергии Морзе возбужденного электронного состояния, продемонстрировать Франк-Кондон принцип и вычислить факторы Франка-Кондона.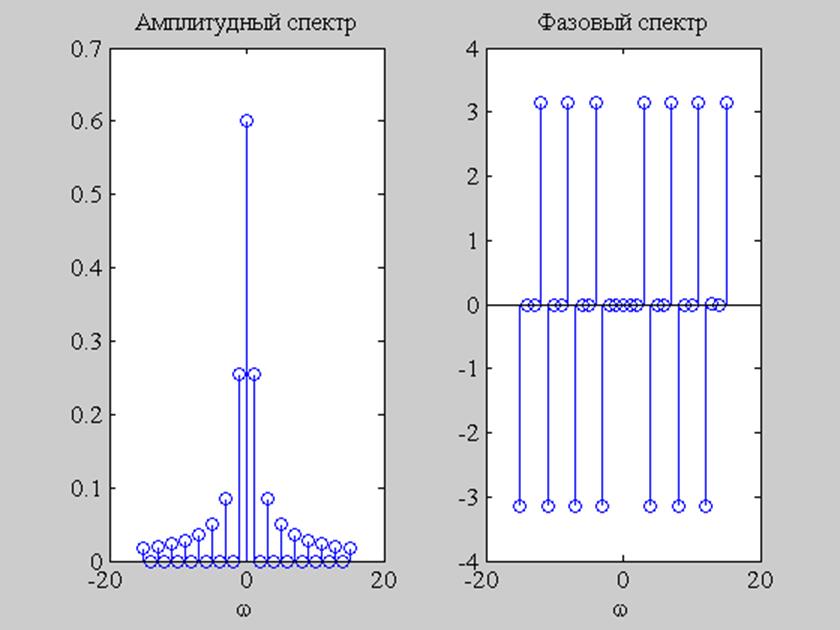 Этот документ Mathcad служит шаблоном для расчета возбужденного состояния Морзе потенциальная кривая для йода из экспериментального спектра. шаблон также может быть использован для расчета возбужденного состояния Морзе потенциал для любой двухатомной молекулы, которая имеет четко определенный вибронный спектр, т.е. Br2 или CO. Целевые характеристики: после Выполняя работу, описанную в этом документе, вы должны быть в состоянии 1. рассчитать параметры потенциала Морзе конкретное электронное состояние двухатомной молекулы из соответствующий вибронный спектр этой молекулы; 2. объяснить понятие ангармонизма и показать, как это понятие влияет на расчет; 3. объяснить термины фактор Франка-Кондона и Принцип Франка-Кондона и показать, где эти принципы применимы в расчет; 4. предсказывать изменения внешнего вида Морзе диаграмма потенциала с учетом изменений потенциальной функции Морзе параметры.Создано: 19 марта97 Изменено: 5 июля 1998 г. IodineSpectrum.mcd страница 1 Авторы: Джордж Лонг Тереза ​​Джулия Zielinski

Часть 1. Предварительные сведения В этом введении мы рассмотрим типичные студенческие данные, полученные из спектра УФ-видимого йода. Этот набор данные содержат 30 пиков, перечисленных в вектор-столбце. Эти переходы были идентифицированы как исходящие от земли вибронное состояние йода. Анализ показанных данных студента здесь подготавливается почва для определения спектроскопического свойства и равновесная длина связи для возбужденного состояния йода, который студент наблюдал в спектре.i 0 .. 29ViVi

47

i

19586,9 19552,3 19504,8 19465,9 19418,3 19375,1 19323,2 19275,7 19223,8 19167,6 19111,4 19050,9 18990,4 18925,6 18860,7 18795,9 18722,4 18653,3 18579,8 18506,3 18428,5 18342,1 18259,9 18177,8 18091,5 17996,3 17909,8 17814,8 17719,7 17624,6

Колебательные квантовые числа для возбужденных электронных состояния Vi идентифицируются индексом массива i. Здесь мы используем тот факт, что линия, ближайшая к 542,1 нм (18428 см-1), отнесена квантовое число V = 27. (Позже мы будем использовать v для колебательного квантовое число.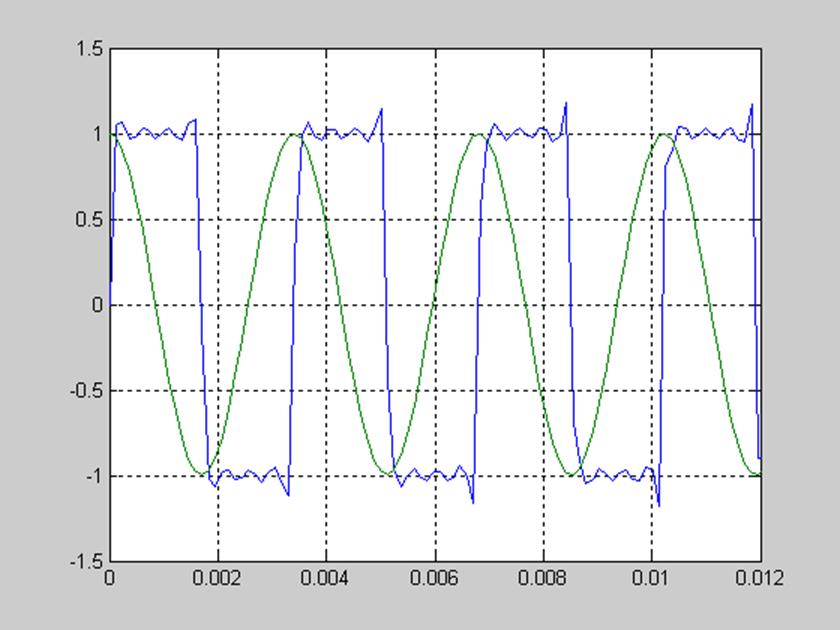 ) Это присвоение квантового числа 27 происходит от литературе (Sime, стр. 668) и определялся с использованием высоких разрешающая спектроскопия, которая позволила идентифицировать переходит в квантовое состояние V=0. Все спектральные строки однозначно помечены относительно этой. Линия V=27 не является первой строкой в ​​списке слева; так как это 10-е мы вычитаем 10 и добавляем 30, чтобы получить верхний предел, 47 в этом случай. (Помните, что в списке 30 элементов, обозначенных индекс i.) В пространстве справа попросите Mathcad показать содержимое векторы i, Vi и 47-i. Убедитесь, что в векторе 47-i 27-я запись связана с пиком при 18428 см-1. Обратите внимание, как индексы разнятся. Что происходит с нумерацией энергетических уровней когда мы используем 47-я? В каком диапазоне находятся колебательные квантовые числа? для частот, наблюдаемых в приведенных здесь спектральных данных? Что колебательный энергетический уровень основного состояния является источником каждого наблюдаемый здесь переход? Подсказка: рассмотрим состояние I2 в ваш образец. Теперь, когда пики назначены, мы можем построить частоту по сравнению с квантовым числом. Кривизна на графике показывает ангармонизм вибрации, а также позволяет оценить вибронный переход 0 — 0 путем экстраполяции на V = 0. кривизна линии не влияет на расчет Морзе потенциал, который будет сделан позже. признавая, что наблюдаемое вибронные переходы исчезают на пределе диссоциации, т. где спектр становится непрерывным, позволяет вычислить энергия диссоциации Do из вибронного спектра двухатомного молекула. Для этого мы будем использовать график Бирге-Спонера. Мы обсуждаем график Бирге-Спонера в следующем разделе этого документа.

Создано: март 1997 г. Модифицировано: 5 июля 1998 г.

йодинеспитр. 104

15

20

25

30

35

40

45

50

V I Vibration QUANTUM CANTUM

Вопросы для части 1. 1. Как будет выглядеть на графике. вибрации были гармоническими? 2. Насколько точна, по вашему мнению, ваша ценность для энергии электронного перехода? Подсказка: рассчитать E для перехода 0-0.

Создано: март 1997 г. Изменено: 5 июля 1998 г. энергия, Do, константа ангармонизма, ee, и колебательный постоянная e из графика Бирджа-Спонера. Вывод Уравнения Бирджа-Спунера доступны в сопутствующем Mathcad. документ, BirgeSponer.mcd. Для конкретных определений энергии диссоциации D o и De и другие свойства Морзе потенциал см. в сопутствующем документе MorsePotential.mcd. Дополнительный информацию можно найти в ссылках в конце этого задокументируйте, в частности, статьи Лессинджера и Макнота. В типичный график Бирджа-Спонера, вы строите график разницы энергий между последовательные спектральные полосы в зависимости от колебательного квантовое число полосы плюс один, т.е. v+1. Обратите внимание, как индексы здесь используются для этого.i 46 .. 19

Мы не можем включить самые высокие и самые низкие частоты, потому что мы будет вычитать соседние пары частот. ци это индекс, обозначающий вектор разности частот по возрастанию заказ. Проверьте это, отобразив массив qi. Тот же индекс массива используется для квантовых чисел. 1 Примечание Mathcad: мы изменили имя переменной квантового числа здесь. V выше на странице 2 был индексом имя переменной. Здесь это имя вектора. .

qi v

46 i

i

q i

q

1.i

2

i

1

i

1

. см

1

Вычислить разность частот между соседними колебательные состояния с использованием уравнения 4 из BirgeSponer.mcd.

Проверить индекс, квантовые числа и разность частот на эту точку, отображая различные векторы в пространстве справа. Обратите внимание, как изменение индекса позволяет отображать частоты в правильный порядок с правильным квантовым числом. Вам может понадобиться изменить точность отображения числового формата, чтобы показать достаточную цифры для вычисления . Проверьте вручную некоторые записи эти векторы, чтобы убедиться, что вы понимаете, как они возникают. )1

m1 = 210,409 м e

точка пересечения( v , )4

Определите наклон и точку пересечения графика Бирджа-Спонера.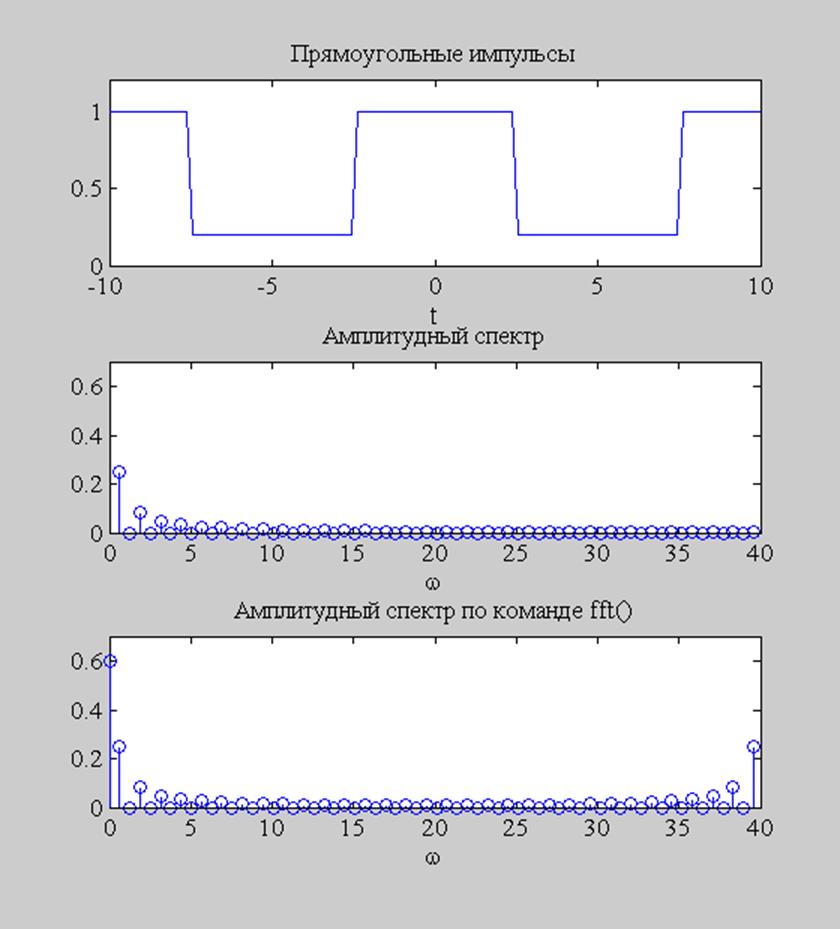 e — это точка пересечения с графиком Бирджа-Спонера. Обратите внимание на использование функции наклона и пересечения Mathcad. Сюжет Бирге-Спонера появляется ниже.

e = 1,383 10

m

1

j

0 .. 64 ( m1. j e )

fit( j )

fit(j) – прямая линия наклона Сюжет Бирге-Спонера.

Создано: март 1997 г. Модифицировано: 5 июля 1998 г.

йодинеспитр.

4

5000

0

0

10

20

30 В., J I

40

50

60

70959

EE

M1 21 1,1

EEE

M1 21115999.

EEE. = 1,052 см

e — колебательная постоянная для возбужденного состояния, а ee — константа ангармонизма для возбужденного состояния.

Пересечение x сообщает вам количество квантовых состояний до диссоциации, а также пределы интегрирования, используемые в расчет энергии диссоциации. Объясните, как x перехватывает получается. Это хорошее время, чтобы вернуться и посмотреть на Снова документ BirgeSponer. mcd. Здесь мы используем уравнение 3 из BirgeSponer.mcd на графике выше. Этот документ назывался G(v’) в уравнении 3 в BirgeSponer.mcd.e 2 . эээ

1 = 64,707

Здесь мы используем уравнение 7 из документа BirgeSponer.mcd для вычислить vмакс.

Таким образом, до диссоциации существует 65 квантовых состояний.

Создано: март 1997 г. Изменено: 5 июля 1998 г. Do , возбужденного состояния молекулы. Вы можете вычислить это энергия диссоциации путем интегрирования функции линии, подходящей для данные. Однако здесь Mathcad выполняет интегрирование численно, можно использовать определенный интеграл функции прямой вместо.

66 DO 0 E 2 FIT (J) DJ DO = 4,542 103

CM

1

DE

DO

DE = 4,611 10

3

1

Уведомление о том, что DO отличаются энергией нулевой точки возбужденное состояние.

Вопросы к части 2: 1. Как вычисляются значения Do и De сравнить с литературными значениями? 2. Какие экспериментальные параметры влияют на точность расчетных значений энергии диссоциации ? 3. Насколько точный результат можно получить с помощью вашего спектрофотометра? 4. Какой тип оборудования вам понадобится для определения диссоциации? энергии точнее?

Создано: март 1997 г. Изменено: 5 июля 1998 г. константа Потенциал Морзе — относительно простая функция, которая используется для моделирования потенциальной энергии двухатомной молекулы как Функция межъядерного расстояния. Потенциал Морзе U( r ) D e. 1 е. r Re2

определяется тремя физическими константами.

Это De , энергия диссоциации (не путать с Do), Re , равновесное межъядерное расстояние, и , азбука Морса. коэффициент ангармонизма (не путать с константа ангармонизма ee). Для получения дополнительной информации об этих константы и их значение см. в сопутствующем документе, MorsePotential.mcd, где практические занятия с Морзе потенциал даст вам большую оценку функции. Сначала вычислим для возбужденного состояния йода. Начать с определение некоторых констант.Ang c 1010.

м1

определите единицу измерения ангстрем скорость света обратите внимание, что предопределены Mathcad34.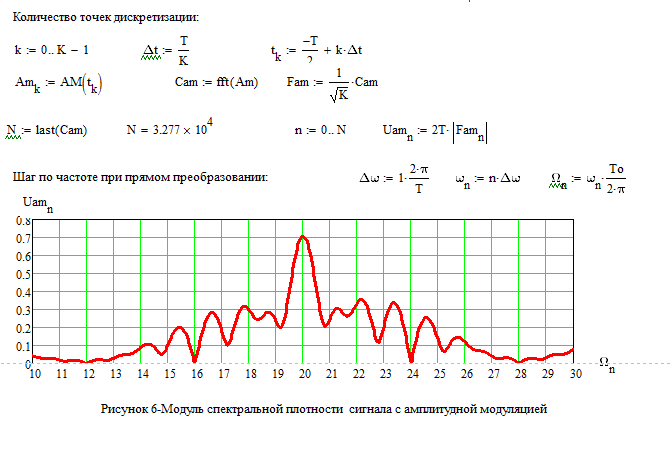

8 2.998. 10 . м. сек

= 3,142 ч 6,6261 . 10 1.053. 10 джоулей. сек

Постоянная Планка приведенная масса йода

25.

кг

Рассчитайте по следующему уравнению. Обратите внимание, как Mathcad сделал правильное преобразование единиц измерения. Когда вы делаете расчет вручную, это Важно отметить, что все количества должны быть указаны в единицах СИ (кг, м, сек, джоули). См-1 не является единицей СИ.2 2 . . . в. э Де. ч

= 1,974 10

10

м

1

Упражнение: Отобразите в Mathcad см-1 в качестве единиц измерения для .

Вопросы к части 3: 1. Откуда взялось уравнение для? Выведите это уравнение из потенциала Морзе. 2. С чем свойство облигации связано? 3. Убедитесь, что размерность длина-1.

Создано: март 1997 г. Изменено: 5 июля 1998 г.0005

Часть 4. Расчет межъядерного расстояния (Re ) возбужденное состояние. Чтобы вычислить Re для возбужденного состояния I2, нам нужно еще две части данных. Во-первых, нам нужна частота максимальное поглощение спектра, и нам нужно равновесие длина связи Re для основного состояния. Частота с максимальное поглощение можно определить по спектру. Хотя Ре можно получить из спектра флуоресценции, его обычно дают студентам для анализа данных в типичном эксперименте с йодом проводится в большинстве бакалавриата физической химии лаборатории.Amax Te 18860.7 . см1 1

Частота максимального поглощения при осмотре спектр. Частота 0 — 0 или основного состояния в основное состояние переход, определенный из данных или полученный из литература. равновесная длина связи для основного состояния как найдено в литературе

15300 . см

R1

2,66. 10

10.

m

Из принципа Франка-Кондона мы знаем, что максимум поглощение будет иметь место там, где есть наибольшее перекрытие между волновой функцией верхнего состояния с колебательным квантом число v ‘и колебательная волновая функция основного состояния с квантовым число v»=0. Величина перекрытия определяется Факторы Франка-Кондона (см. сопутствующие документы FranckCondonBackground.mcd и FranckCondonComputation. mcd для подробное введение в факторы Франка-Кондона). Максимум поглощение значение r в возбужденном состоянии равно R1, равновесная длина связи основного состояния. Итак, если мы знаем, энергии этого перехода, мы можем использовать уравнение потенциала Морзе для решения равновесной длины связи ( Re в используемых обозначениях здесь) возбужденного состояния. Функция потенциальной энергии Морзе есть: Де. 1. р Р e2

U( r )

Te

e

Подставьте R1 вместо длины связи возбужденного состояния при момента электронного перехода, т.е. R1 = r, и Amax для У(р). Когда вы это сделаете, вы получите: De. 1. R1Re 2

Amax Te

e

Измените уравнение для решения Re. Результат: решение на самом деле имеет 2 корня. Больший корень выбран потому, что Re, длина связи в возбужденном состоянии, должна быть больше R1, длина связи основного состояния для йода. Вопрос: Что спектроскопическое наблюдение подскажет нам, какой корень выбрать в расчет здесь?

RE

R1

1.

LN 1

AMAX DE

TE

R E = 2,979 10

10

M

Созданы: март 1997 Модифицирован: 5 июля 1998

IODINESPPT. mcd стр. 8

Авторы: Джордж Лонг Тереза ​​Джулия Зелински

Упражнение: Используйте потенциальные диаграммы Морзе для иллюстрации Факторы Франка-Кондона и объяснить появление максимума абсорбция. Вопрос: Каковы единицы Amax? Это энергия единица? Наконец, мы можем построить потенциалы Морзе как земли, Потенциалы состояния (X) и возбужденного состояния (B) на одном рисунке. график ниже показывает оба .i ri 0 .. 500 ( .5 i .01 ) . Анг

} } это определяет значения r с точки зрения индекса массива, i }

GroundDe g 1.873 Ang

4398. cm Rg e

1

2.66. Ang

} } параметры основного состояния, из литературы }

Теперь рассчитаем потенциальную энергию, используя потенциал Морзе функция.

Возбужденное состояние «В». riRe 2

Ground «X» StategroundDe. 1г. RIG E 2

Bi

De. 1

e

Te

Xi

e

Кривые потенциальной энергии

2 106 Bi X i 1 106

0

2

2,5

3

3,5 10 10 10 I

4

4,5

5

Взволнованный (b) Государственное земля (x) Государство

Создано: март 1997 г. Модифицировано: 5 июля 1998 г.

йодинфиктрий. Zielinski

Общие вопросы. 1. Варьируйте значение в Морзе потенциальное уравнение. Как значение влияет на форму потенциал Морзе? Сделайте то же самое для Re и De. Запишите свой наблюдения в тетрадь. 2. Будет ли получено другое частоты для максимального поглощения имеют большое значение в расчетные параметры? Измените свое значение для Amax и сообщите, что происходит с вычисленными параметрами Морзе. Объясните свои результаты. 3. При каких условиях можно получить другое значение Amax? Почему? 3. Влияет ли какое-либо другое данное на расчеты? Обсудите точность ваших результатов на основе вычислительные манипуляции, выполненные в этом документе.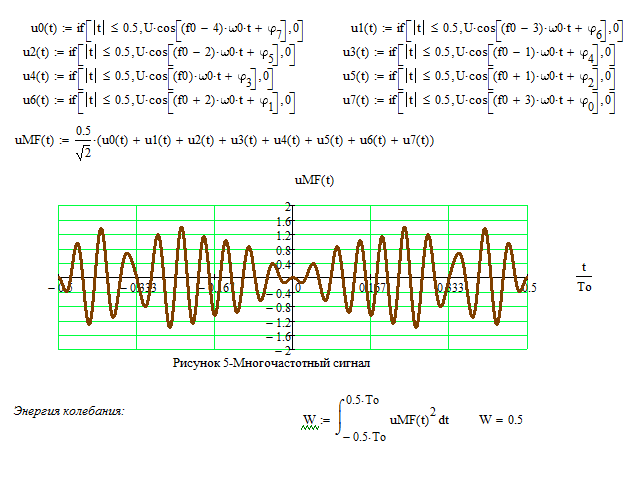 Мастерство Упражнение: Получите УФ-видимый спектр для некоторых других двухатомных молекула. Используйте этот документ в качестве шаблона для построения данных анализ на молекулу. Сравните и сопоставьте спектроскопические свойства молекулы йода по отношению к другой молекуле, которую вы выбрали. Обсудите различия между молекулами в отношении их химические и физические свойства. Благодарность: Авторы благодарят Джордж М. Шалхуб, Университет ЛаСаль, за используемую схему индекса. на сюжете Бирге-Спонера. Ссылки: 1. Д’Альтерио, Р.; Мэттсон, Р.; Харрис, Р. Потенциальные кривые для молекулы I2: An Студенческий физико-химический эксперимент. Дж. Хим. Образовательный 1974, 51, 282-284. 2. Лессингер, Л. Осцилляторы Морзе, Бирдж-Спонер. Экстраполяция и электронный спектр поглощения I2. Дж. хим. Образовательный 1994, 71, 388-391. 3. Макнот И. Дж. The Electronic Новый взгляд на спектр йода. Дж. Хим. Образовательный 1980, 57, 101-105. 4. Сайм, Р. Дж. Физическая химия, методы, приемы и Эксперименты, Колледж Сондерса: Филадельфия; 1990 г.