Уравнения в Mathcad
Практически в каждой лабораторной работе либо курсовом проекте можно столкнуться с необходимостью решения сложного уровня с одной неизвестной. Тратить по несколько десятков минут на нудные вычисления, в ходе коих можно допустить ошибку, не хочется. Оптимальный вариант – воспользоваться специальной математической утилитой, способной дать ответ быстро и корректно. Решение системы уравнений в маткаде можно осуществить двумя основными вариантами: в символьном и численном виде.
Способ первый: применение системы вычислений Given-Find.
Самый широко применяемый и легкий вариат нахождения решений уравнений и неравенств в алегебре. В рабочем поле программы записывается служебная команда Given. Она позволяет задействовать программные модули mathcad, которые необходимы для поиска ответа на уравнение.
Состоят такие модули из различных численных методов решений. После этого записывается само уравнение путем набора с применением символа «равно».
Найти его можно на панели Boolean (Булева алгебра).
Затем записывается команда Find(x), в которой х – искомая переменная. При помощи данной команды и выводят результат. Ее также можно присвоить определенной переменной с целью дальнейшего использования в вычислениях. Чтобы получить решение, после Find(x) вставляют символ «=» либо «→».
При помощи программы MathCad можно вычислить как символьный, так и численный корень. Чтобы получить численный вариант ответа, нужно ввести все приведенные в уравнении переменные, в том числе и искомую. Для MathCad определение нужной переменной – это начальное приближение ответа.
Так как численный способ имеет определенные особенности, в самом начале работы необходимо определить начальное приближение, потому что без него ответ уравнения найти не получится. Отсутствие корня либо его некорректное значение нередко становится последствием неправильного задания начального приближения.
Но ответа может не быть вообще, так как само уравнение может не иметь корней.
Если решение уравнения требуется в символьном виде, то задавать все значения параметров и начальное приближение не обязательно. В таком случае вводится само уравнение в программу через оператора Find(x), после чего ставится «→». Будут задействованы немного другие функции MathCad, которые преобразовывают и упрощают выражения. Ответом также будет определенное выражение. Стоит сразу отметить, что программа может найти решение не каждого уравнения, так что ее возможности весьма ограниченны.
Способ второй: использование метода solve.
Данный метод, по сути, ничем не отличается от вышеописанного, так как корень уравнения находится аналогичным образом. Отличается только оформление: уравнение вносится в программу посредством операторов Find и Given. На панели Symbol после записи уравнения нажимается клавиша solve, через запятую задается нужная переменная, после чего выдается ответ путем нажатия на «→».
Нередко при помощи второго способа можно найти корень уравнения, который не удалось получить первым способом.
Организация численных методов в MathCAD
Библиографическое описание:Имомов, А. И. Организация численных методов в MathCAD / А. И. Имомов. — Текст : непосредственный // Молодой ученый. — 2014. — № 6 (65). — С. 15-19. — URL: https://moluch.ru/archive/65/10618/ (дата обращения: 10.03.2023).
В настоящее время появилась возможность решения математических задач без составления компьютерных программ на языках программирования. Причиной этому является разработка специальных математических программ- математических систем. В научных исследованиях и в вузах на занятиях больше всего применяются следующие математические системы: MathCAD, MATLAB, Maple, Mathematika [1–3].При применении математических систем учебный процесс становится интересным, студенты понимают содержания занятия быстрее, глубоко, и для укрепления понятий и решения задач остаётся больше времени.
В статье возможности MathCAD демонстрируется в курсе «Численные методы» для приближённого решения задач алгебры и анализа.
В MathCADе задачи решаются тремя способами:
1) с помощью стандартных внутренних функций MathCAD,
2) с помощью естественного математического алгоритма решения задачи,
3) с помощью математического алгоритма решения задачи, реализованного во внутреннем языке MathCAD. Мы рассмотрим в основном первые два способа.
Команды в MATHCADE записываются без всякого предопределителя и они не отличаются от математических формул с лишь следующей разницей: комбинация знаков двоеточие и равно (:=) означает определение, знак равно (=) или стрелка (→) означает вывод вычисленного значения. Кроме того, после нажатия знака «открывается площадка для ввода текста- замечания и по окончании ввода и нажатия клавиши Enter остаётся только текст-замечание. Мы в местах, где должно быть текст-замечание записываем знак «и, после него, вводим текст-замечание. Это облегчает понимание алгоритма решения.
1. Приближённое решение одного нелинейного уравнения.
В MathCADе для приближённого решения одного уравнения имеются внутренные стандартные функции: 1) , given.
.find — для произвольных уравнений , 2) -для полиномиального уравнения , здесь — вектор коэффицентов. Коэффициенты вводятся именно в таком порядке.
Пример 1. Решить уравнение .
Записываем в MATHCADе следующие команды:
«начальная итерация и уравнение
«ссылка к внутренней функции и вывод решения.
Пример 2. Определение всех решений уравнения.
Решение:
«внутренние функции
«вывод решения
Организуем теперь алгоритмы методов простой итерации ва Ньютона, они имеют важное значение при изучении методов.
Пример 3. Метод итерации. Решим уравнение . Решение:
«задание начальную итерацию ва их количества
«приведение к виду и построение итераций
«вывод результата
Пример 4.Метод Ньютона. Рассмотрим опять уравнение. Решение:
«задание начальную итерацию ва их количества
«метод Ньютона
«вывод результата
2. Приближённое решение систем нелинейных уравнений.
В MathCADе имеются стандартные функции для приближённого решения систем нелинейных уравнений: блок given.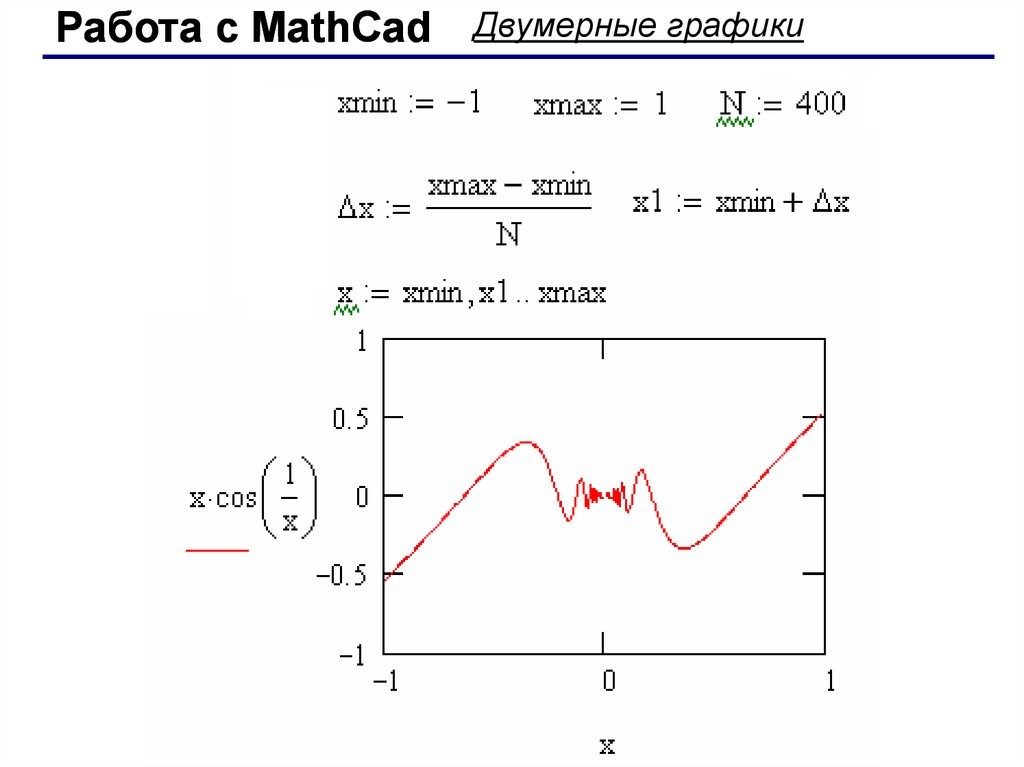
.find, внутренние функции minimize (f(x),x), minerr(x).
В качестве примера рассмотрим систему нелинейных уравнений:
, .
1) использование блока given..find.
Решение:
«задание начальную итерацию
Given «задание системы, равенство жирное
«присвоение решения переменной
«вывод корней
При начальной итерации получаем решение .
2) Метод минимизации. Вышеприведённую систему сведём к задачу .
«задание начальную итерацию ()
«целевая функция
«обращение к внутренней функции
«вывод решения
При начальной итерации получаем решение .
3) Использование внутренней функции minerr(x)
«задание начальную итерацию
Given «задание системы, равенство жирное
«обращение к внутренней функции
«вывод решения
4) Метод итерации. Рассмотрим систему .
«задание итерационых функций,
«задание числа итераций и начальную итерацию
«построение итераций
«вывод последовательности итераций
При начальной итерации получаем решение
«решение
5) Организация метод итераций Ньютона: .
ORIGIN:=1 «установка начального индекса
«задание уравнения
«матрица Якоби и начальная итерация
«итерации Ньютона
«итерации для
«итерации для
Формулу пока удалось реализовать только в MathCADе.
3. Решение задач алгебры. В MathCADе очень многие задачи алгебры решаются достаточно наглядно и этот процесс проводиться в естественном математическом языке. Процесс решения настолько простой, и мы ограничимся демонстраций некоторых основных внутренних функций. Имеем
«матрица, правая часть, начальная итерация
«детерминант, обратная матрица, корни
«собственные значения и векторы
«построение итераций
«расширенная и ступенчатая матрица
«результаты
«результаты
Здесь B расширенная матрица , G-ленточный вид матрицы В после применения метода Гаусса, -итерационный параметр, -метод итерации, lsolve (решение ) augment, rref, eigenvals (собственные значения), eigenvecs (собственные векторы)-внутренние функции MathCAD.
4. Построение интерполяция формул. Пусть .
А) Интерполируем f(x) многочленом Лагранжа 4-ой степени. Наберём в окне MathCADе следующие команды:
«количество точек, функция, отрезок
«узлы, значения «вывод значения функции
«многочлен Лагранжа
«значения многочлена.
Б) Интерполируем f(x) многочленом Ньютона 4-ой степени. Наберём в окне MathCADе следующие команды:
«количество точек, функция, отрезок
«разделённые разности
«результаты
5. Построение квадратурных формул. Интеграл вычислим квадратурными формулами прямоугольников, трапеций, Симпсона и Гаусса.
Записываем следующие команды в MathCADe:
«функция, отрезок, количество точек
«интеграл
«шаг, узлы
«формула прямоугольников
«формула трапеций
«формула Симпсона
«коэффициенты формулы Гаусса
«формула Гаусса
«приближённые значения интеграла
6.
Задача Коши для обыкновенного дифференциального уравнения
Решим приближённо задачу Коши для ОДУ
методами Рунге-Кутта. Записываем следующие команды в MathCAD:
«отрезок, узлы
«ОДУ правая часть, начальное условие
«метод Эйлера
«совершенный метод Эйлера
«метод прогноза коррекции
«коэффициенты метода РК
«коэффициенты метода РК
«формула Рунге-Кутта
Производя вычисления, получим следующую таблицу значений решения:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
yE |
0 |
0,846 |
1,356 |
1,617 |
1,771 |
1,873 |
1,943 |
1,995 |
2,035 |
2,066 |
|
yYE |
0 |
0,772 |
1,284 |
1,575 |
1,746 |
1,857 |
1,933 |
1,989 |
2,03 |
2,063 |
|
yPK |
0 |
0,51 |
1,107 |
1,511 |
1,718 |
1,842 |
1,925 |
1,983 |
2,026 |
2,06 |
|
yRK |
0 |
0,539 |
1,077 |
1,466 |
1,681 |
1,814 |
1,903 |
1,966 |
2,013 |
2,049 |
Все методы, внутренние функции дают достаточно хорошее приближение к решению.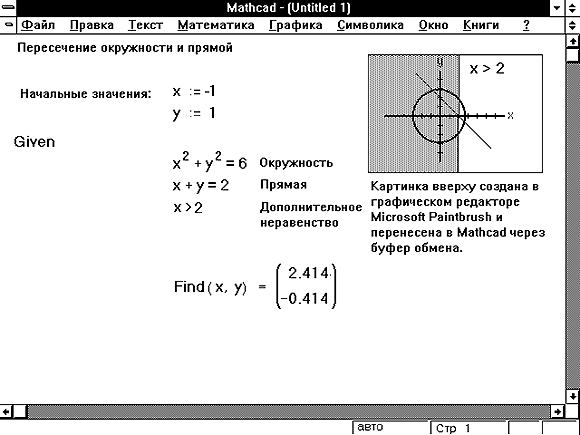
В этом мы убедились, решая одну задачу несколькими методами или решая задачи, с известными точными решениями.
Литература:
1. Алексеев Е. Р., Чеснокова О. В. Решение задач вычислительной математики в пакетах MathCAD, MATLAB, Maple 9. –М.:НТ Пресс, 2006.-496 с.
2. Имомов А. Численные методы и MathCAD. Наманган, НамГУ, Учебно-методическое пособие. 2012 г.-96 с.-znuz_215446_20120119115351.rar.
3. Имомов А. Организация решения дифференциальных уравнений в MathCADе. Усовершенствования преподавания физики, математики и информатики в академических лицеях и коллежах. Материалы 7-традиционной республиканской научно-практической конференции вузов. 1-часть. Ташкент, 2011.-38–41 с.
4. Поршнев С. В., Беленкова И. В. Численные методы на базе MathCAD. СПб, 2005.-464 с.
5. Ракитин В. И. Руководство по ВМ и приложения MathCAD. М.:ФМ, 2005.-264 с.
6. Охорзин В. А. Прикладная математика в системе MathCAD. СПб, Лань,2008–352 с.
7. С. С. Ирискулов, К. Д. Исманова, М.Олимов, А.Имомов. Численные методы и алгоритмы. MathCAD. Учебное пособие. Изд-во “Наманган”, Наманган, 2013.-276 с.
Основные термины (генерируются автоматически): начальная итерация, внутренняя функция, вывод решения, решение, функция, метод итерации, построение итераций, уравнение, MATHCADE, правая часть.
Что эквивалентно MATHCAD’s Given-Find — MATLAB Answers
26 просмотров (последние 30 дней)
Ответ: KSSV 6 июля 2020 г.
У меня есть куча примеров MATHCAD, которые были сделаны в версии 15.0 с помощью функции Given — Find в MATHCAD. Они взяты из «Анализ и проектирование энергетических систем» Ходжа и Тайлора. Я полагаю, что заданное — найти теперь называется блоком решения в MATHCAD Prime.
Пример этого находится на отметке 30 секунд видео с https://www.mathcad.com/en/capabilities о решении систем уравнений
Я хочу сделать то же самое в MATLAB, но не знаю, с чего начать в MATLAB для такого типа решения уравнений, определенных в уравнениях.
Приветствуется любая помощь или направление.
Ответы (2)
Отредактировано: Джерард Нэгл 6 июля 2020 г.
На картинке выше приведен пример из книги Тейлора, рис. 1-14 и 1-15.
Что меня заводит, так это то, как числа Рейнольдса и коэффициенты трения определяются на рис. 1-14, а затем используются в блоке «Дано-найти» на рис. 1-15.
Есть две разные трубы, отсюда и суммирование в блоке «Дано-найти».
У меня это работает в MATHCAD на моем рабочем ПК, но я хочу сделать это с MATLAB, так как университет избавляется от MATHCAD.
Вы можете попробовать это: https://in.mathworks.com/matlabcentral/fileexchange/22441-curve-intersections?focused=5165138&tab=function
Произошла ошибка
Невозможно выполнить действие из-за изменений сделал на странице. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.
Переведено
Выберите веб-сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и увидеть местные события и
предложения.
В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Америка
- Латиноамериканская Америка (Испания)
- Канада (английский)
- США (английский)
Европа
- Бельгия (английский)
- Дания (английский)
- Германия (нем.)
- Испания (Испания)
- Финляндия (английский)
- Франция (французский)
- Ирландия (английский)
- Италия (итальяно)
- Люксембург (английский)
- Нидерланды (английский)
- Норвегия (английский)
- Австрия (немецкий)
- Португалия (английский)
- Швеция (английский)
- Швейцария
- немецкий
- Английский
- французский
- Великобритания (Английский)
Азиатско-Тихоокеанский регион
- Австралия (английский)
- Индия (английский)
- Новая Зеландия (английский)
- 中国
- 简体中文Китайский
- Английский
- 日本Японский (日本語)
- 한국Корейский (한국어)
Обратитесь в местный офис
Рабочие листы RLM MathCAD
MathCAD — одна из нескольких полезных компьютерных математических программ.
которые могут вычислять сложные математические выражения как символически, так и
численно (другие включают Mathematica, Matlab, Maple и IDL).
что математический синтаксис и отображение в MathCAD можно изучить очень
быстро начинающими студентами, но достаточно мощный, чтобы
его можно использовать в студенческой и аспирантской физике и
курсы астрофизики и даже для дипломных исследований.
Учебное пособие по MathCAD
Вот простое учебное пособие по MathCAD, которое можно просмотреть в веб-браузере или загрузить.
MathCAD в астрофизике: демонстрационный доклад
В феврале 2005 года я провел семинар для преподавателей UI и аспирантов.
демонстрация использования MathCAD при решении задач астрофизики.
Темы включают обыкновенные дифференциальные уравнения первого порядка,
взвешенная аппроксимация данных методом наименьших квадратов, фазовые структурные функции,
анализ Фурье, вычисление векторных операторов (дивергенция, ротор,
градиент), а также простую обучающую страницу.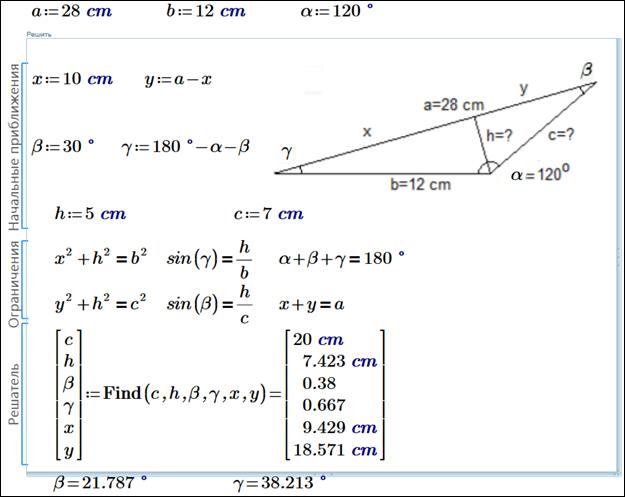
Нажмите здесь, чтобы увидеть таблицу с указателем на каждую тему выступления. (Маскад 11).
Рабочие листы курса астрономии
Эти рабочие листы были написаны, чтобы заменить зачастую неадекватные учебники. количественный материал в учебниках астрономии для начинающих, особенно для классы основного уровня. Нажмите на столбец HTML , чтобы открыть веб-страницу. версию страницы или щелкните правой кнопкой мыши, чтобы загрузить документ MathCAD. Примечание: Большинство рабочих листов были написаны с использованием MathCAD версии 13, но некоторые написано с использованием более ранних версий. Все рабочие листы должны быть читаемы с помощью MathCAD 13. Примечание. Эта таблица будет заполняться по мере нахождения времени!
| Название | Рабочий лист MathCAD | Уровень | Другие материалы |
|---|---|---|---|
| Уголки | Углы | Элементарный | |
| Гравитационное красное смещение, замедление времени | Красное смещение | Промежуточный | |
| Галактики: кривые вращения, темная материя | Галактики-1 | Промежуточный | |
| Законы о радиации | Радиация | Элементарный | |
| Ранняя Вселенная | Ранняя Вселенная | Промежуточный | |
| Галактики: Стандартные свечи, закон Хаббла | Галактики-2 | Элементарный | |
| Широта, долгота | Координаты-1 | Элементарный | |
| Заметки по специальной теории относительности | Специальная теория относительности | Промежуточный | |
| Газовые законы | Газовые законы | Элементарный | |
| Гравитационные черные дыры | Черные дыры | Элементарный | |
| Нейтронные звезды, пульсары | NS-пульсары | Промежуточный | |
| Гравитация: третий закон Кеплера | Кеплер-1 | Элементарный | |
| Оптика, телескопы | Оптика | Элементарный | |
| Звездные свойства | Звездный-0 | Элементарный | |
| Звездная эволюция 1 | Звездный-1 | Промежуточный | |
| Звездная эволюция 2 | Звездный-2 | Промежуточный | |
| Активные галактики, Гравитационные линзы | Линзы AGN | Промежуточный | |
| Синодические, сидерические периоды, небесные координаты | Координаты-2 | Элементарный | |
| Масса с орбиты | Кеплер-2 | Элементарный | |
| Небесная механика — 3-звездочное решение | 3-звездочное решение | Промежуточный уровень | Am. |