For mathcad: Pers.narod.ru. Обучение. Простое число или особенности цикла for в MathCAD

Pers.narod.ru. Обучение. Простое число или особенности цикла for в MathCAD

Pers.narod.ru. Обучение. Простое число или особенности цикла for в MathCAD

Этот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье

Pers.narod.ru. Обучение. Простое число или особенности цикла for в MathCAD

Для иллюстрации применения в MathCAD так называемого цикла типа арифметической прогрессии (обычного цикла for) напишем функцию, определяющую, является ли простым заданное натуральное число n:

Она предполагает, что переданное ей число n – простое (присваивает переменной r значение 1), а затем последовательно проверяет остатки от деления n на значения 2, 3, …, корень(n) – остатки от деления на 1 и n проверять нет смысла, а если число не простое, ни один из его двух целочисленных сомножителей не может быть больше квадратного корня из числа (

5*5=25 и 5 равно корню из 25, а числа, на которое 25 бы делилось нацело, большего 5, не существует).

Остаток от деления нацело значения n на значение i можно найти с помощью стандартной функции mod(n,i). Если найден хотя бы один остаток, равный нулю, функция Simple записывает возвращаемое значение r=0 и прерывает цикл проверок, в противном случае значение r остаётся равным 1, как оно и было назначено до цикла.

Протестировать нашу функцию можно, если написать ещё одну функцию, формирующую вектор из всех простых чисел, не превышающих заданного значения N:

Как видим, наша функция Simple неверна – например, она не считает простыми числа 2 и 3. Проблема состоит в том, что цикл for будет выполняться, даже если начальное значение параметра цикла больше конечного и шаг цикла равен 1 (по умолчанию). Например, для

n=2 граница цикла floor(корень(2))=1 и цикл, проверив остатки от деления n=2 на 2 и 1, равные нулю, решит, что число 2 – не простое.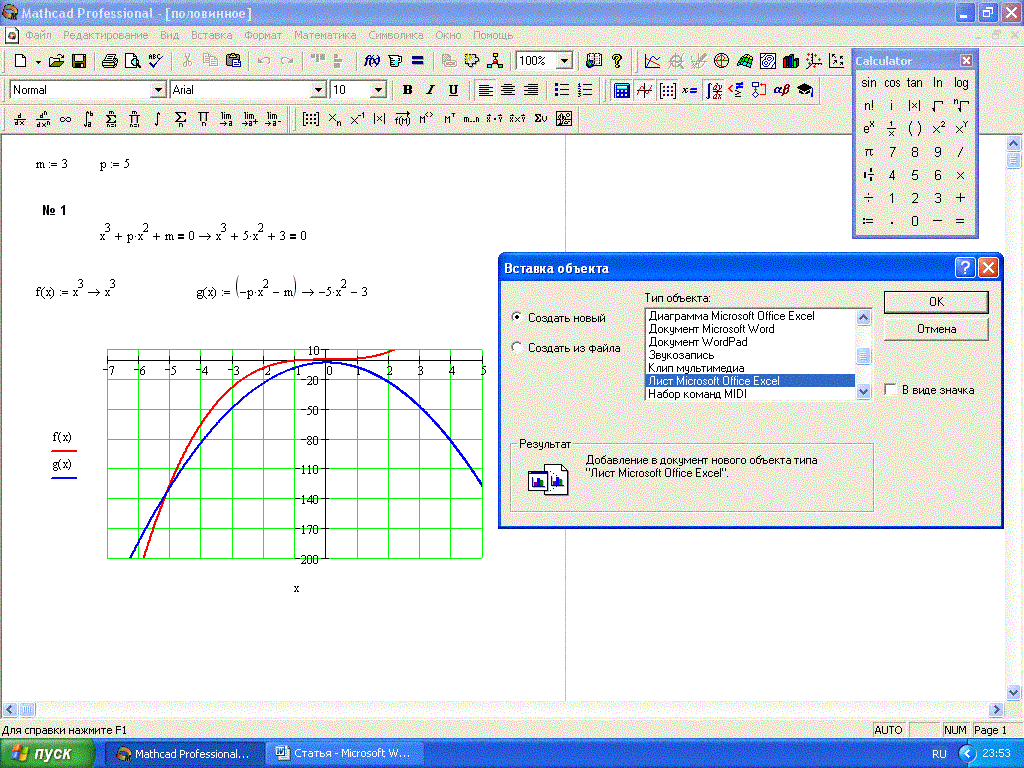

Правильно будет реализовать внутренний цикл через оператор while:

или задать для цикла for явный шаг, равный +1:

В последнем варианте функции числа 2 и 3 пришлось обработать отдельно, чтобы избежать ошибки «Необходимо определить переменную-диапазон с последовательными значениями» — в этом случае она возникнет, если значение floor(корень(n)) окажется меньше трёх.

Второй интересный момент — в классическом цикле for в MathCAD, как известно, справа от знака ∈ обычно ставят дискретный аргумент:

for i ∈ 1..10
 ...

Однако Маткад позволяет поставить вместо дискретной переменной справа от знака ∈ вектор или матрицу. Более того, можно туда поставить список векторов или матриц, перечисленных через запятую. Скалярная переменная слева от знака ∈ по очереди примет значение каждого элемента каждой не-скалярной величины в порядке перечисления. На показанном ниже скриншоте видно, как с помощью переменной i (и счётчика элементов k) программно формируется вектор x из всех положительных элементов векторов-параметров A и B.

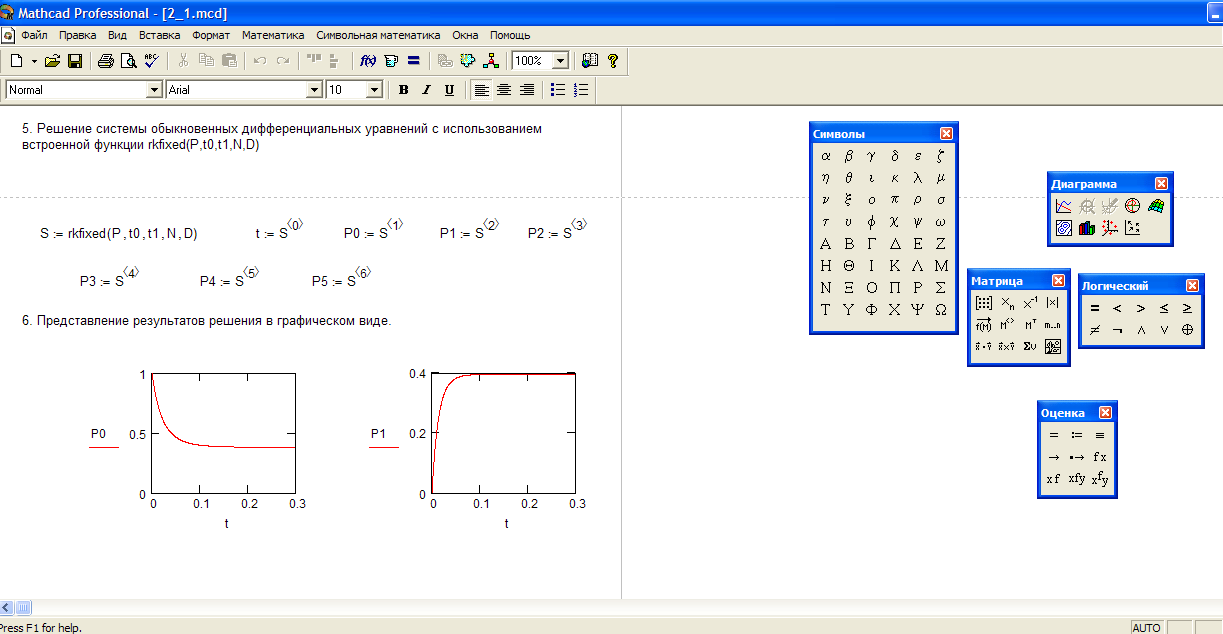
7. Программирование в пакете MathCad

Дополнительные возможности по автоматизации расчетов в пакете MathCAD связаны с возможностью подключения инструментов программирования.

Запрограммировать требуемый алгоритм вычисления в пакете MathCAD можно непосредственно в тексте документа вставляя в него соответствующие операторы и/или функции или, используя программы-функции, содержащие конструкции, подобные тем, что входят в классические алгоритмические языки.

Для использования программ-функций необходимо вначале описать программу-функцию, а затем вызвать ее. Описание включает в себя оригинальное имя, список формальных параметров и тело программы.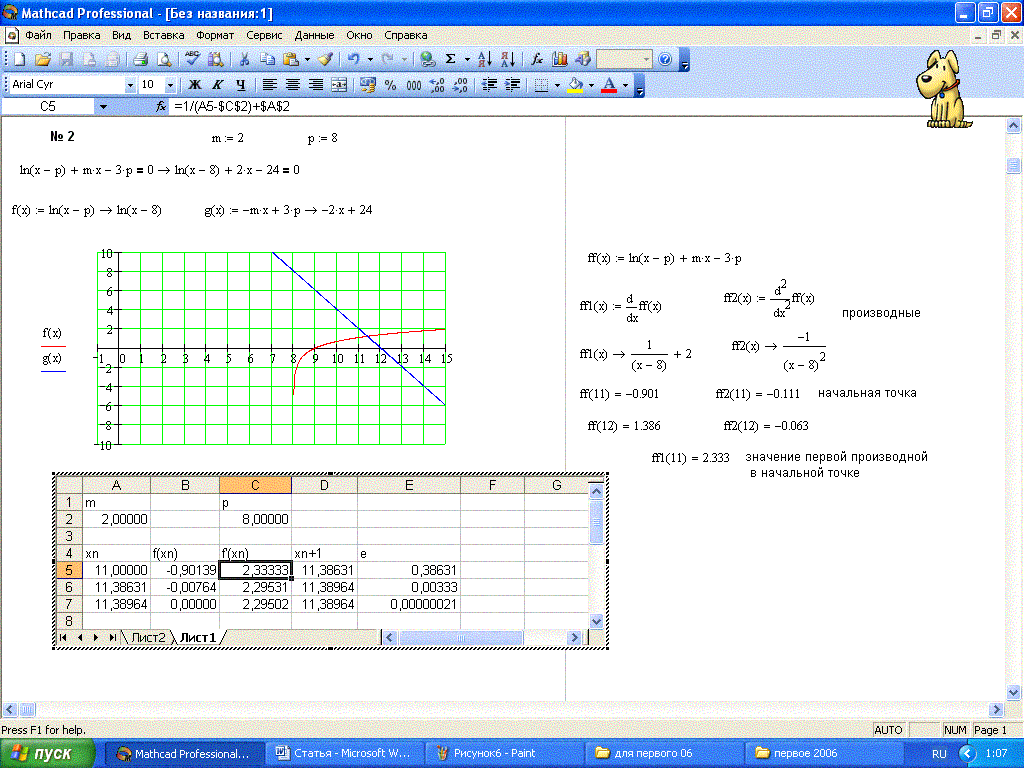

Через оригинальное имя осуществляется обращение к программе и возвращается в рабочий документ результат ее выполнения.

Список формальных параметров записывается в круглых скобках (через запятую) после имени программы. Он необходим для «передачи» внутрь программы данных, необходимых для выполнения вычислений. В качестве формальных параметров могут использоваться имена простых переменных, массивов и функций.

Тело программы, включает локальные операторы присваивания, условные операторы, операторы цикла, а также может включать вызов других программ-функций и функций пользователя.

Для ввода тела программы следует нажать на пиктограмму “Add line” из наборной панели Programming (Программирование). Это создает единый оператор и на экране возникает шаблон-заготовка программы с двумя полями для ввода операторов, образующих ее тело.

Для обращения к программе-функции следует обратиться к ее имени с указанием списка фактических параметров, разделенных запятой. Фактические параметры указывают при каких конкретных значениях осуществляются вычисления в теле программы.

Примеры создания программы-функции и обращения к ней представлены на рис. 19 и 20.

Для программирования линейного алгоритма (вычислительного процесса, в котором необходимые операции выполняются строго последовательно) следует операторы, реализующие его в теле программы — функции также разместить последовательно и выполнять все, с первого и до последнего. Рассмотрим работу этого алгоритма на примере вычисления площади треугольника по формуле Герона:

,

где a, b, c – длины трех сторон треугольника, а p – его полупериметр. На рис. 21 приведен пример реализации этого алгоритма.

Рис. 19. Пример создания программы функции (1)

Рис. 20. Пример создания программы функции (2)

Рис.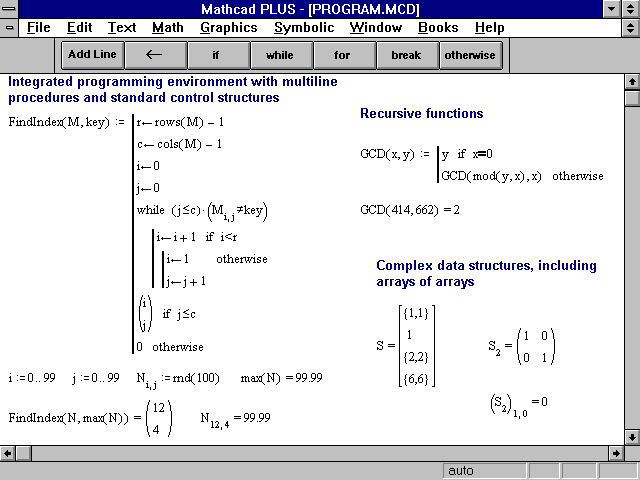

21. Программирование линейного алгоритма

Для программирования разветвляющегося алгоритма, в котором присутствует несколько ветвей вычислительного процесса, следует предусмотреть выбор конкретной ветви в зависимости от выполнения (или невыполнения) заданных условий наложенных на значения переменных алгоритма. С этой целью в MathCAD имеется условный оператор if, позволяющий изменить последовательность выполнение операторов. Оператор позволяет вводить в программу альтернативу с одним плечом и может быть записан только внутри программы. Шаблон-заготовка при вводе этого оператора имеет вид, представленный на рис. 22:

Рис. 22. Шаблон-заготовка для программирования разветвляющегося алгоритма

В поле 2 вводится логическое выражение (выражение отношений), в поле 1 – арифметическое выражение, значение которого используется, если проверяемое логическое выражение истинно, а если оно ложно, то выбирается значение выражения из поля 3.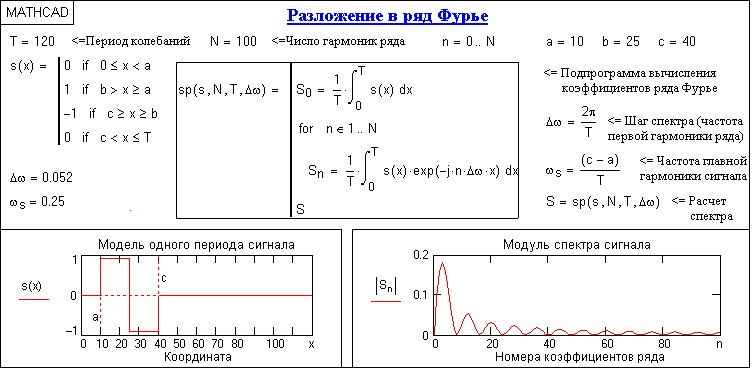

В конструкции условия используются логические выражения, которые, для наиболее часто встречающегося случая отношения двух арифметических выражений имеет вид:

< выражение А > < знак отношения > < выражение В>.

Рис. 23. Программирование разветвляющегося алгоритма

В качестве знака отношения выступают символы, выбираемые из панели Булево (Boolean). Рекомендуется для однозначного вычисления логических выражений использовать круглые скобки. Примеры программирования разветвляющихся алгоритмов представляет фрагмент MathCAD документа представленный на рис. 23. Заметим, что оператор if часто используется совместно с оператором иного выбора –

otherwise, который превращает неполную альтернативу в полную.

Циклические алгоритмы (циклы) содержат повторяющиеся вычисления, зависящие от некоторой переменной, называемой параметром цикла, а сами повторяющиеся вычисления составляют тело цикла . Циклы можно условно разделить на две группы:

• циклы типа арифметической прогрессии для которых количество повторений тела цикла можно определить до начала его выполнения.

• итерационные циклы, для которых окончание определяется не выходом параметра цикла за конечное значение, а более сложными условиями, так что количество повторений заранее определить нельзя;

Рис. 24. Пример программирования цикла (1)

Для программирования цикла типа арифметической прогрессии (с фиксированным числом повторений) используется оператор цикла for, вводимый с наборной панели. Для ввода такого оператора необходимо выполнить следующие действия:

После щелчка на кнопке for возникает заготовка, представленная на рисунке. В заготовку вписываются имя параметра цикла и указывается какие значения он может принимать, например i1. .100 или ii1, i1+D..i2, или дискретный ряд значений: k(1,2,3.7). В нижнее пустое поле (черный квадратик) после помещения туда курсора вводятся операторы, составляющие тело цикла. Если одной строки недостаточно, то дополнительные строки создаются командой Add Line (слева от тела цикла появляется вертикальная черта). На рис. 24 приведен фрагмент документа MathCAD, в котором проиллюстрировано применение цикла типа арифметической прогрессии.

Рис. 25. Пример программирования цикла (2)

Для программирования итерационных циклов используется оператор while («пока»), который формирует цикл с предпроверкой (цикл выполняется, пока выполняется некоторое условие). Нажатие на эту кнопку вызывает появление конструкции с двумя пустыми квадратиками. В первый из них (правее while) записывается булево выражение (переменная), управляющее циклом, а во второй (ниже while) – тело цикла, операторы которого будут выполняться, пока булево выражение возвращает «Да» (числовое значение отличное от нуля). Если в теле цикла более одного оператора, то следует использовать кнопку Add Line.

На рис. 25 представлен фрагмент документа MathCAD, в котором производится расчет квадратного корня по итерационной процедуре, описываемой формулой:

Цикл прерывается, если в результате i-ой итерации удовлетворяется условие , где- заданная точность вычисления.

Рис. 26. Пример программирования цикла (3)

Применение оператора while, без дополнительных средств контроля может привести к зацикливанию (бесконечной работе программы), Так, к зацикливанию может привести задание отрицательного значения точности – < 0. В программе, представленной фрагментом документа MathCAD на рис. 26 реализован цикл с фиксированным числом повторений, а для выхода из цикла (и из программы) используется оператор Break (вводимый с панели Программирование в левое поле оператора if), который проверяет выполнение заданного условия по точности и прерывает выполнение программы, возвращая значение операнда, стоящего за ним.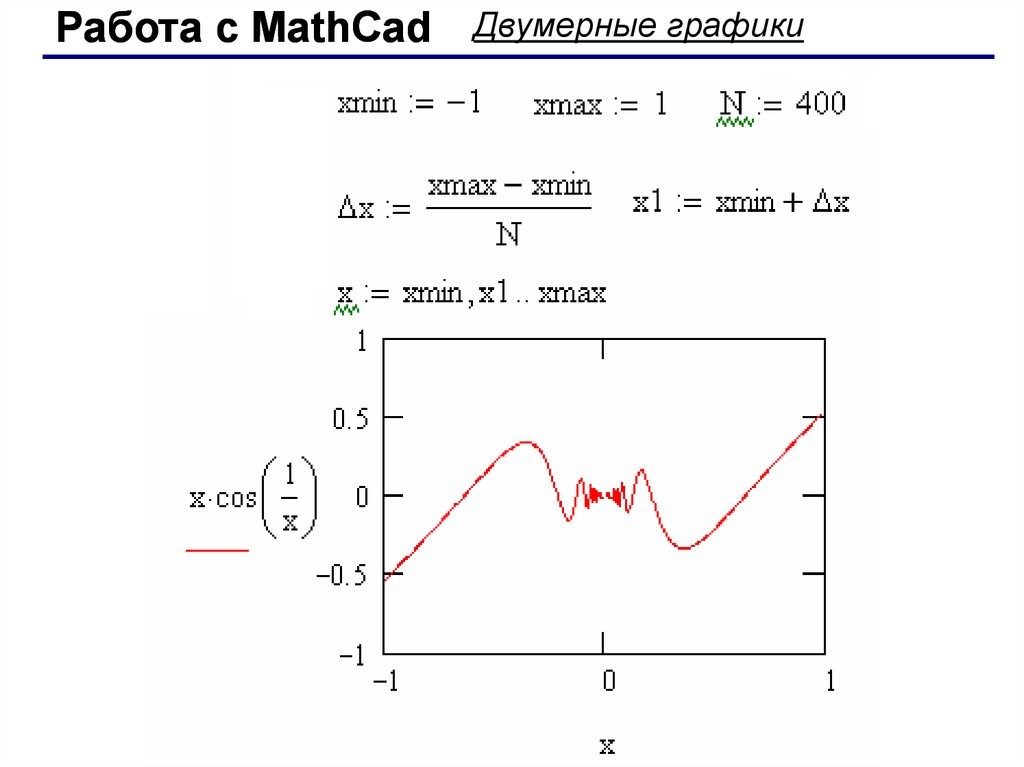

К дополнительным операторам программирования кроме Break относятся: Continue – оператор продолжения выполнения цикла путем возврата в его начало; Return – оператор-функция возврата того или иного значения в зависимости от выполнения условия, On error – оператор обработки ошибок. Эти операторы фактически введены в силу отсутствия в инструментах программирования понятия метки и условного или безусловного перехода к ней.

Рис. 28 представляет фрагмент документа MathCAD, в котором приведен дополнительный пример по составлению программы-функций с использованием циклических процедур.

Рис. 28. Пример выполнения циклического алгоритма

MathsPad’s Shop — Учебные ресурсы

Зарегистрируйтесь бесплатно

Уже зарегистрированы?

Войти

• Mathspad.co.uk
• @mathspadnicola
• Facebook.com

Mathspaduk

Сокровищница.

MathspadUK

Диаграммы Венна Рабочие листы для GCSE 9-1 Математика

Набор рабочих листов, охватывающих все обязательные темы диаграмм Венна для нового учебного плана GCSE 9-1 по математике. Включает в себя: — Затенение разделов диаграмм Венна на основе заданных обозначений — Нахождение вероятностей из диаграмм Венна — Составление диаграмм Венна на основе предоставленной информации — Условная вероятность с диаграммами Венна — Идентификация исчерпывающих, взаимоисключающих и независимых пар событий из диаграмм Венна Эти рабочие листы идеально сочетаются с нашими интерактивными обучающими инструментами на MathsPad. Первый бесплатный, его можно найти на сайте www.MathsPad.co.uk.

MathspadUK

Таинственный иллюстрированный набор трансформаций!

Набор трансформаций: ученики должны отражать, вращать и перемещать различные фигуры, чтобы открыть тайные картинки! Пакет содержит: Переводы Mystery Picture Подходит для младших школьников, которые только изучают переводы и векторы. Размышления Mystery Pictures 1 & 2 Также подходит для младших школьников, которые только начинают изучать отражение в зеркальной линии. Вторая версия использует оси координат и линию y = -x как зеркальные линии. Вращения Mystery Pictures 1 & 2 Учащиеся должны уметь вращать 90 градусов и 180 градусов относительно точки. Большинству студентов понадобится калька. Первая версия находится на координатной плоскости, и все вращения происходят вокруг начала координат. Смешанные Трансформации Картинки 1 & 2 Эти действия требуют, чтобы студенты использовали переводы, размышления и повороты. Комбинированные трансформации Картинки 1 & 2 Это самые сложные изображения, которые требуют от учеников многократных преобразований каждого объекта, чтобы найти его место. Вторая картина имеет место на координатной плоскости. Ответы включены и могут быть проверены с первого взгляда, что позволяет учащимся и учителям легко узнать, все ли в порядке!

MathspadUK

Углы: Нарисуй космический корабль!

Этот набор содержит два упражнения для мотивации аккуратного использования транспортира и линейки. 1. Невозможные конструкции Это задание требует, чтобы учащиеся попытались нарисовать ряд фигур, зная, что хотя бы одна из них невозможна! Например, могут ли они построить треугольник с двумя тупыми углами? Почему? Почему бы нет? 2. Нарисуй этот космический корабль! Это задание требует, чтобы учащиеся попытались сделать точную версию космической ракеты. Они должны точно рисовать линии и углы, чтобы космические корабли получились правильно. Студентам предстоит работать над двумя разными космическими кораблями, сложность которых возрастает! Ответы включены.

MathspadUK

Объем и площадь поверхности: призмы, пирамиды, конусы и сферы

Три задания, предназначенные для учащихся GCSE, работающих с площадью поверхности и объемом призм, пирамид, конусов и сфер. 1. Площадь поверхности прямоугольных параллелепипедов с нечетным значением В этом упражнении учащиеся должны решить, какой прямоугольный параллелепипед в каждом ряду имеет площадь поверхности, отличную от других. Существует также дополнительная деятельность, основанная на поиске недостающих размеров прямоугольных параллелепипедов с учетом их площади поверхности. 2. Рабочий лист объема и площади призмы В этом рабочем листе учащимся предлагается найти площадь поверхности и объем ряда различных призм, включая цилиндр, разрезанный пополам. Рабочий лист предназначен для облегчения проверки понимания, поскольку учащиеся должны записывать свои ответы в приведенную таблицу. 3. Объем пирамид, конусов и т.п. Сферы: Какой объем самый большой? Это задание требует от учащихся сравнения тел и определения в каждом ряду, какое тело самое большое? Включает в себя призмы, пирамиды, конусы и сферы. Теперь обновлено, чтобы включить Дополнительные рабочие листы по сферам, прямоугольным параллелепипедам, призмам, конусам и т.д. цилиндры.

MathspadUK

Подобные и конгруэнтные треугольники Щелчок!

Привязка подобных треугольников: В этом упражнении есть 14 треугольников, и учащиеся должны соединить их в пары, которые подобны. После того, как они сопоставили их в пары подобных треугольников, они должны использовать тот факт, что они подобны, чтобы вычислить недостающие стороны и углы. Привязка конгруэнтных треугольников: Как и выше, есть 14 треугольников, и учащиеся должны составить из них пары, которые определенно конгруэнтны. Затем они должны определить недостающие стороны и углы. В качестве дополнения учащиеся могут также использовать законы синусов и косинусов для определения недостающих сторон и углов в треугольниках. Ответы на это включены. Метки: Сходство, Подобные треугольники, AAA, SAS, SSS, конгруэнтность, конгруэнтность, конгруэнтность треугольников

MathspadUK

Умножение десятичных дробей

Умножение десятичных дробей: использование связанных вычислений Бесплатный рабочий лист, на котором учащиеся должны использовать один заданный расчет, например. 19 x 23 = 437, чтобы получить ответы на соответствующие вычисления, такие как 1,9 x 23 = 437. Включает ответы.

MathspadUK

Задачи на площадь поверхности и сети

Набор задач, в которых учащиеся должны сравнить изображение параллелепипеда и его сети, чтобы вычислить недостающие размеры и площади поверхности. Отзывы ниже очень ценятся 🙂 Нравится этот ресурс? У нас есть действия на площадь поверхности и объем конусов, сфер и пирамид здесь (£).

MathspadUK

Пакет упражнений «Взаимные и экспоненциальные графики»

Этот пакет содержит три задания, предназначенные для помощи учащимся GCSE в построении и интерпретации обратных и экспоненциальных графиков. Оно включает: 1. Рисунок &амп; Понимание взаимного & Экспоненциальные графики Он содержит рабочие листы, на которых учащиеся должны определить координаты для ряда экспоненциальных и обратных функций и построить связанные с ними графики, чтобы увидеть полученную форму. Далее следует набор вопросов, призванных проверить понимание и заставить учащихся задуматься о том, где определены функции и координаты, через которые они будут проходить. 2. Асимптоты Чтобы помочь учащимся понять форму обратных и экспоненциальных графиков, этот набор слайдов PPT разработан, чтобы дать учащимся возможность понять, почему и где возникают асимптоты. 3. Сопоставление графиков Это упражнение предназначено для использования, когда учащиеся изучили ряд графиков, включая обратные и экспоненциальные функции. Он содержит графики квадратичных, кубических, круговых, линейных, обратных и экспоненциальных графиков, которые учащиеся должны сопоставить со своими уравнениями.

MathspadUK

Расширение: Положительные, отрицательные и дробные масштабные коэффициенты

Расширение: Рабочий лист & Пакет действий (положительные, отрицательные и дробные масштабные коэффициенты) В том числе: 1. Три рабочих листа, которые дают учащимся возможность попрактиковаться в использовании положительных, отрицательных и дробных масштабных коэффициентов для увеличения фигуры от заданной точки. 2. Два задания для самопроверки, в которых учащиеся должны увеличить в разном масштабе, чтобы создать загадочную картинку! 3. Увеличение на координатной плоскости. Быстрое практическое задание, которое может стать отличным домашним заданием. Легко проверить и охватывает положительные и дробные увеличения от (0,0). Ответы включены.

MathspadUK

Отрицательные числа: упражнения и головоломки

Этот набор содержит три различных задания, которые помогут учащимся попрактиковаться в вычислениях с отрицательными числами. 1. Добавление & Вычитание отрицательных чисел из таинственных сеток Учащиеся должны решить подсказки, связанные с добавлением и вычитанием отрицательных чисел, чтобы найти недостающие числа в сетке. Например, числа в верхней строке составляют в сумме -10. Включает в себя 3 уровня сложности. 2. Загадочные сетки умножения и деления отрицательных чисел Как и выше, 3 головоломки на умножение и деление негативов. 3. Все 4 операции: головоломки Учащиеся должны выяснить, где в этих головоломках находятся пропущенные числа, чтобы расчеты были верными.

MathspadUK

Вычисление процентов — задания и головоломки

Этот набор содержит три задания, которые помогут учащимся вычислять проценты от суммы: 1. Таинственные сетки процентов Студенты должны использовать набор подсказок, чтобы решить загадочные числа в сетке. Например, «Число в левом верхнем углу составляет 20% от числа в правом нижнем углу». Есть 3 уровня сложности. 2. Головоломки с процентной сеткой В этих упражнениях учащиеся должны решить недостающие числа в серии процентных выражений. Иногда им приходится отрабатывать недостающий процент, а также результат расчета. 3. Стартовые карточки/выходные карточки Набор карточек, которые можно использовать в качестве начала урока или бланка на выходе, чтобы увидеть, насколько хорошо учащиеся поняли. Их можно распечатать с двух сторон, чтобы у учащихся были свои ответы на обратной стороне карточки. В качестве альтернативы ответы предлагаются для проецирования на доску. На каждой странице по 8 карточек. 4. Головоломка «Кто родился когда?» Учащиеся должны использовать подсказки, чтобы выяснить, сколько детей родилось в каждом месяце года. Эта головоломка требует некоторой логики и умения считать простые дроби и проценты от суммы.

MathspadUK

Блок работы по обработке данных для GCSE 9-1 (Высший)

Этот блок работы для GCSE Higher Tier 9-1 включает: Средние значения из частотных таблиц Средние значения из сгруппированных таблиц частот Суммарная частота (построение графиков) Суммарная частота (интерпретация графиков) Квартили & Коробчатые участки Обратные средние задачи (Работая в обратном направлении от заданного среднего, чтобы найти исходные значения данных) Рабочие листы предназначены для использования в качестве буклетов и содержат примеры, на которые учащиеся могут ссылаться, а также несколько страниц с различными вопросами. Ответы включены для всех рабочих листов в удобном для использования формате.

MathspadUK

GCSE 9-1 Transformations Unit Work

Этот раздел GCSE по преобразованиям будет полезен как для студентов старших курсов, так и для учащихся базового уровня. Он включает в себя девять различных рабочих листов: 1. Отражение 1 Отражение в горизонтальных, вертикальных и диагональных зеркальных линиях 2. Отражение 2 Сюда входят зеркальные линии на координатных осях, описываемые как y = a, x = b, y = x и т. д. Вопросы включают создание и описание отражений. 3. Вращение Включает центральные точки на осях и набор вопросов, требующих, чтобы учащиеся выполнили поворот или описали, как была повернута фигура. 4. Перевод Смесь переводов для завершения и описания. 5. Увеличение 1 Включает только положительные коэффициенты масштабирования с вопросами для учащихся, чтобы они завершили увеличение и описали их. 6. Увеличение 2 Сюда входят дробные и отрицательные масштабные коэффициенты. 7. Описание преобразований 1 Этот рабочий лист для смешанной практики дает учащимся возможность попрактиковаться в описании всех четырех различных преобразований. 8. Смешанные преобразования 1 & 2 Эти два рабочих листа объединяют все навыки из всех других рабочих листов для окончательного обзора всей темы.

MathspadUK

Систематическое перечисление и правило продукта для подсчета GCSE 9-1 Математика

Этот пакет содержит три рабочих листа, связанных с новой целью GCSE по систематическому перечислению и стратегиям подсчета. Рабочий лист 1: Систематический список Предназначен для студентов базового уровня, но также является хорошей практикой для более высоких уровней, набор задач основан на систематическом перечислении всех возможных вариантов в различных ситуациях. Рабочий лист 2: Правило продукта (несколько групп) Этот лист требует, чтобы учащиеся использовали правило произведения в ситуациях, когда им нужно вычислить общее количество вариантов из нескольких разных групп. Рабочий лист 3: Правило продукта (одна группа) Это упражнение представляет собой дополнительный набор вопросов о правиле продукта, но немного сложнее, поскольку включает вопросы, в которых учащиеся должны выбрать элементы из одной и той же группы. (Например, количество способов выбрать двух мальчиков из группы 8). Ответы включены для всех трех рабочих листов.

MathspadUK

Округление и оценка: использование значащих цифр

Серия упражнений для учащихся, чтобы попрактиковаться в округлении до заданного количества значащих цифр и оценочных расчетах. 1. Значимые цифры Верная или ложная активность Это упражнение содержит таблицу утверждений о том, как были округлены числа, например, «54,5» было округлено до двух значащих цифр. Студенты должны заштриховать восемь утверждений, которые верны. Формат этого занятия позволяет легко проверить, понимают ли учащиеся концепцию, и есть вторая версия головоломки, которую можно задать позже в качестве домашнего задания для повторения. Ответы включены. 2. Головоломка со значимыми фигурами и сеткой. Вопросы с несколькими вариантами ответов Он содержит два вида деятельности. Во-первых, это головоломка с сеткой, в которой учащийся должен решить, где расположить набор чисел, чтобы сделать ряд утверждений верным.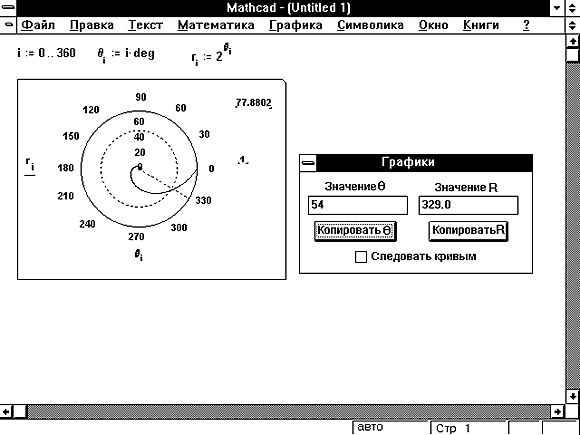 Существует также дополнительный рабочий лист с простой практикой и вопросами с несколькими вариантами ответов о значащих цифрах. Ответы включены. 3. Оценочный лист Это рабочий лист для оценочных расчетов путем округления до 1 или 2 значащих цифр. В нем также есть раздел для практики оценки квадратных корней. Включен набор начальных вопросов для обсуждения со студентами. Включает ответы.

MathspadUK

Вращательная симметрия: рабочий лист и пакет заданий

Вращательная симметрия: набор рабочих листов и заданий по всем темам вращательной симметрии: Вращение вокруг центральной точки Описание вращения (направление, градус и центр) Проекты с симметрией вращения (отличная демонстрационная работа) x 2 Таинственная картина вращательной симметрии Порядок расчетов вращательной симметрии Порядок вращательной симметрии: четырехугольники Симметрия вращения на координатной сетке Ответы прилагаются к каждому рабочему листу.

MathspadUK

Bearings Treasure Map Задание

Учащиеся должны использовать подсказки и карту, чтобы выяснить, где в вымышленном городе спрятаны сокровища.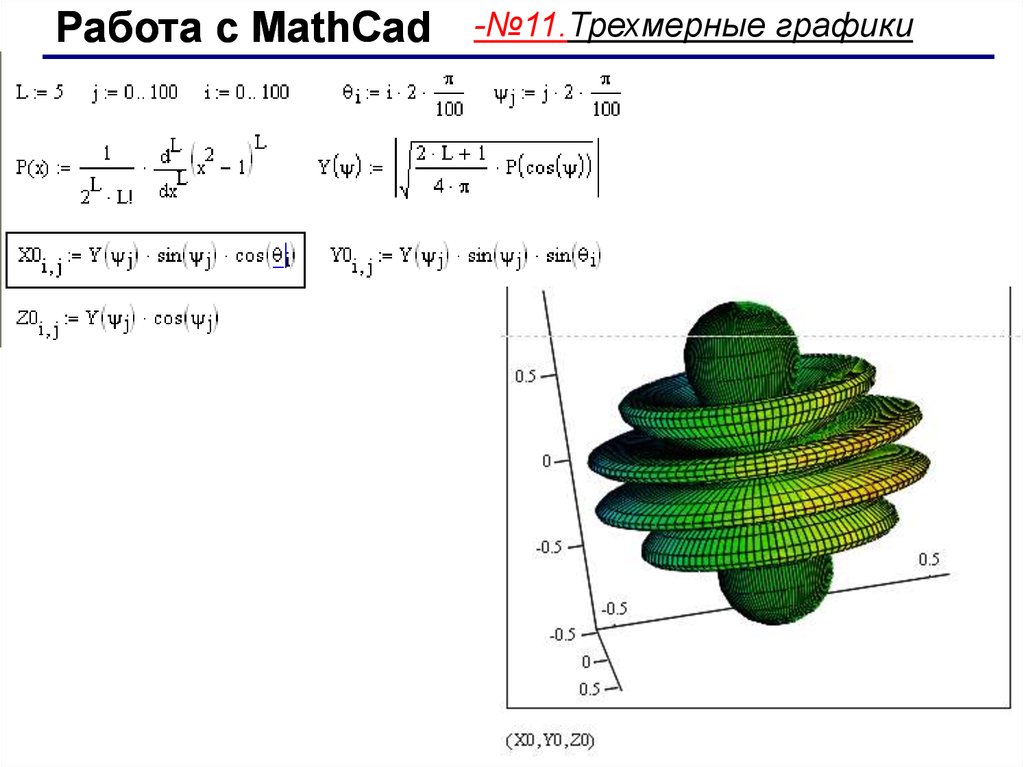 Включает множество измерений/чертежей подшипников. Мы с благодарностью принимаем отзывы, приведенные ниже 🙂

MathspadUK

Головоломки с разрядными значениями и действия с десятичными числами

Три занятия для поддержки учащихся, работающих над разрядными значениями и задачами. десятичные дроби. 1. Чтение & Сопоставление десятичных знаков Учащиеся должны сопоставить числа и утверждения об их разрядности. Например, 0,62 соответствует 2 сотым. Все вопросы связаны с числами 1, 2 и 6, поэтому учащимся действительно нужно подумать о разрядности показанных чисел. Они также могут записывать свои совпадающие пары в таблицу, что позволяет вам легко проверить, правильно ли они понимают их, и предоставить обратную связь. 2. Головоломки со значением места Это задание содержит две страницы головоломок о десятичных дробях и разрядах. Головоломки варьируются от «угадай число», основанного на подсказках о разрядности, до сравнения и упорядочивания десятичных знаков с использованием символов неравенства. 3. Добавление дешифратора десятичных знаков Упражнение по взлому кода, в котором учащиеся должны складывать десятичные знаки, чтобы раскрыть секретное сообщение. Десятичные дроби имеют разную длину, поэтому учащимся потребуется использовать некоторые письменные методы. Ответы включены для всех действий.

MathspadUK

Surds Activity Pack

Три упражнения для повторения умножения, сложения, вычитания и упрощения surds. 1. Головоломка Surds Grid Учащиеся должны решить, куда идут недостающие числа в сетке. Для этого им нужно будет подумать об упрощении surds и использовании всех четырех операций. 2. Головоломки Surds с пропущенными числами Это задание содержит три задания, чтобы сосредоточить внимание учащихся на (а) умножении сурдов, (б) добавлении сурков, (в) использовании всех четырех операций с сурами. В каждом задании учащиеся должны вычислить недостающие числа, чтобы утверждения были верными. 3. Иррациональные последовательности! Это упражнение предназначено для предсказания следующего члена набора последовательностей, которые все содержат surds.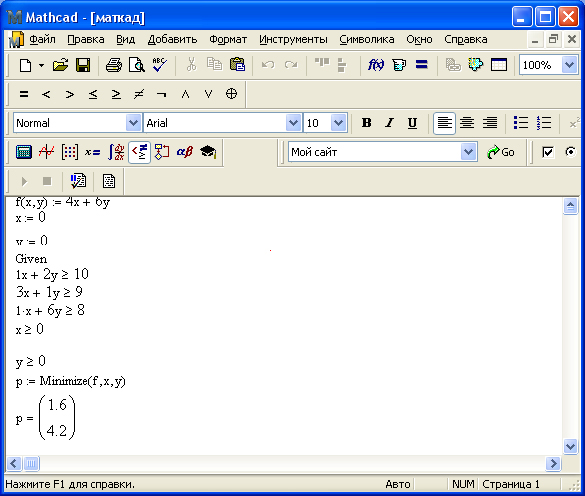 Студенты должны будут думать об умножении, делении, сложении и вычитании surds.

MathspadUK

Умножение и деление дробей Пакет упражнений

Этот ресурс представляет собой набор идей, которые помогут учащимся работать над умножением и делением дробей. В том числе: Умножение дробей на 4 в линейной игре Это задание дает учащимся возможность повторить умножение дробей на дроби в увлекательной игровой деятельности. Они должны играть парами, чтобы умножать дроби, пока не получат четыре блока подряд. Умножение дробей & Обнаружение обратных связей Эта деятельность по сопоставлению побуждает учащихся думать о более разнообразном наборе ситуаций, в которых нам нужно умножать дроби, включая умножение дробей на целые числа и необходимость сокращения. Затем следует задание, которое подводит учащихся от умножения дробей к размышлениям о том, как найти пары дробей, которые умножаются на 1, то есть к обнаружению обратных величин. Умножение & Разделение дробей Это задание направлено на то, чтобы помочь учащимся распознать эквивалентные вычисления.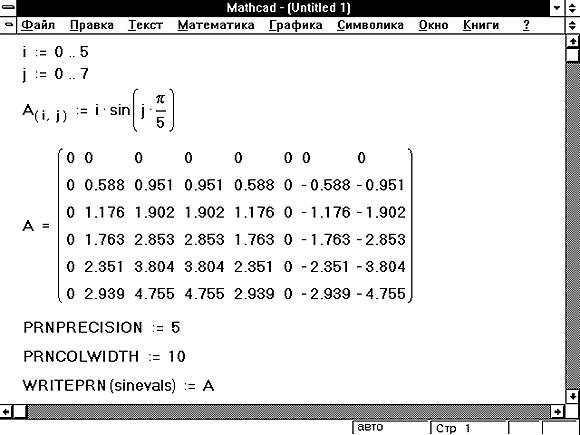 Они должны сопоставить расчеты, которые приводят к одному и тому же ответу, заметив, что умножение на дробь эквивалентно делению на ее обратную величину. Головоломка с делением дробей на пропущенные числа Это задание требует, чтобы учащиеся вычислили недостающие числа, чтобы сделать серию утверждений о делении дробей верными. Он прогрессирует, чтобы включить некоторые случаи деления со смешанными числами. Все действия включают ответы.

5 веб-сайтов, которые вы должны знать… #4

Недавно я запустил новую серию постов под названием «5 веб-сайтов, которые вы должны знать…». Пока что я рассмотрел Corbett Maths, Mr Carter Maths и MathsBot.

Сегодняшняя статья посвящена одному из моих самых любимых MathsPad. Этот веб-сайт требует подписки для доступа к некоторым ресурсам, но многие из них доступны бесплатно. Я использую MathsPad уже много лет, но недавно он стал моим любимым веб-сайтом как для Key Stage 3, так и для новых тем GCSE. Никола (@MathsPadNicola) и Джеймс (@MathsPadJames) добавили несколько совершенно замечательных ресурсов по таким темам, как итерация, диаграммы Венна и систематический список — я не могу рекомендовать их достаточно.

Ресурсы MathsPad очень хорошо разработаны. Их действия увлекательны и умны, их легко распечатать на бумаге формата A5 или отобразить на интерактивной доске. Ответы тоже всегда есть. Я хочу показать вам десятки примеров, но для того, чтобы этот пост был разумным, я просто поделюсь несколькими снимками, начиная с тех, которые относятся к новым темам GCSE.

Новые темы GCSE
На прошлой неделе я преподавал «систематическое перечисление и правило произведения» в 11 классе. Это странная тема — кажется, что она должна быть простой и логичной, но некоторые из примеров вопросов GCSE довольно сложны. Обычно я пишу свои собственные уроки, но в этот раз я делал их прямо из MathsPad. Они подготовили три интерактивных доски, которые я использовал для преподавания, и три рабочих листа для практики студентов. Мои лучшие ученики были действительно вовлечены в течение всего этого урока, и у них была соответствующая задача. Эти ресурсы можно найти здесь.

Еще одна тема, в которой MathsPad пришел мне на помощь, — это диаграммы Венна.

Их ресурсы по этой теме превосходны и включают в себя несколько прекрасных сложных заданий. Для учителей, которые не уверены, что им нужно преподавать для условной вероятности, Worksheet Pack 2 предлагает отличные вопросы.

Последние ресурсы MathsPad находятся на стадии итерации, и снова они превосходны. Для интерактивной доски у них есть умная игра для поиска корней, а также у них есть набор из четырех рабочих листов итераций. Я преподаю эту тему в следующем семестре и обязательно буду использовать эти листы на своих уроках.

Трудно найти ресурсы для нового содержимого GCSE по точечной диаграмме (причинно-следственная связь, экстраполяция и выбросы), но в MathsPad есть прекрасное (бесплатное!) задание True or False.

Преобразование графа? Студентам GCSE больше не нужно знать, как делать растяжки (например, f(2x)). Тем не менее, они все еще должны делать переводы и размышления. Если, как и я, у вас в 11-м классе так мало времени, что у вас есть время только для изучения тем, перечисленных в спецификации GCSE, это означает, что большое количество ресурсов по преобразованию графиков и прошлых вопросов GCSE теперь устарели. Не бойтесь, тем не менее, MathsPad любезно предоставил прекрасную операцию по преобразованию графиков только для переводов и отражений.

Это одна из вещей, в которых Джеймс и Никола преуспели: они производят ресурсы для использования на своих собственных уроках GCSE, поэтому они хорошо знакомы с новой спецификацией GCSE. Я мог бы показать вам множество других замечательных ресурсов для выпускных экзаменов в школе, но сейчас давайте взглянем на некоторые ресурсы, которые подходят для ключевого этапа 3.

Ключевой этап 3

Мои 7-классники обожают взломщики кодов и головоломки. Я постоянно использую с ними ресурсы MathsPad. Например, ранее в этом году им нравились головоломки Place Value.

Им также понравился этот Взломщик Кодов Подстановки…

… и они нашли эту Загадочную Сетку Факторов и Множителей довольно сложной задачей (они были в восторге от этого).

Мне так нравятся ресурсы MathsPad по углам, что я не могу дождаться, чтобы снова преподавать углы!

Уровень A

Я иногда использую ресурсы MathsPad и на уровне A — например, их рационализация знаменателя — это здорово. Недавно, обучая 12-классников дифференциации, я использовал это упражнение, чтобы проверить, правильно ли они понимают дробные индексы (это не так!):

Я знаю, что читатели этого поста не обязательно смогут получить доступ ко всем ссылкам, которыми я поделился (большинство из них требуют подписки), но просмотрите веб-сайт, потому что там есть много бесплатных материалов. И попробуй убедить своего директора по математике подписаться! Если у ваших учеников есть доступ к планшетам на уроках, им также будут полезны интерактивные задания для учащихся.