НОУ ИНТУИТ | Лекция | Встроенные функции MathCAD
Ключевые слова: значение, нумерация, вектор, длина, функция, медиана, биномиальное распределение, натуральное число, параметр, нормальное распределение, вещественное число, графика, опция, массив, координаты, сегменты, математика, значение функции, график функции, радиус, множества, вероятность
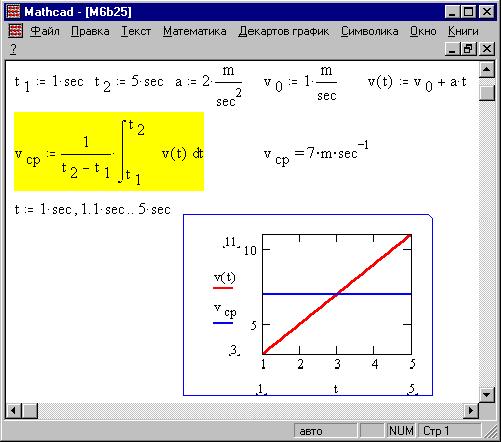
Часто используемые функции
augment(A,B) — Возвращает матрицу, сформированную путем размещения массива В справа от массива А. А и В должны иметь одинаковое число строк:
ceil(y) – возвращает наименьшее целое, большее или равное y. Значение y должно быть вещественным числом:
cols(A) – число столбцов матрицы А.
csort(B,n) – сортирует строки матрицы В таким образом, чтобы расположить элементы столбца n в порядке возрастания. Нумерация столбцов по умолчанию начинается с нуля:
Нумерация столбцов по умолчанию начинается с нуля:
eigenvals(A) – определяет вектор собственных значений для квадратной матрицы А:
find(x,y,…) – возвращает значения x,y,…, удовлетворяющие ограничениям: равенствам или неравенствам, заданным в блоке given решения уравнений. Число уравнений должно равняться числу неизвестных.
floor(y) – возвращает наибольшее целое, меньшее или равное y. Значение y должно быть вещественным числом:
identity(n) – создает единичную матрицу размером
, в которой диагональные элементы равны 1, а остальные элементы равны 0:
length(v) – длина вектора v.
max(v) – максимальный по значению элемент вектора v.
min(v) – минимальный по значению элемент вектора v.
maximize(f,v) – возвращает вектор размерности n, который обеспечивает функции f максимальное значение. Функция f – функция n переменных; вектор v – вектор начальных приближений ответа;
minimize(f,v) — возвращает вектор размерности n, который обеспечивает функции f минимальное значение. Обращение аналогично функции Maximize.
mean(M) – среднее арифметическое элементов вектора или матрицы.
median(v) – медиана вектора. Элементы вектора должны быть заданы в порядке возрастания:
rbeta (m, s 1, s2)Возвращает вектор m случайных чисел, имеющих бэта-распределение. есть параметры формы.
intuit.ru/2010/edi»>rbinom (m, n, p) Возвращает вектор m случайных чисел, имеющих биномиальное распределение. . n есть натуральное число.
rgamma (m, s) Возвращает вектор m случайных чисел, имеющих гамма- распределение, есть параметр формы.
rgeom (m, p) Возвращает вектор m случайных чисел, имеющих геометрическое распределение. .
rlogis (m, l, s) Возвращает вектор m случайных чисел, имеющих логистическое распределение, в котором l является п а раметром расположения, а есть параметр масштаба.
rnorm (m,l, s) Возвращает вектор m случайных чисел, имеющих нормальное распределение. .
rpois (m,d) Возвращает вектор m случайных чисел, имеющих распределение Пуассона. .
intuit.ru/2010/edi»>rt (m, d) Возвращает вектор m случайных чисел, имеющих t-распределение Стьюдента..
runif (m, a, b) Возвращает вектор m случайных чисел, имеющих равномерное распределение, в котором b и a являются граничными точками интервала. .
rnd (x) Возвращает равномерно распределенное случайное число между 0 и x. Эквивалент runif (1, 0, x).
round(y,n) – округляет вещественное число y до n знаков справа от десятичной точки. Если n отсутствует, то y округляется до ближайшего целого числа. Если n<0, то y округляется до n знаков слева от десятичной точки.
rows(A) – число строк матрицы А.
rsort(B,n) – сортирует столбцы матрицы В таким образом, чтобы расположить элементы строки n в порядке возрастания:
intuit.ru/2010/edi»> Нумерация строк по умолчанию начинается с нуля.
submatrix(M,ir,jr,ic,jc) – подматрица, состоящая из элементов матрицы М, содержащихся в строках от ir до jr и столбцах от ic до jc:
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
Имя функции | Возвращается… |
augment (A, B) | Массив,
сформированный расположением A и B бок о бок. |
stack
( | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
submatrix (A, ir, jr, ic, jc) | Субматрица,
состоящая из всех элементов, содержащихся
в строках с ir по jc и столбцах с ic по jc.
Чтобы поддерживать порядок строк
и-или столбцов, удостоверьтесь, что
ir<=jr
и ic<=jc,
иначе порядок строк и-или столбцов
будет обращен. |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
Имя функции | Возвращается… |
eigenvals ( | Вектор,
содержащий собственные значения
матрицы M. |
eigenvec (M, z) | Матрица, содержащая нормированный собственный вектор, соответствующий собственному значению z квадратной матрицы M. |
eigenvecs (M) | Матрица, содержащая нормированные собственные векторы, соответствующие собственным значениям квадратной матрицы M. n-ный столбец возвращенной матрицы — собственный вектор, соответствующий n-ному собственному значению, возвращенному eigenvals . |
genvals (M,N) | Вектор
v собственных значений, каждое из
которых удовлетворяет обобщенной
задаче о собственных значениях . |
genvecs (M,N) | Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям в v, векторе, возвращенном genvals. n-ный столбец этой матрицы — собственный вектор x, удовлетворяющий обобщенной задаче о собственных значениях . Матрицы |
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
упражнений для главы 2 книги Хаге и Харари
упражнение для главы 2 книги Хаге и ХарариУпражнения для главы 2 книги Хаге и Харари книга
- Вернитесь к Упражнению 1 для Главы 1, которая относится к рисунку на стр.
 4 Хаге и Харари.
4 Хаге и Харари.- Сколько ребер было бы в «полном» графе с четырьмя узлами? (Твой ответ должен быть либо числом, либо пояснением того, какие дополнительные Для определения числа потребуется информация.)
- Этот график полный? Объяснять.
- Является ли этот граф «связанным»? Объяснять.
- Какое минимальное количество ребер требуется для четырех узлов? график подключен?
- Если граф НЕ связан, перейдите к следующему пункту. Если он подключен, могли бы вы удалить любое из ребер, но оставить оставшийся граф связанным? (Указать, какие ребра.)
- Если граф связен, пропустите этот пункт. Если он НЕ подключен, сколько в нем компонентов?
- На рис. 1.9, стр. 13, определите каждый узел, который является «узлом разреза». Кратко объяснить
почему человек, занимающий позицию cutnode в социальной сети, может быть в состоянии
оказывать большее влияние, чем лица, занимающие другие должности в узле.

- На рис. 1.9, стр. 13, определите каждое ребро, которое является «мостом». Кратко объяснить, почему люди, занимающие узлы в социальной сети, могут значение для моста, чем для других ребер.
- Постройте матрицу смежности для графа на рис. 1.9., стр. 13, далее соглашение книги о том, что узел НЕ является смежным с самим собой. Подсчитайте количество ребер на рисунке. Подсчитайте количество вхождений числа «1» в матрице. Какие должны быть отношения между два?
- Если матрица смежности A представляет друзей, ее квадрат будет представлять друзей
друзей, его куб друзей друзей друзей и т.д.
Повышение такой большой матрицы до более высоких степеней — утомительная задача.
для которых компьютеры подходят лучше, чем люди. Есть,
однако есть одна трудность в анализе этой конкретной матрицы в
Маткад. Матрица смежности для 11 узлов имеет 11×11=121 элемент, и
Простой способ ввода матрицы в Mathcad работает только для тех,
со 100 и менее элементами.
 Вот два варианта, т.
первый из которых более прост, второй из которых будет
расскажет вам больше об операциях Mathcad для больших матриц. Ты
может выбрать любой вариант:
Вот два варианта, т.
первый из которых более прост, второй из которых будет
расскажет вам больше об операциях Mathcad для больших матриц. Ты
может выбрать любой вариант: - Удалите узел «g» и ребро «gf», которое его касается. Удалите строку g и столбец g из смежности 11×11. матрицы, и приступаем к анализу полученной матрицы 10х10. Или:
- Введите матрицу 11×11 двумя частями, каждая меньшего размера
более 100 элементов; соедините две части, используя «стек»
операция; а затем приступайте к анализу полной матрицы 11×11.
(Примечание: В дополнение к «стеку», для объединения двух матриц один
кроме того, Mathcad также имеет функцию «дополнения» для
объединение двух матриц, расположенных рядом друг с другом.)
Детали: в первых 9 рядах 99, что меньше, чем
100 элементов, чтобы им можно было дать имя, скажем, A, и
вошел обычным способом, набрав A:
и в диалоговом окне «Вставить матрицу», выбрав 9ряды и 11
столбцы и заполнение значений.
Последние две строки с 22 элементами можно было ввести как вторую.

- Используя Mathcad, вычислите квадрат, куб, 4-ю и 5-ю степени матрицы в задаче 5.
- Дайте словесную интерпретацию записи в строке а столбца f 5-го числа. мощность матрицы.
Показать ответ Mathcad в дробях
перейти к содержанию Показать ответ Mathcad в виде дроби31 января 2023 г.
ВРЕМЯ ЧТЕНИЯ: 1,2 МИНУТЫ
Блог • Mathcad
Вам нужно преобразовать ответ Mathcad в дробь ? Mathcad Prime позволяет ввести десятичное число и получить взамен эквивалентную дробь, используя раздел «Результаты» на вкладке «Математическое форматирование» на ленте.
Существует пять вариантов форматирования результатов: общий, десятичный, научный, инженерный и процентный. Вы можете отформатировать конкретный результат или внести изменения на всю страницу в зависимости от того, что вы выберете.
- 1
Щелкните результат, который вы хотите преобразовать
- 2
Выберите пункт меню «Math Formatting»0002 Выберите пункт меню «Проценты» в разделе «Результаты»
Нажмите, чтобы увеличить
Нажмите, чтобы увеличить
Форматирование можно задать для всей страницы или для отдельного результата. Например, если мы хотим, чтобы переменная процентного изменения была представлена только в виде процента, вы можете щелкнуть и настроить определенные параметры. На него не повлияют настройки страницы, если вы не выберете «Математическое форматирование > Очистить формат».
Десятичную точность также можно установить в диапазоне значений от 0 до 15, а также выбрать отображение нулей в конце в разделе «Результаты».
Нажмите, чтобы увеличить
Нажмите, чтобы увеличить
Ищете дополнительную информацию о Mathcad?Ищете дополнительную информацию о Mathcad? Просмотрите наши популярные ссылки ниже:
- Бесплатная пробная версия Mathcad Express
- Что нового в Mathcad 8
- Пакеты Mathcad и цены
- Вебинары Mathcad
- Блоги Mathcad
Или, если вы готовы купить, нажмите здесь!
TriStar PLM Solutions приветствует вопросы.
 Массивы A и B должны иметь одинаковое число строк.
Массивы A и B должны иметь одинаковое число строк.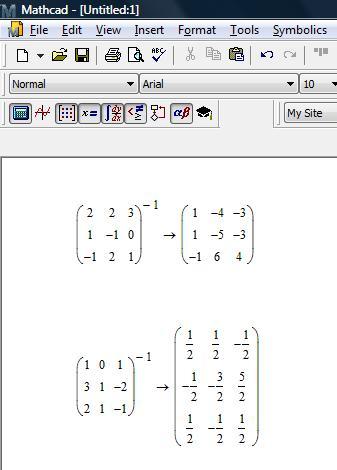

 Матрицы M и N — вещественнозначные квадратные
матрицы одного размера. Вектор x — соответствующий собственный вектор.
Матрицы M и N — вещественнозначные квадратные
матрицы одного размера. Вектор x — соответствующий собственный вектор.