Коэффициент аппроксимации в excel: Аппроксимация в Excel: 5 простых способов

Аппроксимация в Excel: 5 простых способов

Содержание

• Выполнение аппроксимации
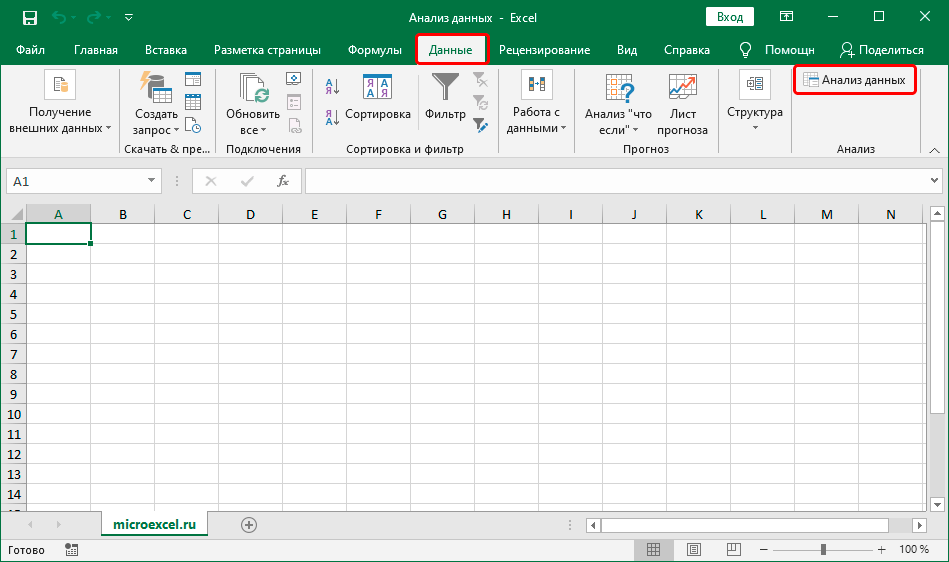
  • Способ 1: линейное сглаживание
  • Способ 2: экспоненциальная аппроксимация
  • Способ 3: логарифмическое сглаживание
  • Способ 4: полиномиальное сглаживание
  • Способ 5: степенное сглаживание
• Вопросы и ответы

Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.

Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов.

Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.

Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.

Но она может быть построена с применением одного из пяти видов аппроксимации:

• Линейной;
• Экспоненциальной;
• Логарифмической;
• Полиномиальной;
• Степенной.

Рассмотрим каждый из вариантов более подробно в отдельности.

Урок: Как построить линию тренда в Excel

Способ 1: линейное сглаживание

Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.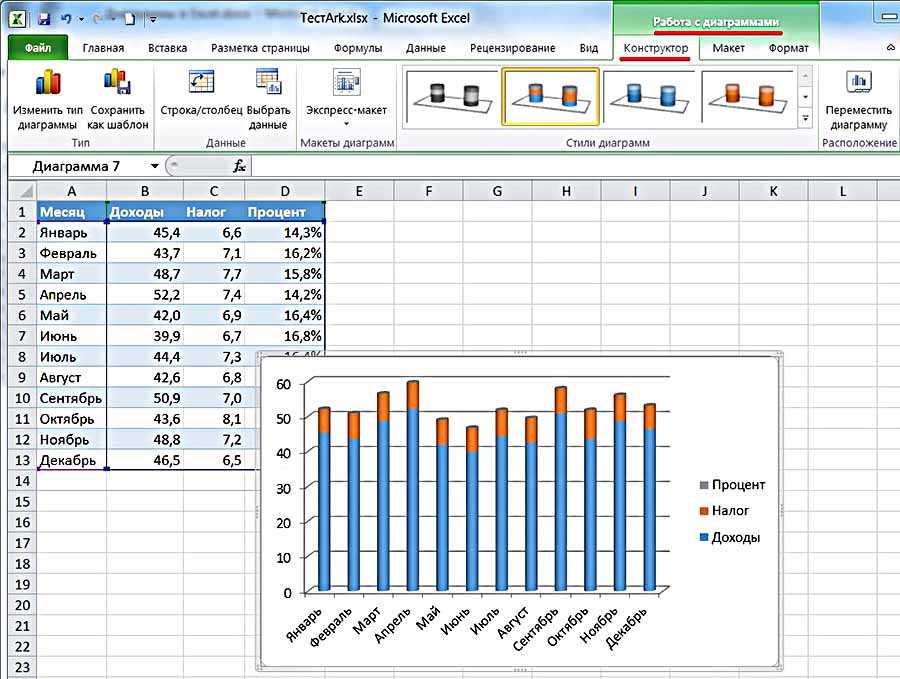

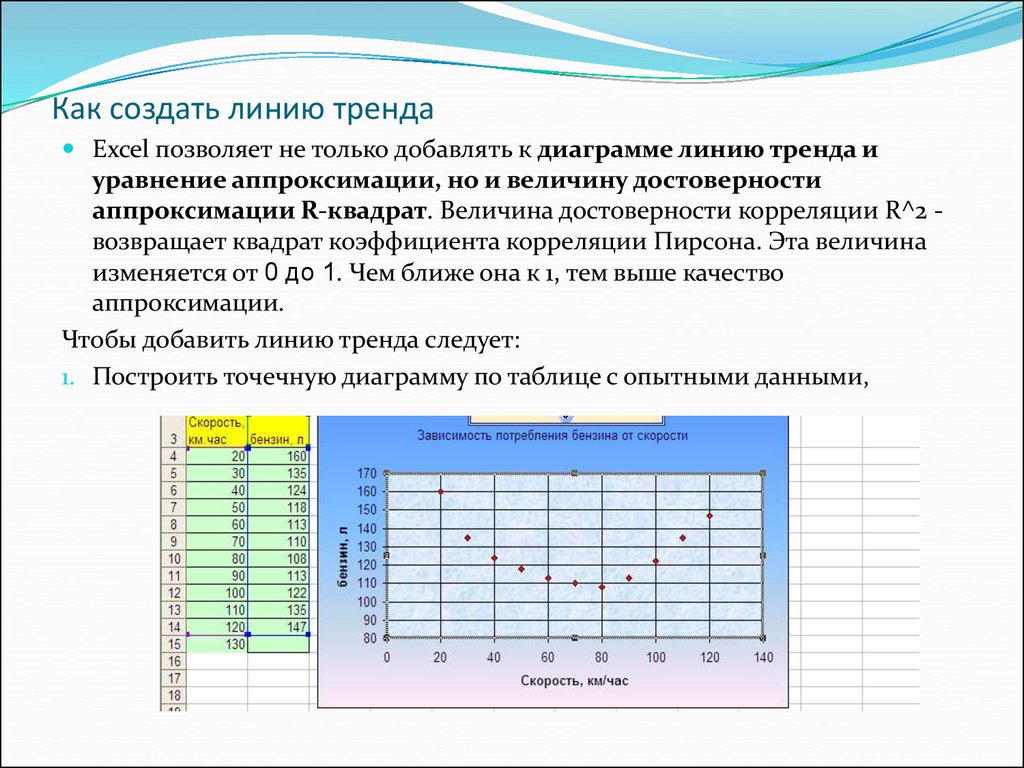
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.

1. Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
2. График построен.
3. Для добавления линии тренда выделяем его кликом правой кнопки мыши. Появляется контекстное меню. Выбираем в нем пункт «Добавить линию тренда…».

   Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».

4. Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
   В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
   При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.

   Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.

   После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.

5. Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.

Сглаживание, которое используется в данном случае, описывается следующей формулой:

y=ax+b

В конкретно нашем случае формула принимает такой вид:

y=-0,1156x+72,255

Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.

Способ 2: экспоненциальная аппроксимация

Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.

1. Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
2. После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
3. После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.

Общий вид функции сглаживания при этом такой:

y=be^x

где e – это основание натурального логарифма. (-0,012*x)

Способ 3: логарифмическое сглаживание

Теперь настала очередь рассмотреть метод логарифмической аппроксимации.

1. Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
2. Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.

В общем виде формула сглаживания выглядит так:

y=a*ln(x)+b

где ln – это величина натурального логарифма. Отсюда и наименование метода.

В нашем случае формула принимает следующий вид:

y=-62,81ln(x)+404,96

Способ 4: полиномиальное сглаживание

Настал черед рассмотреть метод полиномиального сглаживания.

1. Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
2. Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724. 2-2E+07x+2E+09

   Способ 5: степенное сглаживание

   В завершении рассмотрим метод степенной аппроксимации в Excel.

   1. Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
   2. Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.

   Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.

   Общая формула, описывающая данный метод имеет такой вид:

   y=bx^n

   В конкретно нашем случае она выглядит так:

   y = 6E+18x^(-6,512)

   Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.

   Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.

   Коэффициент аппроксимации в excel. Метод аппроксимации в Microsoft Excel

   Полиномиальная аппроксимация непрерывной на отрезке функции.

   Аппроксимация (от латинского «approximate» -«приближаться»)- приближенное выражение каких-либо математических объектов (например, чисел или функций) через другие более простые, более удобные в пользовании или просто более известные. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов.

   Как известно, между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При ведении научных исследований, обработке результатов наблюдения или эксперимента обычно приходиться сталкиваться со вторым вариантом. При изучении количественных зависимостей различных показателей, значения которых определяются эмпирически, как правило, имеется некоторая их вариабельность. Частично она задается неоднородностью самих изучаемых объектов неживой и, особенно, живой природы, частично обуславливается погрешностью наблюдения и количественной обработке материалов. Последнюю составляющую не всегда удается исключить полностью, можно лишь минимизировать ее тщательным выбором адекватного метода исследования и аккуратностью работы. Поэтому при выполнении любой научно-исследовательской работы возникает проблема выявления подлинного характера зависимости изучаемых показателей, этой или иной степени замаскированных неучтенностью вариабельности значений. Для этого и применяется аппроксимация — приближенное описание корреляционной зависимости переменных подходящим уравнением функциональной зависимости, передающим основную тенденцию зависимости (или ее «тренд»).

   При выборе аппроксимации следует исходить из конкретной задачи исследования. Обычно, чем более простое уравнение используется для аппроксимации, тем более приблизительно получаемое описание зависимости.

   Поэтому важно считывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. При описании зависимости эмпирически определенных значений можно добиться и гораздо большей точности, используя какое-либо более сложное, много параметрическое уравнение. Однако нет никакого смысла стремиться с максимальной точностью передать случайные отклонения величин в конкретных рядах эмпирических данных. Гораздо важнее уловить общую закономерность, которая в данном случае наиболее логично и с приемлемой точностью выражается именно двухпараметрическим уравнением степенной функции. Таким образом, выбирая метод аппроксимации, исследователь всегда идет на компромисс: решает, в какой степени в данном случае целесообразно и уместно «пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить зависимость сопоставляемых переменных. Наряду с выявлением закономерностей, замаскированных случайными отклонениями эмпирических данных от общей закономерности, аппроксимация позволяет также решать много других важных задач: формализовать найденную зависимость; найти неизвестные значения зависимой переменной путем интерполяции или, если это допустимо, экстраполяции.

   Здесь будет рассмотрена полиномиальная аппроксимация. Это означает, что наша задача состоит в том, что, опираясь на начальные данные (функция и отрезок), необходимо найти такой полином, отклонение линии которого от графика начальной функции будет минимальным.

   Наиболее популярным методом полиномиальной аппроксимации является метод наименьших квадратов. В Excel он реализуется при помощи диаграммы и линии тренда.

   Разберем данный метод в Excel.

   Начальные данные:

   Сначала нам необходимо разбить данный отрезок при помощи «Чебышевского» разбиения, т.к. данный вид разбиения всегда дает более точный результат.

   В колонке I(рис. 1) записываем числа от 0 до 8, т.к. отрезок разбиваем на 8 частей.

   В колонке z ячейки вычисляем по формуле: COS(3,141593*I/8). Для вычисления каждой ячейки используем соответствующее ей I.

   Значение каждого x находим по формуле: 2*z + 1.

   В колонке F(x) вычисляем значение данной функции для каждого x.

   
   Рисунок 1
   Далее в ячейках h3,I2,J2 задаем начальные значения коэффициентов a, b и c в искомом полиноме (рис. 2).

   
   Рисунок 2
   В столбце F со 2 по 10 ячейки вычисляем значения отклонений, т.е. модуль разности между значением начальной функции и найденным полиномом. 2+$I$2*x+$J$2)).

   В ячейке B11 вычисляется сумма отклонений, а в ячейке B12 среднее отклонение (рис. 3).

   
   Рисунок 3
   С помощью «Мастера диаграмм» строим точечную диаграмму, исходя из данных столбцов x и F(x). Теперь во вкладке «Диаграмма» выбираем «Добавить линию тренда» и устанавливаем необходимый флажок для того, чтобы показать уравнение на диаграмме (рис. 4).

   
   Рисунок 4
   Теперь подставляем коэффициенты из полученного уравнения в ячейки h3, I2 и J2 (рис. 5).

   
   Рисунок 5
   Как видно, среднее отклонение равно 0,117006252.

   Найденный полином: 0,363*x² — 0,6901*x + 2,2203.

   Предложим иной метод полиномиальной аппроксимации.

   Открываем вкладку «Сервис» и выбираем «Поиск решений». В появившемся окне целевой ячейкой указываем F11, причем равной минимальному значению. В поле «изменяя ячейки» указываем h3, I2 и J2.

   Нажимаем кнопку «Выполнить». После выполнения процедуры мы видим, что результаты изменились (рис. 6).

   
   Рисунок 6
   На этот раз среднее отклонение равно 0,106084329.

   Найденный полином: 0,35724*x² — 0,702*x + 2,259158.

   Этот результат существенно точнее предыдущего, что подтверждает преимущество использования минимизации суммы отклонений по сравнению с методом наименьших квадратов.

   ЗАВИСИМОСТЕЙ

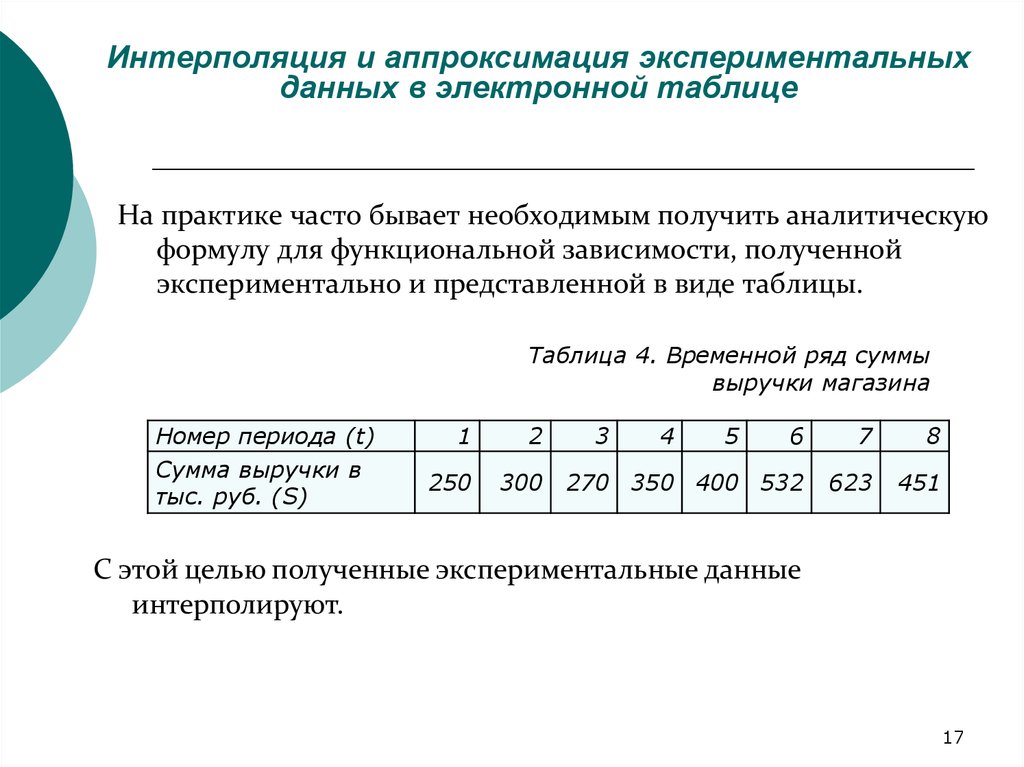
   Excel располагает средствами, позволяющими прогнозировать процессы. Задача аппроксимации возникает в случае необходимости аналитически описать явления, имеющие место в жизни и заданные в виде таблиц, содержащих значения аргумента (аргументов) и функции. Если зависимость удается найти, можно сделать прогноз о поведении исследуемой системы в будущем и, возможно, выбрать оптимальное направление ее развития. Такая аналитическая функция (называемая еще трендом) может иметь разный вид и разный уровень сложности в зависимости от сложности системы и желаемой точности представления.

   10.1. Линейная регрессия

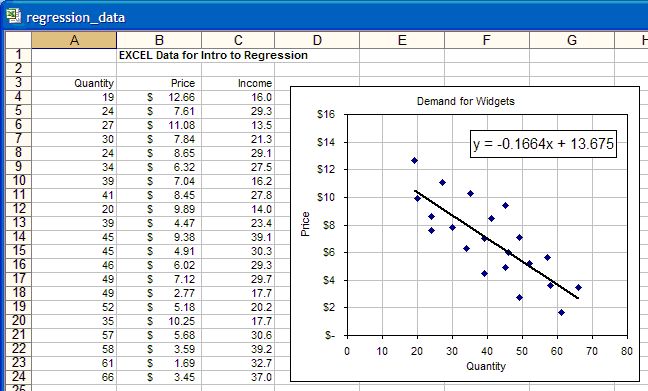
   Самый простой и популярной является аппроксимация прямой линией – линейная регрессия.

   Пусть мы имеем фактическую информацию об уровнях прибыли Y в зависимости от размера X капиталовложений – Y(X). На рис. 10.1-1 показаны четыре такие точки М(Y,X). Пусть также у нас имеются основания предполагать, что зависимость эта линейная, т.е. имеет вид Y=А+ВX. Если бы нам удалось найти коэффициенты A и B и по ним построить прямую (например, такую, как на рисунке), в дальнейшем мы могли бы сделать осознанные предположения о динамике бизнеса и возможном коммерческом состоянии предприятия в будущем. Очевидно, что нас бы устроила прямая, находящаяся как можно ближе к известным точкам М(Y,X), т.е. имеющая минимальную сумму отклонений или сумму ошибок (на рисунке отклонения показаны пунктирными линиями). Известно, что существует только одна такая прямая.

   Для решения этой задачи используют метод наименьших квадратов ошибок. Разность (ошибка) между известным значением Y1 точки М1(Y1,X1) и значением Y(X1), вычисленным по уравнению прямой для того же значения X1, составит

   D1 = Y1 – A – B X1.

   Такая же разность

   для X=X2 составит D2 = Y2 – A – B X2;

   для X=X3 D3 = Y3 – A – B X3;

   и для X=X4 D4 = Y4 – A – B X4.

   Запишем выражение для суммы квадратов этих ошибок

   Ф(A,В)=(Y1–A–B X1) 2 +(Y2–A–B X2) 2 +(Y3–A–B X3) 2 +(Y4–A–B X4) 2

   или сокращенно Ф(B,A) = å(Yi – A – BXi) 2 .

   Здесь нам известны все X и Y и неизвестны коэффициенты A и B. Проведем искомую прямую так (т.е. выберем A и B такими), чтобы эта сумма квадратов ошибок Ф(A,B) была минимальной. Условиями минимальности являются известные соотношения

   ¶Ф(A,B)/¶A=0 и ¶Ф(A,B)/¶B=0.

   Выведем эти выражения (индексы при знаке суммы опускаем):

   ¶[å(Yi–A–B Xi) 2 ]/¶A = å(Yi–A–B Xi)(–1)

   ¶[å(Yi–A–B Xi) 2 ]/¶B = å(Yi–A–B Xi)(–Xi).

   Преобразуем полученные формулы и приравняем их нулю

   Microsoft Excel (также иногда называется Microsoft Office Excel) — программа для работы с электронными таблицами, созданная корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS. Она предоставляет возможности экономико-статистических расчетов, графические инструменты и, за исключением Excel 2008 под Mac OS X, язык макропрограммирования VBA (Visual Basic для приложений). Microsoft Excel входит в состав Microsoft Office и на сегодняшний день Excel является одним из наиболее популярных приложений в мире.

   В MS Excel аппроксимация экспериментальных данных осуществляется путем построения их графика (x — отвлеченные величины) или точечного графика (x — имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции (линии тренда).

   Возможны следующие варианты функций:

   · Линейная — y=ax+b. Обычно применяется в простейших случаях, когда экспериментальные данные возрастают или убывают с постоянной скоростью.

   · Полиномиальная — y=a 0 +a 1 x+a 2 x 2 +…+a n x n , где до шестого порядка включительно (n?6), a i — константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов или минимумов) кривой. Полином второй степени можно описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени — не более трех экстремумов и т.д.

   · Логарифмическая — y=a·lnx+b, где a и b — константы, ln — функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем постепенно стабилизируются.

   · Степенная — y=b·x a , где a и b — константы. Аппроксимация степенной функцией используется для экспериментальных данных с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.

   · Экспоненциальная — y=b·e ax , a и b — константы, e — основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Часто ее использование вытекает из теоретических соображений.

   Степень близости аппроксимации экспериментальных данных выбранной функцией оценивается коэффициентом детерминации (R 2). Таким образом, если есть несколько подходящих вариантов типов аппроксимирующих функций, можно выбрать функцию с большим коэффициентом детерминации (стремящимся к 1).

   MathCAD — это специфический язык программирования, который позволяет облегчить решение математических уравнений. MathCAD — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы. MathCAD идеально подходит для осуществления математического моделирования — осуществляя решение разного рода уравнений и создавая отчет о полученных результатах.

   В MathCAD совсем немного типов данных по сравнению с универсальными языками программирования — всего три. Кратко охарактеризуем их (более детально они будут описаны позже).

   Числа (как действительные, так и комплексные): все числа MathCAD хранит в одном формате (с плавающей точкой двойной точности), не разделяя их на целые и действительные. На одно число выделяется 64 бита. При этом десятичная часть не может превышать по длине 17 знаков, а порядок должен лежать между -307 и 307. Комплексные числа на уровне реализации представляют собой пару действительных чисел. При этом во многих видах расчетов число воспринимается как комплексное, даже если у него нет мнимой части. Описанные особенности чисел в MathCAD касаются только численных расчетов. При работе в символьном режиме совершенно другие уровни точности.

   Строки: в общем случае любой текст, заключенный в кавычки. На практике строки используются в основном для задания сообщений об ошибках, возникших при работе программ на языке MathCAD.

   Массивы: к ним относятся матрицы, векторы, тензоры, таблицы — любые упорядоченные последовательности элементов произвольного типа. К данным этого типа можно отнести и ранжированные переменные. В отдельную группу следует выделить так называемые размерные переменные, то есть единицы измерения, имеющие огромное значение в науке и технике. В MathCAD нет логического типа данных. Для обозначения истины и лжи логическими операторами и функциями используются числа — 0 и 1.

   В MathCAD существует несколько функций, позволяющих выполнить регрессию с использованием зависимостей, наиболее часто встречающихся на практике. Таких функций в MathCAD всего шесть. Вот некоторые из них:

   · expfit(vx,vy,vg) — регрессия экспоненциальной функцией y = a*e b*x +c.

   · sinfit(vx,vy,vg) — регрессия синусоидальной функцией y = a*sin(x+b)+c.

   · pwrfit(vx,vy,vg) — регрессия степенной функцией e = a*x b +c.

   Перечисленные функции используют трехпараметрическую аппроксимирующую функцию, нелинейную по параметрам. При вычислении оптимальных значений трех параметров регрессионной функции по методу наименьших квадратов возникает необходимость в решении сложной системы из трех нелинейных уравнений. Такая система часто может иметь несколько решений. Поэтому в функциях MathCAD, которые проводят регрессию трехпараметрическими зависимостями, введен дополнительный аргумент vg. 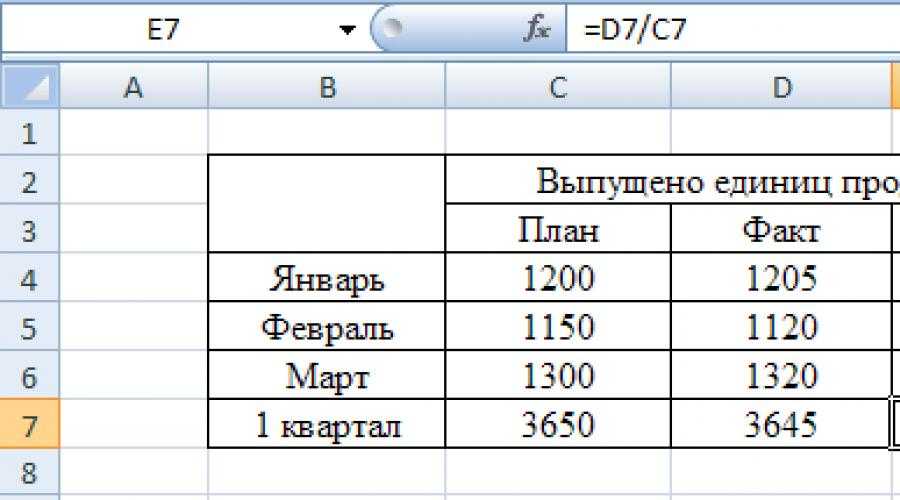Данный аргумент — это трехкомпонентный вектор, содержащий приблизительные значения параметров a,b и c, входящих в аппроксимирующую функцию. Неправильный выбор элементов вектора vg может привести к неудовлетворительному результату регрессии. В MathCAD существуют средства для проведения регрессии самого общего вида. Это означает, что можно использовать любые функции в качестве аппроксимирующих и находить оптимальные значения любых их параметров, как линейных, так и нелинейных. В том случае, если регрессионная функция является линейной по всем параметрам, т.е. представляет линейную комбинацию жестко заданных функций, провести регрессию можно с помощью встроенной функции linfit(vx,vy,F). Аргумент F — это векторная функция, из элементов которой должна быть построена линейная комбинация, наилучшим образом аппроксимирующая заданную последовательность точек. Результатом работы функции linfit является вектор линейных коэффициентов. Каждый элемент этого вектора — коэффициент при функции, стоящей на соответствующем месте в векторе F. 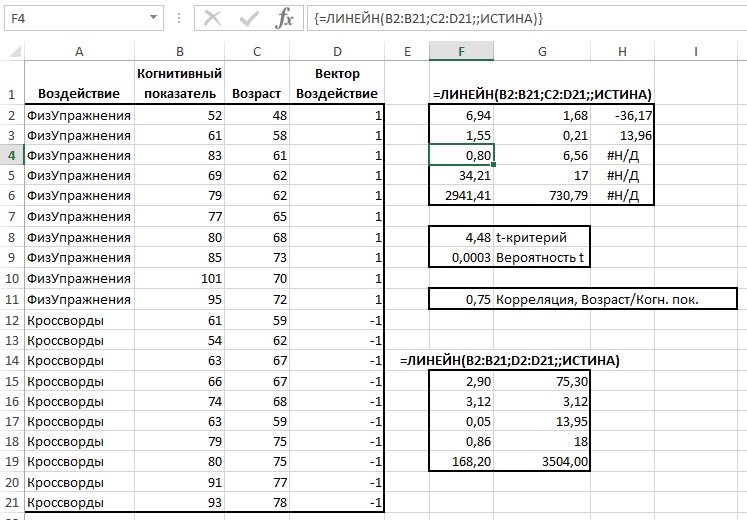Таким образом, для того чтобы получить регрессионную функцию, достаточно скалярно перемножить эти два вектора.

   Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:

   Где y x — расчетное значение по уравнению.

   Значение средней ошибки аппроксимации до 15% свидетельствует о хорошо подобранной модели уравнения.

   По семи территориям Уральского района за 199Х г. известны значения двух признаков.

   Требуется:
   1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
   а) линейной;
   б) степенной;
   в) показательной;
   г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
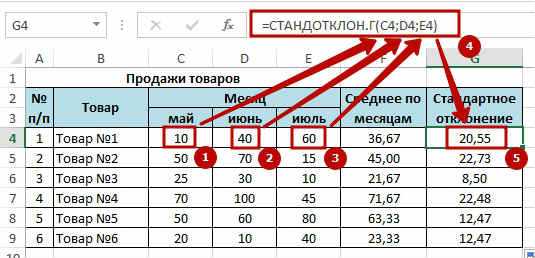
   2. Оценить каждую модель через среднюю ошибку аппроксимации А ср и F-критерий Фишера.

   Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии .
   а) линейное уравнение регрессии;
   Использование графического метода .
   Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
   Совокупность точек результативного и факторного признаков называется полем корреляции .

   На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
   Линейное уравнение регрессии имеет вид y = bx + a + ε
   Здесь ε — случайная ошибка (отклонение, возмущение).
   Причины существования случайной ошибки:
   1. Невключение в регрессионную модель значимых объясняющих переменных;
   2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
   3. Неправильное описание структуры модели;
   4. Неправильная функциональная спецификация;
   5. Ошибки измерения.
   Так как отклонения ε i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
   1) по наблюдениям x i и y i можно получить только оценки параметров α и β
   2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
   Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e i – наблюдаемые значения (оценки) ошибок ε i , а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
   Для оценки параметров α и β — используют МНК (метод наименьших квадратов).

   Получаем b = -0.35, a = 76.88
   Уравнение регрессии:
   y = -0.35 x + 76.88

   x	y	x 2	y 2	x y	y(x)	(y i -y cp) 2	(y-y(x)) 2	|y — y x |:y
   45,1	68,8	2034,01	4733,44	3102,88	61,28	119,12	56,61	0,1094
   59	61,2	3481	3745,44	3610,8	56,47	10,98	22,4	0,0773
   57,2	59,9	3271,84	3588,01	3426,28	57,09	4,06	7,9	0,0469
   61,8	56,7	3819,24	3214,89	3504,06	55,5	1,41	1,44	0,0212
   58,8	55	3457,44	3025	3234	56,54	8,33	2,36	0,0279
   47,2	54,3	2227,84	2948,49	2562,96	60,55	12,86	39,05	0,1151
   55,2	49,3	3047,04	2430,49	2721,36	57,78	73,71	71,94	0,172
   384,3	405,2	21338,41	23685,76	22162,34	405,2	230,47	201,71	0,5699

   Примечание: значения y(x) находятся из полученного уравнения регрессии:
   y(45. 1) = -0.35*45.1 + 76.88 = 61.28
   y(59) = -0.35*59 + 76.88 = 56.47
   … … …

   Ошибка аппроксимации
   Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:

   Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.

   F-статистики. Критерий Фишера.

   3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
   4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
   В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.

   б) степенная регрессия ;
   Решение проводится с помощью сервиса Нелинейная регрессия . При выборе укажите Степенная y = ax b
   в) показательная регрессия;
   г) модель равносторонней гиперболы.
   Система нормальных уравнений.

   Для наших данных система уравнений имеет вид
   7a + 0.1291b = 405.2
   0.1291a + 0.0024b = 7.51
   Из первого уравнения выражаем а и подставим во второе уравнение
   Получаем b = 1054.67, a = 38.44
   Уравнение регрессии:
   y = 1054.67 / x + 38.44
   Ошибка аппроксимации.
   Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

   Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.

   Критерий Фишера.
   Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
   Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

   где m – число факторов в модели.
   Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
   1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H 0: R 2 =0 на уровне значимости α.
   2. Далее определяют фактическое значение F-критерия:

   где m=1 для парной регрессии.
   Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
   Поскольку фактическое значение F

   Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.

   Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.

   Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.

   Но она может быть построена с применением одного из пяти видов аппроксимации:

   • Линейной;
   • Экспоненциальной;
   • Логарифмической;
   • Полиномиальной;
   • Степенной.

   Рассмотрим каждый из вариантов более подробно в отдельности.

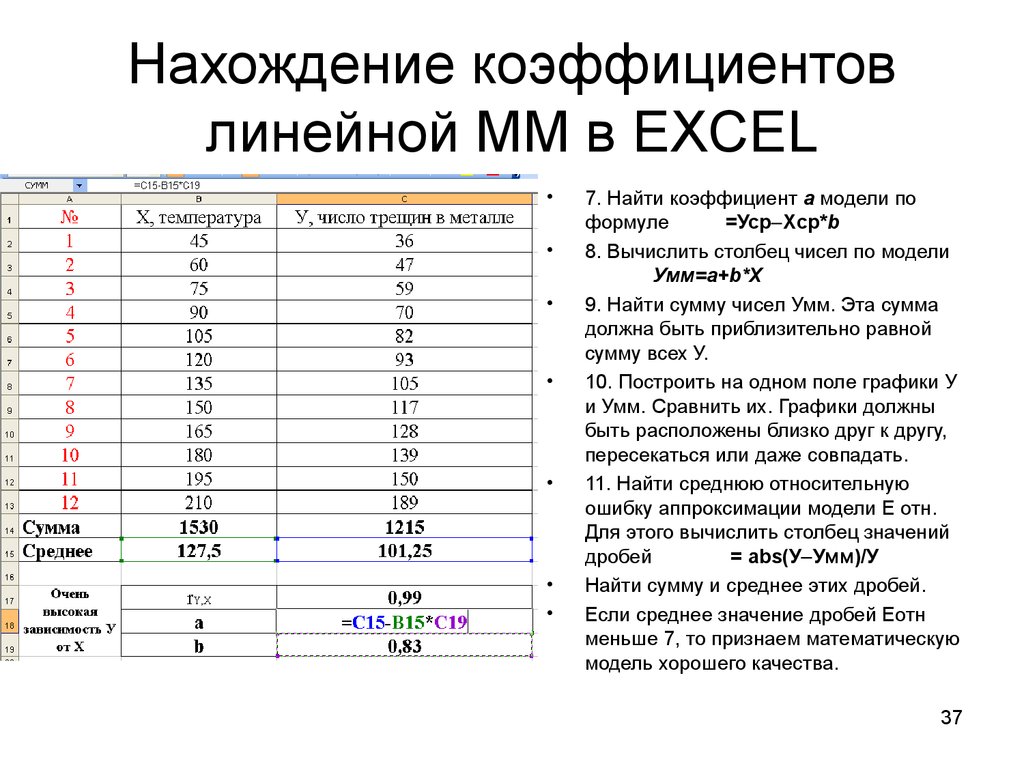
   Способ 1: линейное сглаживание

   Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.

   Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.

   
   

   Сглаживание, которое используется в данном случае, описывается следующей формулой:

   В конкретно нашем случае формула принимает такой вид:

   y=-0,1156x+72,255

   Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное. (-6,512)

   Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844 ), наименьший уровень достоверности у линейного метода (0,9418 ). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.

   Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.

   Использование аппроксимационных моделей в Excel

   16 мая 2016 г.

   Одной из ключевых особенностей pSeven, мощной платформы для исследования пространства проектирования, является возможность обучения аппроксимационных моделей с использованием образцов данных или результатов моделирования. Обученные модели становятся быстрой альтернативой исходному трудоемкому вычислительному коду. В частности, модель аппроксимации в pSeven предоставляет следующие методы:

   • Оценка – вычисляет выходные значения модели в заданной входной точке.
   • Оценка градиента — вычисляет градиенты, частные производные первого порядка выходных функций модели.
   • Оценка точности — вычисляет оценки точности для выходных значений и значений градиента (эти функции доступны, если модель была обучена с опцией GTApprox/AccuracyEvaluation).

   Часто возникает задача экспортировать модель, обученную на pSeven, чтобы использовать ее с другой инженерной платформой. Для этого в pSeven предусмотрены функции экспорта модели в различные распространенные форматы, такие как код, совместимый с MATLAB, или исходный код C. Недавнее улучшение в экспорте моделей — это функция, которая генерирует код C, хорошо совместимый с Microsoft Excel, который остается одной из самых популярных платформ для инженерных расчетов, анализа данных и визуализации.

   Начиная с версии 6.7, pSeven предоставляет возможность экспортировать специальную версию кода модели C, предназначенную для компиляции библиотеки DLL, изначально работающей с Microsoft Excel. Импорт такой DLL в электронную таблицу позволяет вызывать методы модели как пользовательские функции Excel. В этой заметке объясняется общий рабочий процесс импорта и использования моделей pSeven в Excel.

   Рабочий процесс

   Общие шаги для создания аппроксимационной модели pSeven в Excel:

   1. Экспортируйте модель из pSeven в код C.
   2. Скомпилируйте модель DLL.
   3. Импорт DLL модели в Excel.
   4. Определите функции Excel, которые вызывают методы модели из библиотеки DLL.

   Специальный формат экспорта Excel, добавленный в pSeven 6. 7, позволяет значительно упростить процесс импорта. В дополнение к коду модели C, pSeven теперь автоматически генерирует код VBA для Excel, который требует лишь минимального редактирования, чтобы сделать методы модели доступными в ваших электронных таблицах, как описано далее.

   Шаг 1. Экспорт кода модели

   В pSeven модель можно обучить с помощью Model Builder или загрузить из существующего файла. Обучение модели выходит за рамки этой статьи; мы предполагаем, что модель уже создана и добавлена ​​в отчет в Analyze.

   Модели, содержащиеся в отчете, перечислены на панели «Модели» в базе данных отчета. Отсюда вы можете экспортировать код модели, выполнив следующие действия:

   • Откройте панель базы данных отчетов.
   • Выберите модель для экспорта на панели «Модели».
   • Выберите «Экспорт в файл…» в контекстном меню на панели «Модели» или нажмите кнопку экспорта модели на панели быстрого доступа на панели. Это действие откроет диалоговое окно Экспорт модели.

   В диалоговом окне «Экспорт модели»:

   • В качестве формата экспорта выберите «Источник C для Microsoft Excel VBA».
   • Укажите имя файла экспорта в поле ввода «Файл» (pseven_model.c на скриншоте примера).
   • Укажите название функции в поле «Имя функции» (модель в примере).
   • Нажмите кнопку Экспорт. Сгенерированный код будет сохранен в указанный вами файл (по умолчанию находится в текущем каталоге проекта).

   Полученный файл содержит код модели C, который необходимо скомпилировать в DLL, и код VBA для Microsoft Excel. Код VBA находится в блоке комментариев вверху. Поскольку этот код закомментирован, нет необходимости удалять его при компиляции модели. Код VBA требуется при импорте скомпилированной библиотеки DLL в Excel.

   Обратите внимание, что имя функции, указанное в диалоговом окне Экспорт модели , используется в качестве базового имени для методов модели. Большинство моделей предоставляют несколько функций (например, оценку выходных данных модели или градиентов), и, поскольку все методы должны иметь уникальные имена, pSeven добавит к имени каждого метода определенный суффикс. Этот суффикс также указывает на назначение функции, как объяснено далее.

   Шаг 2. Компиляция DLL модели

   После экспорта код модели необходимо скомпилировать в DLL, чтобы его можно было импортировать в Excel. pSeven генерирует код для компилятора Microsoft Visual C++ (MSVC). При использовании MSVC никаких изменений в коде C не требуется. Использование другого компилятора может потребовать определенных изменений кода в зависимости от компилятора.

   Обратите внимание, что при импорте библиотеки DLL в Excel необходимо указать полный путь к файлу DLL. Скомпилированную DLL рекомендуется хранить в удобном месте; далее предполагается, что DLL сохраняется, например, в C:\Users\tmp\pseven_model.dll.

   Если вы используете Microsoft Excel 2010 или более позднюю версию, также рекомендуется обратить внимание на совместимость между 32-разрядной и 64-разрядной версиями. Подробное описание этой темы доступно в MSDN: см. раздел «Совместимость между 32-разрядной и 64-разрядной версиями Office 2010».

   Шаг 3. Импорт библиотеки DLL модели в Excel

   Исходный файл C, экспортированный из pSeven, содержит все необходимое для обеспечения доступа к библиотеке DLL из Excel через модуль VBA. Такой модуль объявляет новые функции, которые делают экспортированные методы модели доступными в Excel. Код модуля VBA находится в комментарии в верхней части исходного кода модели. Вам нужно только скопировать код из комментария в Excel и указать путь к DLL в операторах Declare (поскольку Excel требует указать абсолютный путь к импортируемой DLL).

   Чтобы скопировать код VBA:

   • Откройте панель разработчика в Excel и добавьте новый модуль.
   • Откройте исходный код модели C и скопируйте код VBA из начального комментария. Обратите внимание, что вам нужно скопировать только код, без строк, которые начинаются и заканчиваются комментарием в стиле C («/* … */»).
   • Вставьте скопированный код VBA в новый добавленный модуль.

   Операторы Declare, которые необходимо исправить вручную, находятся в первых строках скопированного кода VBA. Вы должны заменить заполнители в этих строках точным путем к DLL. Операторы объявления в коде VBA, сгенерированном pSeven, выглядят следующим образом:

   Объявить функцию PtrSafe model_impl Lib «<путь к DLL>» Псевдоним «model» (x As Variant, ByVal idx_f As Integer, out As Variant) As Integer

   Существует несколько объявлений, по одному для каждого метода экспортируемой модели. В каждом операторе заполнитель «<поместите здесь путь к DLL>» должен быть заменен фактическим путем к скомпилированной DLL. Например, если DLL находится в папке C:\Users\tmp\pseven_model.dll, отредактированное объявление будет выглядеть так:

   Declare PtrSafe Function model_impl Lib «C:\Users\tmp\pseven_model.dll» Alias ​​»model » (x как вариант, ByVal idx_f как целое число, out как вариант) как целое число

   Шаг 4. Вызов модели из Excel

   После редактирования пути DLL в коде VBA, скопированном в Excel, вы можете использовать объявленные в нем функции для выполнения вычислений в электронной таблице. Как правило, в Excel доступны следующие функции:

   • модель (точка, индекс) — оценивает выходной компонент модели с заданным индексом при заданном входе точка .
   • modelGrad(point, output_index, input_index) — оценивает градиент output_index выходной компонент относительно входной переменной input_index в данной точке .
   • modelAE(point, index) — вычисляет оценку оценки точности для выходного компонента с заданным индексом при заданной входной точке .
   • modelGradAE(point, output_index, input_index) — вычисляет оценку оценки точности для градиентов модели .
   • modelInfo(info) — получает информацию о модели, где аргументом info является одна из следующих строк:
   • «size_x» – получить входной размер модели.
   • «size_f» – получить выходной размер модели.
   • «has_ae» — проверить, поддерживает ли модель оценку точности.

   Обратите внимание, что все функции из одной модели имеют одинаковое базовое имя – то, которое вы указали в поле «Имя функции» в диалоговом окне «Экспорт модели» в pSeven (здесь, например, «модель»).

   Рассмотрим основные правила передачи аргументов в эти функции на примере функции модели (эта функция вычисляет выходные значения модели).

   В общем случае ввод и вывод модели могут быть многомерными. Модель, используемая здесь в качестве примера, имеет входное измерение 3 и выходное измерение 2. В этом случае аргумент точки для модели должен быть диапазоном, включающим 3 столбца, а аргумент index может быть 1 или 2 (Excel использует индексацию на основе 1).

   Мы будем использовать импортированную модель для построения среза вдоль одной из входных осей. Для этого фиксируются два входных значения (столбцы «x2» и «x3» в примере), а значения в столбце «x1» варьируются. Столбцы «y1» и «y2» в электронной таблице примера содержат формулы для вычисления выходных значений:

   • y1 = model(A3:C3; 1)
   • y2 = модель (A3:C3; 2)

   Полученные данные из столбцов «y1» и «y2» можно использовать для дальнейшего анализа, построения графиков и т. д. Например, на графике ниже показан срез выходных данных модели по оси x1.

    

   Алексей Зайцев, научный сотрудник группы разработки приложений, DATADVANCE

   Округление числа — служба поддержки Microsoft

   Допустим, вы хотите округлить число до ближайшего целого, поскольку десятичные значения не имеют для вас значения. . Или вы хотите округлить число до числа, кратного 10, чтобы упростить приближение сумм. Существует несколько способов округления числа.

   Изменить количество отображаемых десятичных разрядов без изменения числа

   На рабочем листе

   org/ItemList»>

   1. Выберите ячейки, которые вы хотите отформатировать.

   2. Чтобы отобразить больше или меньше цифр после запятой, на вкладке Домашняя страница в группе Число нажмите Увеличить десятичное число или Уменьшить десятичное число .

   Во встроенном числовом формате

   1. На вкладке Home в группе Номер щелкните стрелку рядом со списком числовых форматов и выберите Дополнительные числовые форматы .

   2. org/ListItem»>

      В списке Категория , в зависимости от типа данных ваших номеров, нажмите Валюта , Бухгалтерский учет , Процент или Научный .

   3. В поле Десятичных разрядов введите количество десятичных разрядов, которое вы хотите отобразить.

   Округлить число в большую сторону

   Используйте функцию ОКРУГЛВВЕРХ. В некоторых случаях вы можете использовать функции EVEN и ODD для округления до ближайшего четного или нечетного числа.

   Округление числа в меньшую сторону

   Используйте функцию ОКРУГЛВНИЗ.

   Округлить число до ближайшего числа

   Используйте функцию ОКРУГЛ.

   Округление числа до почти дроби

   Используйте функцию ОКРУГЛ.

   Округление числа до значащей цифры

   Значащие цифры — это цифры, влияющие на точность числа.

   В примерах в этом разделе используются функции ОКРУГЛ , ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ . Они охватывают методы округления положительных, отрицательных, целых и дробных чисел, но показанные примеры представляют собой лишь очень небольшой список возможных сценариев.

   Следующий список содержит некоторые общие правила, которые следует учитывать при округлении чисел до значащих цифр. Вы можете поэкспериментировать с функциями округления и подставить свои собственные числа и параметры, чтобы вернуть желаемое количество значащих цифр.

   • При округлении отрицательного числа это число сначала преобразуется в его абсолютное значение (его значение без отрицательного знака). Затем выполняется операция округления, а затем снова применяется отрицательный знак. Хотя это может показаться противоречащим логике, именно так работает округление. Например, использование функции ROUNDDOWN для округления -889 до двух значащих цифр дает -880. Сначала -889 преобразуется в абсолютное значение 889. Затем результат округляется до двух значащих цифр (880). Наконец, снова применяется отрицательный знак, что дает результат -880.

   • Использование функции ОКРУГЛВНИЗ для положительного числа всегда округляет число в меньшую сторону, а ОКРУГЛВВЕРХ всегда округляет число в большую сторону.

   • Функция ROUND округляет число, содержащее дробную часть, следующим образом: Если дробная часть равна 0,5 или больше, число округляется в большую сторону. Если дробная часть меньше 0,5, число округляется в меньшую сторону.

   • Функция ОКРУГЛ округляет целое число в большую или меньшую сторону по тому же правилу, что и для дробных чисел; подставляя кратные 5 вместо 0,5.

   • Как правило, при округлении числа, не имеющего дробной части (целого числа), вы вычитаете длину из числа значащих цифр, до которого хотите округлить. Например, чтобы округлить 2345678 до 3 значащих цифр, вы используете ОКРУГЛВНИЗ функция с параметром -4 следующим образом: = ОКРУГЛВНИЗ(2345678,-4) . Это округляет число до 2340000, при этом часть «234» является значащей цифрой.

   Округление числа до указанного кратного

   В некоторых случаях может потребоваться округление до кратного числа, которое вы укажете.