Прогнозирование значений в рядах — Excel
Если вам нужно спрогнозировать расходы на следующий год или проецировать ожидаемые результаты для ряда в научном эксперименте, вы можете использовать Microsoft Office Excel для автоматического создания будущих значений на основе существующих данных или для автоматического получения экстраполированных значений, основанных на линейных или ростовых трендах.
Вы можете заполнить ряд значений, которые соответствуют простому линейному или экспоненциальному тренду, с помощью маркер заполнения или последовательности. Для расширения сложных и нелинейных данных можно использовать функции или инструмент регрессионный анализ надстройки «Надстройка анализа».
В линейном ряду значение шага или разность между первым и следующим значением последовательного ряда добавляется к начальному значению, а затем добавляется к каждому последующему значению.
Расширенный линейный ряд | |
|---|---|
|
1, 2 |
3, 4, 5 |
|
1, 3 |
5, 7, 9 |
|
100, 95 |
90, 85 |
Чтобы заполнить ряд для линейного тренда, сделайте следующее:
-
Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Если вы хотите повысить точность ряда трендов, выберите дополнительные начальные значения.
-
Перетащите его в нужном направлении.
Например, если в ячейках C1:E1 выбраны начальные значения 3, 5 и 8, перетащите его вправо, чтобы заполнить значениями тенденций, или влево, чтобы заполнить значениями убывания.
Совет: Чтобы вручную управлять тем, как создается ряд, или заполнять ряд с помощью клавиатуры, выберите команду «Ряд»(вкладка «Главная», группа «Редактирование», кнопка «Заполнить»).

Начальное значение | Расширенный цикл роста |
|---|---|
|
1, 2 |
4, 8, 16 |
|
1, 3 |
9, 27, 81 |
|
2, 3 |
4.5, 6.75, 10.125 |
Чтобы заполнить ряд для тенденции роста, сделайте следующее:
-
Выделите не менее двух ячеек, содержащих начальные значения для тренда.
Если вы хотите повысить точность ряда трендов, выберите дополнительные начальные значения.
-
Удерживая нажатой правую кнопку мыши, перетащите указатель заполнения в том направлении, в каком вы хотите заполнить значениями, увеличив или убывнув значения, отпустите кнопку мыши, а затем нажмите кнопку «Рост» на контекстное меню.
Например, если в ячейках C1:E1 выбраны начальные значения 3, 5 и 8, перетащите его вправо, чтобы заполнить значениями тенденций, или влево, чтобы заполнить значениями убывания.
Совет: Чтобы вручную управлять тем, как создается ряд, или заполнять ряд с помощью клавиатуры, выберите команду «Ряд»(вкладка «Главная», группа «Редактирование», кнопка «Заполнить»).
При нажатии кнопки «Ряд» можно вручную управлять тем, как создается линейный или рост тренда, а затем заполнять значения с помощью клавиатуры.
В обоих случаях шаг игнорируется. Созданный ряд эквивалентен значениям, которые возвращаются функцией ТЕНДЕНЦИЯ или функцией РОСТ.
Чтобы заполнить значения вручную, сделайте следующее:
-
Вы выберите ячейку, с которой нужно начать ряд. Ячейка должна содержать первое значение в ряду.
При выборе команды «Ряд» итоговые ряды заменяют исходные выбранные значения. Если вы хотите сохранить исходные значения, скопируйте их в другую строку или столбец, а затем создайте ряд, выбирая скопированные значения.
-
На вкладке Главная в группе Редактирование нажмите кнопку Заполнить и выберите пункт Прогрессия.
-

-
Чтобы заполнить ряд вниз по столбцам, щелкните «Столбцы».
-
Чтобы заполнить ряды на всем телефоне, щелкните «Строки».
-
-
В поле «Шаг» введите значение, на которое нужно увеличить ряд.
Тип ряда | Результат шага |
|---|---|
|
Линейная |
Шаг добавляется к первому начальному значению, а затем к каждому последующему значению. |
|
Геометрическая |
Первое начальное значение умножается на шаг. Результат и каждый последующий результат умножаются на шаг. |
-
В области «Тип»выберите «Линейный» или «Увеличение».
-
В поле «Остановить значение» введите значение, для чего нужно остановить ряд.
Примечание: Если ряд имеет несколько начальных значений и необходимо, чтобы приложение Excel формирует тенденцию, выберите его.
Если у вас есть данные, для которых необходимо спрогнозировать тенденцию, можно создать линия тренда диаграмме. Например, если в Excel есть диаграмма с данными о продажах за первые несколько месяцев года, вы можете добавить на нее линию тренда, которая отображает общую тенденцию продаж (увеличение или убываю или неплоскую) либо отображает прогнозируемый тренд на месяцы вперед.
Например, если в Excel есть диаграмма с данными о продажах за первые несколько месяцев года, вы можете добавить на нее линию тренда, которая отображает общую тенденцию продаж (увеличение или убываю или неплоскую) либо отображает прогнозируемый тренд на месяцы вперед.
В этой процедуре предполагается, что вы уже создали диаграмму, основанную на существующих данных. Если это не так, см. раздел «Создание диаграммы».
-
Щелкните диаграмму.
-
Щелкните ряд данных, к которому вы хотите добавить линия тренда или скользящее среднее.
-
На вкладке «Макет» в группе «Анализ» нажмите кнопку «Линия тренда» и выберите нужный тип линии тренда или скользящего среднего.
-
Чтобы настроить параметры и отформать линию тренда или линию скользящего среднего, щелкните линию тренда правой кнопкой мыши и выберите в shortcut-меню пункт «Формат линии тренда».

-
Выберите нужные параметры линии тренда, линии и эффекты.
-
Если выбрана полиномиальная,введите в поле «Порядок» наивысшую мощность для независимой переменной.
-
При выборе скользящегосреднего введите в поле «Период» количество периодов, используемых для расчета скользящего среднего.
-
Примечания:
-
В поле «На основе ряда» перечислены все ряды данных на диаграмме, поддерживают линии тренда. Чтобы добавить линию тренда к другому ряду, щелкните имя в поле и выберите нужные параметры.
-
При добавлении скользящего среднего на точечная диаграмма скользящие средние значения будут основаны на порядке, в том числе в значении X, относящегося к диаграмме.
 Чтобы получить нужный результат, перед добавлением скользящего среднего может потребоваться отсортировать значения X.
Чтобы получить нужный результат, перед добавлением скользящего среднего может потребоваться отсортировать значения X.
Если вам нужно выполнить более сложный регрессивный анализ, в том числе вычислить оставшиеся остаток и отсчитать оставшиеся остаток, используйте инструмент анализа регрессии в надстройке «Надстройка «Надстройка анализа». Дополнительные сведения см. в подзагонке «Загрузка предоплаченного анализа».
В Excel в Интернете можно проецировать значения ряда с помощью функций или перетащить его, чтобы создать линейный тренд чисел. Но создать тенденцию роста с помощью этого хи2-го нельзя.
Чтобы создать линейный тренд чисел в Excel в Интернете, используйте его Excel в Интернете:
-
Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Если вы хотите повысить точность ряда трендов, выберите дополнительные начальные значения.
-
Перетащите его в нужном направлении.
Интерполяция графика и табличных данных в Excel
Интерполяция – это своего рода «латание» графиков в тех местах, где возникают обрывы линий из-за отсутствия данных по отдельным показателям. Термин интерполяция подразумевает «латание» внутренних обрывов на графике. А если бы «латались» внешние обрывы, то это была-бы уже экстраполяция графика.
Как построить график с интерполяцией в Excel
При работе в Excel приходится сталкиваться с интерполяцией графиков различной сложности. Но для первого знакомства с ней рассмотрим сначала самый простой пример.
Если в таблице еще нет всех значений показателей, но уже нужно сформировать по ним отчет и построить графическое представление данных. Тогда на графике мы наблюдаем обрывы в местах, где отсутствуют значения показателей.
Тогда на графике мы наблюдаем обрывы в местах, где отсутствуют значения показателей.
Заполните таблицу как показано на рисунке:
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«График»-«График с маркерами».
Чтобы устранить обрывы на графике, то есть выполнить интерполяцию в Excel, можем использовать 2 решения для данной задачи:
- Изменить параметры в настройках графика выбрав соответствующую опцию.
- Использовать функцию: =НД() – возвращает значение ошибки #Н/Д.
Оба эти способа рассмотрим далее на конкретных примерах.
Способ 1:
- Сделайте график активным щелкнув по нему левой кнопкой мышки и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
- В появившемся диалоговом окне «Выбор источника данных» кликните на кнопку «Скрытые и пустые ячейки»
- В появившемся диалоговом окне «Настройка скрытых и пустых ячеек» выберите опцию «линию». И нажмите ОК во всех открытых диалоговых окнах.

Как видно на рисунках сразу отображены 2 варианта опций «линию» и «нулевые значения». Обратите внимание, как ведет себя график при выборе каждой из них.
Методы интерполяции табличных данных в Excel
Теперь выполним интерполяцию данных в таблице с помощью функции: =НД(). Для этого нужно предварительно сбросить выше описанные настройки графика, чтобы увидеть как работает данный способ.
Способ 2. В ячейку B3 введите функцию =НД(). Это автоматически приведет к интерполяции графика как показано на рисунке:
Примечание. Вместо функции =НД() в ячейку можно ввести просто значение: #Н/Д!, результат будет тот же.
Кубическая сплайн экстраполяция — CodeRoad
Для простоты я представлю кубическую кривую Bezier в виде 4 точек (A, B, C, D), где A и D-конечные точки кривой, А B и C-«control handle points». (Фактическая кривая обычно не касается точек ручки управления).
Способы преобразования этого представления кубической кривой
Bezier в другие популярные представления см.
интерполяция
Учитывая одну кубическую кривую Bezier (P0, P1, P2, P3), мы используем алгоритм де Кастельжау , чтобы разделить кривую Bezier на левую и правую половины. Это очень просто даже на microcontroller, который не имеет инструкции «multiply», потому что он требует только вычисления нескольких средних значений, пока мы не получим среднюю точку:
P0
F0 := average(P0, P1)
P1 S0 := average(F0, F1)
F1 := average(P1, P2) Midpoint := average(S0, S1)
P2 S1 := average(F1, F2)
F2 := average(P2, P3)
P3
Вся кривая Bezier равна (P0, P1, P2, P3).
Левая половина всей кривой Bezier — это кривая Bezier (P0, F0, S0, M).
Правая половина всей кривой Bezier — это кривая Bezier (M, S1, F2, P3).
Многие микроконтроллеры продолжают делить каждую кривую
на все меньшие и меньшие маленькие кривые
до тех пор, пока каждая часть не станет достаточно маленькой для аппроксимации
прямая линия.
Но мы хотим пойти другим путем-экстраполировать на большую кривую.
экстраполяция
Учитывая либо левую половину, либо правую половину, мы можем выполнить это в обратном порядке, чтобы восстановить исходную кривую.
Представим себе, что мы забыли исходные точки P1, P2, P3.
Учитывая левую половину кривой Bezier (P0, F0, S0, M), мы можем экстраполировать ее вправо с помощью:
S1 := M + (M - S0)
F1 := S0 + (S0 - F0)
P1 := F0 + (F0 - P0)
затем используйте эти значения для расчета
F2 := S1 + (S1 - F1)
P2 := F1 + (F1 - P1)
и наконец
P3 := F2 + (F2 - P2)
экстраполировать и восстановить экстраполированную кривую Базье (P0, P1, P2, P3).
подробности
Экстраполированная кривая (P0, P1, P2, P3)
проходит через каждую точку исходной кривой
(P0, F0, S0, M) —
в частности, начиная с P0 и проходя через среднюю точку M-
и продолжает идти, пока не достигнет P3.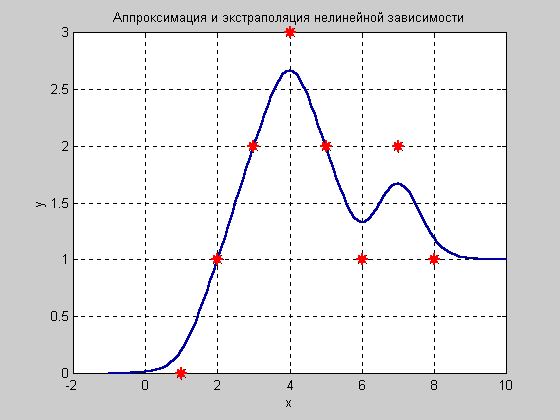
Мы всегда можем экстраполировать из любых 4 точек (P0, F0, S0, M), независимо от того, были ли эти 4 точки первоначально вычислены как левая половина (или правая половина) некоторого большего сплайна Bezier.
Я уверен, что вы уже знаете это, но просто для ясности:
Midpoint = average(F0, F1)
означает «найти среднюю точку точно на полпути между точками F0 и F1», или другими словами,
Midpoint.x = (F0.x + F1.x)/2
Midpoint.y = (F0.y + F1.y)/2
Midpoint.z = (F0.z + F1.z)/2
Выражение
S1 := M + (M - S0)
означает «заданный отрезок линии с одним концом в S0 и средней точкой в M, начинайте с S0 и бегите по прямой мимо M, пока не достигнете другого конца в S1», или другими словами (если у вас нет приличной векторной библиотеки) 3 строки кода
S1.x := M.x + (M.x - S0.x)
S1.y := M.y + (M.y - S0.y)
S1.z := M.z + (M.z - S0.z)
(Если вы делаете 2D, пропустите все «z»-это всегда ноль).
Экстраполяция
Пользователи также искали:
экстраполяция философия,
экстраполяция формула,
экстраполяция графика,
экстраполяция и интерполяция,
экстраполяция онлайн,
экстраполяция пример,
экстраполяция синоним,
экстраполяция в экономике,
экстраполяция,
Экстраполяция,
экстраполяция онлайн,
экстраполяция синоним,
экстраполяция философия,
экстраполяция в экономике,
экстраполяция и интерполяция,
экстраполяция графика,
экстраполяция формула,
графика,
формула,
онлайн,
синоним,
философия,
экономике,
интерполяция,
пример,
экстраполяция пример,
вычислительная математика. экстраполяция,
экстраполяция,
…
Урок 43. Прогнозирование в MS Excel
Урок 43. Прогнозирование в MS Excel
Модели статистического прогнозирования (§18)
О статистике и статистических данныхРассмотрим способ нахождения зависимости частоты заболеваемости жителей города бронхиальной астмой от качества воздуха (третий пример из сформулированных в начале предыдущего параграфа). Любому человеку понятно, что такая зависимость существует. Очевидно, что чем хуже воздух, тем больше больных астмой. Но это качественное заключение. Его недостаточно для того, чтобы управлять уровнем загрязненности воздуха. Для управления требуются более конкретные знания. Нужно установить, какие именно примеси сильнее всего влияют на здоровье людей, как связана концентрация этих примесей в воздухе с числом заболеваний. Такую зависимость можно установить только экспериментальным путем: посредством сбора многочисленных данных, их анализа и обобщения.
При решении таких проблем на помощь приходит статистика.
Статистика — наука о сборе, измерении и анализе массовых количественных данных.
Существуют медицинская статистика, экономическая статистика, социальная статистика и другие. Математический аппарат статистики разрабатывает наука под названием математическая статистика.
Рассмотрим пример из области медицинской статистики.
Известно, что наиболее сильное влияние на бронхиально-легочные заболевания оказывает угарный газ — монооксид углерода. Поставив цель определить эту зависимость, специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (число хронических больных на 1000 жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы (рис. 3.31).
1 Приведенные в примере данные не являются официальной статистикой, однако правдоподобны.
Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер, но верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.
Из полученных данных можно сделать вывод, что при концентрации угарного газа до 3 мг/м3 его влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации наступает резкий рост заболеваемости.
А как построить математическую модель данного явления? Очевидно, нужно получить формулу, отражающую зависимость количества хронических больных Р от концентрации угарного газа С. На языке математики это называется функцией зависимости Р от С: Р(С). Вид такой функции неизвестен, ее следует искать методом подбора по экспериментальным данным.
Понятно, что график искомой функции должен проходить близко к точкам диаграммы экспериментальных данных. Строить функцию так, чтобы ее график точно проходил через все данные точки (рис. 3.4, а), не имеет смысла. Во-первых, математический вид такой функции может оказаться слишком сложным. Во-вторых, уже говорилось о том, что экспериментальные значения являются приближенными.
Строить функцию так, чтобы ее график точно проходил через все данные точки (рис. 3.4, а), не имеет смысла. Во-первых, математический вид такой функции может оказаться слишком сложным. Во-вторых, уже говорилось о том, что экспериментальные значения являются приближенными.
Отсюда следуют основные требования к искомой функции:
• она должна быть достаточно простой для использования ее в дальнейших вычислениях;
• график этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны (рис. 3.4, б).
Полученную функцию, график которой приведен на рис. 3.4, б, в статистике принято называть регрессионной моделью.
Метод наименьших квадратовПолучение регрессионной модели происходит в два этапа:
1) подбор вида функции;
2) вычисление параметров функции.
Первая задача не имеет строгого решения. Здесь может помочь опыт и интуиция исследователя, а возможен и «слепой» перебор из конечного числа функций и выбор лучшей из них.
Здесь может помочь опыт и интуиция исследователя, а возможен и «слепой» перебор из конечного числа функций и выбор лучшей из них.
Чаще всего выбор производится среди следующих функций:
у = ах + b — линейная функция;
у = ах2 + bх + с — квадратичная функция;
у = а lп(х) + b — логарифмическая функция;
у = аеbх — экспоненциальная функция;
у = ахb — степенная функция.
Квадратичная функция называется в математике полиномом второй степени. Иногда используются полиномы и более высоких степеней, например полином третьей степени имеет вид:
у = ах3 + bх2 + сх + d.
Во всех этих формулах х — аргумент, у — значение функции, а, b, с, d — параметры функции, lп(х) — натуральный логарифм, е — константа, основание натурального логарифма.
Если вы выбрали (сознательно или наугад) одну из предлагаемых функций, то далее нужно подобрать параметры (а, Ь, с и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точкам. Что значит «располагалась как можно ближе»? Ответить на этот вопрос значит предложить метод вычисления параметров. Такой метод был предложен в XVIII веке немецким математиком К. Гауссом и называется методом наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была минимальной.
Мы не будем здесь производить подробное математическое описание метода наименьших квадратов. Достаточно того, что вы теперь знаете о существовании такого метода. Он очень широко используется в статистической обработке данных и встроен во многие математические пакеты программ. Важно понимать следующее: методом наименьших квадратов по данному набору экспериментальных точек можно построить любую (в том числе и из рассмотренных выше) функцию. А вот будет ли она нас удовлетворять, это уже другой вопрос — вопрос критерия соответствия. На рис. 3.5 изображены три функции, построенные методом наименьших квадратов по приведенным экспериментальным данным.
Эти рисунки получены с помощью табличного процессора Microsoft Excel. График регрессионной модели называется трендом. Английское слово trend можно перевести как «общее направление» или «тенденция».
Уже с первого взгляда хочется отбраковать вариант линейного тренда. График линейной функции — это прямая. Полученная по МНК прямая отражает факт роста заболеваемости от концентрации угарного газа, но по этому графику трудно что-либо сказать о характере этого роста. А вот квадратичный и экспоненциальный тренды правдоподобны. Теперь пора обратить внимание на надписи, присутствующие на графиках.
Во-первых, это записанные в явном виде искомые функции — регрессионные модели:
линейная функция: у = 46,361x — 99,881;
экспоненциальная функция: у = 3,4302 е0,7555х;
квадратичная функция: у = 21,845x2 -106,97х + 150,21.
На графиках присутствует еще одна величина, полученная в результате построения трендов. Она обозначена как R2. В статистике эта величина называется коэффициентом детерминированности. Именно она определяет, насколько удачной является полученная регрессионная модель. Коэффициент детерминированности всегда заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессионной модели предельно неудачен. Чем R2 ближе к 1, тем удачнее регрессионная модель.
Из трех выбранных моделей значение R2 наименьшее у линейной. Значит, она самая неудачная (нам и так это было понятно). Значения же R2 у двух других моделей достаточно близки (разница меньше 0,01). Если определить погрешность решения данной задачи как 0,01, по критерию R2 эти модели нельзя разделить. Они одинаково удачны. Здесь могут вступить в силу качественные соображения. Например, если считать, что наиболее существенно влияние концентрации угарного газа проявляется при больших величинах, то, глядя на графики, предпочтение следует отдать квадратичной модели. Она лучше отражает резкий рост заболеваемости при больших концентрациях примеси.
Интересный факт: опыт показывает, что если человеку предложить на данной точечной диаграмме провести «на глаз» прямую так, чтобы точки были равномерно разбросаны вокруг нее, то он проведет линию, достаточно близкую к той, что дает МНК.
Мы получили регрессионную математическую модель и можем прогнозировать процесс путем вычислений. Теперь можно оценить уровень заболеваемости астмой не только для тех значений концентрации угарного газа, которые были получены путем измерений, но и для других значений. Это очень важно с практической точки зрения. Например, если в городе планируется построить завод, который будет выбрасывать в атмосферу угарный газ, то, рассчитав его возможную концентрацию, можно предсказать, как это отразится на заболеваемости астмой жителей города.
Существует два способа прогнозирования по регрессионной модели. Если прогноз производится в пределах экспериментальных значений независимой переменной (в нашем случае это концентрация угарного газа С), то это называется восстановлением значения.
Прогнозирование за пределами экспериментальных данных называется экстраполяцией.
Имея регрессионную модель, легко прогнозировать, производя расчеты с помощью электронных таблиц. Выберем для нашего примера в качестве наиболее подходящей квадратичную зависимость. Построим следующую электронную таблицу:
Подставляя в ячейку А2 значение концентрации угарного газа, в ячейке В2 будем получать прогноз заболеваемости. Вот пример восстановления значения:
Заметим, что число, получаемое по формуле в ячейке В2, на самом деле является дробным. Однако не имеет смысла считать число людей, даже среднее, в дробных величинах. Дробная часть удалена — в формате вывода числа указано 0 цифр после запятой.
Экстраполяционный прогноз выполняется аналогично.
Табличный процессор дает возможность производить экстраполяцию графическим способом, продолжая тренд за пределы экспериментальных данных. Как это выглядит при использовании квадратичного тренда для С = 7, показано на рис. 3.6.
В ряде случаев с экстраполяцией надо быть осторожным. Применимость всякой регрессионной модели ограничена, особенно за пределами экспериментальной области. В нашем примере при экстраполяции не следует далеко уходить от величины 5 мг/м3. Вполне возможно, что далее характер зависимости существенно меняется. Слишком сложной является система «экология — здоровье человека», в ней много различных факторов, которые связаны друг с другом. Полученная регрессионная функция является всего лишь моделью, экспериментально подтвержденной в диапазоне концентраций от 2 до 5 мг/м3. Что будет вдали от этой области, мы не знаем. Всякая экстраполяция держится на гипотезе: «предположим, что за пределами экспериментальной области закономерность сохраняется». А если не сохраняется?
Квадратичная модель в данном примере в области малых значений концентрации, близких к 0, вообще не годится. Экстраполируя ее на С = 0 мг/м3, получим 150 человек больных, т. е. больше, чем при 4 мг/м3.
Очевидно, это нелепость. В области малых значений С лучше работает экспоненциальная модель. Кстати, это довольно типичная ситуация: разным областям данных могут лучше соответствовать разные модели.
Вопросы и задания
1.
а) Что такое статистика?
б) Являются ли результаты статистических расчетов точными?
в) Что такое регрессионная модель?
2. Какие из следующих величин можно назвать статистическими: температура вашего тела в данный момент; средняя температура в вашем регионе за последний месяц; максимальная скорость, развиваемая данной моделью автомобиля; среднее число осадков, выпадающих в вашем регионе в течение года?
3.
а) Для чего используется метод наименьших квадратов?
б) Что такое тренд?
в) Как располагается линия тренда, построенная по МНК, относительно экспериментальных точек?
г) Может ли тренд, построенный по МНК, пройти выше всех экспериментальных точек?
4.
а) В чем смысл параметра R2? Какие значения он принимает?
б) Какое значение примет параметр R2, если тренд точно проходит через экспериментальные точки?
5. По данным из следующей таблицы постройте с помощью Excel линейную, квадратичную, экспоненциальную и логарифмическую регрессионные модели. Определите параметры, выберите лучшую модель.
6.
а) Что подразумевается под восстановлением значения по регрессионной модели ?
б) Что такое экстраполяция?
7. Соберите данные о средней дневной температуре в вахпем городе за последнюю неделю (10 дней, 20 дней). Оцените (хотя бы на глаз), годится ли использование линейного тренда для описания характера изменения температуры со временем. Попробуйте путем графической экстраполяции предсказать температуру через 2-5 дней.
8. Придумайте свои примеры практических задач, для которых имело бы смысл выполнение восстановления значений и экстраполяционных
Сущность и методы экстраполяции :: BusinessMan.ru
Сложное слово «экстраполяция» составлено из двух простых. Первое на латыни звучит extra и означает «вне», «за», «снаружи». Второе на той же латыни звучит polire и означает «изменять», «выправлять», «приглаживать». В целом экстраполяция может быть определена как значение вне двух заданных точек. Она считается оценкой того, что извлечено из известных фактов, которые расширяют данные в неизвестной области, чтобы прийти к предполагаемому результату. Эта концепция также может быть отнесена к предсказанию образа будущего, предполагающего истинность настоящих и прошлых тенденций.
Метод экстраполяции предполагает, что данные или наблюдения в будущем будут по-прежнему похожи. Таким образом, будущие результаты могут быть предсказаны. Ее можно рассматривать как математическую гипотезу. При экстраполяции используются данные и факты определенной ситуации и приводятся прогнозы о том, что может произойти в конечном итоге.
История процесса экстраполяции
Этот метод часто называют экстраполяцией Ричардсона или методом Ромберга. Но это не совсем правильно, поскольку на протяжении веков уже существовали похожие численные методы решения подобных задач. Поэтому знаменитая h3 Ричардсона (экстраполяция для численного решения) не является первой. Подобный метод был применим в вычислениях Гюйгенса еще в 1654 году. Сам термин «экстраполяция» был впервые введен Томасом Д. Кларесоном в 1959 году в книге о науке и художественной литературе.
Методы экстраполяции могут пониматься как расширение данных или процессов, предполагающих, что аналогичный процесс будет применяться и за их пределами. Экстраполяция — важная концепция, используемая не только в математике, но и в других областях, таких как социология, психология, прогнозирование. Например, водитель обычно экстраполирует дорожные условия за пределами своего видения. Экстраполяция может быть отнесена к способу, в котором значения данных рассматриваются как точки x1, x2 …, xn, а затем значение приближается к пределу заданного диапазона точек.
Преимущества использования:
- Простой метод прогнозирования.
- Не так много данных требуется.
- Быстрая и дешевая аналитика.
Метод существует в статистических данных. Если какие-то значения периодически убираются, ответ приближается к следующей точке данных. Примером методом экстраполяции является прогноз погоды, в котором рассматривается предыстория данных и экстраполируется прогнозируемая модель будущего. Еще более простой пример, если есть информация о воскресеньях, понедельниках и вторниках, можно экстраполировать среду или четверг.
Недостатки использования экстраполяции:
- Ненадежность, если имеются значительные колебания в исторических данных.
- Предположение, что прошлая тенденция будет продолжаться и в будущем, вряд ли возможно во многих конкурентных бизнес-средах.
- Игнорирует качественные факторы, например изменения вкусов и моды.
Ускорение последовательности
Методы экстраполяции заключается в создании касательной линии в конце известных данных и расширении ее за пределы этой области. Подобно интерполяции, экстраполяция использует множество методов, требующих предварительного знания процесса, который создает существующие точки данных. Метод включает в себя экстраполяцию линейную и полиномиальную, экстраполяцию коники и французской кривой.
Как правило, качество конкретного метода ограничено предположениями о функции. В численном анализе экстраполяция Ричардсона представляет собой метод ускорения последовательности, используемый для улучшения скорости ее сходимости. Он назван в честь Льюиса Фрая Ричардсона. Он представил технику расчета в начале XX века, полезность которой для практических вычислений вряд ли можно переоценить.
Практические применения экстраполяции Ричардсона включают интеграцию Ромберга, которая применяет ее к правилу трапеции и алгоритму Булирша — Стоера для решения обыкновенных дифференциальных уравнений.
Линейный метод
Метод линейной экстраполяции полезен, когда задана линейная функция. Это делается путем рисования касательной линии в конечной точке заданного графика и расширения ее за пределы. Этот метод экстраполяции в прогнозировании дает хорошие результаты, когда точка, которая должна быть предсказана, не слишком далека от данных. Линейная интерполяция полезна при поиске значения между заданными точками. Его можно рассматривать как «заполнение пробелов» таблицы данных.
Стратегия линейной интерполяции заключается в использовании прямой линии для соединения известных точек значений по обе стороны от неизвестной. Линейная интерполяция неточна для нелинейных параметров. Если точки в наборе данных меняются на большую величину, линейная интерполяция может дать неправильную оценку.
Линейная экстраполяция может помочь оценить значения, которые выше или ниже значений в наборе данных. Стратегия ее заключается в использовании подмножества данных вместо всего набора. Для этого типа значений полезно применять в прогнозировании метод экстраполяции, используя последние две или три точки, чтобы оценить значение, превышающее диапазон данных.
Полиномиальная и коническая экстраполяции
Известно, что три точки дают уникальный многочлен. Полиномиальная кривая может быть продолжена после окончания таких данных. Она обычно выполняется методом Ньютона с конечной разностью или с использованием интерполяционной формулы Лагранжа. Полином высшего порядка должен быть экстраполирован с должным вниманием, потому что при полиномиальной экстраполяции есть справедливые шансы на ошибку. Если это произойдет, оценка ошибки будет экспоненциально возрастать вместе со степенью полинома.
В математике минимальная полиномиальная экстраполяция представляет собой преобразование последовательности, используемое для ускорения сходимости. Хотя метод Айткена является самым известным, он часто терпит неудачу, особенно для векторных последовательностей. При этом выполняется итерация, которая строит матрицу. Ее столбцы являются отличиями.
К примеру, методом экстраполяции для конического разреза может быть произведен с помощью 5 точек, указанных ближе к концу данных. В случае, если коническая секция представляет собой круг или эллипс, то она будет образовывать петли назад и воссоединиться с собой. Парабола или гипербола никогда не пересекутся. Но они могут быть изогнуты назад относительно оси X. Экстраполяция конуса может быть выполнена на бумаге с конической секцией или с помощью компьютера.
Математический метод оценки
В этом методе экстраполяции прогнозируется значение за базовый период. Действия, описанные ниже, автоматически выполняются системой и не видны пользователю. Описание предназначено для уточнения алгоритма, который выводит ожидаемые значения из количества, хранящегося в системе, и прогнозирует результат измерения счетчика.
Экстраполяция при использовании определения количества процедуры выполняется с помощью функции: Yt = f (yi, t, aj).
В качестве основы для экстраполяции добавляются округленные данные типичного базового периода, хранящегося в результатах считывания. Система определяет вес Yt данных временного ряда в t (время прогнозируемого периода) для получения правильного решения методом экстраполяции. Где в точке отсчета взяты yi – уровень ряда и aj – параметр уравнения тренда.
Прогнозирование функциональных возможностей
Метод фиксации статистической кривой применим к прогнозированию функциональных возможностей. Статистические процедуры соответствуют прошлым данным одной или нескольких математических функций, таких как линейные, логарифмические, Фурье или экспоненциальные. Наилучшие выбираются статистическим тестом. Тогда этот прогноз экстраполируется из этой математической связи методом математической экстраполяции. Одним из самых простых способов получения приблизительных оценок будущих (или прошлых) условий является экстраполяция данных, которые изменяются со временем.
Например, если нужно провести грубую оценку будущих уровней загрязняющих веществ в питьевых водах на 20 лет вперед, можно экстраполировать эту тенденцию с последних 20 лет. То же наблюдается, если нужно оценить распространенность курения или рак легких в фоновом режиме в будущем. Прогноз можно составить путем расчета тенденции за последние годы. Экстраполяции этого типа можно сделать с использованием менее сложных методов. Во многих случаях (особенно в областях маркетинга и управления бизнесом) традиционно используется метод экстраполяции, например путем просмотра последних данных и интуитивной оценки того, что подразумевается в будущем.
Методы, основанные на правилах, также могут быть использованы путем применения набора предопределенных принципов или ожиданий на основе предварительного понимания системы и учета последних данных для интерпретации будущих событий.
При любом методе в экстраполяции важна осторожность из-за наличия многочисленных неопределенностей. Любая процедура экстраполяции основана на предположении, что в прошлых данных и знаниях имеется достоверная информация. Следовательно, будущее обусловлено теми же факторами, которые действовали ранее.
Ошибки прогнозирования
Ошибочность экстраполяции (точнее, ошибочность неоправданной экстраполяции) возникает, когда явление, ответственное за ряд тривиальных локальных эффектов, считывается в качестве великих глобальных явлений. Еще одна причина ошибки заключается в том, что иногда обобщенные правила выводятся на основе слишком немногочисленных фактов. Так, теория Дарвина об эволюции является фантастическим примером применения метода экстраполяции, в которой механизмы случайных изменений и естественного отбора объявляются для учета развития таких сложных структур, как зрение млекопитающих или иммунная система живых организмов.
При попытке интерпретации результатов исследований ученый должен избегать экстраполяции вне диапазона данных и осознавать лежащие в основе предположения, чтобы избежать принятия недействительных выводов. В общем, экстраполяция является законным научным инструментом. Есть два аспекта, которые помогают различать действительную и ошибочную экстраполяцию. Вероятность ошибочной экстраполяции выше, когда для ее построения были получены точки на недостаточных данных.
Статистические инструменты Excel
Чтобы найти корреляцию между годами и результатами (например, в бизнесе), можно воспользоваться Excel.
Для этих задач используют статистические инструменты для моделирования методом экстраполяции, встроенные во все версии Excel, начиная с 97. Порядок действия:
- Ввести известные значения, например общие продажи за 2016-2017 годы, если нужно определить их за 2018 и 2020 годы.
- Установить утилиту Analysis, функцию, требующую использования надстройки.
- Чтобы установить ее, извлечь из меню «Инструменты», «Дополнения».
- Проверить окно утилиты анализа и подтвердить с помощью «ОК».
- Измерить корреляции между двумя сериями.
- Экстраполяция, которую нужно сделать, имеет смысл только в том случае, если между двумя наборами чисел (годы и продажи) складывается четкая тенденция (корреляция) по методу экстраполяции тенденций.
- Чтобы измерить эту корреляцию, используют меню «Инструменты», «Утилиты анализа».
- В списке «Инструменты анализа» выбирают «Анализ корреляции» и нажимают «ОК».
- В поле Input Range вводят анализируемый диапазон, например A6: B18, Excel добавит символ «$».
- В области «Параметры вывода» проверяют выходной диапазон и вводят в соседнее поле.
- Подтверждают с помощью OK.
- Excel создает массив из двух строк по двум столбцам. Находят расчетное значение (например, 0.981). Поскольку это значение близко к 1, это означает, что существует сильная корреляция между годами и цифрами продаж. Если пользователь получит значение, близкое к нулю, это будет означать, что тенденция не возникает. В этом случае экстраполяция не имеет смысла.
- Запускается оценка будущих значений.
- Выбирают необходимый диапазон и нажимают кнопку «Мастер диаграмм».
- Выбирают диаграмму (например, облака точек) и нажимают «Готово».
Применение скользящих средних
Эти два метода экстраполяции предполагают широкое использование данных по продажам для прогнозирования будущего. Скользящее среднее значение принимает серию данных и «сглаживает» флуктуации в них. Цель состоит в том, чтобы извлекать экстремумы данных из периода в период. Скользящие средние часто вычисляются ежеквартально или еженедельно. Для прогнозирования будущих значений экстраполяция предполагает использование трендов, установленных историческими данными. Основное предположение экстраполяции заключается в том, что образец будет продолжаться и в будущем, если фактические данные не указывают на иное. Чтобы подробнее разобраться в этих методах, можно рассмотреть диаграмму, показывающую продажи гаджетов для крупного бизнеса с 2012 по 2015 годы.
Этот метод экстраполяции расчета показывает фактическую цифру продаж. Как можно увидеть, общая сумма продаж колеблется от года к году, хотя можно догадаться (глядя на данные), что общая тенденция для роста продаж имеется. Черная линия показывает скользящую среднюю. Это рассчитывается путем добавления последних лет продаж (например, Q1 + Q2 + Q3 + Q4), а затем деления на четыре.
Этот метод сглаживает годовые изменения и дает хорошее представление об общей тенденции в годовых продажах. Скользящее среднее помогает указать тенденцию роста, выраженную в процентных значениях. Именно это экстраполяция будет использовать сначала, чтобы предсказать путь будущих продаж. Это можно сделать математически, используя электронную таблицу. В качестве альтернативы экстраполированный тренд можно просто нарисовать на диаграмме в качестве приблизительной оценки.
Корреляция трендов
Всегда одна технология является предшественником другой. Это случается, когда достижения, достигнутые в технологии прекурсоров, могут быть приняты технологией последователей. Когда такие отношения существуют, знание изменений в технологии предшественников может быть использовано для прогнозирования хода технологии последователей в будущем. Кроме того, экстраполяция предшественника позволяет прогнозировать продолжение следования за пределами времени запаздывания.
В этом случае используют метод экстраполяции трендов, в котором сравниваются, например, тенденции скорости боевых и транспортных самолетов. Другим примером прогноза корреляции трендов является прогнозирование размера и мощности будущих компьютеров, основанное на достижениях в области микроэлектронной технологии. Иногда технология последователей зависит от нескольких технологий прекурсоров, а не от одного предшественника.
Фиксированные комбинации предшественников могут влиять на изменение в последовательности, но чаще комбинации не фиксируются, а входы предшественников различаются как по комбинации, так и по силе. Например, увеличение скорости воздушных судов может происходить за счет улучшения двигателей, материалов, элементов управления, топлива, аэродинамики и различных комбинаций этих факторов.
Пример прогноза корреляции, полученной методом экстраполяции трендов: общие пассажирские мили, общие географические мили и средняя посадочная мощность. Экстраполяция статистически определенных тенденций позволяет объективно подходить к прогнозированию. Однако этот подход имеет серьезные ограничения и ловушки. Любые ошибки или неправильный выбор, сделанный при определении исторических данных, будут отражены в прогнозе, что снижает его ценность.
Приложения, атрибуты и лимиты
Метод экстраполяции относится к сфере прогнозирования. Он предполагает, что шаблоны, которые существовали в прошлом, будут продолжаться и в будущем, а также то, что эти шаблоны являются регулярными и могут быть измерены. Другими словами, прошлое является хорошим индикатором будущего. Приложения полезны для разработки базовых данных.
Атрибуты и лимиты — это простые и дешевые инструменты вычислений, как и сложные теоретические модели.
- Данные процесса — графика и наблюдения.
- Ключ — наличие хорошей базы данных и понимание структуры внутри нее.
- Техника — наилучшая подгонка, соотношение и так далее.
Временные стандартные статистические процедуры не приводят к аккуратным подборам тенденций, которые прогнозист может экстраполировать с комфортом, выполняя прогноз методом экстраполяции. В таких случаях прогнозист может «скорректировать» статистические результаты, применяя суждение. Также он может полностью игнорировать статистику и экстраполировать тренд целиком на основе суждения.
Прогнозы, генерируемые таким образом, менее точны, чем статистические, но не обязательно неудовлетворительные. Одним из примеров такой экстраполяции качественного тренда является прогнозирование сложности воздушного судна. Попытки количественной оценки этой тенденции не были успешными. Но процент подвижных или регулируемых частей самолета был экстраполирован с частотой, с которой такие элементы были введены в прошлом. Эти прогнозы были достаточно точными.
Специфические технические изменения не могут быть предсказаны таким образом, но степень изменения может. Это дает полезные материалы для планирования, указывая тенденцию прошлого поведения.
Как сверить выборку с распределением Вейбулла в Excel
ОБНОВЛЕНИЕ: Данный пост все еще актуален, но есть новый: Как сверить выборку с распределением Вейбулла без Excel.
Предупреждение: это очень технический и практический пост.
Оказывается, распределение Вейбулла – довольно распространено среди статистических распределений времени производства в проектах по разработке ПО. Этот инсайт принадлежит Трою Магеннису (Troy Magennis), лидирующему эксперту по симуляциям проектов методом Монте-Карло . Он изучил данные с большого количества реальных проектов. Трой также объясняет как работа со знаниями и ее тенденция к увеличению объема и прерывистости ведет к такому распределению. Рекомендую подробнее изучить его работы на эту тему – за них он стал лауреатом Brickell Key Award. Инсайт о распределении Вейбулла независимо от Троя подтвердил другой лауреат Brickell Key Award, Ричард Хенсли (Richard Hensley). Он изучил большое количество данных из ИТ-подразделения крупной компании.
Совпадают ли ваши лид-таймы с распределением Вейбулла?
Вчера мне пришлось быстро ответить на этот вопрос, а под рукой оказались только Excel и мои знания о статистике. Распределение Вейбулла на самом деле – это группа распределений, формируемых параметром формы (k). На диаграмме выше видно, как изменение этого параметра влияет на форму кривой распределения. Распределение Вейбулла идентично экспоненциальному распределению при k=1 и распределению Рэлея при k=2. При иных значениях k происходит интерполяция/экстраполяция этих распределений. Итак, перед нами два вопроса:
- Соответствует ли данный набор значений распределению Вейбулла?
- Если соответствует, то чему равен параметр формы?
Вот простой алгоритм, которым вы можете следовать, чтобы ответить на эти вопросы для вашей выборки. Я приложу электронную таблицу в конце поста.
Шаг 1. Скопируйте ваш набор значений в колонку А электронной таблицы. Я предпочитаю оставлять первый ряд для заголовков столбцов, так чтобы значения начинались с ячейки А2.
Шаг 2. Отсортируйте значения в колонке А в порядке возрастания.
Шаг 3. Разделите интервал [0; 1] на равные интервалы, согласно количеству значений в вашей выборке. Внесите средние значения этих интервалов в колонку В. Если у вас N=100 значений, то формула Excel для этого будет =(2*ROW(B2)-3)/200 (200 == 2*N). Введите эту формулу в ячейку В2 и растяните на все ячейки колонки В.
Шаг 4. Заполните колонку С натуральными логарифмами значений колонки А. Введите формулу =LN(A2) в ячейку С2 и растяните ее на всю колонку.
Шаг 5. Заполните колонку D значениями, полученными из колонки В как описано дальше. Введите формулу =LN(-LN(1-B2)) в ячейку D2 и растяните ее до конца колонки. По сути, мы линеаризуем функцию накопительного распределения, чтобы линейная регрессия показала нам параметр формы.
Шаг 6. Если выборка совпадает с распределением Вейбулла, то параметр формы будет равен наклону прямой, проведенной через точки с координатами из колонок C и D. Для расчета используйте формулу =SLOPE(D2:D101,C2:C101) (Эта формула рассчитана на выборку, в которой N=100 значений – корректируйте ее исходя из своего количества значений). В приложенной электронной таблице это значение находится в ячейке G2.
Шаг 7. Посчитайте формулу =INTERCEPT(D2:101,C2:C101). (Ячейка G3)
Шаг 8. Посчитайте параметр масштаба для предыдущего шага =EXP(-G3/G2). (Ячейка G4)
Шаг 9. Проверьте, насколько хорошо совпадают значения при помощи формулы =RSQ(C2:C101,D2:D101). Если совпадение идеальное – значение будет равно 1.
Шаг 10. Если совпадение достаточно хорошее, можно еще раз проверить расчет на соответствие реальности. Для этого посчитайте среднее от полученных параметров формы и масштаба и сравните его с общим средним. Формула среднего
В Excel нет встроенной Гамма-функции, но есть функция, возвращающая ее логарифм. Таким образом, мы можем рассчитать прогнозируемое среднее по формуле =G4*EXP(GAMMALN(1+1/G2)). Теперь можно сравнить прогнозируемое среднее и общее среднее, которое получим формулой =AVERAGE(A2:A101).
Обновление
Есть и другой способ сделать линейную регрессию. Шаги выше сократят вертикальные расстояния (по направлению шкалы y) между лучшим совпадением кривой и точками выборки. Это возможно сделать и через сокращение горизонтальных расстояний. Второй метод последовательно переоценивает параметр формы, что нежелательно для практических применений аналитики лид-таймов. Это может приводить к неточностям, когда одно и то же значение встречается в выборке несколько раз, особенно на левой стороне распределения. По этим причинам, я рекомендую использовать метод, изначально описанный в оригинальном посте (линейная регрессия, сокращение вертикальных расстояний).
Я также обновил электронную таблицу более “умными” формулами. Теперь их не нужно корректировать – вне зависимости от количества значений в выборке лид-таймов.
Оригинальная статья опубликована Алексеем Жегловым 1 августа 2013
Перевод: Фролов Максим
Редактура: Артур Нек
Функция ТРЕНД — как прогнозировать и экстраполировать в Excel
Функция ТЕНДЕНЦИЯ — Прогноз и экстраполировать в Excel
Функция ТЕНДЕНЦИЯ — это статистическая функция Excel ФункцииСписок наиболее важных функций Excel для финансовых аналитиков. Эта шпаргалка охватывает сотни функций, которые критически важно знать аналитику Excel, который будет вычислять линейную линию тренда для массивов известных значений y и x. Функция расширяет линейную линию тренда для вычисления дополнительных значений y для нового набора значений x.Это руководство покажет вам шаг за шагом, как экстраполировать в Excel с помощью этой функции.
Как финансовый аналитик Описание работы финансового аналитика В описании должности финансового аналитика ниже приводится типичный пример всех навыков, образования и опыта, необходимых для работы аналитиком в банке, учреждении или корпорации. Выполняйте финансовое прогнозирование, отчетность и отслеживание операционных показателей, анализируйте финансовые данные, создавайте финансовые модели, эта функция может помочь нам в прогнозировании будущих тенденций.Например, мы можем использовать тенденции для прогнозирования будущих доходов конкретной компании. Это отличная функция прогнозирования
Формула
= ТЕНДЕНЦИЯ (известные_г, [известные_x], [новые_x], [const])
Функция ТЕНДЕНЦИЯ использует следующие аргументы:
- Известные_y (обязательный аргумент) — это набор значений y, которые мы уже знаем в отношении y = mx + b.
- Known_x’s (необязательный аргумент) — это набор значений x.Если мы предоставим аргумент, он должен иметь ту же длину, что и набор known_y. Если опущено, набор [known_x’s] принимает значение {1, 2, 3,…}.
- New_x (необязательный аргумент) — предоставляет один или несколько массивов числовых значений, которые представляют значение new_x. Если аргумент [new_x’s] опущен, он устанавливается равным [known_x’s].
- Константа (необязательный аргумент) — указывает, следует ли принудительно установить константу b равной 0. Если const имеет значение ИСТИНА или опущено, b вычисляется нормально.Если false, b устанавливается равным 0 (нулю), а значения m корректируются так, чтобы y = mx.
Функция ТЕНДЕНЦИЯ использует метод наименьших квадратов для поиска линии наилучшего соответствия, а затем использует ИТ для вычисления новых значений y для предоставленных новых значений x.
Как использовать функцию ТЕНДЕНЦИЯ в Excel?
Чтобы понять использование функции ТЕНДЕНЦИЯ, давайте рассмотрим пример. Ниже мы выполним экстраполяцию в Excel с помощью функции прогноза.
Пример — прогноз и экстраполяция в Excel
Предположим, мы хотим построить прогноз или экстраполировать будущую выручку компании.Приведенный набор данных показан ниже:
Для расчета будущих продаж мы будем использовать функцию ТЕНДЕНЦИЯ. Используемая формула будет выглядеть так:
Это вернет массив значений для y, поскольку значения x, которые необходимо вычислить, представляют собой массив x. Таким образом, его необходимо ввести как формулу массива, выделив ячейки, которые необходимо заполнить, введите свою функцию в первую ячейку диапазона и нажмите CTRL-SHIFT-Enter (то же самое для Mac).Получим результат ниже:
Что нужно помнить о функции ТРЕНД
- # ССЫЛКА! error — возникает, если массив known_x и массив new_x имеют разную длину.
- # ЗНАЧЕНИЕ! error — Возникает в следующих случаях:
- Нечисловые значения, указанные в числах known_y, [known_x’s] или [new_x’s]
- Указанный аргумент [const] не является логическим значением.
Щелкните здесь, чтобы загрузить образец файла Excel.
Дополнительные ресурсы
Спасибо за то, что прочитали руководство CFI по функции Excel TREND.Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование в Excel. Что такое финансовое моделирование? Финансовое моделирование выполняется в Excel для прогнозирования финансовых показателей компании. Обзор того, что такое финансовое моделирование, как и зачем строить модель .. Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI:
- Расширенный курс формул Excel
- Расширенные формулы Excel, которые вы должны знать Расширенные формулы Excel, которые необходимо знатьЭти расширенные формулы Excel важно знать, и это позволит вам вывести ваши навыки финансового анализа на новый уровень.Расширенные функции Excel
- Ярлыки Excel для ПК и MacExcel Ярлыки ПК MacExcel Ярлыки — Список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета. Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие статьи
- Станьте сертифицированным финансовым аналитиком Станьте сертифицированным аналитиком финансового моделирования и оценки (FMVA) ®
Как экстраполировать в Excel
Экстраполяция — это математический метод, который используется для прогнозирования за пределами определенного диапазона путем программирования и расширения прошлых известных данных.Так что это разновидность анализа и визуализации данных Excel. В этом руководстве мы узнаем, как экстраполировать данные в Excel.
Формула экстраполяцииЧтобы экстраполировать данные по формуле, нам нужно использовать две точки линейной диаграммы, которую мы построили ранее.
Формула линейной экстраполяции:
Y (x) = b + (x-a) * (d-b) / (c-a)
Вы можете ввести формулу в соответствии с двумя точками значений данных и экстраполировать целевое значение.
Рисунок 1 — Формула линейной экстраполяции в Excel Как экстраполировать график по линии тренда
Экстраполяция графика по линии тренда помогает отображать тенденции визуальных данных. Здесь мы узнаем, как добавить линию тренда на наши диаграммы:
- Выберите диапазон данных.
- Перейдите на вкладку Вставьте вкладку с ленты.
- В разделе диаграмм щелкните диаграмму Line (вы также можете выбрать диаграмму разброса.)
- Щелкните значок Элемент диаграммы и установите флажок Линия тренда.
- Дважды щелкните линию тренда на графике, чтобы открыть панель Format Trendline и применить свои пользовательские настройки.
Рисунок 2 — Как добавить линию тренда к графику Экстраполяция данных функцией прогноза
Если вам нужна функция для прогнозирования данных без создания диаграмм и графиков (внутренняя ссылка), используйте функцию Excel Forecast .Функция прогноза помогает экстраполировать числовые данные на линейный тренд. Кроме того, вы можете экстраполировать шаблон периодического издания или даже экстраполировать лист.
Здесь мы узнаем, как использовать функции Forecast.linear и Forecast.ETS и как экстраполировать лист.
Прогноз.ЛинейныйЭкстраполяция определяет, что взаимосвязь между известными значениями применима и к неизвестным значениям. Эта функция помогает экстраполировать данные, содержащие два набора числовых значений, которые соответствуют друг другу.
Ниже приведен синтаксис функции Forecast.Linear:
= ПРОГНОЗ.ЛИНЕЙНЫЙ (x ؛ известное Ys ؛ известное Xs)
Предположим, у нас есть набор данных, показывающий количество продаж за девять месяцев. Нам нужно спрогнозировать продажи на ближайшие три месяца. Чтобы использовать эту функцию, выполните следующие действия:
- Выберите пустую ячейку.
- Введите = прогноз или = прогноз. Линейный в строке формул .
- Щелкните значение x , которое вы хотите предсказать для себя, и введите точку с запятой или запятую (в соответствии с вашей версией Excel.)
- Выберите все известные Ys , введите точку с запятой, а затем выберите все известные Xs .
- Нажмите Введите .
Рисунок 3 — Синтаксис функции Forecast.Linear Прогноз.ETS
В некоторых случаях у вас есть сезонный шаблон, и этот шаблон периодического издания требует определенной функции для прогнозирования будущего. Здесь у нас есть объем продаж за год, и нам нужно спрогнозировать первые три месяца следующего года.
Синтаксис функции Forecast.ETS:
= FORECAST.ETS (целевая_дата ؛ значения ؛ временная шкала ؛ [сезонность], [data_complation]; [агрегирование])
Target_date : точка, которую нужно спрогнозировать.
Значения : Здесь указаны все известные суммы продаж.
Временная шкала : в данном случае количество месяцев.
[ сезонность ]: длина сезонной модели (необязательный аргумент).
[data_complation] : Хотя временная шкала требует постоянного шага между точками данных, ПРОГНОЗ.ETS поддерживает до 30% отсутствующих данных и автоматически корректирует их (необязательный аргумент).
[ агрегация ]: параметр агрегации — это числовое значение, указывающее, какой метод будет использоваться для агрегирования нескольких значений с одной и той же меткой времени (необязательный аргумент).
Теперь выполните следующие действия, чтобы спрогнозировать целевые значения:
- Выберите пустую ячейку, в которой вы хотите представить результат.
- Введите синтаксис функции и введите аргументы, как мы уже упоминали.
- Нажмите Enter.
Рисунок 4 — Синтаксис функции Forecast.ETS Листы экстраполяции
Excel 2016 и более поздние версии предоставляют инструмент для прогнозирования таблицы. Этот инструмент создает таблицу в соответствии с вашими данными и определяет нижнюю и верхнюю доверительные границы.
Чтобы использовать лист прогноза, перейдите на вкладку Data , из группы Forecast щелкните инструмент Forecast Sheet , чтобы открыть окно Create Forecast Worksheet .Вы можете выбрать линейную или столбчатую диаграмму по их значкам в правом верхнем углу поля.
Рисунок 5 — Инструмент таблицы прогнозов в Excel
Если вам нужно настроить диаграмму прогноза, вы можете отредактировать ее, нажав на опции :
- Где начинается или заканчивается прогноз
- Измените доверительный интервал
- Добавьте статистику прогноза
- Измените временную шкалу и диапазон значений
- И скопируйте дубликат с помощью
Затем нажмите кнопку Create и посмотрите результат.
Рисунок 6 — Результат работы инструмента Таблица прогнозов Функция тренда ExcelЕще одна функция экстраполяции данных без построения графиков — это функция тренда в Excel. Эта статистическая функция будет предсказывать будущие тенденции в соответствии с известными значениями.
Синтаксис функции тренда:
= ТЕНДЕНЦИЯ (известные_Y; [известные_X]; [новые_X]; [const])
Известный Ys : Значения Y, которые мы уже знаем.
Известные Xs : значения X, которые мы уже знаем (необязательный аргумент.)
Const : согласно Y = mX + b, если const ложно, b равно нулю, но если const истинно или пропущено, b вычисляется нормально.
Рисунок 7 — Функция тренда в Excel
Вы можете связаться с нами, задать вопросы нашим специалистам и получить дополнительную поддержку через службу поддержки Excel .
Кроме того, сокращайте расходы, ускоряйте выполнение задач и повышайте качество с помощью служб автоматизации Excel.
Стоимость проекта в серии
Если вам нужно спрогнозировать расходы на следующий год или спрогнозировать ожидаемые результаты для серии в научном эксперименте, вы можете использовать Microsoft Office Excel для автоматического создания будущих значений, основанных на существующих данных, или для автоматического генерирования экстраполированных значений на основе по расчетам линейного тренда или тренда роста.
Вы можете ввести ряд значений, которые соответствуют простой линейной тенденции или тенденции экспоненциального роста, используя маркер заполнения или команду Series . Чтобы расширить сложные и нелинейные данные, вы можете использовать функции рабочего листа или инструмент регрессионного анализа в надстройке Analysis ToolPak.
В линейном ряду значение шага или разница между первым и следующим значением в ряду добавляется к начальному значению, а затем прибавляется к каждому последующему значению.
Первоначальный выбор | Расширенная линейная серия |
|---|---|
1, 2 | 3, 4, 5 |
1, 3 | 5, 7, 9 |
100, 95 | 90, 85 |
Чтобы заполнить ряд для линейного тренда наилучшего соответствия, выполните следующие действия:
Выберите не менее двух ячеек, содержащих начальные значения тенденции.
Если вы хотите повысить точность ряда трендов, выберите дополнительные начальные значения.
Перетащите маркер заполнения в том направлении, в котором вы хотите заполнить увеличивающимися или уменьшающимися значениями.
Например, если выбранные начальные значения в ячейках C1: E1 равны 3, 5 и 8, перетащите маркер заполнения вправо, чтобы заполнить его увеличивающимися значениями тренда, или перетащите его влево, чтобы заполнить уменьшающимися значениями.
Совет: Чтобы вручную управлять созданием серии или использовать клавиатуру для заполнения серии, щелкните команду Series (вкладка Home , группа редактирования , кнопка Fill ).
В возрастающей серии начальное значение умножается на значение шага, чтобы получить следующее значение в серии.Полученный продукт и каждый последующий продукт затем умножаются на значение шага.
Первоначальный выбор | Серия расширенного роста |
|---|---|
1, 2 | 4, 8, 16 |
1, 3 | 9, 27, 81 |
2, 3 | 4.5, 6,75, 10,125 |
Чтобы заполнить ряд для тенденции роста, выполните следующие действия:
Выберите не менее двух ячеек, содержащих начальные значения тенденции.
Если вы хотите повысить точность ряда трендов, выберите дополнительные начальные значения.
Удерживая нажатой правую кнопку мыши, перетащите маркер заполнения в направлении, в котором вы хотите заполнить увеличивающимися или уменьшающимися значениями, отпустите кнопку мыши и затем щелкните Growth Trend в контекстном меню.
Например, если выбранные начальные значения в ячейках C1: E1 равны 3, 5 и 8, перетащите маркер заполнения вправо, чтобы заполнить его увеличивающимися значениями тенденции, или перетащите его влево, чтобы заполнить уменьшающимися значениями. x) для создания серии.
В любом случае значение шага игнорируется. Создаваемый ряд эквивалентен значениям, возвращаемым функцией ТЕНДЕНЦИЯ или РОСТ.
Чтобы ввести значения вручную, выполните следующие действия:
Выберите ячейку, с которой вы хотите начать серию. Ячейка должна содержать первое значение в серии.
Когда вы нажимаете команду Series , полученная серия заменяет исходные выбранные значения.Если вы хотите сохранить исходные значения, скопируйте их в другую строку или столбец, а затем создайте серию, выбрав скопированные значения.
На вкладке Home в группе Editing щелкните Fill , а затем щелкните Series .
Выполните одно из следующих действий:
Чтобы заполнить ряды на листе, щелкните Столбцы .
Чтобы заполнить ряды на листе, щелкните строк .
В поле Шаг значение введите значение, на которое вы хотите увеличить ряд.
Серии тип | Результат значения шага |
|---|---|
линейная | Значение шага добавляется к первому начальному значению и затем добавляется к каждому последующему значению. |
Рост | Первое начальное значение умножается на значение шага. Полученный продукт и каждый последующий продукт затем умножаются на значение шага. |
В разделе Тип щелкните Линейный или Рост .
В поле Stop value введите значение, на котором вы хотите остановить серию.
Примечание: Если в ряду несколько начальных значений и вы хотите, чтобы Excel генерировал тренд, установите флажок Тренд .
Если у вас есть данные, для которых вы хотите спрогнозировать тренд, вы можете создать линию тренда на диаграмме.Например, если у вас есть диаграмма в Excel, которая показывает данные о продажах за первые несколько месяцев года, вы можете добавить к диаграмме линию тренда, которая показывает общую тенденцию продаж (увеличение, уменьшение или фиксированное значение) или прогнозируемый тенденция на месяцы вперед.
Эта процедура предполагает, что вы уже создали диаграмму на основе существующих данных. Если вы еще не сделали этого, см. Раздел Создание диаграммы.
Щелкните диаграмму.
Щелкните ряд данных, к которому вы хотите добавить линию тренда или скользящее среднее.
На вкладке Макет в группе Анализ щелкните Линия тренда , а затем выберите нужный тип линии тренда регрессии или скользящего среднего.
Чтобы установить параметры и отформатировать линию тренда регрессии или скользящее среднее, щелкните линию тренда правой кнопкой мыши, а затем выберите Форматировать линию тренда в контекстном меню.
Выберите нужные параметры линии тренда, линии и эффекты.
Если вы выбрали Полином , введите в поле Порядок наибольшую степень для независимой переменной.
Если вы выбрали Moving Average , введите в поле Period количество периодов, которые будут использоваться для расчета скользящего среднего.
Примечания:
В поле на основе серии перечислены все ряды данных на диаграмме, которые поддерживают линии тренда. Чтобы добавить линию тренда в другую серию, щелкните имя в поле и выберите нужные параметры.
Если вы добавляете скользящее среднее на диаграмму xy (точечная диаграмма), скользящее среднее основывается на порядке значений x, нанесенных на диаграмму.Чтобы получить желаемый результат, вам может потребоваться отсортировать значения x перед добавлением скользящего среднего.
Если вам нужно выполнить более сложный регрессионный анализ, включая вычисление и построение остатков, вы можете использовать инструмент регрессионного анализа в надстройке Analysis ToolPak. Для получения дополнительной информации см. Загрузка пакета инструментов анализа.
В Excel в Интернете вы можете проецировать значения в ряд, используя функции рабочего листа, или вы можете щелкнуть и перетащить маркер заполнения, чтобы создать линейный тренд чисел. Но вы не можете создать тенденцию роста, используя маркер заполнения.
Вот как вы используете маркер заполнения для создания линейного тренда чисел в Excel в Интернете:
Выберите не менее двух ячеек, содержащих начальные значения тенденции.
Если вы хотите повысить точность ряда трендов, выберите дополнительные начальные значения.
Перетащите маркер заполнения в том направлении, в котором вы хотите заполнить увеличивающимися или уменьшающимися значениями.
Формула экстраполяции | Как прогнозировать?
Определение формулы экстраполяции
Формула экстраполяции относится к формуле, которая используется для оценки значения зависимой переменной по отношению к независимой переменной, которая должна находиться в диапазоне, который находится за пределами данного набора данных, который, безусловно, известен, и для расчета линейной разведки. с использованием двух конечных точек (x1, y1) и (x2, y2) на линейном графике, когда значение точки, которое необходимо экстраполировать, равно «x», формула, которую можно использовать, представлена как y1 + [(x − x 1 ) / (x 2 −x 1 )] * (y 2 −y 1 ).
Y (x) = Y (1) + (x- x (1) / x (2) -x (1)) * (Y (2) — Y (1))
Расчет линейной экстраполяции (шаг за шагом)
- Шаг 1 — Данные сначала необходимо проанализировать, следуют ли данные тенденции и можно ли ее спрогнозировать.
- Шаг 2 — Должны быть две переменные, одна из которых должна быть зависимой переменной, а вторая — независимой.
- Шаг 3 — Числитель формулы начинается с предыдущего значения зависимой переменной, а затем нужно добавить обратно долю независимой переменной, как это делается при вычислении среднего для интервалов классов.
- Шаг 4 — Наконец, умножьте значение, полученное на шаге 3, на разницу непосредственно заданных зависимых значений. После добавления шага 4 к значению зависимой переменной мы получим экстраполированное значение.
Примеры
, Пример # 1
Предположим, что значения некоторых переменных указаны ниже в виде (X, Y):
На основании приведенной выше информации вам необходимо найти значение Y (6), используя метод экстраполяции.
Решение
Используйте для расчетов данные, указанные ниже.
- X1: 4,00
- Y2: 6,00
- Y1: 5,00
- X2: 5,00
Расчет Y (6) с использованием формулы экстраполяции выглядит следующим образом:
Экстраполяция Y (x) = Y (1) + ( x) — (x1) / (x2) — (x1) x {Y (2) — Y (1)}
Y (6) = 5 + 6 — 4/ 5 — 4 x (6 — 5)
Ответ будет —
Следовательно, значение Y, когда значение X равно 6, будет равно 7.
, Пример # 2
Г-н M и г-н N являются учениками стандарта 5 th , и в настоящее время они анализируют данные, предоставленные им учителем математики. Учитель попросил их вычислить вес учеников, чей рост будет 5,90, и сообщил, что приведенный ниже набор данных следует линейной экстраполяции.
| X | Высота | Y | Масса |
| X1 | 5.00 | Y1 | 50 |
| X2 | 5,10 | Y2 | 52 |
| X3 | 5,20 | Y3 | 53 |
| X4 | 5,30 | Y4 | 55 |
| Х5 | 5,40 | Y5 | 56 |
| Х6 | 5,50 | Y6 | 57 |
| Х7 | 5.60 | Y7 | 58 |
| Х8 | 5,70 | Y8 | 59 |
| Х9 | 5,80 | Y9 | 62 |
Предполагая, что эти данные соответствуют линейному ряду, вам необходимо вычислить вес, который будет зависимой переменной Y в этом примере, когда независимая переменная x (высота) равна 5,90.
Решение
В этом примере нам теперь нужно узнать значение, или, другими словами, нам нужно спрогнозировать стоимость студентов, рост которых равен 5.90 на основе тенденции, приведенной в примере. Мы можем использовать приведенную ниже формулу экстраполяции в Excel для расчета веса, который является зависимой переменной для данного роста, которая является независимой переменной
Расчет Y (5.90) выглядит следующим образом:
- Экстраполяция Y (5,90) = Y (8) + (x) — (x8) / (x9) — (x8) x [Y (9) — Y (8)]
- Y (5,90) = 59 + 5,90 — 5,70 / 5,80 — 5,70 x (62 — 59)
Ответ будет —
Следовательно, значение Y, когда значение X равно 5.90 будет 65.
, пример # 3
Г-н В. — исполнительный директор компании ABC. Он был обеспокоен тем, что продажи компании имеют тенденцию к снижению. Он попросил свой исследовательский отдел создать новый продукт, который будет соответствовать растущему спросу по мере увеличения производства. Через 2 года они разрабатывают продукт, на который растет спрос.
Ниже приведены данные за последние несколько месяцев:
| X (Производство) | Произведено (шт.) | Y (Спрос) | Спрос (шт.) |
| X1 | 10.0 | Y1 | 20,00 |
| X2 | 20,00 | Y2 | 30,00 |
| X3 | 30,00 | Y3 | 40,00 |
| X4 | 40,00 | Y4 | 50,00 |
| Х5 | 50,00 | Y5 | 60,00 |
| Х6 | 60,00 | Y6 | 70,00 |
| Х7 | 70.00 | Y7 | 80,00 |
| Х8 | 80,00 | Y8 | 90,00 |
| Х9 | 90,00 | Y9 | 100,00 |
Они заметили, что, поскольку это был новый продукт и дешевый продукт и, следовательно, изначально, он будет следовать линейному спросу до определенного момента.
Следовательно, двигаясь вперед, они сначала прогнозируют спрос, а затем сравнивают его с фактическим и производят соответственно, поскольку это потребовало от них огромных затрат.
Менеджер по маркетингу хочет знать, сколько единиц будет востребовано, если они произведут 100 единиц. Основываясь на приведенной выше информации, вам необходимо рассчитать потребность в единицах, когда они произведут 100 единиц.
Решение
Мы можем использовать приведенную ниже формулу для расчета потребности в единицах, которая является зависимой переменной для данных единиц продукции, которая является независимой переменной.
Расчет Y (100) выглядит следующим образом:
- Экстраполяция Y (100) = Y (8) + (x) — (x8) / (x9) — (x8) x [Y (9) — Y (8)]
- Y (100) = 90 + 100-80 / 90-80 x (100-90)
Ответ будет —
Следовательно, значение Y, когда значение X равно 100, будет 110.
Актуальность и использование
В основном используется для прогнозирования данных, выходящих за пределы текущего диапазона данных. В этом случае предполагается, что тенденция будет продолжаться для заданных данных и даже за пределами этого диапазона, что не всегда будет иметь место, и, следовательно, экстраполяцию следует использовать очень осторожно, и вместо этого существует лучший способ сделать то же самое. это использование метода интерполяции.
Рекомендуемые статьи
Эта статья была руководством по формуле экстраполяции.Здесь мы обсуждаем формулу для расчета значения зависимой переменной для независимой переменной, а также практические примеры и загружаемый шаблон Excel. Вы можете узнать больше об экономике из следующих статей —
Курс финансового моделирования (с 15+ проектами)- 16 курсов
- 15+ проектов
- 90+ часов
- Полный пожизненный доступ
- Свидетельство о завершении
Interpolate with Excel — Excel Off The Grid
Интерполяция — это процесс оценки точек данных в существующем наборе данных.Поскольку это блог об Excel, очевидно, что мы хотим ответить на следующий вопрос: можем ли мы выполнять интерполяцию с помощью Excel. Это частый вопрос. Фактически, это был следующий вопрос от читателя, который первым заставил меня изучить эту тему:
«У меня есть вопрос Excel — есть ли способ интерполировать значение из таблицы? У меня есть X и Y, которых нет в таблице, но есть коррелированные данные, поэтому я хочу вычислить интерполированное значение ».
В качестве простого примера, если бы потребовалось 15 минут, чтобы пройти 1 милю в понедельник и 1 час, чтобы пройти 4 мили во вторник, мы могли бы разумно оценить, что это займет 30 минут, чтобы пройти 2 мили.
Не следует путать с экстраполяцией, которая оценивает значения вне набора данных. Оценка того, что пройти 8 миль займет 2 часа, будет экстраполяцией, поскольку оценка выходит за рамки известных значений.
Excel — отличный инструмент для интерполяции, так как в конечном итоге это большой визуальный калькулятор.
Загрузите файл примера
Я рекомендую вам загрузить файл примера для этого поста. Тогда вы сможете работать с примерами и увидеть решение в действии, а файл будет полезен для дальнейшего использования.
Загрузите файл: 0020 Interpolate with Excel.xlsx
Посмотрите видео
Посмотрите видео на YouTube.
Варианты интерполяции в Excel
С точки зрения ответа на вопрос, есть несколько сценариев, которые могут привести к различным решениям.
Во-первых, мы могли использовать простую математику. Это сработало бы, если бы результаты были абсолютно линейными (т.е. значения X и Y перемещались синхронно друг с другом).Но в противном случае мы могли бы получить немного искаженный результат.
В качестве альтернативы мы могли бы использовать функцию ПРОГНОЗ в Excel (или ПРОГНОЗ.ЛИНЕЙНЫЙ в Excel 2016 и последующих версиях). Судя по названию, функция ПРОГНОЗ кажется странным выбором. Казалось бы, это функция специально для экстраполяции; однако это также один из лучших вариантов линейной интерполяции в Excel. ПРОГНОЗ использует все значения в наборе данных для оценки результата; поэтому он отлично подходит для линейных отношений, даже если они не полностью коррелированы.
Тогда еще одна мысль, а что, если отношения X и Y вообще не линейны? Как мы могли интерполировать значение, когда данные экспоненциальны?
Давайте посмотрим на все эти сценарии.
Интерполяция с использованием простой математики
Простая математика хорошо работает, когда есть только две пары чисел или когда отношения между X и Y совершенно линейны.
Вот базовый пример (см. Вкладку Пример 1 во вспомогательном файле загрузки):
Формула в ячейке E4:
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Кому-то это может показаться немного сложным, поэтому вот краткий обзор формулы.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
В последнем разделе (выделенном зеленым цветом выше) вычисляется, насколько изменяется значение Y при изменении значения X на 1. В в нашем примере Y перемещается на 1,67 на каждый 1 из X.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Во втором разделе (зеленом выше) вычисляется, насколько далеко интерполированный X находится далеко от первого X, затем умножается на значение, вычисленное выше. В нашем примере результат равен 17.5 (ячейка E2) минус 10 (ячейка A2), результат умножается на 1,67. Все это равно 12,5.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Наконец, мы переходим к первой части формулы (выделенной зеленым цветом выше), которая складывает первое значение Y. В нашем примере это дает окончательный результат 77,5 (65 + 12,5). Для тех, кто помнит математику в средней школе, формула будет следующей:
Вот результат, наложенный на диаграмму.
Даже если вы не помните линейную интерполяцию в школе, хорошая новость заключается в том, что Excel предоставил нам более простой вариант — функцию ПРОГНОЗ.
Генерируйте точный код VBA за секунды с помощью AutoMacro.
AutoMacro — это мощный генератор кода VBA, который поставляется с обширной библиотекой кода и множеством других инструментов и утилит для экономии времени.
Если вы опытный программист, желающий сэкономить время, или новичок, просто пытающийся заставить вещи работать, AutoMacro — это инструмент для вас.
Интерполяция с использованием функции ПРОГНОЗ
В версии Excel 2016 года было добавлено множество новых статистических функций.Чтобы освободить место для этих новых функций, FORECAST был заменен функцией FORECAST.LINEAR. Хотя ПРОГНОЗ все еще остается на данный момент с целью обратной совместимости с Excel 2013 и более ранними версиями.
Поскольку FORECAST и FORECAST.LINEAR фактически одно и то же, мы будем использовать эти термины как синонимы.
Интерполяция при идеальной линейности
Теперь давайте воспользуемся ПРОГНОЗОМ для интерполяции результата.
Используя те же числа из приведенного выше примера, формула в ячейке E6:
= ПРОГНОЗ (E2, B2: B3, A2: A3)
Функция ПРОГНОЗ имеет следующий синтаксис:
= ПРОГНОЗ (x, известные_y, известные_x)
Три аргумента в функции:
- x — точка данных, для которой мы хотим предсказать значение
- известное_y — диапазон ячеек или массив значений содержащие известные значения Y
- известные_x — диапазон ячеек или массив значений, содержащий известные значения X
При использовании функции ПРОГНОЗ результат ячейки E6 также равен 77.5 (как и в математическом подходе).
Для полноты картины файл примера также содержит использование функции FORECAST.LINEAR. Как и следовало ожидать, результат идентичен устаревшей функции ПРОГНОЗ.
Интерполяция, когда приблизительно линейна
Но … что, если наши данные не совсем линейны? Посмотрите на диаграмму ниже, данные явно имеют линейную зависимость, но она не идеальна. Посмотрите на вкладку Пример 2 во вспомогательном файле.
В этих обстоятельствах функция ПРОГНОЗ даже более полезна, поскольку она не просто интерполирует между первым и последним значениями.Вот данные, используемые в диаграмме.
Функция ПРОГНОЗ в ячейке E4 интерполирует значение Y на основе значения X, равного 17,5.
= ПРОГНОЗ (E2, B2: B11, A2: A11)
В этом сценарии ПРОГНОЗ оценивает значение на основе всех доступных точек данных, а не только начала и конца. Результат функции ПРОГНОЗ в ячейке E4 равен 77,3 (округлено до 1 десятичного знака), что в большинстве случаев будет более точным, чем простая линейная интерполяция, применяемая в математическом подходе.
Помните, что для оценки значений используется интерполяция. 77.3 может быть неточным результатом, но это разумная оценка, основанная на имеющейся у нас информации.
И снова FORECAST.LINEAR вычисляет тот же результат.
Интерполяция, когда данные не линейны
Но вот более сложный вопрос: что, если данные вообще не линейны? Тогда что?
Посмотрите на вкладку Пример 3 во вспомогательном файле. Вот наш новый сценарий графика:
Если бы мы использовали простой линейный подход, это дало бы нам значение 77.5, который, как вы можете видеть ниже, довольно далеко от кривой. Использование функции ПРОГНОЗ даст результат 70,8, что лучше, но также далеко от кривой.
Есть два дополнительных варианта для получения более точной оценки (1) интерполяция экспоненциальных данных с помощью функции РОСТА (2) вычисление внутренней линейной интерполяции
Интерполировать экспоненциальные данные
Функция РОСТА аналогична ПРОГНОЗУ, но может применяться к данным с экспоненциальным ростом.
Результат функции РОСТ в ячейке E10 равен 70. 4. Опять же, это ближе к черте, но все же немного дальше.
Формула в ячейке E10:
= РОСТ (B2: B11, A2: A11, E2)
Функция РОСТ имеет следующий синтаксис:
= РОСТ (известные_y, [известные_x], [новые_x] , [const])
Четыре аргумента в функции РОСТА (просто имейте в виду, что аргументы не в том же порядке, что и функция ПРОГНОЗ).
- known_y’s — диапазон ячеек или массив значений, содержащих известные значения Y
- [известные_x] — диапазон ячеек или массив значений, содержащий известные значения X
- [новые_x] — точка данных, для которой мы хотим спрогнозировать значение
- [Const] — мера истина / ложь, чтобы указать, как должна вычисляться формула. В нашем сценарии мы можем оставить этот последний аргумент.
Квадратные скобки указывают, какие аргументы являются необязательными для функции для вычисления результата.Нам нужны известные_вы , известные_x, и новые_x , но мы проигнорировали аргумент const .
Хотя результат 70,4 является более близким приближением, мы не должны слепо использовать функцию РОСТ. Проверьте свои интерполяции, чтобы убедиться, что они разумны.
Внутренняя линейная интерполяция
Разумным вариантом может быть найти результат выше и ниже нового значения X, а затем применить линейную интерполяцию между этими двумя точками.Это было бы довольно близко.
В нашем примере значения по обе стороны от X, равного 17,5:
- X: 16 и 18
- Y: 66,3 и 68
Используя эти значения, теперь мы можем выполнить стандартную линейную интерполяцию .
Быстрый одноразовый метод
Если бы это было разовое действие, мы могли бы сделать это быстро, включив в формулу только основные ячейки.
= ПРОГНОЗ (E2, B6: B7, A6: A7)
Однако, как только мы изменим интерполированное значение, ПРОГНОЗ может вычислить неточный результат.Итак, давайте перейдем к рассмотрению гибкого метода.
Гибкий подход
Чтобы создать гибкий подход, мы будем использовать вместе функции ИНДЕКС, ПОИСКПОЗ и ПРОГНОЗ. Это может показаться сложным, но не волнуйтесь, мы рассмотрим это медленно. В конечном итоге мы пытаемся достичь того же результата, что и описанный выше одноразовый метод, но автоматически корректируем диапазоны в зависимости от интерполируемого значения.
ПРИМЕЧАНИЕ. Для работы этого метода требуется, чтобы диапазон известных X был указан в порядке возрастания.
Функция ПОИСКПОЗ
Во-первых, мы используем функцию ПОИСКПОЗ, чтобы получить позицию значения ниже 17,5.
= MATCH (E2, A2: A11,1)
Эта формула говорит, что найдите значение в ячейке E2 из диапазона ячеек A2-A11. 1 в конце формулы сообщает функции ПОИСКПОЗ, что мы хотим использовать приблизительное совпадение (т. Е. Ближайшее значение ниже искомого значения). 16 — ближайшее значение ниже 17,5. Поскольку 16 — это 5-й элемент в ячейках A2-A11, ПОИСКПОЗ возвращает значение 5.
Функция ИНДЕКС
Определив на предыдущем этапе, что 5-я позиция содержит значение ниже, мы можем использовать функцию ИНДЕКС, чтобы определить ссылку на ячейку для этого значения.
ИНДЕКС (A2: A11, MATCH (E2, A2: A11,1))
Это вернет ссылку на ячейку A6.
Чтобы найти указанное выше значение, мы можем использовать ту же функцию, но добавить 1 к функции ПОИСКПОЗ.
ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1 )
Приведенная выше формула вернет ссылку на ячейку A7.
Динамический диапазон
Теперь все становится интереснее. Мы можем объединить эти функции с двоеточием (:) посередине, чтобы создать диапазон для двух значений X.
ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1)
Первая функция ИНДЕКС возвращает ссылку в ячейку A6 (результат выделенного зеленым цветом раздела). Вторая функция ИНДЕКС возвращает ссылку на ячейку A7 (результат выделенного фиолетовым цветом раздела).Они разделены двоеточием (:) (выделено красным), чтобы создать диапазон — A6: A7
Мы можем сделать то же самое, чтобы создать диапазон для двух значений Y. Единственная разница в том, что функции ИНДЕКС будут смотреть на ячейки B2-B11.
ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1) +1)
Используя ячейки B2-B11 в ИНДЕКСЕ функция, она вычислит диапазон B6: B7.
ИНДЕКС СООТВЕТСТВИЕ И ПРОГНОЗ
Теперь у нас есть два диапазона; значения X A6: A7 и значения Y B6: B7.Давайте объединим все это в функции ПРОГНОЗ.
= ПРОГНОЗ (E2, ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1) +1), ИНДЕКС (A2: A11, MATCH (E2, A2: A11,1)): INDEX (A2: A11, MATCH (E2, A2: A11,1) +1))
Это довольно большая формула, верно. Но, надеюсь, мне удалось объяснить это так, что это не слишком страшно.
Результат внутренней линейной интерполяции с использованием функции ПРОГНОЗ составляет 67,6 (с точностью до 1 десятичного знака, как показано в ячейке E14). Взгляните на график еще раз; вы увидите, что 67.6 — разумная оценка, основанная на имеющихся данных.
ПРЕДУПРЕЖДЕНИЕ. В конечном счете, это все еще вычисление линейной интерполяции, основанное на двух значениях по обе стороны от значения X. Расстояние между значениями выше и ниже будет иметь прямое влияние на точность интерполяции.
Заключение
Первоначально то, что казалось простым вопросом, привело нас к множеству потенциальных решений для трех различных сценариев. Ключевым моментом является то, что вам необходимо знать свои данные, чтобы выбрать метод, обеспечивающий наиболее точные результаты.
В процессе мы рассмотрели функции FORECAST и FORECAST.LINEAR и увидели, что они полезны как для интерполяции, так и для экстраполяции.
Кроме того, в этом посте мы использовали ИНДЕКС и ПОИСКПОЗ для создания динамических диапазонов, что является очень мощным методом для сложных формул в Excel.
Если вам нужна дополнительная информация о методах прогнозирования в Excel, загляните в Engineer Excel (https://engineerexcel.com/blog). Хотя вы, возможно, не работаете в инженерном контексте, методы применимы во многих других обстоятельствах.
Не забывайте:
Если вы нашли этот пост полезным или у вас есть лучший подход, оставьте комментарий ниже.
Вам нужна помощь в адаптации этого к вашим потребностям?
Я полагаю, что примеры в этом посте не совсем соответствуют вашей ситуации. Все мы используем Excel по-разному, поэтому невозможно написать сообщение, которое удовлетворит потребности всех. Потратив время на то, чтобы понять методы и принципы, описанные в этом посте (и в других местах на этом сайте), вы сможете адаптировать их к своим потребностям.
Но, если вы все еще боретесь, вам следует:
- Читать другие блоги или смотреть видео на YouTube на ту же тему. Вы получите гораздо больше пользы, открыв свои собственные решения.
- Спросите «Excel Ninja» в своем офисе. Удивительно то, что знают другие люди.
- Задайте вопрос на форуме, например в Mr Excel, или в сообществе ответов Microsoft. Помните, что люди на этих форумах обычно проводят свое время бесплатно. Так что постарайтесь сформулировать свой вопрос, сделайте его ясным и кратким.Составьте список всего, что вы пробовали, и предоставьте снимки экрана, фрагменты кода и примеры рабочих книг.
- Воспользуйтесь Excel Rescue, моим партнером-консультантом. Они помогают, предлагая решения небольших проблем с Excel.
Что дальше?
Не уходите, об Excel Off The Grid можно узнать еще много. Ознакомьтесь с последними сообщениями:
Как экстраполировать в Excel
В процессе вычисления значений за пределами известной области числовых данных на помощь приходит Microsoft Excel.Для автоматизации процесса расчета достаточно взять за основу имеющиеся данные и выполнить несколько простых шагов. Вот пошаговая инструкция с объяснениями того, как экстраполировать данные в Excel ниже.
Табличный Da t a Экстраполяция
Например, мы используем данные из следующей таблицы, которая отображает зависимость значений функции от аргумента x.
В данном случае это количество произведенных единиц продукции за определенное время в минутах.
Как мы видим, для нашего примера количество единиц продукции, производимых каждые 15 минут времени от 0 до 120 минут (2 часа) включительно, известно.
Чтобы экстраполировать эти данные в Excel, необходимо последовательно выполнить следующие шаги.
- Определяем число x, относительно которого необходимо сделать прогноз.
В нашем случае это период времени, за который необходимо определить количество произведенной продукции.
Например, нас интересует период 5 часов 15 минут или 315 минут. Добавляем следующее значение интересующего нас аргумента: 315 в столбец «x».
- Выберите ячейку, в которой мы хотим получить желаемый результат, и щелкните значок мастера функций.
- Введите «прогноз» в поле поиска мастера функций и щелкните найденную функцию. Нажмите «Enter» или нажмите кнопку «Вставить функцию».
В открывшемся окне значений функции введите следующие данные:
- В поле «x»: адрес интересующей нас ячейки со значением «x» (в нашем случае это 315) — для этого кликаем по соответствующей ячейке;
- В поле «known_y’s» мы вводим диапазон значений в столбце f (x) (в нашем случае от 100 до 800 штук) — также выбирая этот диапазон мышью;
- В поле «known_x’s» мы вводим соответствующий диапазон значений столбца «x» (в нашем случае от 15 до 120 минут), как в предыдущем подпункте.
- Нажмите «Enter» на клавиатуре или нажмите кнопку «Готово».
- И желаемый результат появится в соответствующей ячейке — в нашем примере это число 2100, т.е. 2100 единиц продукции будет произведено за 3 часа 15 минут с использованием метода экстраполяции.
- Таким же образом мы можем вычислить значение f (x) для любого желаемого значения x. Для этого вы должны добавить известные значения времени (в нашем случае) в столбец значений «x» и скопировать формулу, которую мы ввели в соответствующую ячейку на шаге 2, в следующие ячейки рядом со значениями x.
Итак, мы разобрались, как экстраполировать данные в Excel. Как оказалось, это несложная задача даже для рядового пользователя. Для расчетов достаточно знать нужную функцию и иметь соответствующие числовые данные. Следуя шагам, описанным выше, все шаги по вычислению экстраполяции в Excel будут простыми и понятными.
Линейная интерполяция в Excel — Dagra Data Digitizer
Как работает реализация Excel
Простую реализацию легче всего понять, проанализировав извне и работая внутри.Вот полное уравнение:
= ПРОГНОЗ ( NewX , OFFSET ( KnownY , MATCH ( NewX , KnownX , 1) -1,0,2), OFFSET ( KnownX , MATCH ( NewX) , ИзвестноX , 1) -1,0,2))
Вкратце уравнение состоит из 3 частей:
- функция ПРОГНОЗ для вычисления линейной интерполяции,
- два вызова функции ПОИСКПОЗ, чтобы найти ближайшее табличное значение x, но меньше нового значения x, и
- два вызова функции OFFSET для ссылки на табулированные значения x и значения y чуть выше и чуть ниже нового значения x.
Более подробно, функция ПРОГНОЗ выполняет фактическую интерполяцию, используя уравнение линейной интерполяции, показанное выше. Его синтаксис: ПРОГНОЗ ( NewX , known_y_pair , known_x_pair ).
Первый параметр, NewX — это просто значение для интерполяции. Следующие два параметра, известная_y_ пара и известная_x_ пара , являются значениями по обе стороны от NewX . То есть {x1, x2} и {y1, y2} на диаграмме выше.
Функция ПОИСКПОЗ используется для нахождения табличного значения x чуть ниже NewX . Его синтаксис: MATCH ( lookup_value , lookup_table , match_type ). ПОИСКПОЗ возвращает относительное положение элемента в отсортированном массиве. Итак, lookup_value — это значение для интерполяции, lookup_table — это массив значений KnownX , а match_type — 1, чтобы найти наибольшее значение в массиве, которое меньше или равно NewX .
Функция ПОИСКПОЗ возвращает индекс, но для функции ПРОГНОЗ требуется два диапазона ячеек: один для пары известная_x_ и одна для пары известная_y_ . Таким образом, функция СМЕЩЕНИЕ используется дважды для создания этих диапазонов. Его синтаксис — OFFSET ( ссылка , row_offset , column_offset , row_count , column_count ). Он берет начальную точку, ссылку , и создает ссылку на ячейку с заданным смещением и размером.Чтобы получить диапазон known_y_pair , ссылка устанавливается в таблицу KnownY значений; для диапазона known_x_pair ссылка устанавливается равной массиву KnownX значений. Если табличные значения расположены вертикально, row_offset является результатом функции MATCH минус 1, а row_count равно 2; column_offset равно 0, а column_count равно 1. Это дает нам ссылку на массив ячеек на 2 ячейки в высоту и 1 ячейку в ширину.Если табличные значения расположены горизонтально, строка и столбец переключаются в функции СМЕЩЕНИЕ.
.