Советы и лайфхаки

Замкнутые линии что это такое – Замкнутые и незамкнутые линии. Видеоурок. Математика 1 Класс

Содержание

Замкнутые и незамкнутые линии. Видеоурок. Математика 1 Класс

На этом уроке мы познакомимся с понятиями «замкнутая линия» и «незамкнутая линия», научимся их различать и строить. Также рассмотрим такие понятия, как «звенья» и «вершины» кривой линии. В дальнейшем эти знания будем использовать для решения более сложных задач.

Тема: Знакомство с основными понятиями

Урок: Замкнутые и незамкнутые линии

Задание 1

На данном рисунке видим, что овечке легче будет выбраться из первой ограды, потому что она открыта – незамкнутая. Из-за второй ограды будет выйти сложнее, так как она закрыта. Начертим линии, которые будут соответствовать первой и второй ограде.

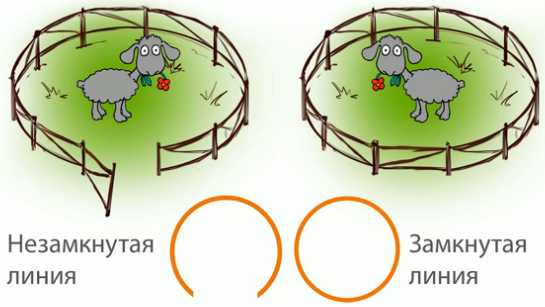
Итак, мы получили две линии, из которых первая замкнутая, а вторая незамкнутая.

Задание 2: 

Определить, какие линии на рис. 3 замкнутые, а какие незамкнутые.

На  рисунке видим, что линии № 1, 3, 6 – это незамкнутые линии. Для того чтобы сомкнуть эти линии, достаточно соединить концы линий вместе. Получим:

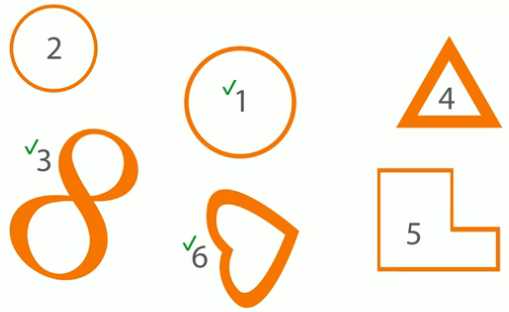
Итак, линия, концы которой не соединены вместе, называется незамкнутой линией. Линия, концы которой соединены вместе, называется замкнутой линией.

Каждая ломаная линия состоит из нескольких отрезков – звеньев. Звенья ломаной не лежат на одной прямой. Конец одного звена является началом другого. Место, где соединяются два звена, а также концы разомкнутой ломаной, называется вершиной.

Итак, на данном уроке мы познакомились с понятиями «замкнутая линия» и «незамкнутая линия». Мы научились их строить, а также применять знания на практике для построения таких линий.

 

Список литературы

  1. Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
  2. Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
  3. Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Фестиваль педагогических идей (Источник).

2. Социальная сеть работников образования (Источник).

3. Фестиваль педагогических идей (Источник).

 

Домашнее задание

1. Определить, какие линии изображены на рисунке.

2. Определить количество звеньев каждой линии.

3. Определить количество вершин каждой линии.

4. Построить незамкнутую линию, у которой 4 вершины.

5. Построить замкнутую линию, у которой 6 звеньев.

 

interneturok.ru

Замкнутая ломаная линия — как она выглядит, и что такое вершины ломаной

Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.

Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:

  1. Картография — для построения изображений улиц и схем маршрутов.
  2. Архитектура — очертания зданий и строений.
  3. Ландшафтный дизайн — декоративное оформление и расположение тропинок.
  4. Химия — молекулярная структура сложных полимерных соединений.
  5. Медицина — мониторы для контроля функционального состояния органов и систем.

Типы ломаных линий

Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.

Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.

Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.

Всего существует 4 типа подобных линий по своей структуре:

  1. Замкнутые, которые не имеют пересечений.
  2. Незамкнутые, которые не имеют пересечений.
  3. Незамкнутые самопересекающиеся.
  4. Замкнутые, имеющие самопересечения.

Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.

Особенности замкнутых линий

Рассмотрим подробнее составляющие части этой геометрической фигуры.

  1. Один отрезок из тех, что составляют описываемую фигуру, называется ее звеном. Ломаной может считаться такая линия, которую составляют как минимум два отрезка — звена. Если звено одно — это просто единичный отрезок.
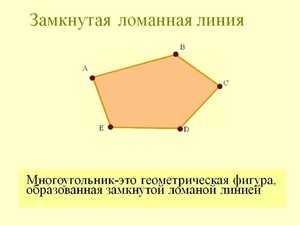
  2. Существует также понятие вершины ломаной. Этим термином принято называть точку, в которой соединяются концы двух звеньев. Такие точки в геометрии принято обозначать с помощью заглавных латинских букв. Сама ломаная называется сочетанием обозначений этих вершин. Например, названием такой линии может послужить сочетание ABCDEF.
  3. Если концы крайних звеньев этого геометрического объекта соединяются в одной точке, такая линия называется замкнутой.
  4. Ломаная линия может пересекать саму себя.
  5. Конечные вершины такой фигуры в геометрии принято называть черными точками.

Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.

Многоугольник как разновидность замкнутой ломаной

Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.

  1. Если вершины принадлежат одной и той же стороне многоугольника — они носят название смежных.
  2. Если отрезок соединяет две любых вершины, не являющиеся смежными, он называется диагональю.
  3. Если у многоугольника имеется n вершин — он называется n-угольником. У такой фигуры имеется количество сторон, равное n.
  4. Такая ломаная делит плоскость на 2 части — внешнюю и внутреннюю.
  5. Если точки многоугольника лежат по одну сторону от прямой и проходят через 2 соседние вершины — его принято называть выпуклым.
  6. Угол выпуклого многоугольника при данной вершине — это угол, который образован двумя его сторонами, для которых эта вершина является общей.
  7. Внешний угол выпуклого многоугольника при определенной вершине — это угол, смежный с внутренним углом многоугольника при этой же самой вершине.

Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.

Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.

Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.

У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.

Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.

Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.

liveposts.ru

звенья, вершины, длина. Замкнутая ломаная

Ломаная линия – это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков – вершинами ломаной.

Построим ломаную из четырёх отрезков:

Отрезки AB, BC, CD и DE – это звенья ломаной. Точки A, B, C, D и E – вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная

ABCDE или ломаная EDCBA.

Замкнутая ломаная

Если концы ломаной совпадают, то такая ломаная называется замкнутой:

ломаная ABCDE.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник ABCED.

Длина ломаной

Длина ломаной – это сумма длин всех её звеньев.

Найдём длину ломаной, сложив длины всех её звеньев:

ABCD = AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

naobumium.info

6. Линии замкнутые, разомкнутые и соединенные

 

В заключение обсуждения моделей линий, используемых в CorelDRAW, следует сказать о еще одной их классификации, оказывающей большое влияние на работу с этими объектами. Эта классификация построена на учете количества и состояния крайних узлов линии.

Крайним узлом называется узел линии, смежный только с одним се сегментом. Выше уже отмечалось, что узел линии, не имеющий предшествующего сегмента, называется начальным.

Линия, имеющая начальный узел, называется незамкнутой (open curve). Линия, в которой крайние узлы отсутствуют, называется замкнутой (closed curve).

Примечание

в замкнутой линии роль начального и конечного узла выполняет один и тот же узел, поэтому у него есть и предшествующий, и последующий сегменты. Таким образом, в замкнутой линии начальный узел отсутствует, хотя на экране при выборе узлов инструментом Shape (Форма) тот узел, в котором произошло замыкание линии при построении, обозначен увеличенным квадратом, так же как начальный узел.

Следует сказать несколько слов о соединенных линиях. Это объекты, состоящие из нескольких ветвей (subpath), каждая из которых представляет собой замкнутую или незамкнутую линию. Соединенные объекты возникают, в частности, при выполнении операции соединения объектов командой Combine (Соединить) и при преобразовании в кривые других объектов (например, текстов). Главным отличительным признаком соединенного объекта является наличие нескольких узлов, отмеченных увеличенными квадратиками, в одном объекте. Кроме того, сведения о наличии в выделенном объекте нескольких ветвей выводятся в строке состояния после количества узлов при выделении линии инструментом Shape (Форма). Соединенные линии можно разъединить, преобразовав их в совокупность линий, каждая из которых состоит всего из одной ветви — замкнутой или разомкнутой.

На рис. 3.6 представлены примеры замкнутых, разомкнутых и соединенных линий.


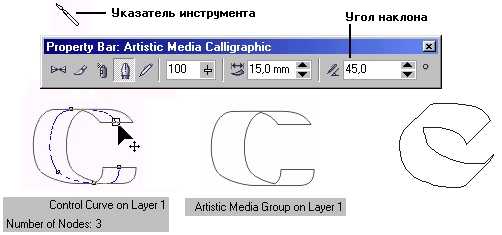
Рис. 3.6. Примеры замкнутых (слева), разомкнутых (в середине) и соединенных (справа) линий

Примечание

Практически любой графический объект CorelDRAW может быть преобразован в кривые. И наоборот, многие сложные объекты, о которых пойдет речь в следующих уроках, строятся на базе одной или нескольких линий. Поэтому понимание модели линии и приемов работы с линиями играют очень важную роль в построении изображения.

Теперь, когда мы знаем о линиях уже достаточно много, можно перейти к приемам их построения. Один из них нам уже известен, поскольку в результате применения инструмента Spiral (Спираль) получается именно кривая, состоящая из сегментов, соответствующих четверти оборота спирали, и разделяющих их сглаженных узлов. В последующих разделах настоящего урока мы познакомимся с инструментами для построения линии, а приемы модификации и редактирования линий будут рассмотрены в уроке 5.

Инструменты, позволяющие строить линии различных типов, сведены в CorelDRAW в одну раскрывающуюся панель инструмента Curve (Кривая), представленную на рис. 3.7. В соответствии с общим стилем пользовательского интерфейса CorelDRAW на кнопке инструмента Curve (Кривая) отображается значок последнего из использованных инструментов, кнопки которых присутствуют на его панели, и щелчок на этой кнопке снова активизирует тот же инструмент. Так же как при выборе инструмента для построения графического примитива, для получения доступа к кнопкам других инструментов достаточно при щелчке мышью на кнопке инструмента Curve (Кривая) задержать кнопку мыши в нажатом состоянии.


Рис. 3.7. Кнопки панели инструмента Curve (Кривая)

 

lib.qrz.ru

Вопрос 35 Чем отличаются замкнутые и разомкнутые сети?

Замкнутые сети обеспечивают наибольшую надежность, по­скольку авария (отключение) на каком-либо участке сети имеет последствия (на­пример, ограничение потребляемой мощности) только для потребителей, непо­средственно подключенных к этому участку. В схемах замкнутых сетей узлы нагрузки могут получать питание с двух и более сторон [20]. Применяют замкнутые сети кольцевой конфигурации, выпол­ненные одинарными (рис.11.2, о) или двойными (рис. 11.2, б), подключенными к одному центру питания, что является некоторым их недостатком. Он устраняется в замкнутой одинарной (рис. 11.2, в) или двойной (рис. 11.2, г) сети, которая по­лучает питание от двух ЦП. Еще большую надежность имеет узловая сеть (рис. 11-2, д), в которой подстанции могут получать питание от трех ЦП. К более слож­ным относятся многоконтурные сети, отдельные участки которых могут выполняться одиночными либо двойными линиями (рис. 11.2, е) или полностью двой­ными линиями (рис. 11.2,
ж).Рис. 11.1. Варианты конфигураций радиальных сетей: а, 6, в — одинарная с одним узлом нагрузки, с несколькими узлами, разветвленная; г, д — с промежуточным распределительным пунктом; е, ж, з — двойная с одним узлом нагрузки, с несколькими узлами, разветвленная В заключение заметим, что при построении схем сетей следует стремиться по возможности применять простые типы конфигураций, но обеспечивающие требуемую степень надежности, например, такие, как двойные радиальные (рис. • 11.1, ж, з), одинарная и двойная с питанием от двух ЦП (рис. 11.2, в, г).

Принцшшально возможны две основные схемы выдачи мощно­сти удаленных электростанций: блочная (рис. 11.3, о) и связанная (рис. 11.3, б).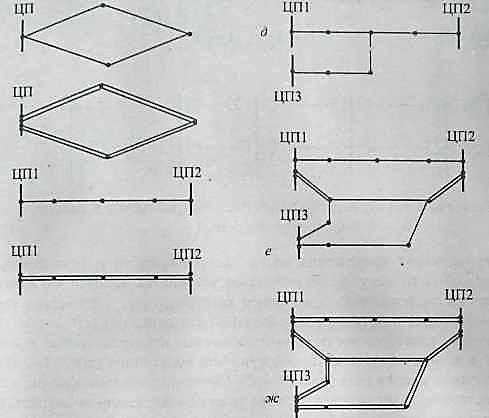

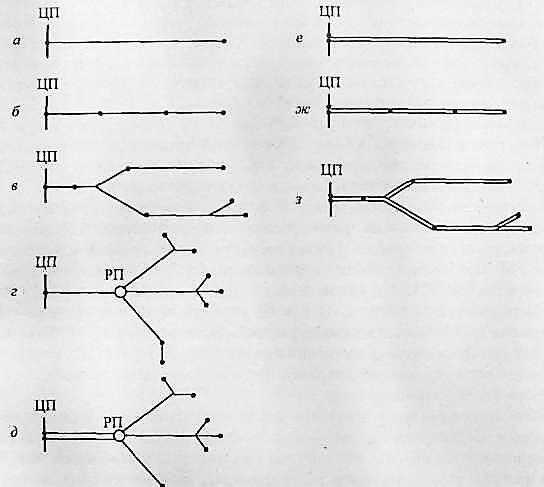
Рис. 11.2. Варианты конфигураций замкнутых сетей:

а — одинарная с питанием от одного ЦП;б — двойная с питанием от одного ЦП;в — одинарная с питанием от двух ЦП;г — двойная с питанием от двух ЦП; д — узловая;

е, ж — многоконтурные

В блочной схеме генератор (группа генераторов) электростанции работают на отдельную цепь линии, соединенную непосредственно с приемной системой С. Она дешевле связанной схемы, но обладает существенным недостатком, который проявляется в том, что при отключении одной из цепей линии мощность части соответствующих генераторов не может быть передана в систему. Этого недос­татка лишена связанная схема, в которой по пути от электростанции к системе выполнены промежуточные подстанции. Между каждой парой из них цепи линии электропередачи соединены параллельно. В результате при отключении одной из Цепей любого участка электропередачи сохраняется связь всех генераторов с сис­темой, хотя в некоторых случаях при этом предельная пропускная способность электропередачи в целом может несколько уменьшится.

Рис. 11.3. Схемы выдачи мощности удаленных электростанций в систему а — блочная; б — связанная.

Для регулирования напряжения вдоль электропередачи и повышения ее пропускной способности могут устанавливаться устройства поперечной компен­сации (шунтирующие реакторы, синхронные компенсаторы, статические тиристорные компенсаторы) и устройства продольной компенсации. Сложно-замкнутые сети дороже радиально-магистральных; их использование выгодно только при большой стоимости перерывов электроснабжения, например, в системах электроснабжения больших городов.

Рис.1.15. Сложно-замкнутая конфигурация сети

Рис. 1.16. Сложно-замкнутая конфигурация сети двух номинальных напряжений

Рис. 1.11. Разомкнутая нерезервированная конфигурация ( а — радиальная; б — магистральная

studfiles.net

Ломаная линия / Виды линий / Справочник по математике для начальной школы

  1. Главная
  2. Справочники
  3. Справочник по математике для начальной школы
  4. Виды линий
  5. Ломаная линия

Ломаная линия состоит из отрезков — звеньев.

Конец одного отрезка — на­чало другого. Ни­какие два соседние звена не лежат на одной прямой.

 Концы каждого звена — это вершины. Их можно обозначать буквами.

Ломаная линия бывает незамкнутая.

Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.

Такая замкнутая ломаная линия называется треугольником.

У нее три вершины.

У треугольника три звена.

Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.

Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.

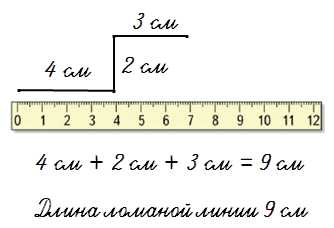
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.

Например,

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точка. Кривая. Прямая линия

Отрезок. Луч

Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине

Виды линий

Правило встречается в следующих упражнениях:

1 класс

Страница 43, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 71, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 101, Моро, Волкова, Степанова, Учебник, 1 часть

Страница 16, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 12. Вариант 1. № 3, Волкова, Проверочные работы

Страница 5, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 25, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 41, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 60, Моро, Волкова, Степанова, Учебник, 2 часть

Страница 32, Моро, Волкова, Рабочая тетрадь, 2 часть

2 класс

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Задание 31, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 20. Вариант 1. № 3, Моро, Волкова, Проверочные работы

Страница 24. Тест 1. Вариант 1, Моро, Волкова, Проверочные работы

Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 110, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 51, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 78, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 6, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 41, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 108, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 5, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 14, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 61, Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 6. Вариант 1. № 2, Моро, Волкова, Проверочные работы

© 2018 — budu5.com, Буду отличником!

budu5.com

Точка, линия, прямая, луч, отрезок, ломанная

Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

точка A, точка B, точка C
ABC
точка 1, точка 2, точка 3
123

Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие?

AAA

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

линия a, линия b, линия c
abc

Линия может быть

  1. замкнутой, если её начало и конец находятся в одной точке,
  2. разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.


Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.


Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
  1. самопересекающейся
  2. без самопересечений
самопересекающиеся линии
линии без самопересечений
  1. прямой
  2. ломанной
  3. кривой
прямые линии
ломанные линии
кривые линии

Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

прямая линия a
a
прямая линия AB
BA

Прямые могут быть

  1. пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
    • перпендикулярными, если пересекаются под прямым углом (90°).
  2. параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии

Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

солнышко

Точка разделяет прямую на две части — два луча A A

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

луч a
a
луч AB
BA

Лучи совпадают, если

  1. расположены на одной и той же прямой,
  2. начинаются в одной точке,
  3. направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBA

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

Через две точки — неограниченное количество кривых, но только одну прямую

кривые линии, проходящие через две точки
BA
прямая линия AB
BA

От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ BA✂

Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок

отрезок AB
BA

Задача: где прямая, луч, отрезок, кривая?

Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752

Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.

Многоугольник — это замкнутая ломанная линия

Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.

Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
ABCDEF120605812298141

Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599

Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.

треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники

shpargalkablog.ru

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *