Восьмеричная система счисления
Рейтинг: / 3- Подробности
- Просмотров: 2979
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 82 + 7 * 81 + 2 * 80 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 82 + 0 * 81 + 0 * 80 = 6410
- < Назад
- Вперёд >
palkins.ru
Восьмеричная система счисления — Мегаобучалка
Основание восьмеричной системы счисления равно 8 (p=8) определяет число цифр входящих в данную систему счисления: {0,1,2,3,4,5,6,7} восемь цифр. Восьмеричная система счисления, так же как и десятичная является позиционной. Формула разложения по степени основания числа записанного в восьмеричной системе счисления имеет следующий вид:
где:
— значение числа в восьмеричной системе счисления;
q – количество разрядов числа записанного в восьмеричной системе счисления.
I – номер разряда;
— значение i-го разряда числа записанного в восьмеричной системе счисления.
Так для четырехразрядного числа, записанного в двоичной системе счисления формула разложения по степени основания будет иметь следующий вид:
Восьмеричная система счисления.
Основание шестнадцатеричной системы счисления равно 16 (p=16) определяет число цифр входящих в данную систему счисления: {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F} шестнадцать цифр. Поскольку в алфавит шестнадцатеричной системы счисления входит больше дести цифр, определенных для десятичной системы счисления, остальные цифры обозначаются буквами латинского алфавита. Шестнадцатеричная система счисления, так же как и десятичная является позиционной. Формула разложения по степени основания числа записанного в шестнадцатеричной системе счисления имеет следующий вид:
где:
— значение числа в шестнадцатеричной системе счисления;
q – количество разрядов числа записанного в шестнадцатеричной системе счисления.
I – номер разряда;
— значение i-го разряда числа записанного в шестнадцатеричной системе счисления.
Так для четырехразрядного числа, записанного в шестнадцатеричной системе счисления формула разложения по степени основания будет иметь следующий вид:
Взаимосвязь систем счисления используемых в вычислительной технике.
Двоичная система счисления, используемая элементами вычислительной техники имеет один недостаток – это громоздкость записи. Для того, чтобы записать число 255
Таблица 2.
megaobuchalka.ru
Десятичная система счисления
Пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, однако информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т. д. Самая правая цифра числа показывает число единиц, вторая справа – число десятков, следующая – число сотен и т. д.
Двоичная система счисления
В этой системе всего две цифры – 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Самая правая цифра числа показывает число единиц, следующая цифра – число двоек, следующая – число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число – представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.
Восьмеричная система счисления
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает, как и в десятичном числе, просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем – 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем – 16 (десятичное), в следующем – 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
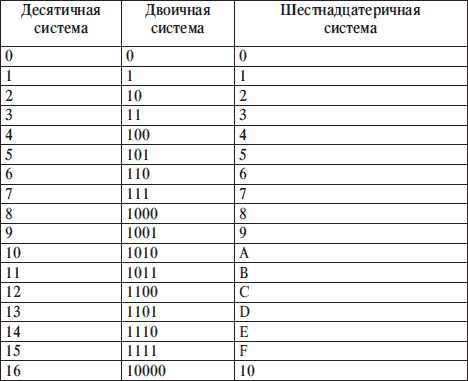
Таблица 1. Соответствие между первыми несколькими натуральными числами всех трех систем счисления
1.4. Кодирование информации
В настоящее время во всех вычислительных машинах информация представляется с помощью электрических сигналов. При этом возможны две формы ее представления – в виде непрерывного сигнала (с помощью сходной величины – аналога) и в виде нескольких сигналов (с помощью набора напряжений, каждое из которых соответствует одной из цифр представляемой величины).
Первая форма представления информации называется аналоговой, или непрерывной. Величины, представленные в такой форме, могут принимать принципиально любые значения в определенном диапазоне. Количество значений, которые может принимать такая величина, бесконечно велико. Отсюда названия – непрерывная величина и непрерывная информация. Слово непрерывность отчетливо выделяет основное свойство таких величин – отсутствие разрывов, промежутков между значениями, которые может принимать данная аналоговая величина. При использовании аналоговой формы для создания вычислительной машины потребуется меньшее число устройств (каждая величина представляется одним, а не несколькими сигналами), но эти устройства будут сложнее (они должны различать значительно большее число состояний сигнала). Непрерывная форма представления используется в аналоговых вычислительных машинах (АВМ). Эти машины предназначены в основном для решения задач, описываемых системами дифференциальных уравнений: исследования поведения подвижных объектов, моделирования процессов и систем, решения задач параметрической оптимизации и оптимального управления. Устройства для обработки непрерывных сигналов обладают более высоким быстродействием, они могут интегрировать сигнал, выполнять любое его функциональное преобразование и т. п. Однако из-за сложности технической реализации устройств выполнения логических операций с непрерывными сигналами, длительного хранения таких сигналов, их точного измерения АВМ не могут эффективно решать задачи, связанные с хранением и обработкой больших объемов информации.
Вторая форма представления информации называется дискретной (цифровой). Такие величины, принимающие не все возможные, а лишь вполне определенные значения, называются дискретными (прерывистыми). В отличие от непрерывной величины, количество значений дискретной величины всегда будет конечным. Дискретная форма представления используется в цифровых электронно-вычислительных машинах (ЭВМ), которые легко решают задачи, связанные с хранением, обработкой и передачей больших объемов информации.
Для автоматизации работы ЭВМ с информацией, относящейся к различным типам, очень важно унифицировать их форму представления – для этого обычно используется прием кодирования.
Кодирование – это представление сигнала в определенной форме, удобной или пригодной для последующего использования сигнала. Говоря строже, это правило, описывающее отображение одного набора знаков в другой набор знаков. Тогда отображаемый набор знаков называется исходным алфавитом, а набор знаков, который используется для отображения, – кодовым алфавитом, или алфавитом для кодирования. При этом кодированию подлежат как отдельные символы исходного алфавита, так и их комбинации. Аналогично для построения кода используются как отдельные символы кодового алфавита, так и их комбинации.
Совокупность символов кодового алфавита, применяемых для кодирования одного символа (или одной комбинации символов) исходного алфавита, называется кодовой комбинацией, или, короче, кодом символа. При этом кодовая комбинация может содержать один символ кодового алфавита.
Символ (или комбинация символов) исходного алфавита, которому соответствует кодовая комбинация, называется исходным символом.
Совокупность кодовых комбинаций называется кодом.
Взаимосвязь символов (или комбинаций символов, если кодируются не отдельные символы исходного алфавита) исходного алфавита с их кодовыми комбинациями составляет таблицу соответствия (или таблицу кодов).
В качестве примера можно привести систему записи математических выражений, азбуку Морзе, морскую флажковую азбуку, систему Брайля для слепых и др.
В вычислительной технике также существует своя система кодирования – она называется двоичным кодированием и основана на представлении данных последовательностью всего двух знаков: 0 и 1 (используется двоичная система счисления). Эти знаки называются двоичными цифрами, или битами (binary digital).
Если увеличивать на единицу количество разрядов в системе двоичного кодирования, то увеличивается в два раза количество значений, которое может быть выражено в данной системе. Для расчета количества значений используется следующая формула:
N=2m,
где N – количество независимо кодируемых значений,
а m – разрядность двоичного кодирования, принятая в данной системе.
Например, какое количество значений (N) можно закодировать 10-ю разрядами (m)?
Для этого возводим 2 в 10 степень (m) и получаем N=1024, т. е. в двоичной системе кодирования 10-ю разрядами можно закодировать 1024 независимо кодируемых значения.
studfiles.net
Двоичная, восьмеричная и шестнадцатеричная системы счисления
Замечание 1
Данные системы счисления относятся к позиционным.
Двоичная система счисления
Эта система счисления свое название получила в результате того, что содержит в своем основании всего две цифры – $0$ и $1$. Таким образом, число $2$ и его степени $2, 4, 8$ и т.д. играют особую роль. Самая правая цифра числа показывает число единиц, следующая – число двоек, следующая — число четверок и т.д.
В двоичной системе счисления для формирования числа используются всего две цифры: $0$ и $1$. Пределом разряда является $1$, и как только при счете разряд достигает своего максимального значения, он обнуляется, а при этом образуется новый разряд. Ниже в таблице приведены соответствия двоичных и десятичных чисел.
Рисунок 1.
Замечание 2
Используя двоичную систему счисления, можно закодировать любое натуральное число, представляя его как последовательность нулей и единиц. В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, изображения, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что оно легко реализуется технически.
Именно на принципе двоичного кодирования работает вся вычислительная техника: $1$ означает, что электрический сигнал прошел, а $0$ – сигнал отсутствует. Наглядно это можно рассмотреть на примере перфокарт, которые использовались в вычислительных машинах первых поколений. Как уже упоминалось выше: в перфокартах пробивались отверстия в соответствующих рядах и столбцах цифр, таким образом, кодировались и сохранялись программы, поскольку жестких дисков, и тем более оптических, в те времена не было. Затем программы считывались при помощи электрического сигнала, который, если проходил в отверстие, значит, это был код $1$ и, наоборот, если не проходил сигнал – это был код $0$. Аналогичным способом в настоящее время записываются оптические диски при помощи лазерного луча, прожигающего невидимые микроотверстия на поверхности специальных дисков. Принцип считывания закодированной информации с диска аналогичен предыдущему.
Из всего вышесказанного можно сделать вывод, что компьютер «понимает» всего два числа: $0$ и $1$. И именно один двоичный разряд и является минимальной единицей измерения памяти компьютера, которая называется «бит», т.е. бит – это ячейка памяти компьютера, в которую можно записать $1$ или $0$.
Другой единицей измерения информации является байт.
Байт – это восемь подряд расположенных битов. Общее количество комбинаций двоичных значений в байте равно $28 = 256$.
$1 \ байт = 8 \ битам$; $1 \ Кб = 210 \ байта = 1024 \ байта$; $1 \ Мб = 210 \ Кбайт = 1024 \ Кбайта$; $1 \ Гб = 210 \ байта = 1024 \ килобайта$; $1 \ Тб = 210 \ гигабайта = 1024 \ гигабайта$.
Замечание 3
Достоинства двоичной системы счисления заключаются в ее простоте, благодаря которой она широко используется в технике. Устройства, работающие в двух состояниях (включено, выключено), наиболее помехоустойчивы, и, как следствие, более надежны.
Восьмеричная система счисления
В основе данной системы счисления находятся $8$ цифр: от $0$ до $7$. Цифра $1$, указанная в самом младшем разряде, означает, как и в десятичном числе просто $1$. Та же цифра $1$ в следующем разряде означает $8$, в следующем $64$ и т.д. Число $100$ (восьмеричное) – это число $64$ (десятичное). Чтобы перевести в двоичную систему, например, число $611$ (восьмеричное), необходимо каждую цифру числа заменить эквивалентной тройкой двоичных чисел. Для перевода многозначного двоичного числа в восьмеричную систему счисления необходимо разбить его на тройки по правую сторону и по левую и заменить каждую тройку соответствующей восьмеричной цифрой.
В таблице приведены соответствия чисел в восьмеричной и десятичной системах.
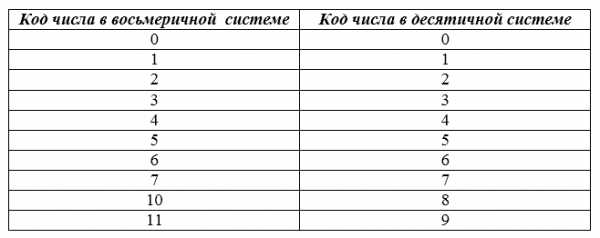
Рисунок 2.
В технике данная система находит широкое применение, так с помощью нее можно компактно записывать двоичные числа.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактная, но еще компактнее она выглядит в шестнадцатеричной системе. В основу данной системы входят цифры от $0$ до $9$ и первые буквы латинского алфавита: $A$, $B$, $C$, $D$, $E$, $F$.
Цифра $1$, записанная в самом младшем разряде, означает просо единицу. Цифра $1$ в следующем разряде – $16$ (десятичное число), в следующем – $256$ и т.д. Цифра, обозначенная латинской буквой $F$, расположенная в самом младшем разряде означает $15$ ( десятичное число).
В таблице приведены соответствия чисел в шестнадцатеричной и десятичной системах.
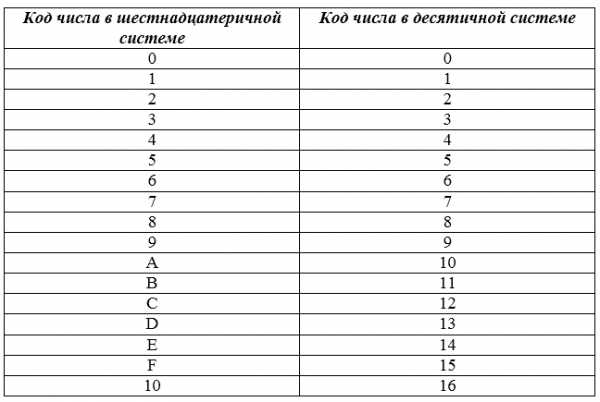
Рисунок 3.
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является $8$-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы $IBM/360$, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с $8$-битными символами, как, например, $PDP-11$ или $БЭСМ-6$) использовали восьмеричную систему.
spravochnick.ru
Системы счисления: двоичная, восьмеричная, шестнадцатеричная, десятиричная
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Существуют системы позиционные и непозиционные. В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число — два, три, четыре, шестнадцать и т. д. Следовательно, возможно бесконечное множество позиционных систем.
Десятичная система счисления
Эта система пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени; 10, 100, 1000 и т. д. Крайняя правая цифра числа показывает число единиц, вторая справа — число десятков, следующая — число сотен и т. д. Причина наибольшей распространенности десятичной системы счисления состоит в том, что первым счетным аппаратом человека являлись его руки. Число пальцев и стало отправным пунктом для системы счета.
Двоичная система счисления
В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Крайняя правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.
Восьмеричная система счисления
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: А, В, С, D, Е, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем разряде — 16 (десятичное), в следующем — 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
shkolo.ru
Восьмеричная система счисления — это… Что такое Восьмеричная система счисления?
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этрусская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Таблица перевода восьмеричных чисел в двоичные
08 = 0002 18 = 0012 28 = 0102 38 = 0112 48 = 1002 58 = 1012 68 = 1102 78 = 1112
Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например: 25418 = [ 28 | 58 | 48 | 18 ] = [ 0102 | 1012 | 1002 | 0012 ] = 0101011000012
Ссылки
dic.academic.ru
Двоичная и восьмеричная системы счисления.
ИНФОРМАТИКА 1 курсы 1 семестр
Раздел «Информация» Системы счисления
______________________________________________________________________________________________________
- Занятие№1
Тема занятия: Системы счисления. Перевод чисел из одной системы в другую.
Цель занятия:
Образовательная:
Познакомить студентов с системами счисления (2СС, 8СС).
Научить переводить числа из одной системы в другую и наоборот.
Развивающая:
Воспитательная:
Оборудование занятия:
- План занятия
Мотивация изучения нового материала
Изучение нового материала
Системы счисления, их типы.
Двоичная система счисления.
Перевод чисел из 2СС в 10СС и из 10СС в 2СС.
Восьмеричная система счисления.
Перевод чисел из 8СС в 10СС и из 10СС в 8СС, 2СС в 8СС, 8СС в 2СС.
Закрепление знаний
Для закрепления на 10 минут самостоятельная работа.
Перевести:
4710 – Х2
10101,012 – Х10
101101100,010112 – Х8
Задание на дом
Примеры:
7910 — Х2,
1011111,112 – Х10,
123,48 – Х10,
83,210 – Х8,
123,48 – Х2.
- Конспект
- Системы счисления
Под системой счисления понимают совокупность приемов для представления и записи чисел с помощью определенного количества знаков (цифр). Существуют позиционные и непозиционные системы счисления. В позиционных системах значение (вес) каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Примером позиционной системы является десятичная система счисления. Проанализируем вместе с учащимися, как представляются числа в этой системе.
Для представления чисел в десятичной системе используются десять цифр: от 0 до 9. Число записанное в десятичной системе, 2359,407 читается как две тысячи триста пятьдесят девять и четыреста семь тысячных и может быть представлено следующим образом:
2*1000 + 3*100 + 5*10 + 9*1 + 4*0,1 + 7*0,001.
Следует обратить внимание студентов, что множители каждого слагаемого представляют собой одну из степеней числа 10, т.е. можно записать:
2*103 + 3*102 + 5*101 + 9*100 + 4*10-1 + 0*10-2 + 7*10-3.
Подчеркнем при этом, что положение (позиция) цифры определяет ее значение. Двойка, стоящая на первом месте, означает количество тысяч в этом числе, а четверка, стоящая после запятой, — количество десятых долей.
Системы счисления, в которых значение цифры зависит от ее позиции в последовательности цифр, изображающих число, принято называть позиционными.
В непозиционных системах значение цифры не зависит от ее позиции. Общеизвестным примером непозиционной системы является римская система счисления. Так, в числе МСХХХII (1132) значение цифры Х не изменяется и всегда равно десяти.
- Двоичная система счисления
Двоичная система счисления – основание этой системы S=2, в ней используют лишь две цифры: 0 и 1. Ее используют в ЭВМ для представления чисел и выполнения над ними различных арифметических и логических операций. Поскольку в ней используют лишь две цифры: 0 и 1, она легко может быть реализована на элементах, обладающих двумя устойчивыми состояниями.
А2= ап * 2п + ап-1 * 2п-1 +… + а0 * 20 + …
Пример:
1010110112 = 1*26 + 0*25 + 1*24 + 0*23+ 1*22 + 1*21 + 0*20 + 1*2-1 + 1*2-2=
= 64 + 16 + 4 + 2+ 0,5 + 0,25=86,7510.
Чтобы перевести число из двоичной системы счисления в десятичную нужно записать его в виде многочлена, где коэффициенты числа будут умножаться на степени двойки и найти сумму слагаемых.
|
|
0 | 0000 |
2 | 0001 |
2 | 0010 |
3 | 0011 |
4 | 0100 |
5 | 0101 |
6 | 0110 |
7 | 0111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
А2 = А*23 + А2*22 + А*21+А*20.
Чтобы перевести число из десятичной системы счисления в двоичную нужно разделить его на два до тех пор пока последнее частное будет меньше 2. Остатки будут являться коэффициентами числа.
Восьмеричная система счисления
А8=ап*8п+…+ап*80+…
|
|
|
0 | 000 | 0 |
1 | 001 | 1 |
2 | 010 | 2 |
3 | 011 | 3 |
4 | 100 | 4 |
5 | 101 | 5 |
6 | 110 | 6 |
7 | 111 | 7 |
- Восьмеричную систему счисления применяют в ЭВМ как вспомогательную при подготовке задачи к решению (в процессе программирования), при проверке работы машины и отладке программы. Эта система дает более короткую запись числа по сравнению с двоичной системой счисления. В восьмеричной системе счисления используют восемь цифр от 0 до 7, а любое число в этой системе представляют самой суммой целых степеней основания S=8, умноженных на соответствующие коэффициенты
Пример:
173,28 – Х10
173,28=1*82+7*81+3*80+2*8-1=64+56+3+2/8=123,2510
Чтобы перевести число из 2 СС в 8 СС нужно разбить его от запятой вправо и влево на триады цифр. Недостающие цифры до 3 записать нулями, и записать эти триады в 8 СС.
Пример:
10101100,101112 – Х8
010 101 100 , 101 110
2 5 4 , 5 6 Ответ: 254,568
Чтобы перевести число из 8 СС в 2 СС нужно записать каждую цифру числа в виде триады цифр в 2 СС.
Пример:
1360,758 – Х2
1 3 6 0 , 7 5
001 011 110 000 , 111 101 Ответ: 1011110000,1111012
Для перевода целого числа из одной позиционной системы с основанием 10 в другую с основанием 8 надо это число последовательно делить на основание 8 новой системы счисления до тех пор, пока не получится частное, меньшее 8.
Для перевода восьмеричных чисел в двоичную систему счисления достаточно каждую их цифру заменить соответственно трех- или четырехразрядным двоичным числом.
Пример:
5718 – Х2 –?
5 7 1
101 111 001
Ответ: 1011110012.
Теория
Системы счисления
В этой главе речь пойдет о представлении числовой информации.
Человеку издревле приходилось считать различные предметы, нужно было и записывать их количество. Самой первой, вероятно, возникла унарная2 система записи, при которой числа обозначались соответствующим количеством черточек (или засечек на деревяшке).
Унарная запись получается очень громоздкой и неудобной, поэтому люди стали искать более компактные способы обозначать большие числа. Появились разные условные обозначения для различных чисел. Например, многие народы использовали в качестве цифр буквы, к которым добавляли специальные значки. На Руси таким знаком было титло
Но, все равно, число получалось сложением цифр, поэтому система оставалась сложной. Представьте: чтобы пользоваться древнерусской системой счисления, нужно было знать числовое значение 30 букв, а еще — несколько особых символов, увеличивавших это значение («тысяча», «тьма», «легион», «леодр»… — все они получались при приписывании к «единице» — букве «аз» разных значков). Вычисления же в таких системах были вообще чрезвычайно затруднены.
В римской системе счисления появилась одна новая идея: хотя там тоже для обозначения чисел использовали буквы (1 — I, 5 — V, 10 — X, 50 — L, 100 — C, 500 — D, 1000 — M), но роль их зависела от порядка записи (значение могло не только прибавляться, но и вычитаться). Развитие этой идеи привело к появлению современных позиционных систем счисления.
Мы настолько привыкли к нашей обычной — десятеричной — системе, что даже не задумываемся, насколько гениальной была идея, положенная в ее основу3: в позиционных системах счисления значение цифры зависит от ее позиции (места) в числе. Например, число 444 записано тремя одинаковыми цифрами, но каждая из них имеет свое значение: четыре сотни, четыре десятка и четыре единицы. То есть его можно записать вот так:
444 = 4.100 + 4.10 + 4.1.
или
444 = 4.102 + 4.101 + 4.100.
Нетрудно заметить, что если обозначить цифры числа как a2, a1 и a0, то любое трехзначное число может быть представлено в виде:
N = a2.102 + a1.101 + a0.100.
Число 10, степени которого используются в этой формуле (и именно столько разных цифр есть в десятичной системе), называют основанием системы счисления, а степени десятки — весами разрядов.
Вообще, выбор в качестве основания позиционной системы именно числа 10 объясняется традицией, а не какими-то особыми свойствами этого числа. С не меньшим успехом можно использовать и любое другое. В общем случае, если основание системы счисления равно p, число, записанное в этой системе, можно представить в виде:
N = aipi + … + a2p2 + a1p1 + a0p0, [1]
причем каждый из коэффициентов-цифр должен быть меньше p.
Пользуясь этой формулой можно легко перевести число из системы счисления с любым основанием в десятеричную.
Пример:
325426 = 3.64 +2.63 + 5.62 + 4.61 + 2.60 = 3.1296 + 2.216 + 5.36 + 4.6 + 2 = 3888 + 432 + 180 + 24 + 2 = 4526
А как выполнить обратный перевод? Для этого нам нужно будет последовательно делить нацело наше число на основание новой системы счисления, запоминая остатки. Пусть нужно перевести число 2000 в восьмеричную систему счисления.
Действуем так:
2000:8=250(ост.0)
250:8=31(ост.2)
31:8=3(ост.7)
3 : 8 = 0 (ост. 3)
Теперь запишем все остатки, не забывая о нулевых, с последнего до первого4:
3720
Это и будет искомое представление.
200010 = 37208.
Контрольные вопросы
Что такое система счисления?
Чем отличаются позиционные системы счисления от непозиционных, в чем их преимущества?
Переведите в десятеричную систему счисления:
а) 47619; б) 33425; в) 221234; г) 110101002.Переведите число 199810 в системы счисления с основаниями 2, 3, 8.
Примечания
От лат. Unus — один
Мы обычно называем такую запись чисел арабской. На самом деле, изобретена она в Индии, но европейцы впервые узнали о ней от арабов
Этим мы, фактически, определили, что 2000 = ((3.8 + 7).8 + 2).8 + 0 или, раскрывая скобки, 3.83 + 7.82 + 2.8 + 0. Сравните этот результат с формулой [1]
6
kopilkaurokov.ru