Ряды Тейлора, Бином, Степенные ряды
Ряд Тейлора функции одной переменной
$f(x)=f(a)+f'(a)(x-a)+\frac{f»(a)(x-a)^2}{2!}+\cdots$$+\frac{f^{(n-1)}(a)(x-a)^{n-1}}{(n-1)!}+R_n$ где $R_n$, остаточный член после n слагаемых, может быть записан в одной из следующих форм:
Форма Лагранжа $R_n=\frac{f^{(n)}(x-a)^n}{n!}$
Форма Коши $R_n=\frac{f^{(n)}(\xi)(x-\xi)^{n-1}(x-a)}{(n-1)!}$
Величина $\xi$, которая может отличаться для двух форм, лежит в промежутке между $a$ и $x$. Результат справедлив, если $f(x)$ имеет непрерывные производные до порядка $n$ как минимум.
Если $\lim_{n\rightarrow\infty} R_n=0$, полученный бесконечный ряд называется рядом Тейлора функции $f(x)$ в окрестности $x = a$. Если $a = 0$, такое разложение часто называют рядом Маклорена. Эти ряды, часто называемые степенными рядами, обычно сходятся для всех значений $x$ из некоторого интервала, который называется интервалом сходимости, и расходятся для всех $x$ вне этого интервала.
Возведение в степень двучленов
$(a+x)^n=a^n+na^{n-1}x+\frac{n(n-1)}{2!}a^{n-2}x^2+$$\frac{n(n-1)(n-2)}{3!}a^{n-3}x^3+\cdots=$
$= a^n+\binom{n}{1}a^{n-1}x+\binom{n}{2}a^{n-2}x^2+$$\binom{n}{3}a^{n-3}x^3+\cdots$
Особо стоит выделить следующие разложения
$(a+x)^2=a^2+2ax+x^2$
$(a+x)^3=a^3+3a^2x+3ax^2+x^3$
$(a+x)^4=a^4+4a^3x+6a^2x^2+4ax^3+x^4$
$(1+x)^{-1}=$$1-x+x^2-x^3+x^4-\cdots,$ $-1
$(1+x)^{-2}=$$1-2x+3x^2-4x^3+5x^4-\cdots,$ $-1
$(1+x)^{-3}=$$1-3x+6x^2-10x^3+15x^4-\cdots$ $-1
$(1+x)^{-\frac{1}{2}}=$$1-\frac{1}{2}x+\frac{1\cdot3}{2\cdot4}x^2-\frac{1\cdot3\cdot5}{2\cdot4\cdot6}x^3+\cdots$ $-1
$(1+x)^{\frac{1}{2}}=$$1+\frac{1}{2}x-\frac{1}{2\cdot4}x^2+\frac{1\cdot3}{2\cdot4\cdot6}x^3-\cdots$ $-1
$(1+x)^{-\frac{1}{3}}=$$1-\frac{1}{3}x+\frac{1\cdot4}{3\cdot6}x^2-\frac{1\cdot4\cdot7}{3\cdot6\cdot9}x^3+\cdots$ $-1
$(1+x)^{\frac{1}{3}}=$$1+\frac{1}{3}x+\frac{2}{3\cdot6}x^2-\frac{2\cdot5}{3\cdot6\cdot9}x^3-\cdots$ $-1
Разложение в ряд показательной и логарифмической функций
$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots$ $-\infty
$a^x=e^{x\ln x}=$$1+x\ln a+\frac{(x\ln a)^2}{2!}+\frac{(x\ln a)^3}{3!}+\cdots$ $ -\infty
$\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots$ $-1
$\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)=$$x+\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7}+\cdots$ $-1
$\ln x=2\left\{\left(\frac{x-1}{x+1}\right)+\frac{1}{3}\left(\frac{x-1}{x+1}\right)^3+\frac{1}{5}\left(\frac{x-1}{x+1}\right)^5+\cdots\right\}$ $x>0$
$\ln x=\left(\frac{x-1}{x}\right)+\frac{1}{2}\left(\frac{x-1}{x}\right)^2+$$\frac{1}{3}\left(\frac{x-1}{x}\right)^3+\cdots$ $x\geq\frac{1}{2}$
Разложение в ряд тригонометрических функций
$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$ $-\infty
$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$ $-\infty
$tg x=x+\frac{x^3}{3}+\frac{2x^5}{15}+\frac{17x^7}{315}+\cdots$$+\frac{2^{2n}(2^{2n}-1)B_nx^{2n-1}}{(2n)!}+\cdots$ $|x|
$\text{ctg} x=\frac{1}{x}-\frac{x}{3}-\frac{x^3}{45}-\frac{2x^5}{945}-\cdots-$$\frac{2^{2n}B_nx^{2n-1}}{(2n)!}-\cdots$ $0
$\sec x=1+\frac{x^2}{2}+\frac{5x^4}{24}+\frac{61x^6}{720}+\cdots$$+\frac{E_nx^{2n}}{(2n)!}+\cdots$ $|x|
$\csc x=\frac{1}{x}+\frac{x}{6}+\frac{7x^3}{360}+\frac{31x^5}{15,120}+\cdots$$+\frac{2(2^{2n-1}-1)B_nx^{2n-1}}{(2n)!}+\cdots$ $0
$\sin^{-1}x=x+\frac{1}{2}\frac{x^3}{3}+\frac{1\cdot3}{2\cdot4}\frac{x^5}{5}+$$\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\frac{x^7}{7}+\cdots$ $|x|
$\cos^{-1}x=\frac{\pi}{2}-\sin^{-1}x=$$\frac{\pi}{2}-\left(x+\frac{1}{2}\frac{x^3}{3}+\frac{1\cdot3}{2\cdot4}\frac{x^5}{5}+\cdots\right)$ $|x|
$\text{tg}^{-1}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots$, когда $|x| $\text{tg}^{-1}x=\pm\frac{\pi}{2}-\frac{1}{x}+\frac{1}{3x^3}-\frac{1}{5x^5}+\cdots$ $[+\ \text{если}\ x\geq1, -\ \text{если}\ x\leq-1]$
$\text{ctg}^{-1}x=\frac{\pi}{2}-\text{tg}^{-1}x =$$\frac{\pi}{2}-\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots\right)$, когда $|x| $\text{ctg}^{-1}x=\frac{\pi}{2}-\text{tg}^{-1}x =$$p\pi+\frac{1}{x}-\frac{1}{3x^3}+\frac{1}{5x^5}-\cdots$, когда [p=0 если x>1, p=1 если x
$\sec^{-1}x=\cos^{-1}\left(\frac{1}{x}\right)=$$\frac{\pi}{2}-\left(\frac{1}{x}+\frac{1}{2\cdot3x^3}+\frac{1\cdot3}{2\cdot4\cdot5x^5}+\cdots\right)$ $|x|>1$
$\csc^{-1}x=\sin^{-1}\left(\frac{1}{x}\right)=$$\frac{1}{x}+\frac{1}{2\cdot3x^3}+\frac{1\cdot3}{2\cdot4\cdot5x^5}+\cdots$ $|x|>1$
Разложение в ряд гиперболических функций
$\text{sh} x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\cdots$ $-\infty
$\text{ch} x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\cdots$ $-\infty
$\text{th} x=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots$$+\frac{(-1)^{n-1}2^{2n}(2^{2n}-1)B_nx^{2n-1}}{(2n)!}+\cdots$ $|x|
$\text{cth} x=\frac{1}{x}+\frac{x}{3}-\frac{x^3}{45}+\frac{2x^5}{945}+\cdots$$+\frac{(-1)^{n-1}2^{2n}B_nx^{2n-1}}{(2n)!}+\cdots$ $0
$\sec\text{h}x=1-\frac{x^2}{2}+\frac{5x^4}{24}-\frac{61x^6}{720}+\cdots$$+\frac{(-1)^
www.math10.com
Ряд Тейлора — это… Что такое Ряд Тейлора?
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Определение
Пусть функция бесконечно дифференцируема в некоторой окрестности точки . Формальный ряд
называется рядом Тейлора функции в точке .
Связанные определения
- В случае, если , этот ряд также называется рядом Макло́рена.
Свойства
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке равны нулю.
Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена
В форме Лагранжа:
В форме Коши:
В интегральной форме:
Ослабим предположения:
- — остаточный член в асимптотической форме (в форме Пеано, в локальной форме)
Ряды Маклорена некоторых функций
Формула Тейлора для функции двух переменных
Пусть функция имеет полные производные вплоть до -го порядка включительно в некоторой окрестности точки . Введём дифференциальный оператор
- .
Тогда разложением в ряд Тейлора функции по степеням и в окрестности точки будет
где — остаточный член в форме Лагранжа:
В случае функции одной переменной , поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе .
См. также
Литература
- Ильин В. А., Садовничий В. А., Сендов Б. Х. Математический анализ, ч. 1, изд. 3, ред. А. Н. Тихонов. М.: Проспект, 2004.
- Киселёв В. Ю., Пяртли А. С., Калугина Т. Ф. Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
- Петрова С. С., Романовска Д. А. К истории открытия ряда Тэйлора. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 10-24.
- Письменный Д. Т. Конспект лекций по высшей математике, изд.: АЙРИС-пресс, 2002.
dic.academic.ru
Лекция 19. Формула Тейлора. Ряд Тейлора
19.1. Формула Тейлора1.
Рассмотрим произвольный многочлен степени n:
.
Пусть  – любое фиксированное число. Полагая,
получим:
– любое фиксированное число. Полагая,
получим:
. (19.1)
Запишем также в виде
, (19.2)
где
– числа, зависящие от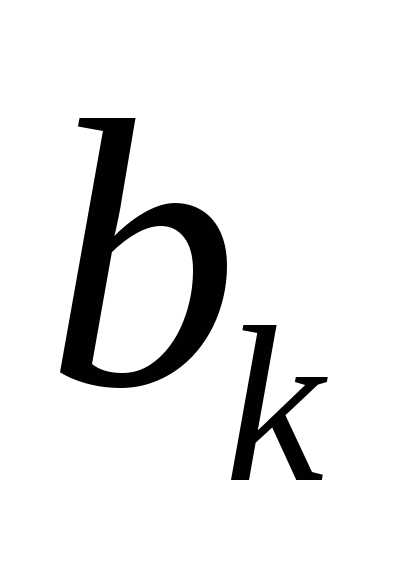 и
и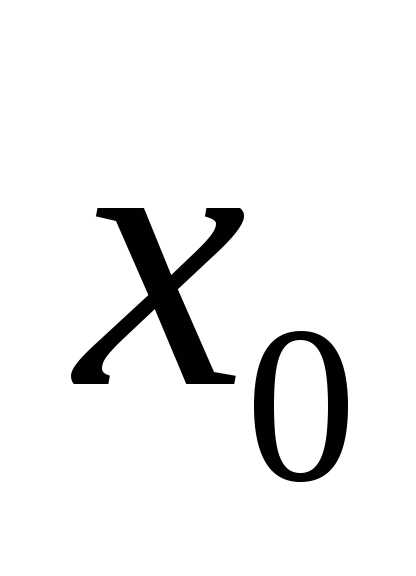 – коэффициенты разложения
– коэффициенты разложения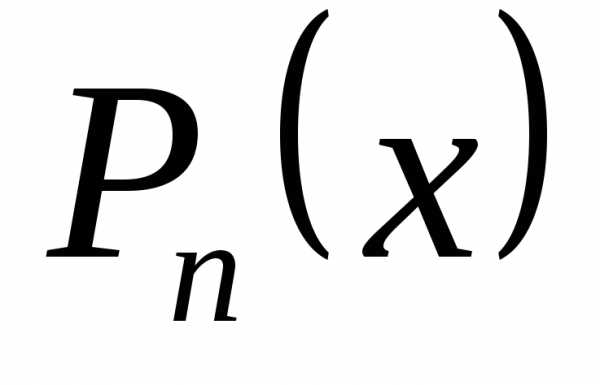 по степеням
по степеням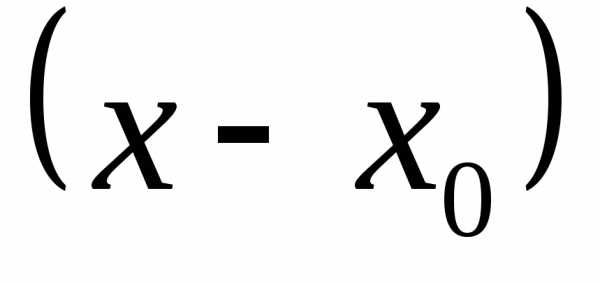 .
Например,.
.
Например,.
Из (19.1) не видно, что 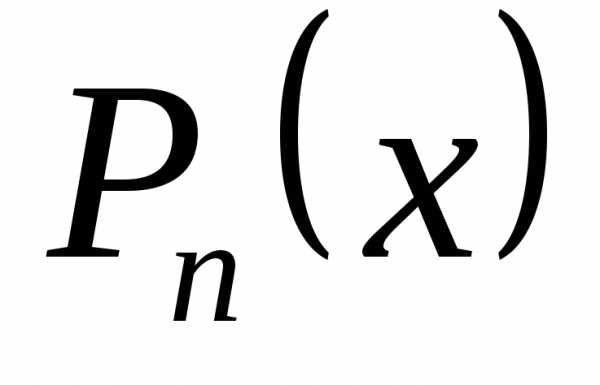 от
от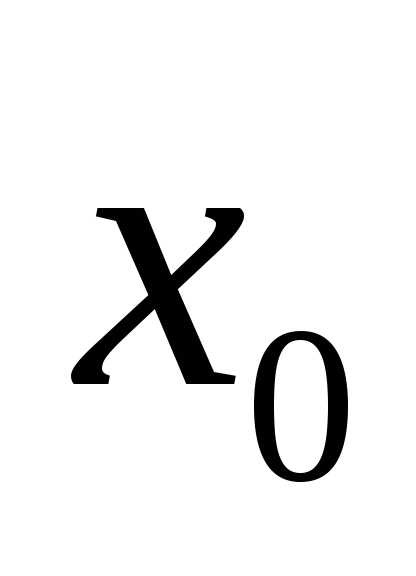
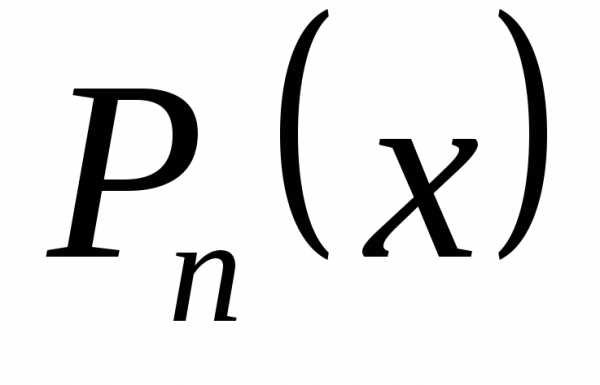 :
:. (19.3)
Следующие производные равны нулю.
Полагая в формулах (19.2) и (19.3)  ,
получаем:
,
получаем:
,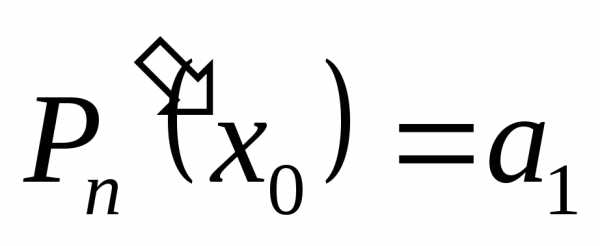 ,,
,, ,,
,,
то есть
 .
(19.4)
.
(19.4)
Таким образом,
. (19.2*)
Это формула Тейлора для многочлена  по степеням
по степеням .
.
Отметим, что правая часть (19.2*) фактически
не зависит от 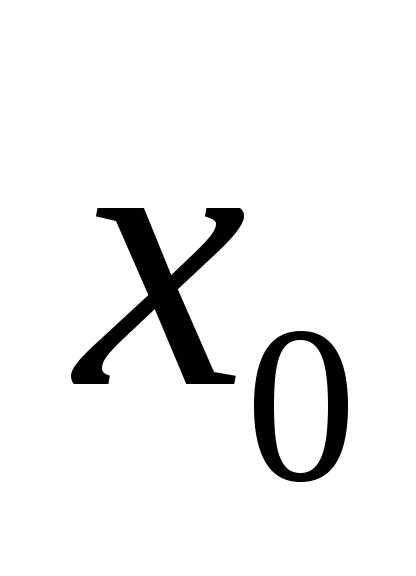
Пример 19.1.Пусть,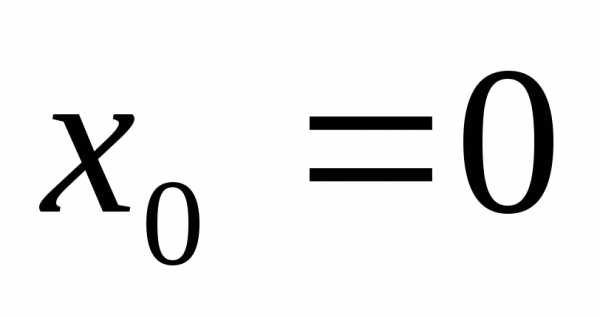 .
.
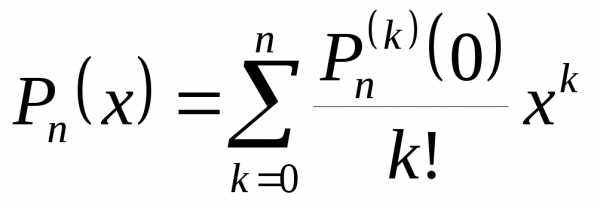 ,
,
,,
после чего получаем формулу бинома Ньютона
.
19.2. Остаточный член формулы Тейлора.
Рассмотрим любую функцию 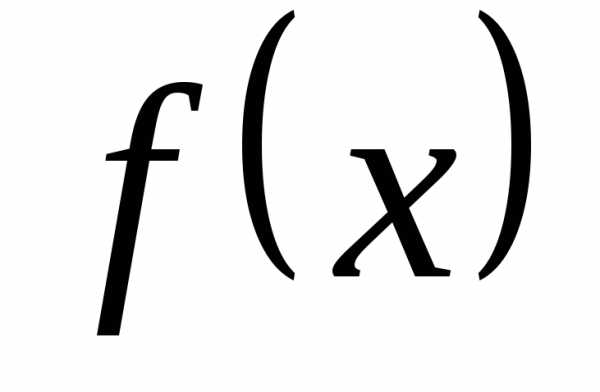 ,
которая имеет непрерывные производные
до
,
которая имеет непрерывные производные
до -го
порядка в некоторой окрестности точки
-го
порядка в некоторой окрестности точки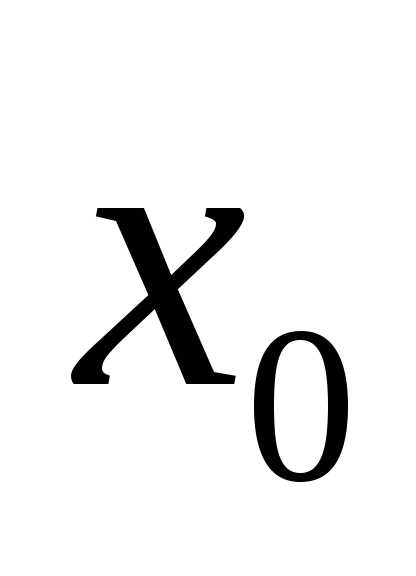 .
Составим многочлен Тейлораn-й
степени по степеням
.
Составим многочлен Тейлораn-й
степени по степеням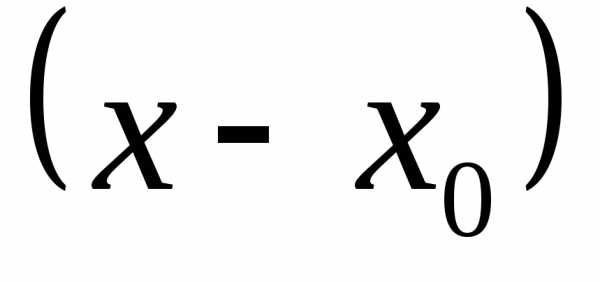 :
:
. (19.5)
 в точке
в точке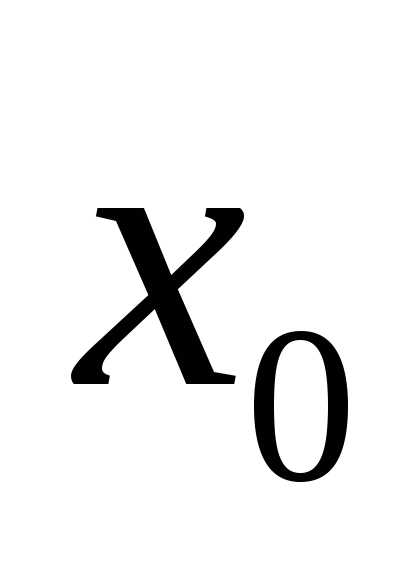 ,
но для всехxон не
равен
,
но для всехxон не
равен  .
Кроме того,
.
Кроме того, , ,.
,.
Положим
. (19.6)
Здесь  –остаточный член формулы Тейлора.Он показывает, какую погрешность мы
допускаем при замене
–остаточный член формулы Тейлора.Он показывает, какую погрешность мы
допускаем при замене  на многочлен Тейлора (19.5).
на многочлен Тейлора (19.5).
Если функция  имеет в окрестности точки
имеет в окрестности точки  непрерывную производную
непрерывную производную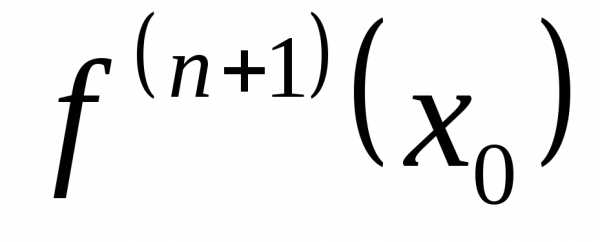 ,
то для
,
то для
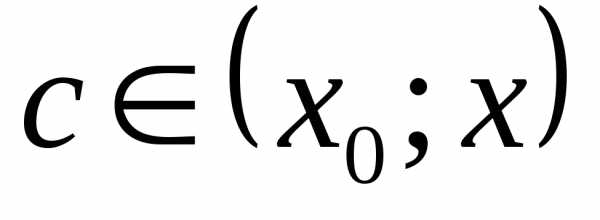 такая, что
такая, что(остаточный член в форме Лагранжа).
Функцию 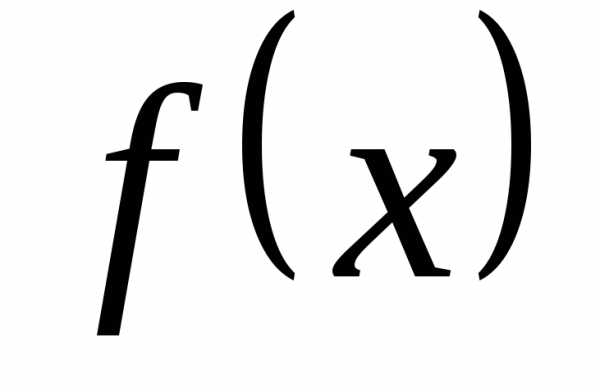 можно записать в виде:
можно записать в виде:
. (19.6*)
Если  ,
то формулу (19.6*) называютформулой
Маклорена1.
,
то формулу (19.6*) называютформулой
Маклорена1.
Известны и другие формы остаточного члена формулы Тейлора.
Остаточный член в форме Коши:, где .
Формула Тейлора с остаточным членом в смысле Пеано2:
.
Эта формула приспособлена для изучения
функции 
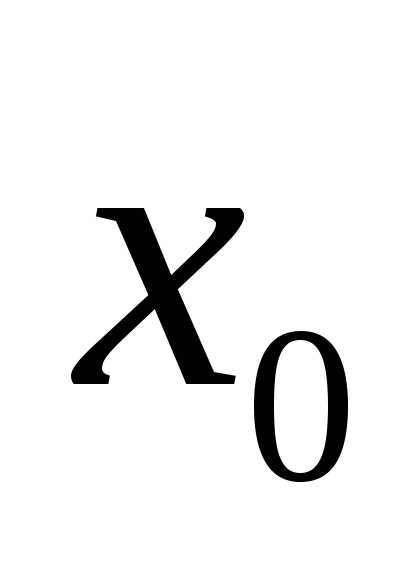 .
.19.3. Ряд Тейлора.
Определение 19.1.Выражение вида
, (19.7)
или
 , (19.7*)
, (19.7*)
где 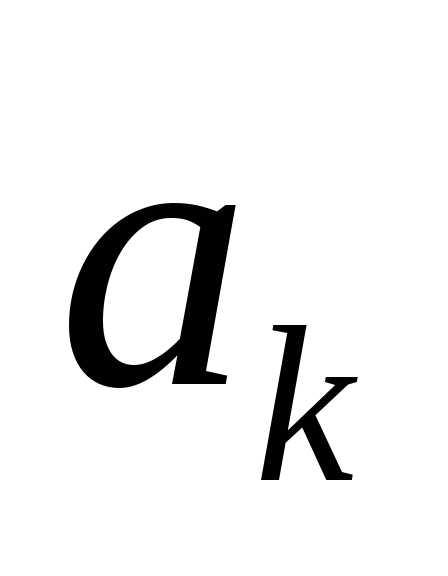 – числа, зависящие от индекса k,
называется рядом (числовым рядом).
– числа, зависящие от индекса k,
называется рядом (числовым рядом).
Определение 19.2.Конечные суммы 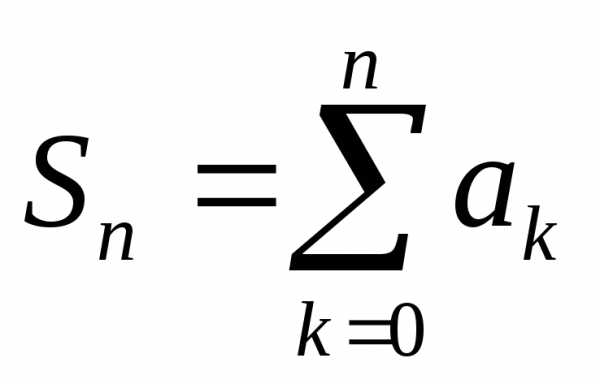 называются частичными суммами
ряда(19.7).
называются частичными суммами
ряда(19.7).
Определение 19.3.Если существует конечный предел
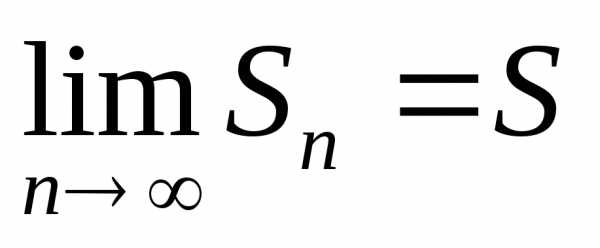
то говорят, что ряд(19.7)сходится к числу S и называют S суммой ряда:
.
Определение 19.4.Если предел
частичных сумм Sn  ряда(19.7)не существует или равен
ряда(19.7)не существует или равен  ,
то ряд(19.7)называется расходящимся
рядом.
,
то ряд(19.7)называется расходящимся
рядом.
Если функция  имеет производные любого порядка в
окрестности точки
имеет производные любого порядка в
окрестности точки ,
то можно функцию
,
то можно функцию  представить в виде суммы
представить в виде суммы
.
Такое разложение называется рядом Тейлора функции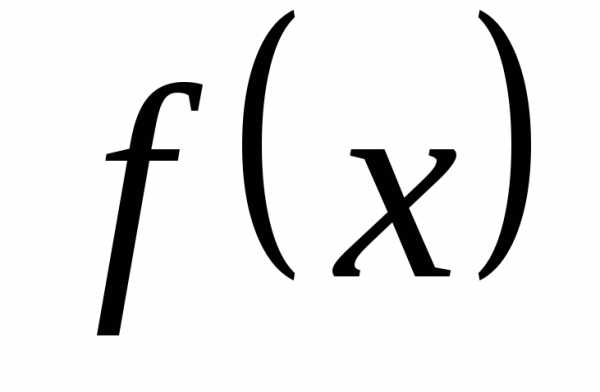 по степеням
по степеням .
Если
.
Если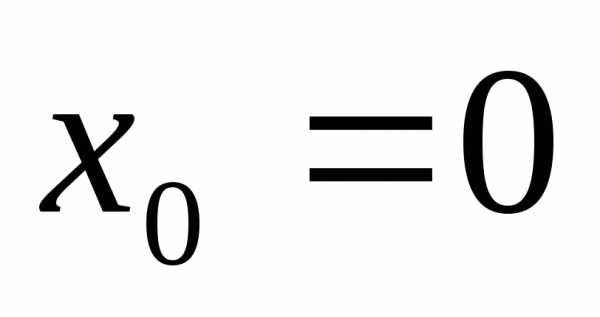 ,
то это будетряд Маклорена.
,
то это будетряд Маклорена. Особый интерес представляет тот случай,
когда ряд Тейлора функции  по степеням
по степеням сходится в некоторой окрестности точки
сходится в некоторой окрестности точки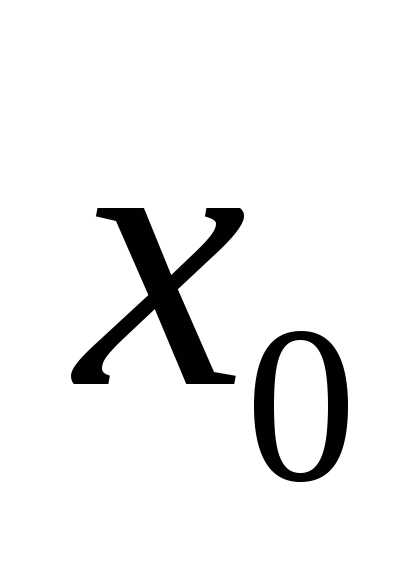 и при том к самой функции
и при том к самой функции 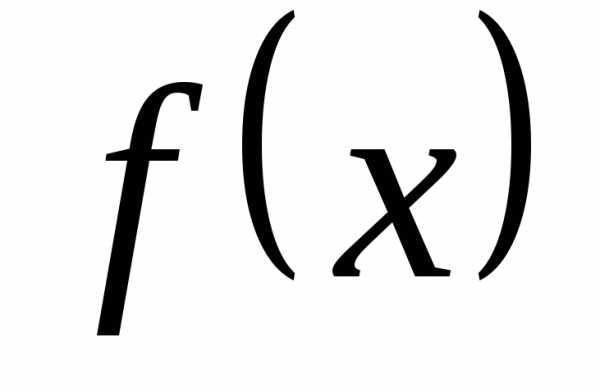 .
Если это имеет место, то
.
Если это имеет место, то
,, (19.9)
то есть функция  есть сумма её ряда Тейлора в некоторой
окрестности точки
есть сумма её ряда Тейлора в некоторой
окрестности точки
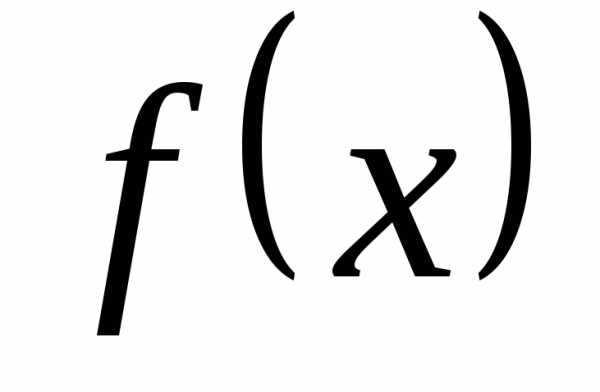 разлагается в ряд Тейлора по степеням
разлагается в ряд Тейлора по степеням 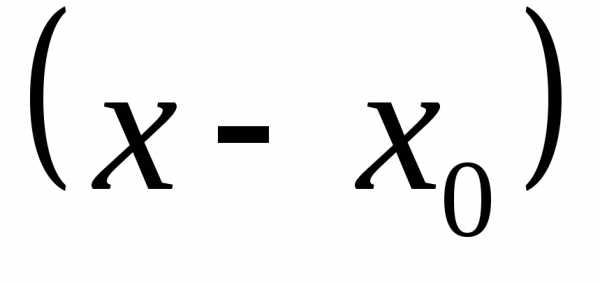 ,
сходящийся к ней.
,
сходящийся к ней. ♦ Теорема 19.1. Пусть функция  на отрезке имеет производные любого порядка и
остаток её формулы Тейлора стремится
к нулю при на этом отрезке:
на отрезке имеет производные любого порядка и
остаток её формулы Тейлора стремится
к нулю при на этом отрезке:
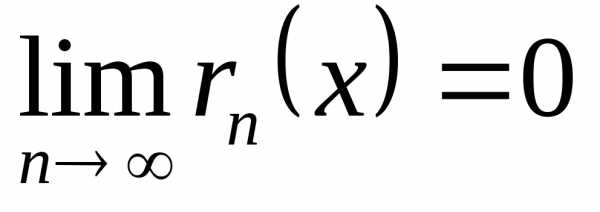 .(19.10)
.(19.10)
Тогда функция 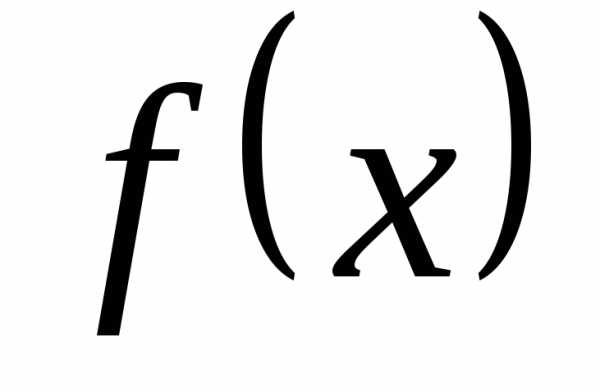 разлагается в ряд Тейлора на этом
отрезке.
разлагается в ряд Тейлора на этом
отрезке.
Доказательство.Пусть функция  имеет на отрезке
производные любого порядка. Тогда эти
производные непрерывны на
,
потому что если
имеет на отрезке
производные любого порядка. Тогда эти
производные непрерывны на
,
потому что если 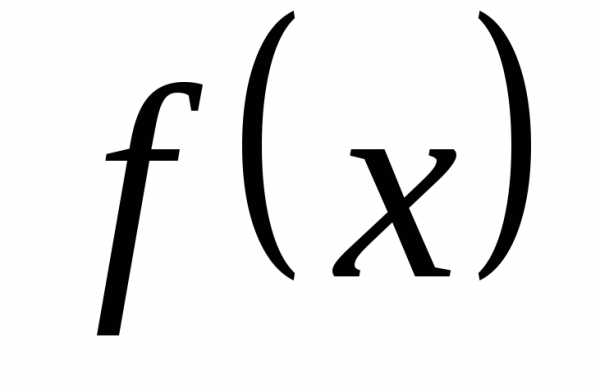 имеет производную
имеет производную  на
,
то производная
на
,
то производная  непрерывна на
.
непрерывна на
.
Поэтому для нашей функции 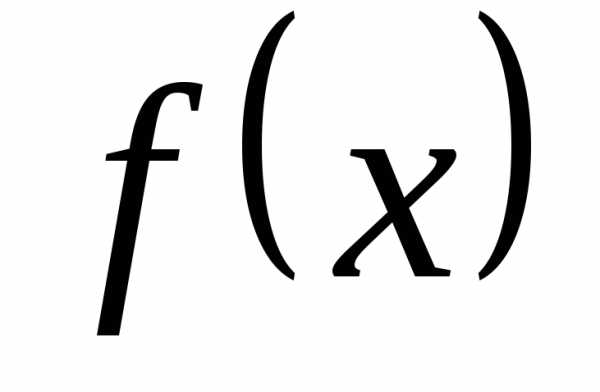 имеет смысл формула Тейлора:
имеет смысл формула Тейлора:
 ,.
,.
В силу (19.10)
.
То есть в этом случае многочлен Тейлора
функции 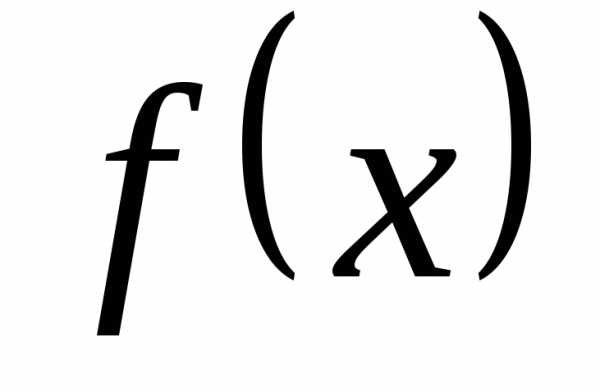 по степеням
по степеням стремится при
к самой функции:
стремится при
к самой функции:
,. (19.11)
А это означает, что ряд Тейлора функции  сходится на
и имеет своей суммой
сходится на
и имеет своей суммой 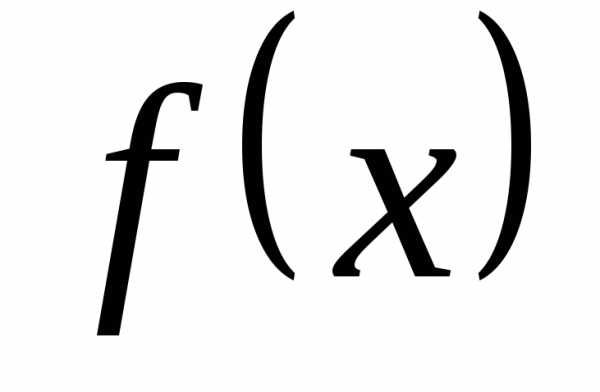 :
:
,.■
♦ Теорема 19.2 (достаточный
критерий сходимости остатка формулы
Тейлора к нулю). Если функция 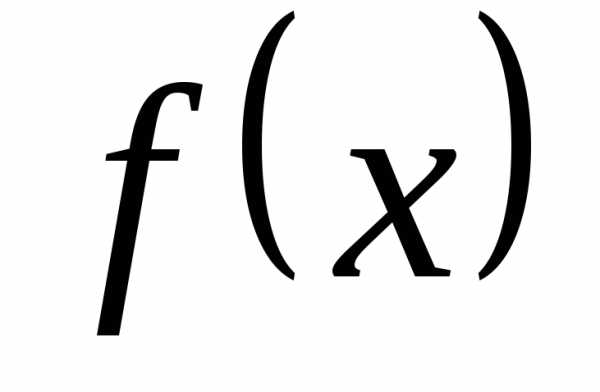 имеет на отрезке производные любого порядка, ограниченные
одним и тем же числом
имеет на отрезке производные любого порядка, ограниченные
одним и тем же числом 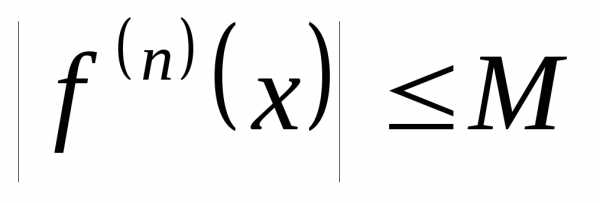 ,,
то остаток её формулы Тейлора на этом
отрезке стремится при к нулю:
,,
то остаток её формулы Тейлора на этом
отрезке стремится при к нулю:
 .(19.12)
.(19.12)
Доказательство.Воспользуемся формой Лагранжа остаточного члена:
. (19.13)
Так как правая часть (19.13) стремится к нулю при , то имеет место (19.12).■
19.4. Формулы и ряды Тейлора элементарных функций.
1)  .Эта функция бесконечно дифференцируема
на
.Эта функция бесконечно дифференцируема
на  :
:
,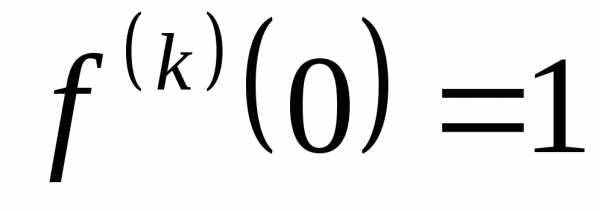 ,,.
,,.
Формула Тейлора с 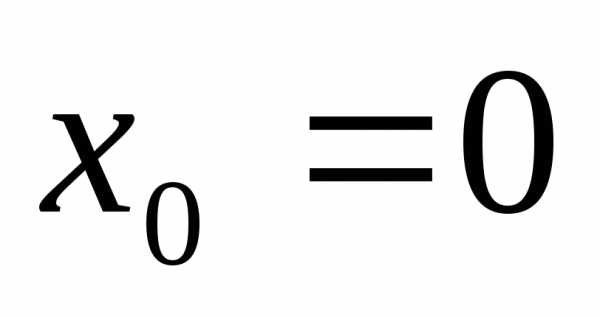 и остаточным членом в форме Лагранжа
имеет вид:
и остаточным членом в форме Лагранжа
имеет вид:
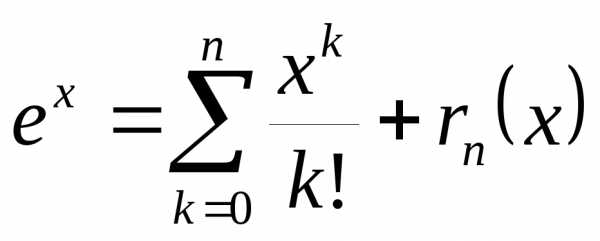 ,
,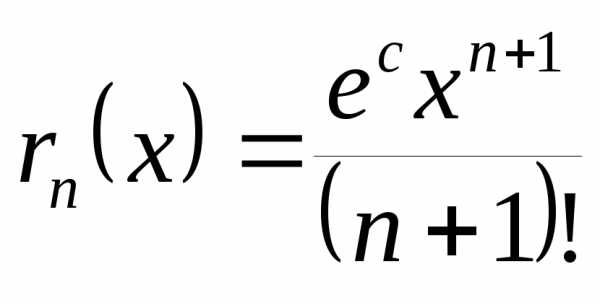 ,
,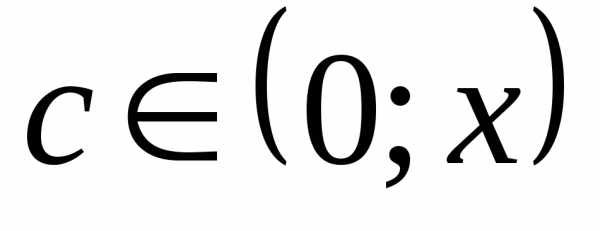 .
.
На отрезке 

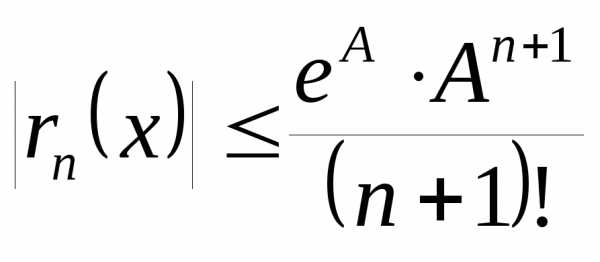 ,
,
где 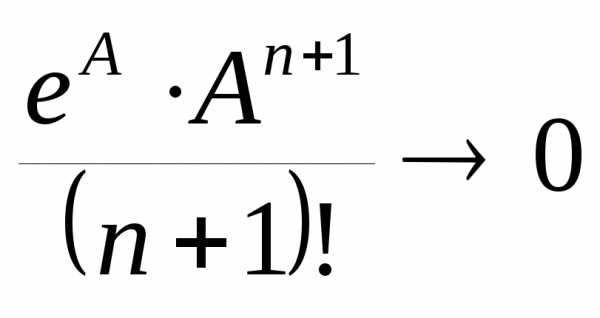 при
.
То есть нафункция
при
.
То есть нафункция 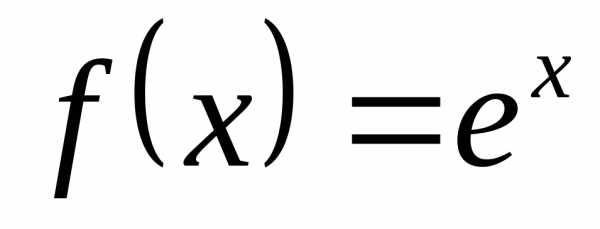 разлагается в ряд Маклорена по степенямx:
разлагается в ряд Маклорена по степенямx:
 .
.
Пример 19.2.Вычислимeс точностью до 0,001:
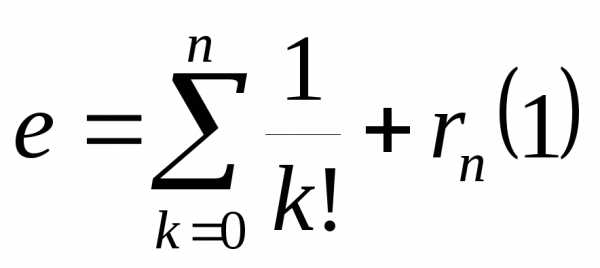 ,
где
,
где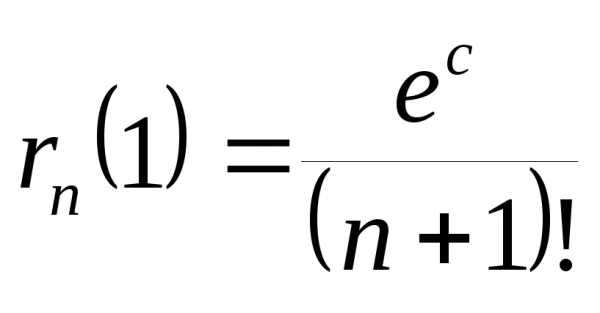 ,.
,.
Надо подобрать nнастолько большим, чтобы .
Так как
.
Так как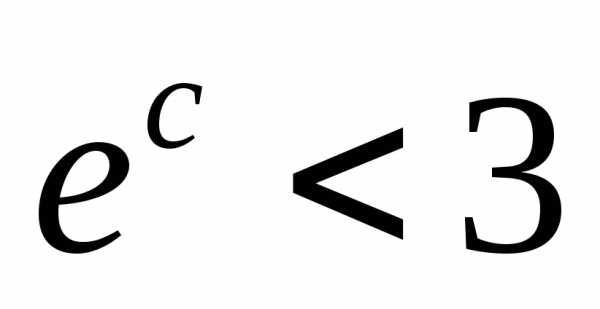 ,
решим неравенство
,
решим неравенство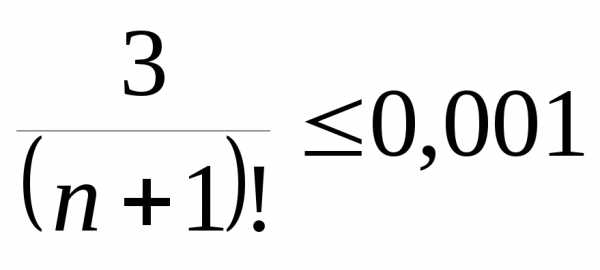 .
Оно начинает выполняться при
.
Оно начинает выполняться при .
Следовательно,
.
Следовательно,
.
2) . Данная функция имеет производную любого порядка и
 .
.
Надо учесть, что
Функция
разлагается в сходящийся к ней на  ряд Тейлора по степенямx:
ряд Тейлора по степенямx:
.
Формула Тейлора функции по степенямxимеет вид:
,
где
,.
Отсюда следует, что и
.
Пример 19.3.Вычислим 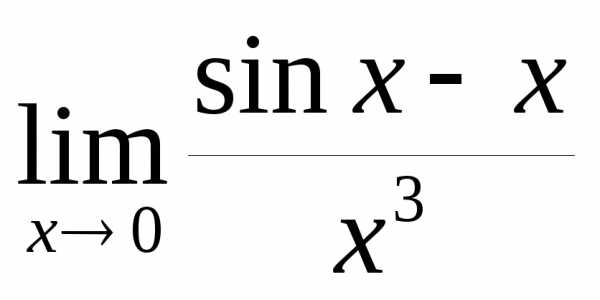 .
.
Ряд Тейлора для синуса . Поэтому
,
то есть 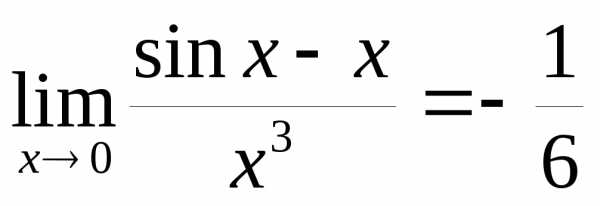 .
.
На самом деле остаток имеет вид  ,
но для наших целей достаточно
,
но для наших целей достаточно 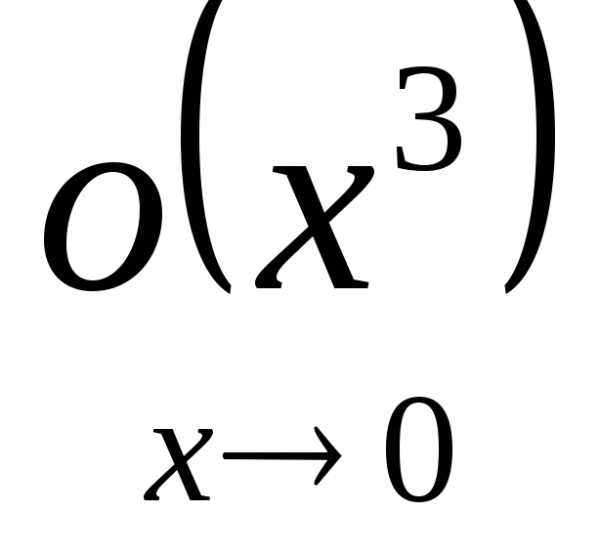 .
Надо иметь в виду, что если некоторая
функция отxесть
.
Надо иметь в виду, что если некоторая
функция отxесть  ,
то она есть также
,
то она есть также 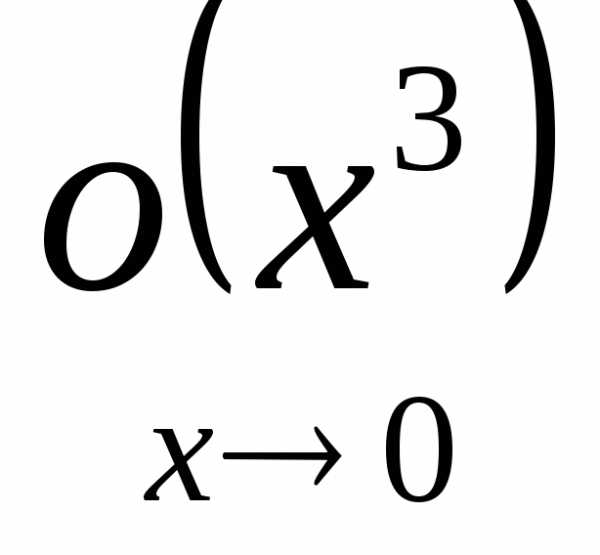 (но вообще не наоборот).
(но вообще не наоборот).
3) . Аналогично можно получить, что
.
Пример 19.4.(с точностью до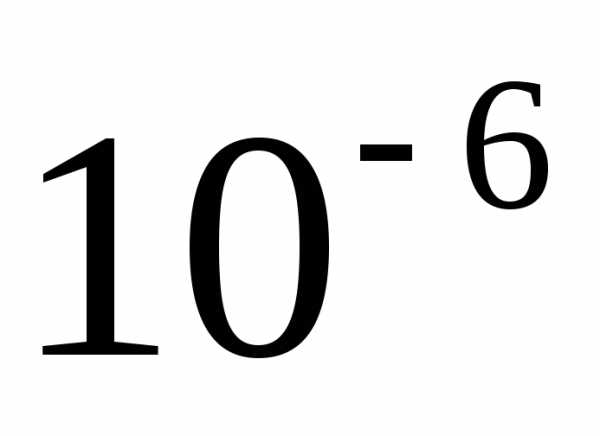 ).
).
Пример 19.5.Вычислим 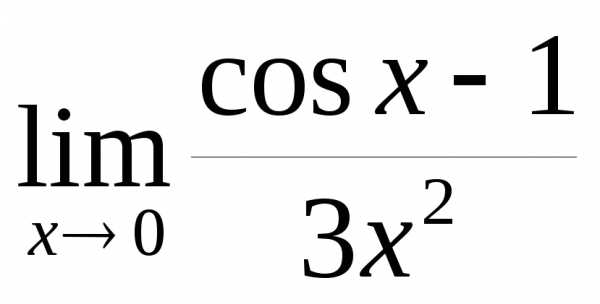 .
.
По аналогии с примером 19.3 получим
,
то есть 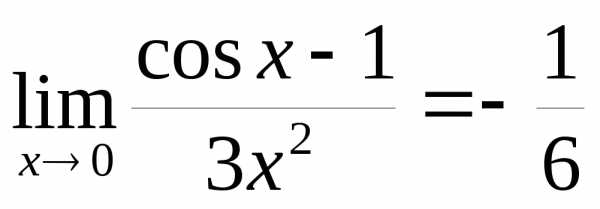 .
.
4)Функцияопределена и сколько угодно раз
дифференцируема для  .
Для
.
Для 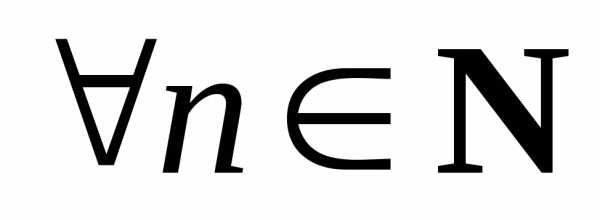 при
при  запишем формулу Тейлора. Так как,,
то формула Тейлора имеет вид:
запишем формулу Тейлора. Так как,,
то формула Тейлора имеет вид:
.
При 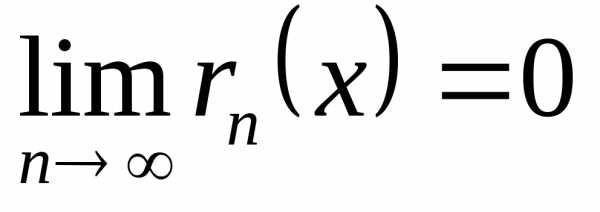 ,
поэтому
,
поэтому
.
Например, .
5)Функция. Производные,. Формула Тейлора по степенямxимеет вид:
.
Для  при
,
поэтому
при
,
поэтому
.
Если  ,
то функцияесть многочлен. В этом случае
,
то функцияесть многочлен. В этом случае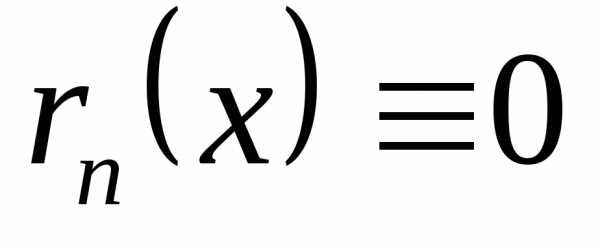 для
для и ряд представляет собой конечную сумму
– многочлен Тейлора.
и ряд представляет собой конечную сумму
– многочлен Тейлора.
1Тейлор Брук (1685-1731) – английский математик.
1Маклорен Колин (1698-1746) – шотландский математик.
2Пеано Джузеппе (1858-1932) – итальянский математик.
91
studfiles.net
Разложение некоторых элементарных функций в ряд Тейлора.
Задача разложения
функции в ряд Тейлора в окрестности
точки  решается в следующем порядке:
решается в следующем порядке:
Находятся последовательно .
Записываются (1).
Находим интервал сходимости ряда (1): .
Записываем остаточный член
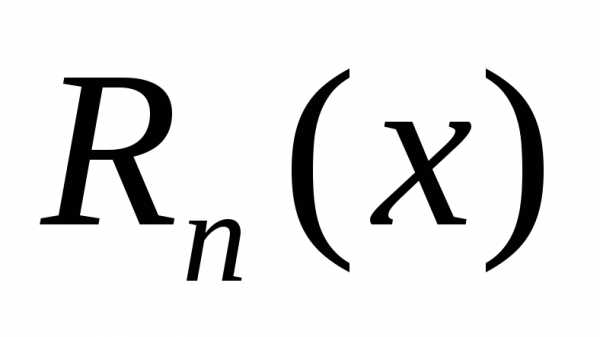 в каком-то виде.
в каком-то виде.Находим те точки , для которых.
После выполнения
этих пунктов в (1) вместо  можно поставить равенство
можно поставить равенство .
.
Функция  .
.
Пусть задана
функция 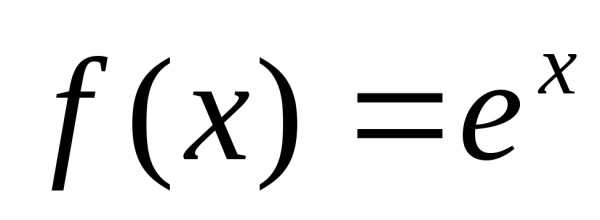 ,
она бесконечно дифференцируемая и
,
где
,
она бесконечно дифференцируемая и
,
где .
.
Найдем коэффициенты разложения , тогда
-это
ряд Маклорена для функции  ,
который сходится к этой функции на всей
числовой прямой.
,
который сходится к этой функции на всей
числовой прямой.
Функция .
Найдем ее производные
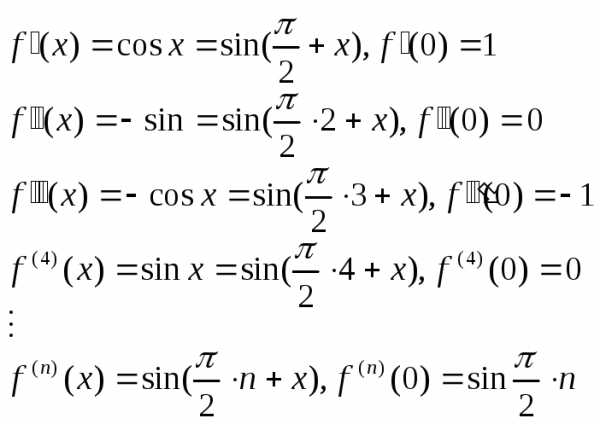
Вычислим коэффициенты в формуле Тейлора:
 .
Пусть
.
Пусть  ,
тогда
,
тогда  ,
если
,
то так как
,
то по теореме 2, можно утверждать, что
ряд Тейлора сходится к функции
,
если
,
то так как
,
то по теореме 2, можно утверждать, что
ряд Тейлора сходится к функции .
.
.
Функция . Можно провести аналогично разложение, а можно разложить другим способом. Мы знаем, что степенной ряд можно дифференцировать в интервале его сходимости. Тогда .
Ряд Маклорена для функции.
Так как функция  и ее производные не определены в точке
и ее производные не определены в точке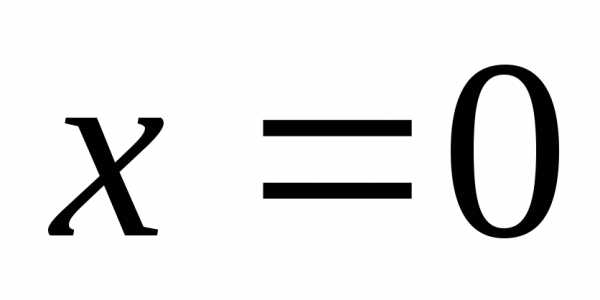 ,
поэтому будем рассматривать функцию ,
которая определена
,
вместе с производными. Продифференцируем
,
поэтому будем рассматривать функцию ,
которая определена
,
вместе с производными. Продифференцируем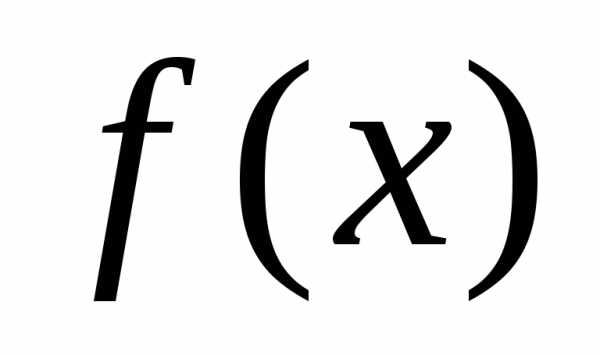 :
:
 —
как сумма бесконечно убывающей
геометрической прогрессии
—
как сумма бесконечно убывающей
геометрической прогрессии 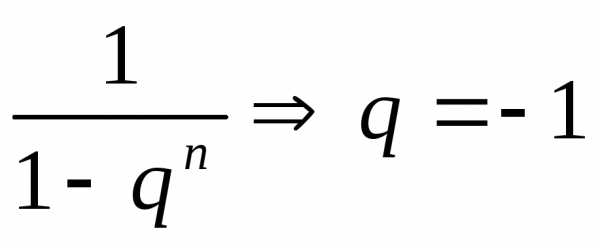 (имеет сумму при
(имеет сумму при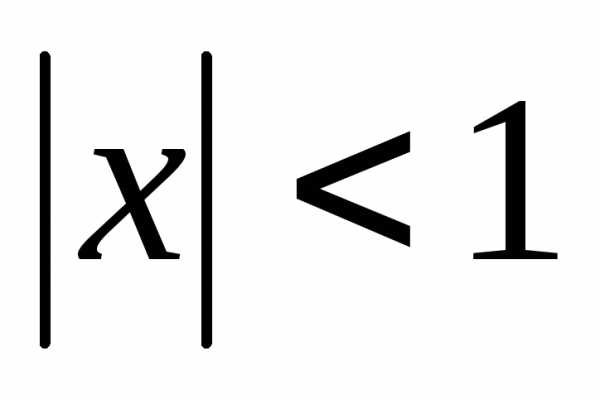 ).
).
Проинтегрируем
этот ряд почленно по любому отрезку от 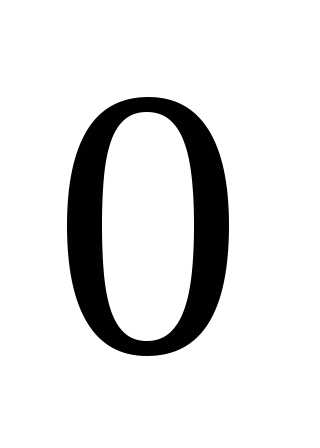 до
до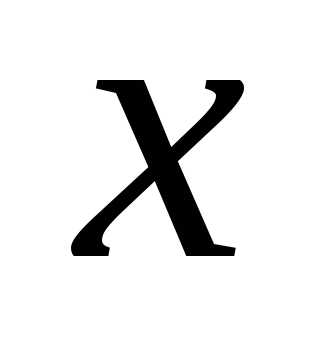 ,
где
.
Получим
он сходится при
,
где
.
Получим
он сходится при .
Проверим сходится ли ряд на границах
интервала
.
Проверим сходится ли ряд на границах
интервала :
:
при 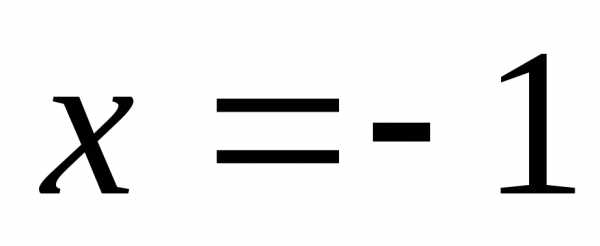 ряд вообще суммы не имеет, при
ряд вообще суммы не имеет, при получается знакочередующийся рядпо теореме Лейбница он сходится, покажем,
что он сходится к
получается знакочередующийся рядпо теореме Лейбница он сходится, покажем,
что он сходится к ,
то есть.
Воспользуемся теоремой (достаточным
условием разложимости в ряд Тейлора).
Для этого оценим остаточный член в
формуле Лагранжа.при
,
то есть.
Воспользуемся теоремой (достаточным
условием разложимости в ряд Тейлора).
Для этого оценим остаточный член в
формуле Лагранжа.при
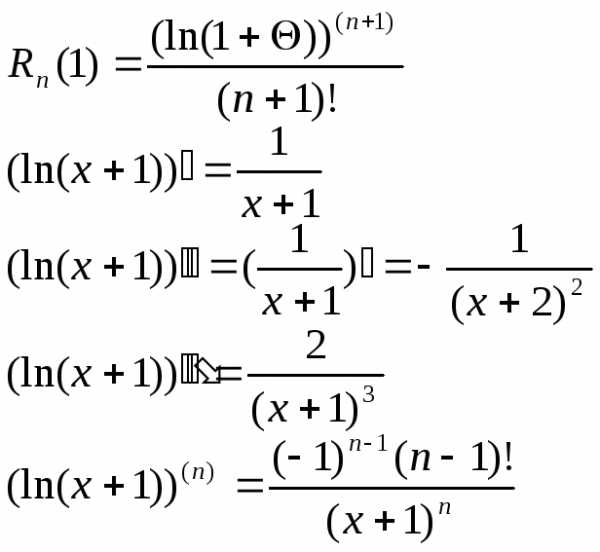 Тогда
.
Тогда
.
Таким образом, , то есть ряд сходится при.
При 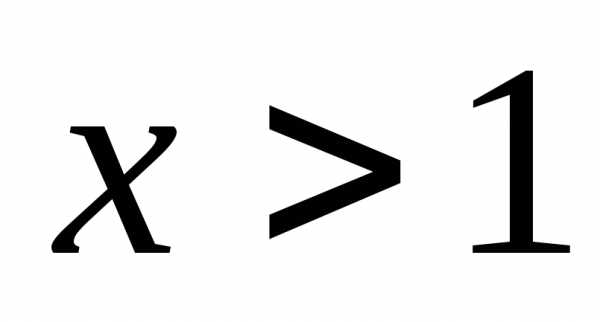 ряд расходится, так как не выполнено
необходимое условие сходимости ряда,
так как
ряд расходится, так как не выполнено
необходимое условие сходимости ряда,
так как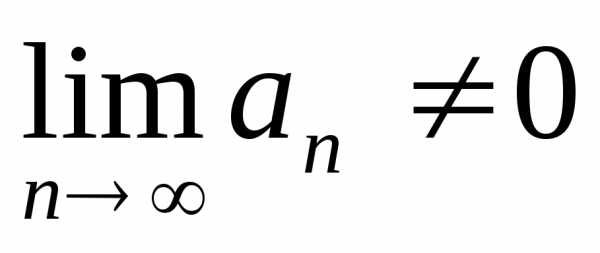 .
.
Разложение степенной функции в ряд Тейлора.
Рассмотрим функцию . (5).
Область сходимости ряда . на границе интервала надо проверять отдельно для каждого конкретного ряда
Отметим наиболее часто встречающиеся частные случаи биномиального ряда:
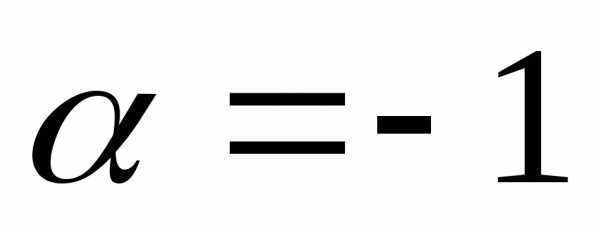 , тогда
—
бесконечно убывающая геометрическая
прогрессия, сходится при
, тогда
—
бесконечно убывающая геометрическая
прогрессия, сходится при  .
.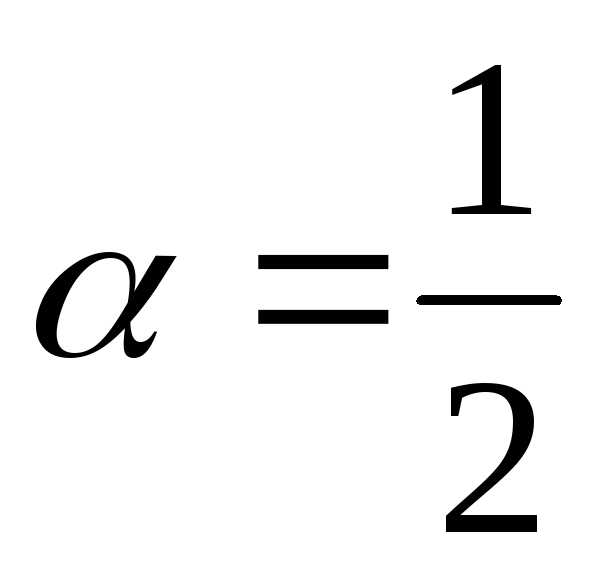 ,
тогда
,
тогда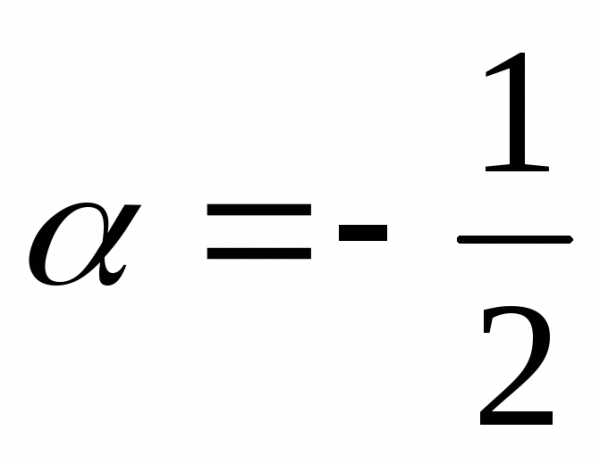 ,
тогда
,
тогда
Используя свойство степенных рядов о почленном интегрировании и дифференцировании внутри области сходимости можно получить следующие разложения:
Пример 1: сходится при  .
Проинтегрируем внутри отрезка сходимости:Пример
2:
.
Проинтегрируем внутри отрезка сходимости:Пример
2:
Сходится
при
.
Проинтегрировав по на
на получим:
.
получим:
.
Дробно-рациональная функция.
—
многочлены. Чтобы разложить  в ряд Тейлора, вначале приводим к
правильной дроби, далее полученную
дробь разбиваем на сумму более простых
методом неопределенных коэффициентов.
Эти более простые дроби раскладываем
в ряд Тейлора, используя разложение в
геометрическую прогрессию.
в ряд Тейлора, вначале приводим к
правильной дроби, далее полученную
дробь разбиваем на сумму более простых
методом неопределенных коэффициентов.
Эти более простые дроби раскладываем
в ряд Тейлора, используя разложение в
геометрическую прогрессию.
.
.

Ряд Тейлора. Разложение основных элементарных функций в степенные ряды.
Теорема: Всякая функция, бесконечно дифференцируемая
в интервале 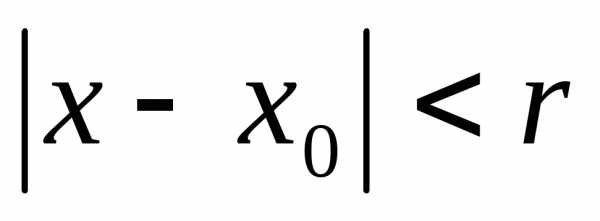 ,
то есть,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд Тейлора.
,
то есть,
может быть разложена в этом интервале
в сходящийся к ней степенной ряд Тейлора.
,
если в этом интервале выполняется
условие
,
где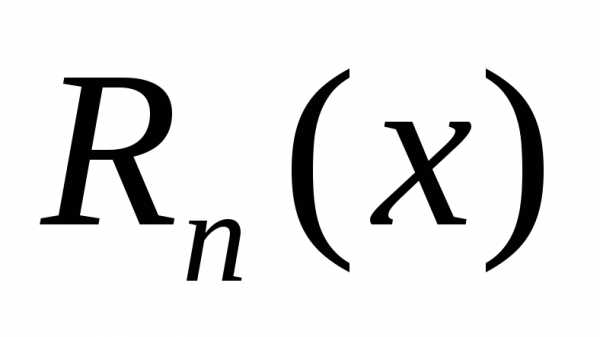 —
остаточный член формулы Тейлора,.
При
—
остаточный член формулы Тейлора,.
При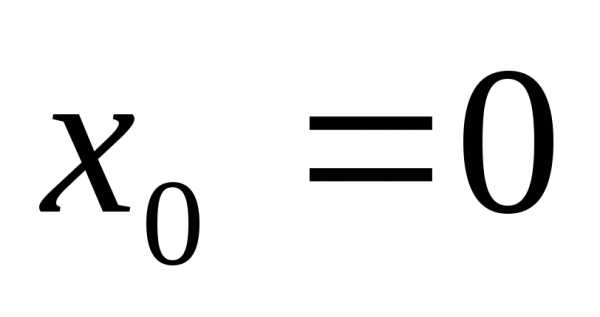 получается ряд Маклорена:.
Если в некотором интервале, содержащем
точку
получается ряд Маклорена:.
Если в некотором интервале, содержащем
точку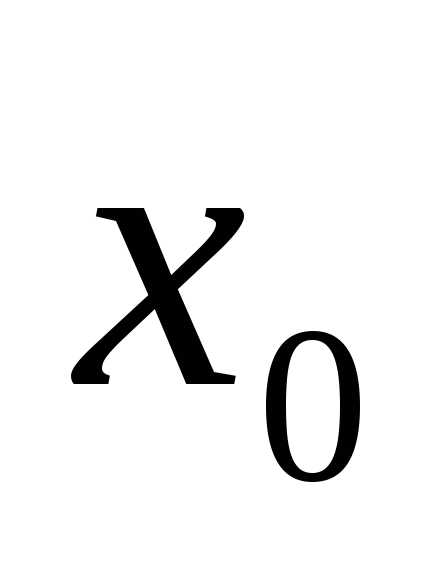 ,
при любом
,
при любом 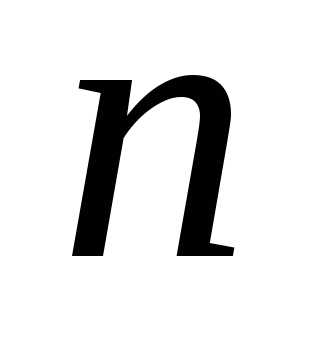 выполняется неравенство
,
где
выполняется неравенство
,
где —
положительная постоянная, то
—
положительная постоянная, то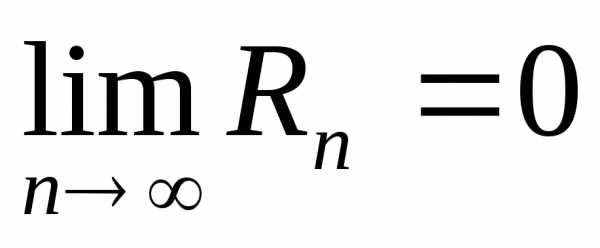 и функция
и функция разложима в ряд Тейлора.
разложима в ряд Тейлора.
studfiles.net
Ряд Тейлора | Математика | FANDOM powered by Wikia
Ряд Тейлора — разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора.
Пусть функция $ f(x) $ бесконечно дифференцируема в некоторой окрестности точки $ {a} $, тогда ряд
- $ f(x) = f(a)+\sum_{k=1}^\infty {f^{(k)} (a) \over k!} (x — a)^k $
называется рядом Тейлора функции $ f $ в точке $ a $.
В случае, если $ a=0 $, этот ряд иногда называется рядом Маклорена.
Если $ f $ есть аналитическая функция, то её ряд Тейлора в любой точке $ a $ области определения $ f $ сходится к $ f $ в некоторой окрестности $ a $.
Формула Тейлора Править
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
- Пусть функция $ f(x) $ имеет $ n+1 $ производную в некоторой окрестности точки $ a $, $ U(a, \epsilon) $
- Пусть $ x\in U(a, \epsilon) $
- <I>Пусть $ p $ — произвольное положительное число,
тогда: $ \exists $ точка $ \xi\in (x,a) $ при $ x < a $ или $ \xi\in (a,x) $ при $ x > a $:
$ f(x) = f(a) + \sum_{k=1}^n {f^{(k)} (a) \over k!} (x — a)^k + \left({x — a \over x — \xi}\right)^p{(x — \xi)^{n+1}\over n! p}f^{(n+1)}(\xi) $
Это формула Тейлора с остаточным членом в общей форме (форме Шлемильха — Роша).
Различные формы остаточного члена Править
В форме Лагранжа:
- $ R_{n+1}(x) = {(x — a)^{n+1} \over (n+1)!}f^{(n+1)} [a + \theta(x — a)] \qquad p = n+1 $
В форме Коши:
- $ R_{n+1}(x) = {(x — a)^{n+1} (1 — \theta)^n \over n!}f^{(n+1)} [a + \theta(x — a)] \qquad p = 1 $
Ослабим предположения:
- Пусть функция $ f(x) $ имеет $ n-1 $ производную в некоторой окрестности точки $ a $
- И $ n $ производную в самой точке $ a $, тогда:
- $ R_{n+1}(x) = o[(x — a)^n ] $ — остаточный член в асимптотической форме (форме Пеано)
Ряды Тейлора некоторых функций Править
- Экспонента: $ \mathrm{e}^{x} = \sum^{\infin}_{n=0} \frac{x^n}{n!} $ для всех $ x $
- натуральный логарифм: $ \ln(1+x) = \sum^{\infin}_{n=0} \frac{(-1)^n}{n+1} x^{n+1} $ для $ \left| x \right| < 1 $
- $ \frac{1}{1-x} = \sum^{\infin}_{n=0} x^n $ для $ \left| x \right| < 1 $
- Биномиальное разложение: $ (1+x)^\alpha = \sum^{\infin}_{n=0} {\alpha \choose n} x^n $ для всех $ \left| x \right| < 1\quad\mbox{ and all complex } \alpha $
- Тригонометрические функции:
- $ \sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1} $ для всех $ x $
- $ \cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n} $ для всех $ x $
- $ \operatorname{tg} x = \sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1} $ для $ \left| x \right| < \frac{\pi}{2} $
- $ \sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n} $ для $ \left| x \right| < \frac{\pi}{2} $
- $ \arcsin x = \sum^{\infin}_{n=0} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} $ для $ \left| x \right| < 1 $
- $ \operatorname{arctg} x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1} $ для $ \left| x \right| < 1 $
- Гиперболические функции:
- $ \operatorname{sh} \left(x\right) = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1} $ для всех $ x $
- $ \operatorname{ch} \left(x\right) = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n} $ для всех $ x $
- $ \operatorname{th}\left(x\right) = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1} $ для $ \left|x\right| < \frac{\pi}{2} $
- $ \operatorname{areash} \left(x\right) = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1} $ для $ \left| x \right| < 1 $
- $ \operatorname{areath} \left(x\right) = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1} $ для $ \left| x \right| < 1 $
Интересные факты
Несмотря на то, что фамилия Тейлор правильно произносится с ударением на первом слоге, некоторые преподаватели старой закалки любят говорить Тейлóр и таким образом проверять кто же из студентов ходил на лекции, а кто нет. В некоторых случаях подобный трюк проделывают с фамилией <a data-rte-meta=»%7B%22type%22%3A%22internal%22%2C%22text%22%3A%22%5Cu0411%5Cu0430%5Cu043d%5Cu0430%5Cu0445%5Cu0430%22%2C%22link%22%3A%22%5Cu0411%5Cu0430%5Cu043d%5Cu0430%5Cu0445%22%2C%22wasblank%22%3Afalse%2C%22noforce%22%3Atrue%2C%22wikitext%22%3A%22%5B%5B%5Cu0411%5Cu0430%5Cu043d%5Cu0430%5Cu0445%7C%5Cu0411%5Cu0430%5Cu043d%5Cu0430%5Cu0445%5Cu0430%5D%5D%22%7D» data-rte-instance=»2561-7752124154f252a814fc05″ href=»/index.php?title=%D0%91%D0%B0%D0%BD%D0%B0%D1%85&amp;action=edit&amp;redlink=1″ title=»Банах (такой страницы не существует)»>Банаха</a>.
hu:Taylor-sornl:Taylorreeks pl:Szereg Taylorasl:Taylorjeva vrsta sv:Taylorserie
ru.math.wikia.com
Ряд Тейлора. Разложение функции в ряд Тейлора.
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1), где f(x) — функция, имеющая при х=а производные всех порядков. Rn — остаточный член в ряде Тейлора определяется выражением
2)
k-тый коэффициент (при хk) ряда определяется формулой
3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при a=0
члены ряда определяются по формуле
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
- Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
- Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.tehtab.ru
69. Формула Тейлора. Разложение функции по формуле Тейлора.
Пусть функция y= f(x) задана на (a, b) и x0 (a, b). Поставим следующую задачу: найти многочлен P(x), значения которого в окрестности точки x0 приближенно совпадали бы со значениями функции f(x) в соответствующих точках. Тогда можно будет считать, что f(x)≈P(x) и задачу вычисления значенийf(x) в окрестности точки x0 можно заменить более легкой задачей вычисления значений P(x).
Пусть искомый многочлен имеет степень n P(x) = Pn(x). Будем искать его в виде
(1) |
В этом равенстве нам нужно найти коэффициенты .
Для того чтобы этот многочлен был «близок» к функции f(x) потребуем выполнения следующих равенств:
Пусть функция y= f(x) имеет производные до n-ого порядка. Найдем коэффициенты многочленаPn(x) исходя из условия равенства производных.
Введем обозначение n! = 1·2·3…n, 0! = 1, 1! = 1.
Подставим в (1) x = x0 и найдем , но с другой стороны. Поэтому
Далее найдем производную и вычислимСледовательно,.
Учитывая третье условие и то, что
,
получим , т.е..
Далее . Значит,, т.е..
Очевидно, что и для всех последующих коэффициентов будет верна формула
Подставляя найденные значения коэффициентов в формулу (1), получим искомый многочлен:
Обозначим и назовем эту разностьn-ым остаточным членом функции f(x) в точке x0. Отсюда и, следовательно,если остаточный член будет мал.
Оказывается, что если x0 (a, b) при всех x (a, b) существует производная f (n+1)(x), то для произвольной точки x (a, b) существует точка, лежащая между x0 и x такая, что остаток можно представить в виде:
Это так называемая формула Лагранжа для остаточного члена.
Формула
где x (x0, x) называется формулой Тейлора.
Если в этой формуле положить x0 = 0, то она запишется в виде
где x ( x0, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.
.
РАЗЛОЖЕНИЕ ПО ФОРМУЛЕ МАКЛОРЕНА НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Рассмотрим функцию f(x)=ex. Представим ее по формуле МакЛорена в виде суммы многочлена и некоторого остатка. Для этого найдем производные до (n+1) порядка:
Таким образом, получаем
Используя эту формулу и придавая x различные значения, мы сможем вычислить значение ex.
Например, при x=1, ограничиваясь n=8, получим формулу, позволяющую найти приближенное значение числа e:
причем остаток
Отметим, что для любого x R остаточный член
Действительно, так как ξ (0; x), то величина eξ ограничена при фиксированном x. При x> 0 eξ < ex. Докажем, что при фиксированном x
Имеем
Если x зафиксировано, то существует натуральное число N такое, что |x|<N.
Обозначим Заметив, что 0<q<1, приn>N можем написать
Но , не зависящая отn, а так как q<1. ПоэтомуСледовательно,
Таким образом, при любом x, взяв достаточное число слагаемых, мы можем вычислить ex с любой степенью точности.
Выпишем разложение по формуле МакЛорена для функции f(x)=sin x.
Найдем последовательные производные от функции f(x)=sin x.

Подставляя полученные значения в формулу МакЛорена, получим разложение:
Несложно заметить, что преобразовав n-й член ряда, получим
.
Так как , то аналогично разложениюex можно показать, что для всехx.
Пример. Применим полученную формулу для приближенного вычисления sin 20°. При n=3 будем иметь:
Оценим сделанную погрешность, которая равна остаточному члену:
Таким образом, sin 20°= 0,342 с точностью до 0,001.
f(x) = cos x. Аналогично предыдущему разложению можно вывести следующую формулу:
Здесь также для всехx. Докажите формулу самостоятельно.
f(x)=ln (1+x). Заметим, что область определения этой функции D(y)=(–1; +∞).
Найдем формулу МакЛорена для данной функции.
Подставим все найденные производные в ряд МакЛорена.
Можно доказать, что если x (–1;1],то , т.е. выведенная формула справедлива приx ( –1;1].
f(x) = (1+x)m, где m R, m≠0.
При m≠Z данная функция определена при x> –1. Найдем формулу МакЛорена для этой функции:
И следовательно,
Можно показать, что при |x|<1
studfiles.net