Sup в математике – Список математических аббревиатур

Содержание

Грани множеств | Царица Математика

Определение. Число $m$ называется нижней гранью множества $E$, если оно является наибольшим из нижних границ множества $E$.

Обозначается нижняя грань: $m = \inf E$. Произносится $\inf$, как «инфимум» (от латинского infimum — самый низкий).

$m=\inf E \Leftrightarrow \left\{ \begin{align} &\forall x \in E \; (x \ge m), \\ &\forall \varepsilon > 0 \; \exists x’ \in E \; (x’ < m + \epsilon). \\\end{align} \right.$

Определение. Число $M$ называется верхней гранью множества $E$, если оно является наименьшим из верхних границ множества $E$.

Обозначается верхняя грань: $M = \sup E$. Произносится $\sup$, как «супремум» (от латинского supremum — самый высокий).

$M = \sup E \Leftrightarrow \left\{ \begin{align} &\forall x \in E \; (x \le M), \\ &\forall \varepsilon > 0 \; \exists x» \in E \; (x» > M — \epsilon). \\\end{align} \right.$

Пример.

Рассмотрим множество $E=\left\{\frac{1}{n} \right\}$. Оно ограничено и сверху и снизу.

$\sup E = 1 \in E$, $\inf E = 0 \notin E$.

Некоторые свойства граней

1. Если множество $A$ является подмножеством множества $B$ или совпадает с ним, то верхняя грань множества $A$ меньше либо равна верхней грани множества $B$, а нижняя грань множества $A$ больше либо равна нижней грани множества $B$.

$A \subseteq B \Rightarrow$ $\sup A \le \sup B$, $\inf A \ge \inf B$

2. Для любых множеств $A$ и $B$ супремум (верхняя грань) суммы $A$ и $B$ равен сумме супремумов этих множеств. Аналогично для инфимума (нижней грани): инфимум суммы множеств $A$ и $B$ равен сумме инфимумов этих множеств.

$\forall A, B$: $\sup (A+B) = \sup A + \sup B$, $\inf (A + B) = \inf A + \inf B$.

$A + B = \{x + y, x \in A, y \in B \}$.

3. Для любых множеств $A$ и $B$ супремум (верхняя грань) произведения $A$ и $B$ равен произведению супремумов этих множеств. Аналогично для инфимума (нижней грани): инфимум произведения множеств $A$ и $B$ равен произведению инфимумов этих множеств.

$\forall A, B$: $\sup (A \cdot B) = \sup A \cdot \sup B$, $\inf (A \cdot B) = \inf A \cdot \inf B$.

$A \cdot B = \{x \cdot y, x \in A, y \in B \}$.

4. Для любого множества $A$, являющегося подмножеством множества действительных чисел супремум $-A$ равен минус инфимуму $A$, а инфимум $-A$ равен минус супремуму $A$.

$\forall A \subset R$: $\sup (-A) = — \inf A$, $\inf (-A) = — \sup (A)$.

$-A = \{-x, \; x \in A\}$.

mathematike.ru

Правила ввода математических выражений

Ввод чисел:

Целые числа вводятся обычным способом, например: 4; 18; 56
Для ввода отрицательного числа необходимо поставить знак минус: -19; -45; -90
Рациональные числа вводятся с использованием символа /, например: 3/4; -5/3; 5/(-19)

Вещественные числа вводятся с использованием точки в качестве разделителя целой и дробной частей: 4.5; -0.4

Ввод переменных и констант:

Переменные и константы вводятся латинскими буквами, например: x; y; z; a; b.
Для ввода переменных можно также использовать целые числа после соответствующей буквы: x1; y3; a4.
Константы π и e вводятся как pi и e — соответственно.
Символ бесконечности ∞ вводится двумя маленькими латинскими буквами oo или словом inf.
Соответственно, плюс бесконечность задается как +oo, и минус бесконечность как -oo.

Сумма и разность:

Сумма и разность задаются при помощи знаков + и — соответственно, например: 3+a; x+y; 5-4+t; a-b+4; ВНИМАНИЕ! Никаких пробелов между операндами быть не должно, например ввод: x + a — неправильный, правильно вводить так: x+a — без пробелов.

Умножение:

Умножение задается знаком *, например: 3*t; x*y; -5*x.
ВНИМАНИЕ! Ввод знака * необходим всегда, т.е. запись типа: 2x — недопустима. Следует всегда использовать знак *, т.е правильная запись: 3*x.

Деление:

Деление задается знаком /, например: 15/a; y/x;.

Степень:

Степень задается знаком ^, например: x^2; 4^2; y^(-1/2).

Приоритет операций:

Для указания (или изменения) приоритета операций необходимо использовать скобки (), например: (a+b)/4 — тут вначале будет произведено сложение a+b, а потом сумма разделится на 4, тогда как без скобок: — сначала b разделится на 4 и к полученному прибавится a. ВНИМАНИЕ! В непонятных случаях лучше всегда использовать скобки для получения нужного результата, например: 2^4^3 — неясно как будет вычислено это выражение: cначала 2^4, а затем результат в степень 3, или сначала 4^3=64, а затем 2^64? Поэтому, в данном случае, необходимо использовать скобки: (2^4)^3 или 2^(4^3) — смотря что нужно.
Также распространенной ошибкой является запись вида: x^3/4 — непонятно: вы хотите возвести x в куб и полученное выражение разделить на 4, или хотите возвести x в степень 3/4? В последнем случае необходимо использовать скобки: x^(3/4).

Ввод функций:

Функции вводятся с использованием маленьких латинских букв: sin; cos; tan; log.
ВНИМАНИЕ! Аргумент функции всегда берется в скобки (), например: sin(4); cos(x); log(4+y).
Запись типа: sin 4; cos x; log 4+y — недопустима. Правильная запись: sin(4); cos(x); log(4+y).
Если необходимо возвести функцию в степень, например: синус x и все это в квадрате, это записывается вот так: (sin(x))^2. Если необходимо возвести в квадрат аргумент, а не функцию (т.е синус от x^2), тогда это выглядит вот так: sin(x^2). Запись типа: sin^2 x — недопустима.

www.mathforyou.net

Верхний и нижний индекс | WebReference

Индексом по отношению к тексту называется смещение символов относительно базовой линии вверх или вниз. В зависимости от положительного или отрицательного значения смещения, индекс называется, соответственно, верхним или нижним. Они активно применяются в математике, физике, химии и для обозначения единиц измерения. HTML предлагает два элемента для создания индекса: (от англ. superscript) — верхний индекс и (от англ. subscript) — нижний индекс. Текст, помещённый в один из этих контейнеров, обозначается меньшим размером, чем базовый текст, и смещается относительно него вверх или вниз. В примере 1 приведено совместное использование указанных элементов и стилей для изменения вида текста.

Пример 1. Создание верхнего и нижнего индекса

<!DOCTYPE html>
<html>
 <head>
  <meta charset="utf-8">
  <title>Верхний и нижний индекс</title>
  <style>
   .formula { font-size: 1.4em; /* Размер текста формулы */ }
   sup, sub {
    font-style: italic; /* Курсивное начертание */
    color: red; /* Красный цвет символов */
   }
   sub {
    color: blue; /* Синий цвет символов */
   }
  </style>
 </head>
 <body>
  <p>Характеристическое уравнение поверхности второй степени</p>
  <p>λ<sup>3</sup> - I<sub>1</sub>λ<sup>2</sup> +
    I<sub>2</sub>λ - I<sub>3</sub> = 0</p>
 </body>
</html>

В примере одновременно встречается как нижний, так и верхний индекс. Для изменения начертания шрифта индекса применяются стили, которые задают единое оформление (рис. 1).

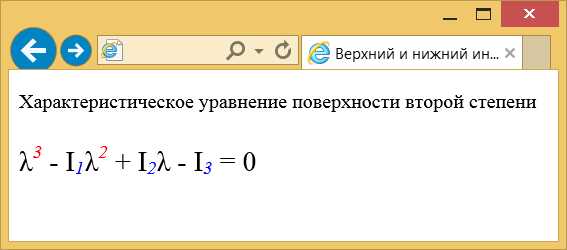
Рис. 1. Вид индексов после применения стилей

Можно вообще отказаться от использования и в пользу стилей. Аналогом этих элементов служит свойство vertical-align, заставляющее текст смещаться по вертикали на заданное расстояние. В частности, в примере 2 в качестве значения применяется 0.8em для верхнего индекса и -0.5em для нижнего. Em — это относительная единица, равная размеру текущего шрифта. Например, 0.5em говорит о том, что текст надо сдвинуть на половину размера шрифта.

Пример 2. Использование стилей для управления индексами

<!DOCTYPE html>
<html>
 <head>
  <meta charset="utf-8">
  <title>Верхний и нижний индекс</title>
  <style>
   .formula { 
    font-size: 1.6em; /* Размер текста */ 
    font-style: italic; /* Курсивное начертание */
   }
   .sup,  .sub {
    font-style: normal; /* Нормальное начертание */
    font-size: 0.6em; /* Размер индекса */
    color: red; /* Цвет верхнего индекса */
    vertical-align: 0.8em; /* Сдвигаем текст вверх */
   }
   .sub {
    color: blue; /* Цвет нижнего индекса */
    vertical-align: -0.5em; /* Сдвигаем текст вниз */
   }
  </style>
 </head>
 <body>
  <p>Многочлен степени <em>n</em></p>
  <p>f(x) = a<span>0</span> + a<span>1</span> x + ... + 
   a<span>n-1</span> x<span>n-1</span> + 
   a<span>n</span> x<span>n</span></p>
 </body>
</html>

В примере сама формула выводится увеличенным размером, символы верхнего индекса устанавливаются красным цветом, а нижние — синим (рис. 2).

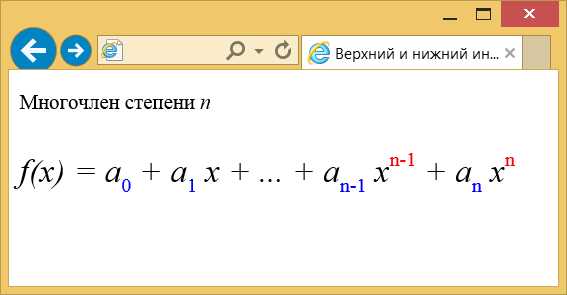
Рис. 2. Управление положением и видом нижнего и верхнего индекса

Использование элемента делает код громоздким, поэтому лучше переопределить стили и , в частности, задать положение индекса, цвет и курсивное начертание.

Автор и редакторы

Автор: Влад Мержевич

Последнее изменение: 05.09.2017

Редакторы: Влад Мержевич

webref.ru

Как набирать функции и константы

В отличие от форума и учебных материалов, где для ввода формул используется язык LaTex, в онлайн сервисе существуют свои правила ввода функций — более простые и наглядные.

Как вводить функции и некоторые константы:

Простейшие математические операции
Сумма: +; Вычитание: -; Умножение: * или пробел; Деление и дроби: /
Некоторые константы
e — основание натурального логарифма с приближенным числовым значением 2.71828… EulerGamma — постоянная Эйлера с числовым значением 0.577216…	pi — константа 3.14159… равная отношению длины окружности к ее диаметру GoldenRatio — число 1.6180… определяющее деление отрезка по правилу золотого сечения
Элементарные функции
sqrt(x) — квадратный корень значения x, x^y — x в степени y, exp(x)=e^x — экспонента значения x,	log(a,x) — логарифм с основанием a, log(x)=ln(x) — натуральный логарифм, dilog(x) — дилогарифм значения x,
Тригонометрические функции
sin(x) — синус значения x cos(x) — косинус значения x tan(x) — тангенс значения x	cot(x)=ctg(x) — котангенс значения x sec(x) — секанс значения x, sec(x)=1/cos(x) csc(x) — косеканс значения x, csc(x)=1/sin(x)
Обратные тригонометрические функции
arcsin(x) — арксинус значения x, arccos(x) — арккосинус значения x, arctan(x) — арктангенс значения x,	arccot(x) — арккотангенс значения x, arcsec(x) — арксеканс значения x, arccsc(x) — арккосеканс значения x,
Примеры:
sqrt(1-pi x^2) — cos(x) x-e^x+log(4,x) —	sec(EulerGamma x)/5 —

Что делать, если вместо решения пустой экран

Если вы ввели функцию, нажали на кнопку «решить», открылось поле с решением, но оно пустое, как, например, изображено ниже:

или

значит, имеется конфликт браузера с заголовками сервера. Исправить ситуацию можно отключив в браузере CSP (Content Security Policy). Для браузера Chrome это реализуется установкой расширения, которое скачать можно здесь: Disable Content-Security-Policy. Для остальных браузеров можно найти аналогичные решения.

Однако крайне рекомендуем после окончания работы с сайтом matematikam.ru включить CSP снова. Это повысит безопасность при работе в интернете.

matematikam.ru

Теория множеств — Википедия

Материал из Википедии — свободной энциклопедии

Тео́рия мно́жеств — раздел математики, в котором изучаются общие свойства множеств — совокупностей элементов произвольной природы, обладающих каким-либо общим свойством. Создана во второй половине XIX века Георгом Кантором при значительном участии Рихарда Дедекинда, привнесла в математику новое понимание природы бесконечности, была обнаружена глубокая связь теории с формальной логикой, однако уже в конце XIX — начале XX века теория столкнулась со значительными сложностями в виде возникающих парадоксов^[⇨], поэтому изначальная форма теории известна как наивная теория множеств^[⇨]. В XX веке теория получила существенное методологическое развитие, были созданы несколько вариантов аксиоматической теории множеств^[⇨], обеспечивающие универсальный математический инструментарий, в связи с вопросами измеримости множеств тщательно разработана дескриптивная теория множеств^[⇨].

Теория множеств стала основой многих разделов математики — общей топологии, общей алгебры, функционального анализа и оказала существенное влияние на современное понимание предмета математики^[1]. В первой половине XX века теоретико-множественный подход был привнесён и во многие традиционные разделы математики, в связи с чем стал широко использоваться в преподавании математики, в том числе в школах. Однако использование теории множеств для логически безупречного построения математических теорий осложняется тем, что она сама нуждается в обосновании своих методов рассуждения. Более того, все логические трудности, связанные с обоснованием математического учения о бесконечности, при переходе на точку зрения общей теории множеств приобретают лишь бо́льшую остроту^[2].

Начиная со второй половины XX века представление о значении теории и её влияние на развитие математики заметно снизились за счёт осознания возможности получения достаточно общих результатов во многих областях математики и без явного использования её аппарата, в частности, с использованием теоретико-категорного инструментария (средствами которого в теории топосов обобщены практиче

ru.wikipedia.org

Sup в математике – Список математических аббревиатур — Википедия