Учебно-методическое пособие «Техника выполнения сопряжений» — Информио
При изучении дисциплины «Начертательная геометрия и инженерная графика» студенты должны усвоить правила и последовательность выполнения геометрических построений и сопряжений. В этом отношении лучшим способом приобретения навыков построения являются задания по вычерчиванию контуров сложных деталей.
Прежде чем приступить к выполнению контрольного задания,
нужно изучить технику выполнения геометрических построений и сопряжений по
методическому пособию.
Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжения дугой заданного радиуса нужно найти:
- Центр сопряжения – центр, из которого проводят дугу;
- Точки сопряжения (касания) – точки, в которых одна линия переходит в другую.
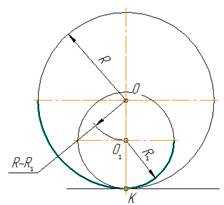
Центр сопряжения находится от точек сопряжения на одинаковых расстояниях, равных радиусу сопряжения R. Переход от прямой к окружности будет плавным в том случае, если прямая касается к окружности. Точка сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой (рис. 1)

рис. 1
Переход от одной окружности к другой будет плавным, если окружности касаются.
Различают два случая
касания дуг окружностей: внешнее (рис.
2) и внутреннее (рис.3).
При внешнем касании центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО1 равно сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1, соединяющей их центры.
При внутреннем касании центры окружностей лежат по одну сторону от их общей касательной L. Расстояние между их центрами ОО1 равно разности их радиусов R-R1 и точка касания К окружностей лежит на продолжении прямой ОО1 (рис. 3).
| |
рис. 2 | рис. 3 |
Касание дуг окружностей:
рис. 2 – сопряжение двух окружностей (внешнее касание)
рис. 3 – сопряжение двух окружностей (внутреннее касание)
Сопряжение двух пересекающихся прямых
Даны пересекающиеся под прямым, острым и тупым углами прямые линии.
Требуется построить сопряжения этих прямых дугой заданного радиуса R.
рис. 4
- Для нахождения центра сопряжения проводят вспомогательные прямые, параллельные данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и будет центом дуги сопряжения (рис. 4).
- Перпендикуляры, опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки касания К и N.
- Из точки О, как центра, описывают дугу заданного радиуса R.
рис. 5
Примечание.Для прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).
Сопряжение дуги окружности и прямой линии дугой заданного радиуса.
Внешнее касание
Дана окружность радиуса R и прямая АВ. Требуется соединить их дугой радиусом R1.
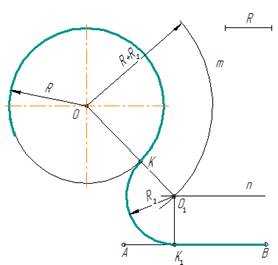
рис. 6
- Для нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R1 и на расстоянии R1 – прямую n // AB. Точка О1 пересечения прямой n и дуги m будет центром сопряжения.
- Для получения точек сопряжения: К и К1 проводят линию центров ОО1 и восстанавливают к прямой АВ перпендикуляр ОК1.
- Из центра сопряжения О1 между точками К и К1 проводят дугу сопряжения радиусом R1
Внутреннее касание
В случае внутреннего касания выполняют те же построения, но дугу m вспомогательной окружности проводят радиусом R — R1.
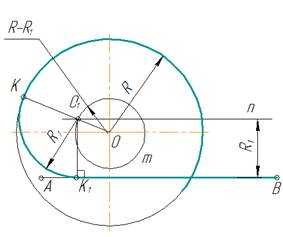
рис. 7
Сопряжение двух окружностей дугой заданного радиуса
Заданы две окружности радиусом R1 и R2. Требуется построить сопряжение дугой заданного радиуса R.
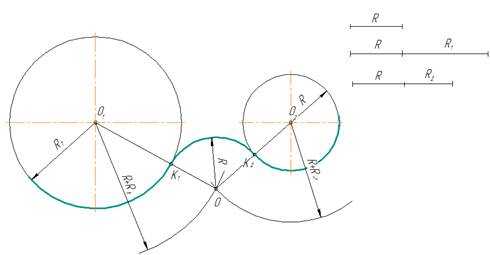
рис. 8
Внешнее касание
- Для определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом R + R1 и из центра О2 окружности радиуса R + R2. Точка О пересечения этих дуг является центом сопряжения.
- Соединяя центры О и О1, а так же О и О2 , определяют точки сопряжения (касания) К1 и К2.
- Из центра О радиусом R проводят дугу сопряжения между точками К1 и К2
Внутреннее касание
При внутреннем касании выполняют те же построения, но дуги проводят радиусами
R -R1 и R — R2.

рис. 9
Смешанное касание
рис. 10
Центр сопряжения О находится в пересечении двух дуг, описанных из центра О1 радиусом R — R1 и из центра О2 радиусом R + R2
Примечание. При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.
Частные случаи
Нахождение центра дуги заданного радиуса.
Задана дуга радиусом R, соединяющая две параллельные прямые mи n и проходящая через точку А ∈ m (рис. 11). Требуется найти центр О заданной дуги.
рис. 11
В основу построения положено нахождение точки О, равноудаленной от заданных прямых (рис. 11).
- Из точки А ∈ m, как из центра, проводят дугу вспомогательной окружности с заданным радиусом R.
- Точка О – точка пересечения этих вспомогательных линий является центром заданной дуги. (рис. 12)
рис. 12
- Боголюбов С.К. Инженерная графика: Учебник для средних специальных учебных заведений. – 3-е изд., испр. И доп. — М.: Машиностроение, 2006. – с.392: ил.
- Куприков М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил.
- Федоренко В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение. 1976. 336 с.
www.informio.ru
Сопряжение дуг окружностей дугой окружности | Начертательная геометрия
Сопряжение дуг окружностей дугой окружности могут быть выполнены: — когда расстояние между центрами O и O1 сопрягаемых дуг больше суммы их радиусов R и R1, т. е. A>R+R1; — когда расстояние между центрами O и O1 сопрягаемых дуг меньше суммы их радиусов R и R1, т. е. R+R1>A. Во всех случаях решение задачи сводится к нахождению центра сопряжения O2 и точек сопряжения C и B.
Построим сопряжение дуг окружностей дугой окружности когда A>R+R1

Сопряжение дуг окружностей дугой окружности
Заданы дуги окружностей радиусов R и R1 и расстояние между их центрами OO1 = A и радиус сопряжения R2. Находим центр сопряжения O2: — из центра O проводим дугу радиуса R+R2; — из центра O1 проводим дугу радиуса R1+R2. Пересечение этих дуг определит центр сопряжения O2.
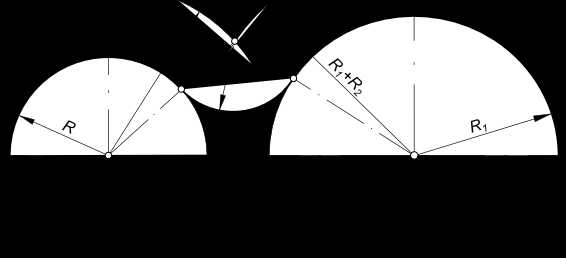
Сопряжение дуг окружностей дугой окружности
Находим точки сопряжения C и B: — из точки O2 проводим прямые в центр O и O1; — находим на пересечении этих прямых с соответствующими дугами точки сопряжения C и B;
точки сопряжения C и B соединяем дугой радиуса R2.
Для случая когда R+R1>A
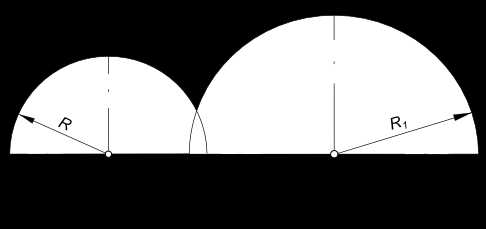
Сопряжение дуг окружностей дугой окружности
построение выполняется аналогично
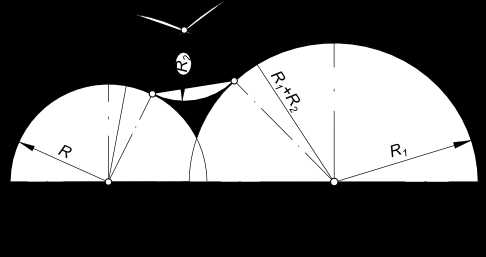
Сопряжение дуг окружностей дугой окружности
Построим сопряжение дуг окружностей дугой окружности когда A>R+R1

Сопряжение дуг окружностей дугой окружности
Заданы дуги окружностей радиусов R и R1 и расстояние между их центрами OO1 = A и радиус сопряжения R2. Находим центр сопряжения O2: — из центра O проводим дугу радиуса R2-R; — из центра O1 проводим дугу радиуса R2-R1. Пересечение этих дуг определит центр сопряжения O2.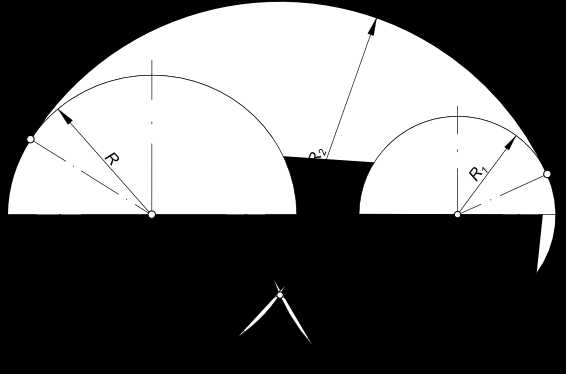
Сопряжение дуг окружностей дугой окружности
Находим точки сопряжения C и B: — из точки O2 проводим прямые в центр O и O1; — находим на пересечении этих прямых с соответствующими дугами точки сопряжения C и B;
точки сопряжения C и B соединяем дугой радиуса R2.
Сопряжение дуг окружностей дугой окружности когда R+R1>A Заданы дуги окружностей радиусов R и R1 и расстояние между их центрами OO1 = A и радиус сопряжения R2
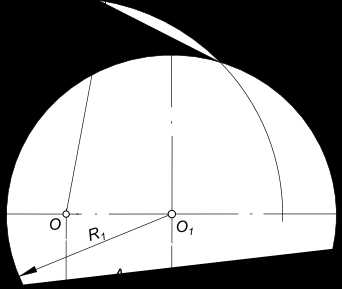
Сопряжение дуг окружностей дугой окружности
Находим центр сопряжения O2: — из центра O проводим дугу радиуса R-R2; — из центра O1 проводим дугу радиуса R1-R2. Пересечение этих дуг определит центр сопряжения O2.

Сопряжение дуг окружностей дугой окружности
Находим точки сопряжения C и B: — из точки O2 проводим прямые в центр O и O1; — находим на пересечении этих прямых с соответствующими дугами точки сопряжения C и B;
точки сопряжения C и B соединяем дугой радиуса R2
Применение приведенных выше примеров для построения сопряжений элементов рычага,
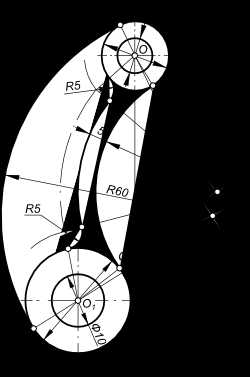
Сопряжение дуг окружностей дугой окружности
для построения сопряжений окружностей диаметров 20 и 30 мм дугами AB и EC радиусов R60 и R35 соответственно.
Применение приведенных выше примеров для построения сопряжений элементов однорогого крюка,

Сопряжение дуг окружностей дугой окружности
Заданы: фa40; b=24; h=36; d=25; d1=20; d2=16,4; d0=M20; l=60; l1=20; l2=30; R=6; R1=20; R2=20; R3=20; R4=15; R5=40; R6=45; R7=6,5; R8=2; c=2; f=4,5
Сопряжения крюка — это наиболее сложный пример на построение сопряжений. Вычерчивание крюка выполняем в следующем порядке: — проводим оси и вычерчиваем шейку крюка; — проводим из центра O1 пересечения осей основную окружность внутреннего очертания крюка. Радиус этой окружности равен a/2.; — находим центр O2 и проводим из него радиусом R3 основную дугу окружности внешнего очертания крюка. Для построения центра O2 проводим из центра O1 прямую n под углом 45 к осям и засекаем ее из точки N дугой окружности радиуса R3. Точка N удалена от центра O1 на расстояние h+a/2; — строим сопряжение внешней окружности правым прямолинейным контуром верхней части крюка. Сопрягаемая дуга имеет радиус R4. Центр сопряжения O3 и точки сопряжения K и M находим по общему правилу сопряжения дуги с прямой; — строим сопряжение внутренней окружности диаметра a с левым прямолинейным контуром верхней части крюка. Радиус сопряжения R4. Центр сопряжения O4 и точки сопряжения A и B определяются аналогично точкам O3, K и M; — строим очертания носка крюка. Пользуемся построениями приведенными на рисунках … и … . Находим центры O5, O6 и O7. Носок крюка должен касаться прямой e, проведенной на расстоянии m от горизонтальой оси крюка. Кроме того, зев крюка должен быть равен размеру O. Расстояние O измеряется по линии центров дуг O4O5, ограничивающих контур зева. Определяем центр O5 дуги радиуса R6. Для этого делаем две засечки: первую из центра O4 радиусом R5+R6+O; вторую — из центра O1 радиусом a/2+R6. Точка сопряжения E лежит на линии центров O1 — O5. Из центра O5 проводим дугу радиуса R6, начиная от точки E. Находим центр O7 дуги радиуса R7. Засекаем дугой радиуса R6-R7 из центра O5 и засекаем дугой радиуса R6-R7 из центра O6. Точка сопряжения C лежит на линии центров O5 — O7. Проводим из центра O7 дугу радиуса R7. Определяем центр O6 дуги радиса R6, сопрягающей носок крюка с внешним контуром крюка. Для этого делаем засечку из центра O2 радиусом R3+R6. Точки сопряжений T и P лежат на линии центров O6 — O7 и O6 — O2. Из центра O4 проводим дугу, соединяющую точки T и P.
+
ngeo.fxyz.ru
Сопряжение окружностей (дуг) Внешнее сопряжение дуг окружностей
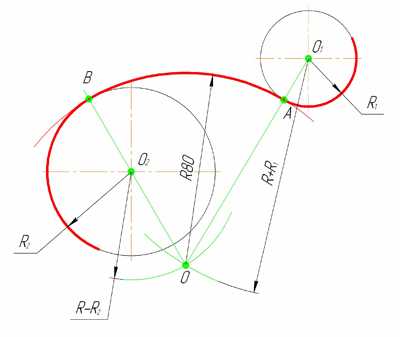
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей (дуг) O1 ( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг (рис.5). Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
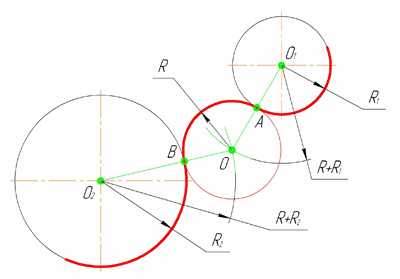
Рисунок 5. Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На рис.6 приведён пример построения внутреннего сопряжения окружностей (дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1 и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Рисунок 6. Внутреннее сопряжение дуг окружностей |
Рисунок 7. Смешанное сопряжение дуг окружностей |
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На рис.7 приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+ R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
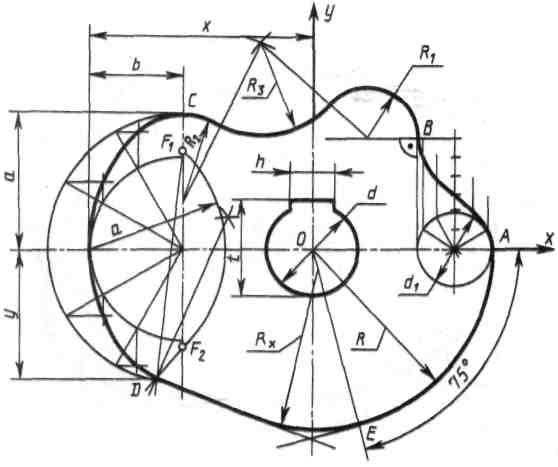
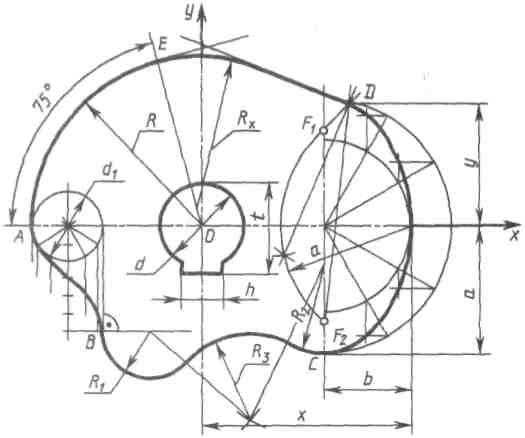
Построение кулачка
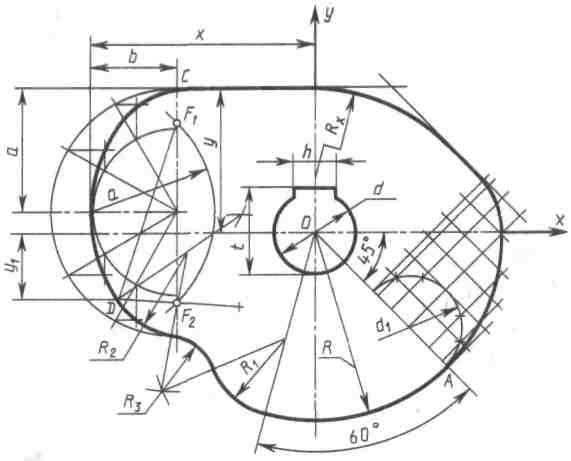
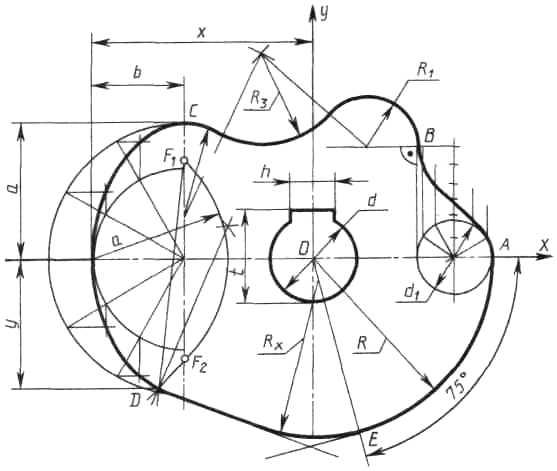
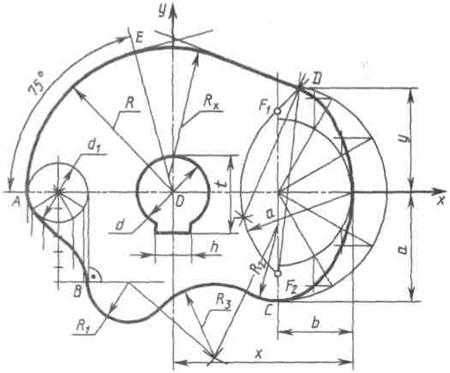
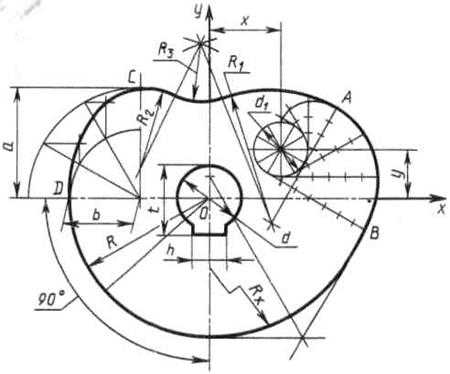
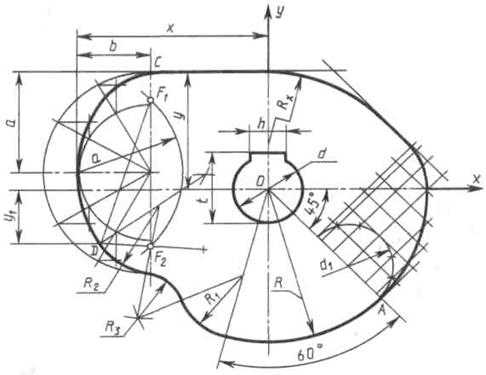
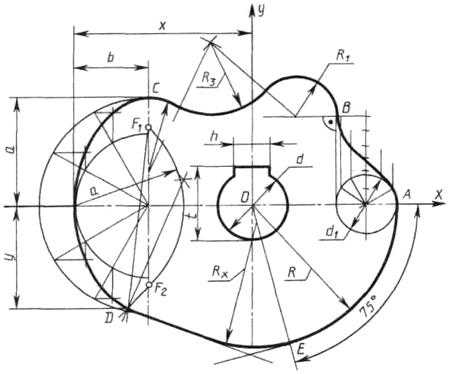
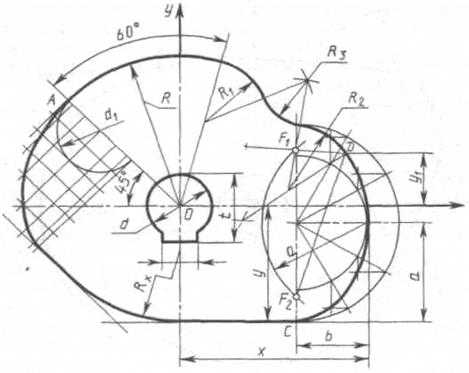
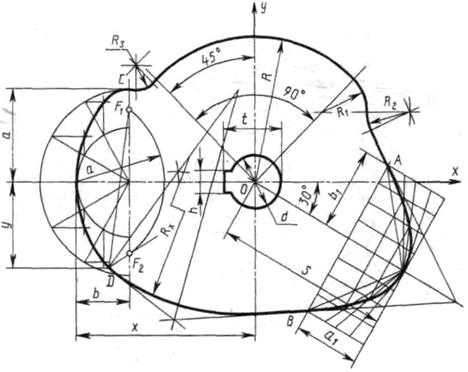
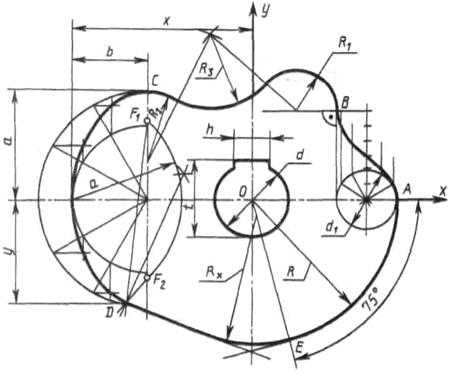
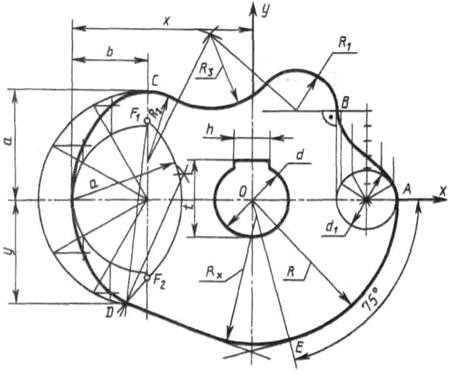
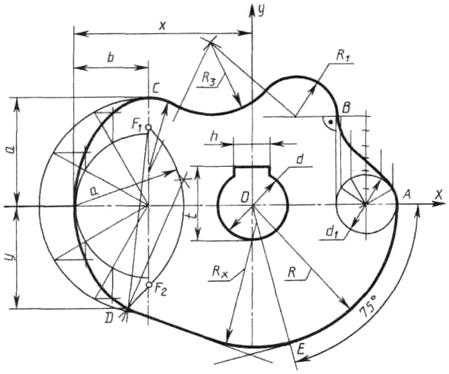
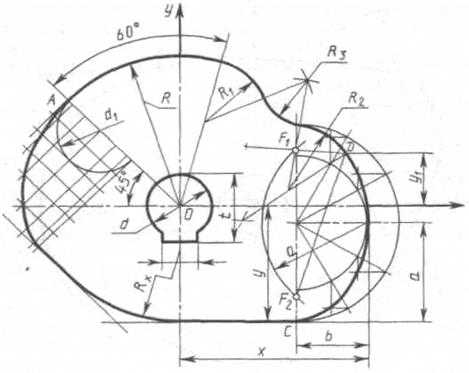
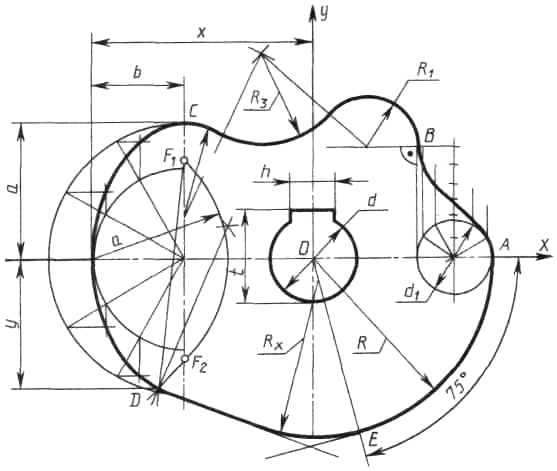
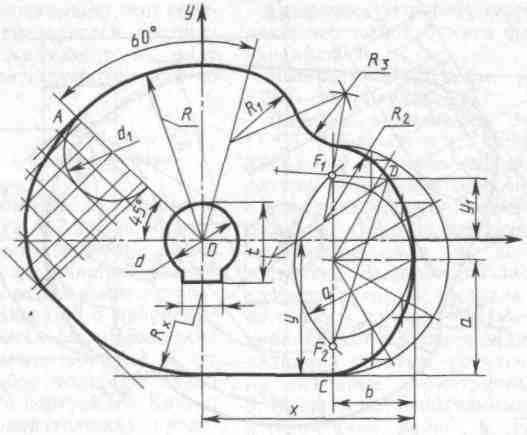
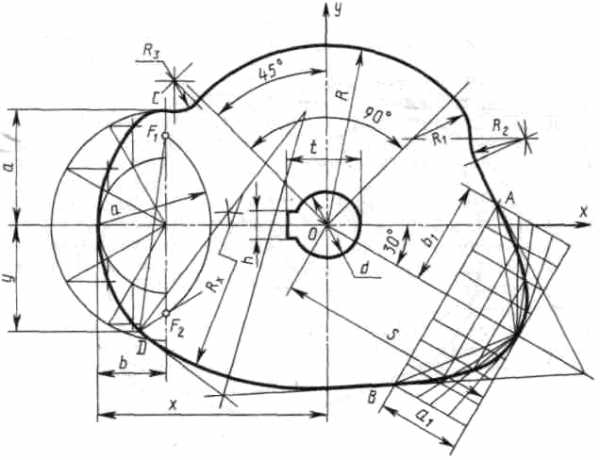
Построение очертания кулачка в каждом варианте следует начинать с нанесения осей координат Ох и Оу. Затем строят лекальные кривые по их заданным параметрам и выделяют участки, входящие в очертание кулачка. После этого можно вычертить плавные переходы между лекальными кривыми. При этом следует учесть, что во всех вариантах через точку D проходит касательная к эллипсу.
Обозначение Rx показывает, что величина радиуса определяется построением. На чертеже вместо Rx надо проставить соответствующее число со знаком «*».
Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.
Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.
Эллипс — кривая второго порядка. Одним из способов построения эллипса является способ построения эллипса по двум осям рис.8. При построении проводим окружности радиусами r и R из одного центра О и произвольную секущую ОА. Из точек пересечения 1 и 2 проводим прямые, параллельные осям эллипса. На их пересечении отмечаем точку М эллипса. Остальные точки строим аналогично.
Рисунок 8. Способ построения эллипса по двум осям | Рисунок 9. Построение параболы |
Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки называемой фокусом параболы, расположенных в той же плоскости.
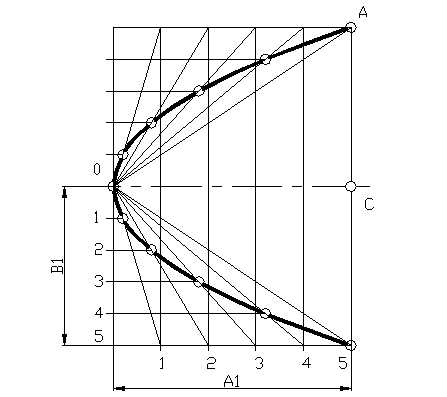
На рисунке 9 приведен один из способов построения параболы. Даны вершина параболы О, одна из точек параболы А и направление оси – ОС. На отрезке ОС и СА строят прямоугольник, стороны этого прямоугольника в задании – А1 и В1, делят на произвольное одинаковое число равных частей и нумеруют точки деления 1, 2, 3, 4… 10. Вершину О соединяют с точками деления на А1, а из точек деления отрезка В1 проводят прямые параллельные оси ОС. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяют ряд точек параболы.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 10) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
Рисунок 10. Построение синусоиды
Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис.11): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n, на второй – два и т.д.
Рисунок 11. Построение эвольвенты | Рисунок 12. Спираль Архимеда |
Спираль Архимеда – плоская кривая, которую описывает точка, движущаяся равномерно-поступательно от центра О по равномерно вращающемуся радиусу (рис.12).
Для построения спирали Архимеда задается шаг спирали – а, и центр О. Из центра О описывают окружность радиусом Р = а (0-8). Делят окружность на несколько равных частей, например, на восемь (точки 1, 2, …, 8). На столько же частей делят отрезок О8. Из центра О радиусами О1, О2, и т.д. проводят дуги окружностей, точки пересечения которых с соответствующими радиусами-векторами принадлежат спирали (I, II, …,YIII)
Таблица 2
1
| ||||||||||||||||||||||||||
2
|
3 Кулачок
| ||||||||||||||||||||||||||||
4 Кулачок
| ||||||||||||||||||||||||||||
5 Кулачок
| ||||||||||||||||||||||||||||||
6 Кулачок
|
7 Кулачок
| ||||||||||||||||||||||||||||||
8 Кулачок
| ||||||||||||||||||||||||||||||
9 Кулачок
| ||||||||||||||||||||||||||
10 Кулачок
|
11 Кулачок
| ||||||||||||||||||||||||||
12
| ||||||||||||||||||||||||||
13 Кулачок
| ||||||||||||||||||||||||||||
14 Кулачок
|
studfiles.net
Сопряжение окружностей (дуг) — МегаЛекции
Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей (дуг) O1 ( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг (рис.5). Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
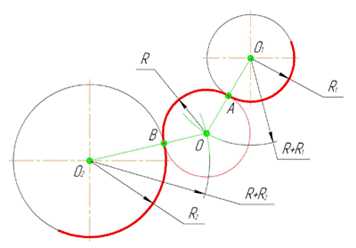
Рисунок 5. Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На рис.6 приведён пример построения внутреннего сопряжения окружностей (дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1 и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
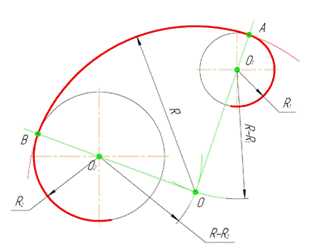 Рисунок 6. Внутреннее сопряжение дуг окружностей
Рисунок 6. Внутреннее сопряжение дуг окружностей
|  Рисунок 7.Смешанное сопряжение дуг окружностей
Рисунок 7.Смешанное сопряжение дуг окружностей
|
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На рис.7 приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+ R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Построение кулачка
Построение очертания кулачка в каждом варианте следует начинать с нанесения осей координат Ох и Оу. Затем строят лекальные кривые по их заданным параметрам и выделяют участки, входящие в очертание кулачка. После этого можно вычертить плавные переходы между лекальными кривыми. При этом следует учесть, что во всех вариантах через точку D проходит касательная к эллипсу.
Обозначение Rx показывает, что величина радиуса определяется построением. На чертеже вместо Rx надо проставить соответствующее число со знаком «*».
Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.
Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.
Эллипс — кривая второго порядка. Одним из способов построения эллипса является способ построения эллипса по двум осям рис.8. При построении проводим окружности радиусами r и R из одного центра О и произвольную секущую ОА. Из точек пересечения 1 и 2 проводим прямые, параллельные осям эллипса. На их пересечении отмечаем точку М эллипса. Остальные точки строим аналогично.
 Рисунок 8. Способ построения эллипса по двум осям
Рисунок 8. Способ построения эллипса по двум осям
|
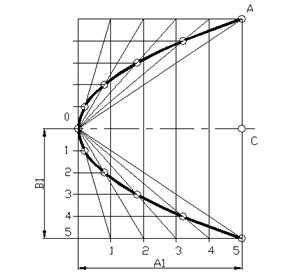 Рисунок 9. Построение параболы
Рисунок 9. Построение параболы
|
Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки называемой фокусом параболы, расположенных в той же плоскости.
На рисунке 9 приведен один из способов построения параболы. Даны вершина параболы О, одна из точек параболы А и направление оси – ОС. На отрезке ОС и СА строят прямоугольник, стороны этого прямоугольника в задании – А1 и В1, делят на произвольное одинаковое число равных частей и нумеруют точки деления 1, 2, 3, 4… 10. Вершину О соединяют с точками деления на А1, а из точек деления отрезка В1 проводят прямые параллельные оси ОС. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяют ряд точек параболы.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 10) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
Рисунок 10. Построение синусоиды
Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис.11): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n, на второй – два и т.д.
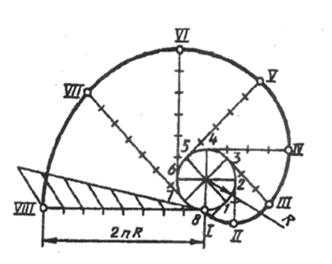 Рисунок 11. Построение эвольвенты
Рисунок 11. Построение эвольвенты
|
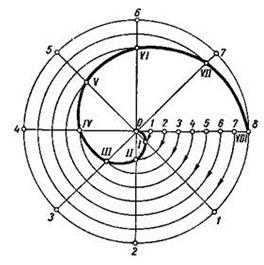 Рисунок 12. Спираль Архимеда
Рисунок 12. Спираль Архимеда
|
Спираль Архимеда – плоская кривая, которую описывает точка, движущаяся равномерно-поступательно от центра О по равномерно вращающемуся радиусу (рис.12).
Для построения спирали Архимеда задается шаг спирали – а, и центр О. Из центра О описывают окружность радиусом Р = а (0-8). Делят окружность на несколько равных частей, например, на восемь (точки 1, 2, …, 8). На столько же частей делят отрезок О8. Из центра О радиусами О1, О2, и т.д. проводят дуги окружностей, точки пересечения которых с соответствующими радиусами-векторами принадлежат спирали (I, II, …,YIII)
Таблица 2
 Кулачок Кулачок
| ||||||||||||||||||||||||||
 Кулачок Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||
 Кулачок Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
 Кулачок
Кулачок
| ||||||||||||||||||||||||||||||
 Кулачок
Кулачок
|
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
4.2. Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые а и b (рис. 18). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Рис. 18
На расстоянии R от пересекающихся прямых проводим вспомогательные прямые, параллельные заданным прямым а и b, до пересечения в точке О. Из центра О опускаем перпендикуляры к прямым а и b и получаем точки сопряжения К1 и К2. Из точки О, как из центра, проводим дугу сопряжения радиуса R между точками К1 и К2.
4.3. Сопряжения прямой с окружностью
Возможны три случая построения сопряжений с окружностью:
задан радиус дуги сопряжения;
задана точка сопряжения на прямой;
задана точка сопряжения на окружности.
В каждом из трех случае сопряжение может быть внешним или внутренним.
Рассмотрим первый случай — сопряжение прямой с окружностью с заданным радиусом дуги сопряжения. Пусть задана окружность радиусом R1 с центром в точке O1 и прямая а. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 19, а).
Из центра О1 проведем вспомогательную дугу радиусом R1+R до пересечения с прямой, проведенной параллельно прямой а на расстоянии R от нее. Получаем точку О — центр дуги сопряжения. Точку сопряжения К1 находим как основание перпендикуляра, проведенного из точки О к прямой а. Чтобы построить точку сопряжения К2, необходимо провести линию центров OO1. Проведем дугу сопряжения К1К2 радиусом R. Построенное сопряжение будет внешним, поскольку OO1=R1+R.
При построении внутреннего сопряжения (рис. 19, б) последовательность построений остается та же, что и в предыдущем примере. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра О1, радиусом R – R1.

Рис. 19
Принцип построений для сопряжения прямой с окружностью, если на прямой задана точка сопряжения, и, наоборот, если точка сопряжения дана на окружности, аналогичен описанному выше.
4.4. Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным.
Построим сопряжение с внешним касанием двух данных окружностей и с радиусами R1 и R2 дугой заданного радиуса R (рис. 20). Из центра О1 радиусом R+R1, а из центра О2 радиусом R+R2 проводим дуги до их пересечения в точке О — центре дуги сопряжения. Точки сопряжения К1 и К2 лежат на пересечении прямых, соединяющих точку О с центрами О1 и О2 сопрягаемых окружностей. Из точки О, как из центра, проведем дугу сопряжения К1К2.
Построим сопряжение с внутренним касанием двух данных окружностей с радиусами R1 и R2 дугой радиусом R (рис. 21). Из центров О1 и О2 проведем две дуги радиусами соответственно R–R1 и R–R2. На их пересечении найдем центр сопряжения О. Точку сопряжения К1 найдем как точку пересечения линии центров ОО1 с первой заданной окружностью. Точку сопряжения К2 найдем как точку пересечения линии центров OO2 cо второй окружностью. Проведем дугу сопряжения К1К2 с центром в точке O.
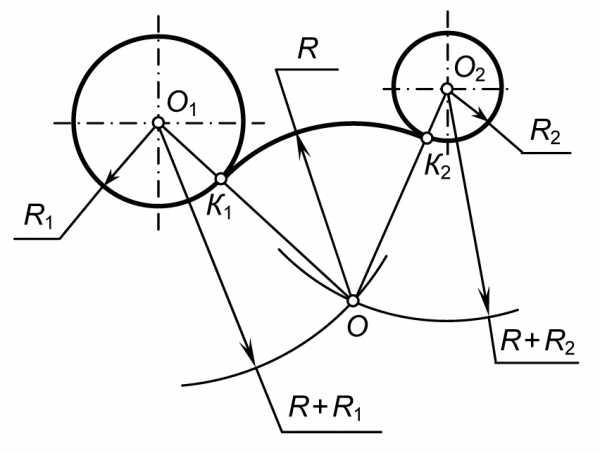
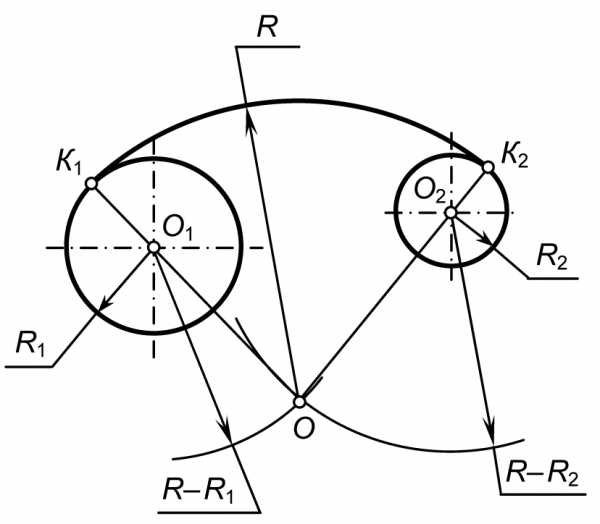
Рис. 20
Рис. 21
Пример построения сопряжения двух окружностей со смешанным касанием приведен на рис. 22.
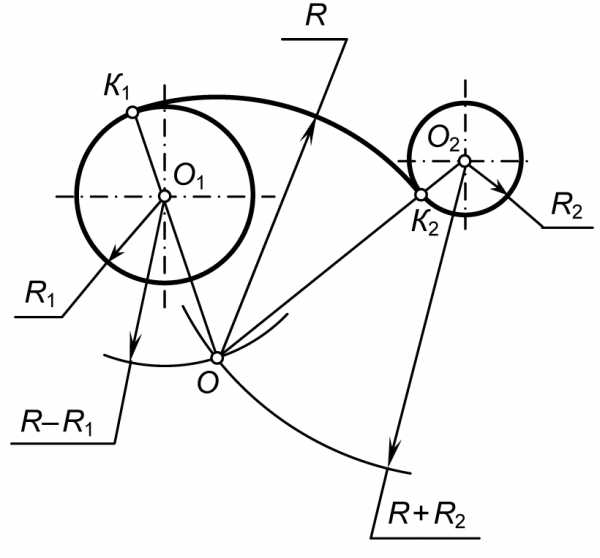
Рис. 22
Принцип построения сопряжений двух окружностей, когда задана некоторая точка на одной из окружностей, аналогичен рассмотренным выше примерам.
studfiles.net
4. Глава 3. Некоторые геометрические построения
§ 22. Лекальные кривые
Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.
Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее
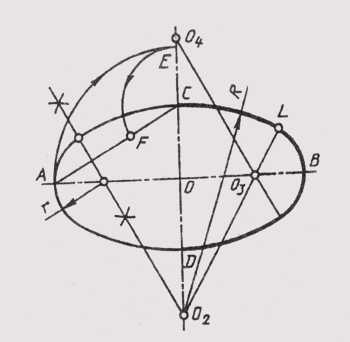
Рис. 36

Рис. 37
точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности — прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.
Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи. В пересечении одноименных лучей получают точки эллипса.
Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данной прямой — директрисы.
Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.
Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и ну-
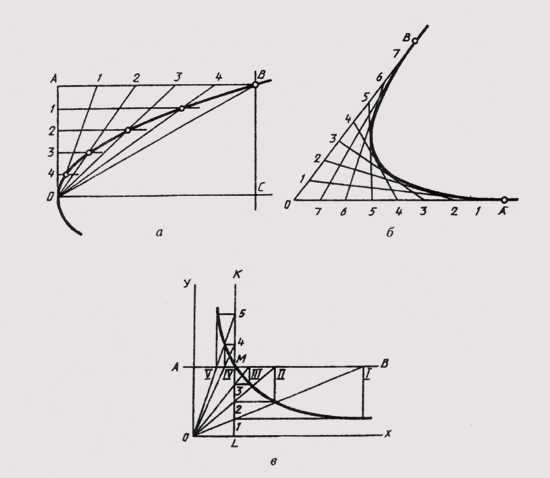
Рис. 38
меруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.
Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.
Рис. 39
Рис. 40
Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА], отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О1, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
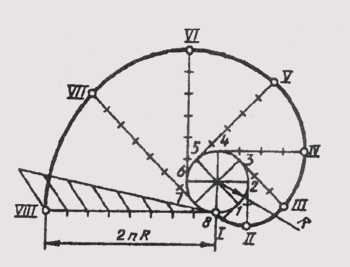
Рис. 41
Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис. 41): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n , на второй — два и т. д.
Полученные точки соединяют плавной кривой и получают эвольвенту окружности.
lib.qrz.ru
Сопряжение дуги окружности с прямой | Начертательная геометрия
Построим Сопряжение дуги окружности с прямой. Задана дуга окружности радиуса R и прямая l
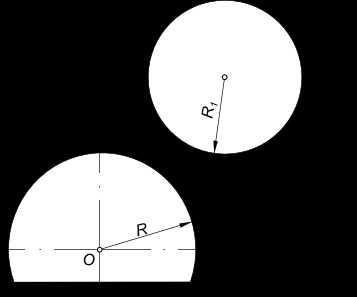
Сопряжение дуги окружности с прямой
Находим центр сопряжения O1: — из центра O проводим дугу радиуса R+R1; — параллельно прямой l на расстоянии R1 от нее проводим прямую m; — в пересечении дуги радиуса R+R1 и прямой m находим центр сопряжения O1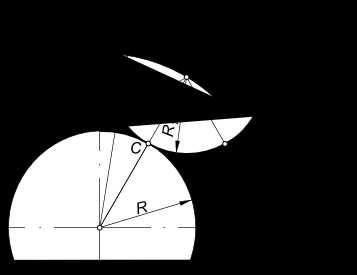
Сопряжение дуги окружности с прямой
Находим точки сопряжения A и C: — проводим линию, соединяющую центры O и O1 и в пересечении ее с дугой радиуса R находим точку сопряжения C; — из центра O1 опускаем перпендикуляр на прямую l и находим точку сопряжения A.
Из центра сопряжения O1 соединяем дугой радиуса R1 точки сопряжения A и C.
Построим Сопряжение дуги окружности с прямой. Задана дуга окружности радиуса R, прямая l и точка сопряжения A. Найти радиус сопряжения R1 и точку сопряжения C.

Сопряжение дуги окружности с прямой
Находим центр сопряжения O1: — через точку A проводим перпендикуляр к прямой l и на нем откладываем отрезок AK, равный R; — соединяем центр O с точкой K; — проводим через середину OK перпендикуляр до пересечения с прямой AK в точке O1.
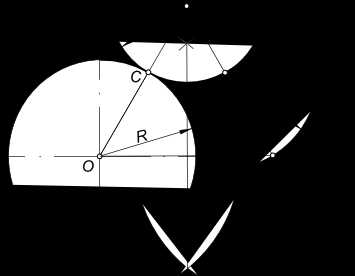
Сопряжение дуги окружности с прямой
Находим точку сопряжения C: — проводим линию, соединяющую центры O и O1 и в пересечении ее с дугой радиуса R находим точку сопряжения C
Из центра сопряжения O1 соединяем точки сопряжения A и C дугой радиуса R1.
Применение приведенных выше примеров для построения сопряжений заготовки рычага,
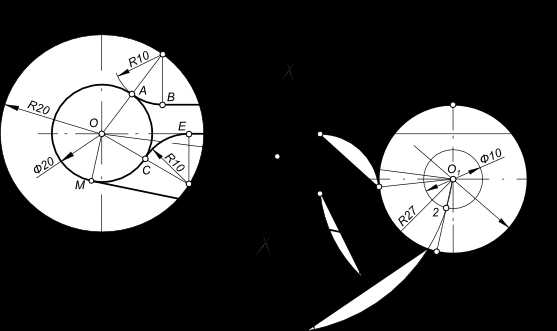
Сопряжение дуги окружности с прямой
для построения сопряжений окружностей диаметрами 20 и 30 мм с прямыми BD и EH.
+
ngeo.fxyz.ru




 Кулачок
Кулачок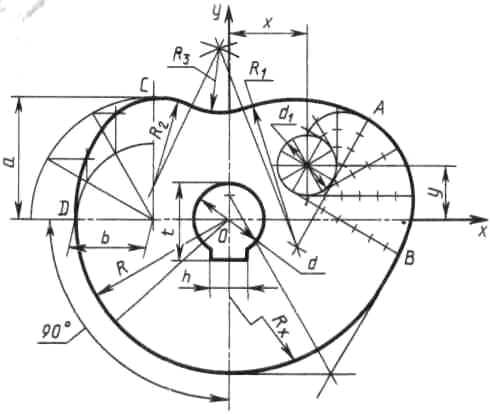 Кулачок
Кулачок



 Кулачок
Кулачок