Решение нелинейных уравнений маткад – 2. Решение систем нелинейных уравнений. Метод простых итераций (последовательных приближений).

Урок 23. Нелинейные уравнения в Mathcad

Mathcad может решать системы линейных и нелинейных уравнений с помощью встроенных алгоритмов. На самом деле, «решать» — не совсем верное определение того, что делает программа. Лучше рассуждать так: Вы задаете приближенное значение, затем программа уточняет эту оценку. Поэтому, используя такую технологию решения, нужно знать, что Вы делаете. Вы должны понимать, как ведет себя функция, которую исследуете. Иначе Вы можете быть разочарованы.

Изучение «решения» начнем с уравнений с одной переменной. В этом случае поведение уравнения можно понять, построив график. Позже мы рассмотрим системы уравнений.

Уравнения с одной переменной

Уравнение, которое мы рассмотрим, достаточно простое:

Рассмотрим это уравнение как пересечение прямой линии (левая часть) и парабола (правая часть). Построим графики трех прямых линий и посмотрим, что произошло:

Первая (самая верхняя) линия дважды пересекается с параболой около точек x=-0.3 и x=1.3. У второй линии – одно пересечение (или два близко расположенных) возле точки x=0.5. Пересечений с третьей прямой (самой нижней) нет.

Решения

Сначала рассмотрим самую верхнюю линию. Чтобы получить решение, нам нужен Блок решения (вкладка Математика –> Области –> Блок решения). Заполним блок для решения первого уравнения:

Здесь есть три области для различных записей:

— начальные приближения;

— ограничения;

— решатель.

В области ограничений мы записали уравнение, которое хотим решить. В первой области мы задали приближенное решение этого уравнения. Функция Find(), которую мы записали в последней области – это решатель.

Как видно, решение 1.366 – это правое пересечение прямой и параболы. Начальное приближение не критично – можно ввести 1.6, щелкнуть мышью вне блока и получить тот же результат:

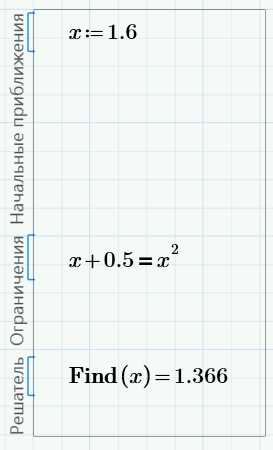
Изменим начальное приближение на значение, близкое к левому пересечению, скажем, -0.5. Решение изменится на -0.366:

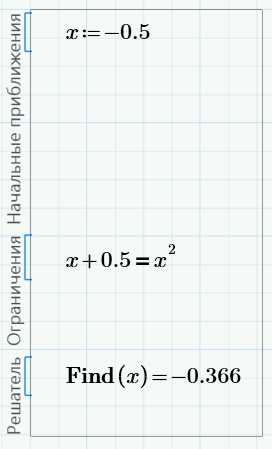
Измените начальное приближение обратно на 1.3.

Теперь поменяем константу 0.5 в уравнении на -0.25. Решение изменится на 0.5:

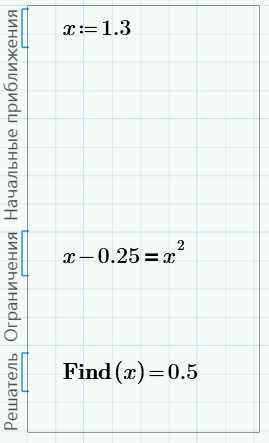
Этот же ответ мы будем получать для любого значения начального приближения – это единственное решение.

Наконец, изменим константу в уравнении на -1 (последнее уравнение). Щелкнем вне блока и получим сообщение об ошибке:

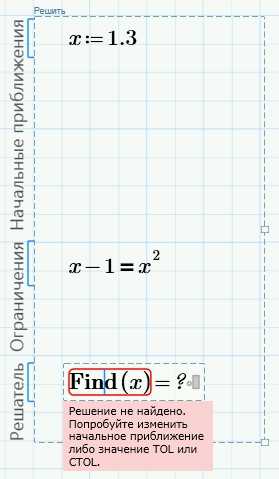
Решения нет. Изменим константу обратно на 0.5.

Вывод решения

Переменные в блоке решений локальны. Вы не можете использовать их значения вне блока. Вернемся к уравнению, где приближенное значение задано 1.3. Мы решили уравнение, чтобы найти более точное решение x=1.366. Однако если мы попробуем вывести значение x, мы получим вектор, которые определили для нашего графика.

Если Вы хотите использовать результат решения в дальнейших вычислениях, нужно присвоить функцию решателя переменной:

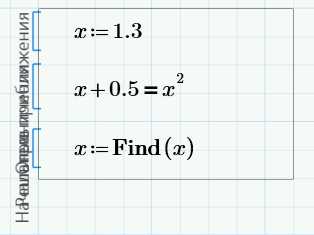
Тогда получим верный результат:

Решение систем уравнений

Для примера решим систему трех уравнений: два линейных и одно кубическое. Здесь три неизвестных – начальное приближение даем для всех трех:

Все три ответа можно вывести в вектор:

Удалите последнее из трех уравнений. Решение все равно будет найдено, с учетом двух оставшихся уравнений:

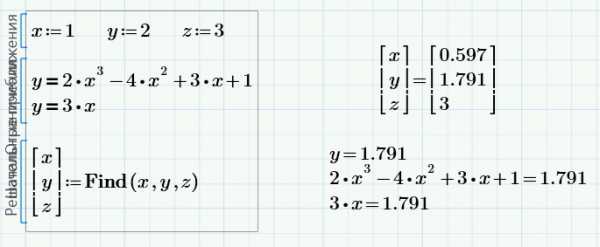
Однако, такое решение может быть не тем, которое Вам нужно.

Обратите внимание еще на некоторые детали. В блоке решения используются два вида знака «равно»: знак присваивания для начальных приближений и для решателя Find, и знак булева равенства в уравнении. Эта разница очень важна. Еще один момент – щелкните по слову Find в области решателя, откройте вкладку Математика. В строке Обозначения должно быть отмечено «Ключевое». Некоторые другие ключевые слова мы рассмотрим в последующих уроках.

Растворимость вещества

Рассмотрим растворение вещества DOH. Это двухстадийный процесс: сначала растворяется твердая фаза, затем растворенные части диссоциируют на D и OH. Малую растворимость можно повысить, добавив небольшое количество сильной кислоты HA. Она диссоциирует, и ионы водорода вступают в реакцию с гидроксильной группой:

Как зависит общая растворимость D от количества добавленной кислоты? Концентрацию будем считать в моль/л. Концентрация насыщения нерастворенной кислоты:

Начнем с концентрации кислоты:

Константы равновесия реакции:

Блок решения начинается с трех неизвестных и их начальных приближений:

Решение:

Общая концентрация вещества:

Расчет для построения графика (подробнее о таких расчетах поговорим в следующем уроке):

График показывает концентрацию как функцию от количества добавленной кислоты. Концентрация ионов водорода на порядки меньше, чем концентрации других элементов. Поэтому мы изменили масштаб в миллион раз, чтобы показать этот график в тех же осях:

Если концентрация кислоты мала, решение содержит низкую концентрацию DOH, которая диссоциирует только частично. При увеличении концентрации кислоты, все больше и больше вещества диссоциирует.

Резюме

1. Если есть уравнение или система уравнений, Вы можете дать приближенное решение, а Mathcad улучшит эту оценку. Такой способ используется в Блоке решения.
2. Первая часть блока решения – начальные приближения, т.е. Ваши оценки. Здесь используется знак присваивания «:=». Эти значения могут быть помещены и до блока.
3. В области «Ограничения» (уравнения) нужно использовать булево равенство [Ctrl+=]. Это единственный знак, по обе стороны от которого могут быть выражения.
4. Блок решения заканчивается функцией для решения. Мы рассмотрели Find(), которая содержит неизвестные, которые нужно найти.
5. Чтобы использовать результат решения в дальнейших расчетах, присвойте Find() переменной. Это может быть как одна переменная, так и вектор.
6. Для решения системы нелинейных уравнений нужно быть внимательным. Число уравнений должно быть равно числу неизвестных. Кроме того, приближенные значения должны быть как можно ближе к решению.
7. Если решение не было найдено, не спешите обвинять Mathcad. Нелинейные уравнения являются головной болью для любого языка программирования. Попробуйте понять поведение Ваших уравнений, прежде чем приступать – часто уравнения могут не иметь решения.

Другие интересные материалы

sapr-journal.ru

Решение нелинейных уравнений и систем уравнений в пакете MathCAD

Pers.narod.ru. Обучение. Лекции по MathCAD. Решение нелинейных уравнений и систем уравнений в пакете MathCAD

Этот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье

 

 

Вычисление корней численными методами включает два основных этапа:

·      отделение корней;

·      уточнение корней до заданной точности.

Рассмотрим эти два этапа подробно.

 

Отделение корней нелинейного уравнения

 

Учитывая легкость построения графиков функций в MathCAD, в дальнейшем будет использоваться графический метод отделения корней.

Пример. Дано алгебраическое уравнение

.

Определить интервалы локализации корней этого уравнения.

 

 

Пример. Дано алгебраическое уравнение

.

Определить интервалы локализации корней этого уравнения.

На рисунке приведен график функции , построенный в MathCAD. Видно, что в качестве интервала изоляции можно принять интервал

. Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨

 

Уточнение корней нелинейного уравнения

 

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

Функция root. В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root, которая может иметь два или четыре аргумента, т.е.  или , где  – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению,  – скалярная переменная, относительно которой решается уравнение,

 – границы интервала локализации корня.

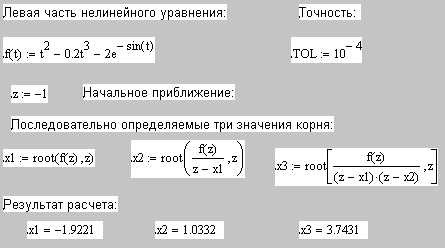
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.

 

 

Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨

 

Функция root с двумя аргументами требует задания (до обращения к функции) переменной  начального значения корня из интервала локализации.

 

Пример 8.1.5. Используя функцию root, вычислить изменения корня нелинейного уравнения   при изменении коэффициента а от 1 до 10 с шагом 1.

 

 

 

Функция polyroots. Для вычисления всех корней алгебраического уравнения порядка  (не выше 5) рекомендуется использовать функцию polyroots. Обращение к этой функции имеет вид polyroots(v), где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.

Пример. Используя функцию polyroots, найти все три корня уравнения , включая и два комплексных

 

 

Блок Given. При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given, имеющий следующую структуру:

 

 

Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логичес­кий.

Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

 

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find(x), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr(x), которая возвращает приближенное значение корня.

 

Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find(x) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.

 

Аналогично можно задать алгоритм решения и для функции   Minerr(x).

 

Использование численных методов в функциях Find(x), Minerr(x) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.

 

Пример. Используя блок Given, вычислите корень уравнения  в интервале отделения .

 

 

 

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

·      алгебраические системы уравнений;

·      трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

 

Системы линейных алгебраических уравнений

 

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

 

В матричном виде систему можно записать как

 

,

где  – матрица размерности ,  – вектор с  проекциями.

 

Для вычисления решения СЛАУ следует использовать функцию lsolve, обращение к которой имеет вид: lsolve(А,b), где А – матрица системы,  – вектор правой части.

Решение систем нелинейных уравнений

 

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD2001i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

 

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

Пример. Дана система уравнений:

Определить начальные приближения для решений этой системы.

 

 

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨

Вычисление решения системы уравнений с заданной точностью. Для этого используется уже известный вычислительный блок Given.

 

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find(x), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке < Начальные условия >. Число аргументов функции должно быть равно числу неизвестных.

 

Следующие выражения недопустимы внутри блока решения:

·      ограничения со знаком ¹;

·      дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

·      блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr).

 

Пример. Используя блок Given, вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

 

 

Пример. Используя функцию , вычислите решение системы уравнений

 

 

 

 

 

pers.narod.ru

2.5.1. Поиск корней нелинейных уравнений в MathCad

Благодаря встроенным функциям root, Find и Minerr система MathCAD обеспечивает получение готового решения уравнений без составления программы. Однако не во всех случаях результат может оказаться верным, даже при отсутствии видимых ошибок. Ниже рассматриваются примеры решения задач в MathCAD, обсуждаются вычислительные проблемы и способы их преодоления.

MathCAD освобождает пользователя от необходимости программирования алгоритма решения уравнений. Однако основной принцип работы в MathCAD – решение без программирования – имеет помимо очевидных достоинств и обратную сторону: неуверенность в результате вычислений. Эта неуверенность объясняется тем, что процесс решения скрыт от пользователя и не может быть проконтролирован непосредственно. Примеры вычислений с ошибочным результатом приведены ниже.

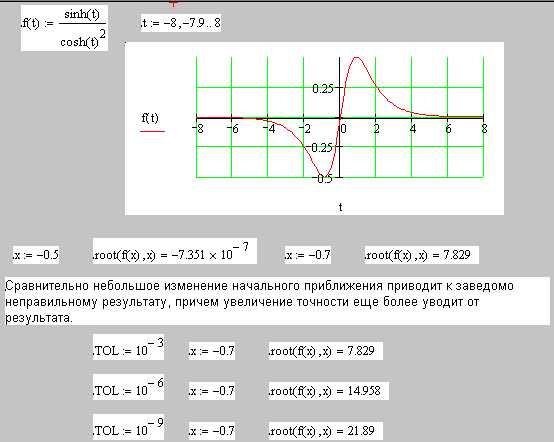
Зададим функцию, содержащую гиперболические синус и косинус: f(x) = sh(x) / (ch(x))². График этой функции в интервале –8 < x < 8 представлен на рис. 14, а.

Корнем этой функции является x = 0. Слева и справа от этой точки f(x) имеет минимум и максимум, а при удалении от начала координат f(x) приближается к нулю. С формальной точки зрения решение уравнения f(x) = 0 не должно вызывать проблем, поскольку функция не содержит разрывов и имеет один корень во всей области определения неизвестного –∞ < x < +∞.

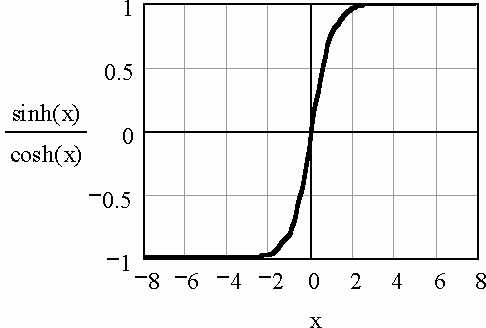
а б

Рис. 14. Графики функций f(x) = sh(x) / (ch(x)) ^{2 ­­}

и f(x) = sh(x) / (ch (x))

При начальном приближении x = –0,5 процедура root довольно уверенно определяет значение корня:

_{x := —0.5 f(x) := sinh(x)∙(cosh(x))}^–2

^{root(f(x),x)=—7.351×10–7}

Однако сравнительно небольшое изменение начальной точки – до x = –0,7 приводит к заведомо неверному результату. Причём с увеличением требований к точности (параметр TOL) результаты удаляются от корня:

x := -0.7	TOL:=10–3	root(f(x),x) = 7.829
x := -0.7	TOL:=10–6	root(f(x),x) = 14.958
x := -0.7	TOL:=10–9	root(f(x),x) = 21.89

Причина ошибок кроется как в характере зависимости f(x), так и в особенностях работы процедуры, обеспечивающей решение.

При начальном приближении x = -0,7 алгоритм root (в основу которого положен метод секущих) попадает на внешний правый по отношению к x = 0 склон зависимости f(x) (рис. 14, а) и «скатывается» по этому склону в поисках нуля f(x) в сторону +∞. Это видно по возвращаемым функцией root числам. Очевидно, что результаты решения неверны.

Однако система не выдаёт никаких сообщений об ошибке. Это объясняется тем, что MathCAD считает корнем не то значение x, при котором f(x) точно равна нулю, а то, при котором f(x) не превышает значения системной переменной TOL, равной по умолчанию 10^–3. Данное условие во всех трёх случаях выполняется. С увеличением требований к точности расчёта (то есть с уменьшением TOL) возвращаемые root числа все больше отклоняются от корня x = 0, так как с ростом | x | функция f(x) приближается к нулю.

Расчёты при различных начальных значениях x показывают, что границы области сходимости в рассматриваемой задаче примерно соответствуют условию | x | < 0,6.

Для успешного решения уравнения необходимо правильно выбирать не только начальное приближение, но и критерий точности расчёта. Иллюстрацией этого служит пример решения модифицированного уравнения, отличающегося от рассмотренного множителем 10^—3: _{x:=–0.5 TOL:=10}^–3­­­­

_{root(f(x)∙ 10}^–3_,x)=0.307

Корни исходного уравнения f(x) = 0 и нового f(x)∙10^–3= 0 должны совпадать. Однако MathCAD выдаёт неверный результат. Эта ошибка объясняется тем, что функция f(x)∙10^–3при любых значениях x не превышает значения параметра TOL. Чтобы получить разумный результат, необходимо скорректировать требования к точности, выбрав, например, TOL = 10^–6. В этом случае MathCAD возвращает x = –7,35117∙10^-7

_{Опасность ошибок,подобныхрассмотреннымвыше,состоитвтом,что} они могут остаться незамеченными, поскольку MathCAD не выдаёт никаких предупреждающих сообщений. Поэтому при решении уравнений желательно придерживаться следующих правил.

Во-первых, необходимо сначала провести отделение корней уравнения. Во-вторых, желательно выполнить поиск решения несколько раз от различных начальных точек. Решение следует подвергать проверке, если его правильность не очевидна. Приведённые примеры не свидетельствуют о слабости встроенных в MathCAD процедур решения уравнений. С подобными проблемами можно столкнуться и при использовании других средств, например, MATLAB или пакетов прикладных программ для численных расчётов.

studfiles.net

3.4. Решение нелинейных алгебраических и трансцендентных уравнений в среде MathCad

Отделение корня способом 1 (по графику функции y = f(x))

Информация к решению

На этапе отделения корня рекомендуется выбирать такой участок [a; b], на котором функция f(x) монотонна.

Встроенная функция root(f(x),x) предназначена для решения уравнений вида:

f(x) = 0. (3.72)

В основе функции root() лежит численный итерационный метод вычисления приближенного значения корня x* уравнения с заданной точностью.

Функция root() требует предварительного задания начального приближения переменной x. В качестве начального приближения x можно принимать одну из границ интервала [a; b] или приближённое значение корня, определённое на этапе отделения корней.

Корень уравнения будет определён с точностью, заданной системной (встроенной) переменной TOL (по умолчанию TOL = 0,001).

ПРИМЕР 3.2. Дана математическая модель в форме нелинейного трансцендентного уравнения

^(3.73)

Произвести отделение корня способом 1 (по графику функции y = f(x)).

Фрагмент рабочего документа MathCad

1.  Построение графика функции f(x) на заданном интервале [-2; 2] .

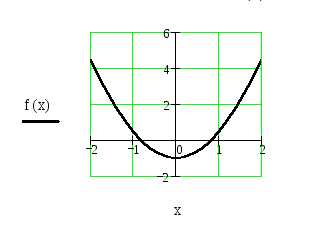
На интервале [-2; 2] уравнение имеет два корня.

Отделим корень, лежащий в области x > 0 (положительный корень).

2.  Устанавливаем визуально по графику границы a_ут и b_ут отрезка, в пределах которого заключен только один корень x* (положительный): принимаем a_ут = 0,2 b_ут = 1,5 . Следовательно искомый отрезок — [0,2; 1,5]. Называем этот отрезок уточненным.

Фрагмент рабочего документа MathCad

3.  Построение графика функции f(x) на уточнённом интервале [0,2; 1,5]:

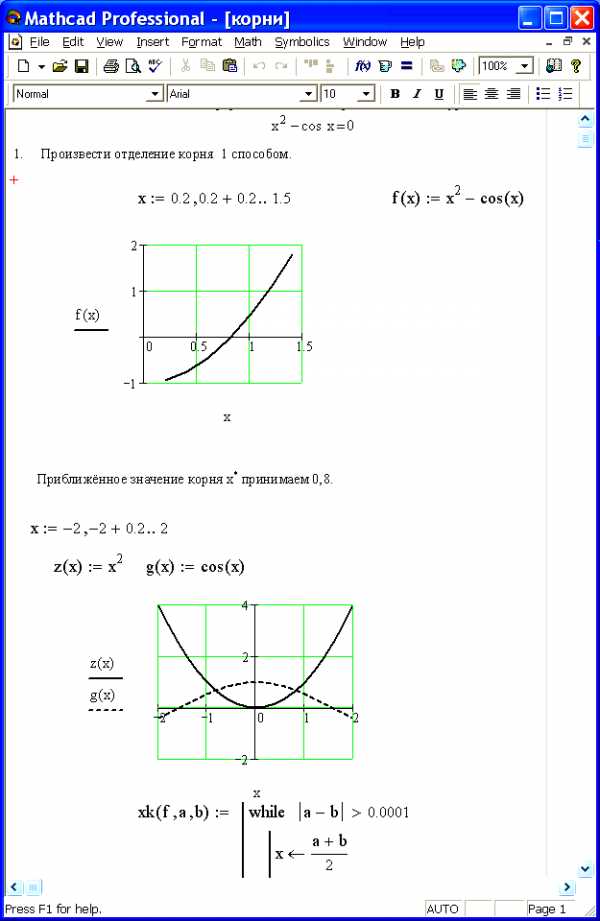
4.  Приближённое значение корня x^* принимаем 0,8. То есть x^* ≈ 0.8

ПРИМЕР 3.3. Для заданного нелинейного трансцендентного уравнения (3.73) произвести отделение корня способом 2 (заменой уравнения).

1.  Замена исходного уравнения равносильным:

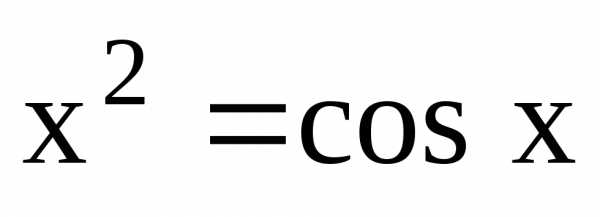
Фрагмент рабочего документа MathCad

2.  Построение графиков двух полученных функций на уточненном интервале [0,2; 1,5]:

3.  Приближённое значение корня x* принимаем 0,8. То есть x^* ≈ 0.8

ПРИМЕР 3.4. Уточнить приближённое значение корня уравнения (3.73) с помощью встроенной функции MathCAD root(…).

Фрагмент рабочего документа MathCad

studfiles.net

Реализация численных методов решения нелинейных уравнений в пакете Mathcad

Для уравнений вида f(x) = 0 решение находится с помощью функции: root(f(х),х,a,b), которая возвращает значение х, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции x и f(x) должны быть скалярами, а аргументы a, b – являются необязательными и, если используются, то должны быть вещественными числами, причем a < b. Предварительно, перед заданием функции должно быть указано зачение начального приближения. Функция позволяет находить не только вещественные, но и комплексные корни уравнения (при выборе начального приближения в комплексной форме).

Если уравнение не имеет корней, они расположены слишком далеко от начального приближения, начальное приближение было вещественным, а корни – комплексные, функция f(х) имеет разрывы (локальные экстремумы между начальными приближениями корня) то появится сообщение (отсутствует сходимость). Причину ошибки можно выяснить, исследуя графикf(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет сходиться функция root.

Если увеличить значение системной переменной TOL (tolerance), то функция root будет сходиться быстрее, но ответ будет менее точен, а при уменьшении TOL более медленная сходимость обеспечивает более высокую точность, соответственно. Последнее необходимо, если требуется различить два близко расположенных корня, или же, если функция f(x) имеет малый наклон около искомого корня, поскольку итерационный процесс в этом случае может сходиться к результату, отстоящему от корня достаточно далеко. В последнем случае альтернативой повышения точности является замена уравнения f(x) = 0 на g(x) = 0, где.

Для выражения f(x) с известным корнем а нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x)=f(x)/(x‑a). Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения f(x)=0, выбирая различные начальные приближения. Подобный прием полезен для нахождения корней, расположенных близко друг к другу, он реализован в приведенном на рис. 8.9 фрагменте документа Mathcad:

Рис. 8.9а. Применение функции root для решения нелинейных уравнений.

Альтернативным вариантом решения является изменение начального приближения представленное на фрагменте документа Mathcad, который приведен на рис. 8.9б.

Рис. 8.9б. Альтернативный способ поиска корней с помощью функции root

Блок решений с ключевыми словами (Given – Find или Given – Minerr) или функция solve позволяют найти решение произвольного нелинейного уравнения, если предварительно задано начальное приближение. Соответствующий фрагмент документа Mathcad приведен на рис. 8.10.

Отметим, что между функциями Find и root наблюдается своеобразная конкуренция. С одной стороны, Find позволяет искать корни, как уравнений, так и систем. С этих позиций функция root как бы и не нужна. Но с другой стороны, конструкцию Given—Find невозможно вставить в Mathcad программы. Поэтому в программах приходится подстановками сводить систему к одному уравнению и использовать функцию root.

Рис. 8.10. Применение функции solve и блока решений.

Mathcad освобождает пользователя от необходимости программирования алгоритма решения уравнений. Однако основной принцип работы в Mathcad – решение без программирования – имеет помимо очевидных достоинств и обратную сторону: неуверенность в результате вычислений. Эта неуверенность объясняется тем, что процесс решения скрыт от пользователя и не может быть проконтролирован непосредственно. Примеры вычислений с ошибочным результатом приведены ниже.

Зададим функцию, содержащую гиперболические синус и косинус:

График этой функции в интервале –8 < x < 8 представлен на рис. 3.12, которая представляет собой фрагмент соответствующего документа Mathcad. Корнем этой функции является x = 0. Слева и справа от этой точки f(x) имеет минимум и максимум, а при удалении от начала координат f(x) приближается к нулю. С формальной точки зрения решение этого уравнения не должно вызывать проблем, поскольку функция не содержит разрывов и имеет один корень во всей области определения неизвестного.

Причина ошибок кроется как в характере зависимости f(x), так и в особенностях работы процедуры, обеспечивающей решение. При начальном приближении x = -0,7 алгоритм root (в основу которого положен метод секущих, являющийся модификацией метода Ньютона) попадает на внешний, правый по отношению к x = 0, склон зависимости f(x) (см. рис. 8.11) и «скатывается» по этому склону в поисках нуля f(x) в сторону +∞. Это видно по возвращаемым функцией root числам. Очевидно, что результаты решения неверны. Однако система не выдаёт никаких сообщений об ошибке. Это объясняется тем, что Mathcad считает корнем не то значение x, при котором f(x) точно равна нулю, а то, при котором f(x) не превышает значения системной переменной TOL, равной по умолчанию 10^-3. Данное условие во всех трёх случаях выполняется. С увеличением требований к точности расчёта (то есть с уменьшением TOL) возвращаемые root числа все больше отклоняются от корня x = 0, так как с ростом |x| функция f(x) приближается к нулю. Расчёты при различных начальных значениях x показывают, что границы области сходимости в рассматриваемой задаче примерно соответствуют условию |x| < 0,6.

Рис.8.11. Пример неправильного действия функции root

К аналогичному решению приводит запись результата методом Ньютона, что представлено на рис. 8.12.

Рис. 8.12. Метод Ньютона решения нелинейного уравнения.

Для успешного решения уравнения необходимо правильно выбирать не только начальное приближение, но и критерий точности расчёта. Иллюстрацией этого служит пример решения модифицированного уравнения, отличающегося множителем 10^-3:

Рис. 8.13

Корни исходного уравнения f(x) = 0 и нового f(x)10^-3 = 0 должны совпадать. Однако Mathcad выдаёт неверный результат. Эта ошибка объясняется тем, что функция f(x)10^-3 при любых значениях x не превышает значения параметра TOL. Чтобы получить разумный результат, необходимо скорректировать требования к точности, выбрав, например, TOL = 10^-6. В этом случае Mathcad возвращает правильный результат.

В ряде случаев особенности уравнения могут привести к неработоспособности алгоритма поиска корня. Так на рис. 8.14 приведен такой пример.

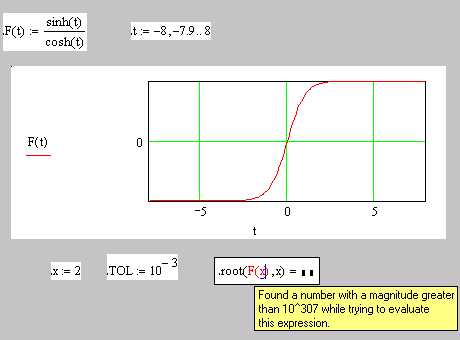
Рис. 8.14 Пример неработоспособности функции root

Неудача объясняется тем, что функция имеет пологие участки слева и справа от точки x = 0. Поскольку алгоритм root на каждом итерационном шаге делит значения функции f(x) на численный эквивалент её производной, возникает переполнение (overflow), так как производная 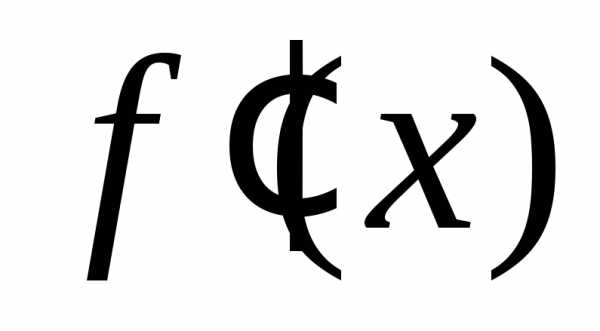при |x| ≥ 2 близка к нулю.

Опасность ошибок, подобных рассмотренным выше, состоит в том, что они могут остаться незамеченными, поскольку Mathcad не выдаёт никаких предупреждающих сообщений. Поэтому при решении уравнений желательно придерживаться следующих правил. Во-первых, необходимо сначала провести отделение корней уравнения. Во-вторых, желательно выполнить поиск решения несколько раз от различных начальных точек. Решение следует подвергать проверке, если его правильность не очевидна.

Символьное (аналитическое) решение уравнений в пакете MathCAD

Во многих случаях, MathCAD позволяет найти аналитическое решение уравнения. Для того чтобы найти решение уравнения в аналитическом виде необходимо записать выражение и выделить в нем переменную. После этого выбираем из пункта меню Symbolic (Символы) подпункт Variables (Переменные) и Solve (Вычислить). Другими вариантами нахождения решения в символьной форме являются – использование функции solve из палитры математических операций использование блока решения (с ключевыми словами Given — Find). Данные методы проиллюстрированы на рис. 8.15, который представляет фрагмент соответствующего документа пакета Mathcad.

Рис8.15. Методы аналитического решения уравнения.

studfiles.net

Работа с массивами и решение систем уравнений в Mathcad

Содержание

Введение

3. Решение систем линейных уравнений

4. Решение нелинейных уравнений

5. Решение систем нелинейных уравнений

Заключение

Библиографический список

Введение

Одна из задач ЭВМ — автоматизация труда, повышение эффективности научных исследований. Основная особенность ЭВМ — ориентация на применение пользователями, не владеющими языками программирования. Такой подход позволяет преодолевать языковой барьер, отделяющий человека от машины. С этой целью разрабатываются пакеты прикладных программ, рассчитанные на широкие круги специалистов. К подобным пакетам относится MATHCAD.

MATHCAD — универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Основное преимущество пакета — естественный математический язык, на котором формируются решаемые задачи.

Объединение текстового редактора с возможностью использования общепринятого математического языка позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда.

Цель работы: изучение выполнения основных операций с массивами, решения систем линейных и нелинейных уравнений в Mathcad.

В математике часто возникает необходимость в задании некоторого ряда значений. Например, при вычислении

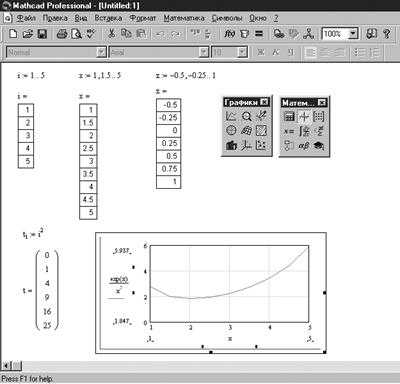
нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Для создания таких рядов в Mathcad используются ранжированные переменные . В простом случае для создания ранжированной переменной используется выражение

Name:=Nbegin…Nend,

Где Name – имя переменной, Nbegin – начальное значение переменной, Nend – ее конечное значение. Символ «…» (он вводится с клавиатуры знаком точка с запятой «;») указывает на изменение переменной в заданных границах. Если Nbegin<Nend, то шаг изменения переменной будет равен +1, в противном случае –1. Например, выражение a:=1…10 описывает ранжированную переменную a со значениями от 1 до 10.

Для создания ранжированной переменной общего вида используется выражение

Name:=Nbegin, (Nbegin+Step)…Nend,

где Step — заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend и отрицательным в противном случае).

Например, выражение a:=1, 1.5, …10 описывает ранжированную переменную a со значениями от 1 до 10 с шагом 0,5.

Ранжированные переменные широко применяются для представления функций в виде таблиц вывода , а также для построения их графиков.

Если после некоторого выражения с ранжированной переменной поставить знак равенства, то после щелчка мышью на экране будет выведена таблица значений этого выражения. Такие таблицы называются таблицами вывода .

Необходимо учитывать следующее свойство таблиц вывода: если количество значений ранжированной переменной и, соответственно, строк в таблице вывода больше 16, то выводятся первые 16 строк. Если указатель мыши находится в пределах таблицы, то щелчок левой кнопкой мыши приводит к появлению вертикальной полосы прокрутки, позволяющей просмотреть все строки таблицы.

Помните, что задание ранжированных переменных эквивалентно заданию конечных циклов.

Примеры использования ранжированных переменных приведены на рисунке 1.1.

Ранжированная переменная отличается от вектора (одномерного массива) тем, что невозможно использование ее отдельных значений. При необходимости иметь доступ к каждому значению переменной со многими компонентами она должна быть задана в виде одномерного (вектора) и двумерного (матрицы) массива.

Местоположение элемента массива задается одним индексом для вектора и двумя для матрицы. Индексы могут быть только положительными целыми числами . Для ввода индекса используется знак « [ » – прямая открывающая скобка.

Для задания массивов можно либо воспользоваться командой Matrices меню Math, либо нажать комбинацию клавиш Ctrl+V , либо щелкнуть на значке с изображением шаблона матрицы. Любое из этих действий вызывает появление диалогового окна, в котором надо указать количество строк m и столбцов n в массиве. При m=1 получим вектор-столбец, а при n=1 – вектор-строку.

В отношении массивов действуют те же правила присваивания и вывода, что и для обычных переменных. В частности, с помощью оператора присваивания можно создать массив заданного размера и заданного типа без ручного заполнения шаблона (рисунок 2.1.).

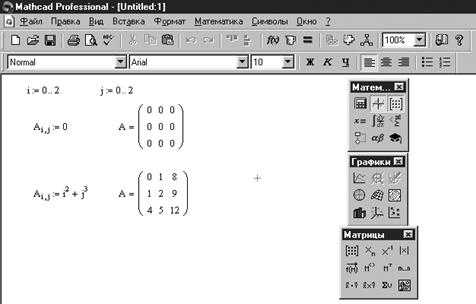
Рис. 2.1 Пример создания матриц без использования шаблонов матриц

Для работы с массивами Mathcad содержит ряд операторов и функций. Ниже представлены операторы для работы с векторами и матрицами. В таблице используются следующие обозначения: V – для векторов, M – для матриц, Z – для скалярных величин.

Существует ряд встроенных векторных и матричных функций . Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц.

Примеры работы с матрицами приведены на рисунке 2.2.

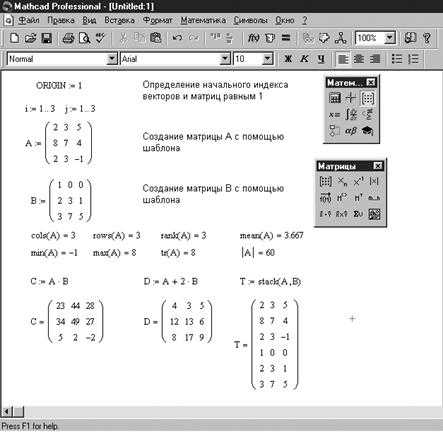
Рис. 2.2. Примеры работы с матрицами

3. Решение систем линейных уравнений

Векторные и матричные операторы и функции позволяют решать широкий круг задач линейной алгебры.

Например, если задана матрица A и вектор B для системы линейных уравнений в матричной форме

, то вектор решения X можно получить из уравнения .

Поскольку решение систем линейных уравнений довольно распространенная задача, то в Mathcad введена специальная функция lsolve(A,B) , которая возвращает вектор X для системы линейных уравнений

при заданной матрице коэффициентов A и векторе свободных членов B. Если уравнений n, то размер вектора B должен быть n, а матрицы A — n´n.

Пусть необходимо решить систему уравнений

.

mirznanii.com

Решение системы уравнений в Mathcad

Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.

Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.

Пример решения СЛАУ:

Для решения системы нелинейных уравнений используются два блока: given…find() и given…minerr (). Так как система нелинейных уравнений может иметь несколько решений, то полученные результаты зависят от начальных значений искомых переменных. В обоих случаях получаются приближенные решения, для которых рекомендуется делать проверку. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики может быть получено точное решение и при меньшем количестве уравнений, данное условие может быть нарушено. На листинге представлены примеры использования блоков given…find() и given…minerr () для решения систем нелинейных уравнений.

www.allmathcad.com