Разложение дроби на элементарные дроби – .

2.Разложение дроби на элементарные

Лемма 1. Пусть 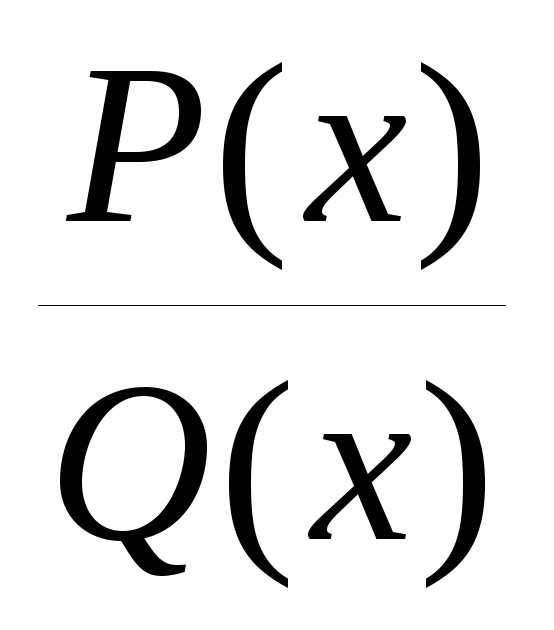правильная дробь иa – вещественный корень многочлена Q(x), т.е. Q(x)=(x—a)^Q₁(x), Q₁(a)0,1. Тогда существует A и многочлен P₁(x) такие, что

,

где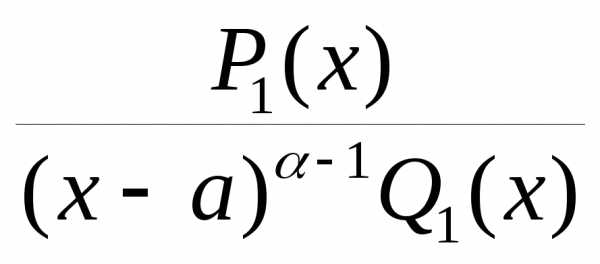 — правильная дробь.

Доказательство: Рассмотрим разность ( где A — некоторое, пока неопределенное число)

.

Дробь справа правильная, так как порядок

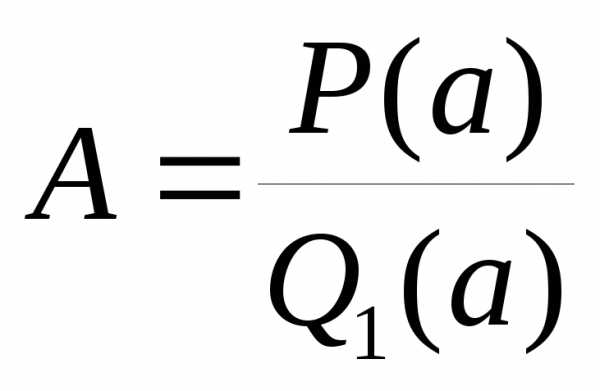P(x) и AQ₁(x) меньше порядка знаменателя. Положим , тогда для числителя число a будет корнем и 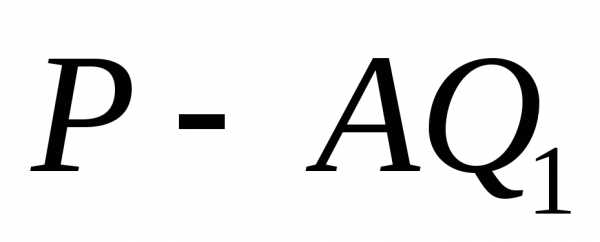=(x—a)P₁(x). Если это выражение поделить на Q(x), то получиться требуемое равенство.

Лемма 2. Пусть 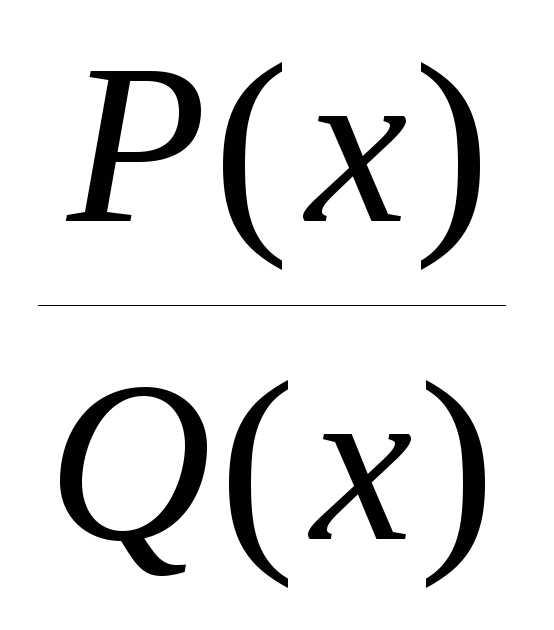правильная дробь иw=u+iv (v0) – комплексный корень многочлена Q(x), т.е. Q(x)=(x²+px+q)^Q₁(

x), Q₁(w)0, 1. Тогда существуют вещественные числа M, N и многочлен P₁(x) с вещественными коэффициентами такие, что

,

где — правильная дробь.

(без доказательства).

Определение. Дроби вида

называются элементарными.

Теорема. Пусть P(x)/Q(x) – правильная дробь, P, Q – многочлены с вещественными коэффициентами, старший коэффициент Q равен 1 и

разложение многочлена по парно простым корням

a₁,a₂,…,a_r,w₁,w₂,…,w

_s, (x-w_k)(x-)=x²+p_kx+q_k

кратностей ₁,…,_r,₁,…,_s . Тогда дробь P(x)/Q(x) может быть представлена в виде суммы элементарных дробей. Каждому сомножителю будет соответствовать сумма дробей вида, а каждому сомножителю будет соответствовать сумма дробей .

Другими словами существуют вещественные числа ,такие, что справедлива формула

=+…+++…+ (*)

Доказательство. По лемме 1

.

Таким образом, у второго слагаемого 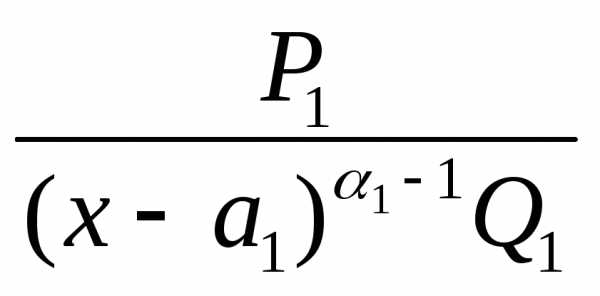кратность корня

a₁ в знаменателе понижена на единицу и к 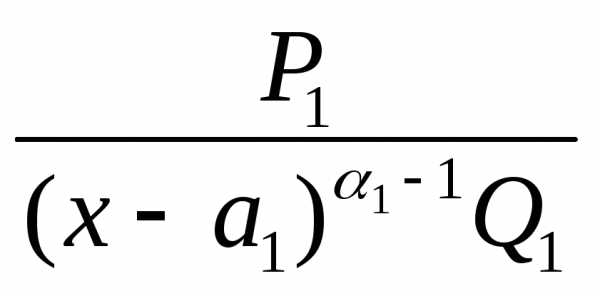применяем лемму 1 еще раз. Повторяя эту процедуру нужное число раз мы получим последнее слагаемое, знаменатель которого не будет иметь своим корнемa₁.

=+.

Точно также поступаем с остальными действительными корнями знаменателя.

=+…++.

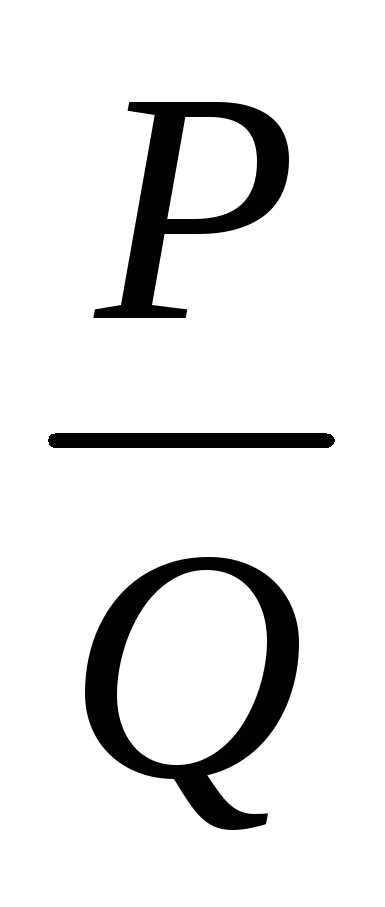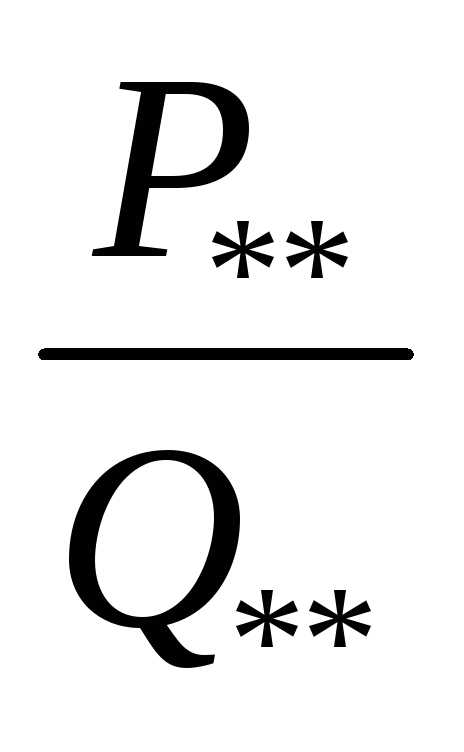У последнего слагаемого 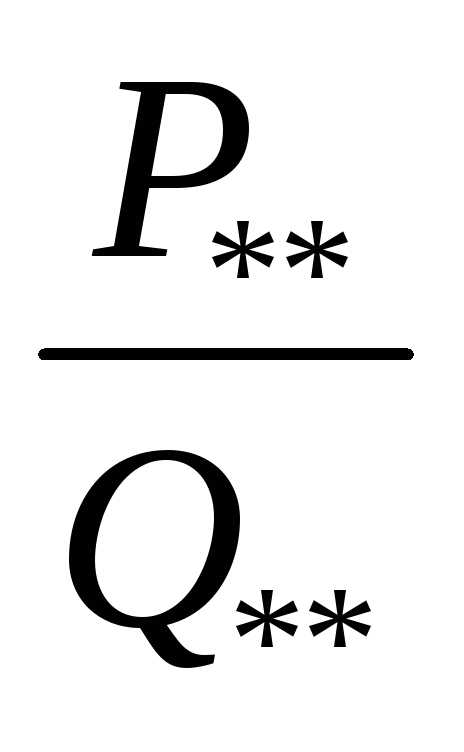знаменатель имеет только комплексные корни и к нему применяется лемма 2. В результате, появляется последняя серия слагаемых, соответствующих комплексным корням.

3.Метод неопределенных коэффициентов

Для нахождения коэффициентов разложения (*) выписывают это разложение с неопределенными коэффициентами, приводят правую и левую часть к общему знаменателю. В полученном равенстве для числителей приравнивают коэффициенты при одинаковых степенях x. В результате получают систему уравнений для определения коэффициентов разложения.

Пример.

1 = A(x²+4x+4)+B(x²+x-2)+C(x-1)

A+B=0

4A+B+C=0

4A-2B-C=1,

A=-B, 3A+C=0,6A-C=1, A=1/9, B=-1/9, C=-1/3.

4.Вычисление интегралов от элементарных дробей

I. Дроби вида .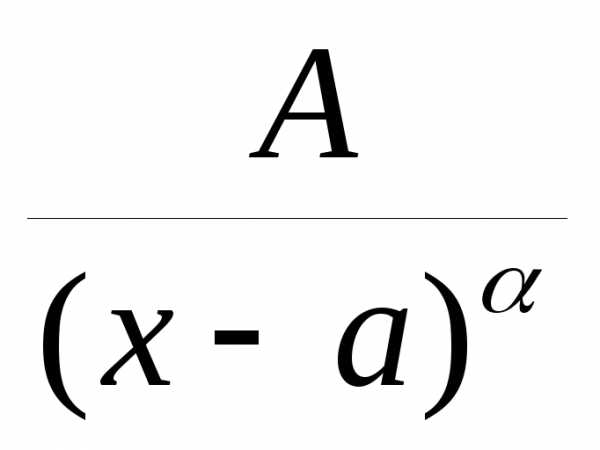

для 1 и

II. Дроби вида .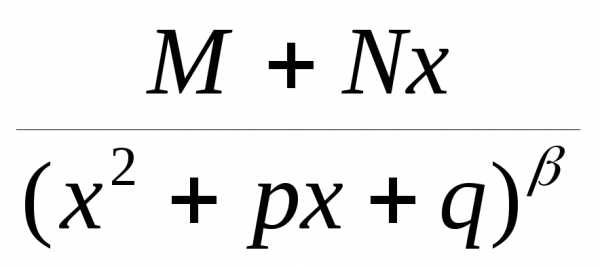

1. =1

, где u=x+p/2,a

2=q — p²/4. Далее ln ( u²+a² )+С.

+C.

2. >1.

Рассмотрим интегралы вида 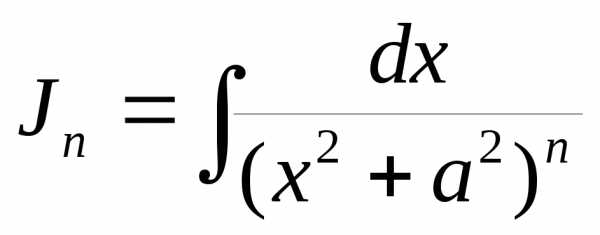. Интегрируя по частям, получим

===.

Откуда получаем рекуррентное соотношение

, ,

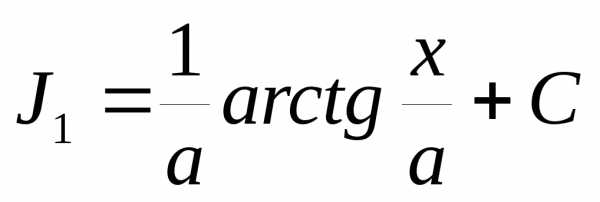позволяющее вычислять интегралы J_n .

§4 Интегрирование некоторых иррациональностей

1.

Через R(u,v,…,w) здесь обозначается рациональная функция, то есть выражение, которое может быть получено с помощью конечного числа операций сложения и деления над выражениями u,v,…,w и произвольными константами. Отметим, что суперпозиция рациональных функций будет также рациональной функцией. Дифференциал от рациональной функции равен рациональной функции, умноженной на дифференциал независимого переменного.

Пример рациональной функции

=.

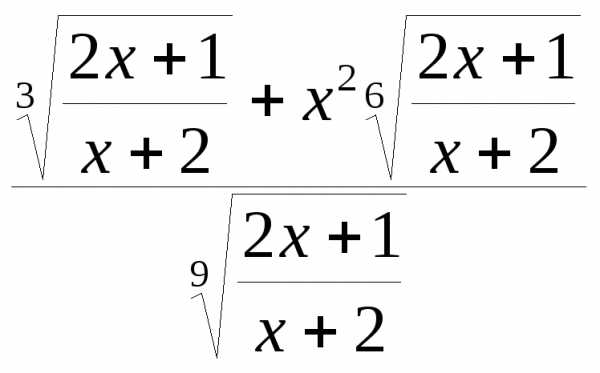Интегралы такого вида приводятся к интегралам от рациональных функций с помощью замены 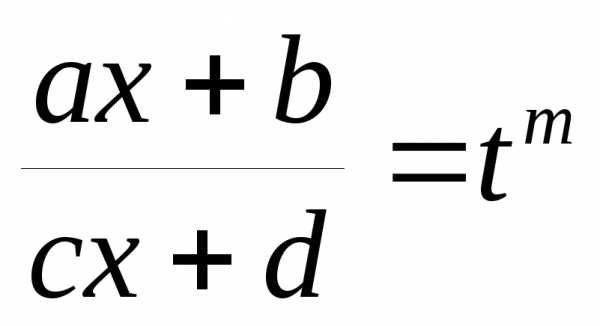,m – общий знаменатель дробей ,…, (берут наименьшее общее кратное знаменателей этих дробей). В рассмотренном выше примере, наименьшее общее кратное m=18.

2.Интегралы вида .Подстановки Эйлера

a) a>0,

В этом случае ax²+bx+c=ax²+2 xt+t

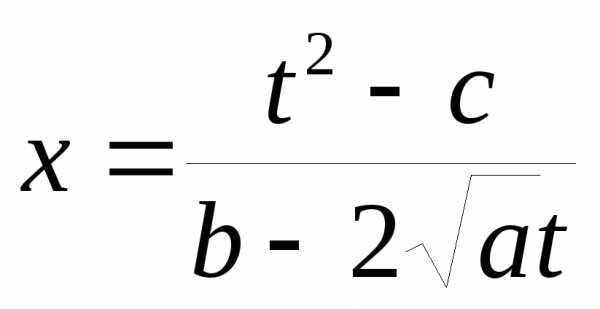², откуда -рациональная функция. Таким образом, подинтегральное выражение примет вид

=R₁(t)-рациональная функция от t. Кроме того dx=R₂(t)dt.

b) Корни x₁,x₂ квадратного трехчлена ax²+bx+c вещественные, тогда ax²+bx+c =a(x — x₁)(x — x₂).

Если x₁ = x₂ , то =|x – x₁

| и иррациональность отсутствует. Если x₁  x₂, то полагают и задача сводится к ранее рассмотренной

.

В этом случае можно так же сделать замену .

c) c>0

. В этом случае

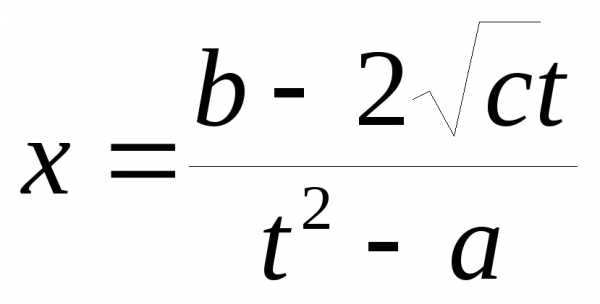ax²+bx+c= x²t²+2 xt+ с, ax+b= xt² +2t, — рациональная функция. После замены получим

=R₁(t) — рациональная функция от t, dx=R₂

(t)dt.

Можно показать, что этими тремя подстановками исчерпываются всевозможные случаи. Действительно, если a<0 и c<0 и действительных корней нет, то выражение ax²+bx+c=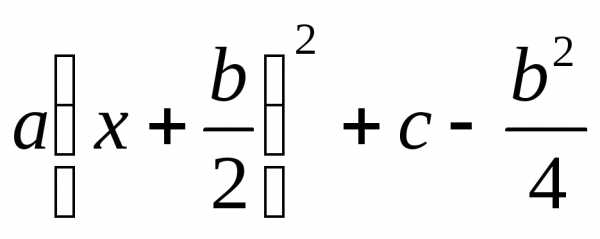< 0для всех x и область определения выражения пуста.

3. Интегрирование дифференциальных биномов m, n, p – рациональные числа.

Сделаем замену x=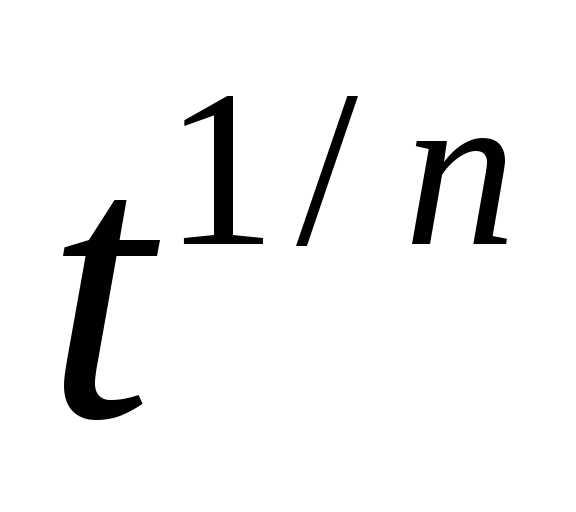,x^m(a+bxⁿ)^pdx=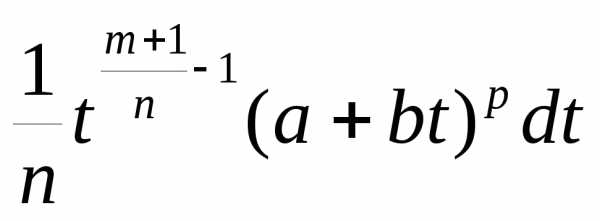.Таким образом, задача свелась к интегрированию биномов вида. Интегралы можно вычислить в следующих трех случаях:

а) p – целое (a+bt)^p t^q=R( t, t^q )

б) q – целое (a+bt)^p t^q=R( t, (a+bt)^p )

в) p+q – целое (a+bt)^p t^q=

studfiles.net

Разложение дроби на простейшие

Информация предоставлена с сайта www.cleverstudents.ru

Разложение дроби на простейшие.

Для начала разберем теорию, далее решим парочку примеров для закрепления материала по разложению дробно рациональной функции на сумму простейших дробей. Подробно остановимся на методе неопределенных коэффициентов и методе частных значений, а также на их комбинации. Простейшие дроби часто называют элементарными дробями. Различают следующие виды простейших дробей:

где A, M, N, a, p, q – числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля. Называют их соответственно дробями первого, второго, третьего и четвертого типов. Для чего вообще дробь раскладывать на простейшие? Приведем математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов. К примеру, требуется взять интеграл от дробно рациональной функции . После разложения подынтегральной функции на простейшие дроби, все сводится к достаточно простым интегралам Но об интегралах в другом разделе. Пример. Разложить дробь на простейшие.Решение. Вообще отношение многочленов раскладывают на простейшие дроби, если степень многочлена числителя меньше степени многочлена в знаменателе. В противном случае сначала проводят деление многочлена числителя на многочлен знаменателя, а уже затем проводят разложение правильной дробно рациональной функции. Выполним деление столбиком (уголком): Следовательно, исходная дробь примет вид:Таким образом, на простейшие дроби будем раскладыватьАлгоритм метода неопределенных коэффициентов.

• Во-первых, раскладываем знаменатель на множители. Здесь все методы хороши – от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй). Об этом подробнее в разделе теории – разложение многочлена на множители. В нашем примере все просто – выносим х за скобки.

• Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами. Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.

  • Если в знаменателе что-то вроде этого , количество линейных множителей роли не играет, (будь их2 или 22), то дробь представится в виде суммы простейших дробей первого типа: a, b, c и d — числа, A, B, C и D — неопределенные коэффициенты.

• Если в знаменателе что-то вроде этого количество множителей роли не играет и не играют роли степени этих множителей (хоть 221ая степень), то дробь представится в виде суммы простейших дробей первого и второго типов:a, b, c — числа, — неопределенные коэффициенты. Возьмите на заметку: какая степень – столько и слагаемых.

• Если в знаменателе что-то вроде этого количество квадратичных выражений роли не играет, то дробь представится в виде суммы простейших дробей третьего типа:p, q, r и s — числа, P, Q, R и S — неопределенные коэффициенты.

• Если в знаменателе что-то вроде этого количество множителей роли не играет и не играют роли степени этих множителей, то дробь представится в виде суммы простейших дробей третьего и четвертого типов:p, q, r и s — числа, — неопределенные коэффициенты. ОБЫЧНО ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ (как правило, довольно простая).

Хватит теории, на практике все равно понятнее. Пришло время вернуться к примеру. Дробь раскладывается в сумму простейших дробей первого и третьего типов с неопределенными коэффициентами A, B и C.

• В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х. То есть, пришли к равенству:Приx отличных от нуля это равенство сводится к равенству двух многочленов А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.

• В-четвертых, приравниваем коэффициенты при одинаковых степенях х. При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:

• В-пятых, решаем полученную систему уравнений любым способом (при необходимости смотрите статью решение систем линейных алгебраических уравнений, методы решения, примеры), который нравится Вам, находим неопределенные коэффициенты. О решении систем линейных уравнений подробнее в разделе – решение систем линейных алгебраических уравнений.

P.S. Пожалуйста, не ленитесь, проверяйте ответ, приводя к общему знаменателю полученное разложение. Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие. Очень удобно использовать метод частных значений, если знаменатель представляет собой произведение линейных множителей, то есть имеет вид схожий с Рассмотрим на примере, чтобы показать плюсы этого метода.Пример. Разложить дробь на простейшие.Решение. Так как степень многочлена в числителе меньше степени многочлена в знаменателе, то производить деление нам не придется. Переходим к разложению знаменателя на множители. Для начала выносим х за скобки. Находим корни квадратного трехчлена(например, по теореме Виета):Следовательно, квадратный трехчлен можно записать какТо есть, знаменатель примет видПри данном знаменателе, исходная дробь раскладывается в сумму трех простейших дробей первого типа с неопределенными коэффициентами:Полученную сумму приводим к общему знаменателю, но в числителе при этом скобки не раскрываем и не приводим подобные приА, В и С (на этом этапе как раз отличие от метода неопределенных коэффициентов): Таким образом, пришли к равенству:А теперь, для нахождения неопределенных коэффициентов, начинаем подставлять в полученное равенство «частные значения», при которых знаменатель обращается в ноль, то естьх=0, х=2 и х=3 для нашего примера: При х=0 имеем: Прих=2 имеем: Прих=3 имеем: Ответ: Как видите, различие метода неопределенных коэффициентов и метода частных значений лишь в способе нахождения неизвестных. Эти методы можно совмещать для упрощения вычислений. Рассмотрим пример.Пример. Разложить дробно рациональное выражение на простейшие дроби.Решение. Так как степень многочлена числителя меньше степени многочлена знаменателя и знаменатель уже разложен на множители, то исходное выражение представится в виде суммы простейших дробей следующего вида: Приводим к общему знаменателю:Приравниваем числители.Очевидно, что нулями знаменателя являются значениях=1, х=-1 и х=3. Используем метод частных значений. При х=1 имеем: Прих=-1 имеем: Прих=3 имеем: Осталось найти неизвестныеиДля этого подставляем найденные значения в равенство числителей:После раскрытия скобок и приведения подобных слагаемых при одинаковых степенях х приходим к равенству двух многочленов:Приравниваем соответствующие коэффициенты при одинаковых степенях, тем самым составляем систему уравнений для нахождения оставшихся неизвестныхи. Получаем систему из пяти уравнений с двумя неизвестными:Из первого уравнения сразу находим, из второго уравненияВ итоге получаем разложение на простейшие дроби:Примечание. Если бы мы сразу решили применить метод неопределенных коэффициентов, то пришлось бы решать систему пяти линейных алгебраических уравнений с пятью неизвестными. Применение метода частных значений позволило легко отыскать значения трех неизвестных из пяти, что значительно упростило дальнейшее решение. Удачных решений!

studfiles.net

Разложение рациональных дробей на элементарные (простейшие) дроби. Третья часть.

Пример №5

Разложить рациональную дробь $\frac{5x^2+13x+6}{(x+4)(x^2+x+5)}$ на элементарные дроби.

Решение

Выражая заданную правильную рациональную дробь через элементарные дроби (см. пример №2) будем иметь:

$$ \frac{5x^2+13x+6}{(x+4)(x^2+x+5)}=\frac{A}{x+4}+\frac{Bx+C}{x^2+x+5}=\frac{A(x^2+x+5)+(Bx+C)(x+4)}{(x+4)(x^2+x+5)};\\ A(x^2+x+5)+(Bx+C)(x+4)=5x^2+13x+6;\\ (A+B)x^2+(A+4B+C)x+5A+4C=5x^2+13x+6;\\ \left\{ \begin{aligned} & A+B=5;\\ & A+4B+C=13;\\ & 5A+4C=6. \end{aligned} \right. $$

Для разнообразия применим метод Крамера для решения полученной системы линейных уравнений.

$$ \Delta=\left| \begin{array} {ccc} 1 & 1 & 0\\ 1 & 4 & 1 \\ 5 & 0 & 4 \end{array}\right|=17; \Delta_A=\left| \begin{array} {ccc} 5 & 1 & 0\\ 13 & 4 & 1 \\ 6 & 0 & 4 \end{array}\right|=34; \Delta_B=\left| \begin{array} {ccc} 1 & 5 & 0\\ 1 & 13 & 1 \\ 5 & 6 & 4 \end{array}\right|=51; \Delta_C=\left| \begin{array} {ccc} 1 & 1 & 5\\ 1 & 4 & 13 \\ 5 & 0 & 6 \end{array}\right|=-17. \\ A=\frac{\Delta_A}{\Delta}=\frac{34}{17}=2;\; B=\frac{\Delta_B}{\Delta}=\frac{51}{17}=3; \; C=\frac{\Delta_C}{\Delta}=\frac{-17}{17}=-1. $$

Подставляя значения $A=2$, $B=3$, $C=-1$ в равенство

$$ \frac{5x^2+13x+6}{(x+4)(x^2+x+5)}=\frac{A}{x+4}+\frac{Bx+C}{x^2+x+5} $$

будем иметь:

$$ \frac{5x^2+13x+6}{(x+4)(x^2+x+5)}=\frac{2}{x+4}+\frac{3x-1}{x^2+x+5}. $$

Ответ: $\frac{5x^2+13x+6}{(x+4)(x^2+x+5)}=\frac{2}{x+4}+\frac{3x-1}{x^2+x+5}$.

Ну, и для полноты картины разберём пару частных случаев разложения на элементарные дроби. Мы ограничимся преобразованиями, которые даже не потребуют введения неизвестных параметров.

Пример №6

Разложить рациональные дроби на элементарные:

1. $\frac{x^2}{(x-1)^8}$;
2. $\frac{1}{x^2(x^2+1)^2}$.

Решение

1) Для разложения дроби $\frac{x^2}{(x-1)^8}$ можно, конечно, пойти стандарным путём:

$$ \frac{x^2}{(x-1)^8}=\frac{A_1}{x-1}+\frac{A_2}{(x-1)^2}+\frac{A_3}{(x-1)^3}+\frac{A_4}{(x-1)^4}+\frac{A_5}{(x-1)^5}+\frac{A_6}{(x-1)^6}+\frac{A_7}{(x-1)^7}+ \frac{A_8}{(x-1)^8}. $$

Привести к одному знаменателю, а затем применить метод неопределённых коэффициентов, получив систему из восьми уравнений с восемью неизвестными. А можно сделать попроще, добавив и вычтя в числителе $1$ (согласитесь, что при этом числитель остаётся неизменным):

$$ \frac{x^2}{(x-1)^8}=\frac{x^2-1+1}{(x-1)^8}. $$

Теперь, так как $x^2-1=(x-1)(x+1)$, то получим следующее:

$$ \frac{x^2}{(x-1)^8}=\frac{x^2-1+1}{(x-1)^8} =\frac{(x-1)(x+1)+1}{(x-1)^8}=\frac{(x-1)(x+1)}{(x-1)^8}+\frac{1}{(x-1)^8}=\\ =\frac{x+1}{(x-1)^7}+\frac{1}{(x-1)^8}=\frac{x-1+2}{(x-1)^7}+\frac{1}{(x-1)^8}=\\ =\frac{x-1}{(x-1)^7}+\frac{2}{(x-1)^7}+\frac{1}{(x-1)^8}=\frac{1}{(x-1)^6}+\frac{2}{(x-1)^7}+\frac{1}{(x-1)^8}. $$

Можно сделать и по-иному, сразу выделив $x-1$:

$$ \frac{x^2}{(x-1)^8} =\frac{((x-1)+1)^2}{(x-1)^8} =\frac{(x-1)^2+2(x-1)+1}{(x-1)^8}=\\ =\frac{(x-1)^2}{(x-1)^8}+\frac{2(x-1)}{(x-1)^8}+\frac{1}{(x-1)^8} =\frac{1}{(x-1)^6}+\frac{2}{(x-1)^7}+\frac{1}{(x-1)^8} $$

Задача решена, разложение получено. Понятно, что в общем случае такой метод малопригоден, но иметь его в виду стоит. Хотя бы для того, чтобы избежать громоздких преобразований, если есть для этого хоть малейшая возможность.

2) Здесь добавим и вычтем в числителе $x^2$. Сделать это преобразование придётся два раза:

$$ \frac{1}{x^2(x^2+1)^2}=\frac{1+x^2-x^2}{x^2(x^2+1)^2}=\frac{x^2+1}{x^2(x^2+1)^2}-\frac{x^2}{x^2(x^2+1)^2}=\\ =\frac{1}{x^2(x^2+1)}-\frac{1}{(x^2+1)^2}=\frac{1+x^2-x^2}{x^2(x^2+1)}-\frac{1}{(x^2+1)^2}=\\ =\frac{x^2+1}{x^2(x^2+1)}-\frac{x^2}{x^2(x^2+1)}-\frac{1}{(x^2+1)^2} =\frac{1}{x^2}-\frac{1}{x^2+1}-\frac{1}{(x^2+1)^2}. $$

Ответ: 1) $\frac{x^2}{(x-1)^8}=\frac{1}{(x-1)^6}+\frac{2}{(x-1)^7}+\frac{1}{(x-1)^8}$; 2) $\frac{1}{x^2(x^2+1)^2}=\frac{1}{x^2}-\frac{1}{x^2+1}-\frac{1}{(x^2+1)^2}$.

math1.ru

Алгоритм разложения правильной дроби на простейшие.

1) Знаменатель дроби представить в виде произведения:

где корень многочлена. Если корни повторяются k раз, то записывают если корни комплексные то

2) Каждому множителю в знаменателе поставить в соответствие простейшую дробь:

множителю — простейшую дробь 1 типа ,

множителю сумму

множителю — дробь III типа

множителю — сумму

3) записать правильную исходную дробь суммой простейших дробей, найденных в п.2.

4) найти коэффициенты А,В,С,… методом неопределенных коэффициентоводним из способов.

 

Способ «сравнения коэффициентов«

· сложить простейшие дроби, приведя их к общему знаменателю;

· отбросить знаменатель, а в числителе привести подобные члены по степеням ;

· сравнивая коэффициенты при степенях полученного числителя и числителя исходной дроби, составить систему уравнений относительно неизвестных А, В, С,…,N;

· решить полученную систему любым способом.

Способ «подборачастных решений»:

· расставить дополнительные множители для приведения дробей к общему знаменателю;

· составить тождество, в левой части которого – сумма произведений числителей простейших дробей на дополнительные множители, а в правой части – числитель исходной дроби;

· придавая переменной различные значения ( в первую очередь значения корней многочлена, разложенного на множители в 1-ом пункте алгоритма, а также тривиальные значения) составить систему относительно неизвестных коэффициентов А,В,С,…;

· решить полученную систему.

ПРИМЕР 1.11. Найти интеграл

Подынтегральная функция – правильная рациональная дробь. Представляем её в виде суммы простейших дробей.

Находим коэффициенты А, В, С.

1. Способ «сравнения коэффициентов».

Решаем систему матричным методом Гаусса.

 

2. Способ «подбора частных решений».

При

При

При

Подставляем значения А, В, С и находим интеграл.

ПРИМЕР 1.12. Разложить дробь на простейшие.

РЕШЕНИЕ.

Дробь правильная рациональная, поэтому

=

Способом подбора частных решений находим коэффициенты .

При

При

При

При

Вычтя 2-е уравнение из 1-го, получаем:

Делим 1-е уравнение на 2, и из него получаем:

Подставляем коэффициенты и получаем искомое разложение исходной правильной дроби на простейшие.

=

Интегралы от иррациональных функций.

Не от всякой иррациональной функции интеграл выражается через элементарные функции, то есть интегрируется. Рассмотрим некоторые интегрирующиеся функции.

 

1.8.1. Интегралы вида , (1.16.)

где означает, что над величинами производятся только рациональные операции;

— целые числа.

Применяя подстановку (1.17.)

где — наименьший общий знаменатель дробей ,

указанный интеграл преобразуется в интеграл от рациональной функции.

ПРИМЕР 1.13. Найти интеграл

РЕШЕНИЕ.

|общий знаменатель дробей и является 4,

следовательно, заменяем переменную =

=

=

1.8.2. Интегралы вида . (1.18.) Подстановкой (1.19.)

где — наименьший общий знаменатель дробей ,

указанный интеграл преобразуют в интеграл от рациональной функции.

ПРИМЕР 1.14. Найти интеграл

а)

РЕШЕНИЕ.

Общий знаменатель дробей и является 6, следовательно, замена переменной: .

=

б) .

РЕШЕНИЕ.

Делаем подстановку: .

 

1.8.3. Интегралы вида (1.20.) приводятся к интегралам от рациональных функций подстановками

Эйлера.

Я подстановка Эйлера.

Если то полагаем (1.21.)

Положим знак плюс и возведем в квадрат обе части равенства

откуда рациональная функция от

Тогда

ПРИМЕР 1.15. Найти интеграл .

РЕШЕНИЕ.

Принимаем: тогда ;

Я подстановка Эйлера.

Пусть и — действительные корни трехчлена

тогда применяется подстановка (1.22.)

Возводим в квадрат и выражаем квадратный трехчлен через его корни ;

рациональное выражение.

и также рационально зависят от

Данная подстановка применима как при так и при , но многочлен должен иметь два действительных корня.

ПРИМЕР 1.16. Найти интеграл

 

РЕШЕНИЕ.

Корни трехчлена = — 4; = 1 – действительные числа, поэтому

Полагаем .

Возведём в квадрат обе части и сократим на ( ).Получаем:

; = = . Тогда:

= +C =

= +C = .

 

Искусственные приемы.

ПРИМЕР 1.17. Найти интегралы а) б)

= в) | |=

Последнее слагаемое — есть исходный интеграл поэтому, перенеся его влево от знака равенства и разделив на 2, получаем:

Интегрирование иррациональных функций, содержащих квадратные трехчлены, рассмотрены в п.1.5.

 

1.8.5.Тригонометритческие подстановки.

Если подынтегральная функция содержит корни вида: то применяются тригонометрические подстановки.

Для интегралов вида —

подстановка (1.23.)

вида —

подстановка или (1.24.)

вида —

подстановка или (1.25.)

 

ПРИМЕР 1.18. Найти интегралы.

stydopedia.ru

Разложение дроби на простейшие

Закон равноускоренного движения

Равноускоренное движение в поле тяжести Земли

Закон равноускоренного движения получается в результате решения простейшего дифференциального уравнения вида:

Общее решение этого уравнения дается формулой:

;

Здесь и — произвольные константы, соответствующие начальной координате и начальной скорости.

Движение с постоянным ускорением называют равноускоренным. Движение с постоянным ускорением подчиняется закону:

;

.

При этом уравнения движения в координатной форме имеют аналогичный вид:

;

.

В этом случае часто говорят о равноускоренном движении, если знаки и совпадают и о равнозамедленном, если и имеют противоположные знаки. При этом знак каждой из величин зависит от начального выбора системы отсчета.

Частный случай равноускоренного движения — равномерное движение. В этом случае . Тогда движение описывается закону:

 

2 http://www.math34.ru/уравнения-с-разделяющимися-переменными.html

 

3 Рассмотрим, как решать уравнения вида y’=f(ax+by+c), где a,b,c — некоторые числа. Это — дифференциальные уравнения, приводимые к уравнениям с разделяющимися переменными.

Такие уравнения приводятся к уравнениям с разделяющимися переменными с помощью замены z=ax+by+c. Дифференцируем обе части этого равенства по иксу:

Поскольку x’=1, а так как y’=f(ax+by+c), то y’=f(z).

Соответственно, получаем, что

 

При условии a+bf(z)≠0 переменные можем разделить:

Интегрируем полученное уравнение

В полученном решении возвращаемся к исходным переменным z=ax+by+c.

Если a+bf(z)=0, то значит, и dz/dx=0, то ax+by+c=С.

6 Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель

получим

используем правило дифференцирования произведения

что, после интегрирования обеих частей, дает нам

Таким образом, решение линейного дифференциального уравнения первого порядка

(в частности, с постоянными коэффициентами) имеет вид

где является константой интегрирования.

Пример[

Возьмём дифференциальное уравнение первого порядка с постоянными коэффициентами:

Это уравнение имеет особое значение для систем первого порядка, таким как RC-схемы и масс-демпфер^{системы.}

В этом случае, p(x) = b, r(x) = 1.

Следовательно, решение будет:

 

7 Уравнение Бернулли

Обыкновенное дифференциальное уравнение вида:

называется уравнением Бернулли (при или получаем неоднородное или однородное линейное уравнение).

При является частным случаем уравнения Риккати. Названо в честь Якоба Бернулли, опубликовавшего это уравнение в 1695 году.

Метод решения с помощью замены, сводящей это уравнение к линейному, нашёл его брат Иоганн Бернулли в 1697 году.^[1]

Первый способ[править | править вики-текст]

Разделим все члены уравнения на

получим

Делая замену

и дифференцируя, получаем:

Это уравнение приводится к линейному:

и может быть решено методом Лагранжа (вариации постоянной) или методом интегрирующего множителя.

Второй способ

Заменим

тогда:

Подберем так, чтобы было

для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка. После этого для определения получаем уравнение — уравнение с разделяющимися переменными.

Пример

Уравнение

разделим на получаем:

Замена переменных

дает:

Делим на ,

Результат:

Линейные дифференциальные уравнения второго порядка

Дифференциальное уравнение второго порядка имеет вид . Определение. Общим решением уравнения второго порядка называется такая функция , которая при любых значениях и является решением этого уравнения. Определение. Линейным однородным уравнением второго порядка называется уравнение . Если коэффициенты и постоянны, т.е. не зависят от , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так: . Уравнение будем называть линейным неоднородным уравнением. Определение.Уравнение , которое получается из линейного однородного уравнения заменой функции единицей, а и — соответствующими степенями , называется характеристическим уравнением. Известно, что квадратное уравнение имеет решение, зависящее от дискриминанта : , т.е. если , то корни и — действительные различные числа. Если , то . Если же , т.е. , то будет мнимым числом, а корни и — комплексными числами. В этом случае условимся обозначать .

12 Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого действительного и комплексного числа выполнено следующее равенство:

,

где — одна из важнейших математических констант, определяющаяся следующей формулой: ,

— мнимая единица.

 

 

14 Метод неопределённых коэффициентов ― метод, используемый в математике для нахождения искомой функции в виде точной или приближённой линейной комбинации конечного или бесконечного набора базовых функций. Указанная линейная комбинация берётся с неизвестными коэффициентами, которые определяются тем или иным способом из условий рассматриваемой задачи. Обычно для них получается система алгебраических уравнений.

Разложение дроби на простейшие

Классическим примером применения метода неопределённых коэффициентов является разложение правильной рациональной дроби в комплексной или вещественной области на элементарные дроби.

Пусть и — многочлены с комплексными коэффициентами, причём степень многочлена меньше степени многочлена . Будем полагать, что степень многочлена равна , коэффициент при старшем члене многочлена равен 1, а , ― различные корни многочлена с кратностями , соответственно. Отсюда имеем

Функция представима, и притом единственным образом, в виде суммы элементарных дробей

где ― неизвестные пока комплексные числа (их число равно ). Для их отыскания обе части равенства приводят к общему знаменателю. После его отбрасывания и приведения в правой части подобных членов получается равенство, которое сводится к системе линейных уравнений относительно .

Примечание. Нахождение коэффициентов упрощается, если имеет только некратные корни , , т.е. все и

После умножения на последнего равенства и подстановки непосредственно получаем значение соответствующего коэффициента

.

Обращение ряда

Если функция , не равная нулю при разложена в ряд Маклорена:

то существует ряд Маклорена противоположной функции:

Коэффициенты этого ряда можно найти, перемножив эти два равенства и применив метод неопределённых коэффициентов. Получится бесконечная треугольная система линейных уравнений, из которой последовательно найдутся искомые коэффициенты.

Аналогичным, но более громоздким, образом можно найти коэффициенты ряда обратной функции:

При этом используется соотношение , то есть весь ряд для подставляется вместо в ряд для .

Сумма степеней

В качестве частного примера можно привести задачу о нахождении формулы k-х степеней: . Будем искать ответ в виде многочлена -ой степени от . Коэффициенты же этого многочлена найдём с помощью метода неопределённых коэффициентов.

Пример. Ищем в виде .

По определению , а также . Подставляя многочлен в приведённой форме и приравнивая коэффициенты при одинаковых степенях, получаем систему для их определения:

откуда получаем ответ:

 

15 Числовой ряд — числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Рассматриваются числовые ряды двух видов:

· вещественные числовые ряды — изучаются в математическом анализе;

· комплексные числовые ряды — изучаются в комплексном анализе;

Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.

Числовые ряды применяются в качестве системы приближений к числам.

Обобщением понятия ряда является понятие двойного ряда.

Пусть — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность

каждый элемент которой представляет собой сумму первых k членов исходной последовательности, называемой частичной суммой вида:

Рядом называется совокупность этих двух последовательностей. Вообще, для обозначения ряда используется символ:

поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.

В соответствии с этим говорится о сходимости числового ряда:

· числовой ряд сходится, если сходится последовательность его частичных сумм;

· числовой ряд расходится, если расходится последовательность его частичных сумм;

· числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.

Если числовой ряд сходится, то предел последовательности его частичных сумм носит название суммы ряда:

 

 

Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится^[1]. Элементы ряда представляют собой комплексные числа (в частности, вещественные).

Пусть — числовой ряд. Число называется n-ой частичной суммой ряда .

Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число , то в этом случае пишут . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.

Дальнейшим обобщением понятия суммы ряда является понятие суммирующей функции ряда.

17 Необходимое условие сходимости ряда (Необходимый признак сходимости ряда):

Для сходимости ряда необходимо, чтобы последовательность была бесконечно малой.

Доказательство

По условию последовательность , а следовательно, и её остаток имеют общий конечный предел , но и поэтому , что равносильно бесконечной малости .

19 Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов.

Содержание

Формулировка

Доказательство

Обозначим частные суммы ряда . Из неравенств следует, что Поэтому из ограниченности вытекает ограниченность а из неограниченности следует неограниченность Справедливость признака вытекает из критерия сходимости для

 

stydopedia.ru

Разложение дроби на элементарные

Количество просмотров публикации Разложение дроби на элементарные — 24

Лемма 1. Пусть правильная дробь и a – вещественный корень многочлена Q(x), ᴛ.ᴇ. Q(x)=(x-a)^aQ₁(x), Q₁(a)¹0,a³1. Тогда существует A и многочлен P₁(x) такие, что

,

где- правильная дробь.

Доказательство: Рассмотрим разность ( где A — неĸᴏᴛᴏᴩᴏᴇ, пока неопределœенное число)

.

Дробь справа правильная, так как порядок P(x) и AQ₁(x) меньше порядка знаменателя.Положим , тогда для числителя число a будет корнем и =(x-a)P₁(x). В случае если это выражение поделить на Q(x), то получиться требуемое равенство.

Лемма 2. Пусть правильная дробь и w=u+iv (v¹0) – комплексный корень многочлена Q(x), ᴛ.ᴇ. Q(x)=(x²+px+q)^bQ₁(x), Q₁(w)¹0,b ³1. Тогда существуют вещественные числа M, N и многочлен P₁(x) с вещественными коэффициентами такие, что

,

где- правильная дробь.

(без доказательства).

Определœение. Дроби вида

называются элементарными.

Теорема. Пусть P(x)/Q(x) – правильная дробь, P, Q – многочлены с вещественными коэффициентами, старший коэффициент Q равен 1 и

разложение многочлена по парно простым корням

a₁,a₂,…,a_r,w₁,w₂,…,w_s, (x-w_k)(x-)=x²+p_kx+q_k

кратностей a₁,…,a_r,b₁,…,b_s . Тогда дробь P(x)/Q(x) должна быть представлена в виде суммы элементарных дробей. Каждому сомножителю будет соответствовать сумма дробей вида , а каждому сомножителю будет соответствовать сумма дробей .

Другими словами существуют вещественные числа , такие, что справедлива формула

=+…+++…+ (*)

Доказательство. По лемме 1

.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, у второго слагаемого кратность корня a₁в знаменателœе понижена на единицуи к применяем лемму 1 еще раз. Повторяя эту процедуру нужное число раз мы получим последнее слагаемое, знаменатель которого не будет иметь своим корнем a₁ .

=+.

Точно также поступаем с остальными действительными корнями знаменателя.

=+…++.

У последнего слагаемого знаменатель имеет только комплексные корни и к нему применяется лемма 2. В результате, появляется последняя серия слагаемых, соответствующих комплексным корням.

referatwork.ru