Логарифмическая бумага — Википедия
Материал из Википедии — свободной энциклопедии
 Логарифмическая бумага с числовыми координатами от (1; 1) до (100; 100)
Логарифмическая бумага с числовыми координатами от (1; 1) до (100; 100)Логарифми́ческая бума́га — разновидность масштабно-координатной бумаги, на которой координатная сетка построена в логарифмическом масштабе. Обычно изготовляется типографским способом. Также используется полулогарифмическая бумага, на которой вдоль одной оси отложена равномерная шкала, по другой — логарифмическая.
Логарифмическая и полулогарифмическая бумаги применяются для построения графиков функций, которые в логарифмическом масштабе принимают более простой вид (в некоторых случаях — прямая). Они удобны для графического представления данных, изменяющихся в очень большом диапазоне значений (на несколько порядков). Естественно, аргумент и (или) функция, отложенные по логарифмической шкале, должны принимать только положительные значения.
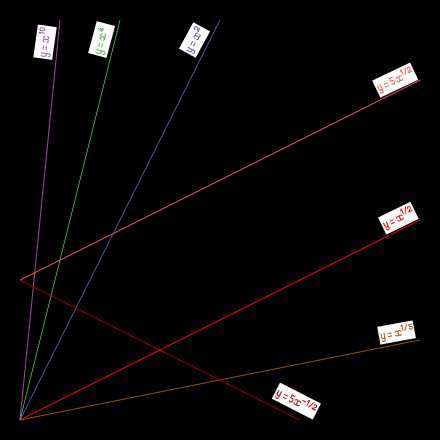
На логарифмической бумаге вид прямых имеют графики степенных функций вида y=axb{\displaystyle y=ax^{b}}, поскольку путём логарифмирования степенная зависимость приводится к линейной: lgy=lga+blgx{\displaystyle \mathrm {lg} \,y=\mathrm {lg} \,a+b\,\mathrm {lg} \,x}. Наклон прямой (угловой коэффициент) определяется показателем степени b. При b>0{\displaystyle b>0} эта функция возрастающая, а при b<0
ru.wikipedia.org
Полулогарифмический масштаб — Большая Энциклопедия Нефти и Газа, статья, страница 1
Полулогарифмический масштаб
Cтраница 1
Полулогарифмический масштаб, при котором по оси ординат откладывается не цена акций, а ее логарифм, полезен, когда цена акции меняется очень сильно, например, с 3 до 90 долларов. Должны ли быть линии канала абсолютно параллельными. [2]
В полулогарифмическом масштабе по оси абсцисс ( горизонтальная) откладывается логарифм величины, а по оси ординат ( вертикальная) — истинная величина в линейном масштабе. Такой масштаб удобен при изображении, например, частотных или амплитудных характеристик приемника. [3]
В полулогарифмическом масштабе с линейной шкалой времени экспоненциальный рост изображается прямой линией, представляющей, таким образом, особенно большой соблазн с точки зрения возможности экстраполяции. [4]
В полулогарифмическом масштабе распределение скорости изображается прямой линией. Влияние теплообмена или шероховатости стенки сводится только к параллельному сдвигу этой прямой. [5]
В случае полулогарифмического масштаба по одной из осей откладывают не самое величину, а ее логарифм. Такой масштаб удобен, если в рассматриваемом интервале одна из величин изменяется весьма значительно. Вторую величину откладывают в линейном масштабе. На рис. 8 — 2 приведена в качестве примера зависимость tg б от температуры для цирконового фарфора в полулогарифмическом масштабе. [6]
Применение ( полулогарифмического масштаба на рис., 50.3 позволяет легко производить интерполяцию и находить ненанесенные на график кривые, соответствующие промежуточным значениям RP / RS, ( поскольку эти кривые при выбранном способе изображения становятся симметричными. Для упрощения интерполяции на рисунке нанесена пунктирная линия, на которой расположены все минимумы. [7]
Если в полулогарифмическом масштабе вместо прямой линии lg / f ( t) получается кривая, это свидетельствует о наличии в препарате более чем одного радиоактивного изотопа. [8]
Естественно, что
Эта зависимость в полулогарифмическом масштабе выражается прямой. Для установления указанной зависимости необходимо экспериментально определить вязкость раствора данной партии полимера для двух различных концентраций. [10]
Концентрация примеси изображена в полулогарифмическом масштабе в зависимости от расстояния ( в мкм) в глубь прибора. Размытие границы скрытого слоя ( а также границы эпитаксиального слоя) происходит при последующих высокотемпературных операциях диффузии, проводимых после сформирования этого слоя. [11]
При составлении графика в полулогарифмическом масштабе получаем, что абсолютная активность убывает со временем попрямей. [12]
Кривые распада строятся в полулогарифмическом масштабе; по оси абсцисс в линейном масштабе откладывается время, по оси ординат в логарифмическом масштабе — интенсивность излучения. На рис. 24 приведены кривые распада радиоактивного натрия для нефтеносных и водоносных песчаников в эксплуатационной скв. Наведенная активность в нефтеносном пласте, измеренная сразу после окончания облучения, больше, чем в водоносном. [14]
На рис. 2.6 в полулогарифмическом масштабе представлена кривая распределения ионов по состояниям для двух различных материалов электродов. В отличие от высоковольтного искрового пробоя для дугового наиболее характерно наличие двух-и трехзарядных ионов. Вероятность появления высокозарядных ионов, однако, уменьшается более быстрыми темпами, чем в случае высокочастотной искры. [15]
Страницы: 1 2 3 4 5
www.ngpedia.ru
Полулогарифмический график — Справочник химика 21
Полулогарифмический график уравнения (П1,71) или (П1.72) представляет собой прямую линию с наклоном k (рис. П1-20). [c.86]Полученные полярограммы обрабатывают графически и путем построения полулогарифмического графика (см. рис. 2.19) рассчитывают Ег/ и число электронов, участвующих в электродном процессе. Значения Ег/ц для полярограммы неизвестного раствора сравнивают с найденными значениями Еу. для стандартных растворов и табличными данными. Делают вывод о качественном составе анализируемого раствора, [c.149]
Наиболее показательно в этом плане уточнение условий и способа регистрации Тц (рис. XII. 5). Данные относятся к полиизобутилену. Строится полулогарифмический график зависимости частоты, при которой регистрируется Тц, от обратной температуры. С небольшими вариациями и для разных полимеров картина получается одна и та же. Действительно, Тц, как и другие температуры релаксационных переходов (в отличие от фазовых ), зависит от частоты, смещаясь с ростом частоты 306 [c.306] Если полярографически активным веществом является продукт реакции первого порядка, то константа скорости ее также может быть найдена из полулогарифмического графика [c.252] Точно так же, как и в анализе скорости десорбции, параметры, определяющие стационарное состояние, могут быть в общем случае определены из семейства кривых выделения газа. Полулогарифмический график зависимости плотности газа N при постоянной поверхностной концентрации п от /ЯТ дает
Доля обмена F ко времени t определяется путем измерения изотопного состава АХ или ВХ, и из полулогарифмического графика зависимости F от I можно оценить время половинного обмена и, следовательно, R. Из экспериментов, проведенных при разных концентрациях АХ и ВХ, можно найти зависимость от а и 6 и путем обычного рассмотрения кинетических данных можно постулировать механизм реакции, приводящей к обмену. Количественное изучение реакции обмена требует разделения реагентов АХ и ВХ для изотопного анализа в разные моменты реакции. [c.108]
На полулогарифмическом графике типа рис. 7 зависимость /д от 8 изобразится прямой линией, наклонной к оси абсцисс. Выполняя подобное построение для каждой фракции нашей системы, получают набор прямых, пересекающих в различных точках оси абсцисс и ординат, и в определенной мере характеризующих зависимость (А = 1,2,. ..). Затем для каждого значения абсциссы суммируют значения ординат всех этих прямых, выраженные в натуральных единицах интенсивности, и откладывают на том же графике логарифм найденной суммы но оси ординат для соответствующего значения 8 . [c.50]На рис. 8-2 представлены так называемые тафелевские кривые, используемые по той причине, что при высоких поверхностных перенапряжениях один из членов в равенстве (8-2) становится пренебрежимо малым и на полулогарифмическом графике получается прямая линия. Таким образом, [c.30]
Необходимо построить два графика полулогарифмический график для образца 1 и график зависимости активность — время для образцов 1, 2 и 3. [c.125]
Рассмотрим далее методику определения кинетических параметров нуклеации по уравнению (184). Результаты экспер№ ментов наносятся на полулогарифмический график с координатами [— 1п (1 — 2 э) — ], на котором функция распределения по уравнению (184) имеет выпуклость вверх. В начале процесса (1 = 0) наклон функции распределения равен сумме скоростей гомогенной и гетерогенной нуклеации в образце,
Функция распределения на полулогарифмическом графике асимптотически приближается к некоторой прямой линии [c.110]
Основное соотношение — это линейная зависимость между логарифмами приведенных времен удерживания членов гомологического ряда и числом их углеродных атомов. Для определения индексов удерживания нужно только построить полулогарифмический график, как показано на рис. 10. Здесь число углеродных атомов умножается на 100, а расстояние между н-алканами разделено на 100 единиц. Сначала на ординате в логарифмической шкале наносятся приведенные времена удерживания соответствующих н-алканов и строится калибровочная прямая н-алканов. Затем, как указано выше, вычисляют приведенное время удерживания 1 х каждой из интересующих компонент хроматограммы и находят индекс удерживания 1х по калибровочному графику, как показано на рис. 10. [c.184]
Гель-фильтрация восстановленных полипептидных цепей в 6М гуанидингидрохлориде позволяет производить оценки молекулярного веса в диапазоне 80000—1000 [147]. В поддиапазоне 40 000—10 000 точность метода 7% и на краях диапазона — 10%. В качестве среды для гель-фильтрации используют колонку Био-Гель А-5М с номинальным содержанием агарозы 6%. Определение молекулярного веса осуществляется по принципу сравнения с белками-маркерами известного молекулярного веса на полулогарифмическом графике зависимости молекулярного веса от коэффициентов распределения либо от где Ve — объем элюирования и Уо — исключенный объем (см. разд. 5.3 и 5.5). [c.427]
Как видно из уравнений (1) и (2), для вычисления коэффициента самодиффузии необходимо определить зависимость амплитуды спинового эха от O или g. На основании того что пМ линейно зависит от из полулогарифмического графика зависимости легко определить величину D. В наших опытах коэффициенты самодиффузии (КСД) адсорбированных молекул определялись из зависимости амплитуды спинового эха от ширины o градиентного импульса [1, 2], а величина Д рассматривалась как независимая переменная. Времена наблюдения составляли 1—3 мс при использовании методики первичного эха и 3—100 мс в методике стимулированного эха. Практически во всех опытах использовался накопитель сигналов типа EMG-666 (Венгрия) и определялись средние значения из 16—128 сигналов амплитуды спинового эха, что существенно повышало точность
Для проведения анализа по поглощению нейтронов часто применяют специальные кюветы (рис. 74). Во внутренний цилиндр кюветы помещают детектор, а во внешний — анализируемое вещество или стандартный образец с известным содержанием данного элемента. Массу анализируемого элемента находят, пользуясь калибровочным полулогарифмическим графиком, полученным на основании измерений активностей детекторов после облучения нейтронами проб с известным содержанием определяемого элемента. [c.233]
Результаты измерений наносят на полулогарифмический график. По оси абсцисс откладывают толщину слоя, а по оси ординат— логарифм интенсивности излучения. В случае однокомпонентного излучения получается близкая к теоретической линия (см. рис. 34), тангенс угла наклона которой соответствует коэффициенту поглощения излучения. [c.51]
М, НС1 добавляли до необходимого pH). До pH 7,0 полулогарифмические графики представляют собой прямые, которые с ростом pH смещаются к отрицательным потенциалам с заметным увеличением наклона [в качественном согласии с уравнениями (121) — (124)]. При pH > 7,0 на графиках появляется перегиб — верхняя часть волн имеет больший наклон, чем нижняя. При pH >8,3 появляется второй перегиб—крутизна самой верхней части волны увеличивается по сравнению с ее величиной в средней части. Для сильнощелочного раствора график становится прямолинейным с наклоном, близким наклону верхней части волн при pH = 8,3. Такой характер изменения логарифмических графиков волн объясняется 8-образной формой изотермы адсорбции непротонированной формы деполяризатора. В кислых растворах, где потенциалы близки к й , имеют место очень высокая адсорбируемость и высокое заполнение. В этом случае, видимо, адсорбиру- [c.186]
Перегибы на полулогарифмических графиках волн встречаются довольно часто. Так, например, графики, очень напоминающие по виду приведенные на рис. 43, наблюдали Ф. Эльвинг и Э. Олсон при восстановлении ароматических нитрозогидроксиламинов (см. рис. 3 в работе [486]). [c.187]
При полярографировании растворов К-этил-пиридиния на фоне тет-раалкиламмониевой соли среднее значение обратной величины наклона полулогарифмических графиков волн,построенных по уравнению (133), также падает с увеличением концентрации органического растворителя (см. кривые 2 на рис. 73 и 74), [c.258]
Для 1-го и 2-го порядков реакции на полулогарифмическом графике зависимости (l/P)ln[n( i)/n] или IT )[n ti)—n]j[nn ti)] от XjRT получаются прямые линии с наклоном, равным энергии активации десорбции. Пренебрежение последним членом в уравнении (18) вносит ошибку (менее 1%) для хемосорбционных систем. Эта ошибка может быть скорректирована с удовлетворительной точностью для случая очень малых величин энергии адсорбции, в котором этот член может стать заметным. Для любой [c.131] При исиользовании выражения (2. И) отпадает необходимость градуировки термопары, а темн охлаждения тп но абсолютной величине может быть найден из полулогарифмического графика 1пф=7 (т) как тангенс угла наклона прямой, характеризуюгцей регулярный режим. На рис. 2. 6 представлены графики режимов охлаждения одного из крекипг-остатков при одной и той же температуре опыта (58,7° С) для бикалориметра с зазором соответственно 4,06 и 2,05 мм. Приведенные данные параллельных опытов свидетельствуют о достаточно высокой стабильности результатов и хорошей воспроизводимости их. [c.67]Несколько других методов, успех которых также зависел от формы двух сравниваемых ионизационных кривых, было названо Никольсоном логарифмическими методами . Первый из них, разработанный Хонигом и Ванье [965], не исключает влияния распределения электронов по энергиям и дает аналитическое выражение, указывающее, что при энергиях, ниже потенциала ионизации примерно на 1 эв, зависимость носит экспоненциальный характер. На полулогарифмическом графике эффективности ионизации кривая имеет наклон 2/ ЗкТ) в области потенциала ионизации. Допускают, что все кривые в этих координатах имеют аналогичную форму. Другие методы, подобные рас- [c.479]
На рис. 50 можно видеть, что кривая, показывающая зависимость коэффициента погашения от длины волпы, имеет параболическую форму. Однако внутри значительного интервала длин волн вблизи видимого спектра кривая может быть представлена прямой на полулогарифмическом графике. Холт, Мак-Лейн и Олденберг считают, что при длинах волн, значительно меньших, чем исследованные, иа кривой поглощения возможно наличие максимума. На кривой рис. 50 можно наметить две точки перегиба, расположенные соответственно у обоих концов исследованного интервала длин волн. Однако, прежде чем утверждать, что эти точки перегиба действительно существуют, потребуются дополнительные исследования. Признаки перегиба вблизи 1920А, намечающиеся по данным Холта, Мак-Лейна и Олденберга [181], по мнению Идсе [185], подтверждают положение Шарма [177] о существовании четкого [c.245]
Функция распределения времени ожидания появления первого центра кристаллизации при различных переохлаждениях и перегревах расплава олова исследовалась в работах Ланге [172 ], Шейля[173,174] (для переохлаждений 3 — 11°С) и Делабройля [176] (для переохлаждений 47— 59°С).По Ланге и Шейлю,скорость зарождения центров кристаллизации возрастает с увеличением переохлаждения и уменьшением предварительного перегрева расплава. Функция распределения времени ожидания появления первого центра кристаллизации обычно соответствует уравнению (91), т. е. после некоторого периода нестационарности Тн скорость зарождения центров кристаллизации достигает постоянного стационарного значения. При малых пере-охлаледениях (3—6°) и больших перегревах (100—400°) расплава функция распределения на полулогарифмическом графике [—1п (1— ) — ] имеет выпуклость либо вверх, т. е. скорость зарождения центров кристаллизации со временем уменьшается (см. рис. 18, IV, 3), либо вниз, т. е. скорость зарождения центров кристаллизации со временем возрастает (см. рис. 18, IV, 2). В работах [130, 173] представлены также, результаты этих исследований на вероятностной бумаге закона Вейбулла — Гнеденко. [c.83]
При переохлаждениях 50 и 54°, соответствуюш их положению минимумов кривой /(АГ), функция распределения времени олодания появления первого центра кристаллизации описывается более общим гиперэкспоненциальным законом [см. уравнение (83) ] с выпуклостью вниз на полулогарифмическом графике [—1п(1 — Р) — I]. Скорость зарождения центров кристаллизации со временем возрастает от /(0), асимптотически приближаясь к стационарному значению /(оо) (см. рис. 18, IV,2). Стационарная скорость зарождения центров кристаллизации (/ст) монотонно возрастает с увеличением переохлаждения расплава и соответствует классической зависимости 1 АТ) [см. уравнения (4) (11)1- Значения нестационарной скорости зарождения центров кристаллизации (/(0)) образуют экстремальную зависимость /(АГ), соответствующую эксперимен- [c.85]
chem21.info
Презентация на тему: Динамический график

Характеристика динамики
При изображении динамики с помощью линейной диаграммы на ось абсцисс наносят характеристики времени (дни, месяцы, кварталы, годы), а на оси ординат – значения показателя

Полулогарифмическая сетка
Однако линейные диаграммы с равномерной шкалой искажают относительные изменения экономических показателей. Кроме того, их применение теряет наглядность и даже становится невозможным при изображении рядов динамики с резко изменяющимися уровнями, что характерно для динамических рядов за длительный период времени. В таких
случаях, вместо равномерной шкалы используют полулогарифмическую сетку, в
которой на одной оси наносится линейный масштаб, а на другой – логарифмический.

Полулогарифмическая сетка
В этом случае логарифмический масштаб наносится на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (год, квартал и пр.). Для построения логарифмической шкалы необходимо: найти логарифмы исходных чисел, начертить ординату и разделить ее на несколько равных частей.

Полулогарифмическая сетка
Затем нанести на ординату отрезки, пропорциональные абсолютным приростам этих логарифмов, и записать соответствующие логарифмы чисел и их антилогарифмы.
Полученные антилогарифмы дают вид искомой шкалы на ординате.

Пример
Рассмотрим пример использования логарифмического масштаба для отображения динамики производства контрольно-кассовыхмашин в России:

Логарифмический масштаб
Найдя минимальные и максимальные значения логарифмов производства контрольно-кассовыхмашин, строим масштаб с таким расчетом, чтобы все они разместились на графике. Затем находим соответствующие точки (с учетом масштаба) и соединяем их прямыми линиями. Полученный график с использованием логарифмического масштаба называется диаграммой на полулогарифмической сетке.
studfiles.net
Сравнение равномерной, логарифмической и степенной шкал
Выбор типа шкал для графика, всегда казалось мне интуитивно понятной задачей. Однако, когда мне нужно было объяснить, чем они отличаются, то я не смог привести понятных аргументов. В интернете хорошей информации мне не попалось. Поэтому решил разобраться, откуда растут ноги у разных видов шкал и как их следует применять. Я решил рассмотреть три самых распространенных вида шкал — равномерную, логарифмическую и степенную.
Равномерная шкала
Самый распространенный и привычный вид шкал. Также их называют арифметическими или линейными шкалами. На такой шкале значения равноудалены друг друг от друга.
Например значения 100 и 200, и 200 и 300 отстают друг от друга на одно и тоже расстояние.
Например, на этом графике по оси Y — равномерная шкала с шагом в 20 лет средней продолжительности жизни, а по оси X — равномерная шкала с шагом 10 календарных лет.

Логарифмическая шкала
Этот вид шкал тоже используется достаточно часто, особенно когда речь идёт о научных исследованиях. Она используется для отображения широко диапазона величин, когда значения, которые попадают на график отличаются на много порядков. То есть когда мы хотим одновременно видеть и значения 0.1, 0.2 и значения 100, 200 на одном графике. Зачастую это связанно с физикой процесса. Так, например, в музыке ноты, различающиеся по частоте в два раза это ноты на октаву выше (Ля и Ля следующей октавы). Чтобы показать частоты двух нот будет удобно использовать логарифмическую шкалу.
Но бывает, что в наборе данных просто содержаться большой разброс данных. Например, как на этом графике из Beautiful Evidence Тафти, где он использует логарифмические шкалы для сравнения массы тела и мозга различных существ. Так как бывают и крошечные рыбки и огромные киты, то на таком графике удобно использовать логарифмические шкалы.

Чаще всего используются логарифмические шкалы с основанием 10. Это значит, что одинаковые расстояние на графике откладываются между значениями отличающимися на один порядок. Но бывают логарифмические шкалы с другими основаниями. Например 2.
Степенная шкала
Это менее известный тип шкал. Он отличается от остальных тем, что расстояние между рисками, соответствует числам возведенным в степень. То есть получается, что расстояние между соседними рисками постоянно растёт или уменьшается. Такие шкалы удобны, когда мы хотим показать на одном графике более детально какую-то группу значений, но при это не хотим потерять из вида, значения которые, сильно отличаются от этой группы. Чем-то это похоже на логарифмическую шкалу, но здесь идёт акцент не на всем промежутке, а только на отдельной его части. Это хорошо видно на примере РИА новости, где они использовали степенные шкалы, чтобы сгладить выбросы по доходам отдельных депутатов.
Со степенной шкалой

С равномерной шкалой
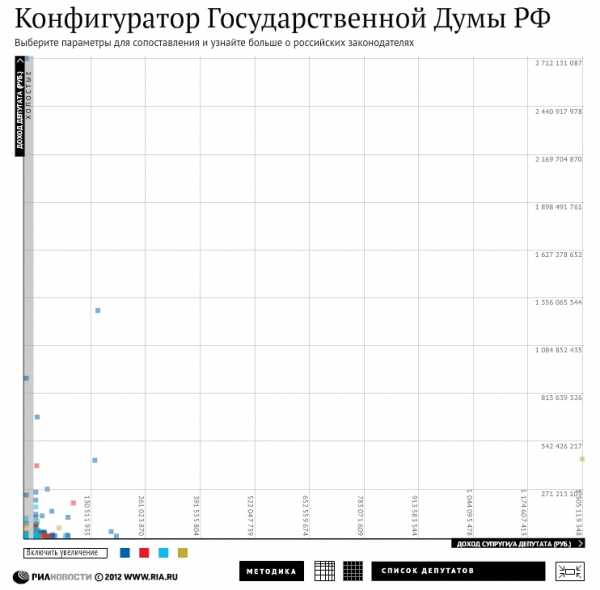
То есть степенные шкалы используются когда данные смещены в ту или иную сторону.
Сравнение шкал
Чтобы удобно сравнить и понять как использовать ту или иную шкалу, я сделал небольшой инструмент. На нём можно выбрать разные наборы данных и понять, как они выглядят на разных шкалах.
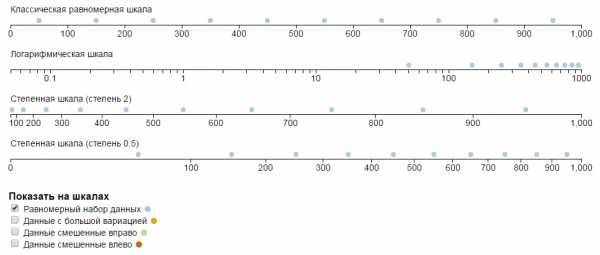
revealthedata.com
Полулогарифмический масштаб — Большая Энциклопедия Нефти и Газа, статья, страница 2
Полулогарифмический масштаб
Cтраница 2
На рисунке представлена в полулогарифмическом масштабе зависимость от времени амплитуды затухающих колебаний. По оси абсцисс отложено время в линейном масштабе, по оси ординат — амплитуда в логарифмическом. [16]
Как известно, в полулогарифмическом масштабе закон радиоактивного распада выражается прямой линией; однако в области высоких загрузок экспериментальная кривая будет идти ниже прямой, экстраполированной из области малых загрузок ( рис. 9.12), указывая тем самым на потери в скорости счета, причем разность между экстраполированной прямой и кривой распада будет равна Igp ( при данной скорости счета пэ ксп) По полученным данным можно непосредственно построить кривую зависимости поправки на разрешающее время от скорости счета. [17]
По полученным данным в полулогарифмическом масштабе строится график охлаждения калориметра — эталона и калориметра с испытуемым материалом. [18]
На рис. 3 в полулогарифмическом масштабе показано изменение концентрации индия в растворе ( С в зависимости от продолжительности контакта ионита с раствором. Иными словами, значения констант в уравнении реакции ионного обмена убывают с уменьшением величины диэлектрической проницаемости раствора. [20]
Результаты испытаний приведены в полулогарифмическом масштабе. Найдено, что в композициях, содержащих до 20 % пластификатора, предел прочности при растяжении не зависит от типа пластификатора. Эта зависимость справедлива в пределах ошибки опыта, что следует из разброса точек для трех непластифицированных контрольных пленок. Даже образцы, пластифицированные касторовым маслом, не являющимся растворителем, имеют практически такую же прочность. При более высоком содержании пластификатора наступает значительное различие в эффективности действия пластификаторов. Для образцов, пластифицированных камфорой, предел совместимости которой равен 50 %, получены высокие значения предела прочности при растяжении, очень мало снижающиеся с повышением содержания пластификатора. Разница между пределом прочности при растяжении для пленок, содержащих 50 % камфоры, и пленок без пластификатора равна 1 8 кгс / мм. Несмотря на то что касторовое масло является нерастворителем нитрата целлюлозы, а дибутилфталат растворяет нитрат целлюлозы, эти пластификаторы одинаково снижают предел прочности изделий при растяжении. Понятно, что дибутилфталат, являющийся хорошим растворителем нитрата целлюлозы, вызывает несколько большие снижения предела прочности пленок при растяжении. [21]
На рис. 52 в полулогарифмическом масштабе графически изображены результаты определения испарения палатинола С в зависимости от длительности испытаний. Испытывались пленки, приготовленные при 115 ( критическая температура растворения поливинилхлорида) и при 160 С. Из графика следует, что испарение пластификатора при 100 С больше, чем при 70 С. [23]
Можно предположить, что необходимость полулогарифмического масштаба связана с волной, находящейся в процессе ускорения. Имея некоторую ценовую цель и предполагая определенную длительность во времени, каждый может нарисовать гипотетически удовлетворительный волновой канал Эллиотта из одной и ой же начальной точки как в арифмг тическом. Таким образом, вопрос о том, следует ли ожидать параллельного канала в арифметическом и и полулогарифмическом масштабе, до сих пор не решен — — он находится в стадии разработки. Если развитие цены в некоторой точке не оказывается внутри двух параллельных линий в том мягш iane. Чтобы полностью контролировать pajBHTi — ic событий, следует использовать оба масштаба. [24]
На рис. 3.3 приведена в полулогарифмическом масштабе) зависимость pV / RT от р при Т const — 300 К для некоторых газов по современным данным. [25]
На рис. 9 дана в полулогарифмическом масштабе зависимость термоэдс от концентрации носителей при комнатной температуре для ряда образцов электронного теллуристого свинца ( 1), электронного ( 2) и дырочного ( 3) селенистого свинца. [27]
Зависимость ( 24) в полулогарифмическом масштабе на графике изобразится прямой линией, тангенс угла наклона которой в соответствии с ( 25) будет равен постоянной радиоактивного распада. [28]
На рис. 83 показаны в полулогарифмическом масштабе кривые жизни капроновых образцов длиной 25 мм и 250 — 300 мм при j3 мм / мин, ру 45 ом-м, / 43 кгц. [30]
Страницы: 1 2 3 4 5
www.ngpedia.ru
Полулогарифмический график зависимости изменения — Справочник химика 21
Алюминиевые экраны должны иметь толщину 0,1—0,15 мм. Число экранов увеличивают до тех пор, пока активность не будет близка к величине фона. Активность сильных препаратов может аналогичным образом измеряться в электрометре. В этом случае препарат помещают на дно ионизационной камеры и последовательно закрывают алюминиевыми экранами. Измеряется изменение величины ионизационного тока в зависимости от толщины поглощающего слоя. По полученным данным строят полулогарифмический график толщина экран а—а к т и в-ность, откладывая на оси абсцисс толщину экранов в г см , а на оси ординат—логарифм активности. [c.145]На рис. 8 представлена зависимость силы анодного тока, изменения потенциала деформируемого образца и нагрузки от степени деформации. Как видно из графика, нагружение ниже макроскопического предела текучести в области деформации анодного тока, тогда как пластическая деформация сопровождается резким его увеличением. В полулогарифмических координатах эти кривые приведены на рис. 9. На участке АБ характер кривой I соответствует уравнению (81). На стадии деформационного упрочнения наблюдается четкая линейная корреляция между его величиной (кривая Р) и деформационным приростом тока (кривая ) в соответствии с линейным приближением теории. [c.67]
На рис. 2 показана типичная экспериментальная кривая химической релаксации в ферментативной системе, измеренная с помощью флуоресцентного контроля изменения концентрации раствора. Эти опыты были проведены на одной из первых установок для реализации метода температурного скачка, обсуждаемого ниже в разд. II. Важно отметить, что короткая верхняя горизонтальная линия соответствует начальному равновесному значению, изменяющемуся при разрыве кривой в момент г= 0. Быстрый начальный спад кривой определяется процессами, которые не могут быть разделены во времени. Последующая гладкая экспоненциально убывающая кривая связана с исследуемым химическим процессом. Из-за шума в измерительной аппаратуре эта кривая менее четко выражена, чем кривая, приведенная на рис. 1. Поэтому в данном случае целесообразно перенести точки этой кривой на полулогарифмическую бумагу. Абсциссой такого графика служит г, а ордината соответствует сигналу Д5, отсчитываемому от нижней линии сетки, показанной на рис. 2. Верхняя кривая на рис. 3 получена непосредственным перенесением зависимости А5 от на полулогарифмическую бумагу. Эта кривая не является прямой линией, как требуется от полулогарифмической зависимости, описываемой уравнением (18). Если из Д5 вычесть 10 мВ, получается нижняя кривая, которая также изогнута, но в направлении, проти- [c.371]
В заключение — несколько слов о влиянии температуры на форму волны. Обратимые волны с ростом температуры становятся более пологими в соответствии с изменением значения RTjnF. Таким образом изменяется, например, наклон 1-й квазиобратимой волны на полярограммах аниона динитрометана [130]. Так же, по-видимому, изменяется наклон необратимых волн, которые отвечают электродным процессам, не осложненным адсорбционными явлениями. При этом принимается, что в сравнительно узкой области изменения температуры значение а не меняется. У волн, отвечающих процессам, осложненным адсорбционными эффектами, наклон при повыщении температуры в зависимости от условий может как увеличиваться, так и уменьшаться, на полулогарифмических графиках могут появляться или исчезать перегибы, т. е. наблюдаются все те явления, которые происходят с подобными волнами при изменении pH раствора (у волн с поверхностной пред-ществующей протонизацией) или состава водно-органической смеси. Если на волне имеется спад, обусловленный десорбцией деполяризатора (или его неактивной формы — в случае кинетических или каталитических волн), то, в зависимости от того, увеличивается ли сильнее с ростом температуры константа скорости электрохимической (или предшествующей химической) реакции или быстрее уменьшается адсорбируемость, спады на волнах могут либо исчезать, либо становиться глубже. Так, при повышении температуры спад на волне фенолфталеина становится менее глубоким [139] наоборот, углубление спада с ростом температуры часто наблюдается на поверхностных каталитических волнах водорода имеет место оно и на волне восстановления метилового эфира 5-хлор-2-тиофенкарбоновой кислоты [140]. [c.78]
Зависимость величины Ег/ от периода капания видна из уравнений (21) и (12) А увеличивается линейно с lg ty, тогда как ЭЛ -от не зависит. Таким образом, 1/, квазидиффузионных поверхностных волн с ростом /ь как и в случае обычных необратимых волн, становится положительнее, однако величина сдвига 1/2 с lg /1 (который для сравнительно узкого интервала изменения ii можно считать приближенно линейным) в общем случае отличается от половины наклона полулогарифмического графика волны (последнее характерно для сдвига 1/3 с lg обычных необратимых волн). Действительно, например, для волн бромацетилтиофена в боратном буфере с pH 9,3 величина 1/2 становится на 73 мв положительнее при десятикратном увеличении 4, тогда как наклон [c.375]
На рис. Х1Х-10 нвображен график этой зависнмости, из которого видно, что с изменением х переменная у изменяется нелинейно. На полулогарифмической сетке (рис. XIX-11) эта зависимость обращается в линейную поэтому имеем [c.542]
В работе [408] описан один из методов прогнозирования работоспособности клеевых соединений во влажных условиях. Показано, что воздействие воды при 60 °С и влажного воздуха (60°С, ф = 99—100%) одинаково влияет на изменение прочностных свойств. Поэтому рекомендуется проведение ускоренных испытаний клеевых соединений в воде при 60 °С в течение 1000 ч. Данные об изменении их прочности представляют графически в полулогарифмических координатах Тсд—1д1 при этом получается линейная зависимость. Далее клеевые соединения испытывают под нагрузкой, воздействующей на них в реальных условиях, в термовлажностной камере при 60°С и ф = 99—100% до разрушения. Получив таким образом одну точку, наносят ее на тот же график и проводят через нее линию, параллельную линии, характеризующей изменение прочности клеевых соединений в воде при 60 °С. [c.241]
Если прямолинейные участки на кривых установлены, то на полулогарифмической диаграмме можно произвести прямолинейную экстраполяцию катодной и анодной поляризационной кривых до значений плотностей токов, приближающихся к величине порядка 10 —10″ а1см (граница, при которой логарифмический закон зависимости потенциала от плотности тока еще выполняется). Дальнейшая прямолинейная экстраполяция для получения значений потенциалов и Уд на нулевой ординате должна уже проводиться на графике в обычных координатах, так как при малых плотностях тока уже имеет место линейная зависимость между изменением потенциалов катода и анода и плотностью тока. [c.212]
chem21.info