Десятичная система счисления
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 6 классы | Материал для любознательных | Десятичная система счисления
Десятичная система счисления
Обычная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления.
В привычной нам системе счисления для записи чисел используются десять различных знаков (цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9). Поэтому ее называют десятичной. Из двух написанных рядом одинаковых цифр левая в 10 раз больше правой. Не только сама цифра, но и ее место, ее позиция в числе имеют определяющее значение. Поэтому данную систему счисления называют позиционной.
В десятичном числе 255 = 2 • 100 + 5 • 10 + 5 • 1 цифры 5, находящиеся на разных позициях, имеют различные количественные значения — 5 десятков и 5 единиц. При перемещении цифры на соседнюю позицию ее «вес» изменяется в 10 раз.
Потребовалось много тысячелетий, чтобы люди научились называть и записывать числа так, как это делаем мы с вами. Начало этому было положено в Древнем Египте и Вавилоне. Дело в основном завершили индийские математики в V — VII веках нашей эры. Важным достижением индийской науки было введение особого обозначения для пропуска разрядов — нуля. Арабы, познакомившись с этой нумерацией первыми, по достоинству ее оценили, усвоили и перенесли в Европу. Получив название арабской, эта система в XII веке нашей эры распространилась по всей Европе и, будучи проще и удобнее остальных систем счисления, быстро их вытеснила. Сегодня десятичными цифрами выражаются время, номера домов и телефонов, цены, бюджет, на них базируется метрическая система мер.
Время многократно изменяло облик десятичных цифр, пока они не приобрели привычный для нас вид. Некогда написание цифр было таким:
Такое изображение десятичных цифр не случайно: каждая цифра обозначает число, соответствующее количеству углов в ней. Подсчитайте и убедитесь в этом сами!
Арифметические действия над десятичными числами производятся с помощью достаточно простых операций, в основе которых лежат известные каждому школьнику таблицы умножения и сложения, а также правило переноса: если в результате сложения двух цифр получается число, которое больше или равно 10, то оно записывается с помощью нескольких цифр, находящихся на соседних позициях.
Изучаемые в самом раннем возрасте, эти правила в результате повседневной практики усваиваются так прочно, что мы оперируем ими уже подсознательно. По этой причине сегодня многие люди даже не догадываются о существовании других систем счисления.
xn—-7sbbfb7a7aej.xn--p1ai
Десятичная система счисления
Количество просмотров публикации Десятичная система счисления — 4676
Десятичная система счисления известна всем нам очень подробно, мы ею пользуемся каждый день (при оплате за транспорт, подсчёте количества штук чего либо, арифметические операции над числами). В десятичную систему счисления входят 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Десятичная система счисления является позиционной системой, потому что зависит от того, в каком месте числа (в каком разряде, на какой позиции) стоит цифра. Т.е. 001 – единица, 010 — ϶ᴛᴏ уже десять, 100 – а это сто. Мы видим, что менялась только позиция одной цифры (единицы), а число менялось очень значительно.
В любой позиционной системе счисления позиция цифры представляет собой цифру, помноженную на число основания системы счисления в степени позиции этой цифры. Посмотрите на пример, и станет всё ясно.
Число десятичное 123 = (1 * 10^2) + (2 * 10^1) + (3 * 10^0) = (1*100) + (2*10) + (3*1)
Число десятичное 209 = (2 * 10^2) + (0 * 10^1) + (9 * 10^0) = (2*100) + (0*10) + (9*1)
Двоичная система счисления
Двоичная система счисления нам должна быть и вовсе не знакома, но поверьте, она намного проще, чем привычная нам десятичная система. В двоичную систему счисления входят всего 2 цифры: 0 и 1. Это сравнимо с лампочкой, когда она не горит — ϶ᴛᴏ 0, а когда свет включен — ϶ᴛᴏ 1.
Двоичная система счисления, как и десятичная, является позиционной.
Число двоичное 1111 = (1*2^3) + (1*2^2) + (1*2^1) + (1*2^0) = (1*8) + (1*4) + (1*2) + (1*1) = 8 + 4 + 2 + 1 = 15 (десятичное).
Число двоичное 0000 = (0*2^3) + (0*2^2) + (0*2^1) + (0*2^0) = (0*8) + (0*4) + (0*2) + (0*1) = 8 + 4 + 2 + 1 = 0 (десятичное).
Хотели мы того, или нет, но мы уже преобразовали 2 двоичных числа в десятичные. Рассмотрим более подробно дальше.
Из двоичной в десятичную систему счисления
Из двоичной системы счисления в десятичную систему счисления переводить не сложно, нужно выучить степени двойки от 0 до 15, хотя в большинстве случаев будет достаточным от 0 до 7. Это связано с восемью битами каждого октета в ip адресе.
Для преобразования двоичного числа нужно будет каждую цифру помножить на число 2 (основание системы счисления) в степени позиции той цифры, а затем сложить те цифры. В примерах ниже всё будет ясно.
Начнем с простых чисел и закончим числами из восьми цифр.
Число двоичное 111 = (1*2^2) + (1*2^1) + (1*2^0) = (1*4) + (1*2) + (1*1) = 4 + 2 + 1 = 7 (десятичное).
Число двоичное 001 = (0*2^2) + (0*2^1) + (1*2^0) = (0*4) + (0*2) + (1*1) = 0 + 0 + 1 = 1 (десятичное).
Число двоичное 100 = (1*2^2) + (0*2^1) + (0*2^0) = (1*4) + (0*2) + (0*1) = 4 + 0 + 0 = 4 (десятичное).
Число двоичное 101 = (1*2^2) + (0*2^1) + (1*2^0) = (1*4) + (0*2) + (1*1) = 4 + 0 + 1 = 5 (десятичное).
Точно таким же образом можно преобразовать любое двоичное число в десятичное.
Число двоичное 1010 = (1*2^3) + (0*2^2) + (1*2^1) + (0*2^0) = (1*8) + (0*4) + (1*2) + (0*1) = 8 + 0 + 2 + 0 = 10 (десятичное).
Число двоичное 10000001 = (1*2^7) + (0*2^6) + (0*2^5) + (0*2^4) + (0*2^3) + (0*2^2) + (0*2^1) + (1*2^0) = (1*128) + (0*64) + (0*32) + (0*16) + (0*8) + (0*4) + (0*2) + (1*1) = 128 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 129 (десятичное).
А так же когда вам нужноест считать действия с нулями, то пропускайте их. Ваши подсчёты станут краткими и красивыми.
Число двоичное 10000001 = (1*2^7) + (1*2^0) = (1*128) + (1*1) = 128 + 1 = 129 (десятичное).
Число двоичное 10000011 = (1*2^7) + (1*2^1) + (1*2^0) = (1*128) + (1*2) + (1*1) = 128 + 2 + 1 = 131 (десятичное).
Число двоичное 01111111 = (1*2^6) + (1*2^5) + (1*2^4) + (1*2^3) + (1*2^2) + (1*2^1) + (1*2^0) = (1*64) + (1*32) + (1*16) + (1*8) + (1*4) + (1*2) + (1*1) = 64 + 32 + 16 + 8 + 4 + 2 + 1 = 127 (десятичное).
Число двоичное 11111111 = (1*2^7) + (1*2^6) + (1*2^5) + (1*2^4) + (1*2^3) + (1*2^2) + (1*2^1) + (1*2^0) = (1*128) + (1*64) + (1*32) + (1*16) + (1*8) + (1*4) + (1*2) + (1*1) = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255 (десятичное).
Число двоичное 01111011 = (1*2^6) + (1*2^5) + (1*2^4) + (1*2^3) + (1*2^1) + (1*2^0) = (1*64) + (1*32) + (1*16) + (1*8) + (1*2) + (1*1) = 64 + 32 + 16 + 8 + 2 + 1 = 123 (десятичное).
Число двоичное 11010001 = (1*2^7) + (1*2^6) + (1*2^4) + (1*2^0) = (1*128) + (1*64) + (1*16) + (1*1) = 128 + 64 + 16 + 1 = 209 (десятичное).
Вот и справились. Теперь переведём всё обратно из двоичной в десятичную.
referatwork.ru
Практическая работа системы счисления (материалы http://vestikinc.Narod.Ru/ab/index.Htm)
Привычная нам десятичная система счисления имеет, по сравнению с другими системами счета, физиологическое преимущество – большинство людей от рождения обладают «встроенным» в собственное тело калькулятором – двумя руками и двумя ногами, и, соответственно, двадцатью пальцами. В «живом» калькуляторе пальцы могут служить одновременно числами (1-20), разрядами (100 — 1020) и индикаторами (включено/выключено, т.е. согнут/разогнут). Наглядность представления чисел предопределило успех этой системы счисления в древности, поскольку позволяло осуществлять, скажем, торговлю между группами людей, говоривших на разных языках. Высокая разрядность «биологического» калькулятора (до 1020) не использовалась в полной мере, и двадцатеричные системы счисления в истории человечества встречались редко (чукчи, майя, баски, кельтские народы в прежние времена, народы Франции — достаточно вспомнить отголоски ее во французских числительных — роман Виктора Гюго «93 год» по-французски «Quatre-vingts-treize» — «четыре двадцатки тринадцать»). Зато существовали другие, более простые системы счета – например, пятеричная у китайцев (по количеству пальцев на одной руке или ноге) или двенадцатеричная у англичан.
За всю свою историю человечество смогло создать только два типа систем счисления или записи цифр – позиционную и непозиционную, или знаковую. Непозиционные системы записи цифр появились раньше позиционных.
Непозиционная система счисления применялась в Древнем Риме – для записи цифр использовались буквы латинского алфавита, обозначавшие определенные количества:
I — единица
V — пять
X — десять
L — пятьдесят
C — сто
D — пятьсот
M — тысяча
В этой системе цифры записывались так, чтобы при суммировании цифровых эквивалентов букв получалось требуемое число, например:
MDCLXVI = 1000+500+100+50+10+5+1=1666
Если младшая цифра стоит перед старшей, то эта цифра вычитается:
MCDXLIV = 1000-100+500-10+50-1+5=1444
Возникает ощущение, что одну и ту же цифру можно записать разными способами – например, XIX и XVIIII, однако специальное правило запрещает запись буквы I в цифре более трех раз подряд.
Позиционная система счисления подразумевает более сложный уровень абстракции – для записи цифр используется базовый набор символов, число которых составляет основание системы счисления. Место каждого символа в числе называется позицией, а номер позиции символа (за вычетом единицы) называется разрядом. Разряды увеличиваются, начиная с нулевого: нулевой, первый, второй и т.д., причем нулевой называется младшим разрядом, а последний – старшим разрядом.
В позиционных системах счисления любое положительное число может быть записано при помощи формулы, составить которую можно, введя следующие обозначения:
Пусть p — основание системы счисления, Ap — количественный эквивалент числа A , состоящего из n цифр ak, где k =0, …, n-1 . Тогда число A можно представить как последовательность цифр Ap= an-1an-2…a1a0 , причем всегда ak < p.
В общем случае количественный эквивалент любого положительного числа в позиционной системе счисления можно представить в виде:
Ap = an-1·pn-1+an-2·pn-2 + … + a1·p1+a0·p0, [1]
где a — цифра данной системы счисления , n — номер старшего разряда числа.
Проанализировав это выражение, можно сформулировать следующее общее правило: количественный эквивалент числа в некоторой позиционной системе счисления равен сумме произведений количественных значений цифр и степеней основания, показатели которых равны номерам разрядов, причем нумерация разрядов начинается с нуля.
В привычной нам десятичной системе счисления любое положительное число может быть представлено по формуле [1] аналогично следующему примеру:
1254698357 = 1·109+2·108+5·107+4·106+6·105+9·104+8·103+3·102+5·101+7·100
studfiles.net
Почему мы используем десятичную систему исчисления?
Система деления, приведенная в статье «Деление на части» удобна и практична, ее легко применять в повседневной жизни, и кое-кто даже жалеет о том, что в основе нашей системы исчисления лежит 10, а не 12. У числа 10 есть только два множителя, это 2 и 5. Десять не делится ни на 3, ни на 4. Единственная причина, по которой в основе системы оказалось число 10, – это то, что у нас по 5 пальцев на каждой руке. А вот если бы их было бы по 6…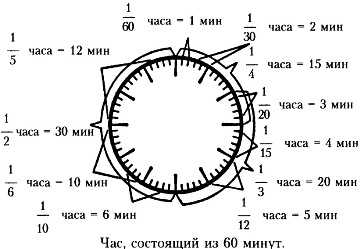
У числа 10 есть одно преимущество перед 12. Число 10 делится на 5, а 12 – нет. Древние вавилоняне пытались соединить в одном числе все достоинства чисел 10 и 12. Такое число должно делиться не только на 2, 3, и 4, но и на 5. Наименьшим таким числом является 60. Это число используется и в астрономии. Год составляет 365 дней и несколько часов. Год – это то время, за которое Солнце совершает свой (кажущийся) круговой путь по небу относительно неподвижных звезд. Если полный круг разделить на величину пути, которое Солнце проходит за день (то есть на «путь-день»). Мы получим 365 долей круга.
У вавилонян год равнялся 360 дням (либо они неправильно вычислили продолжительность года, либо просто округлили 365 до 360 для удобства вычислений). С этим числом удобно работать, поскольку 360 – это 60х60. Поэтому они делили небесную сферу и другие круги на 360 равных частей, которые мы в наши дни называем градусами. Затем каждый градус они делили на 60 частей, которые мы называем минутами, а каждую минуту еще на 60 частей, на 60 секунд. Мы до сих пор придерживаемся вавилонской системы. Более того, поскольку время измеряется по движению крупных небесных тел на небосклоне, наш час разделен на 60 минут, а минута – на 60 секунд.
При подсчете времени мы находим также следы системы, основанной на 12. День и ночь разделены на 12 часов. В древности, до того как были изобретены часы, длина часа менялась в зависимости от времени года. Зимой дневные часы были короче, чем летом, а ночные длиннее. В наши дни продолжительность часа принята постоянной, поэтому летом светлое время длится дольше, чем зимой, ночное, наоборот, – короче.
Тем не менее на циферблате наших часов только 12 чисел, и, следовательно, мы определяем время между 1 часом ночи и 1 часом дня. (Принято считать время после 12 как 13, 14 и так далее часов, но обычно в быту мы не используем таких обозначений.)
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Десятичная система счисления. Основание системы счисления
Система счисления (иначе называемая нумерацией) – это способ именования и записи чисел с помощью определённого набора символов.
Практическая деятельность потребовала от людей не только умения считать, но и умения записывать числа. В давние времена для записи чисел люди использовали особые рисунки, чёрточки, буквы и другие способы обозначения количества предметов. В настоящее время используется десятичная система счисления, в которой для записи числа используют следующие десять знаков:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Знаки, употребляемые для записи чисел, называются цифрами.
Название системы счисления зависит от её основания. Основание системы счисления – это количество цифр, которые используются в данной системе счисления для записи чисел. Так как в системе счисления, которой мы пользуемся 10 цифр, то она имеет основание 10, поэтому система счисления называется десятичной
.
В десятичной системе значение одной и той же цифры зависит от её позиции в записи числа. Для примера возьмём число 777, которое состоит из трёх одинаковых цифр. В этом числе первая слева цифра означает семь сотен, вторая – семь десятков, а третья – семь единиц. Так как значение цифры зависит от её позиции в записи числа, десятичную систему счисления также называют
Позиционной называют такую систему счисления, в которой значение цифры зависит от её позиции в записи числа.
Числа, которые записаны с помощью одной цифры, называют однозначными, записанные с помощью двух – двузначными, так же по количеству цифр в числе дают названия и другим числам:
1, 2, 4 – однозначные числа.
14, 77, 92 – двузначные числа.
122, 345 – трёхзначные числа.
537633, 987345 – шестизначные числа.
Двузначные, трёхзначные, четырёхзначные, пятизначные и т. д. числа называют многозначными.
Следует помнить, что цифра и число не одно и то же.
Цифра – это только письменный знак, используемый для записи числа. Число может быть обозначено не одной, а несколькими цифрами (например, 75) или может быть выражено словами (семьдесят пять).
naobumium.info
Простая информатика — Система счисления
Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:
11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.
345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.
XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).
В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.
Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.
Основание системы счисления – это количество знаков, которое используется для записи цифр.
Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 264 — трехразрядное число, 00010101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка — третий).
Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)
Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.
Двоичная система счисления
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 82 + 7 * 81 + 2 * 80 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 82 + 0 * 81 + 0 * 80 = 6410
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
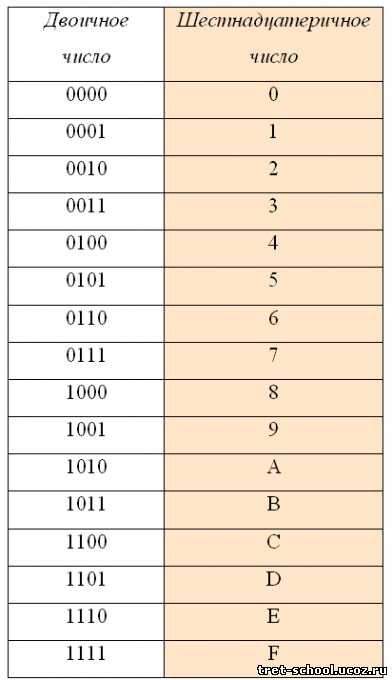
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние
informatic.my1.ru
Десятичная система — счисление — Большая Энциклопедия Нефти и Газа, статья, страница 1
Десятичная система — счисление
Cтраница 1
Десятичная система счисления весьма наглядна и удобна для чтения на перфорированной ленте. Достаточно сложным является и дешифрирующее устройство, которое должно иметь 10п дешифраторов, чтобы иметь возможность прочитывать каждую позицию. Импульсы же подаются в систему управления только с рабочих позиций, в которых пробиты отверстия. [1]
Десятичная система счисления крайне неудобна для использования в ЭВМ, но она общепринята, и поэтому, несмотря на свои недостатки, так же применяется в вычислительной технике. Для того чтобы ввести в ЭВМ десятичные числа, отобразить их состояниями двухпозиционных элементов, используют двоично-десятичную форму представления десятичных чисел. [2]
Десятичная система счисления общепринята и широко применяется для индикации и регистрации. При изображении больших чисел она имеет примерно втрое меньшее число разрядов, чем двоичная система. Для автоматических вычислений десятичная система удобна только при наличии достаточно надежных и простых элементов, имеющих десять хорошо различимых состояний. [3]
Десятичная система счисления, привычная для нас в повседневной жизни, не является наилучшей для использования в ЭВМ. Это объясняется тем, что известные в настоящее время функциональные элементы с десятью устойчивыми состояниями ( элементы на основе сегнетокерамики, декатроны и др.) имеют низкую скорость переключения и, таким образом, не могут удовлетворять требованиям, предъявляемым к ЭВМ по быстродействию. Поэтому в большинстве случаев в ЭВМ используют двоичные или двоично-кодированные системы счисления. Широкое распространение этих систем обусловлено тем, что элементы ЭВМ способны находиться лишь в одном из двух устойчивых состояний. Например, полупроводниковый транзистор в режиме переключения может быть в открытом или закрытом состоянии, а следовательно, иметь на выходе высокое или низкое напряжение. Ферритовый сердечник в устойчивом состоянии может иметь положительную или отрицательную остаточную магнитную индукцию. Такие элементы принято называть двухпозицион-ными. Если одно из устойчивых положений элемента принять за О, а другое — за 1, то достаточно просто изображаются разряды двоичного числа. [4]
Десятичная система счисления возникла в глубокой древности. Люди стали пользоваться ею потому, что привыкли считать десятками, имея на руках десять пальцев. [5]
Десятичная система счисления, привычная для нас в повседневной жизни, не является наилучшей системой счисления для использования в ЭВМ. Это объясняется тем, что известные в настоящее время функциональные элементы с десятью устойчивыми состояниями ( элементы на основе сегнетокерамики, декатроны и др.) имеют низкую скорость переключения и, таким образом, не могут удовлетворять требованиям, предъявляемым к ЭВМ по быстродействию. Поэтому в подавляющем большинстве случаев в ЭВМ используют двоичные или двоично-кодированные системы счисления. [6]
Десятичная система счисления, привычная для нас, не является наилучшей системой счисления при использовании в ЭВМ. Для изображения любого числа в десятичной системе требуется десять различных символов. При реализации в ЭВМ этой системы счисления требуются функциональные элементы, реализующие десять устойчивых состояний. Имеющиеся в настоящее время функциональные элементы не могут удовлетворить этим требованиям. [7]
Десятичная система счисления используется для записи исходной информации и результатов решения задачи. [8]
Десятичная система счисления крайне неудобна для использования в ЭВМ, но она общепринята, и поэтому, несмотря на свои недостатки, так же применяется в вычислительной технике. Для того чтобы ввести в ЭВМ десятичные числа, отобразить их состояниями двухпозиционных элементов, используют двоично-десятичную форму представления десятичных чисел. [9]
Десятичная система счисления используется главным образом в цифровых индикаторных и регистрирующих устройствах. Для изображения чисел в ней требуется меньшее число разрядов по сравнению с двоичной системой, поэтому при регистрации дестичных знаков затрачивается и меньшее время. Однако реализация цифровых устройств в десятичной системе требует сложных элементов с десятью устойчивыми состояниями. [10]
Десятичная система счисления применяется в ЭЦВМ редко, так как устройства, используемые для представления и хранения информации в десятичных числах, должны иметь десять различных состояний. Такие устройства, например, декатроны, разработаны и существуют, но ЭЦВМ, построенные на них, широкого применения не нашли из-за ненадежной работы и сложности. [11]
Десятичная система счисления по этой оценке приблизительно в 1 5 раза уступает троичной, а двоичная и четверичная близки к троичной. [12]
Десятичная система счисления распространена почти повсеместно. Многие видят причину такой распространенности в том, что каждый человек с детства привыкает считать при помощи десяти пальцев обеих рук. Однако десятичное счисление не является самым удобным. Например, в некоторых отношениях удобнее была бы двенадцатеричная система, которая, не требуя для изображения чисел большого числа цифр, обладает важным свойством, что основание ее делится без остатка на 2, на 3, на 4 и на 6, тогда как основание наглей системы делится только на 2 и на 5; подобные же соображения послу жили, вероятно, основанием шестидесятеричной системы счисления, употреблявшейся в древнем Вавилоне. Употребляемые нами цифры и самая система обозначения чисел заимствованы европейцами у арабов ( около ХПв. Вот почему эти цифры называются арабскими. Но есть основание думать, что арабы в свою очередь заимствовали эту систему у индусов. [13]
Десятичная система счисления в системах ЧПУ практически не применяется, так как в системе управления в этом случае надо различать десять различных символов. Она применяется иногда в станках с непосредственным набором программы на пульте управления. [14]
Десятичная система счисления укоренилась, вероятно, потому, что люди ( возможно, еще в первобытном обществе) стали считать предметы при помощи своих десяти пальцев. А сегодня мы так привыкли к десятичной системе счисления, что воспринимаем ее как нечто само собой разумеющееся, вполне обычное, совершенно не задумываясь ни над ее происхождением, ни над возможностью создания иных систем счисления. [15]
Страницы: 1 2 3 4
www.ngpedia.ru