Обратная матрица matlab – C Matlab

Команды (линейная алгебра) Maple Matlab

Пакеты linalg и LinearAlgebra системы Maple

Функции пакетов linalg и LinearAlgebra подключаются командой with(название пакета)

addcol — формирует линейные комбинации из столбцов матрицы

addrow — формирует линейные комбинации из строк матрицы

adj — возвращает матрицу, умножение которой на исходную квадратную матрицу дает единичную матрицу

angle — вычисляет угол между векторами

basis — находит базис для векторного пространства

BlockDiagonal — создает блок-диагональную матрицу

blockmatrix — создает блок-матрицу

charmat — создает характеристическую матрицу

charpoly — возвращает характеристический полином матрицы

сurl — ищет ротор векторного поля

definite — тест на положительные (отрицательные) определенные матрицы

delcols — удаляет столбцы матрицы

delrows — удаляет строки матрицы

del — вычисляет детерминант матрицы

diverge — ищет дивергенцию векторного поля

eigenvals — вычисляет собственные значения матрицы

eigenvects — вычисляет собственные векторы матрицы

evalm — выполняет операции над матрицами (сложение: «+», умножение: «&*», и т.д.)

extend — расширяет матрицу

GramSchmidt — вычисляет ортогональные векторы

hermite — Эрмитовая нормальная форма матрицы

hessian — вычисляет Hessian-матрицу выражения

hilbert — создает матрицу Гильберта

intbasis — определить базис для пересечения пространства

inverse — вычисляет обратную матрицу

linsolve — решение линейных уравнений

Ludecomp — осуществляет LU-декомпозицию

matrix — создает матрицу

minor — вычисляет миноры матрицы

norm — норма матрицы или вектора

normalize — нормирует вектор

rank — возвращает ранг матрицы

references — выводит список основополагающих работ по линейной алгебре

trace — возвращает след матрицы

transpose — вычисляет транспонированную матрицу

vector — создает вектор

wronskian — матрица Вронскиана векторных функции

Matlab

inv — вычисление обратной матрицы

orth — вычисление ортонормированного базиса

rank — ранг матрицы

det — определитель матрицы

Вычисление собственных значений и сингулярных чисел

eig, cdf2rdf — собственные значения и собственные векторы матрицы

Полиномы и операции над ними

polyval — вычисление полинома

deconv — деление полиномов

roots — вычисление корней полиномов

poly — вычисление характеристического полинома

residue, resi2 — разложение на простые дроби

Математические функции

sin, cos, tan, acos, asin, exp, log, sqrt, rand, round fix abs angle real imag conj

Арифметические и матричные операции

+ — сложение чисел, векторов, матриц

— — вычитание чисел, векторов, матриц

* — умножение чисел, совместные матриц и векторов

.* — поэлементное умножение векторов и матриц одного размера

/ — деление чисел, умножение на обратную матрицу справа

./ — поэлементное деление векторов и матриц одного размера

\ —умножение на обратную матрицу слева

^ — возведение числа или квадратной матрицы в степень

.^ — поэлементное возведение матрицы в степень

’ — транспонирование

size — возвращение размеров матрицы или вектора

length — возвращение числа компонент вектора

sum —суммирование элементов вектора

norm — вычисление норма матрицы или вектора

Символьные вычисления в Matlab

В Matlab версии 5 и выше встроен интерфейс прямого вызова команд системы компьютерной алгебры Maple. Для этого используется функция maple в той или иной форме:

1) maple (statement) — устанавливает выражение statement для ядра Maple. statement является строкой, записанной в формате команд Maple. Возвращает результат в форме строки с нотацией системы Maple V;

2) maple (’function’, arg1, arg2,…) — даёт доступ к Maple-функциям с заданными аргументами;

3) [result, status]=maple(…) — возвращает результат и статус сообщений/ошибок, если они возникают в ходе вычислений заданной функции.

Пример.

» maple(’sin(1)’) ans= sin(1)

» maple(’evalf(sin(1))’) ans= .84147098480789650665250232163030

» maple(’sqrt’,2) ans= 2^(1/2)

» maple(’evalf(sin)’, 1) ans= sin(1)

Пример. Найти 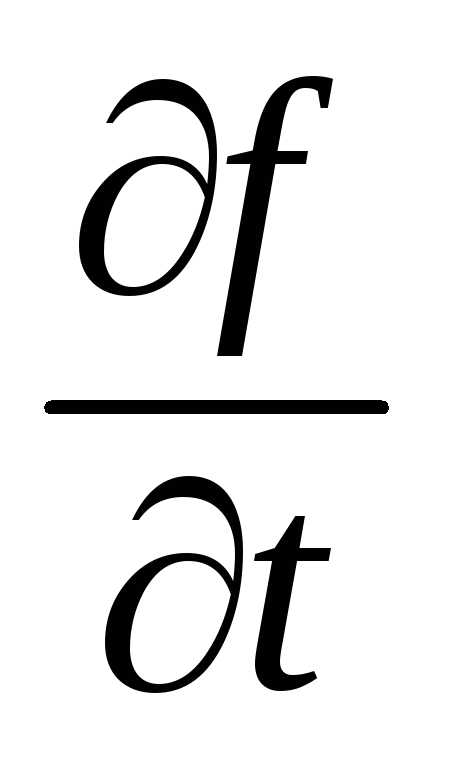для. Решить относительноy уравнение .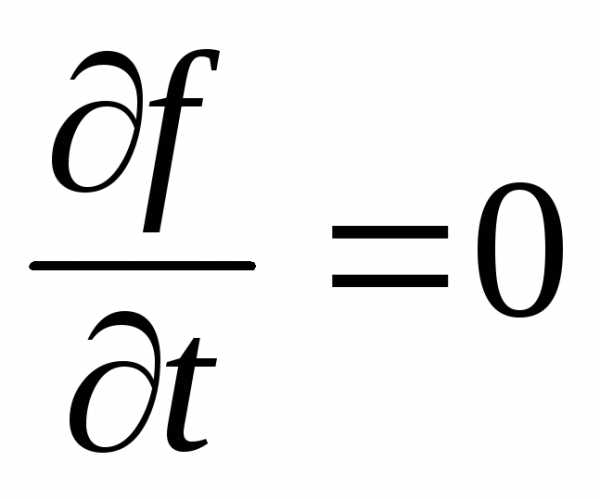

Необходимо выполнить:

» maple(’ f:=x+2*t*y-t-2*t^3;’)

» maple(’ g:=diff(f,t)’)

» maple(’ h:=solve(g,y)’)

Matlab имеет интерактивную систему помощи, которая реализуется в командном режиме с помощью ряда команд. Одной из них является команда

» help

Чтобы получить дополнительную информацию по Maple, необходимо набрать

» mhelp

или

» maple(’help’).

Для получения справке по команде maple ввести:

» mhelp имя_команды

studfiles.net

Обращение матриц — функции inv, pinv MatLab

Урок 11. Матричные операции линейной алгебры
Вычисление нормы и чисел обусловленности матрицы
Определитель и ранг матрицы
Определение нормы вектора
Определение ортонормированного базиса матрицы
Функции приведения матрицы к треугольной форме
Определение угла между двумя подпространствами
Вычисление следа матрицы
Разложение Холецкого
Обращение матриц — функции inv, pinv
LU- и QR-разложения
Вычисление собственных значений и сингулярных чисел
Приведение матриц к форме Шура и Хессенберга
Что нового мы узнали?

Обращение матриц — одна из наиболее распространенных операций матричного анализа. Обратной называют матрицу, получаемую в результате деления единичной матрицы Е на исходную матрицу X. Таким образом, Х^-1=Е/Х. Следующие функции обеспечивают реализацию данной операции:

 inv(X) — возвращает матрицу, обратную квадратной матрице X. Предупреждающее сообщение выдается, если X плохо масштабирована или близка к вырожденной.

Пример:

» inv(rand(4,4)) 

ans =

2.2631 -2.3495-0.4696-0.6631

-0.76201.2122 1.7041 -1.2146

-2.04081.4228 1.5538 1.3730 

1.3075 -0.0183-2.54830.6344

На практике вычисление явной обратной матрицы не так уж необходимо. Чаще операцию обращения применяют при решении системы линейных уравнений вида Ах=b. Один из путей решения этой системы — вычисление x=inv(A)*b. Но лучшим с точки зрения минимизации времени расчета и повышения точности вычислений является использование оператора матричного деления х=А\b. Эта операция использует метод исключения Гаусса без явного формирования обратной матрицы.

В = pinv(A) — возвращает матрицу, псевдообратную матрице А (псевдообращение матрицы по Муру-Пенроузу). Результатом псевдообращения матрицы по Муру-Пенроузу является матрица В того же размера, что и А’, и удовлетворяющая условиям А*В*А=А и В*А*В=В. Вычисление основано на использовании функции svd(A) и приравнивании к нулю всех сингулярных чисел, меньших величины tol;

В = pinv (A. tol) — возвращает псевдообратную матрицу и отменяет заданный по умолчанию порог, равный max(size(A))*norm(A)*eps.

Пример:

» pinv(rand(4,3))

ans =

-1.3907-0.0485-0.24931.8640

-0.87751.1636 0.6605 -0.0034 

2.0906 -0.5921-0.2749-0.5987

 

radiomaster.ru

Доступ к элементам — MatLab Руководство для начинающих

1   2   3   4   5   6 Доступ к элементам матриц осуществляется при помощи двух индексов — номеров строки и столбца, заключенных в круглые скобки, например команда B(2,3) выдаст элемент второй строки и третьего столбца матрицы B. Для выделения из матрицы столбца или строки следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием. Например, запишем вторую строку матрицы A в вектор z Также можно осуществлять выделение блоков матриц при помощи двоеточия. Например, выделим из матрицы P блок отмеченный цветом Если необходимо посмотреть переменные рабочей среды, в командной строке необходимо набрать команду whos. Команда who выводит только имена переменных Видно, что в рабочей среде содержатся один скаляр (p), четыре матрицы (A, B, P, P1) и вектор-строка (z). 2.3. Основные матричные операции При использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус а умножение — знаком звездочка *. Введем матрицу размером 3×2 Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева. Возведение квадратной матрицы в целую степень производится с использованием оператора ^ 2.4. Создание матриц специального вида Заполнение прямоугольной матрицы нулями производится встроенной функцией zeros Единичная матрица создается при помощи функции eye Матрица, состоящая из единиц, образуется в результате вызова функции ones MatLab предоставляет возможность заполнения матриц случайными числами. Результатом функции rand является матрица чисел, равномерно распределенных между нулем и единицей, а функции randn — матрица чисел, распределенных по нормальному закону с нулевым средним и единичной дисперсией.  Функция diag формирует диагональную матрицу из вектора, располагая элементы по диагонали. Пример. Команда z = magic(3) генерирует магический квадрат размера 3 x 3 2.5. Матричные вычисления MatLab содержит множество различных функций для работы с матрицами. Так, например, транспонирование матрицы производится при помощи апострофа ‘ Нахождение обратной матрицы проводится с помощью функции inv для квадратных матриц Псевдообратную матрицу можно найти с помощью функции pinv.  Более подробно про обработку матричных данных можно узнать, если вывести список всех встроенных функций обработки данных командой help datafun, а затем посмотреть информацию о нужной функции, например help max. 2.6. Справочник по формированию и операциям над матрицами Формирование массивов специального вида ZEROS — формирование массива нулей ONES — формирование массива единиц EYE — формирование единичной матрицы RAND — формирование массива элементов, распределенных по равномерному закону RANDN — формирование массива элементов, распределенных по нормальному закону CROSS — векторное произведение KRON — формирование тензорного произведения LINSPACE — формирование линейного массива равноотстоящих узлов LOGSPACE — формирование узлов логарифмичесокй сетки MESHGRID — формирование узлов двумерной и трехмерной сеток : — формирование векторов и подматриц Операции над матрицами DIAG — формирование или извлечение диагоналей матрицы TRIL — формирование нижнетреугольной матрицы (массива) TRIU — формирование верхнетреугольной матрицы (массива) FLIPLR — поворот матрицы относительно вертикальной оси FLIPUD — поворот матрицы относительно горизонтальной оси ROT90 — поворот матрицы на 90 градусов RESHAPE — преобразование размеров матрицы Специальные матрицы COMPAN — сопровождающая матрица характеристического многочлена HADAMARD — матрица Адамара (Hadamard matrix) HANKEL — матрица Ганкеля (Hankel matrix) HILB, INVHILB — матрица Гильберта (Hilbert matrix) MAGIC — магический квадрат PASCAL — матрица Паскаля (Pascal matrix) ROSSER — матрица Рессера (Rosser matrix) TOEPLITZ — матрица Теплица (Toeplitz matrix) VANDER — матрица Вандермонда (Vandermonde matrix) WILKINSON — матрица Уилкинсона (Wilkinson matrix) 2.7. Присвоение матрице математического выражения Организация всех переменных системы MATLAB как матрицы вызывает следующие ограничения применения их в выражениях. Например: t=1:5 t= 1 2 3 4 5 y=cos(t) y=1 0.5 -0.4 -1 -0.6 0.2 z=y/t z=-0.08 Результат — получается одно число, а ожидали функцию z(t)=cos(t)/t. Для организации поэлементного деления одного массива на другой, в MATLAB предусмотрена специальная операция — «./» — поэлементное деление. Результат этого выражения будет другой: z=y ./ t z= 0.5403 -0.2081 -0.3300 -0.1634 0.0567. 3. Математические функции В системе MATLAB имеется обширная библиотека математических функций. Каждой функции соответствует определенное имя. Функция ставит в соответствие значениям своих аргументов значение результата. Аргументы функции всегда указываются в круглых скобках после имени функции и, если их больше одного, разделяются запятыми. В качестве аргументов могут использоваться другие функции и любые выражения языка MATLAB (при условии соответствия типов аргументов). Элементарная математическая функция — это, как правило, функция от одной переменной, и в этом случае устанавливается соответствие между массивами значений аргумента и результата. Аргумент указывается в круглых скобках после имени функции. Имя переменной, которой присваивается значение функции, располагается слева от знака равенства. Если имя присваиваемой переменной не указано, значение функции присваивается служебной переменной ans. Тип результата вычисления математической функции всегда совпадает с типом ее аргумента. Например, если аргументом функции является вектор-столбец, то значением этой функции также будет вектор-столбец. Рассмотрим встроенные математические функции системы MATLAB, которые применяются к числам, скалярным переменным и к массивам (поэлементно). Базовые функции ABS — абсолютное значение ANGLE — аргумент комплексного числа REAL, IMAG — действительная и мнимая части комплексного числа CONJ — операция комплексного сопряжения SIGN — вычисление знака числа CEIL, FIX, FLOOR, ROUND —  функции округления REM — функция остатка GCD — наибольший общий делитель LCM — наименьшее общее кратное RAT, RATS — представление результата в виде рационального числа или цепной дроби Трансцендентные функции SQRT — квадратный корень EXP — экспоненциальная функция LOG — функция натурального логарифма POW2 — экспонента по основанию 2 NEXTPOW2 — ближайшая степень по основанию 2 LOG2 — фунции логарифма LOG10 — функции логарифма Тригонометрические функции SIN, SINH — функции синуса ASIN, ASINH — функции обратного синуса CSC, CSCH — функции косеканса ACSC, ACSCH — функции обратного косеканса COS, COSH — функции косинуса ACOS, ACOSH — функции обратного косинуса SEC, SECH — функции секанса ASEC, ASECH — функции обратного секанса TAN, TANH — функции тангенса ATAN, ATAN2, ATANH — функции обратного тангенса COT, COTH —  функции котангенса ACOT, ACOTH — функции обратного котангенса Преобразования системы координат CART2POL — преобразование декартовой системы координат в полярную и цилиндрическую CART2SPH — преобразование декартовой системы координат в сферическую POL2CART — преобразование полярной и цилиндрической систем координат в декартову SPh3CART — преобразование сферической системы координат в декартову Специальные функции BESSEL — функции Бесселя BETA, BETACORE, BETAINC, BETALN — бета-функции ELLIPJ — эллиптические функции Якоби ELLIPKE — полные эллиптические интегралы ERF, ERFCORE, ERFC, ERFCX, ERFINV —  функции ошибок GAMMA, GAMMAINC, GAMMALN —  гамма-функции 1   2   3   4   5   6

topuch.ru