Иллюстрированный самоучитель по SPSS 10/11 › Корреляции › Корреляции [страница — 202] | Самоучители по математическим пакетам
Корреляции
В этой главе речь пойдет о связи (корреляции) между двумя переменными. Расчеты подобных двумерных критериев взаимосвязи основываются на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок.
Если в качестве примера мы возьмем данные об уровне холестерина для первых двух моментов времени из исследования гипертонии (файл hyper.sav), то в данном случае следует ожидать довольно сильную связь: большие значения в исходный момент времени являются веским поводом для ожидания больших значений и через 1 месяц.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая; пара значений маркируется при помощи определенного символа. Такой график, называемый «диаграммой рассеяния» для двух зависимых переменных можно построить путем вызова меню Graphs… (Графики) › Scatter plots… (Диаграммы рассеяния) (см. гл. 22.8).
Образовавшееся скопление точек показывает, что обследованные пациенты с высокими исходными показателями, как правило, имеют высокие значения холестерина и при повторном опросе через месяц. Это, конечно же, не является неожиданностью; данный пример был выбран, чтобы продемонстрировать наличие явной связи.
Статистик говорит о корреляции между двумя переменными и указывает силу связи при помощи некоторого критерия взаимосвязи, который получил название коэффициента корреляции. Этот коэффициент, всегда обозначаемый латинской буквой г, может принимать значения между -1 и +1, причем если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой.

Рис. 15.1.Диаграммы рассеяния
Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой. Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следующие градации:
| Значение | Интерпретация |
| до 0.2 | Очень слабая корреляция |
| до 0.5 | Слабая корреляция |
| до 0.7 | Средняя корреляция |
| до 0.9 | Высокая корреляция |
| свыше 0.9 | Очень высокая корреляция |
Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные.
- Переменные с интервальной и с номинальной шкалой: коэффициент корреляции Пирсона (корреляция моментов произведений).
- По меньшей мере, одна из двух переменных имеет порядковую шкалу либо не является нормально распределенной: ранговая корреляция по Спирману или т (тау-грого-соая) Кендала.
- Одна из двух переменных является дихотомической: точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применен расчет ранговой корреляции.
- Обе переменные являются дихотомическими: четырехполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства (см. гл 15.4).
Расчет коэффициента корреляции между двумя недихотомическими переменными не лишен смысла только тогда, кода связь между ними линейна (однонаправлена). Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю. В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Еше один раздел специально посвящен частной корреляции.
samoychiteli.ru
ЛБ_6
Дисциплина: Теоретические основы статистических исследованийЛабораторная работа №6
Корреляционный анализ
При проведении корреляционного анализа различают параметрические и непараметрические методы анализа наличия зависимости.
1. Параметрические методы оценки корреляции. Коэффициент линейной корреляции Пирсона
Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной или количественной шкале.
1.1. Реализация в SPSS
Для того, чтобы рассчитать коэффициент линейной корреляции Пирсона необходимо использовать следующую последовательность команд:
Analyze (Анализ) – Correlate (Корреляция) –
В результате чего, откроется диалоговое окно (рис.1), в котором необходимо указать переменные, для которых будет рассчитан коэффициент корреляции Пирсона. И установить флажок в поле Pearson.
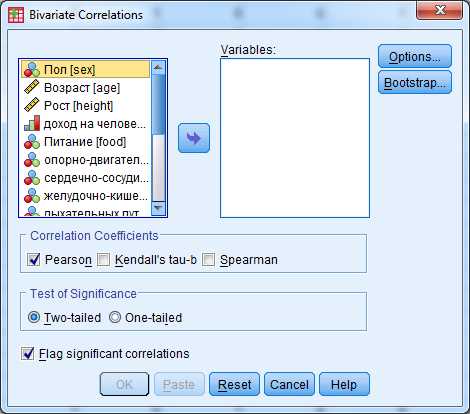
Рис.1. Диалоговое окноBivariateCorrelations
После нажатия на кнопку ОКна экран будет выведена матрица корреляций Пирсона для указанных переменных.
Пример расчета коэффициентов линейной корреляции Пирсона для переменных height,weight_1,index_1 приведен на рис.2.

Рис.2.Матрица коэффициентов корреляции Пирсона
Значимая положительная корреляция в этой таблице наблюдается для всех переменных. Например, коэффициент корреляции между переменными heightиweight, равный 0,732 (уровень значимости р=0,001), говорит о тесной положительной связи между этими переменными. Т.е. Чем больше рост респондента, тем больше его вес.
1.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициент линейной корреляции Пирсона необходимо использовать следующую последовательность команд:
Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) – Correlation matrices (Корреляционные матрицы)
В результате откроется диалоговое окно (рис.3.), в котором необходимо указать переменные для расчета линейного коэффициента корреляции Пирсона

Рис.3. Диалоговое окно Product-Moment and Partial Correlations
После нажатия на кнопку Summary: Correlationsна экран будет выведена корреляционная матрица.
Пример расчета коэффициентов линейной корреляции Пирсона для переменных height,weight_1,index_1 приведен на рис.4.
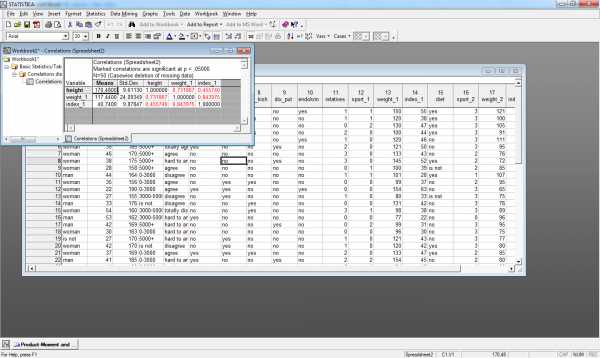
Рис.4.Матрица коэффициентов корреляции Пирсона
2. Непараметрические методы оценки корреляции.
Коэффициенты Спирмена и Кенделла
Оба показателя, основаны на корреляции не самих значений рассматриваемых признаков, а их рангов. С их помощью можно изучать и измерять связь не только между количественными, но и качественными (атрибутивными) признаками, ранжированными определенным образом.
2.1. Реализация в SPSS
Для того, чтобы рассчитать коэффициенты ранговой корреляции Спирмена и Кенделла, необходимо использовать следующую последовательность команд:
Analyze (Анализ) – Correlate (Корреляция) – Bivariate (Двумерная)
В открывшемся диалоговом окне Bivariate Correlations(рис.1.) установить флажок в полеKendall’s tau—b иSpearman.После нажатия на кнопкуОКна экран будет выведена матрица корреляций Спирмена и Кендалла для указанных переменных.
Пример расчета коэффициентов ранговой корреляции Спирмена и Кендалла для переменных sex,diet,weight_2,sport_2 приведен на рис.5.
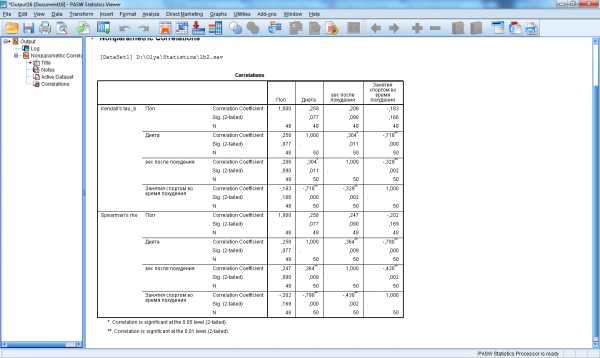
Рис.5.Матрица корреляций Спирмена и Кенделла
Из полученной матрицы видно, что переменные dietиsport_2 имеют тесную обратную связь. Т.к. переменнаяdietпринимает два значения: 1- соблюдает и 2-не соблюдает, то коэффициент корреляции равный -0,718 по Кендаллу и -0,79 по Спирмену можно трактовать так: если респондент при программе похудения придерживался диеты, то он чаще занимался спортом. Также обратную корреляцию имеет пара переменныхsport_2 иweight_2, что можно трактовать так: чем больше респондент занимался спортом, участвуя в программе похудения, тем меньше стал вес после программы похудения.
Значительную прямую корреляцию имеют пары переменных: sexиdiet(учитывая кодировку данных переменных это означает, что женщины соблюдают диету чаще, чем мужчины),weight_2 иdiet(учитывая кодировку переменнойdiet– если респондент не соблюдал диету во время программы похудения, то его вес после программы похудения окажется выше).
2.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициенты ранговой корреляции Спирмена и Кенделла, необходимо использовать следующую последовательность команд:
Statistics (Статистики) – Nonparametrics (Непараметрические) –
Correlations (Корреляции)
В результате чего откроется диалоговое окно (рис.6.), в котором необходимо указать переменные, для которых будут рассчитаны коэффициенты корреляции.
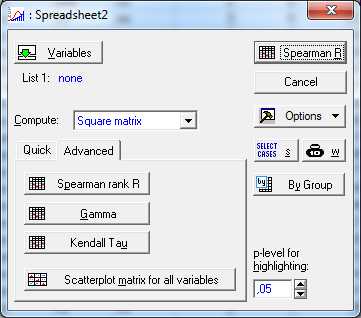
Рис.6.Диалоговое окноCorrelations
После нажатия на кнопку Spearman rank R на экран будет выведена матрица корреляций Спирмена, а после нажатия кнопкиKendall Tau– матрица корреляций Кенделла.
Пример расчета коэффициентов ранговой корреляции Спирмена и Кендалла для переменных sex,diet,weight_2,sportприведен соответственно на рис.7. и рис.8.
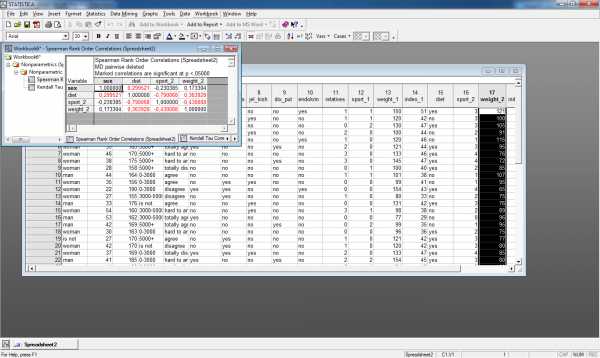
Рис.7. Матрица корреляций Спирмена
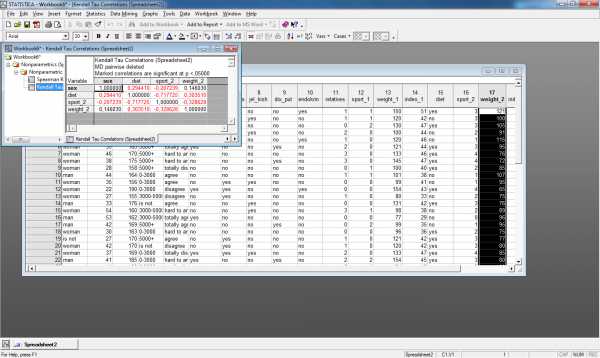
Рис.8. Матрица корреляций Кендалла
Полученные результаты схожи с результатами расчета коэффициентов ранговой корреляции в пакете SPSS.
3. Частные корреляции. Выявление ложных корреляций.
На практике иногда возникают ситуации, когда в результате корреляционного анализа обнаруживаются логически необъяснимые, противоречащие объективному опыту исследователя корреляции между двумя переменными (например, оказывается, что между уровнем дохода респондентов и количеством детей в семье существует статистически значимая зависимость). В этом случае говорят о так называемой ложной корреляции, исследовать которую помогают частные коэффициенты корреляции.
3.1. Реализация в SPSS
В SPSS коэффициент частной корреляции можно рассчитать используя следующую последовательность команд:
Analyze (Анализ) – Correlate (Корреляции) – Partial (Частные)
В результате откроется диалоговое окно (рис.9.), в котором необходимо ввести в поле Variables переменные для которых нужно вычислить коэффициент корреляции, а в окно Controlling for – переменную, значение которой нужно исключить
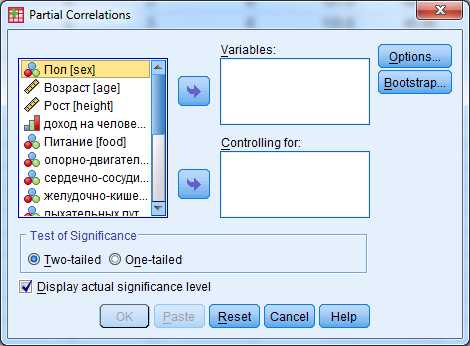
Рис.9.Диалоговое окноPartial Correlations
После нажатия на кнопку ОКна экран будет выведена матрица частных коэффициентов корреляции.
Пример расчета коэффициентов частной корреляции для переменных heightиindex_1 за исключением переменнойweight_1 приведен на рис.10.
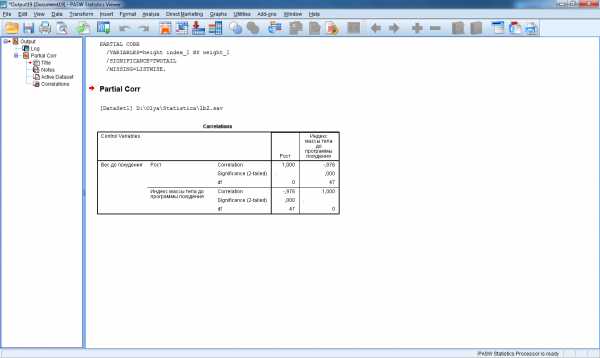
Рис.10. Матрица коэффициентов частной корреляции.
Рассчитанный коэффициент корреляции с высокой точностью (p<0,001) говорит о том, что существует тесная обратная связь между переменнымиheightиindex_1 (за исключением переменнойweight_1), т.е. чем выше рост респондента, тем ниже его индекс массы тела. Заметим, что коэффициент линейной корреляции Пирсона для этих переменных с высокой точностью (p=0,001) давал значение 0,45 (рис.2.), что свидетельствует о прямой связи переменных.
3.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициент частной корреляции необходимо использовать следующую последовательность команд:
Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) – Correlation matrices (Корреляционные матрицы)
В открывшемся диалоговом окне Product—Moment and Partial Correlations (рис.3.) необходимо перейти на вкладкуAdvanced / plotгде, щелкнув на кнопкуPartial correlations. В открывшемся окне, в полеFirst listуказать переменные для которых нужно вычислить коэффициент корреляции, а в полеSecond list— переменную, значение которой нужно исключить.
После нажатия на кнопку ОКна экран будет выведена матрица частных коэффициентов корреляции.
Пример расчета коэффициентов частной корреляции для переменных heightиindex_1 за исключением переменнойweight_1 приведен на рис.11.

Рис.11.Матрица коэффициентов частной корреляции.
Индивидуальное задание:
Для имеющихся данных в пакетах MS Excel (или Mathcad),SPSSиStatistica рассчитать:
значениековариации и коэффициента корреляции Пирсона,
коэффициенты корреляции Спирмена и Кенделла,
корреляционную матрицу,
коэффициент множественной корреляции ,
коэффициент частной корреляции,
коэффициент детерминации,
коэффициент конкордации.
Сделать выводы о наличии или отсутствии связи в каждом конкретном случае и о ее силе.
studfiles.net
КОРРЕЛЯЦИЯ В SPSS ОБЗОР — PDF
Транскрипт
1 КОРРЕЛЯЦИЯ В SPSS ОБЗОР Корреляция это двумерное измерение близости (силы) связи между двумя переменными. Она варьируется от 0 (случайная связь) до 1 (абсолютная линейная связь) или -1 (абсолютная негативная линейная связь). О ней обычно сообщается в терминах ее квадрата (r 2 ), интерпретируемого как процент объясняемой дисперсии. Например, если r 2 =.25, то говорят, что данная независимая переменная объясняет 25% дисперсии в зависимой переменной. В SPSS выберите Анализ, Корреляция, Двумерный; отметьте Пирсон. Существуют несколько распространенных заблуждений в отношении корреляции. Корреляция является симметричной, и поэтому она не может говорить о направлении каузальной связи. Если другие переменные также вызывают зависимую переменную, тогда любая ковариация, которую они разделяют с рассматриваемой независимой переменной, может быть ошибочно отнесена к этой независимой переменной. Также, в той степени, в которой связь между двумя коррелируемыми переменными оказывается нелинейной, корреляция будет недооценивать такую связь. Корреляция будет также ослабляться в степени, в которой присутствует ошибка измерения, включая использование суб-интервальных данных или искусственное сужение [artificial truncation] диапазона данных. Корреляция может также вводить в заблуждение, если связь изменяется в зависимости от величины независимой переменной («отсутствие гомоскедастичности»). И, конечно, не имевшие теоретического обоснования расчеты, или расчеты «задним числом» большого количества корреляций, влекут за собой вероятность, что 5% коэффициентов могут оказаться значимыми исключительно случайно. Кроме широко распространенной Пирсоновской корреляции (r), существуют другие специфические разновидности корреляции, приспособленные к работе со специфическими особенностями таких переменных, как дихотомические, а также другие меры связи для номинальных и порядковых переменных (см. файл «Измерение связей в SPSS»). Регрессионные процедуры рассчитывают множественную корреляцию, R, которая является корреляцией множества независимых переменных с единственной зависимой. Также существует частная корреляция, которая является корреляцией одной переменной с другой при контроле обеих переменных (независимой и зависимой) со стороны третьих, или дополнительных переменных. КЛЮЧЕВЫЕ ПОНЯТИЯ И ТЕРМИНЫ Отклонение [deviation]. Отклонение это значение минус его среднее: x — среднее x. В SPSS выберите Анализ, Корреляция, Двумерный; щелкните Установки; отметьте Векторное произведение отклонений и ковариантов. Ковариация [covariance]. Ковариация это степень согласованности отклонений двух переменных. Ее уравнение: cov(x,y) = СУММА[(x — среднее x )(y — среднее y )]. При высокой степени согласованности высокие позитивные отклонения в х будут согласовываться с высокими позитивными отклонениями в y, высокие негативные с высокими негативными и так далее. Такая высокая согласованность парных значений по каждому случаю будет приводить к высокой сумме в формуле. В SPSS выберите Анализ, Корреляция, Двумерный; щелкните Установки; отметьте Векторное произведение отклонений и ковариантов. Стандартизация [standardization]. Мы не можем сравнить ковариацию одной пары переменных с ковариацией другой пары переменных, поскольку переменные различаются по величине (среднему значению) и дисперсии (стандартному отклонению). Стандартизация это процесс, позволяющий сделать переменные сравнимыми по величине и дисперсии: из каждой переменной вычитается среднее значение и делится на ее стандартное отклонение, в результате чего все переменные приобретают среднее 0 и стандартное отклонение 1. Корреляция [correlation] это ковариация стандартизованных переменных. То есть, ковариация переменных после создания возможности их сравнения путем вычитания среднего и деления на стандартное отклонение. Стандартизация включена в расчет корреляции, и поэтому ее нужно специально запрашивать в SPSS или других программах. Корреляция представляет собой отношение наблюдаемой ковариации двух стандартизованных переменных к максимально возможной ковариации, когда порядковая величина значений обеих переменных идеально соответствует друг другу (напр., 5 и 5, 3 и 3, 6 и 6 и т.д.). Когда наблюдаемая ковариация оказывается такой же высокой, как максимально возможная ковариация, корреляция принимает значение 1, указывающее на абсолютное соответствие порядков значений обеих переменных. Значение -1 указывает на абсолютную негативную ковариацию, на совпадение самых высоких позитивных значений одной переменной с самыми высокими негативными значениями другой. Значение 0 указывает на случайную связь порядков значений между двумя переменными. Пирсоновский r [Pearson’s r] — наиболее распространенная мера корреляции, иногда называемая корреляцией смешанного момента [product-moment correlation]. Пирсоновский r является мерой связи, которая варьируется от -1 до +1 с 0, указывающим на отсутствие связи (случайные порядки значений переменных), и 1, указываю-
2 щей на связь, принимающую форму «чем больше х, тем больше y и наоборот». Значение -1 указывает на абсолютную негативную связь, принимающую форму «чем больше х, тем меньше y и наоборот». В SPSS выберите Анализ, Корреляция, Двумерный; отметьте Пирсон (отмечен по умолчанию). Примечание. В старых работах, написанных до появления персональных компьютеров, предлагались специальные формулы для ручного расчета корреляции. Для определенных типов переменных, особенно для дихотомических, использовались отличавшиеся друг от друга вычислительные формулы (напр., коэффициент Фи для двух дихотомий, точечно-бисериальная корреляция для оценки связи между интервальной и дихотомической переменной). Однако сегодня SPSS рассчитает точную корреляцию для переменной любого типа. Значимость коэффициентов корреляции обсуждается ниже в разделе «Частые вопросы». Коэффициент детерминации [coefficient of determination], r 2. Коэффициент детерминации это квадрат Пирсоновского коэффициента корреляции. Он характеризует процент дисперсии в зависимой переменной, объясняемый независимой. Разумеется, поскольку корреляция является двунаправленной, r 2 есть также процент дисперсии в независимой переменной, объясняемый зависимой. То есть, исследователь должен постулировать направление связи на основе внешних по отношению к корреляции соображений, поскольку сама корреляция не может что-либо сказать о каузальности. Корреляция дихотомических и порядковых переменных. Для бинарных и порядковых данных были разработаны специальные процедуры. Некоторые исследования показывают, что использование этих типов коэффициентов корреляции редко существенно влияет на конечные результаты. Ранговая корреляция является непараметрической и не требует допущения о нормальности распределения. Она также менее чувствительная к отклоняющимся случаям. Порядковые Смотри файл «Порядковая связь в SPSS». Роу Спирмена [Spearman’s rho]. Одно из наиболее популярных измерений для двух порядковых переменных или порядковой и интервальной переменной. Роу для ранговых данных соответствует Пирсоновскому r для ранговых данных. Обратите внимание, что SPSS назначит средний ранг связанным значениям. Формула для Роу Спирмена: rho = 1 — [(6*СУММА(d 2 )/n(n 2-1)], где d = разность в рангах. В SPSS выберите Анализ, Корреляция, Двумерный; отметьте Спирмен. Тау Кендалла [Kendall’s tau] — другое популярное измерение для двух порядковых переменных или порядковой и интервальной переменной. До эпохи персональных компьютеров роу предпочиталось тау из-за простоты вычислений. Сейчас такой проблемы не существует, и поэтому чаще предпочитается тау. Также доступен частный тау Кендалла, являющийся порядковым аналогом частной Пирсоновской корреляции. В SPSS выберите Анализ, Корреляция, Двумерный; отметьте тау-b Кендалла. Полисериальная корреляция [polyserial correlation]. Используется, когда интервальная переменная коррелируется с дихотомической или ординальной переменной, которая предположительно отражает лежащую за ней непрерывную переменную. Интерпретируется так же, как Пирсоновский r. Хи-квадрат тест полисериальной корреляции и связанное с ним значение p проверяет допущение о двумерной нормальности, требуемое полисериальным коэффициентом; при р >.05 допущение о двумерной нормальности отвергается. Полисериальная корреляция поддерживается модулем PRELIS в LISREL, пакета программ структурного моделирования (SEM), распространяемого Scientific Software International. Полихорическая корреляция [polychoric correlation] используется, когда обе переменные являются дихотомическими или порядковыми, однако в обоих случаях предполагаются лежащие за ними непрерывные переменные. То есть, полихорическая корреляция экстраполирует, каковы были бы распределения дихотомических переменных, если бы они являлись непрерывными, путем добавления концов к данному распределению. Как таковая эта оценка сильно опирается на допущение о лежащем в основе переменных непрерывном двумерном нормальном распределении. Полихорическая корреляция поддерживается модулем PROC FREQ в SAS и модулем PRELIS в LISREL, пакета программ структурного моделирования (SEM), распространяемого Scientific Software International, и широко используется в приложениях SEM, а также при оценках межоценочной согласованности [inter-rater agreement] инструментов. Тетрахорическая корреляция является частным случаем полихорической корреляции для дихо-
3 томических переменных. Веб-страница Джона Юберсака приводит список программ для оценки полихорической корреляции, которая недоступна в SPSS. Дихотомические Точечно-бисериальная корреляция [point-biserial correlation] используется, когда непрерывная переменная коррелируется с настоящей дихотомической переменной. Является особым случаем Пирсоновской корреляции, и Пирсоновский r равен точечно-бисериальной корреляции, когда одна переменная является непрерывной, а другая дихотомической. Поэтому, в известном смысле, верно, что дихотомическую или искусственную переменную [dummy variable] можно использовать «подобно непрерывной переменной» в обычной Пирсоновской корреляции. (В учебниках приводятся специальные формулы для ручных вычислений точечно-бисериальной корреляции; точечно-бисериальная корреляция то же самое, что Пирсоновская корреляция, когда та применяется к дихотомической и непрерывной переменной.) Однако даже когда порядок значений дихотомической переменной полностью совпадает с порядком значений непрерывной переменной, величина r будет меньше 1.0, что нужно учитывать при соответствующей интерпретации. В частности, точечно-бисериальная корреляция будет иметь максимум 1.0 для наборов данных только с двумя случаями и максимальную корреляцию в районе.85 для крупных наборов данных, когда независимая переменная нормально распределена. Величина r может приближаться к 1.0, когда непрерывная переменная является бимодальной, а значения дихотомической расщеплены поровну, 50/50. Неравное расщепление значений в дихотомической переменной и криволинейность в непрерывной будут снижать максимально возможную точечно-бисериальную корреляцию даже при идеальном совпадении порядков их значений. Кроме того, если дихотомическая переменная в действительности репрезентирует скрывающийся за ней континуум, корреляция будет слабее по сравнению с той, какой она бы была, если бы вместо дихотомии использовалась такая непрерывная переменная. Бисериальная корреляция [biserial correlation] используется, когда интервальная переменная коррелируется с дихотомической переменной, которая отражает лежащую за ней непрерывную переменную. Бисериальная корреляция всегда выше, чем соответствующая точечно-бисериальная корреляция. Бисериальная корреляция может быть выше, чем 1.0. Бисериальная корреляция используется довольно редко, сегодня ей предпочитают полисериальную/ полихорическую корреляцию. Бисериальная корреляция не поддерживается в SPSS, но доступна в SAS. Преобразование точечно-бисериальной в бисериальную корреляцию. Бисериальная корреляция это точечно-бисериальная корреляция, скорректированная (путем умножения) фактором, отражающим расщепление в дихотомии. Чтобы получить бисериальную корреляцию из точечнобисериальной корреляции, умножьте точечно-бисериальную корреляцию на геометрическое среднее расщепления (на квадратный корень из (P 1 P 2 ), где Р это пропорции дихотомических значений), деленное на ординату нормальной кривой в точке, где эта нормальная кривая расщепляется на те же самые пропорции (большинство таблиц нормальной кривой дают ординату, а также z- оценку и ее область). Ранговая бисериальная корреляция [rank biserial correlation]. Используется, когда порядковая переменная коррелируется с дихотомической переменной. Ранговая бисериальная корреляция не поддерживается в SPSS, но доступна в SAS. Фи [phi]. Используется, когда обе переменные являются дихотомическими. В учебниках приводятся специальные формулы для ручных вычислений; фи есть то же самое, что Пирсоновская корреляция для двух дихотомий в выводимых SPSS результатах корреляционного анализа, которая использует точные алгоритмы. Или же в SPSS выберите Анализ, Статистика, Перекрестные табличные данные; щелкните Статистика; отметьте Phi and Cramer’s V. Не рассматриваемый здесь Cramer`s V является расширением фи на более крупные таблицы. Тетрахорическая корреляция [tetrachoric correlation]. Используется, когда обе переменные являются дихотомиями, которые предположительно отражают лежащие за ними двумерные нормальные распределения, как это могло бы быть в случае, когда дихотомический тестовый пункт используется для измерения некоторого показателя достижений. Тетрахорическая корреляция иногда используется в структурном моделировании (SEM) на подготовительной фазе создания входной корреляционной матрицы и рассчитывается модулем PRELIS в LISREL, пакете программ структурного моделирования (SEM), распространяемом Scientific Software International. То есть, LISREL, EQS и другие пакеты SEM
4 часто по умолчанию рассчитывают тетрахорическую корреляцию вместо Пирсоновской для корреляций, вовлекающих дихотомические переменные. Тетрахорические корреляции, оцениваемые различными пакетами SEM, могут заметно различаться в зависимости от метода оценивания (напр., последовательное или одновременное). Тетрахорическая корреляция рассчитывается модулем PROC FREQ в SAS. В SPSS для расчета тетрахорической корреляции доступен макрос r tetra. Обратите внимание, что матрицы тетрахорической корреляции в SEM часто дают завышенные хивадрат значения и недооценивают стандартные ошибки оценок из-за более сильной вариативности, чем Пирсоновская корреляция. Кроме того, тетрахорическая корреляция может приводить к не положительно определенной [nonpositive definite] корреляционной матрице, поскольку собственные значения могут быть негативными (из-за нарушения нормальности, ошибки выборки, отклоняющихся значений или мультиколлинеарности переменных). Эти проблемы могут побудить исследователя отказаться от SEM в пользу анализа на основе логит или пробит регрессии (см. файл «Логит, пробит и лог-линейный модели в SPSS»). Корреляционное отношение, эта [correlation ratio, eta]. Эта, коэффициент нелинейной корреляции, известный как корреляционное отношение, обсуждается в разделе дисперсионного анализа (см. файл «Одномерный GLM, ANOVA и ANCOVA в SPSS»). Эта является отношением суммы квадратов к общей сумме квадратов в дисперсионном анализе. Степень, в которой эта выше, чем r, является оценкой того, насколько изучаемые связи оказываются нелинейными. В SPSS выберите Анализ, Сравнение средних, Средние; щелкните Установки; отметьте ANOVA таблица и этта. Эта также рассчитывается в Анализ, Линейная модель, Многомерный; и еще в некоторых местах в SPSS. Коэффициент внутригрупповой корреляции, r [coefficient intraclass correlation, r]. Этот основанный на ANO- VA тип корреляции измеряет сравнительную однородность внутри групп в отношении к общей вариации [total variation] и используется, например, в оценке межоценочной надежности [inter-rater reliability]. Внутригрупповая корреляция, r = [Межгрупповая MS — Внутригрупповая MS]/[Межгрупповая MS + (n-1)*внутригрупповая MS], где n среднее количество случаев в каждой категории независимой переменной. Внутригрупповая корреляция является высокой и позитивной, когда отсутствует вариация внутри групп, но различаются групповые средние. Она будет высокой и негативной, когда групповые средние не различаются, но существует большая вариация внутри групп. Ее максимальное позитивное значение составляет 1.0, однако ее максимально негативное равно [-1/(n-1)]. Негативная внутригрупповая корреляция возникает, когда межгрупповая вариация меньше внутригрупповой вариации, указывая на то, что некоторая третья (контрольная) переменная оказывает неслучайные влияния на различные группы. Внутригрупповая корреляция обсуждается также в файле «Анализ надежности в SPSS». ДОПУЩЕНИЯ 1. Интервальный уровень данных (для Пирсоновской корреляции). 2. Линейная связь. Предполагается, что двумерный (x-y) график рассеяния точек двух коррелируемых переменных лучше описывается прямолинейной, чем криволинейной функцией. В той мере, в которой он будет лучше описываться криволинейной функцией, Пирсоновский r и другие линейные коэффициенты корреляции будут недооценивать истинную корреляцию, вплоть до того, что иногда такие оценки будут оказываться бесполезными или уводящими в сторону. Линейность можно проверить визуально при помощи диаграммы рассеяния. В SPSS выберите Визуализация, Разброс/ Точка; выберите Простой разброс; щелкните Определить; разрешите независимой переменной располагаться на оси х, а зависимой на оси y; щелкните ОК. Можно также изучать одновременно несколько диаграмм рассеяния, запросив матрицу диаграмм рассеяния [scatterplot matrix]: в SPSS выберите Визуализация, Разброс/ Точка, Разброс матрицей; щелкните Определить; переместите интересующие вас переменные в список Переменные матрицы; щелкните ОК. 3. Гомоскедастичность [homoscedasticity]. То есть, предполагается, что дисперсия ошибки остается той же самой в любой точке на протяжении всей линейной связи. В противном случае коэффициент корреляции будет завышаться или, наоборот, занижаться. 4. Отсутствие выбросов [no outliers]. Выбросы могут ослаблять коэффициенты корреляции. Для визуального выявления выбросов можно использовать диаграммы рассеяния (см. выше). На присутствие
5 выбросов также может указывать большое различие между Пирсоновской корреляцией и Спирменовским Роу. 5. Минимальная ошибка измерения [minimal measurement error]. Требуется, поскольку низкая надежность ослабляет коэффициент корреляции. По определению, корреляция измеряет систематическую ковариацию двух переменных. Ошибка измерения обычно, за редкими исключениями, уменьшает систематическую ковариацию и снижает коэффициент корреляции. Такое снижение называется ослаблением [attenuation]. Ограниченная дисперсия, рассматриваемая ниже, также приводит к ослаблению. Корректировка ослабления [correction for attenuation]. О надежности можно думать как о корреляции переменной с самой собой. Корректировка ослабления корреляции, r xy, является функцией надежностей двух переменных, r xx и r yy. скорректированный r xy = r xy / [квадратный корень{r xx r yy }] 6. Неограниченная дисперсия [unrestricted variance]. Если дисперсия в одной или обеих переменных оказывается усеченной или ограниченной в результате, например, плохой выборки, это также может приводить к ослаблению коэффициента корреляции. Это также происходит в результате усечения диапазона переменной, например, при дихотомизации непрерывных данных, или сведением 7-балльной шкалы к 3-балльной. 7. Одинаковые распределения [similar underlying distributions] необходимы для целей оценки силы корреляции. То есть, если переменные имеют разные распределения, их корреляция может не достигать +1 даже при абсолютном соответствии порядков значений обеих переменных. Таким образом, чем больше различий в форме распределений двух переменных, тем существеннее ослабление коэффициента корреляции и тем чаще исследователь должен склоняться к рассмотрению альтернативных коэффициентов, например, ранговой корреляции. Это допущение может нарушаться, когда интервальная переменная коррелируется с дихотомической или даже с порядковой переменной. 8. Нормальные распределения обеих переменных [common underlying normal distributions] необходимы для целей оценки значимости корреляции. Также, в связи с целями оценки силы корреляции следует иметь в виду, что в случае не нормальных распределений диапазон коэффициента корреляции может быть уже, чем от -1 до +1 (см. Shih & Huang, 1992). Теорема о центральном пределе [central limit theorem] демонстрирует, однако, что в больших выборках показатели, использующиеся при оценке значимости, будут нормально распределяться, даже когда сами переменные не имеют нормальных распределений, что позволяет использовать тесты значимости. Исследователь может воспользоваться Спирменовской или другого типа ранговой корреляцией, когда наблюдаются заметные нарушения этого допущения, хотя такая стратегия влечет за собой опасность ослабления корреляции. 9. Нормально распределенные члены ошибки [normally distributed error terms]. Здесь также применима теорема о центральном пределе. ЧАСТЫЕ ВОПРОСЫ 1. Какие существуют правила для определения подходящего уровня значимости при проверке коэффициентов корреляции? 2. В каких случаях требуется односторонняя и двусторонняя значимость? 3. Как преобразовать корреляции в z-оценки? 4. Как рассчитывается значимость коэффициента корреляции? 5. Как мне рассчитать значимость различий между двумя коэффициентами корреляции? 6. Как определить доверительные границы для моих коэффициентов корреляции? 7. У меня порядковые переменные, и поэтому я применил Спирменовский роу. Как мне использовать эти корреляции в SPSS в частных корреляциях, регрессиях и других процедурах? 8. Как корреляция соотносится с ANOVA? 1. Какие существуют правила для определения подходящего уровня значимости при проверке коэффициентов корреляции? Предлагаются два правила: 1. Исходя из соображения, что чем больше проверяется коэффициентов, тем более консервативным должен быть тест, некоторые утверждают, что уровень отсечки для значимости должен устанавливаться на отметке.05/с, где С количество проверяемых коэффициентов. Таким образом, если проверяются 5 коэффициентов, то уровень значимости должен составлять.01.
6 2. Менее консервативное правило, опирающееся на те же соображения, предлагает проверять самый высокий коэффициент на уровне.05/с, следующий по величине на уровне.05/(с-1), третий — на уровне.05/(с-2), и т.д. Даже менее консервативное правило оказывается очень строгим, когда проверяется много коэффициентов. Например, если проверяется 50 коэффициентов, самый высокий коэффициент должен проверяться на уровне 05/50 =.001. Поскольку в социальных науках связи часто не бывают сильными, а исследователь часто не может собирать крупные выборки, такая проверка будет предполагать высокий риск ошибки II типа. На практике большинство исследователей независимо от количества коэффициентов применяют к каждому уровень значимости.05, однако следует осознавать, что при использовании традиционного доверительного уровня 95% значимость 1 из 20 коэффициентов может оказываться иллюзорной. В первую очередь, такая опасность возникает при анализе «задним числом», в отсутствие предварительно сформулированных гипотез. 2. В каких случаях требуется односторонняя и двусторонняя значимость? Обычно исследователь предпочитает двустороннюю [two-tailed] значимость, которая указывается по умолчанию в выводимых SPSS результатах. Она оценивает вероятность того, что наблюдаемая корреляция значимо отличается от нуля, в позитивном и негативном направлении. Если по каким-то теоретическим соображениям одно направление корреляции (напр., негативное) можно исключить из рассмотрения, то тогда следует выбрать одностороннюю значимость [one-tailed]. В SPSS выберите Анализ, Корреляция, Двумерный; отметьте Двусторонний (отмечен по умолчанию) или Односторонний. 3. Как преобразовать корреляции в z-оценки? Преобразование в z-оценку Пирсоновского r. Коэффициенты корреляции можно преобразовывать в z-оценки, например, для проверки гипотезы о различиях между двумя корреляциями. Для этого разделите корреляцию плюс 1 на ту же самую корреляцию минус 1; затем возьмите натуральный логарифм абсолютного значения полученного результата; затем разделите полученное значение на 2. Конечный результат представляет собой преобразование Пирсоновского r в Фишеровскую z- оценку. Преобразование Фишера уменьшает смещение (асимметрию) и приближает выборочное распределение к нормальному с увеличением размера выборки. Например, возьмем r =.30. Затем следуем формуле Z = ln[ (r+1)/r-1) ]/2 в этом случае Z = ln( 1.3/-.7 )/2 = ln(1.8571)/2 =.6190/2 =.3095 = значению, показанному в таблице ниже Таблица Z-преобразований для Пирсоновского r. r z’
7
8 Как рассчитывается значимость коэффициента корреляции? Значимость r. Проверяет гипотезу о том, что корреляция равна нулю (р = 0) с использованием следующей формулы: t = [r*квадратный корень(n-2)]/[квадратный корень(1-r 2 )] где r коэффициент корреляции и n размер выборки. Затем следует найти критериальное значение t в таблице t- распределения для (n-2) степеней свободы. Если рассчитанное значение t превышает табличное значение t, тогда исследователь делает вывод, что корреляция является значимой (то есть, значимо отличается от нуля). На практике большинство компьютерных программ рассчитывают значимость корреляции, поэтому исследователю нет необходимости обращаться к ручным расчетам. 5. Как рассчитать значимость различий между двумя коэффициентами корреляции? Значимость различий между двумя корреляциями для двух независимых выборок. Чтобы рассчитать значимость различий между двумя корреляциями из независимых выборок, таких как корреляция для мужчин против корреляции для женщин, выполните следующие шаги: 1. Используйте таблицу z-преобразований или преобразуйте обе корреляции в z-оценки, как описано выше. Заметьте, что если корреляция негативная, то z-значение также должно быть негативным. 2. Оцените стандартную ошибку различия между двумя коэффициентами корреляции как: SE = квадратный корень[(1/(n 1-3) + (1/(n 2-3)], где n 1 и n 2 размеры двух независимых выборок. 3. Разделите разность между двумя z-оценками на стандартную ошибку. 4. Если z-значение разности, рассчитанное на шаге 3, равно или выше 1.96, различие в корреляциях значимо на уровне.05. Используйте критериальное значение 2.58 для проверки значимости на уровне.01. Пример. Возьмем выборку из 15 мужчин, имеющих корреляцию между доходом и образованием.60, и возьмем выборку из 20 женщин, имеющих корреляцию.50. Мы хотим посмотреть, нет ли между ними значимых различий. Z-преобразования обеих корреляций составят.6931 и.5493, соответственно, с разницей в Оценка SE = квадратный корень [(1/12)+(1/17)] = квадратный корень [.1422] = Отсюда z-значение разности.1438/.3770 =.381, что гораздо ниже 1.96 и, следовательно, не значимо на уровне.05. Значимость различий между двумя зависимыми корреляциями из той же самой выборки. Для проверки различий двух зависимых корреляций из той же самой выборки используется t-тест. Рассчитываем значение t с использованием приведенной ниже формулы, затем ищем рассчитанное значение в таблице t- распределения для (n-3) степеней свободы, где n размер выборки. Пусть х будет переменной, такой как образование и давайте проверим значимость различий корреляции x с доходом (y), а также корреляции социальноэкономического статуса родителей (z) с доходом. Используется следующая формула: t = (r xy — r zy )* квадратный корень [{(n — 3)(1 + r xz )}/ {2(1 — r xy 2 — r xz 2 — r zy 2 + 2r xy *r xz *r zy )}] Если рассчитанное значение t превышает критериальное значение t в таблице, тогда различие в корреляциях является значимым на интересующем нас уровне (в таблице t-распределения приводятся разные критериальные значения для различных уровней значимости, таких как.05,.01,.001). Тесты для проверки различий между двумя зависимыми корреляциями или различий между более чем двумя независимыми корреляциями см. У Чен и Попович (2002). 6. Как определить доверительные границы для моих коэффициентов корреляции? SPSS не рассчитывает доверительных границ [confidence limits] отдельно. (См. файл «Значимость в SPSS».) Однако регрессионный модуль в SPSS рассчитает доверительные границы, если вы стандартизуете две интересующие вас переменные, а затем регрессируете одну на другую. Получившийся регрессионный коэффициент (наклона, b) идентичен коэффициенту корреляции, а его доверительные границы идентичны доверительным границам коэффициента корреляции. Однако если вы используете такой способ когда корреляции являются
9 очень высокими и/ или надежности очень низкими, верхние и/ или нижние доверительные границы могут выходить за пределы диапазона коэффициента корреляции от -1 до У меня порядковые переменные, и поэтому я применил Спирменовский Роу. Как мне использовать эти корреляции в SPSS в частных корреляциях, регрессиях и других процедурах? Вы получили эти данные, выбрав Статистика, Корреляция, а затем отметив Спирменовский роу в качестве типа корреляции. Это вызвало процедуру NONPAR CORR, однако диалоговые окна (как в версии 7.5) не обеспечивали матрицу выводимых результатов. Перезапустите Спирменовские корреляции из окна синтаксиса, которое вызывается через Файл, Создать, Синтаксис. Введите синтаксис по приведенному ниже образцу, а затем запустите его: NONPAR CORR VARIABLES= horse engine cylinder /MATRIX=OUT(*). После этого в Редакторе данных SPSS появится корреляционная матрица, где вы измените значения переменной ROWTYPE_ на CORR вместо RHO. По усмотрению вы можете выбрать Файл, Сохранить. На этот момент, чтобы сохранить вашу матрицу. Затем выберите Статистика, Корреляция, Частные корреляции (или другую процедуру) и SPSS будет использовать на входе Спирменовскую матрицу. Или, в качестве альтернативы, в окне синтаксиса введите MATRIX=IN(*) in PARTIAL CORR или другой процедуре, которая использует на входе корреляционную матрицу. 8. Как корреляция соотносится с ANOVA? Уровень значимости коэффициента корреляции для корреляции интервальной переменной с дихотомической будет тем же самым, что и для ANOVA интервальной переменной, использующий дихотомию в качестве единственного фактора. (См. файл «Одномерный GLM, ANOVA и ANCOVA в SPSS».) Такое сходство не распространяется на категориальные переменные с более чем двумя значениями.
docplayer.ru